Application of an Improved ABC Algorithm in Urban Land Use Prediction
Abstract
:1. Introduction
2. Related Works
2.1. ABC Algorithm
2.2. Land Use Prediction
3. Improved ABC Algorithm
3.1. Standard ABC Algorithm
3.2. MHABC Algorithm
3.2.1. Mutation Method of Inferior Solutions
3.2.2. Binary Crossover Operation
3.2.3. MHABC Algorithm
4. Interval Model based on CA
4.1. Basic Model of CA
4.2. Interval Model Based on CA
4.2.1. Construction of Interval Model of CA
4.2.2. Normalization Processing
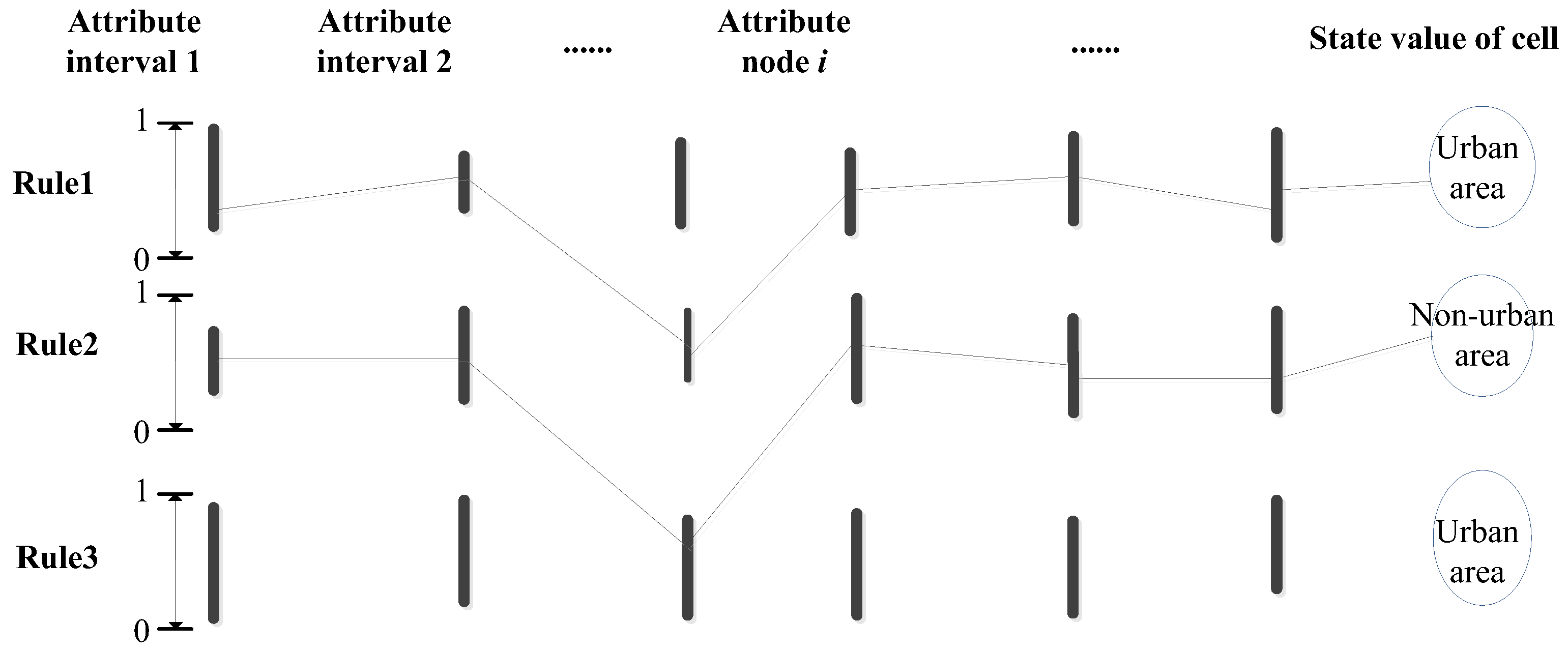
4.3. Conversion of Interval Model based on CA
where n is the number of attributes; the Lower_k and Upper_k are the best lower and the best upper threshold value of the interval on the k-th attribute, respectively, ; Ci refers to a cell status value ; and m is the number of cell state.IFAttribute1 ≥Lower_1 and Attribute1 ≤ Upper_1AndAttribute2 ≥Lower_2 and Attribute2 ≤Upper_2And......AndAttributen ≥Lower_n and Attributen ≤ Upper_nTHENCell state is Ci
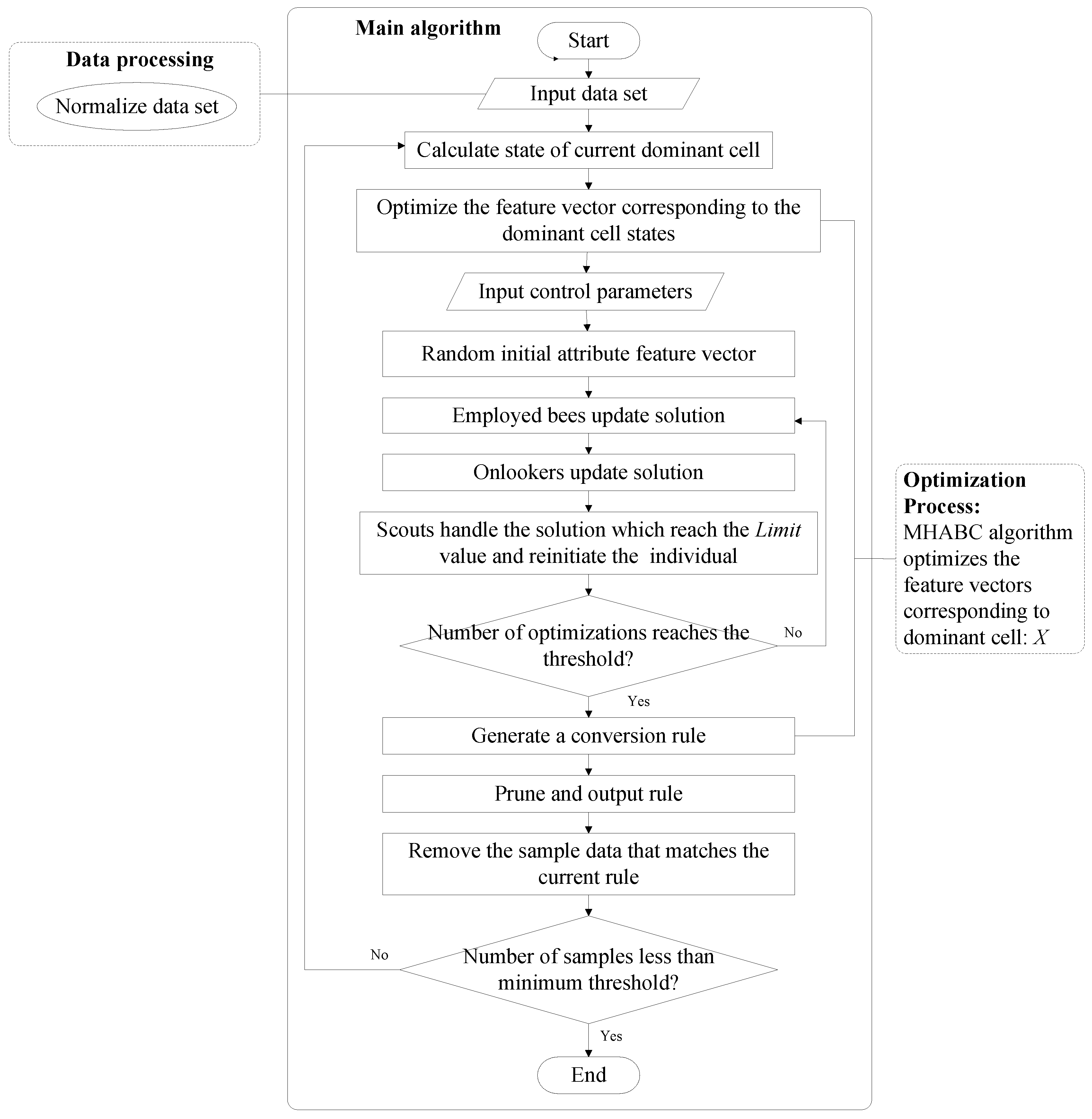
5. CA Rule Mining Algorithm based on MHABC Algorithm
| Algorithm 1. MHABC-CA algorithm. |
| SwarmNumber: Number of bee swarm. FoodNumber: Number of foods sources. FoodNumber = SwarmNumber/2. Trial: Stagnation number of a solution. Limit: Maximum number of trial for the scouts to abandon a food source, and re-initiate a new solution. MFE: Maximum number of iterations. As the number of iterations reaches this value, the iteration process of algorithm will be stopped. MSN: Minimum number of samples. As the number of samples lower than this value, the mining process will be stopped. Begin Input pre-processed data_set; While (Number of samples > MSN) Calculate state of current dominant cell C; For iter = 1 to MFE Input control parameters; Initialization; SendEmployedBees(); SendOnlookerBees(); SendScoutBees(); End For best_rule = GenConvRule(); // Generate a conversion rule. PruneRule(best_rule); // prune the unnecessary conditions from the current rule. UpdateDataSet(data_set, best_rule); // remove the sample data that matches the current rule. UpdateRuleSet(RulesSet, best_rule); // update the current rule into the rules set. End While Return RulesSet; // return and output the rules set. End Function SendEmployedBees() Begin For i = 0 to FoodNumber − 1 Generate a crossover probability cr in the range of [0, 1]; If rand (0, 1) <= cr new_rule = BinaryCrossover(Rule(i)); // crossover operation with the global optimal value Else new_rule = GenNewRule(Rule(i)); // generate a new candidate rule End If If fitness(new_rule) > fitness(Rule(i)) // Calculate and compare the fitness value Rule(i) = new_rule; // Update the rule by the new rule. Trial[i] = 0; // Reset its Trial to 1 Else Trial[i] = Trial[i] + 1; // Increase its Trial by 1 End If End For End Function SendOnlookerBees() Begin index = 0, t = 0; Prob = CalculateProb(); // Calculate the select probabilities of each solution; While (t < FoodNumber) If rand (0, 1) >= Prob(index) new_rule = Mutation (Rule(index)); // mutation operation with the global optimal value Else new_rule = GenNewRule(Rule(index)); // generate a new candidate rule End If If fitness(new_rule) > fitness(Rule(index)) // Calculate and compare the fitness value Rule(index) = new_rule; // Update the rule by the new rule. Trial[index] = 0; // Reset its Trial to 1 Else Trial[i] = Trial[i] + 1; // Increase its Trial by 1 End If End While End Function SendScoutBees() Begin index = 0; For i = 1 to FoodNumber − 1 If Trial(i) > Trial(index) Index = i; End If End For If Trial(index) > Limit Re-Initialize(rule(index)) Trial(index) = 0 End If End |
5.1. Data Processing of MHABC-CA Algorithm
5.2. Optimization Process of MHABC-CA Algorithm
5.3. Pruning Rule and Updating Sample Set
6. Case Study of MHABC-CA Algorithm
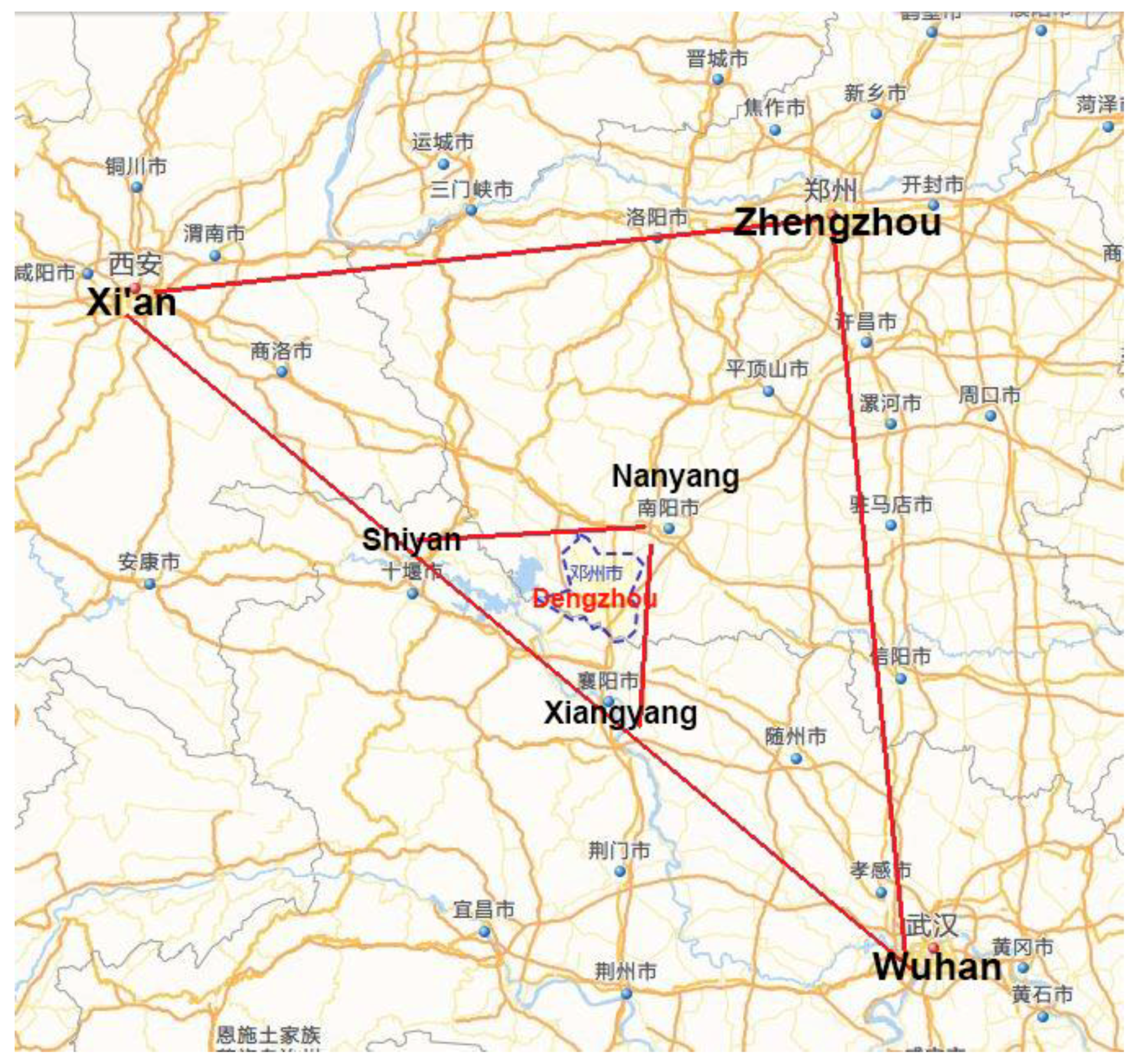
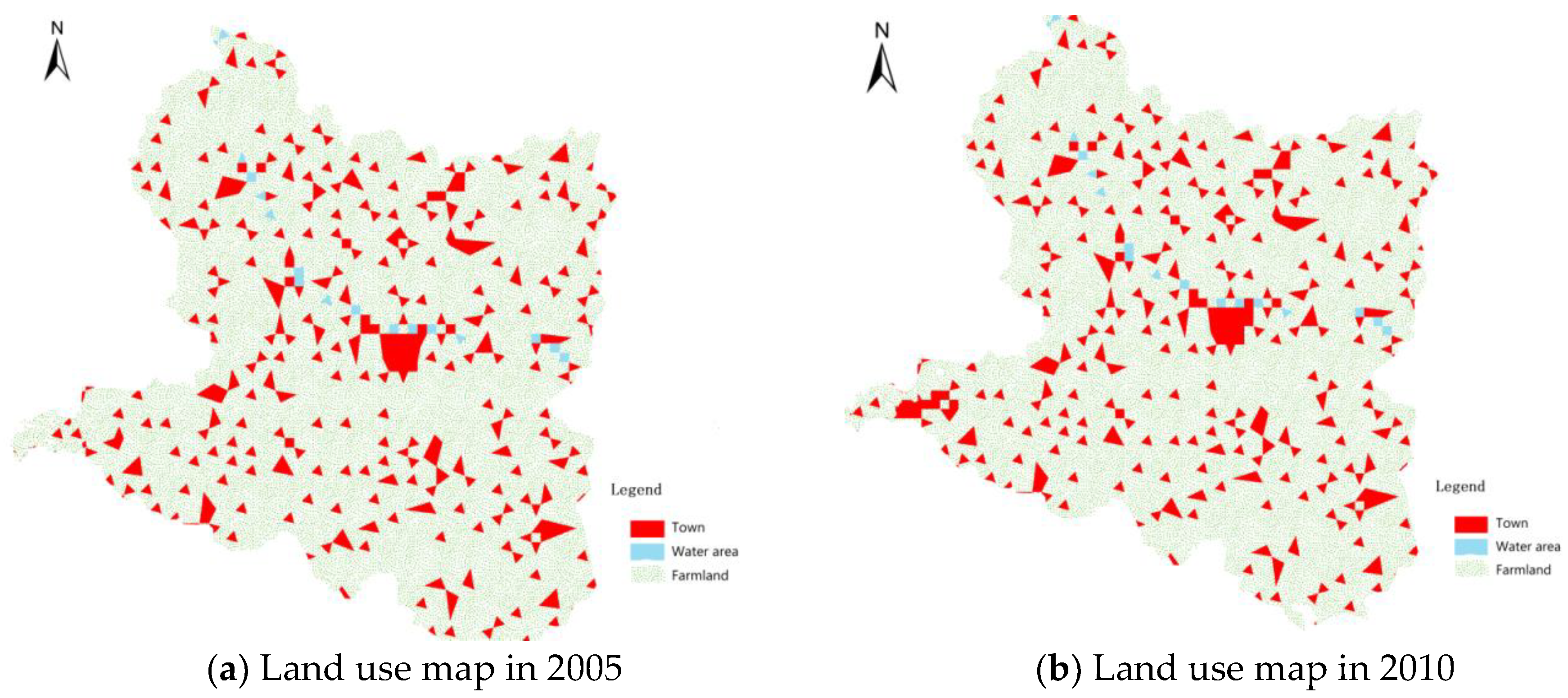
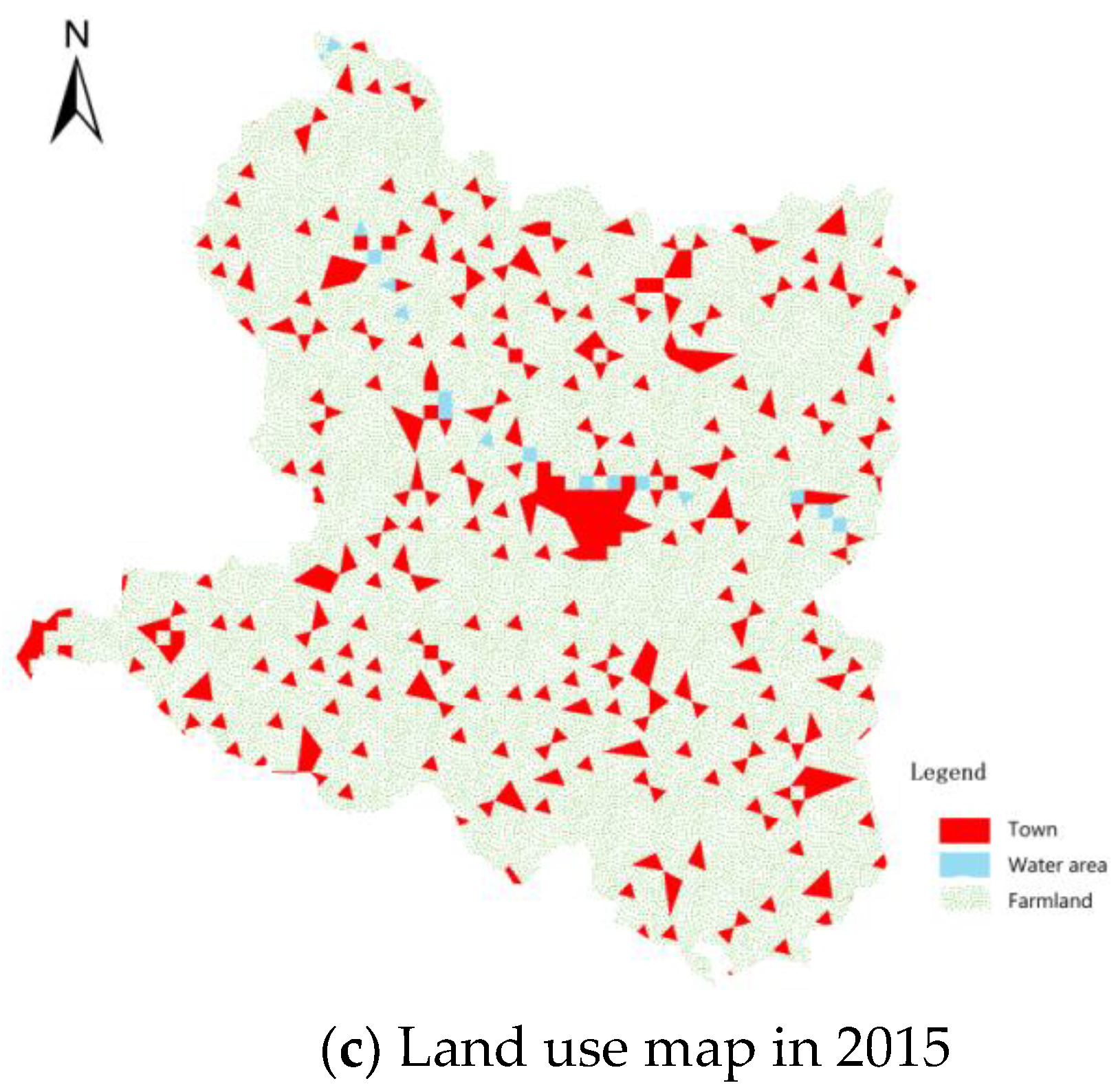
6.1. Selection of Study Area
6.1.1. Study Area
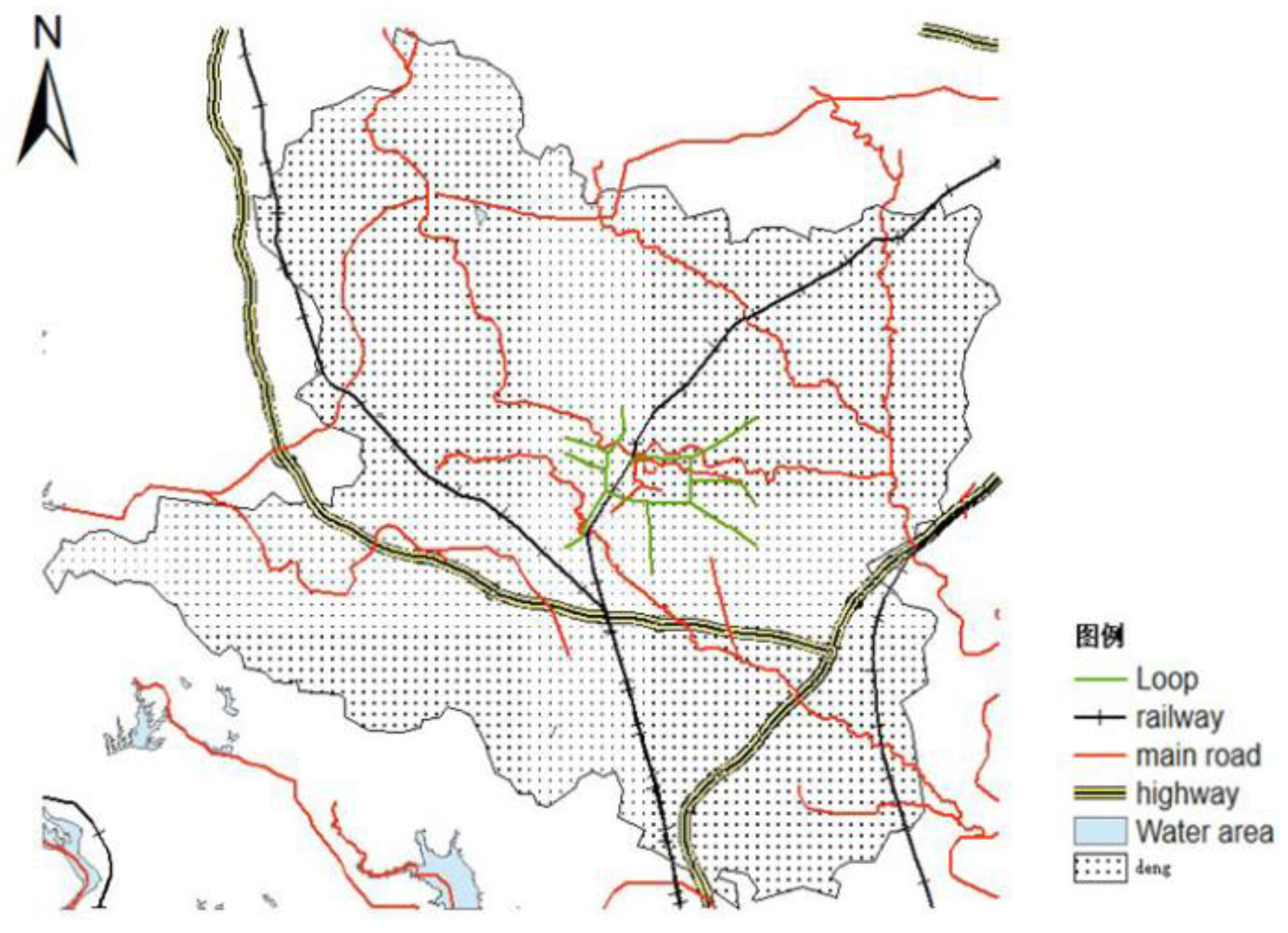
6.1.2. Road Network Data
6.1.3. Urban Land Use Type
6.2. Data Pre-Processing
6.3. Prediction Experiment of Urban Land Use Type
| IF DIST_TL < 6955.7 and DIST_GS > 1674.4 and DIST_GD < 280.0 and DIST_SD < 6771.5 and DIST_HL < 3183.1 and NEIGHBOR < 21.5 THEN DEV STATUS = I IF DIST_TL < 345.55 and DIST_GS > 8700.35 and DIST_GD < 80.25 and DIST_SD < 1771.5 and DIST_HL < 383.1 and NEIGHBOR < 30.2 THEN DEV STATUS = 0 IF DIST_TL < 996.15 and DIST_GS > 364.4 and DIST_GD < 890.0 and DIST_SD < 3771.5 and DIST_HL < 183.1 and NEIGHBOR < 27.3 THEN DEV STATUS = I ...... |
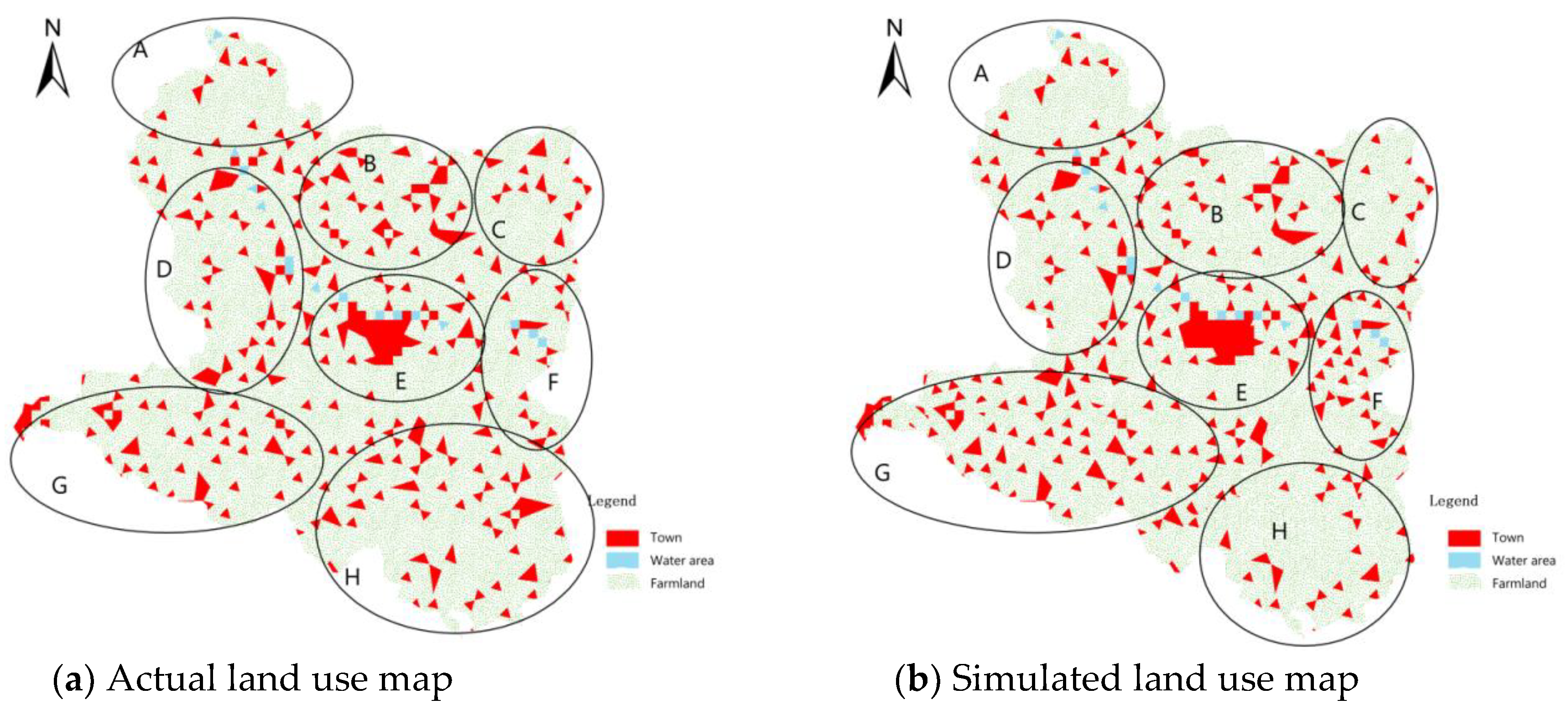
6.4. Analysis of Simulation Results
6.4.1. Comparison of Visual Features
6.4.2. Quantitative Analysis of Simulation Accuracy
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Van Vliet, J.; Bregt, A.K.; Brown, D.G.; van Delden, H.; Heckbert, S.; Verburg, P.H. A review of current calibration and validation practices in land-change modeling. Environ. Model. Softw. 2016, 82, 174–182. [Google Scholar] [CrossRef]
- Brown, D.G.; Verburg, P.H.; Pontius, R.G., Jr.; Lange, M.D. Opportunities to improve impact, integration, and evaluation of land change models. Curr. Opin. Environ. Sustain. 2013, 5, 452–457. [Google Scholar] [CrossRef]
- Wang, J.; Lin, Y.; Glendinning, A.; Xu, Y. Land-use changes and land policies evolution in China’s urbanization processes. Land Use Policy 2018, 75, 375–387. [Google Scholar] [CrossRef]
- Dong, N.; You, L.; Cai, W.J.; Li, G.; Lin, H. Land use projections in China under global socioeconomic and emission scenarios: Utilizing a scenario-based land-use change assessment framework. Glob. Environ. Chang. 2018, 50, 164–177. [Google Scholar] [CrossRef]
- Ustaoglu, E.; Castillo, C.P.; Jacobs-Crisioni, C.; Lavalle, C. Economic evaluation of agricultural land to assess land use changes. Land Use Policy 2016, 56, 125–146. [Google Scholar] [CrossRef]
- Blecic, I.; Cecchini, A.; Trunfio, G.A. How much past to see the future: A computational study in calibrating urban cellular automata. Int. J. Geogr. Inf. Syst. 2015, 29, 349–374. [Google Scholar] [CrossRef]
- Yang, H.B.; Du, L.J.; Guo, H.L.; Zhang, J. Tai’an Land Use Analysis and Prediction Based on RS and Markov Model. Procedia Environ. Sci. 2011, 10, 2625–2630. [Google Scholar]
- Fu, X.; Wang, X.H.; Yang, Y.J. Deriving suitability factors for CA-Markov land use simulation model based on local historical data. J. Environ. Manag. 2018, 206, 10–19. [Google Scholar] [CrossRef] [PubMed]
- Veldkamp, A.; Fresco, L.O. CLUE: A conceptual model to study the Conversion of Land Use and its Effects. Ecol. Model. 1996, 85, 253–270. [Google Scholar] [CrossRef]
- Kennedy, J. Swarm intelligence. In Handbook of Nature-Inspired and Innovative Computing; Springer: Boston, MA, USA, 2006; pp. 187–219. [Google Scholar]
- Karaboga, D.; Basturk, B. A Powerful and Efficient Algorithm for Numerical Function Optimization: Artificial Bee Colony (ABC) Algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Kabalci, Y.; Kockanat, S.; Kabalci, E. A modified ABC algorithm approach for power system harmonic estimation problems. Electr. Power Syst. Res. 2018, 154, 160–173. [Google Scholar] [CrossRef]
- Amarjeet; Chhabra, J.K. FP-ABC: Fuzzy-Pareto dominance driven artificial bee colony algorithm for many-objective software module clustering. Comput. Lang. Syst. Struct. 2018, 51, 1–21. [Google Scholar]
- Zhong, F.; Li, H.; Zhong, S. A modified ABC algorithm based on improved-global-best-guided approach and adaptive-limit strategy for global optimization. Appl. Soft Comput. 2016, 46, 469–486. [Google Scholar] [CrossRef]
- Qin, Q.D.; Cheng, S.; Li, L.; Shi, Y.H. A survey of artificial bee colony algorithm. J. Intell. Syst. 2014, 9, 127–135. [Google Scholar]
- Boztoprak, H.; Özbay, Y.; Güçlü, D.; Küçükhemek, M. Prediction of sludge volume index bulking using image analysis and neural network at a full-scale activated sludge plant. Desalination Water Treat. 2015, 57, 1–11. [Google Scholar] [CrossRef]
- Santhi, V.; Nandhini, S. An Efficient Algorithm for Job Scheduling Problem-Enhanced Artificial Bee Colony Algorithm. Asian J. Inf. Technol. 2016, 15, 2210–2216. [Google Scholar]
- Zhu, G.; Kwong, S. Gbest-guided artificial bee colony algorithm for numerical function optimization. Appl. Math. Comput. 2010, 217, 3166–3173. [Google Scholar] [CrossRef]
- Huo, J.Y.; Zhang, Y.N.; Zhao, H.X. An improved artificial bee colony algorithm for numerical functions. Int. J. Reason.-Based Intell. Syst. 2015, 7, 200–208. [Google Scholar] [CrossRef]
- Niu, F.Q.; Li, J. Modeling the population and industry distribution impacts of urban land use policies in Beijing. Land Use Policy 2018, 70, 347–359. [Google Scholar] [CrossRef]
- Amici, V.; Marcantonio, M.; Porta, N.L.; Rocchini, D. A multi-temporal approach in MaxEnt modelling: A new frontier for land use/land cover change detection. Ecol. Inform. 2017, 40, 40–49. [Google Scholar] [CrossRef]
- Zhao, L.Y.; Peng, Z.R. LandSys II: Agent-Based Land Use-Forecast Model with Artificial Neural Networks and Multiagent Model. J. Urban Plan. Dev. 2014, 141, 04014045. [Google Scholar] [CrossRef]
- Huang, T.; Zhang, C.Z. Simulation and Prediction of Land Use Based on the Markov Model. In Proceedings of the 9th International Symposium on Linear Drives for Industry Applications; Springer: Berlin/Heidelberg, Germany, 2014; Volume 2, pp. 373–377. [Google Scholar]
- Anputhas, M.; Janmaat, J.J.A.; Nichol, C.F.; Wei, X.H. Modelling spatial association in pattern based land use simulation models. J. Environ. Manag. 2016, 181, 465–476. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.M.; Song, G.; Lu, S.; Wang, H.; Xu, S.G. Prediction of land use change in Harbin based on CA-Markov model. Chin. Agric. Resour. Reg. Plan. 2017, 38, 41–48. [Google Scholar]
- Huang, P.; Yuan, Y.B.; Dong, H. Study on land use change in Qingjiang basin using CA-Markov model. Surv. Sci. 2017, 42, 102–109. [Google Scholar]
- Zhang, X.J.; Zhou, Q.G.; Wang, Z.L.; Wang, F.H. Land use evolution simulation and prediction based on MCE-CA-Markov in the Three Gorges reservoir area. Chin. J. Agric. Eng. 2017, 33, 268–277. [Google Scholar]
- Yuntana, D.; Su, G.C.; Sun, W.R.; Tu, Y. Land use change analysis based on GIS and CA-Markov model in the Cullen County. J. Yangtze Univ. China 2017, 14, 79–82+85. [Google Scholar]
- Lu, N.; Li, Z.H.; Bao, Y.J.; Li, Z.L.; Zhang, J.; Liu, L.; Liu, X.; Tan, Y.C.; Gong, X.S. Analysis and Prediction of Land Use Dynamic Change Based on CA-Markov Model in Balikun Lake Basin. Tianjin Agric. Sci. 2017, 23, 63–65. [Google Scholar]
- Wang, C.X.; Zhang, C. Land Use Change Prediction Model Based on Genetic BP Neural Network Model. Surv. Mapp. 2017, 40, 52–55. [Google Scholar]
- Zhang, J.P.; Li, J. Prediction and Analysis of Land Use Change in Ganzhou District Based on CA-Markov Model. Chin. Agric. Sci. Bull. 2017, 33, 105–110. [Google Scholar]
- Yu, D.G.; Wu, Q. Research and Application of Multi-factor Driven Prediction Model for Land Use Structural Change based on Logistic-Markov Method. Bull. Soil Water Conserv. 2017, 37, 149–154. [Google Scholar]
- Jiang, M.Y.; Yuan, D.F. Artificial Bee Colony Algorithm and Its Application; Science Press: Beijing, China, 2014. [Google Scholar]
- Huo, J.Y.; Zhang, Z.; Meng, F.M. A hybrid artificial bee colony algorithm guided by mutation strategy. Comput. Appl. Softw. 2018, 35, 267–272. [Google Scholar]
- Yang, J.Y. Research on Mining Methods of Geographic Cellular Automata Transformation Rules Based on Bee Colony Intelligence; Nanjing Normal University: Nanjing, China, 2014. [Google Scholar]
- Li, X.; Ye, J.A.; Liu, X.P.; Yang, J.S. Geographic Simulation System: Cellular Automata and Multi-Agent; Science Press: Beijing, China, 2007. [Google Scholar]
- Yang, J.; Tang, G.; Cao, M.; Zhu, R. An intelligent method to discover transition rules for cellular automata using bee colony optimization. Int. J. Geogr. Inf. Sci. 2013, 27, 1849–1864. [Google Scholar] [CrossRef]
- Shukran, M.A.M.; Chung, Y.Y.; Yeh, W.C.; Wahid, N.; Zaidi, A.M.A. Artificial Bee Colony based Data Mining Algorithms for Classification Tasks. Mod. Appl. Sci. 2011, 5, 217–231. [Google Scholar] [CrossRef]
- Tang, J.; Chai, T.Y.; Liu, Z.; Yu, W.; Zhou, X.J. Adaptive Ensemble Modelling Approach Based on Updating Sample Intelligent Identification. Acta Autom. Sin. 2016, 42, 1040–1052. [Google Scholar]
- Veček, N.; Liu, S.H.; Črepinšek, M.; Mernik, M. On the Importance of the Artificial Bee Colony Control Parameter ‘Limit’. Inf. Technol. Control 2017, 46, 566–604. [Google Scholar] [CrossRef]
- Karaboga, D.; Akay, B.; Ozturk, C. Artificial Bee Colony (ABC) Optimization Algorithm for Training Feed-Forward Neural Networks. Model. Decis. Artif. Intell. 2007, 4617, 318–329. [Google Scholar]
- Yang, X. Research on Visual Feature Expression and Learning for Image Classification and Recognition; South China University of Technology: Guangzhou, China, 2014. [Google Scholar]
- Wang, D.; Li, C.S.; Wu, H. Optimal closed-form solution of array error matrix based on eigenvectors. J. Appl. Sci. 2009, 27, 592–600. [Google Scholar]
- Feng, Y.; Liu, Y.; Tong, X.; Liu, M.L.; Deng, S.S. Modeling dynamic urban growth using cellular automata and particle swarm optimization rules. Landsc. Urban Plan. 2011, 102, 188–196. [Google Scholar] [CrossRef]
- Rabbani, A.; Aghababaee, H.; Rajabi, M.A. Modeling dynamic urban growth using hybrid cellular automata and particle swarm optimization. J. Appl. Remote Sens. 2012, 6, 063582. [Google Scholar] [CrossRef]
- Mernik, M.; Liu, S.H.; Karaboga, D.; Črepinšek, M. On clarifying misconceptions when comparing variants of the Artificial Bee Colony Algorithm by offering a new implementation. Inf. Sci. 2015, 291, 115–127. [Google Scholar] [CrossRef]
- Črepinšek, M.; Liu, S.H.; Mernik, M. Replication and comparison of computational experiments in applied evolutionary computing: Common pitfalls and guidelines to avoid them. Appl. Soft Comput. J. 2014, 19, 161–170. [Google Scholar] [CrossRef]
- Nozohour-Leilabady, B.; Fazelabdolabadi, B. On the application of artificial bee colony (ABC) algorithm for optimization of well placements in fractured reservoirs; efficiency comparison with the particle swarm optimization (PSO) methodology. Petroleum 2016, 2, 79–89. [Google Scholar] [CrossRef]
- Pontius, R.G.; Boersma, W.; Castella, J.C.; Clarke, K.; de Nijs, T.; Dietzel, C.; Duan, Z.; Fotsing, E.; Goldstein, N.; Kok, K.; et al. Comparing the input, output, and validation maps for several models of land change. Ann. Reg. Sci. 2008, 42, 11–37. [Google Scholar] [CrossRef]
- Chen, H.; Pontius, R.G., Jr. Sensitivity of a Land Change Model to Pixel Resolution and Precision of the Independent Variable. Environ. Model. Assess. 2011, 16, 37–52. [Google Scholar] [CrossRef]
- Jantz, C.A.; Goetz, S.J.; Shelley, M.K. Using the SLEUTH Urban Growth Model to Simulate the Impacts of Future Policy Scenarios on Urban Land Use in the Baltimore-Washington Metropolitan Area. Environ. Plan. B Plan. Des. 2004, 31, 251–271. [Google Scholar] [CrossRef]
- Jesenko, D.; Mernik, M.; Žalik, B.; Mongus, D. Two-level Evolutionary Algorithm for Discovering Relations Between Nodes’ Features in a Complex Network. Appl. Soft Comput. 2017, 56, 82–93. [Google Scholar] [CrossRef]


| Symbol | Description |
|---|---|
| SN | The number of food sources (SN = SNe = SNo) |
| SNe | The number of Employed bees |
| SNo | The number of onlookers |
| n | Feature dimension of Cell |
| X | Bee populations of Employed bees, |
| Spatial Variables | Description | Ranges (Unit) | Standardized Range |
|---|---|---|---|
| DIST_TL | The distance from a grid unit to the railway | 0–35,200 (m) | 0–1 |
| DIST_GS | The distance from a grid unit to the highway | 0–56,100 (m) | 0–1 |
| DIST_GD | The distance from a grid unit to the national road | 0–42,100 (m) | 0–1 |
| DIST_SD | The distance from a grid unit to the provincial road | 0–14,400 (m) | 0–1 |
| DIST_HL | The distance from a grid unit to the city loop | 0–35,400 (m) | 0–1 |
| NEIGHBOR | The number of city cells in the 7 × 7 window | 0–49 | 0–1 |
| DIST_TL | DIST_GS | DIST_GD | DIST_SD | DIST_HL | NEIGHBOR | DEV_STATUS |
|---|---|---|---|---|---|---|
| 362.49 | 108.16 | 7682.46 | 416.77 | 8607.12 | 49 | 0 |
| 8.16 | 41.6.77 | 7682.46 | 48.26 | 3540 | 0 | 0 |
| 48.26 | 5122.53 | 8607.12 | 212.13 | 94.86 | 2 | 1 |
| 108.15 | 4249.52 | 305.941 | 3768.2 | 94.86 | 0 | 1 |
| 5050.34 | 2421.65 | 3703.02 | 7567.19 | 4012.04 | 1 | 0 |
| 4193.35 | 8554.68 | 8554.68 | 228.473 | 342.05 | 1 | 0 |
| 3396.49 | 5023.27 | 23.69 | 4484.47 | 8160.49 | 49 | 1 |
| 254.55 | 27.27 | 254.55 | 816.08 | 300 | 3 | 1 |
| 14,460.78 | 27.27 | 329.45 | 3789.55 | 355.78 | 49 | 0 |
| Parameter | Value | Description |
|---|---|---|
| Food sources number (SN) | 20 | The number of food sources which is equal to the number of employed or onlooker bees. |
| Individual search limit (Limit) | 250 | If the fitness value of a honey source has not been improved in the number of Limit iterations, the honey source will be discarded. |
| Number of iterations | 2500 | The maximum number of iteration of the algorithm |
| Rule convergence threshold | 500 | The maximum number of convergence rules. |
| Minimum fitting ratio | 0.01 | When the ratio of remaining samples to total number of samples reaches this parameter, the mining algorithm will be stopped. |
| Effective coverage | 0.005 | The ratio of minimum samples to total number of samples that matches a rule which is to control the quality of the rule. |
| Urban Land in Actual Situation | Non-Urban Land in Actual Situation | |
|---|---|---|
| Urban land in simulation results | a | b |
| Non-urban land in simulation results | d | c |
| Simulation accuracy | (a + c)/(a + b + c + d) × 100% | |
| Algorithm | Execution Time (Unit: Second) | |||
|---|---|---|---|---|
| Max | Min | Mean | SD | |
| PSO-CA | 1.013 × 102 | 9.677 × 101 | 9.886 × 101 | 4.021 × 100 |
| MHABC-CA | 1.098 × 102 | 9.733 × 101 | 1.034 × 102 | 3.475 × 100 |
| Urban Land in Actual Situation | Non-Urban Land in Actual Situation | |
|---|---|---|
| Urban land in simulation results | 34,168 | 5796 |
| Non-urban land in simulation results | 7557 | 42,029 |
| Simulation accuracy | 85.09% | |
| Urban Land in Actual Situation | Non-Urban Land in Actual Situation | |
|---|---|---|
| Urban land in simulation results | 32,285 | 7833 |
| Non-urban land in simulation results | 8684 | 40,748 |
| Simulation accuracy | 81.56% | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huo, J.; Zhang, Z. Application of an Improved ABC Algorithm in Urban Land Use Prediction. Information 2018, 9, 193. https://doi.org/10.3390/info9080193
Huo J, Zhang Z. Application of an Improved ABC Algorithm in Urban Land Use Prediction. Information. 2018; 9(8):193. https://doi.org/10.3390/info9080193
Chicago/Turabian StyleHuo, Jiuyuan, and Zheng Zhang. 2018. "Application of an Improved ABC Algorithm in Urban Land Use Prediction" Information 9, no. 8: 193. https://doi.org/10.3390/info9080193
APA StyleHuo, J., & Zhang, Z. (2018). Application of an Improved ABC Algorithm in Urban Land Use Prediction. Information, 9(8), 193. https://doi.org/10.3390/info9080193





