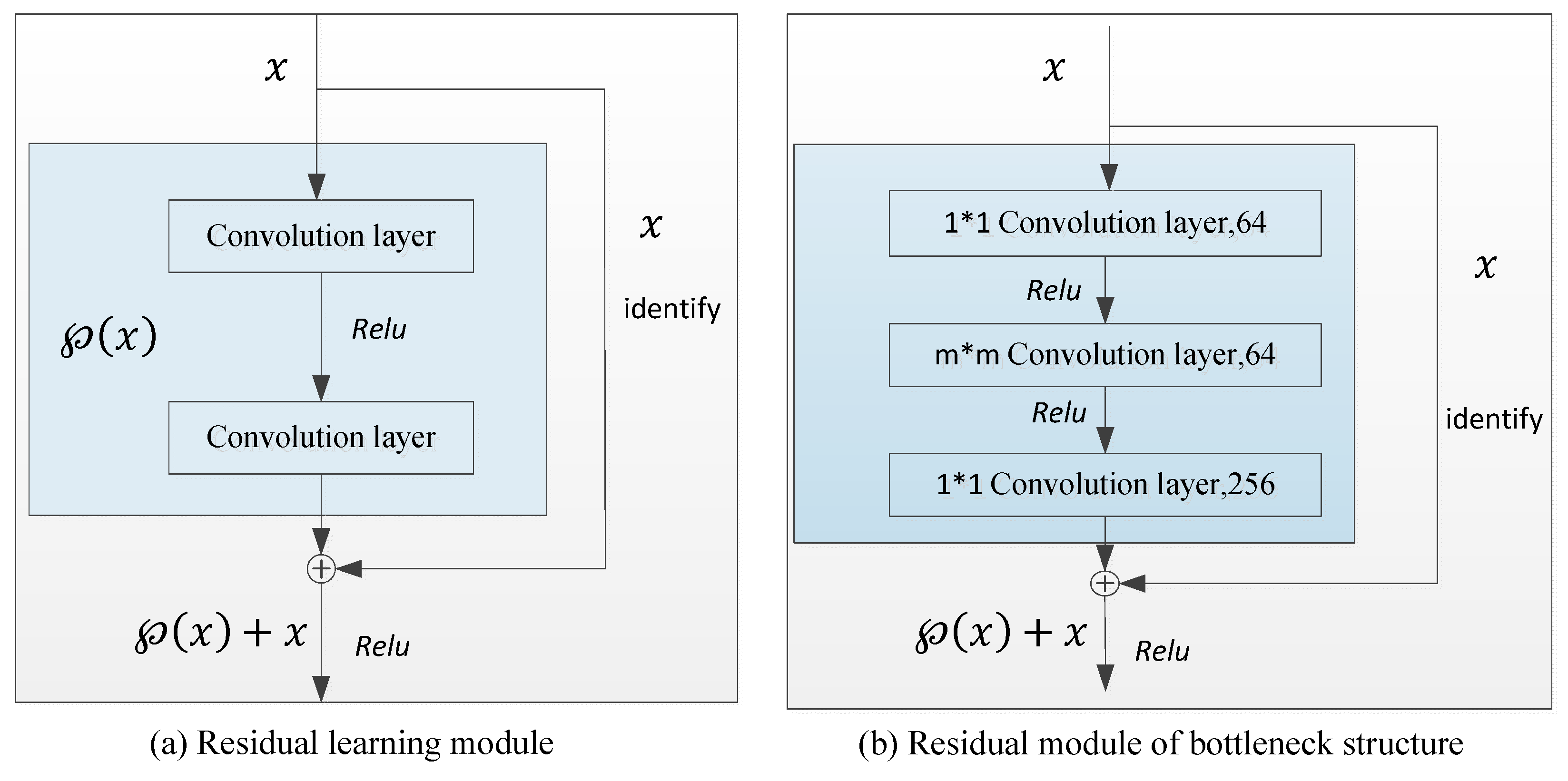
Figure 1.
Residual learning network.
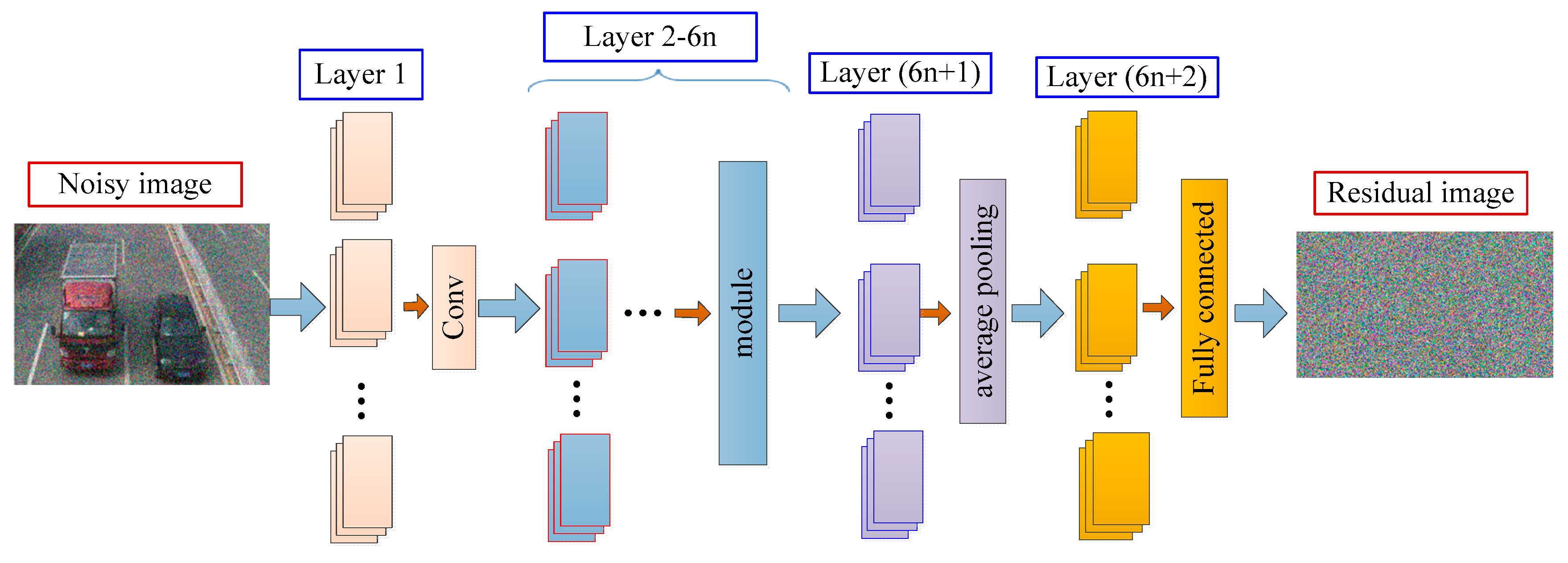
Figure 2.
The architecture of the model for aerial-image denoising;
is the number of learning modules (the size of
is discussed in
Section 4.2.3), and the module is a multi-scale residual learning module (see
Figure 4).
Figure 3.
Reconstruction phase of the proposed model.
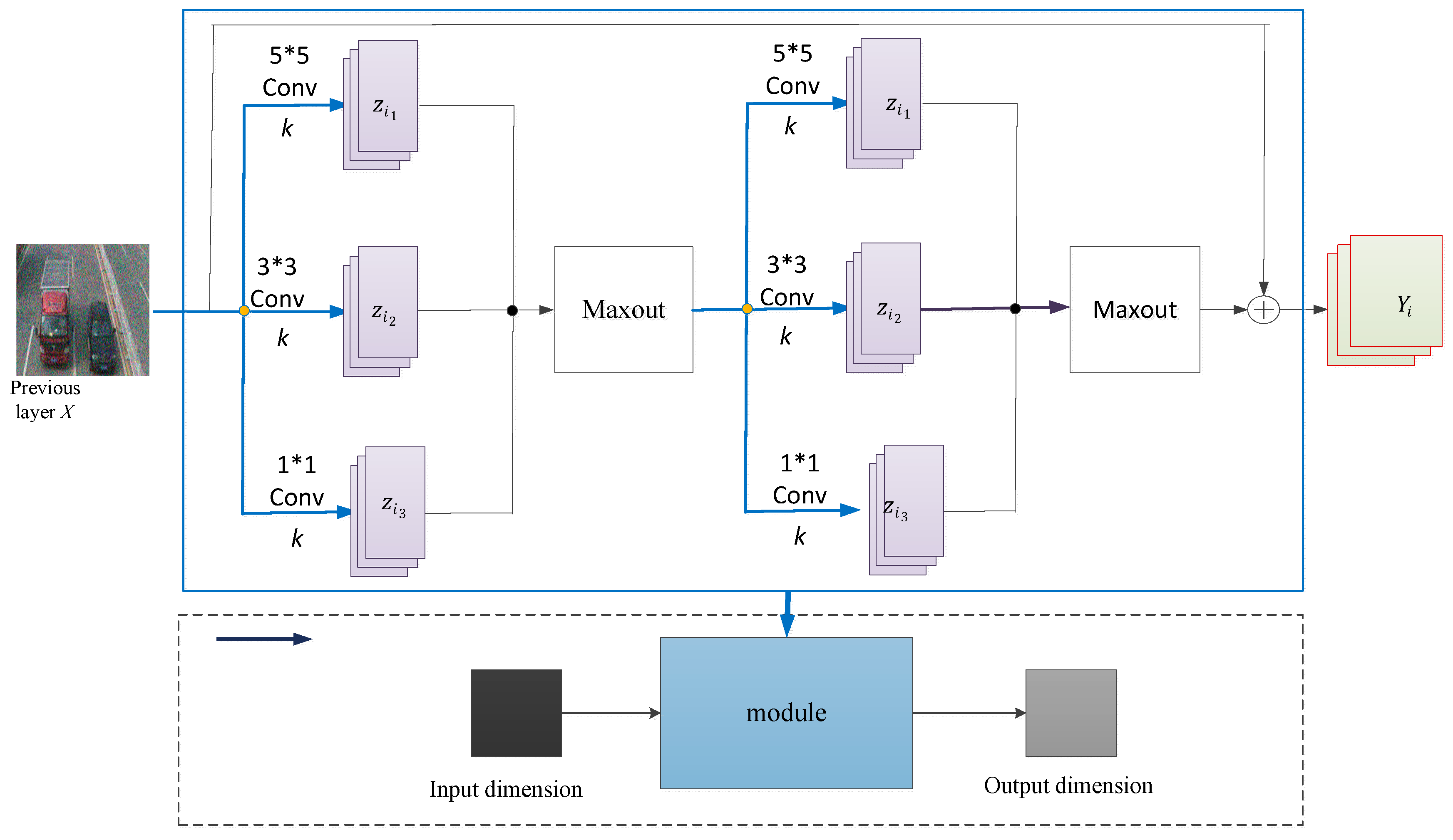
Figure 4.
Multi-scale residual learning module.
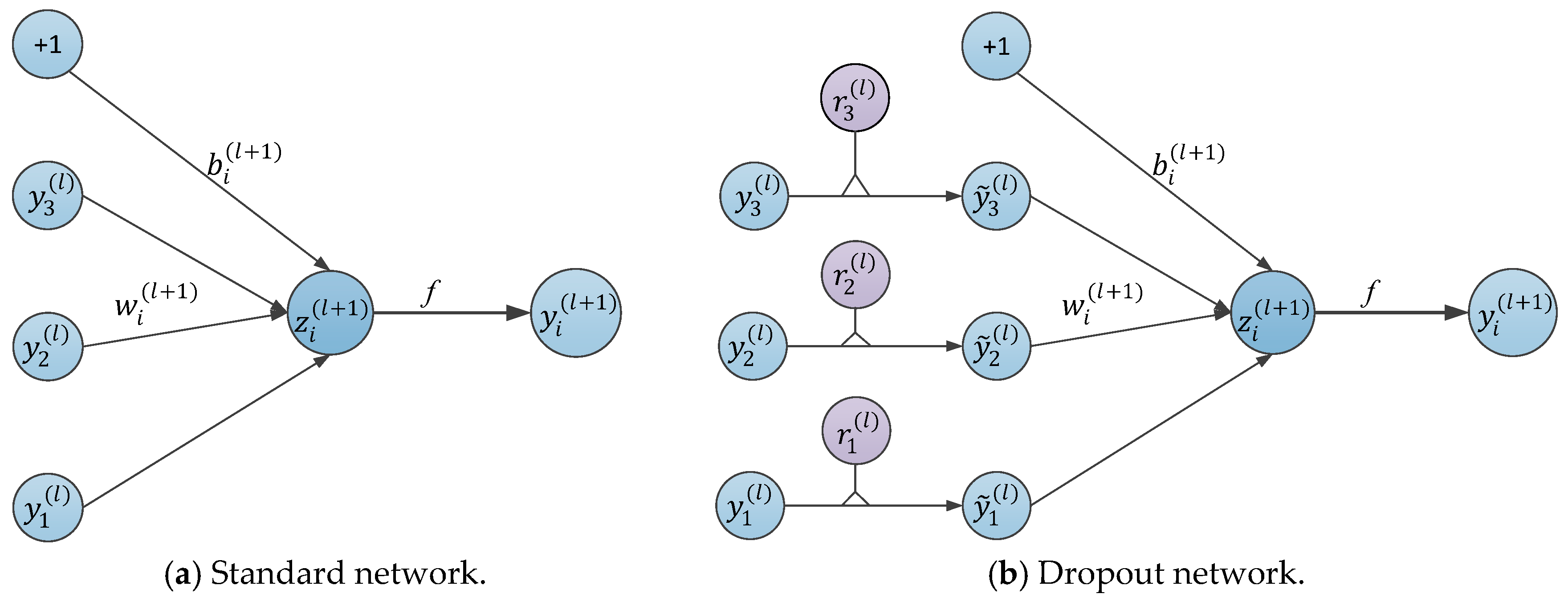
Figure 5.
A comparison of the basic operations between the standard and dropout networks.
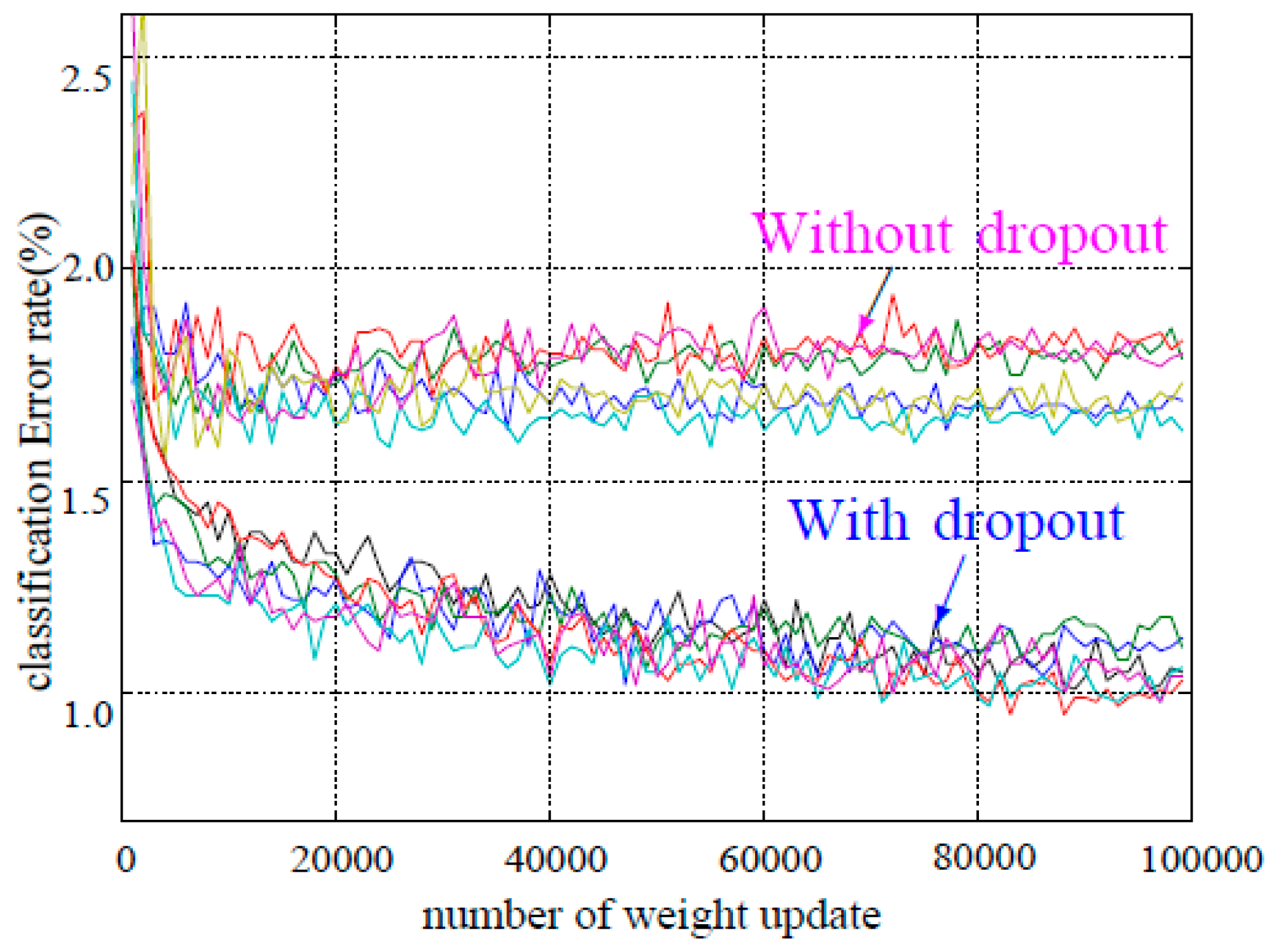
Figure 6.
Test error for different datasets with and without dropout.
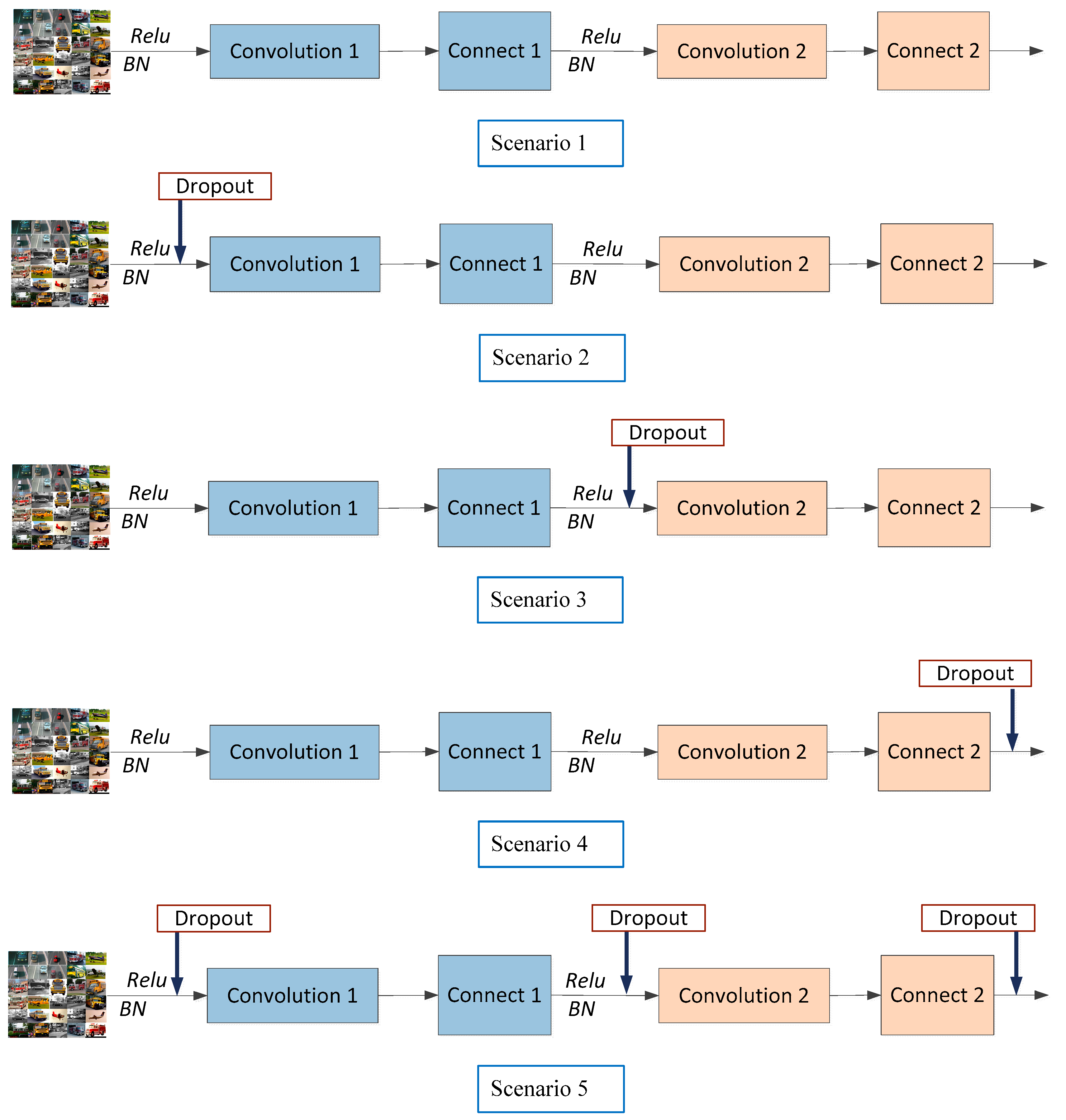
Figure 7.
The module structure of different dropout locations.
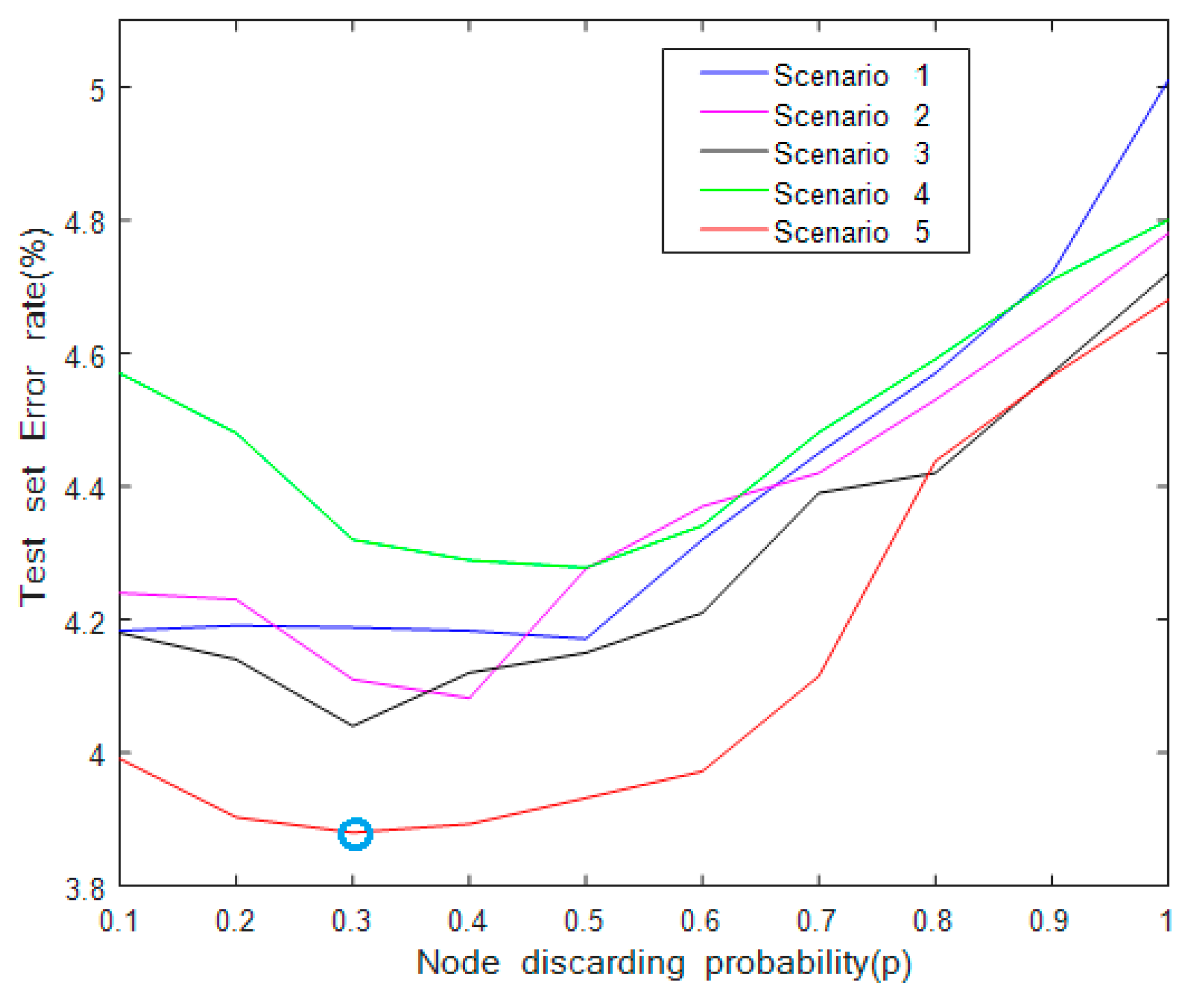
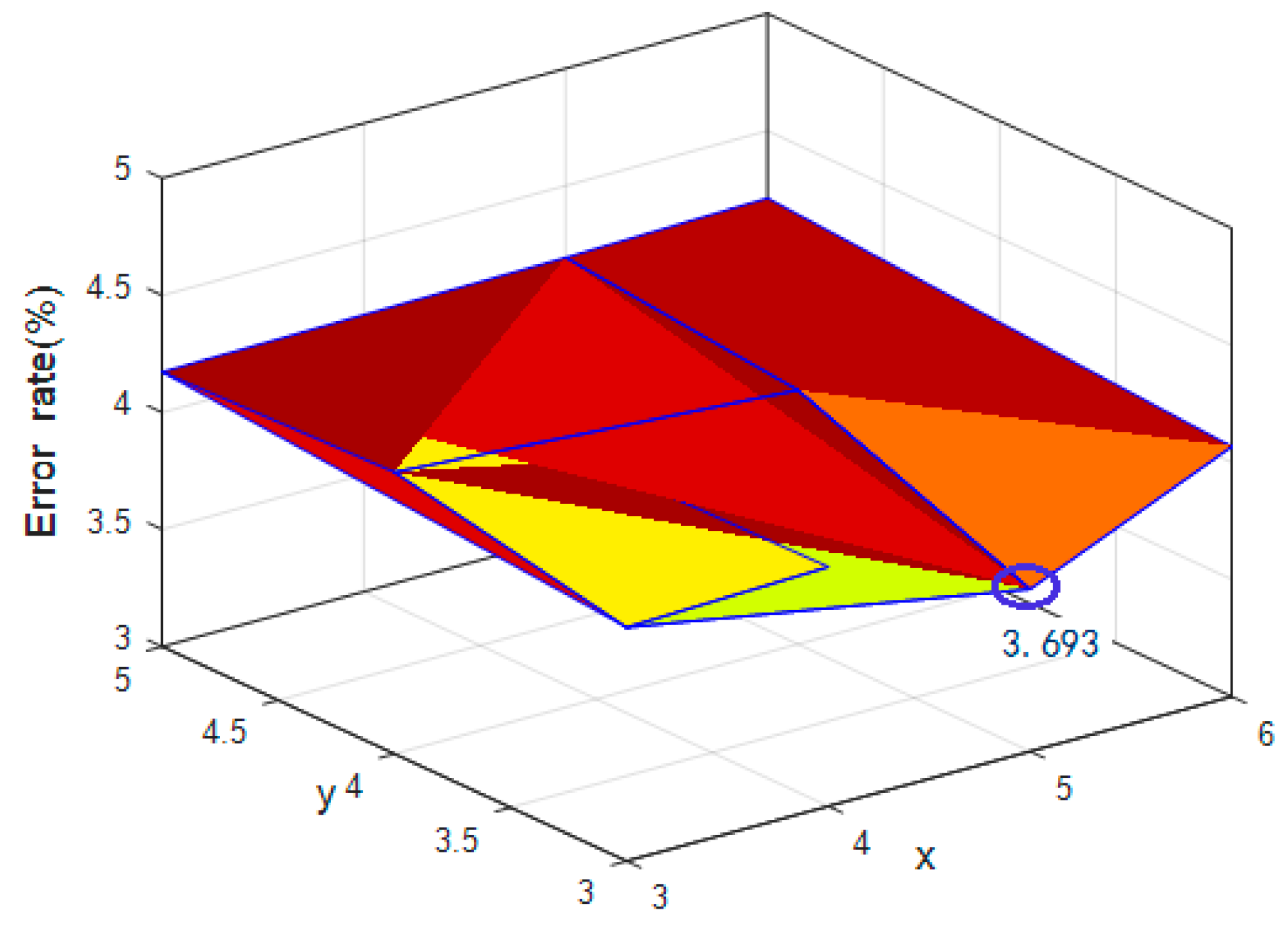
Figure 8.
The influence of parameter and dropout for multi-scale residual learning network (ResNet).
Figure 9.
The curve for the training times and the error rates for the test set.
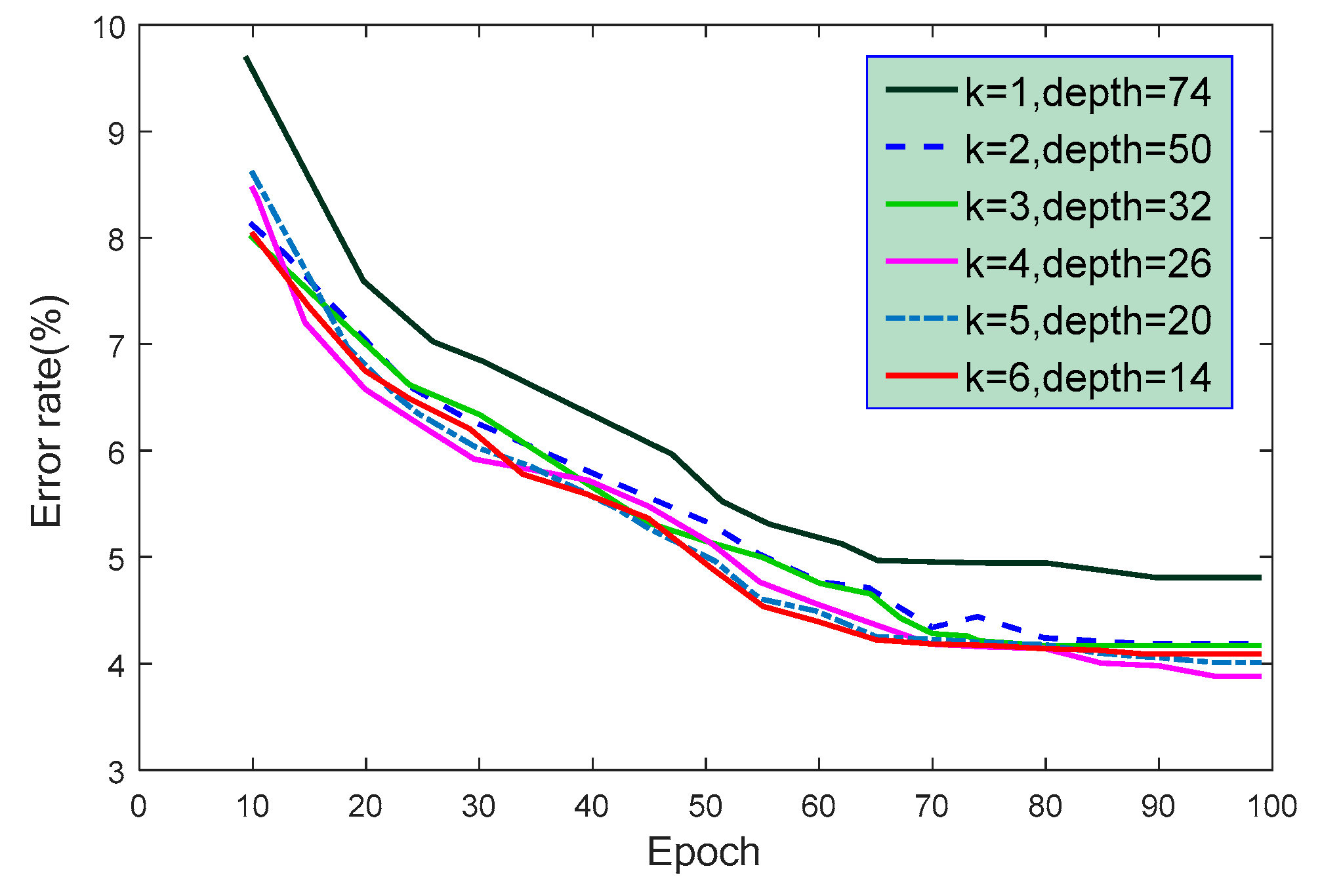
Figure 10.
The error rate of test set under different learning module numbers (where z = 4).
Figure 11.
Vehicle images: model performance trained with 64 × 64 image size. (A1) The original image; (A2) the noisy image; (A3) denoised image with .
Figure 12.
Vehicle images: model performance trained with 64 × 64 image size. (A1) The original image; (A2) the noisy image; (A3) denoised image with .
Figure 13.
Vehicle images: model performance trained with 64 × 64 image size. (A1) The original image; (A2) the noisy image; (A3) denoised image with .
Figure 14.
Vehicle images: model performance trained with 180 × 180 image size. (A1) The original image; (A2) the noisy image; (A3) denoised image with .
Figure 15.
Vehicle images: model performance trained with 180 × 180 image size. (A1) The original image; (A2) the noisy image; (A3) denoised image with .
Figure 16.
Vehicle images: model performance trained with 180 × 180 image size. (A1) The original image; (A2) the noisy image; (A3) denoised image with .
Figure 17.
Aerial images: model performance trained with 180 × 180 image size. (A1,A4,A7,A10) Original images; (A2) noisy image with 64 × 64 image size and ; (A3) denoised image with 64 × 64 image size and ; (A5) noisy image with 64 × 64 image size and ; (A6) denoised image with 64 × 64 image size and ; (A8) noisy image with 180 × 180 image size and ; (A9) denoised image with 180 × 180 image size and ; (A11) noisy image with 180 × 180 image size and ; (A12) denoised image with 180 × 180 image size and .
Table 1.
The machine configuration used in experimental environment.
| Computer Configuration |
|---|
| Processor | Intel(R) Core(TM) i7-7700HQ CPU @ 2.90 GHz |
| GPU | NVIDIA GeForce GTX1050 Ti |
| RAM | 8 GB |
| Hard disk | SSD 256 GB |
| Operating system | Windows 7 @ 64 bit |
| Test framework | Tensorflow |
Table 2.
The parameter in experimental environment.
| Parameter |
|---|
| Loss Function | Initial Learning Rate | Drop Probability | Momentum | Weight Decay |
|---|
| Cross-entropy | 0.1 | 0.3 | 0.9 | 0.0005 |
Table 3.
The error rate of test set under different network structures, where is the scaling parameter and is the number of learning modules.
| Model States |
|---|
| Model Number | | | Network Depth | Parameters | Error Rate |
|---|
| i | 1 | 12 | 74 | 12.9 M | 4.813% |
| ii | 1 | 16 | 98 | 18.7 M | 4.913% |
| iii | 1 | 20 | 122 | 22.8 M | 4.965% |
| iv | 2 | 8 | 50 | 36.1 M | 4.191% |
| v | 3 | 5 | 32 | 47.8 M | 4.178% |
| vi | 3 | 6 | 38 | 59.1M | 4.238% |
| vii | 4 | 4 | 26 | 66.4 M | 3.883% |
| viii | 5 | 3 | 20 | 76.4 M | 4.012% |
| ix | 6 | 2 | 14 | 81.3 M | 4.099% |
Table 4.
The running state of model under different scaling parameters and network depths, where “—” indicates that GPU resources were exhausted and could not be trained (blue font indicates the best).
| Model State | | | |
|---|
| | Network Depth | Parameters (M) | Training Situation | Error Rate (%) |
|---|
| 1 | 20 | 122 | 22.8 | Normal training | 4.965 |
| 1 | 21 | 128 | 25.3 | — | |
| 1 | 22 | 134 | 26.8 | — | |
| 2 | 8 | 50 | 36.1 | Normal training | 4.229 |
| 2 | 9 | 56 | 40.9 | — | |
| 2 | 10 | 62 | 43.9 | — | |
| 3 | 6 | 38 | 59.1 | Normal training | 4.232 |
| 3 | 7 | 44 | 68.0 | — | |
| 3 | 8 | 50 | 69.5 | — | |
| 4 | 4 | 26 | 66.4 | Normal training | 3.883 |
| 4 | 5 | 32 | 83.6 | — | |
| 4 | 6 | 38 | 88.5 | — | |
| 5 | 3 | 20 | 76.4 | Normal training | 4.012 |
| 5 | 4 | 26 | 105.5 | — | |
| 5 | 5 | 32 | 108.3 | — | |
| 6 | 2 | 14 | 81.3 | Normal training | 4.099 |
| 6 | 3 | 20 | 110.2 | — | |
| 6 | 4 | 26 | 114.7 | — | |
Table 5.
The average results of our aerial-image model, where the multi-scale residual learning network (ResNet) was the proposed aerial-image denoising method in the paper. The corresponding experimental parameters were = 5, = 3, scaling parameter = 4, and network depth of 26 (blue font indicates the best).
| Noise Level () | Methods | Image Size of 64 × 64, with Dropout |
|---|
| PSNR/SSIM | PNN | Multi-Scale ResNet | SRCNN | BM3D | WNNM | DnCNN |
|---|
| = 10 | 38.485/0.9000 | 39.482/0.9271 | 38.551/0.9211 | 38.494/0.9004 | 38.494/0.9001 | 39.466/0.9271 |
| = 15 | 36.388/0.8881 | 38.607/0.9202 | 37.112/0.9000 | 36.993/0.9001 | 36.379/0.8746 | 38.007/0.9202 |
| = 25 | 35.553/0.7003 | 36.998/0.9193 | 36.996/0.9303 | 36.261/0.9184 | 36.118/0.7839 | 36.767/0.9192 |
Table 6.
The average results of our aerial-image model, where the multi-scale residual learning network (ResNet) was the proposed aerial-image denoising method in the paper. The corresponding experimental parameters were = 5, = 3, scaling parameter = 4, and network depth of 26 (blue font indicates the best).
| Noise Level () | Methods | Image Size of 180 × 180, with Dropout |
|---|
| PSNR/SSIM | PNN | Multi-Scale ResNet | SRCNN | BM3D | WNNM | DnCNN |
|---|
| = 10 | 40.114/0.9009 | 40.987/0.9652 | 40.478/0.9622 | 40.115/0.9195 | 40.114/0.9191 | 40.582/0.9642 |
| = 15 | 38.572/0.9441 | 40.208/0.9597 | 39.442/0.9501 | 39.028/0.9447 | 39.005/0.9448 | 39.881/0.9597 |
| = 25 | 37.316/0.9311 | 38.448/0.9421 | 37.411/0.9400 | 37.401/0.9338 | 37.189/0.9278 | 37.644/0.9420 |
Table 7.
The average results of our aerial-image model, where the multi-scale residual learning network (ResNet) was the proposed aerial-image denoising method in the paper. The corresponding experimental parameters were = 5, = 3, scaling parameter = 4, and network depth of 26 (blue font indicates the best).
| Noise Level () | Methods | Image Size of 180 × 180, without Dropout |
|---|
| PSNR/SSIM | PNN | Multi-Scale ResNet | SRCNN | BM3D | WNNM | DnCNN |
|---|
| = 10 | 37.660/0.8796 | 39.481/0.9424 | 38.003/0.9008 | 38.104/0.9103 | 37.661/0.9001 | 38.117/0.9424 |
| = 15 | 36.782/0.8982 | 38.115/0.9331 | 37.180/0.9115 | 37.178/0.9112 | 36.703/0.8954 | 37.380/0.9321 |
| = 25 | 35.116/0.8716 | 36.662/0.9004 | 35.333/0.8894 | 35.371/0.8990 | 35.003/0.8541 | 35.773/0.9010 |