Abstract
Our understanding of the natural universe is far from being comprehensive. The following questions bring to the fore some of the fundamental issues. Is there a reality of information associated with the states of matter based entirely on natural causation? If so, then what constitutes the mechanism of information exchange (processing) at each interaction of physical entities? Let the association of information with a state of matter be referred to as the representation of semantic value expressed by the information. We ask, can the semantic value be quantified, described, and operated upon with symbols, as mathematical symbols describe the material world? In this work, these questions are dealt with substantively to establish the fundamental principles of the mechanisms of representation and propagation of information with every physical interaction. A quantitative method of information processing is derived from the first principles to show how high level structured and abstract semantics may arise via physical interactions alone, without a need for an intelligent interpreter. It is further shown that the natural representation constitutes a basis for the description, and therefore, for comprehension, of all natural phenomena, creating a more holistic view of nature. A brief discussion underscores the natural information processing as the foundation for the genesis of language and mathematics. In addition to the derivation of theoretical basis from established observations, the method of information processing is further demonstrated by a computer simulation.
1. Introduction and Definitions
Information plays a central role in our lives. Even our thoughts are constituted of information involving objects and relations, objects may be as elemental as a numerical value, a visual pixel, a tonal sound, and as complex or abstract as laws of physics, mathematical expressions, social order, etc. It is generally accepted that the entire gamut of information processing takes place in the brain, a highly organized neural system. These neurons and their networks are implicated to possess mechanisms to represent as well as to discover inter-relations among objects to guide our actions towards certain goals. From a different standpoint, we note that all models of physical phenomena and all mathematical structures have been developed using the resource (capacity to represent and process information) that the human brain provides. Yet, we do not have a scientific understanding of how such a resource is made available by natural processes. What physical processes, methods, and relations may give rise to such a resource? Are these processes mathematically describable or are they supra-mathematical in their manifestation? Is there a fundamental property of the physical universe that has been left out of consideration which must be taken into account in order to understand the genesis of such a resource? These questions assume center stage in light of the stated void in our understanding. The work presented here addresses these issues at the fundamental level, where the correlation of information with the states of matter is derived from the first principles of cause and effect relation in nature. For the moment, we consider matter as a form of energy (e.g., particle, wave, field, and their composites), generically referred to as ‘a physical entity’ or ‘a system’, and ‘a state’ as a description of quality of a system that can be accounted for or modeled to have an effect on the observable consequence. First principles also enable us to formulate the mechanism of information processing that occurs at each interaction. Based on the mechanism, a quantitative method of information processing is founded that yields object descriptions of unlimited complexity and abstraction.
Defining natural causality: The natural universe, as observed from within, undergoes change. Changes exhibit a certain uniformity and regularity (constancy), such that an observable state, S, of a physical entity, P, bears dependence on certain other states within limits, where may include relative static or dynamic quantities (rates of change). That is, if were not to form a part of contextual reality within the limits, the state, S, of P could not have an existential reality either. Therefore, if a state, C, bore a dependence on B, and B on A, then it is possible to define an order on the sequence of dependence. A mutual dependence indicates conjugate state variables evolving together. It is ascertainable then that A is a precursor to B, while A and B are to C. It is noteworthy that A is not said to cause B, but rather B depends on A, and B may depend on other factors in conjunction or disjunction. This relation of ‘precursor to the consequence’ is referred to here as ‘natural causality’. It is referred to as ‘natural’ to imply the independence of this relation from any model or interpretation to mean what really exists, an ontological connotation. Given a possibility of a limited indeterminism, as discussed in Section 5.2, it becomes impossible to assert a globally objective order of causal dependence for the non-uniqueness of state description as observed by different entities and for multiplicity of paths to the same end state. Therefore, the limits of determinism define the limits of causality. Moreover, as the processes of change exhibit constancy of relative rates of evolution of elements and their interactions, a notion of time emerges, as discussed in Section 4.1.
In this work, the specifics of the laws and limits of causation are not important, as long as there is a constancy in the nature of change; no new law of causation is being proposed here. It is immaterial here if there exists a degree of indeterminism in the form of one-to-many and many-to-one mapping from precursor to the consequence so far as mapping is bounded. As discussed in Section 4.1, the universe would have no predictability if there was no constancy in the nature of change. Therefore, each observed state must naturally (without requiring an interpretation based on a model) correlate with the information of causal limits (precursor states and their inter-relations).
The purpose here is to work out how this information of correlation is exchanged at each interaction that amounts to its processing, resulting in the representation of higher level complex and abstract semantics.
Information, as used here, is not limited to the way it is used by Shannon [1] to deal with the quantity of it, measured in bits or other units and represented by discrete physical states. In physical sciences too, so far, information has been limited to the description of discrete states which are often counted and quantified in bits or qubits. In this work, a state description depends only on the natural limits of causation, discrete or otherwise, as observed by each interacting entity. Therefore, the perspective of information is intrinsic to each interacting entity in contrast to what is currently the norm in physical sciences, where it is based on what an interpreter can determine from an observation within the model laws of causality and contextual constraint as analyzed by the interpreter. Moreover, information here refers to the ‘semantic value (or semantics)’, rather than the quantity of it (see [2] for a related discussion). In order to contain digression and misinterpretation, in this text, the term ‘semantics’ is limited to what an information conveys or expresses and what properties, function, and relations define an object. Therefore, here, semantics is the primitive of meaning. For example, mass of a physical entity, Q, bears a meaning—it conveys its causal power in an interaction which constitutes Q’s function or the basis of its relation with other objects. If an entity, P, interacts with Q and gains a state, S, due to the causal power of mass of Q, then the S of P is said to correlate with the information of mass of Q. Therefore, the information of the causal value of mass corresponds to a semantic value; this is how semantics gets grounded, without any need for semantic attribution (see [3]). Similarly, ‘right angle’ is a semantic value that describes an abstract object, a relation; relations among primitives create more complex semantics. In contrast to the views expressed by several authors regarding semantic information, semantic memory, semantic knowledge, semantic processing, or semantic categories [4,5,6,7], here, all information is semantic by definition, and all information processing is semantic processing.
A representation of information, natural or artificial, by definition is always an association of information with a state of physical substrate. For this reason, sometimes it is referred to as ‘physical information’ [8,9,10,11]. The physical substrate of information may be a binary register in a digital processing unit, or a neuron in the neural system, or any physical entity, elemental or composite, whose specific state is implied to represent information. An element of information is necessarily relative as it qualifies a distinction; therefore, semantic value is the relation implied or expressed. A semantic value may be atomic, e.g., a numerical constant, an element of state description, a symbol that stands for an object, or structured, e.g., a right angle, a paper, etc. The semantics of number five expresses its relative ordinal position among natural numbers, the symbol ‘A’ stands for the first letter in an alphabet, and ‘right angle’ expresses a relation between lines, planes, or vectors. Each of these semantic values forms an example of objects. Since an object has a description only in relation to other objects, or as a structural (internal) relation among its components, it is always expressed in relative terms; therefore, an object description or definition is equivalent to a semantic value. Therefore, the term ‘semantic value’ may be used for an element of information, or equivalently, for the description of an object in a transparent manner.
The work presented here is meant to cover, universally, all expressible semantics; therefore, the expressions and statements must hold true to this generality. We need a term to refer to elements of reality, relations, processes, and expressions alike. The term ‘object’ is used in the text as an unified reference to all that is referable. An object is referable only when a representation is constructed from its observable relations or functions in the physical domain or in the domain of representation. The domain of discourse here covers the space of all objects, referred to as the ‘universal scope’.
A state of a physical entity that is said to represent an object does not embody the properties of the object represented; a state is not said to represent itself. This is one of the primary ways the treatment here differs from the established norm in physical sciences, where the information contained in a physical system is the ‘true value’ (description) of its state. In contrast, here, it is always a state of physical entity that is said to bear correlation with the semantic value of information, henceforth rephrased as ‘semantics of correlation of the state’; this expression is used extensively in the text. In fact, there does not exist a possibility to refer to an element of information that does not have a relational basis in the physical substratum. That is, all semantics originate from relations based on interactions among the physical entities that refer to them. An interaction is defined by the ‘observable transitions in the states of physical entities’ that are accountably interdependent on the causal power of the states. Stated differently, the observable transformations in the physical substrate are causally accountable to the quantifiable state description of the physical entities. The physical consequences of interaction make it possible to organize a system, where the states of the elements of the system not only represent the objects but may also carry out the function of the objects by their interactions. In fact, it becomes possible then to define the functions of the objects that may not even have a priori existence. Binary registers of a processing unit that represent artificially assigned objects interact under well defined rules to carry out the functions of the objects represented. While this may form an artificial example of such a system, the same may be achieved from the natural processing that occurs with each physical interaction. The represented object may or may not have a physical reality in itself. For example, ‘right angle’ is unrealizable in the physical domain; an instance of ‘right angle’ may be marked or may have a visual representation but not the ‘right angle’ itself, since it refers to a class defined by a relation where the individual lines have no particular orientation. Such a term describes an emergent abstract object. The term ‘abstract’, as an adjective, is used as a qualifier to refer to a definitive class of objects or instances, or to a relation that describes the class, and ‘abstraction’ refers to the process of forming a class, or the emergence of a class from its instances. This definition functions as a concrete constructor method which is applicable across all object types and domains. Therefore, a representation may be constructed to refer to an abstract object that has no correspondence in the physical universe; in fact, by and large this is the case, as described in this work. In other words, all constituent elements of our thoughts and experiences are represented objects without exception.
In literature, the term ‘representation’ has been used in varied contexts, but none corresponds to the information associated with a state of a physical entity by virtue of its correlation in the universal context, as per natural causation and how such values are transmitted. Even though, the causal dependence may not appear in strict sequential order to an external observer at the finest observable scales, intrinsically (or subjectively), for each resultant state, the causal influence defines the order of events, which, in conjunction with implied indeterminism (discussed in Section 5.2), gives rise to the arrow of time. Fred Dretske [12] makes a reference to the representation of information by states, but he refers to them as what the states indicate as per their design. Barwise and Seligman’s approach [13] requires either a system of coding and decoding or a model of regularity (constraint) as a basis of information. Similarly, Roederer’s approach [14] also requires an evolved system of coding/decoding, or a mechanism of interpretation. These approaches differ from this work in certain fundamental ways—information is grounded by a framework to create a basis, and all intentional or interpretation-based systems already require elemental information (datum) to work with under a frame of reference.
With due respect and consideration, we set aside the work in the domain of philosophy, for it is not always possible to ground the ideas and terms to physical function. In the physical sciences, a reference to information occurs in diverse contexts [15,16]. It refers to (1) a description of state that can be associated with a physical entity (a system) such that a measurement in specific context conforms to it, which is necessarily relative to a model and a reference frame; (2) the a priori probability distribution of possible outcomes on measurement (this is an extension of point 1); (3) the quantity of information contained in a system, which is the number of different quantifiable discrete states that an instance (description) of a state discriminates against, as in the consideration of entropy, where the measure of information is the log of the number; or (4) the values artificially assigned to the discrete physical states for the purpose of storage, transmission, or for processing, as in the case of binary registers in digital devices. In this work, information does not refer to any of the above. Instead, it is the causal correlation of the observable state that constitutes the information associated ‘with the state’. This is in contrast to point 1, where information is associated with the system itself, information being its own state description, which limits the semantic build up. Here, a state description, observable post-interaction, is said to bear a natural correlation with the information constituted of the causal limits of the precursor states of interacting entities without a reference to any a priori model. The accountable identity of physical entities, models of states, and the laws of interaction emerge from such a consideration, rather than being the basis of information. In order to make a clear distinction from all such prior usage, it is referred to here as ‘natural representation’. Natural representation should not be taken to refer to similar usage either in the ‘Mathematics of Symmetric Groups’ or elsewhere in other domains.
The plan of the presentation is as follows: (1) First, we take note of the perspective of the reality of information associated with physical states and what is referred to as primitive semantics; (2) from established experiments, the causal basis of interaction is interpreted to show the natural association of information with states; (3) from the perspective of a resultant state, the causal interaction is interpreted as the ‘disjunction of conjunctions’ of specific state descriptions of interacting entities; this expression then forms the constructor of higher level semantics. The same constructor also applies to interpret the semantics of correlation of a macroscopic state, describable in terms of the state descriptions of the components; (4) this brings to the fore the centrality of state description, which is then defined with specificity; (5) attention is then shifted to show how the constructor method forms the basis of expressing universally all semantics; (6) the quantitative formulation of the constructor method is then laid down. In particular, what constitutes the mechanics of abstraction and the process of emergence of symbolism suitable for language and mathematics is determined; (7) in light of the new development of natural representation of information, certain aspects of physical sciences are revisited for completeness; (8) definitive postulates are advanced to bring into scientific account the reality of natural representation; (9) a basic level simulation is carried out to show how the constructor method in fact results in quantitative processing of information; and (10) finally, the results are interpreted to draw a wide range of inferences.
2. The Basis of Natural Representation
How may the phenomenon of representation arise from natural function of the physical universe? Here, I need to develop the conceptual background stepwise, which requires some of the points to be revisited successively in more formal ways, so that not only we arrive at the robust definition of natural representation, but we also relate some of the dependent concepts in reasonable detail to achieve a degree of completeness. Additionally, a reader encounters the rationality of an argument before it is made. To begin with, we equate the natural representation with causal correlation, but the term is refined in the text as the inferences permit.
From the first principle consideration of causation, if an interaction among physical entities results in an observable state, S, of a physical entity, P, then the S of P must remain congruent with, or correlate with, the causal context of the transition to the state. Otherwise, measurements do not have an interpretation relating to their cause. A representation involves two natural entities—one is an accountable physical entity, P, that may cause a consequence upon interaction by virtue of its state, S, in a context, and another is a semantic value, C, a natural correlation of the state with the limits of reality and relations that may cause the S of P. P is referred to as the ‘Physical Substrate of Representation’ (PSR). In general, there is no unique or default description of state—it is relative to the observation. A PSR may be elementary or composite that has the capacity to interact as an accountable coherent unit.
In order to fix the sense and meaning of ‘correlation with information’ as used in the text here, consider a gedanken experiment with a chamber of argon gas, as shown in Figure 1. A passing energetic heavy ion (say, an alpha particle or a nucleus of carbon or oxygen atom) knocks out several electrons from their respective atoms (argon is chosen to avoid a quick reunion of a free electron with another atom), which leaves the atoms in ionized states. Let the circle in Figure 1 designate a composite instrument that could detect the electrons ejected into the neighborhood of (x,t) and the heavy ion passing through it. Each of these electrons’ existential state must bear a positive correlation with the point of interaction in the neighborhood of (x,t) and a negative (anti) correlation with the rest of the space, since, if the instrument sampled electrons at any other place except around x, or at any other time except t, it would not detect these electrons. The existential state is a notional description of state that is as comprehensive as permitted by the causality. The point (x,t) constitutes an element of information, but only in relative terms. Stated differently, if space and time, and distances and durations, play any causal roles in the function of the universe such that different points in space and time cause relative differential effects, then an ejected electron’s state bears a specific correlation with the point of ejection in contrast to all other points in space and time. We label a point as (x,t) for the convenience of communication to relatively differentiate it from other points. In a model dependent description of (x,t), the model provides the relative frame of reference, a context, but then, the information is dependent on the model, not a natural correlation. The point (x,t) is not even referable in absolute isolation, even though the state of electrons distinctively correlates with it. The instrument, observing in the neighborhood of (x,t), imparts a relative meaning to the states of detected electrons in relation to itself, which distinguishes the neighborhood of (x,t) from the rest of space and time, due to the constraints of causation. A point to note here is that as per historical evolution, the observed state of an electron or the instrument may have a priori correlation with the limits of space and time, the current interaction only adds to the constraint in conjunction. This point is worked out in detail in the text. This semantic value is independent of any language or interpreter.
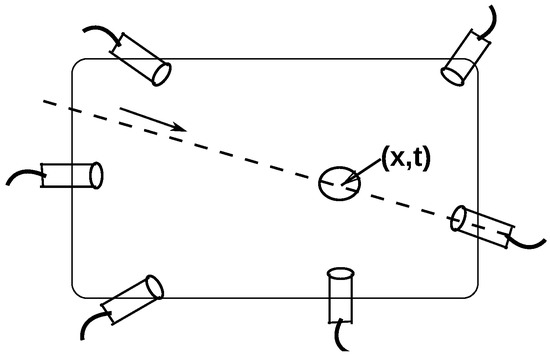
Figure 1.
A chamber to observe electrons ejected by a passing heavy ion.
Now, if a coincidence detection is required between the process of heavy ion and the release of electrons, the result will bear a positive correlation with the process. Instead, if the electrons were ejected by any other process but the heavy ion passing through it, the result will bear a negative correlation with the heavy ion process. Each of these electrons correlate positively with the bounded region of interaction with the heavy ion in the neighborhood of (x,t). Let us refer to this exclusive limit of information of correlation common to each ejected electron as C.
Instead of the instrument centered at x, if there were several instruments located away from x, but pointed exclusively in the direction of x, as shown in Figure 1, then several of these instruments would detect the same electrons, and one of them would also detect the heavy ion. From the perspective of a single instrument, its resultant state correlates positively with a limited range of angles and times of incidence of an electron, and negatively with the rest of the parametric space. Let us refer to the directly observed limits of states as level one (L1) correlation of the resultant state. Due to natural causation, the specific state of the observing instrument, at this very moment, must also correlate with the causal limits of the history of the electron that could make it possible for the specific electron to arrive within the limits of observation, which includes the information, C. We may refer to this as a level two (L2) correlation for clarity. From a third person perspective, this correlation is out of bounds for the lack of consideration of complete contextual specification of the history. Now, if the coincidence detection is required among a sufficient number of these instruments including the one that detected the heavy ion within suitable time limits, then the conjunction of correlation limits of these instruments would be limited to information profile C, even from an external perspective. In fact, any set of three or more recipient instruments in a non-coplanar arrangement with point x would suffice. Therefore, there exists a disjunctive (inclusive) relation among several specific combinations (conjunctions) of correlation profiles that yield the same information, C. This clarifies the distinction between the intrinsic vs. external limits of correlation.
In order to have further clarity on the distinction between the intrinsic vs. externally interpreted correlations, we consider an experimental setup, as shown in Figure 2. Photons emerging from two uncorrelated sources, P1 and P2 (where a measurement identifies the source of a given photon), pass through a beam splitter (BS) before arriving at one of the two uncorrelated detectors, D1 and D2. When a photon is detected at say D1, from a third person consideration, the state of D1 can not be interpreted to distinguish between the photon sources. Intrinsically though, the state of D1 at this very point of time not only must correlate with the causal limits of photon’s state, S, as observed, but also with what S itself correlated with, which includes the causal history within limits including the source. An external agent would require a coincidence detection between the source and the detection at D1 to fix the correlation. To bring to the fore the distinction between the intrinsic vs. externally interpreted correlation constitutes one of the central aims of this work.
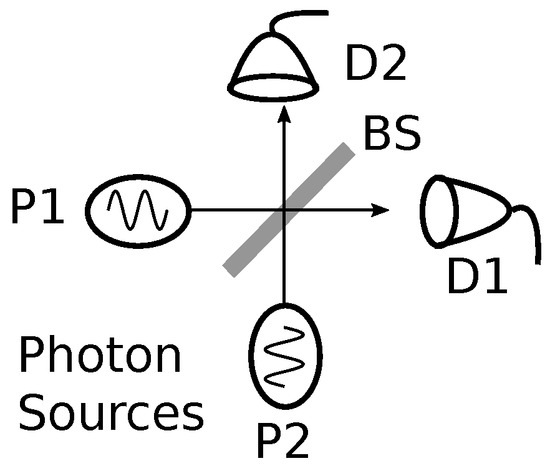
Figure 2.
Quantum randomization of a photon passing through a beam splitter.
We extend the idea of Figure 1 to a real but idealized experimental setup of an ionization chamber consisting of a pair of electrodes with suitable electric potential difference between them, as shown in Figure 3a (see [17]). The preliminary purpose of the experiment is to detect heavy ion events.
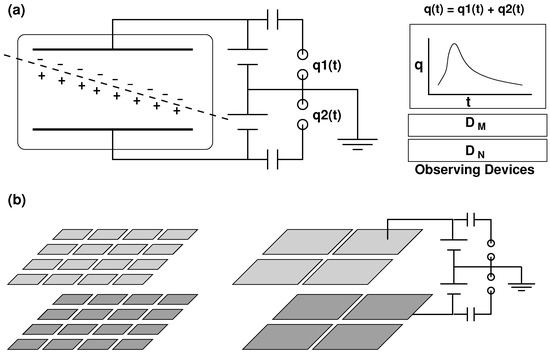
Figure 3.
Ionization chamber. (a) The figure shows a schematic of an idealized experimental setup. A heavy ion passing between the two parallel plates (electrodes), knocks out electrons from the argon atoms. The electric potential difference between the plates accelerates the electrons towards the anode. The positively charged ions move slowly towards the other electrode. and designate rate of charge flow (current) on respective plates as a function of time. The plot on the right shows one possible profile of sum of the currents, which is the net current between the plates. and are threshold current detectors. The setup is idealized only in the sense of a precision instrument that can measure small currents (about nanoamps) over small times (micro-seconds). An alpha particle with 1.5 MeV/nucleon energy, argon gas at STP, and a potential difference of about 250 volts across a plate separation of 10 cm can give rise to such values. (b) The electrodes are divided into smaller parts to form a grid. Temporal current profiles are recorded at each of the electrodes in a pair. The perpendicular electric field between the two parallel plates bends the charged particles towards the closest points on the respective plates.
The response of an observing device, as shown in Figure 3a, could either be plotted on a paper, or the device could simply produce a two state response as a measure of the limit of coherence among the electrons, where a positive response to the current above certain threshold would correlate with a generic semantic value of ‘heavy ion event’, but without the specific details of the event such as the identity, energy, or trajectory of the heavy ion. In a primitive sense, this is what is referred to as natural representation by a state of a PSR.
2.1. Causal Correlation, Coherence Relation, and Representation
The experimental setup described in Figure 3 offers an opportunity to analyze three levels of interactions in a temporal sequence with causal connections. First, the interaction of a heavy ion with atoms ejects the electrons out of their atomic shells. Second, the electrons and positive ions guided by the force field are absorbed at the respective electrodes. Third, the current profile at the electrode pair is either recorded by an external device, or the devices, and , respond to the current peak above a threshold. This allows us to discuss the transmission of information at micro as well as macro level interactions.
Given a free electron, in physics, one usually worries only about its temporal evolution in the physical state space from a classical or quantum consideration. Moreover, in several contexts, the electrons are treated as a class—one electron is considered non-differentiable from another, or the states are not fully qualified. For example, identity is not assigned as to which electron is ejected from an atom, or what is an electron’s state before its accumulation at the anode, not even which specific atom has contributed a given electron. In the physical sciences, this leads to the probabilistic consideration of the consequences of a physical process. On the contrary, from the representation point of view, the correlation of a state of a PSR in the universal scope carries as much importance as physical consequences. With respect to analyzing correlations with information, first, we deal with micro and macro states in an uniform manner. Later, we show that a quantum consideration remains transparent to the analysis.
To begin with, one may presume that the observable state of an electron in relation to the rest of the universe represents contextual elements, causal states of entities and their inter-relations, that the state depends on, and the subsequent elements that causally depend on the state. As we noted earlier, from the causal viewpoint, it suffices to consider the correlation with the configuration of immediate precursor states (L1) and what those states themselves correlate with (L2). It is important to bear in mind that for a given resultant state of an electron (a PSR), precursor states also include the existential state of the very electron (PSR) itself or of whatever system that has engendered it. In a spatially and temporally localized consideration, the causal correlation of a knocked out electron absorbed at the anode includes the interaction with the force field created by the heavy ion and the electric field that has guided the electron to the anode. From the perspective of the state of anode, the current profile is limited by the selection of electrons from within the structured spatio-temporal confinement, a state constraint that each electron satisfies. Therefore, the anode state must also correlate with the constraint of this selection. At this point, a correlation is not taken as a reference to representation. The correlation with each of the factors within relevant parametric spaces may have a profile extending to a range of values. For example, the energy-momentum state of an electron neither correlates with the unique identity and state of the heavy ion, nor with all possible identities and energy-momentum states of heavy ion uniformly [17]. The limits on the range of correlation are rather wide, since the state of an electron is not even evaluated in conjunction with the state of the atomic ion in recoil or with the states of other electrons ejected in the same process. We investigate further, keeping in mind a distinction between two possible types of correlation, one, where no distinction is made among values of states within causally permitted range of correlation, and another where a probability is assigned with different values.
Purely from the perspective of a structureless electron in presumed state of isolation, if we ask, “How did it come to exist in a specific state/context?”, there is nothing in the measurable state of the electron that could address the question with any specificity, even though the existential state intrinsically must correlate with the states of interacting entities and their inter-relations that are responsible for its transition into its present observable state. We refer to the causal correlations of existential state as intrinsic or subjective. From the external perspective of a decoupled observer, if we wish to determine the cause of an electron’s freedom from its atom from the measurement of the state of the electron alone, it is impossible. The measurement here essentially refers to an electron’s interaction with an observing system, such that different resultant states of the system bear direct correspondence with the relevant states of the electron. That is, a natural correlation is not the information encoded into the state that could be decoded from the measurement of the state. An external perspective then forms a projection of this correlation onto the limits of context under consideration by the external agent. Furthermore, if it was possible to encode the causal correlations, then the structure of the state would need to become more complex with every interaction to be able to differentially encode more contextual elements as it evolved, causing a rapid divergence of structural detail. The same rationale must also apply to the active states of neurons in the brain—a neural signal cannot encode the structured cause and the context, its state just correlates with the cause and the context.
Instead, if the measured state of an electron is interpreted in relation to the overall state of the device, there could have been several other possible pathways of interactions and processes. An electron could have been freed due to the causes other than the heavy ion, such as the atom’s interaction with another atom, or it received a photon of appropriate energy, or it was knocked out by another accelerating electron in the electric field, or it was released from the cathode end of the electrode pair. Even though an individual electron intrinsically must correlate with one of these processes only, with respect to an external observer, its identity is not separated from the other electrons, and its specific state transition is not differentially evaluated against the evolving state of the rest of the universe. Therefore, its state of being free is interpreted as correlating with a disjunction (inclusive) of all possible processes with respective probabilities as measured or as per the prior models (knowledge) of interaction.
Similarly, if the natural processes are intrinsically indeterminate in the sense that from the perspective of the specific transition in the state of an electron, there exists multiple possible descriptions of reality, then the resultant state will naturally correlate with the disjunction of all possible descriptions or range of states of interacting entities even intrinsically. That is, the causal correlation of a state is a perspective (a projection) of reality.
If a large fraction of free electrons created in that singular process, coherently accumulate at the anode and generate a current above a certain threshold and of a specific profile, which has negligible probability of being produced by any other process within the structural constraints of the coupled system, only then the observable macro-state of the anode is said to correlate with the heavy ion event for an external observer. The term ‘coherent accumulation’ is used here to signify the fact that a large number of electrons interact with the anode in an unified manner to produce a combined (integral) effect that is sufficiently distinctive in nature, due to the specific relation among the electrons. In this sense, the group of electrons functions as a composite system with its own identity, even if it is transient. A definite and observable relation among states of PSRs is referred to as coherent if the relation maintains a degree of constancy over time and allows a common process to observe the relation resulting in a specific state of the observing system. The ‘coherence relation’ neither requires, nor is limited to, a congruence with respect to only one observable property, such as a phase relation in waves. Here, the coherence relation among electrons can be stated as the “freedom from the bound states of atoms with a common direction of movement within a spatio-temporal confinement” that correlates with the heavy ion event and the electric field, among other factors.
The anode captures this coherence, and gains a distinctive state which is interpreted as correlating with what the coherence relation among the electrons correlates with. For an external observer, it does not matter much which electrons combine back with the ionized argon ions and which electrons are created spontaneously unrelated to the heavy ion event, as the accumulated effect can rarely (negligible probability) be created without a passing heavy ion. Therefore, the state is interpreted as representing the heavy ion event, even though the anode has not interacted with the heavy ion directly. Even from a third person perspective, indirect (higher level) correlations are rationally acceptable. The probabilistic viewpoint comes into consideration, for no knowledge can be assigned to the causal correlation of availability of each electron independently.
An indicative calculation is in order. Let us consider the experiment described in Figure 3a. Let the number of argon atoms in the spatial confinement be N. Under a dynamic balance the number of electrons freed by stochastic processes and those that get absorbed either in the medium or at the anode balance out. Absorption at the anode causes a perturbation of current of mean size . This corresponds to a probability of release and absorption of an electron at anode per atom per unit time under normal distribution (Gaussian) to p, such that . The constant K takes care of the scale and the unit. Considering the Gaussian distribution as a limiting case of discrete binomial distribution with a probability, p, the mean and variance are given by , and , respectively. Since p is expected to be tiny for a large N and small currents, is nearly unity. Therefore, the numerical value of variance is approximately the same as that of the mean:
If the threshold current cutoff, c, is taken to be () times the mean current due to stochastic processes, , the probability, , falls off as . That is, with the release of a sufficiently large number of electrons relative to the stochastic processes, the anode current above a large enough threshold is said to represent the heavy ion event. This definition of representation has always been implicitly used in the physical sciences, which corresponds to the third person derivable correlation of a state, where the specific contexts of individual physical entities are ignored.
From the considerations of symmetry and determinism of the physical systems, the state of an energetic heavy ion passing through the ionization chamber in conjunction with the given electric field between the electrode pairs correlates with the current above threshold on an electrode pair, even before the build up of the current. It is only natural to expect this temporal reciprocity of correlation due to the structure and determinism that exist in the natural processes. That is, in relation to the experimental setup, current above a certain threshold correlates with the heavy ion event in the past, while the heavy ion event in conjunction with the experimental setup correlates with the current above threshold in the future. The limits of causality enforce the symmetric correlation with contexts back and forth in time. The only requirement here is that there must be a physical state that correlates with both the state of the heavy ion and the context of the device in conjunction. The coherent relation among the emitted electrons as a composite system apparently bears such a state.
A preliminary working definition of representation is as follows. Natural representation refers to a semantic value expressed by the disjunction of all causal correlations of an observable state description of a physical entity. Disjunction and conjunction as semantic quantification operators are discussed in Section 3.1. The emphasis here is on the semantics of class relation expressed by the disjunction operator, as worked out in Section 3.1, rather than on decoherent histories [18]. A disjunction of all possible decoherent histories would refer to a class of causal processes.
A more detailed re-examination of this event enables us to understand and construct more robust definitions. At this point, some of the relevant questions are as follows: (a) How to formulate a rationale for a symbolic expression to quantify the semantic value of correlation of a state? (b) Are there different observable descriptions of state of a physical object that correlate with different semantic values? (c) Are there descriptions of semantic values such that different observable states correlate with the same semantic value? (d) Could more abstract representation be created modularly in hierarchy?
2.2. Non-Uniqueness of State and Transmission of Correlation
The state of the anode as referred to in the previous discussion, the current peak above a certain threshold, is naturally not an unique or complete description of the state. A large number of highly specific details of an anode’s internal micro states meet that requirement. In order to determine the information, a description of the state that the electrode pair correlates with, we consider a modification to the ionization chamber experiment. It is conceivable that the electrode pair in the experiment is replaced with a two dimensional grid of isolated, but smaller, electrode pairs, as shown in Figure 3b, such that the same geometrical configuration is achieved as before. For each of the electrodes in a pair, a separate device is used to measure respective temporal current profiles. A simple sum of the current profiles on the two electrodes gives the current profile of the electrode pair, as in Figure 3a.
With the setup depicted in Figure 3b, two different kinds of coherence detection could be performed. First, the electrode pairs close to the path of the heavy ion in the horizontal plane would receive more charged particles than those away from it. A relation among specific currents (conjunction of specific values of currents) on respective pairs would correlate with the projection of the heavy ion path in the horizontal plane. Second, the difference in points in time of the current peaks of electrons and positive ions at their respective electrodes in a pair would correlate with the relative distance of the heavy ion path from the respective plates. A conjunction (combination) of the two specific sets of measurements allows the recreation of the path in three dimensions within limits, barring the direction of motion for relativistic heavy ion. Care must be taken to accept the correlation only if the sum of all currents crosses the threshold set for the unified detector, as shown in Figure 3a, to limit the consequences of fluctuations due to stochastic processes.
Now, one can imagine combining the nearest four electrodes into one, as shown in the figure, and trying to determine the trajectory. The extra details of the trajectory would be lost, i.e., the tolerance on the trajectory of the heavy ion is much larger now. This is attributed to the disjunctive relation among all possible current profiles of the earlier four elements in each of the integrated electrodes; it is indistinguishable as to which of the earlier four elements contributes how much of the current. Similarly, one could keep on reducing the number of electrodes by joining the nearest four to get back to the same state as shown in Figure 3a. In the process, the details are gradually lost to a level where no information is available on the trajectory of the heavy ion. The unified current profile is equivalent to a disjunctive relation among all possible conjunctions where each conjunction is a specific set of causally possible current profiles of elemental electrodes, erstwhile correlating with different specific trajectories. In the way that a state of integrated electrode is describable as a disjunction of specific current distributions on elemental electrodes, the semantics of correlation also corresponds to the disjunction of the semantics of correlations of the respective current distributions, i.e., the specific trajectories. Therefore, the resultant state, described as ‘a current profile crossing a threshold’, correlates with the disjunction of all possible trajectories, which makes it independent of any specificity with respect to the trajectory. The state continues to correlate with ‘the occurrence of a heavy ion event’ but without any particular dependence on specific trajectory, as was the primary intent of the experiment. The process described here captures the description of a state as a disjunction of conjunctions of elemental values, as well as the construction of a generic semantic value from elemental values of specifics by the same expression. It establishes a mechanism to comprehend the semantics of correlation of a macro state, in terms of the disjunction of correlations of ensemble of micro state configurations.
Taken to the microscopic level, with respect to the experiment depicted in Figure 3a, a noteworthy point is that the observable consequence of the coherence among the electrons is the distinction between the two states of the anode, whether the current measured is above or below a threshold. Let us say that an accumulation of at least N electrons are required within the time interval of measurement to build the threshold current on the anode. Let us also presume that the number of primary electrons released in the interaction with the heavy ion is K, where . The context specific to individual electrons may not permit its accumulation at the anode within a given period, such as absorption back into the medium or direction of motion away from the anode. Some electrons may even cause the production of secondary electrons or the time of release and transmission may not fall within the given period of measurement. An accumulation of electrons within an unit of time makes the anode cross the threshold, activating the measuring devices and . A few of the noteworthy points are as follows:
- While the existential state of the anode at the moment of measurement must correlate with the conjunction of specific correlations of states of M electrons which, in reality, converge on the anode, the state of the observing device, , even intrinsically, can not distinguish between the accumulation of N electrons or more on the observed anode.
- The device, , functions as a filter responding to certain state description of the anode that is neither comprehensive nor absolute. Similarly, the observed state of the anode depends on the electron’s state of availability within spatio-temporal limits; the energy-momentum component remains irrelevant to this state description. All PSRs, microscopic or macroscopic, function as filters, selecting only certain relative measures. Therefore, with respect to the correlation with information, a default comprehensive description of state of a PSR is immaterial and irrelevant—it is the observed state that remains relevant.
- As per the natural limits of causation, the active state of also must correlate with what the threshold current at the anode correlates with. The transmitted value of the semantics of correlation from one physical entity to another is dependent on the limit of state of one, as observed by another—the greater the specificity of the state observed, the more specific its transmitted semantics of correlation is.
- The state description of the anode as observed by can be satisfied by all combinations of N or more electrons accumulating during the period of measurement. Each combination is a conjunction of specific set of electrons. Therefore, the active state of correlates with terms in disjunction, where each term evaluates a conjunction of relevant states of subsets of greater than or equal to N electrons. The disjunctive relation is not equivalent to the conjunction of M electrons; therefore, the semantics of correlation of the observed state is not equivalent to that of the comprehensive existential state of the anode.
- Each combination of N or more electrons together must correlate with the conjunction of correlations of their specific states relevant for their convergence. The disjunction of such conjunctions makes the semantics independent of individually specific correlations of electrons and of their conjunctions, where each conjunction correlates with the heavy ion event. Therefore, the state of is said to represent the generic semantics of the ‘heavy ion event’ but without the particular correlations of electrons and their conjunctions. Here, the usage shows a distinction between the terms ‘correlation’ and ‘representation’, while the state is said to correlate with each conjunction, but it represents the value of disjunction of all correlations. This forms a mechanism to transmit the semantics of relation among the states and their respective correlations but without the specifics of states. Correlation is a more general term than representation, since correlation may also refer to the value represented by a state.
- A ‘heavy ion event’ is a generic, but constant, discrete semantic value which does not describe a real unique physical heavy ion or a real physical process, because the ions with a range of states and events with different specifics are all be referred to by the same value. Yet, even in scientific parlance, it is usually taken to be an objective description of physical reality. In fact, it describes an object (a process) corresponding to a common noun semantic value, an equivalence class. While the primary aim of the experiment is to detect the ‘heavy ion events’, that happens to be a class description, not an element of physical reality.
- The interaction of a heavy ion with the atoms, and of the electrons with the anode, causes the creation of a relation among the interacting entities, the PSRs. Every physical entity (PSR) plays the role of an observer, specific interaction as the mode of observation, and causally accountable descriptions of interacting entities as objects observed. Under a quantum mechanical consideration, an interaction is complete when decoherence occurs; therefore, the separation of the observer and the observed has no issues here. A PSR acquires a relative identity due to differential causal accountability. One may refer to Chris Fields [19] for a discussion on other notions of what constitutes an observer.
- Let us consider two possible instances for the threshold activated device—one, which turns active when N or more electrons accumulate within the specified time, , and another, when M or more electrons accumulate in the same period of time, . In the case considered, the anode receives M or higher number of electrons activating both the devices. Descriptions of specific configurations of physical states or processes that could not cause sufficiently greater than N electrons to be deposited in the given time duration to activate , then the class of such states, C, would negatively correlate with the state of the anode, which indeed receives electrons, and with the active state of . Class C may include specific combinations of high energy ions in conjunction with specific lower densities of the argon gas. However, the instances of the same class are positively correlated with the state of the device that activates with N electrons only. If the purpose of the experiment is merely to count the events, then detects more events than , i.e, the active state of is more specific than that of . Moreover, the instances that negatively correlate with correlate positively with for the same experiment. Furthermore, a conjunction of these two correlates must conform to the one with greater specificity, whereas a disjunction of the two must correlate with the one that encapsulates both, since it is not guaranteed that the more specific correlation is the one that caused the result of the disjunction; the less specific correlation always encapsulates the more stringent limits. Therefore, while a conjunction of the two yields a negative correlation with class C, the disjunction yields a positive correlation.
A general statement on the transmission of semantic values on interaction is as follows. The state description of a physical system as observed by another is equivalent to the disjunction of all possible conjunctions (configurations) of elemental state descriptions that can cause, observably, the same indistinguishable state of the observing system. Similarly, the semantics of correlation of an observed state within limits is equivalent to the disjunction of the semantics of correlations of all causally indistinguishable configurations of elemental states. Since the observing system is a part of the same interaction, the correlation of its a priori state forms part of the conjunctive terms, serving as a contextual constraint. The statement of transmission holds good for all interactions at the micro or macro levels.
2.3. State as a Non-Discrete Value and Its Semantics of Correlation
Given the fundamental nature of this work, which seeks to establish a basis of the relation between a state and the semantic value represented by the state, it is as imperative to develop an understanding of state as it is for the realism of the represented value. Even though the term ‘state’ is one of the most basic units of description of the physical world, a concrete definition of state in physical sciences does not exist. In this work, one may not make a presumption of the notional meaning of a state—it needs to be established from an even more fundamental consideration of the emergence of definable state. Since the concept of state is always associated with a physical entity, we cannot define one without also referring to the other.
For our purposes here, the constitutional definition of a physical entity is as follows. An elementary physical entity is constituted of a quantifiable resource that enables it to effect an observable change—the form of the resource affords it an accountable and referable identity bearing a quantifiable and modifiable ‘coherent state’ where a change effected by the entity is accounted for by quantitative change in state. The emergent quantifiable resource is labeled as ‘energy’. This resource is exchangeable in quanta, but it can never be zero without a loss of identity. All physical interactions are temporal events without exception—a real interaction is not possible at an instant of time. Therefore, a measurement captures only an emergent property that is attributable to the whole process that takes place over a time duration. The term ‘coherent state’ is a generalized reference to a state due to the indistinguishability of internal dynamics, temporal evolution, or of internal coherence among elements of a physical entity over the course of interaction. In this text, the term ‘state’ refers to ‘coherent state’ as opposed to existential state. A structured or composite physical entity is constituted of relatively more elemental physical entities, such that in an interaction, it exhibits an observable coherence among its elements to afford a referable identity for the unified whole. Such an identity necessarily entails a degree of variability in its detailed internal structure that allows for the same observable consequences. A state of the composite entity refers to the qualities of this emergent identity.
A component state of a physical entity refers to an associable measure of a quality or of a relation within limits, classifiable under a parametric space, that may effect an accountable observable consequence. With respect to an yet undesignated state, a parametric space is defined by an inferable class of measures, where different relative measures for the state relate to different relative measures of the consequence where the medium of interaction is always physical. Examples of parametric space include charge, mass, momentum, color, shape, coordinates in space and time, orientation, etc. As is evident, each of these is inferable from the observable class of effects. Therefore, they can only be referred to as emergent. A state then refers to a relative measure within the parametric space, which can also be thought of as an instance of a class of values. A parametric space, therefore, is an arbitrarily definable domain of values which offers classification and differentiation among the states or results of interaction. Therefore, the classical or quantum description of states emerge from the same process of accounting for their consequences. Parametric spaces are not necessarily independent of each other.
The only way that a descriptive relation in the degrees of a quality of state can be meaningfully constructed is based on the relation in the consequences they cause in their interactions. Under a given context and mode of interaction, the states are distinguishable if the results of interaction are distinguishable. A model of a relation among the consequences allows a relation to be modeled among the states of the interacting objects and the context, which must be such that the model remains uniform for all interaction types and contexts. In a given context, and with respect to the resultant state of a physical entity, different processes or states of interacting physical entities may exist that could give rise to the same resultant state.
Nature does exhibit the equivalence of states and processes at all levels of interaction. For example, a spherically symmetric distribution of charge/mass generates the same effect at a distance that is caused by another similar distribution of equivalent charge/mass with a different radius centered at the same point. It is indistinguishable whether an object is under acceleration or is in the neighborhood of a suitably distributed mass. Quantum systems exhibit inherent uncertainty and ambiguity. For example, conjugate observables are not simultaneously determinable with unlimited precision. In Figure 2, the detection of a photon on one detector does not disambiguate the source, and when the source is known, it is not predictable which path a photon would take at beam splitter or which detector would receive the photon. The model-dependent descriptions of states within the limits of observation are indistinguishable. That is, the states modeled as a point on a real line with arbitrary precision can only be the artifact of the model. In other words, the quantification of states can only be performed with measurement of the resulting states of an interaction, but the resulting states also suffer from the same limitations of state determination.
As concluded above, a state description is non-discrete and never absolute with infinite precision in any physical state spaces. Here, the term ‘value’ for a state of a PSR is always used in this sense which includes a width of resolution or a zone/range of indistinguishability in a parametric space, as limited by the causal relation. This value is never intended to be a discrete point with respect to a state, unless specified otherwise in the text to allow certain logical conclusions. Even if a state, as conceived of in the physical sciences as a discrete value, may not be absolute in reality, by virtue of the equivalence of state descriptions or their inter-relations within limits, an element of semantics of correlation could still be the same for all equivalent states or relations, which could even be a discrete value, as noted earlier and exemplified by the ‘heavy ion event’. A state description includes contextual relations, as discussed in the next section. While elementary physical entities exhibit a much larger degree of relative uncertainty in their measurements, ensembles of a large number of elements in a coherent relation or as a structured entity may exhibit measurably stable and nearly discrete macroscopic states, as modeled in classical physics and thermodynamics. Such macroscopic state descriptions, in turn, correlate with sufficiently stable semantics, as is the case with the coherent beam of electrons in ionization chamber experiments. For a large number of components functioning coherently together, active neural states are nearly discrete and distinguishable from the default state.
In this work, we attempt to establish the limits and mechanisms of the transmission of information with interactions, rather than determining the a priori correlation of a state. Neurons in a neural system select or respond to only certain correlations among their evolving states.
An electron is knocked out as the result of an interaction with the force field created by the passing heavy ion. The electron responds to the qualities of the force field and gains a certain state of energy and momentum while leaving the ionized argon atom in recoil. In fact, a heavy ion with different energy and trajectory could have also caused the same transition of state of the electron. Are all combinations of charge, mass, energy states, and trajectories of the heavy ion equally capable of causing this transition to the resultant state of electron? From prior knowledge of physical processes, the answer is clearly in the negative [17]. In fact, from a simple application of mechanics, if the specific state of the electron is conjugated with the specific state of the ionized atom in recoil, the correlation limits of the heavy ion narrow down considerably. Therefore, the existential state of an electron even intrinsically correlates with a range of values of heavy ion states. Noteworthy points are as follows: From the perspective of the resultant state of the electron, all causally permissible states of the heavy ion are non-differentiable, even though the probability of occurrence of one parametric combination may be different from that of another. These combinations of parametric states of heavy ions form an equivalent class of positive correlations. Similarly, the combination of parametric states of a heavy ion that cannot effect this transition form another class of negative correlation since the transition has occurred.
The probability distribution of correlation with different possible processes and states is not represented by an observable resultant state of an interaction. The probability distribution is the result of a model building exercise aggregated over a sufficiently large number of observations. This is one of the aspects where the treatment of semantics of correlation differs from the way it is done in the physical sciences. An element of reality remains uncorrelated with a state unless the element has direct causal effect on the state.
A model of the states of a heavy ion could be constructed either classically, in terms of charge, mass, energy, etc., where a quantitative value of a state could be described with a width of resolution, or quantum mechanically, in terms of a wave function or in terms of a vector space conforming to the superposition of states. With respect to the limitation of state determination and the corresponding limits on the semantics of correlation, as stated above, the specific choice of formulation of a state description becomes immaterial for multiple reasons. First, the superposition and the wave function description do not form an observable reality of states; they are model descriptions that provide a mechanism to predict the possible outcomes of observation. Only observable states are elements of reality. Moreover, intrinsic correlations are based on causally limited descriptions of state of one as observed by another, which has no model dependence. In fact, a model emerges from the interpreted requirement of constancy in the cause and effect relation, as determined by an external agent based on limited access to the existential state. Second, in contexts where a state description includes multiple possible outcomes if observed, the correlation itself is describable as the disjunction of observable states which already takes into account such considerations of state description. Third, a definitive communication of information may occur only when the observation is completed (post decoherence). The observed state must be an accountable element of the reality of nature, irrespective of a model description. The EPR-like [20] consideration does not apply here. The point to note here is that given the description of semantics of correlation in terms of the disjunction of all possible observable states, the correlation with a model state described in terms of the superposition of quantum states does not need to be defined as superposition of semantic values. Moreover, as noted in Section 6, deterministic unitary evolution does not alter the correlation. Furthermore, a superposition is replaceable with the disjunction of all causally possible observable outcomes. In fact, the description (model) of the superposition of states in itself is one of the possible semantics of the correlations with the existential states.
The lack of independent or absolute reference frames of physical states grounds the system of representation purely on the constancy of relations; hence, a state can only be referred to as an emergent value. Indeed, the emergent values may have direct correspondence with the EPR-like reality, but since reality is not exactly measurable, it is impossible to assert. All measured values are derived from the same principle of constancy of causal relations, which does not require one-to-one mapping between the cause and its effect. For instance, if the number of possible states (values) for A is , and for B it is , but if the total number of causally possible combinations of states (values) is less than the Cartesian product , then they are related. Even though, for a given state (value) of A, B can have one of multiple possible states (values), a constancy of relation still holds, since a state of A fixes the state of B within a limited class and vice versa. The limit of uncertainty in the measurement of conjugate quantities is one such relation.
2.4. Relative Measures Form Elements of State Description
The reality of information that conveys semantics is based on the relation among the states of PSRs that result in observable transformation (change). For example, the observable state of an anode is the result of specific spatio-temporal relation among ejected electrons and the anode that form the basis of correlation of the anode’s state with the heavy ion event.
In the physical sciences, a state not only refers to the modeled fundamental or emergent qualities of physical entities that are responsible for causing interactions under the influence of force fields, but also to the relative measures, such as spatial and temporal placement, orientation, momentum, etc. While maintaining this norm, we extend it to all possible contextual and relative measures that can be determined to have an effect on the consequence of an interaction. For example, even though the spatial separation between two entities cannot be assigned as an element of state of any one of the two entities without a reference frame, relative to each the location of other can be assigned as the state of the other as observed by the first. That is, the perspective of the state of the other PSRs is relative to the one under consideration. In fact, even the polarity or neutrality of the charge states of interacting entities is relative to the PSR under consideration. This method allows for the creation of a reference frame relative to each of the PSRs respectively, such that the relevant elements of the context form elements of relative state description.
Consider, for example, the observed macroscopic state description of an anode. The current above threshold is not sensitive to, or dependent on, the energy and momentum state components of electrons. Therefore, the observed state of the anode bears no correlation with the specifics of semantics exclusively associated with these component states of electrons. In the same instance, the observed current within a given limit of time is the result of the selection of electrons in a specific relation among themselves, and with respect to space and time. As noted earlier, the relation creates an identity for the group of electrons as a coherent entity. The same number of electrons may accumulate at the anode over a longer period of time, which does not bear so restrictive a correlation in the universal scope. That is, the electrode pair in conjunction with the observing device acts as a relation filter to pick only the electrons available in a localized space and time. While this contextual limit remains irrelevant for the state description of an electron in isolation, the same limit forms a necessary element of state description of such electrons with respect to the specific resultant state of the anode.
The term ‘interaction’ serves as a label for the relation of transformation from a set of state descriptions to the next or resultant set. Therefore, from the perspective of a resultant state, an interaction is necessarily describable as a disjunction of conjunctions of elements of state under the limits of natural causation. Hence, this expression forms the basis of all emergent semantics associated with the resultant state.
In conclusion, in an interaction, a PSR P selects, and therefore responds to, certain specific relative measures among the states of interacting PSRs. It is noteworthy that P’s response is based on the relation among states, not on what semantic values the states correlate with. It is the states that interact, not the information represented; therefore, information remains non-measurable and subjective. However, since the information arises from the objectivity of the natural causation, the causal power of the states in a context gets translated into causal power of the represented information. Moreover, the states in correlated contexts may share elements of correlated information as the electrons in a spatio-temporal relation share a contextual relation with the elements of heavy ion event. This coherence in the semantics of correlation of the respective states of electrons is termed the ‘semcoherence’ of the states. The profile of correlation of the resultant state of a PSR must reflect the selected relation among the interacting PSRs. As discussed below in Section 3.1, the disjunction of conjunctions of selected states achieves this. Space and time constitute two of the most natural and fundamental contextual relations that cause the emergence of semantics of universal localization. Therefore, it may be suggested that the neurons in a neural system may build and enforce temporal synchronization among the states of the neurons that semcohere with the prevailing constancy of relation in the context.
3. Symbolic Interpretation of the Semantics of Correlation
The semantics of correlation are dependent on the parametric context of states selected by an observing system which can be arbitrary and unlimited. Hence, a functional description of the unique or complete semantics of correlation of a physical entity is not always possible. However, systems with elements of nearly discrete states in limited contexts may exist, where the observations are based on such limits—e.g., neural systems and artificial digital systems. Therefore, we limit the discussion to the correlation with a specific state, rather than with a PSR in general.
A correlation is describable as a multi-dimensional profile. A profile of values in a parametric space is defined by the limits of positive and negative correlations with the state under consideration. We may denote a semantic value by a symbol, x, in the parametric space, X. An n dimensional value is described by , corresponding to n dimensional space, . Then, the question we ask is what may constitute a general method to express an n dimensional correlation? As noted earlier, the expression, ‘disjunction of conjunctions’, forms the constructor of the semantic values. It also immediately suggests how the correlation profile may propagate with each interaction.
One way to express the semantics of correlation, C, is to use a function of n dimensional semantic space as n arguments for semantic values, as shown in Equation (2); the function can take one of the three values, Positive, Negative, or Null. A simple interpretation of the function is a conjunctive relation among its arguments. A value of Positive for C implies that the conjunction of arguments correlates positively with, or is in consonance with, a state, S—a value of Negative implies an anti-correlation or dissonance, while a Null implies no (null) correlation. Consonance refers to the fact that the history of physical interactions that gave rise to the state, S, under consideration, also formed the basis of the emergence of semantic value C, as per the method laid down here; dissonance refers to the incongruity between the two. The observed state of anode could be the result of certain combination of values of charge, mass, energy, and momentum states of heavy ion, while the state could not have been possible for certain other combination of values. This form of function description is stated to be symmetric with respect to n parametric spaces.
In addition, it is noteworthy that for given values of charge and mass, the energy range of a heavy ion that may correlate with the anode’s state description may be different from when a different values of charge and mass states are taken into consideration. That is, the correlation range in one semantic space depends on the semantic value under consideration in another. In other words, the state of the anode correlates with a relation among semantic values in different parametric spaces. For this reason, a functional form is better suited. Given a set of semantic values in any of the domains, the function expresses the range of correlation in the remaining nth space (Equation (3)). This is referred to as the asymmetric form where one parametric space is isolated from the rest.
where C is a correlation function, and denotes a value within the space, . The function’s value is denoted with binary numerals {01, 00, and 11} which are to be interpreted as symbols for positive, negative, and null correlations respectively. The additional significance of this symbolic method is discussed below, as well as in Table 1 in Section 3.1. The following points are noteworthy for proper interpretation of the expressions.

Table 1.
The table specifies the results of conjunction and disjunction as binary operators on two correlation values, Corr1 and Corr2, that refer to a correlation with the same semantic value irrespective of the type of the value. Therefore, the entire range of semantic space under consideration may be accounted for as elemental ranges of values of overlap to determine the results of conjunction or disjunction operators. While the table gives comprehensive results for the conjunction operator, it falls short in quantifying the abstraction as a result of disjunction, as discussed in the text.
- A given set of arguments merely covers one possible instance within the limits of all possible correlations. In addition, the state description of the PSR under consideration may itself be one of the parameters in the list expressing the correlation of the state with other values in the list.
- In order to have all objects represented in complete generality, the parametric space and its respective argument values may come from all realities and all expressible semantics.
- It is possible though that a state may bear a positive correlation with a contrast relation among semantic values; this is not to be confused with the positive and negative correlations with the contrasting values. For example, active states of some retinal ganglion cells may positively correlate with either on-center or off-center receptive fields [21,22] that bear contrast relation between the center and the surround in the field of view. Yet, this is not the same as the positive correlation with the center and the negative correlation with the surround or vice versa. However, it may be true that a positive correlation with an on-center contrast relation may imply a negative correlation with the off-center relation. This is equivalent to the statement that if a state correlates positively with , then it bears negative correlation with .
In order to take note of the correspondence that the functional form of expressing correlation bears with mathematical functions, we consider the graphical representation of a generic function, , where x is an independent variable. The linear function shown in Figure 4 depicts only a special case of what the asymmetric form of correlation in Equation (3) expresses. First, asymmetric form also identifies the semantic range that correlates negatively. Second, the range of values is non-probabilistic, so there is no need for error bars. Third, the values in the parametric space for x may be discrete or non-discrete arbitrary ranges, similar to the values in y. Fourth, the values for x or y may emerge from arbitrary domains of abstraction which may not be directly quantifiable, except for symbolically from their respective consequences.
Figure 4.
The figure shows the correlation profile of an active state of a system on the y-axis in the context of orientation of a line presented to the system, as denoted on the x-axis. While this may be a trivial example where the domain and codomain are same, it serves to illustrate the difference from function-based representation. The color bands on the vertical bars represent the extents of values in a domain that correlate with the state of a physical entity in the context of a value in another, as represented on the x-axis. The green band indicates the range of positive correlations, while the blue band designates the negative correlations. The line in red represents the value of the function at respective x-values. The data is taken from a run of the simulation, as presented in Section 7. Here, the x-value represents the orientation of an object in discrete steps of 1 degree of arc in the field of observation, while the different ranges on the bar shows the correlation bands of the state.
The symmetric form merely includes the value of in the list of arguments, , for which there are only three possible values, as listed in Equation (2). Here, denotes a value in a multi-dimensional space.
The processing of information in the physical domain allows a method of direct mapping of values from the dimensional space to the nth which encapsulates the functional form within limits. There is no restriction on the types of values or semantics of objects that are mapped. This method of mapping may, in fact, be achieved in an evolving physical system, to create modules in hierarchy. Schematically, Figure 5 depicts one such mapping of two variables, the distance and incident angular size of a physical object at an observer, to the emergent constant size of the object. This mapping scheme directly corresponds to the method of disjunction of conjunctions discussed here. It is apparent that all expressions of mathematical equations and functions can be mapped in this scheme with a finite limit of precision. Moreover, a coarse coding method of mapping may achieve much greater dynamic specificity of values, as shown by a simulation presented in Section 7.
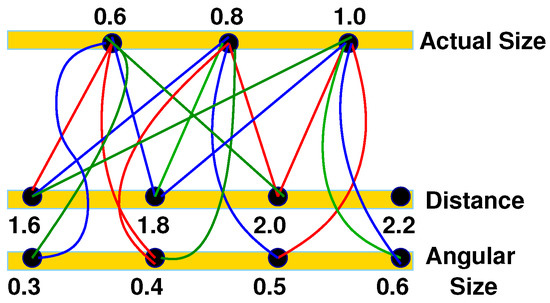
Figure 5.
Schematic of a mapping from two variables, distance and angular size, to the emergent constant size of an object. The yellow bands show parametric spaces, while a black dot within the space represents a range of values. A convergent mapping in the same color onto the dots in the upper band represents a conjunction of values in distance and angular size that map to the resultant value in size. The convergence of multiple color combinations on the same dot represents terms in disjunction.
The method further allows for an n-way processing, where given any of the values, the map yields a correlating value in the remaining space. In a more general sense, values in the space may map to sets of values in the remaining m space. Furthermore, it allows the inverse even for one-to-many and many-to-one mapping going beyond the limitations of a mathematical function. A noteworthy point is that one or more of the parametric domains in Figure 5 could be time or a function of time. Like all other parametric spaces, the values here can also be relative to some arbitrary point, T, such as . Like all other values, can have variation within limits. The mapping then corresponds to a temporal process. For a re-entrant system, this may function as a predictor of context at future times.
3.1. Conjunction and Disjunction as Semantic Quantifiers
If the states of physical entities must represent universally all semantics, then we must also expect a method of expression that is universal. Here, the qualitative and quantitative function of conjunction and disjunction as operators are shown to encompass all expressible and referable semantics. The emergence of abstract objects (semantics) is especially quantified, which establishes the basis for universal expressions.
There are two basic forms to express relations that describe objects. First, an object is described as a common entity among its manifestations within the objects of greater complexity, we refer to it as a top-down method. In an extreme form, the method allows the description of most fundamental indivisible objects. A visual point or a structureless electron can only be described as a common elemental entity bearing certain relations with other entities within encapsulating systems. Second, an object can also be described as a structured relation among its components; we refer to it as a bottom-up description. Either method is shown to be potent enough to build descriptions of objects at all levels of complexity in terms of relations.
We begin by taking note of the fact that the specifics of all descriptions are expressions of the conjunction of values in one or more parametric spaces. The greater the number of elements in conjunction, or the narrower the limits on the semantic values of individual elements, the greater the specificity is. Here, a semantic value refers to an arbitrary object (including temporal events/relations); therefore, a conjunctive relation does not pose any limitations to the descriptive power of arbitrary semantics. We may reach the same conclusion of specificity if we consider all physical entities, relations, processes, and representations as generalized objects. Then, all specifics, without limitation, can be described as the conjunction of such objects. A generalized object is one where the specification admits more than one instance in the scope of all expressible semantics. In fact, it is apparent that given the arbitrary consideration of parametric spaces, a description can never be stated to be uniquely complete. Therefore, the assertion of greater specificity with the inclusion of each independent element in conjunction forms a trivial conclusion. For example, a specific paper is describable as a conjunction of properties (objects) that are specific values of physical material, weight, size, shape, thickness, coordinates in time and space, color, texture, reflectance, its particular movement in air under free fall, and the purposes that it serves. Apparently, each of these values (objects) is describable as an abstraction of a certain relation, either in a bottom-up build up from the respective constituents or as a common class description among higher level complex objects. The specificity is naturally higher when more independent parametric spaces are added to the list.
In contrast, a generalization can be expressed as a disjunction of multiple possible specifics within the limits of respective domains that removes the dependence on the particularities of the specific values—recall how the specification of heavy ion trajectory information is lost, as depicted in Figure 3. A disjunction operation generalizes the description, creating a class, a common noun object, serving as an inverse to the conjunction operation. For example, the term ‘paper’ describes a disjunctive relation among the values in each of the domains of material, shape, size, thickness, color, texture, and coordinates in time and space. Large variation is tolerated in each domain giving rise to a class of equivalence. Similarly, ‘velocity’ is an object that expresses a relation without any specification of entities in directed motion or even the quantum of displacement per unit of time. Similarly, the ‘accumulation of electronic charge on the anode’ refers to a process (a temporal event) without the specifics of the times and points of incidence, momentum, and energy of respective electrons.
The expression in Equation (3) describes a correlation profile with limits on values with either positive or negative correlation; the modeled values of null correlation are not a part of a profile, because from the perspective of the observed state of a PSR, there is no dependence on the domains or range of values for null correlation. The semantic description of an object corresponds to the internal and external relations among objects in the universal scope, where each component of a relation functions as a constraint. The semantics of conjunction of a set of correlation profiles specifies an object that satisfies all constraints, which naturally describes an object that is more specific than individual elements, unless the profiles are all identical (Figure 6). If two correlation profiles overlap in a parametric space, then the conjunction specifies an object with a narrower positive correlation where both have a positive correlation, and a wider negative correlation where at least one has negative correlation. On the other hand, when the parametric spaces of correlation are different or the limits are non overlapping, i.e., in a given range of values only one object bears a positive or negative correlation, while the other has a null correlation, the conjunction yields a correlation overriding the null, effectively extending the scope of the parametric space and the constraint towards a more specific description.
Figure 6.
Illustration of the functions of disjunction and conjunction. Left: When a rectangular object (e.g., a paper) rotates about one of its vertices, its four edges sweep through different orientations. The conjunction of two neighboring edges is shown in one color in the lower left corner; its mapping on the orientation space (displayed vertically) is shown as a pair of horizontal lines. A disjunction of all such conjunctions that cover the entire space specifies the orientation-independent right angle, an abstract quantity, that is physically a non-realizable object. Right: The results of the conjunction on the correlation profiles in the orientation space are shown with two examples. Each horizontal color bar represents a correlation profile of an active agent (say, a neuron) in the orientation space. The correlation index is shown on the top (green: Positive, blue: Negative, gray: Null). All color bars cover the same range of orientation space with a resolution of 1 degree of arc. The rest of the space extending to the left and to the right of the bars bears a negative correlation. The result of conjunction on the columns of values is displayed below the black line in respective diagrams. The data is taken from a simulation, as presented in Section 7. In fact, the results stay consistent, even when each column within the band of values is taken from arbitrary different semantic spaces or when the bar represents a continuous range in a space.
In contrast, the disjunction of two or more profiles specifies an object that does not necessarily depend on the specifics of individual profiles. The resultant object can only be formally described as the disjunction of all profiles, each serving as a term in the list. When one of the two correlations is positive, while the other is negative, for a given range of values, the disjunction results in a positive correlation, as discussed above with the two threshold triggered devices, and . While it may hold true for most parametric spaces that the negative and positive correlations cover the entire space or have no correlation at all, here, we do not presume so, since the process of evaluating the results of conjunction and disjunction remain transparent to the null correlation sharing the space. That is, a negative correlation with a range of values is not necessarily, or in general, interpreted as a positive correlation with the complement of the range in a parametric space, since that would demand an explicit correlation with the entire parametric space. That is, the expression of the semantics of correlation with positive and negative values is not equivalent to in propositional calculus that is always true. Similarly, when one of the two profiles specifies a positive or negative correlation with a value, while another bears a null correlation with the same, the disjunction simply disregards a particular dependence on (correlation with) the value. We ask, if there exists an expression that the semantic value of the disjunction of profiles necessarily satisfies, then it can only be a class description, a relation that exclusively includes each of the correlation profiles as particular instances of the class. If the terms in disjunction include all possible values in a parametric space, then the disjunction specifies a complete class of equivalence with respect to the space, where all instances within the space are admissible without explicit dependence on any particular value. The complete class is akin to the ‘for all’ quantifier in predicate logic. For instance, the term ‘right angle’ describes a complete class relation with respect to orientation space; the semantics of ‘right angle’ do not depend on any particular orientation of the lines, as long as the relation between the lines is constant at a right angle. Similarly, the term ‘angle’ specifies a relation between two lines without any particular association with relative angular distance or the orientation of lines. Even though the class does not depend on any specific values in particular, an instance must depend on one of the values of the class—e.g., ‘right angle’ is an instance of class ‘angle’. A description of a relation that admits more of the instances than are particular to a given disjunction, the class is referred to as a superclass (with the prefix super), whereas the relation that admits fewer instances or a subset is referred to as a subclass. Similarly, if a class description includes only as many values as there are in a disjunction, it may be especially designated as a ‘proper class’. For example, the ‘heavy ion event’ is a superclass description for the events that take place in the ionization chamber experiment, since it is not limited only to the instances of actual events that have taken place during the run of the experiment, yet such class descriptions are taken as meaningful descriptions of the events that ignore the variety of limits of actual observation. In a top down reference to an object in a neural domain, a neuron often admits more instances of a class than observed. Andrei [23] notes the function of ignoring information to form categories, but only via signatures of probability distribution, not via the mechanism of disjunction.
A correlation profile that includes either a wider range of values within a domain, or that includes specific attributes from fewer domains, specifies a relatively generic object that includes a multitude of possible instances. In contrast, when the permissible range of values within a domain is narrow, or specific attributes from other independent domains are further associated with a profile, this describes relatively a more specific object, effectively with fewer possible instances. With this rationale, a contour is more specific object than a component line segment that does not impose any limits on the kinds of contours, objects, and contexts that the line segment could be a part of. In this sense, a structured object is always more specific than a component which includes a relation that holds among the elements of the structure. Therefore, a reference to an object as generic or specific is relative to the context. That is, given the arbitrary nature of parametric spaces, superclass and subclass descriptions are always possible for all objects.
The semantics of conjunction and disjunction as quantitative binary operators are shown in Table 1. Notably, the operands are correlation values {01, 00, and 11} that designate positive, negative, and null correlations, respectively, with the arbitrary semantics of the context. That is, conjunction and disjunction serve as semantic type independent operators—the operands may refer to any object in the universal scope. In addition, the disjunction causes the emergence of a class that forms an implicit type, as shown below.
A few additional significant properties of correlation values {01, 00, 11} in mathematical and computational terms are as follows. With this binary representation, the results of the conjunction and disjunction operations can be computed with the binary AND and the binary OR (inclusive OR) operations, respectively. This allows for a simple method of evaluating the semantic correlations of arbitrary expressions with these operators, as aptly used in the simulation of propagation of correlation in Section 7. Moreover, the set of correlation values {01, 00, 11}, together with the conjunction and disjunction operators, bears the following properties and structure. The set is closed, commutative, and associative under both the operators independently, and the conjunction is distributive over disjunction. In fact, the same properties also hold for any set of one or two values, since the conjunction or disjunction on two correlation values always results in one of the values in operands. Null is a conjunctive identity without an inverse, and Negative is a disjunctive identity without an inverse.
There is, in fact, no need for an unary negation operator as the negation is inbuilt in the values of the operands. Functionally, the negation of a semantic value is equivalent to the negative correlation with the value. Even in cases where the states of two different entities form an exclusive existential relation—it has the simple interpretation of a default correlation of one in conjunction with the negative correlation with another. Because Null is a default correlation as well as a conjunctive identity, the exclusivity of semantics can always be interpreted as a conjunction of Null and Negative. This form of negation is already in use in the digital (as a NOT gate) as well as in neural (as an action of inhibition not resulting in superposition) systems.
For simplicity, we consider the neural system of the brain where the neurons serve the purpose of PSRs and their action potentials (APs) as states that correlate with semantic values. APs do not constitute static states of neurons that can be observed any time other than when it is active, i.e., the specificity of the moment of time forms a critical limit of the state description of a neuron. Therefore, it may carry very specific correlations of the moment as a result of re-entrant activity into the network, even though the neuron itself may have selectivity to a broad range of values as well as sensitivity to multiple domains [24,25]. At a given point of time, a neuron’s AP may bear positive and negative correlations with limits of values in width, length, orientation, and location of a line segment. A conjunction of such limits from synchronized activities of neurons may evaluate to values with greater specificity of a line segment. A disjunction of a number of such conjunctions of groups of neurons evaluates to the base class defined by the qualities of a line segment common to all conjunctions, but without any dependence on particular correlations of specific neurons and their particular conjunctions.
In order to formulate the emergence of abstract semantics more formally, we review the disjunctive relation from a different perspective. Consider and as infix binary operators of conjunction and disjunction, respectively, with having higher precedence:
The expression expresses the object p without an explicit dependence on any one of the s. If s form instances of objects in an object space, and p is a relation that holds for all, then the expression describes a generic object, p, independent of the specific instances—the way ‘right angle’ is independent of a specific orientation (Figure 6) and ‘heavy ion event’ is independent of a specific trajectory or identity. For clarity, the expression may be compared against an expression in propositional logic, . Here, the equivalence of is achieved by the enumeration of all possible values or the entire range not covered by q. In fact, p need not be an independent object to begin with, as long as the property/relation, p, holds for all objects in disjunction. For instance, if a conjunction of two adjunct lines is represented by , while the object, a non pre-existent, independently referable semantics of the ‘relation of a right angle on two lines’, is expressed by p, then expresses an instance of a right angle. Hence, the expression expresses a class descriptor, p, an abstraction of a relation between two adjunct lines. For the emergence of p, the instances must be referable objects. The relation, p, serves as an equivalence class, to which the specific instances belong as members. The noteworthy points are as follows:
- The s are not necessarily discrete, making it more general and potent to represent entire object space with a finite number of elements.
- The expression permits overlaps among the profiles of s, again enhancing the generality and the scope for achieving arbitrary precision.
- The list of s may not necessarily cover the entire space to form a class, even though a partial class allows for representation of abstract objects within the range of observation at the cost of completeness—a good method for observing systems to build abstractions that do not have access to the entire space or when entirety of space is undefined.
Now, if for a specific network of a neural circuit, a neuron gains an active state only when one or more of the instances of right angles are present in the context, irrespective of their orientation and placement, then such a state naturally correlates with the disjunction of instances of a ‘right angle’, an orientation and placement independent semantics of ‘right angle’. This exemplifies a bottom-up reference to the abstract semantics of ‘right angle’.
A referable disjunction of objects, where each object is described as a conjunction of elements, makes it possible to refer to the semantics of an abstract object as a symbol. This makes an implementable potent mechanism available to represent and refer to the emergent semantics, i.e., the method of forming a disjunction in itself becomes the process of abstraction. This is what the neural system of the brain may have evolved to achieve in hierarchy, making the emergent abstract objects referable in bottom up and top down methods. In a hierarchical representation of objects, in a bottom up reference to ‘right angle’, instances refer to the class, while in a top down reference, a common base class object among objects of greater complexity is referred to as an unit which is a non-reducible emergent entity. Structureless electrons and abstract notions of a point can only be referred to as common base elements among their manifestation in various encapsulating contexts. Functionally, this is also achievable through the same method of disjunction of conjunctions, as expressed in Equation (4), where each of the s refer to a conjunction of any number of elemental units in the context, where the element p is common to all. For example, papers, tables, boxes, and walls all have the object ‘right angle’ as one of the base class elements, among others.
Another important point to note here is that a conjunction may include the two component line segments as well as the explicit relation p between the two to create the unified semantics of , where the relation p is an independently referable element at higher level neural hierarchy. This provides a resolution to what is known as the ‘binding’ phenomenon or perceptual unity in the neural domain [26,27,28] (for reviews, see Neuron 24, 1999). The process described above may form the central mechanism to unify the processes and features together that belong to different domains. The multi-modal binding of features and attributes from visual, auditory, and tactile domains constitutes a particular example [29,30].
It is possible that the list of values in disjunction does not cover the entire range of a parametric space; therefore, the emergent relation does not truly express the complete class, yet it could be used as such, as a part of higher level more specific objects in real physical systems like the brain. One may recall that if a state has no correlation with a value, neither the existence, nor the negation of the value bear any relevance to the state. Therefore, in a limited domain of functional operation, the semantics of correlation of a neural state may serve as a symbol of an abstract object, which characterizes a class or a type object, for example, the term angle is learned as a rule from the observations of a limited set of measures of angles.
In this description of emergent objects, no limits exist on p as long as the right selection of s is made in the domain of instances of p among more elemental objects or in the manifestations of p among the objects of greater complexity, including the objects from the domain of representation of abstract objects. The method has no limits whatsoever in creating abstract semantics of objects of arbitrary kind.
The method of abstraction also suggests that generalized mechanisms may exist to build models of relations among objects, regardless of their types. That is, the process of learning could be implemented in a given elemental structure of processing which could then be repeated for all domains, at all levels of hierarchy as may be the case with ubiquitous six-layered structure in the neo-cortex where processing is organized into what is referred to as canonical micro circuits (see [31] and references therein). The implementation of canonical networks may vary depending on the resource constraints and the requirements of the model for behavior [32,33].
In addition, an object expressed in terms of relations offers an idealization of measure zero, such as the abstraction of ‘right angle’ or ‘heavy ion event’. A relation is not necessarily limited by the finiteness (limits of minimum resolution) of the physical world. A reference to the relation itself does not require an actual construction of its instance. A reference to objects constructed out of relations makes them entirely separable and discrete, giving rise to the abstract notion of countability, infinite or unlimited precision, differentiation, and absoluteness. Such objects permit the genesis of symbolic languages, including the language of mathematics with symbols of discrete semantics, as discussed in Section 8.4. Moreover, the abstraction of a relation takes the form of a rule that can be used to construct or to test an instance of the relation. For example, the relation of the ‘right angle’ functions as a rule to construct an instance with orientation as a free parameter.
4. Transience of Information and Emergence of Models
In the experiment depicted in Figure 3, the state of the anode merely correlated with the heavy ion event, not with the specific identity, energy, or trajectory of the ion. From the temporal and spatial distribution of currents on the electrodes in Figure 3b, the trajectory was inferred, but no further interaction captured this specific distribution.
Each of the knocked out electrons or ions left behind bears a correlation with the point of interaction. Consider an observing system whose specific response depends on selection of ions from within a width of the path of heavy ion—i.e., the states of selected ions correlates positively with small regions (points) of space and negatively with regions outside the width of the path. Then, the resultant state of the system will correlate with the disjunction of conjunctions of points of interaction within the same path. As discussed above, the disjunction of all possible distributions of points on the same path express the semantics of the path. This requires an observing device that captures this relation among the ions. In place of a chamber of gas, a solid state device may serve the purpose better, which receives damage to the medium in a way that the electrons get knocked out of the atoms/molecules along the path of the heavy ion, but the ions stay ionized within the same region, as will happen if the device is an insulator plastic, such as CR-39 [34,35]. Then, it is possible to capture this coherence relation among these ionized atoms and molecules. A chemical processing that etches out the material along the path of the damage [34,36] faster than the rest creates a conical hole in the material (see Figure 7).
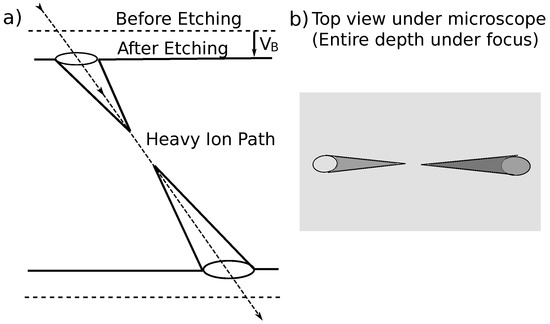
Figure 7.
A simplified view of etched out heavy ion track in CR-39. (a) A cross sectional schematic of the track in the plastic sheet; is the bulk etch rate under lab conditions. (b) Top view under microscope.
The etched out precise shape and size of conical hole in the plastic correlates with the high precision path, energy, and the identity of the particle [35,37,38] that has traversed the medium causing the loss of uniformity in the medium. The chemical etching rate at a given point correlates with the amount of damage received which, in turn, correlates with the rate of energy loss by the ion. The total path length correlates with the energy for a given ion in a medium. Different nuclei have their own characteristic energy loss rates at specific energy and charge states in a given medium [34,39]. Therefore, the energy loss rate per unit path length vs. the distance covered in the medium constitutes the signature of the specific ion—its identity. That is, the observable specific ‘shape and size’—a state of a PSR—of the hole naturally correlates with the path, identity, and energy of the ion. The interaction of a passing heavy ion within a medium remains the same, but what specific coherence relation among the resultant states is captured in a medium determine what information of the process is represented by the state of the medium.
We especially note that the specific information regarding the path, energy, and identity is not a part of ‘specific correlation’ of any one of the ejected electrons or ionized atoms; it is the observation of a specific contextual relation among the states that makes the information available and recordable. A record of the information is created where none existed; thus, information is not a conserved quantity—it can be created. If the same plastic material is melted away with heat, then three points can be noted about the process. First, the measurable coherence that existed among the elements (molecules) of the material that maintained the hole is destroyed. Second, a physical process to reconstruct the same coherence post-facto may not exist. Third, the process of multiple molecular/ionic interactions during melting and thereafter, where, with each interaction certain degree of information is lost due to the uncertainty inherent in physical interactions, leads to the loss of specific information regarding an ion’s correlation vis-a-vis the hole in the plastic erstwhile, annihilating even a trace of information about the shape of the hole. Therefore, information can also be destroyed. A similar phenomenon is expected if the electrons released in the ionization chamber is not collected by the anode—the opportunity to capture a specific coherence and semantic value of correlation is lost for ever. The trajectory information that is available in the specific coherence relation among the knocked out electrons and ions could be lost with the loss of coherence due to multiple interactions of individual electrons and ions. For the same reason, a new active state of a neuron is not expected to carry forward correlations of its prior active state from a while ago.
4.1. Emergence of Quantitative Models, Units, and Scale
In the light of the origin of semantics and methods of transmission of information, as dealt with so far, what may constitute a general method of building models of objects (physical entities, relations, processes) of the universe? A model is expressed in terms of relations which are expressions of the constancy in the characteristics and functions of objects that lead to definite predictions, even if within finite limits of variation. A universe without a degree of constancy in its function is an impossibility. Therefore, a general method of building models may rely on determining the limits of constancy in the variations of objects that define the relation among objects.
All interactions exhibit certain constancy, at least the causal relations. In a model expression such as , where the electric current is defined as the flow of electric charge per unit of time, the ratio preserves the constancy of the relation. The function of the relation constitutes one kind of constancy, whereas a multitude of values of variables (here, charge flow and duration of time) producing the same outcome (current), forms another. The enumeration of possible combinations of values giving rise to the same result is describable as the disjunction of specific conjunctions of values, as depicted in Figure 5. On one hand, the disjunction captures the abstraction of the functions of multiplication and division; on the other, it also captures the outcomes of the functions given the values of the variables. For instance, at a given potential difference, V, the measure of current, I, relates to the amount of work done per unit of time: . A given multiple, m, of the charge flow in a time duration corresponds to the same multiple, m, in the amount of work done, , in the same duration of time. A given quantum of work per unit of time, say W, may form the reference unit for the measure of current, I, and vice versa. Then, different multiples of W become the measure of current and vice versa, via the mapping shown in Figure 5. The constancy of a relation, a given variation in one quantity reflected in a definite change in another, as in , captures both the unit and scale by the same method of disjunction. With the emergence of units and scale, the models become quantitative. While this forms a trivial example from the perspective of the present day understanding of models of physical phenomena, the noteworthy point here is that each component of such a model is entirely representable by the mapping of the disjunction of conjunctions of semantic values.
The scope of the method to model a generic object is greater than that of the mathematics. First, since objects are definable by the method of enumeration of terms in disjunction, where each term is a conjunction of arbitrary number and type of objects, any arbitrary object or relation with any degree of complexity may be modeled. A model gets reduced to a mapping from the set of elements of an object along with the elements of context to its functional consequence. In a hierarchical organization, it may even have a referable identity. Second, if an object bears a limited determinism, i.e., the same result occurs for different initial conditions or vice versa, disjunction allows it to be expressed, without having to create only a probabilistic model. Third, since the method of building a model is based on the reality of the natural function of the objects, the limits of tolerance emerge from the observed variations in their function, which allows for modeling of objects with observed limits of accuracy and precision without any implicit or implied precision. Even if the object displays a limited semcoherence with other objects, exhibiting fuzziness, it can be modeled. Fourth, even though the physical interactions do not exhibit unlimited precision, the relations represented may have infinite precision and be discrete by virtue of symbolic reference to the equivalence class made possible by disjunction. That is, the models are not limited by the limits of uncertainty and resolution in the physical domain. Fifth, the disjunction of instances gives rise to a referable abstraction as a symbolic entity, even if the class of instances is incomplete. Sixth, processing via disjunction and conjunction offers a mechanism to create a system with entirely physical means and rules of operation that can have unlimited modeling abilities, potent enough to create language and mathematics, including a model of itself.
The following examples bring to the fore how the models take shape due to disjunctive relations among the processes of nature. A photon released in electronic transition between two hyperfine ground states of the cesium-133 atom completes 9,192,631,770 oscillations in a given condition when a stimulated photon from hydrogen maser completes about 1,420,405,751 oscillations. When earth rotates about its axis once (sidereal period), the sun moves by about 18,956,080 km around the galactic center in its orbit. With respect to the duration of time, a constant relation exists among the processes of natural phenomena at all scales. The abstraction of realism of time with its own unit emerges from this equivalence in the completion of different processes in specified contexts, which is modeled by a disjunctive relation. Similarly, there exists a constancy with respect to the measure of work done, or to the measure of stored potential to achieve the same degree of work, in the processes of nature; the disjunction of such equivalent processes establishes the abstraction of energy. The indistinguishability or equivalence among certain fundamental physical entities or processes establishes the model of a type object for the physical entities or processes, such as electron, paper, water, time, energy, current, etc., with its own measures, units, and scale. It is proposed here that the neural system of the brain may construct models of the universe by capturing the constancy and equivalence exhibited in different phenomena via the disjunctive relation in the hierarchy of modules. At the same time, objects of greater specificity or complexity may be represented by the conjunctive relation.
5. Implications of Representation on Physical Sciences
In this section, we explore if the correlations of information with states of physical entities, as presented here, offer any new insights or perspectives into our understanding of the laws of the physical universe.
5.1. Preservation of Correlation on Extreme Scales
The following empirically established results set the ground to discuss further implications. Radio waves originating from stellar systems maintain coherence within, and correlation with, the events and processes that took place a long time ago at a large distance away in the universe. The radio waves emitted as part of a stellar process leave the source and travel for thousands of years through interstellar space, and then through the ionosphere of the earth before arriving at radio antennae spread over a distance scale of a few kilometers (see Figure 8).
Figure 8.
Radio antennae receiving signals from a distant source. The distance d between the antennae, and the angle of incidence (from the vertical) cause a differential distance of between the parts of coherent waves arriving at the two antennae.
Even though the magnetic field of the interstellar space does interact with the radio waves altering the orientation of polarization, the coherence within the wave and the correlation with the stellar system are not lost. The ionosphere further disturbs the waves, yet a degree of coherence is maintained. On the other hand, the distance of a few kilometers for waves of a meter long wavelength will make them lose their coherence nearly entirely if the delay correction is not applied to the signals received by different antennae (see Figure 8) in a multiple antennae setting. Given the direction of the source, if signals are correlated in such a way that compensates for the relative temporal delay that has occurred between the coherent waves in transit before arriving at the respective antennae, the coherence is restored [40,41]. It is also possible to model the disturbance caused by the ionosphere to a certain extent to compensate for that, to allow better coherence in the signals, which yields a better correlation with the event at the stellar system [42,43]. One of the implications of this is that it allows us to conceive a system that organizes itself on the basis of temporal coherence in the observable states of elements that respond to physical phenomena. A feedback looping system can even synchronize the flow of information back and forth to select the invariant relations in the processes of the systems being observed.
This example brings to the fore the evidence that with respect to the sustenance of coherence and the correlation with the events at source, a long period of time and large physical distance are of little consequence. The relative evolution of physical entities sustains a constancy if not subjected to mutually decohering interactions. In fact, the PSRs may even undergo certain interactions that alter some of their physical characteristics substantially, yet preserve their mutual coherence and therefore, their correlation. From the uniformity, homogeneity, and isotropy arguments, it is natural to expect that the photons leaving the same source in a coherent state and traveling in different directions would not lose mutual coherence by virtue of time or distance; difficulty is expected only in making the observation that captures this coherence. As happened in this radio source observation, even when a part of the wave is captured at one antenna, the other part of the wave maintains the time evolution of the coherence relation with the first part, together with the processes at the source that were common to both. One of the implications is that the determinism inherent in the wave function description of state captures more of the constancy of relative evolution, rather than the observable reality of the intrinsic state of the physical entities in a deterministic sense; the uncertainty in the measurement of the individual component remains as expected.
In the next set of examples, we consider experiments based on variants of the Mach–Zehnder Interferometer (MZI) that investigate wave particle duality or complimentarity, which is considered central to the distinction between classical and quantum systems [44,45,46]. A quantum system, such as a photon from a coherent source, considered to be a beam of light, is split by a beam splitter, BS1, into two different paths where a phase difference is introduced between the two paths before recombining them at BS2 (see Figure 9). The output from BS2 is observed by two detector systems placed on two possible paths.
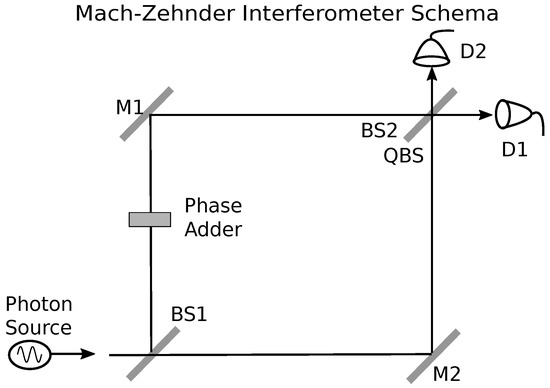
Figure 9.
Schematic diagram of the Mach–Zehnder Interferometer.
In one of the experiments, Jacques et al. [44] arranged the selection of the presence or absence of BS2 arbitrarily by making a local choice that is separated from BS1 in a space-like separation, such that the photon had already passed through BS1 before the choice was made. They observed that when BS2 was not present in the path, the two detectors observed the photons with the probability half that carried the information of which path the photon had arrived. In contrast, when BS2 was introduced in the path, they observed an interference pattern, as expected for the phase difference between the two paths.
In the other two experiments, Kaiser et al. and Peruzzo et al. [45,46], used a quantum beam splitter (QBS) in place of BS2. The QBS was configured to be in a quantum state of superposition of being open (absent) and closed (present). This observation is interpreted as being in conformance with non-local nature of quantum systems, and the choice of state recorded is delayed until it is forced by the detection process. They suggested that the wave particle duality, where only one aspect is observed in any measurement, is a naive view of the state description.
These observations offer us insight into the exchange or sustenance of correlation on extreme scales.
- Interaction-free evolution of states over large distances and long times preserves objective causal correlation.
- Interaction-free evolution of coherent systems preserve mutual coherence, and therefore preserve the semcoherence.
- Interactions of correlated microscopic states with macroscopic systems that do not differentially probe the correlated states preserve the mutual correlation, as is evident from radio waves interacting with the interstellar magnetic field, and coherent photons encountering a lens, or beam splitters that modify their state.
- Non-local spatio-temporal causations, if any, remain transparent to the natural correlations.
- Every interaction results in the exchange of information among interacting entities. Observer-observed relation must hold among the entities. Therefore, each resultant state must bear the semantics of the correlation of the limits of states observed, irrespective of their micro or macro physical limits. That is, even the resultant states of macroscopic entities must correlate with exchanged semantics of correlation of microscopic entity (the implications are to be discussed elsewhere).
5.2. Physical Sciences in the Light of Natural Representation
If the description of nature, as defined by classical physics, and as supported by mathematical expressions with analog functions were to be true and exact, then the states could be described with infinite precision, and interactions would have evolved via all intermediate states. In such a consideration, the number of states between the initial and final states of interaction would be uncountably infinite. This implies that in order for an interaction to be completed within a finite amount of time, the physical entity must traverse an uncountably infinite number of intermediate states, each being a likely stable end point of the interaction. This is possible only if the rate of change of states under the specification of the interaction is infinite too, but then the consequence of the interaction would become indeterminate, making the universe implausible with no specific pattern or conservation laws. In addition, this also implies that the only possible way that a universe may become a reality is when the physical entities superposed in their state spaces, yet the observable states changed only in quanta. Without the superposition in states, there could be no interaction, and without the quantum change, there could be no determinism. The superposition requires a description of state akin to the wave function formalism in quantum mechanics.
The wave function description remains non-comprehensive, for it does not express the qualitative basis of the underlying physical substrate, and it does not identify the causes of randomness in the measurement; this requirement is not the same as that of EPR [20] reality. Henceforth, we refer to the generalized, but unknown, function of state as the state function. Moreover, in an interaction, the state function should never collapse to give rise to a quantitative measure of width zero; it must remain describable by a state function that still extends (superposes) over a range of space. Moreover, no interaction could be completed in an instant of time, i.e., duration of width zero, for if this was possible, all state transitions would be required to proceed at infinite rate, including the energy and momentum transfer, or compositional/structural change, giving rise to mathematical singularity. Therefore, an interaction necessarily evolves over a period of time and over a region of space, making it impossible to sample instantaneous values of states. In fact, it would be in natural contradiction to expect static values for states, or realism of instants of measurable states. That is, the transitions are in quanta, not in any intrinsic quality of reality of instants. For this reason, even the instant of time with measure zero is an ill-defined term. Moreover, in an interaction, each entity being an observer, if the state of the observed remains unmodified, the observer must remain unmodified too, yielding no measurement and no exchange of information. The same can also be inferred from the assumption of causally bounded (finite) universe; if an interaction permits an entity to undergo a non-causal change, it must be an isolated system (universe). That is, in a finitely bounded system, entities do not have absolute independent existence. Accounting for entities in an interaction only provides working definitions of identities, not absolute independence. Therefore, observed states also could never have absolute definitions without reference to other entities.
From another consideration, if the interactions were deterministic in absolute sense, and if the universe began in a correlated state, or the universe was ever smaller than the speed of information exchange multiplied by its age, the universe would remain in correlated state forever as a single thread of possible evolution. That is, only the distribution of states would change with time, but not the historical correlation. Every interaction would be predetermined, and every state would be predictable at all times. In a true deterministic universe with finite elements to describe the complete reality of states and their interactions, a decoherence can never occur. The picture of perspectives based on PSRs, or incompleteness of state description of correlation would vanish. Notably, actual physical states would always exist within the reality of the completeness of context in a deterministic universe. The universal evolution would be entirely time reversible.
In such a scenario, states would have had unique definitions, and their correlations with semantics would encompass all physical reality that lead to the respective states in respective contexts, including all phenomena of nature that formed the basis of deterministic interactions. For a finite universe, with sufficient time for states of all elements to affect all others, a state of any physical entity would correlate with the state of the universe for all times—past, present, and future. In his essay [47], Laplace articulated a similar viewpoint, even though the interpretation differed.
Now, if the states have differential correlations, this necessarily implies that the interactions are non-deterministic, even if within limits. It does not matter much whether the interactions are describable by linear or non-linear models, or how great the number of components the universe has, as long as it is finite with transitions only in quanta, a degree of non-linearity and the number of elements cannot bring about indeterminism. This further indicates that in order to achieve limited uncertainty and randomness, each element must individually have the qualities to give rise to uncertain outcome within limits. It may be inferred that within the limits of measurement, a physical entity has analog/continuous detail that cannot be described with a finite number of discrete parametric values (to be discussed elsewhere). Stated differently, it is impossible to admit fundamental uncertainty in the function of the universe when both the states of fundamental elements and their modes of interaction are taken to be finite, complete, and stable. Moreover, from the perspective of natural representation, an entirely deterministic universe cannot have an origin or an end, and the fundamental laws must remain immutable. A finite universe would be cyclic, and an infinite universe indeterminate. Non-determinism does not remain a premise, it becomes the only reality. It is the limited non-determinism that causes the emergence of localization and arrow of time, where the effect of an interaction cannot immediately be a part of a correlated evolution of the observable universe. In such a scenario, the perspective of a PSR is based on a reference frame of its own. In fact, one may consider a view that the finite speed of information travel is the outcome of the limited determinism, or non-localization is expected as long as the evolution of a system is deterministic.
An individual’s ability to observe things as different, an outcome of the first principles of natural correlation, constitutes a non-violable evidence for the states to have differential intrinsic correlation, which implies both that nature must be non-deterministic at the fundamental level, while bearing a degree of constancy of relation to give rise to correlations with differentiated semantics. By virtue of the fact that this is non-violable evidence, from now on, we may consider the conclusion of limited indeterminism and randomness as part of the natural universe as a demonstrated fact beyond the necessity of further evidence. As an addendum, it is noted, the stated wisdom of ‘Cogito, ergo sum’ takes a totally new dimension, far greater in scope and far richer in its applicability.
A world simulator that predicts the future for all times is an impossibility, and so is the exact temporal reversibility. A model of the universe even partly based on descriptions of unitary evolution at its most fundamental level may only be conceived of with respect to uncertainty in the transitions, i.e., given a set of equivalent transformations on interaction, it will remain uncertain as to which one in reality will take place.
Furthermore, if a measurement is made of a macroscopic property, as is the case in thermodynamics and statistical mechanics, which correlates with a large number of indistinguishable micro states, the completeness of the state descriptions of individual elements is necessarily lost; therefore, it is undefinable to regain the same state of initial condition that existed prior to the interaction from the considerations of thermodynamics alone, making the process irreversible. It does not remain only a question of whether the initial state can be regained, the sequence of state transitions could never be entirely repeatable, even if the initial state is regained in principle by virtue of microscopic quantum states being finite.
6. The Laws of Natural Representation
A set of laws for the genesis of natural representation is proposed here that incorporates the natural association of information with state descriptions of physical entities as a reality of the universe. Furthermore, the laws also establish an objective mechanism of transmission of information with each interaction that results in observable change in states.
In this text, the term ‘existential state’ has been used to construct a logical basis to conceive the semantics of correlation of an observed state; the observed state is considered equivalent to the disjunction of all causally possible existential states that could satisfy the same observation. We bear in mind that any change in observable state, even intrinsic to a system, that alters the correlation, is considered to be a definite transition. Since the existential state is neither observable nor determinable in reality, it remains largely a notional state for the convenience of construction of logical steps. Therefore, the natural representation is stated only with respect to the observable state. Moreover, the semantics of the term state, as used here, does not refer to an absolute description of physical reality, it refers to an emergent or a relative measure.
The identity of a physical entity is characterized by the elements of its state that are responsible for the observable consequence upon interaction. The state description is relative to the context as observed by another system. An interaction may alter the identity characterizing elements of state. Therefore, an expression such as ‘a change in state of a PSR P’ is not entirely accurate, since P is not a stable qualifier of an identity across interactions. This poses great difficulty when referring to a change in state with respect to the identity of a PSR that itself is transient. With this caveat, we continue to use this expression without intending to refer to P as a stable identity qualifier across interactions.
The statement of the basis of natural representation:
- The genesis of an accountable physical entity and its associated state is based exclusively on the limits of constancy (uniform regularity) of cause and effect relation in the nature of change.
- The perspective of the semantic value of representation is based on the observable state of a physical entity that serves as a reference state of a reference physical entity.
- Post-interaction, the observable resultant state, S, of a physical entity, P, represents a definite semantic value, C, that is derived from all causally equivalent configurations of reality, describable in terms of states of interacting entities, that result in the state S of entity P. The semantic value C is constituted of the following components.
- (a)
- A value that is equivalent to disjunction of conjunctions of values of respective states in each configuration.
- (b)
- A value that is equivalent to disjunction of conjunctions of semantic values of correlation of respective states in each configuration.
It can not be overemphasized that observing and observed systems are parts of the same interaction with mutually relative roles embedded within an unified whole. The observed state of an accountable system has a description within the parametric space of relevance to the transformation in the observing system. Hence, the disjunction of conjunctions of observed states under Rule 3a naturally includes the relation, R, of the constraint over observed states required by the observing system to undergo the transformation to state S of P; no separate rule is required for the inclusion of R.
Corollary: When there is a one-to-one mapping between the earlier states to the next, there is only one term in the expression of disjunction. This takes care of interaction free unitary evolution of a system.
An external system cannot gain access to the correlation profile of another PSR without an interaction that selects or responds to the relevant state of the PSR. Therefore, it is the transmission of semantics of correlation that remains central to the laws of natural representation.
7. A Simulation of Information Processing
The primary purpose of this simulation is to demonstrate the mechanism of processing of information presented here. It also illustrates the internal consistency and simplicity of the formulation that must be the hallmark of natural methods.
In this simulation, we consider a set of pseudo neural agents, referred to as lower level (LL) agents, that assume an active state in the pre-assigned context; the context defines the associated semantic value. These agents’ output states are mapped (connected) to higher level (HL) similar agents in accordance with the pre-assigned sensitivity ranges of HL agents which may turn active when a sufficient number of LL agents that they receive input from are active. Using the rules of the laws stated above, the specifications of the values represented by the HL agents are then evaluated.
Specifics of the Method
For each run of the simulation, each of the LL agents is assigned a random orientation range of pseudo line segments, i.e., when a line segment with a certain orientation is presented in the simulated field of observation, respective LL agents that are sensitive to the orientation are set to turn active. To initiate the mapping, each of the HL agents is also assigned a preliminary sensitivity field in the orientation domain; a connection map is then created from those LL neural agents that overlap in the sensitivity field. Since the orientation is not associated with a vector, the range is limited to {0–180} degrees of arc with a resolution of 1 degree. The random assignment of static ranges of positive, negative, and null correlations to the LL agents cover the entire field {0–180} deg and are usually much larger than 1 deg; the values of range assigned to LL agents follow normal distribution which constitutes a variable of the simulation. Another variable is the activation limit common to all HL agents that defines the fraction of total number of input connections from LL agents that must turn active in order to activate an HL agent. The simulation proceeds by presenting a line segment of specific orientation with a resolution of 1 degree at a time and determining the correlation profiles of HL agents if they turn active. A single run is completed when all values in {0–180} are generated once and statistics collected.
The results presented below are based on the following specific values. There were 360 pseudo neural agents in lower as well as in higher level modules. Each of the LL agents was assigned a mid-value angle of positive correlation range randomly within {0–180} and a range of 15 deg 3 sigma (standard deviation = 2.5 deg) such that the range varied between {7–23} deg around the mid-angle as per a normal distribution. For one type of simulation, the remaining range was statically assigned to bear negative correlation, i.e., the orientation value in this range could not activate the LL agent. In another simulation, a fixed range of 16/2 degrees of null correlation was assigned between positive and negative correlation ranges on either side; the purpose here was simply to study how the null correlation evolved with varying ranges of positive and negative correlations. For the HL agents, it was desirable to sample semantics of correlation at each simulated orientation equally. Therefore, the mid values of positive correlation were uniformly distributed among 360 agents, while the range assignment remained similar to LL agents for the purpose of making a connectivity map. A projection map was created from LL to HL agents if there was an overlap in positive correlation. Moreover, since the mapping remained static during a run, there was no need to simulate the same orientation value multiple times, or in a random order. The activation limit of the HL agents was varied from {0.3–0.55} in steps of 0.05 during different runs of the simulation.
When an HL agent turned active in response to the number of active inputs from LL agents crossing the activation limit, the conjunction of correlation profiles of respective LL agents constituted one term of correlation for the HL agent. When the number of active inputs was larger than the minimum required, then all possible combinations of inputs from LL agents that met the required minimum formed distinct terms in the disjunctive relation of the correlation. When the number of terms was very large, a limited set of randomly chosen conjunctions were selected to determine the profile of the HL agent. It is to be noted that in this simulation, if we chose 100 terms, or a 1000, the results of the disjunction did not change at all, implying that 100 randomly selected terms were sufficient for the purpose here. Thus, the correlation profile of an HL agent computed against the simulation of an orientation value determined the value represented by the HL agent for that instance, whereas the entire range of orientation that could activate an HL agent determined its sensitivity field. In figures Figure 10 and Figure 11, some of the results of the simulation are presented, followed by an interpretation.
Figure 10.
A bar represents the correlation profile in the range of orientation as marked below each figure (green: positive, blue: negative, gray: null); a negative correlation is implied for the rest of the space. The results of conjunction or disjunction are shown below the black line in each figure, while the red mark on each black line shows the instance of orientation presented for simulation. The data for (a,b) were drawn from a run when entire orientation space was divided into negative and positive correlations, while for (c,d), the null range was also included. (a,c) show the result of a conjunction of profiles of active LL agents mapped to an HL agent, while (b,d) shows the results of the disjunction of such conjunctions. The list of terms in disjunction may not be exhaustive, even though the result is the same. The activation limit was 0.4, i.e., 40 percent of input connections had to be active to activate the HL agent.
Figure 11.
The results presented here include the means and standard deviations of variation in the range of positive and null correlation that resulted from conjunction and disjunction operations for different activation limits. To spare the clutter in the graphs, the standard deviation for a given mean (filled square) is shown as a separate point (filled triangle) in the same color, except for the sensitivity data in (a), for which the scale on the right hand y-axis applies. For (a), the entire orientation space was divided between positive and negative correlations, whereas for (b), a constant null range of correlation was included for LL agents. For activation limits >, several of HL agents did not turn active for any orientation values.
A few of the generic interpretations are as follows. Case of zero range of null correlation: Even for a low activation limit, the mean of ranges of positive correlation of HL agents resulting from the conjunction was dramatically limited relative to the individual ranges of LL agents. Notably, even the disjunction of conjunctions yielded a substantially limited range. With an increasing activation limit, the range of positive correlations fell further. In case of disjunction, the fall was sharper approaching the limits resulting from conjunction alone. This implies that at higher limits of activation requirement, the terms in disjunction do not vary much in their respective profiles.
Case of non-zero range of null correlation: Due to the conjunction of null and positive correlation values being positive, the range of positive correlations stayed wide for HL agents, even though the range of null correlation shrunk, as seen in Figure 10c and Figure 11b. When the static range of null correlation assigned to LL agents was very wide, the positive correlation range grew post-conjunction (not shown in the figure).
The values of standard deviation of variation in the range of positive or negative correlation also become limited by the operation of conjunction, which was reflected in the disjunction results as well. Moreover, the variation fell even with increasing activation limit.
A few of the important interpretations are as follows:
- It is evident from the results of the simulation that the specificity of the correlation profile of an HL agent, when it turns active, is far greater than what is originally assigned to LL or HL agents, yet it remains consistent with the presented orientation. The enhancement in specificity is a result of diverse negative correlation range of LL agents.
- This method of processing forms a good example of coarse coding, yet it achieves high specificity in its results. When the method is conjugated with the relation mapping scheme, as shown in Figure 5, the potential in generic information processing becomes apparent. Mapping represents relations among arbitrary objects, and coarse coding achieves greater specificity.
- Comparing the results of conjunction and disjunction, as shown in Figure 10a,b, with that of Equation (1), we note that the specificity achieved in either case is high. While the former is based on first principles of processing that occur at each interaction, the later requires an interpretation based on a model of probabilities.
- The results of the simulation suggest that for a re-entrant system of processing, when the new set of active states are fed back in a controlled loop within the same level of processing as well as to the lower level, the evolving profile of positive correlation could get more and more specific closer to the maximum resolution of reality presented. For this reason, it did not matter much if the range of null correlation was wide to begin with, since, initially, the positive range of correlation would grow wider, but the null correlation would decay out quickly, and then, the positive correlation would also begin to gain specificity.
- Considering how the conjunction of correlation profiles limits the range of positive correlation sharply around the specifics of reality present in the observed system, it is an advantage to a processing system to capture or sample as much of a diversity in the correlation profiles as possible with the agents [24,48,49] within the sampling domains. Even the feedback profiles could initially bear greater diversity. This may appear as noise to an external system that makes measurements on the signals and correlation profiles of the agents [50,51].
8. Discussion, Interpretation, Implication, and Conclusions
Here, we discuss additional interpretations and conclusions that could not be embedded in the specific contexts of the multiple branches of the analysis above.
8.1. Realism of Natural Representation
Since the association of information with physical states is based entirely on the limits of functional relations in the nature of change, it neither depends on any hypothesis or interpretation, nor is it falsifiable, nor does it have any existential status without physical substrate of representation. This perspective is in direct contrast with ‘It from Bit’ [52], and the ‘Mathematical Universe Hypothesis’ [53], that require the a priori reality of information. Moreover, for the same dependence on a causal pattern, the reality of semantics of correlation forbids descriptions of universes that are not congruent with observable reality; speculative multiverses with different causal functions cannot interact with the one observed to be violating the causal pattern and the semantics of undeniable correlation. Therefore, the causal description of the observed universe must remain complete within itself. Since the classical or quantum physical descriptions of properties, states, and physical entities constitute model descriptions of reality derived from relative measurements in non-absolute reference frames, a possibility always remains that there could be an alternative description for the same reality.
8.2. Function of Natural Representation
A represented semantic value is not a physical substance or a form of energy that may have its basis in interaction, such as mass or force fields, that can be physically probed. The value may not in itself be the source or the cause of further physical interactions, but it is necessarily associated with a physical state in a context that has a physical consequence. Natural representation is an inseparable consequence of causal relations in physical processes, making independent existence of each other an impossibility; in fact, any expression of independence would be a natural contradiction. In this sense, a represented value can be associated with a correlatable difference in the physical world. There may even be a representation of the consequence of the function of represented objects. Therefore, it is entirely possible that systems may evolve towards the creation of a certain specific representation that describe an object, actions by the object, and the consequences of the actions within specific contexts, along with the referable records (memories) of the actions and their consequences, which may, in turn, become a source of further organization towards actions based on prior memories of relation between actions and consequences. In fact, the object may even be the representation of the very system of representation at a level of abstraction that has the abilities to organize the memories and actions in the context of its own abstract self.
8.3. Role of Natural Representation in the Universe
Certain coherent characteristic of a structured physical object are rarely represented by an element of the same object; in order for an element to be able to represent the coherent characteristic of the whole, its state must depend on the coherent properties of the whole. For instance, consider a description of a physical object such as a leaf. The semantics corresponding to the constancy of its shape and color are represented only by a system that has states that depend on the specific, but unified, view of the entire contour of the shape in all its variations and certain relations of its reflectivity over its extent with that of the surroundings. It is apparent that no element of the leaf or the tree bears a state that especially correlates with the shape and the contrast. In fact, the chromosome sequence controlling the shape and reflectivity of the surface merely encode the function of the cells in specific contexts that give rise to emergent shape and reflectivity. A system like the brain forms an exception—it organizes the representation in hierarchy, where the states of higher level neurons correlate with the unified properties of objects.
The function of representation is profound. Without a recourse to natural representation as a function of the universe, which constitutes the semantics embedded in all natural phenomena, the description of universe could remain structureless, formless, timeless, colorless, purposeless field of fundamental elements with ever changing states without any unity among its elements—without a holistic view and without any informational content about causal connections whatsoever. However, this is possible only when there is no constancy in natural phenomena. Moreover, without a system such as the human brain, hierarchically unified representations of objects, abstractions of higher level structures, models of physical phenomena, and laws of natural function could not be possible. A description of the universe that does not include the laws of representation cannot be worth calling the ‘theory of everything’. It is noteworthy that even the notion of the ‘theory of everything’ is construed within the realm of representation of semantics; therefore, such a theory must have explanatory power to include the basis in which it is expressed.
8.4. Symbolism as a Powerful Tool of Language and Mathematics
In nature, where all objects, without exception, are described in terms of relations, the only way a meaningful description can be constructed is by relating an object to the symbolic abstraction of other objects without requiring the complete semantic construction of the other objects. This constitutes the boot strapping method of building semantic structure.
Constructing the description of an object purely from its internal and external relations does not depend on the description of qualities in any absolute frame of reference. Therefore, it is entirely possible to create objects of arbitrary types with arbitrary inter-relations that may or may not have any natural basis in physical realm, but can be referred to by assigning symbols of physical forms to them. Then the processing (or evolution) of such objects could be expressed symbolically, as exemplified below.
A constant feature in any physical domain, even in the visual or aural domain, may function as a symbol; the specific physical forms, e.g., may serve as symbols. The forms may be conjugated to create more symbols. The lexical forms (graphemes), or the forms of aural sounds for the same, may serve as states that represent objects even without any natural association with the objects represented. The characteristic forms may be thought of as mathematical symbols or as letters, marks, syllables, or words in a language. It then becomes possible to assign arbitrary semantic values or objects with such forms, making the assigned objects referable. These symbols may refer to objects of action (operators) or the objects acted upon (operands) in an uniform manner which may serve the purpose of expressing relations among the objects. The semantics of an operator or an operand are dependent only on the interpretation and the context; in a general sense, they are equivalent, since a change of an operator or an operand in an expression changes the semantics or the value uniformly. For the sake of uniformity, we refer to the forms of symbols as terms of an expression. Furthermore, the semantics can also be assigned to the transformation of their forms (equivalent to change in states) individually or in specific conjugation, which may then serve the purpose of syntax; syntax is merely a pre-defined semantics [54] assigned to certain terms (forms), and to their transformation schema that sets or limits a context and expresses relations among the terms of the expression. The schema may also associate semantics with the order or proximity of appearance of terms in space or time to allow operations within the semantic space by the relative placement of the terms, thereby forming a part of the linguistic feature. When the assigned semantics itself includes associations only with certain types of objects, the proximity of terms that refer to these objects suffice. Moreover, the symbolic forms may also serve as variables where the assignment of new semantic values is expressed in the same language. The artificial assignment of semantics to the terms substitutes the natural association of semantics with state descriptions. Then, the general interpretation of application of these symbols within the linguistic schema is the disjunction of conjunctions of assigned semantics, that includes the relations among objects as expressed in the schema, which only requires Rule 3b. Disjunction allows for the variation in the semantics associated with the terms or the usage. Thus, all forms of linguistic or mathematical expressions are made possible under Rule 3.
8.5. Limitations of Processing in the Physical Domain
As we noted earlier, descriptions of discrete properties with infinite precision may only be the consequence of rule formation via disjunction. First, as the information is processed by a physical system, the rules are formed by observations of objects, simple, complex, or abstract, where all possible cases for the rule within the domain of applicability are usually not observed, making the rule a generalization beyond verified limits. The applicability of the symbolic rule so formed may not be absolute. Second, even an evaluation of the application of rules may lead to ambiguity when the field of applicability presents contexts of overlap or of arbitrary proximity due to insufficiency of parameters or for ill-defined rules unless there exists a rule to determine the applicability. Therefore, either the system of evaluating the applicability may be based on subjective processing, or the applicability of rules may become self referential, whereby they are never satisfied without the application of a subjective evaluation at certain level of abstraction. Third, descriptions of forms, meanings of symbols, and the definitions of rules may require a language, where the semantic values of terms and their inter-relations may only be acquired from subjective observations with a degree of variability and without an absolute reference frame; hence, they, in turn, are interpreted by a subjective consideration [55]. Fourth, even in mathematics, whereever a list of all instances of a class is expressed and interpreted as an abstraction of a class, the interpretation necessarily depends on the interpreter’s subjective processing of the method of disjunction. For instance, an expression, such as, if a property is true for N then it must also be true for N + 1, requires a subjective distinction of class of N, and also of the operation of successor, particularly if the class is an infinite (inexhaustible) set. Given the limitations to subjective processing due to the uncertainties inherent in the physical systems, it is impossible to assert that the processing is mathematically consistent without limitation as is the subject matter of the theorems of Kurt Gödel. Macroscopic systems of processing, or the application of multiple systems of processing may reduce the evaluation errors arbitrarily, but cannot eliminate it altogether—i.e., subjective evaluations would continue to be limited by the limits of physical processing. Therefore, one is at a liberty to infer that information processing by physical systems can never be described by an entirely consistent mathematical system, and therefore, processing by physical systems will always remain outside the realm of the applicable limitations of completeness and derivability of theorems, as established by Kurt Gödel. Stated differently, the Gödel’s theorems do not apply to physical systems which may achieve an arbitrary degree of consistency and completeness in their processing and prediction, except for the limiting case. Moreover, there are no established obstacles that could limit the correctness of a proof, therefore, the proofs arrived at by such systems may, in fact, remain unassailable [56].
A consistent mathematical system may not describe the processing by physical systems entirely, whereas the processing in physical system may describe entirely consistent mathematics. In the context of Penrose’s triangle, does not hold entirely [56,57].
8.6. State vs. Specificity of Representation
Given the large variation and uncertainty inherent in the interactions at microscopic level, the semantics of correlation of consequent states are not sufficiently specific to represent a complex structure. As noted above, an ejected electron correlates with a wide range of state descriptions of the heavy ion. This requires a conjunction of large number of electrons in a specific relation to correlate with the specific properties of the heavy ion. On the other hand, a specific macroscopic state already exhibits a coherence among a large number of components, resulting in very specific correlations, as is the case with the state of anode. It is unlikely, therefore, that the quantum states of microscopic entities could be used in neural systems to represent such complex semantics as we communicate (see [58]).
8.7. Sparseness of Objects With Greater Specificity
The symbolic formation of a class from observation of a fewer elements than the comprehensive set that may belong to the class enables a system to make a leap into the domain of relation which may lie beyond the realm of mathematically consistent methods. As we noted, the construction of a symbol of class for ‘right angle’ may employ primitives, such as line segments, but at higher levels of abstraction, the elements of observation could be highly complex notions and rules. While, as expected, several such leaps may not hold good when tested with mathematical rigor or empirical verification, some of them could indeed lead to novel methods that remain unassailable. Furthermore, when the domains of elements are varied, the number of elements large, the level of complexity and specificity high, the domain of objects having elements such as these become highly sparse and discrete. That is, meaningful relations (objects) with greater specificity are not contiguously distributed. Therefore, the probability of correctness of a good suggestion (so called intuition) for higher level class relations, that avoid immediately bad examples, improves dramatically over combinatorial enumeration.
8.8. A New Perspective of Physical Universe
One of the important aims of the present work was to augment the perspective of the natural universe. For example, robust definitions have been worked out for basic scientific terms, such as ‘physical entity’, ‘physical state’, ‘physical interaction’, ‘natural causality’, ‘natural representation’, ‘semantic value’, etc. The reality of natural association of information with a state is especially presented as new physics. Moreover, an interaction was shown to be entirely describable by ‘disjunction of conjunctions of semantics of relative state descriptions’. This expression forms the basis of all quantitative processing of associated information. Furthermore, the phenomena of emergence of abstract semantics were especially worked out to exhibit the sufficiency of the method. The disjunction and conjunction operators may be viewed as ‘the basic tools of language of nature’ to express all semantics.
8.9. Reality vs. Measurability
Studies in natural phenomena began with classical observations classified under physics, where the elements of reality were stable and measurable within the limits of measuring instruments, allowing deterministic dynamical models to be constructed, even though certain states and processes remained indistinguishable. This also allowed the construction of the concept of real line to represent analog or continuous change. The concept of conserved quantities took root in the stability of reality. With the advent of quantum physics, measurements within models of reality with unlimited precision went out of scope; only probabilistic measures could be assigned with different possible outcomes. The models were constructed to determine these probabilities. Moreover, one of the fundamental suggestions of these models is that the reality itself contains uncertainty within limits; the lack of absolute specificity in the measurements is not limited to the instruments alone, it is part of the reality as well. For macroscopic physical objects, the situation was still, by and large, stable within tolerable degree of uncertainty. Conservation laws were seen in the light of new limits, where for limited periods of time, conservation may not hold in the strictest possible sense. In this work, for the first time ever, we dealt with a fundamental reality of nature that is so deeply embedded in all physical processes, associated with all physical states, yet fundamentally non-tangible, non-measurable, and non-detectable by experiments using physical devices. The very notion of direct measurement goes out of scope. One has to contend with the idea of objectivity in the mechanism of creation, transmission, sustenance, and destruction of such elemental reality. This allows for the creation as well as evolution of systems to achieve arbitrary limits of analytical processing and abstraction. The idea of conservation of elements of reality remains limited to the duration of the record of observable states, or the latent observable consequence specific to the states.
Furthermore, the reality of information comes into existence entirely due to the causal relations in natural processes. One remarkable fact that emerges from this consideration is that the information is directly associated with the states of physical entities, such as with neurons in the human brain, which offers us a direct access to one of the fundamental elements of reality of nature. This then becomes the window to collect information, to sense, and to build knowledge about all of nature.
8.10. Method of Information Processing
As detailed in the text and demonstrated by a simulation in part, we note that the mechanism of information processing, as modeled here, is sufficiently potent, not only to deal with the abstract and emergent quantities, but also with processing the specifics of quantitative values. Moreover, it is capable of constructing rules and applying them in proper contexts, while creating the descriptions with symbols. With the knowledge that this method may be used in the neural system of the brain, it offers a definitive basis to build a theory of processing in the human brain. It becomes possible to map the fine structure of connectivity to determine or to model how the processing takes place in the brain that allows it to model the natural phenomena.
In this work, the rationale of structured semantics of specifics, and of abstractions is systematically developed from the consideration of state transitions alone due entirely to the natural limits of causation. The consequent microscopic or macroscopic observable states are shown to represent those semantics. This, not only leads to a more holistic understanding and comprehension of the natural universe, but also establishes a robust foundation, a platform to develop a scientific understanding of one of the most enigmatic phenomena of all, the human consciousness!
Funding
This research received no external funding.
Acknowledgments
I wish to thank N. Krishnan, TIFR, for useful comments on a part of the manuscript. I also thank an anonymous reviewer whose comments shed light on certain important and relevant issues requiring sharper distinctions to be made, and for pointing to relevant literature. A word of thanks is due to the member of MDPI who made linguistic improvements to this article.
Conflicts of Interest
The author declares no conflict of interest.
References
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Hintikka, J. On Semantic Information. In Physics, Logic, and History; Yourgrau, W., Breck, A.D., Eds.; Springer: Boston, MA, USA, 1970; pp. 147–172. [Google Scholar]
- Dietrich, E. Semantics and the computational paradigm in cognitive psychology. Synthese 1989, 79, 119–141. [Google Scholar] [CrossRef]
- Ralph, M.A.L.; Jefferies, E.; Patterson, K.; Rogers, T.T. The neural and computational bases of semantic cognition. Nat. Rev. Neurosci. 2017, 18, 42–55. [Google Scholar] [CrossRef] [PubMed]
- Binder, J.R.; Desai, R.H. The neurobiology of semantic memory. Trends Cogn. Sci. 2011, 15, 527–536. [Google Scholar] [CrossRef] [PubMed]
- Kiefer, M.; Pulvermüller, F. Conceptual representations in mind and brain: Theoretical developments, current evidence and future directions. Cortex 2012, 48, 805–825. [Google Scholar] [CrossRef] [PubMed]
- McClelland, J.L.; Rogers, T.T. The parallel distributed processing approach to semantic cognition. Nat. Rev. Neurosci. 2003, 4, 310–322. [Google Scholar] [CrossRef] [PubMed]
- Landauer, R. Information is a physical entity. Physics A 1999, 263, 63–67. [Google Scholar] [CrossRef]
- Vedral, V. Information and physics. Information 2012, 3, 219–223. [Google Scholar] [CrossRef]
- Karnani, M.; Pääkkönen, K.; Annila, A. The physical character of information. Proc. R. Soc. A 2009, 465, 2155–2175. [Google Scholar] [CrossRef]
- Davies, P. Information and the nature of reality: From physics to metaphysics. In Universe from Bit; Davies, P., Gregersen, N.H., Eds.; Cambridge University Press: Cambridge, UK, 2010; pp. 65–91. [Google Scholar]
- Dretske, F.I. Naturaliozing the Mind; MIT Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Barwise, J.; Seligman, J. Information Flow: The Logic of Distributed Systems; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Roederer, J.G. On the Concept of Information and Its Role in Nature. Entropy 2003, 5, 3–33. [Google Scholar] [CrossRef]
- Bais, F.A.; Farmer, J.D. The Physics of Information. arXiv, 2007; arXiv:0708.2837v2. [Google Scholar]
- Goyal, P. Information Physics-Towards a New Conception of Physical Reality. Information 2012, 3, 567–594. [Google Scholar] [CrossRef]
- Knoll, G.F. Radiation Detection and Measurement, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Gell-Mann, M.; Hartle, J.B. Decoherent histories quantum mechanics with one real fine-grained history. Phys. Rev. A 2012, 85, 062120. [Google Scholar] [CrossRef]
- Fields, C. If Physics Is an Information Science, What Is an Observer? Information 2012, 3, 92–123. [Google Scholar] [CrossRef]
- Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 1935, 47, 777–780. [Google Scholar] [CrossRef]
- Hirsch, J.A. Synaptic Physiology and Receptive Field Structure in the Early Visual Pathway of the Cat. Cereb. Cortex 2003, 13, 63–69. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.B. Receptive field structure in the primate retina. Vis. Res. 1996, 36, 631–644. [Google Scholar] [CrossRef]
- Khrennikov, A. Quantum-like model of processing of information in the brain based on classical electromagnetic field. Biosystems 2011, 105, 250–262. [Google Scholar] [CrossRef] [PubMed]
- Basole, A.; White, L.E.; Fitzpatrick, D. Mapping multiple features in the population response of visual cortex. Nature 2003, 423, 986–990. [Google Scholar] [CrossRef] [PubMed]
- Albright, T.D. Direction and orientation selectivity of neurons in visual area MT of the macaque. J. Neurophys. 1984, 52, 1106–1130. [Google Scholar] [CrossRef] [PubMed]
- Treisman, A. The binding problem. Curr. Opin. Neurobiol. 1996, 6, 171–178. [Google Scholar] [CrossRef]
- Roskies, A.L. The Binding Problem. Neuron 1999, 24, 7–9. [Google Scholar] [CrossRef]
- Singer, W. Consciousness and the Binding Problem. Ann. N. Y. Acad. Sci. 2001, 929, 123–146. [Google Scholar] [CrossRef] [PubMed]
- McNorgan, C.; Reid, J.; McRae, K. Integrating conceptual knowledge within and across representational modalities. Cognition 2011, 118, 211–233. [Google Scholar] [CrossRef] [PubMed]
- Yuval-Greenberg, S.; Deouell, L.Y. What You See Is Not (Always) What You Hear: Induced Gamma Band Responses Reflect Cross-Modal Interactions in Familiar Object Recognition. J. Neurosci. 2007, 27, 1090–1096. [Google Scholar] [CrossRef] [PubMed]
- Harris, K.D.; Shepherd, G.M.G. The neocortical circuit: Themes and variations. Nat. Neurosci. 2015, 18, 170–181. [Google Scholar] [CrossRef] [PubMed]
- Harris, K.D. Cortical computation in mammals and birds. Proc. Natl. Acad. Sci. USA 2015, 112, 3184–3185. [Google Scholar] [CrossRef] [PubMed]
- Calabrese, A.; Woolley, S.M.N. Coding principles of the canonical cortical microcircuit in the avian brain. Proc. Natl. Acad. Sci. USA 2015, 112, 3517–3522. [Google Scholar] [CrossRef] [PubMed]
- Durrani, S.A.; Bull, R.K. Solid State Nuclear Track Detection: Principles, Methods, and Applications; International Series of Monographs in Natural Philosophy; Pergramon Press: Oxford, UK, 1987. [Google Scholar]
- Fleischer, R.L.; Price, P.B.; Walker, R.M. Nuclear Tracks in Solids: Principles and Applications; University of California Press: Berkeley, CA, USA, 1975. [Google Scholar]
- Yadav, J.S.; Singh, R.K. Error analysis for particle identification in CR-39 track detectors. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms. 1990, 51, 69–75. [Google Scholar] [CrossRef]
- Henke, R.P.; Benton, E.V. On geometry of tracks in dielectric nuclear track detectors. Nucl. Instrum. Methods 1971, 97, 483–489. [Google Scholar] [CrossRef]
- Yadav, J.S.; Singh, R.K. Space Lab-3 Anuradha detector response and the expected charge resolution. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms. 1990, 51, 63–68. [Google Scholar] [CrossRef]
- Benton, E.V. On latent track formation in organic nuclear charged particle track detectors. Radiat. Eff. 1970, 2, 273–280. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics, 6th ed.; Pergoman Press: Oxford, UK, 1980; Chapter X. [Google Scholar]
- Thompson, A.; Moran, J.; Swenson, G., Jr. Interferometry and Synthesis in Radio Astronomy, 2nd ed.; Wiley-VCH: Weinheim, Germany, 2001. [Google Scholar]
- Bhatnagar, S.; Cornwell, T.; Uson, J. Correcting direction-dependent gains in the deconvolution of radio interferometric images. Astron. Astrophys. 2008, 487, 419–429. [Google Scholar] [CrossRef]
- Intema, H.; Van der Tol, S.; Cotton, W. Ionospheric calibration of low frequency radio interferometric observations using the peeling scheme-I.Method description and first results. Astron. Astrophys. 2009, 501, 1185–1205. [Google Scholar] [CrossRef]
- Jacques, V.; Wu, E.; Grosshans, F.; Treussart, F.; Grangier, P.; Aspect, A.; Roch, J.F. Experimental Realization of Wheeler’s Delayed-Choice Gedanken Experiment. Science 2007, 315, 966–968. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, F.; Coudreau, T.; Milman, P.; Ostrowsky, D.B.; Tanzilli, S. Entanglement-Enabled Delayed-Choice Experiment. Science 2012, 338, 637–640. [Google Scholar] [CrossRef] [PubMed]
- Peruzzo, A.; Shadbolt, P.; Brunner, N.; Popescu, S.; O’Brien, J.L. A Quantum Delayed-Choice Experiment. Science 2012, 338, 634–637. [Google Scholar] [CrossRef] [PubMed]
- Marquis de Laplace, P.S. A Philosophical Essay on Probablities; John Wiley and Sons: Hoboken, NJ, USA, 1902. [Google Scholar]
- Binzegger, T.; Douglas, R.J.; Martin, K.A.C. Stereotypical Bouton Clustering of Individual Neurons in Cat Primary Visual Cortex. J. Neurosci. 2007, 27, 12242–12254. [Google Scholar] [CrossRef] [PubMed]
- Potjans, T.C.; Diesmann, M. The Cell-Type Specific Cortical Microcircuit: Relating Structure and Activity in a Full-Scale Spiking Network Model. Cereb. Cortex 2014, 24, 785–806. [Google Scholar] [CrossRef] [PubMed]
- Tabareau, N.; Slotine, J.J.; Pham, Q.C. How Synchronization Protects from Noise. PLoS Comput. Biol. 2010, 6, e1000637. [Google Scholar] [CrossRef] [PubMed]
- Stein, R.B.; Gossen, E.R.; Jones, K.E. Neuronal variability: Noise or part of the signal? Nat. Rev. Neurosci. 2005, 6, 389–397. [Google Scholar] [CrossRef] [PubMed]
- Wheeler, J.A. Information, Physics, Quantum: The Search for Links. In Proceedings of the 3rd International Symposium on Foundations of Quantum Mechanics, Tokyo, Japan, 28–31 August 1989; pp. 354–358. [Google Scholar]
- Tegmark, M. The Mathematical Universe. Found. Phys. 2008, 38, 101–150. [Google Scholar] [CrossRef]
- Kako, E.; Wagner, L. The semantics of syntactic structures. Trends Cogn. Sci. 2001, 5, 102–108. [Google Scholar] [CrossRef]
- Hutten, E.H. On Semantics and Physics. Proc. Aristot. Soc. 1948, 49, 115–132. [Google Scholar] [CrossRef]
- Penrose, R. Shadows of the Mind: A Search for the Missing Science of Consciousness; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Hut, P.; Alford, M.; Tegmark, M. On Math, Matter and Mind. Found. Phys. 2006, 36, 765–794. [Google Scholar] [CrossRef]
- Hameroff, S.; Penrose, R. Consciousness in the universe: A review of the ‘Orch OR’ theory. Phys. Life Rev. 2014, 11, 39–78. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).