Long-Short-Term Memory Network Based Hybrid Model for Short-Term Electrical Load Forecasting
Abstract
:1. Introduction
2. Methodologies
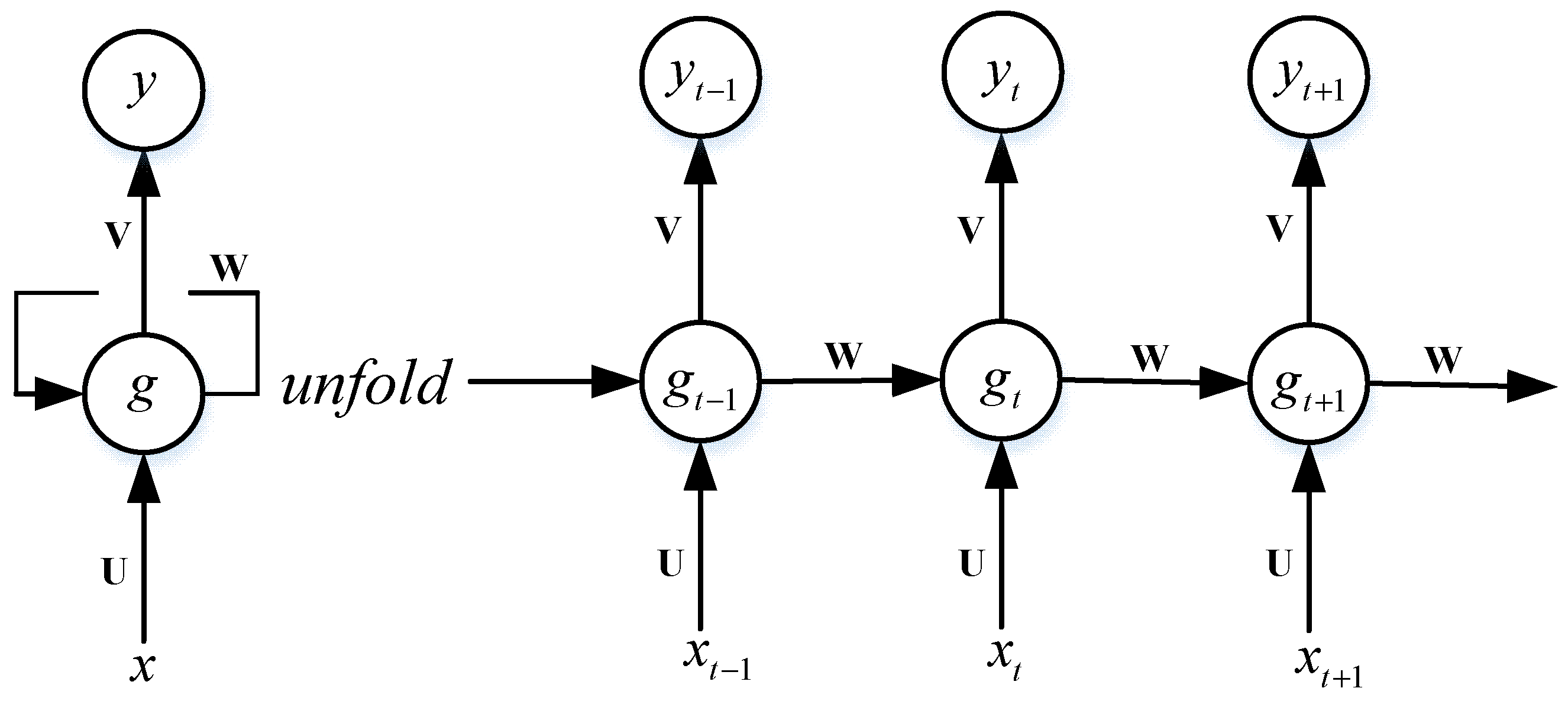
2.1. Recurrent Neural Network
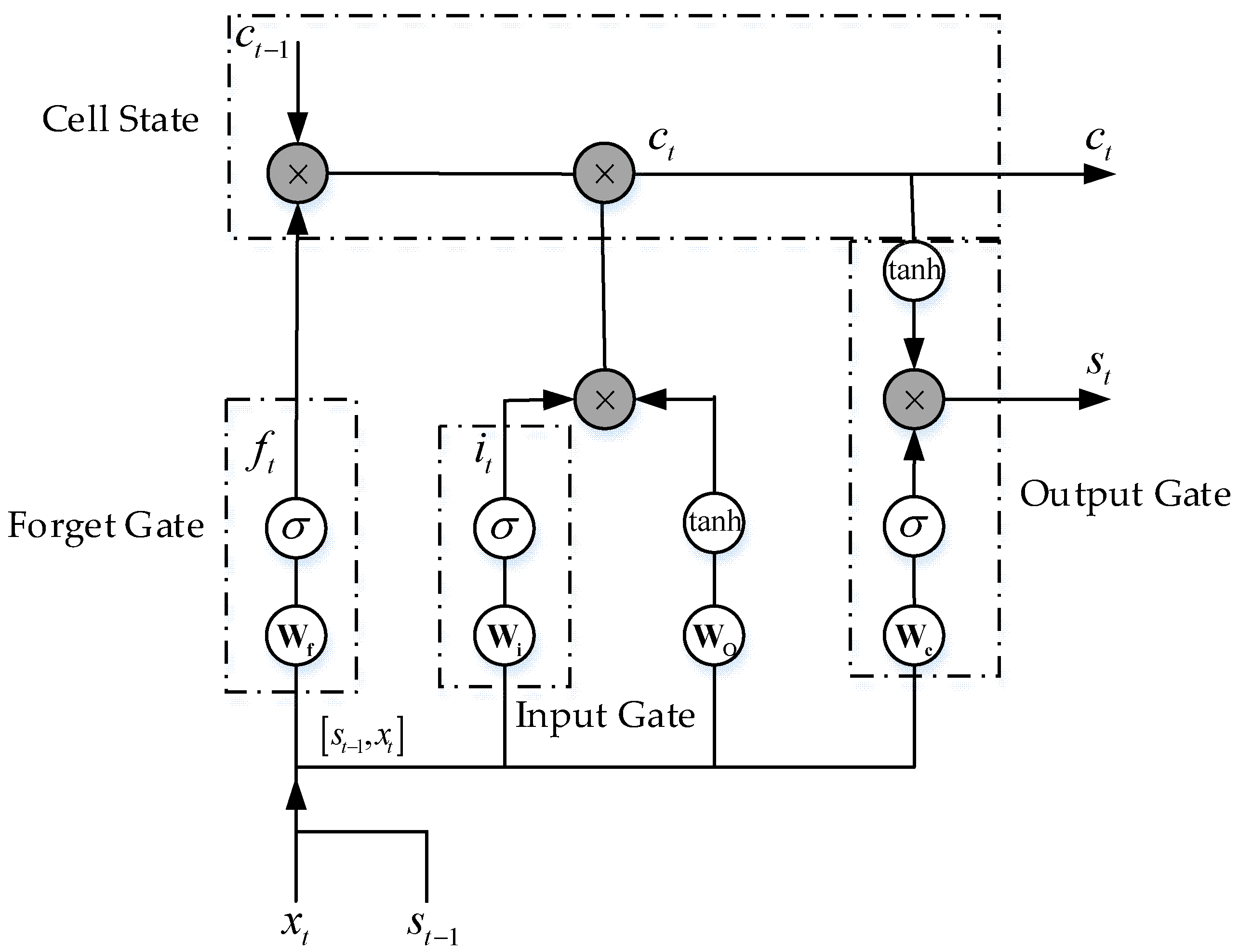
2.2. Long-Short-Term Memory Network
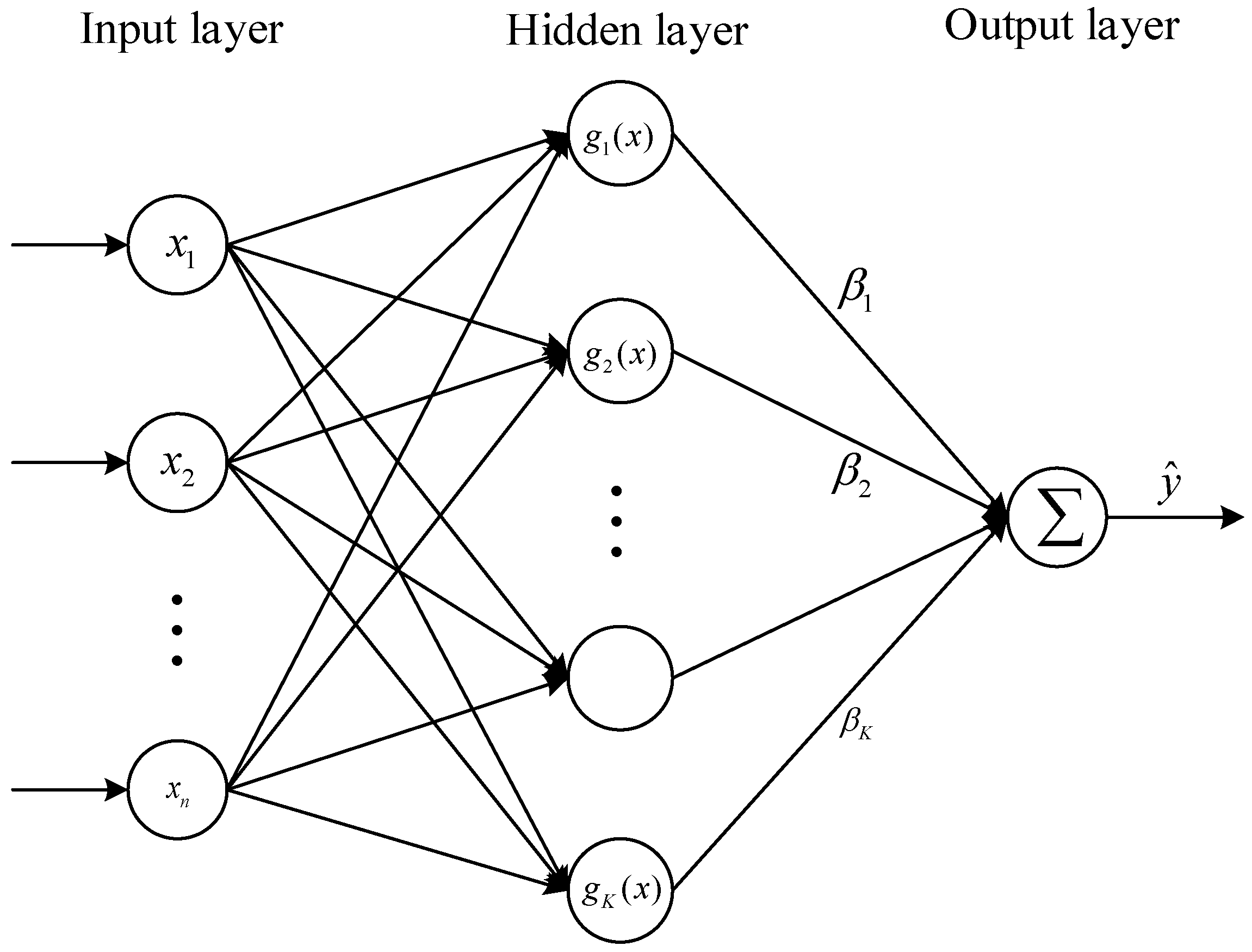
2.3. Extreme Learning Machine
3. The Proposed Hybrid Model
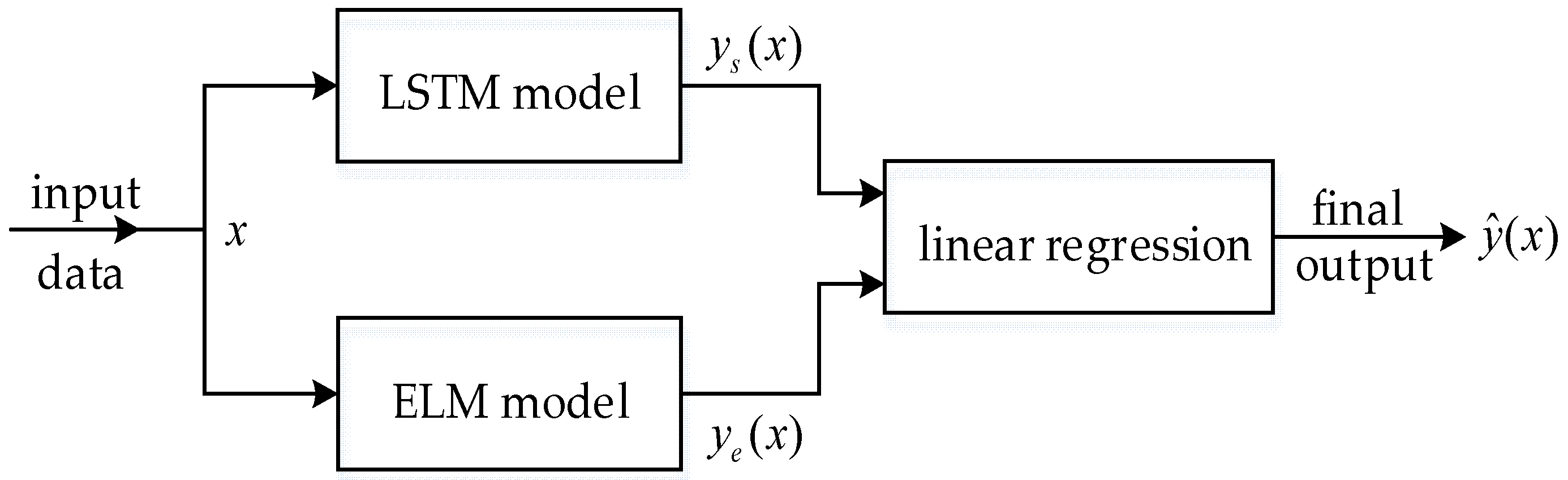
3.1. The Hybrid Model
3.2. Model Evaluation Indices
3.3. Data Preprocessing
4. Experiments and Comparisons
4.1. Electrical Load Forecasting of the Albert Area
4.1.1. Applied Dataset
4.1.2. Experimental Setting
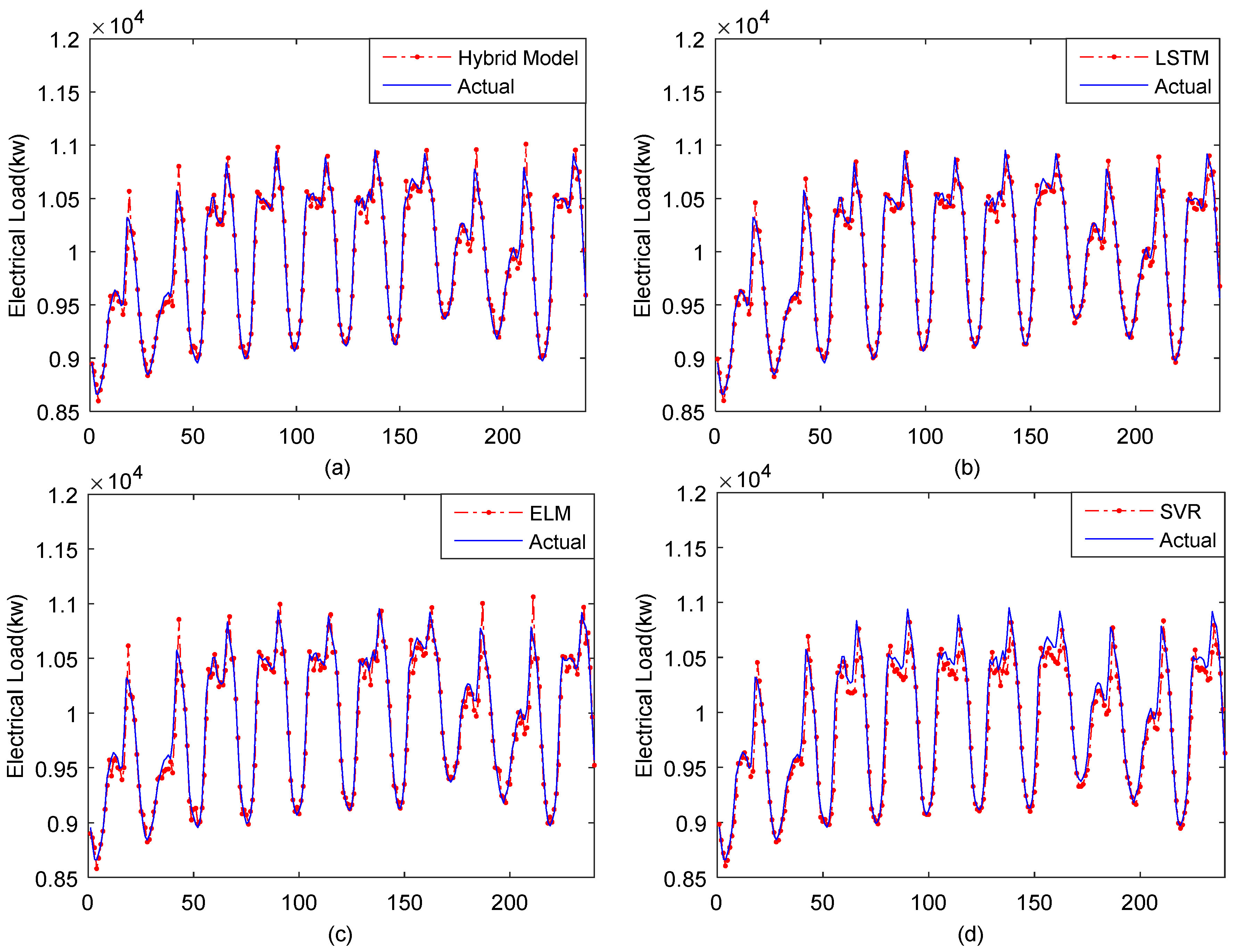
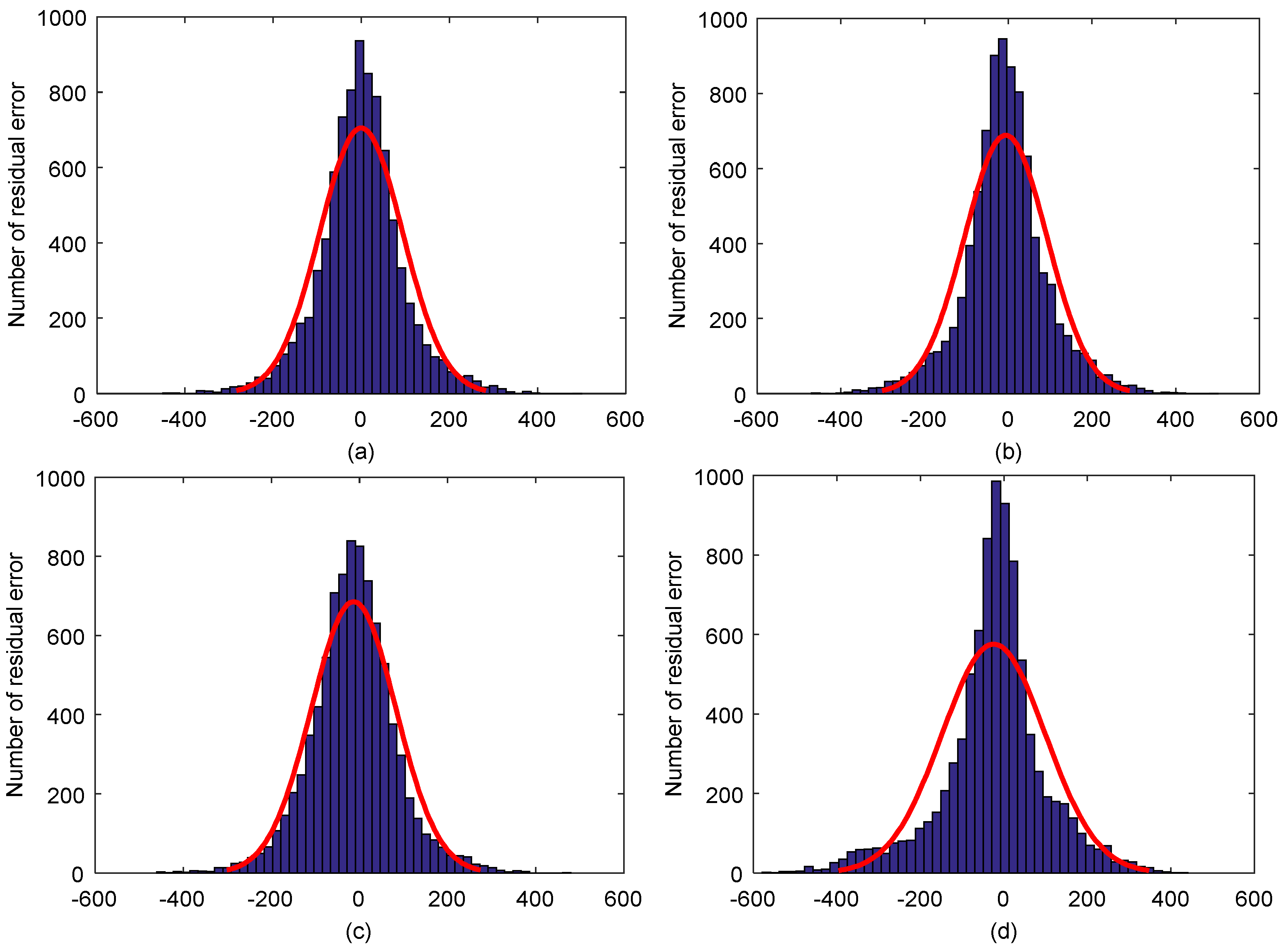
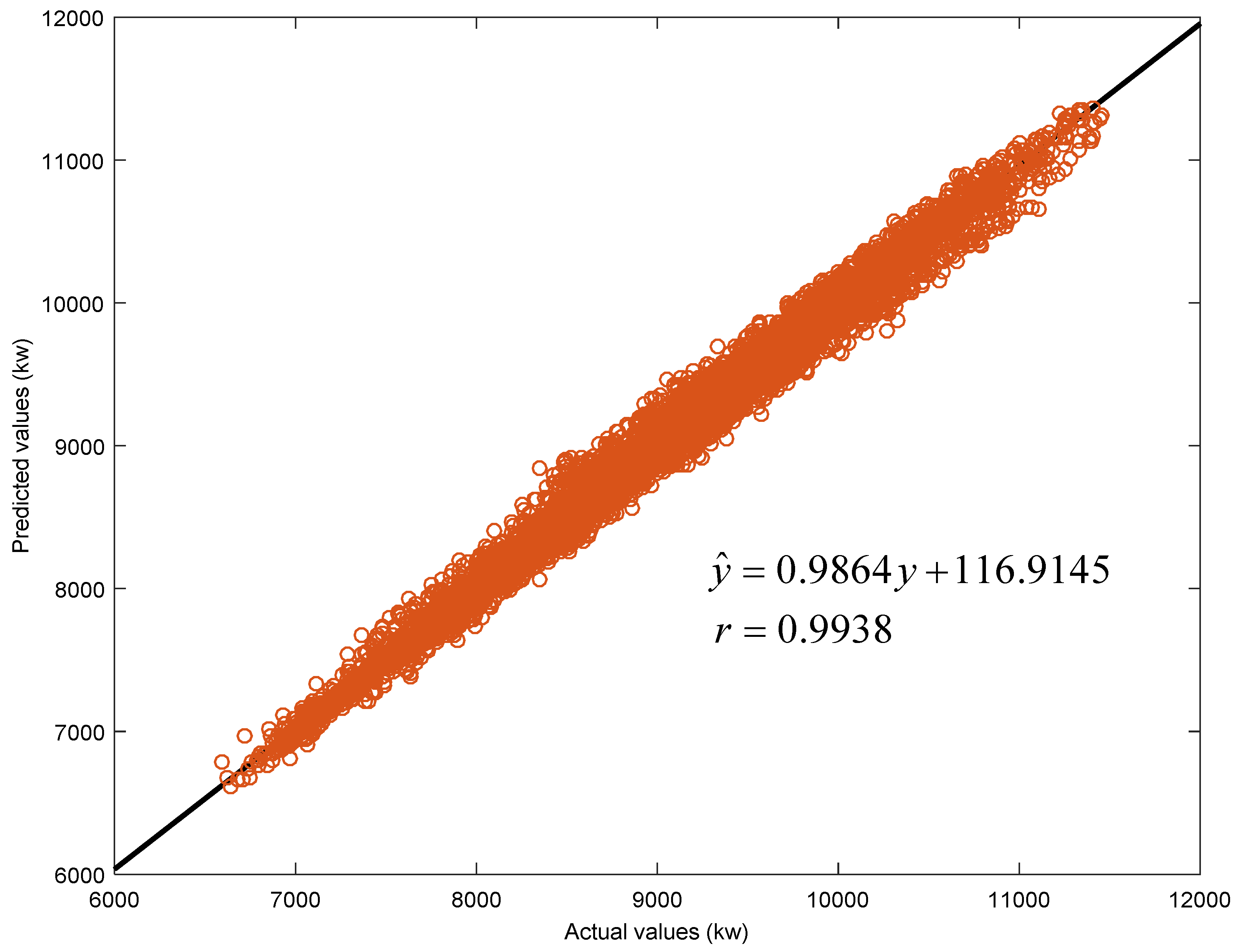
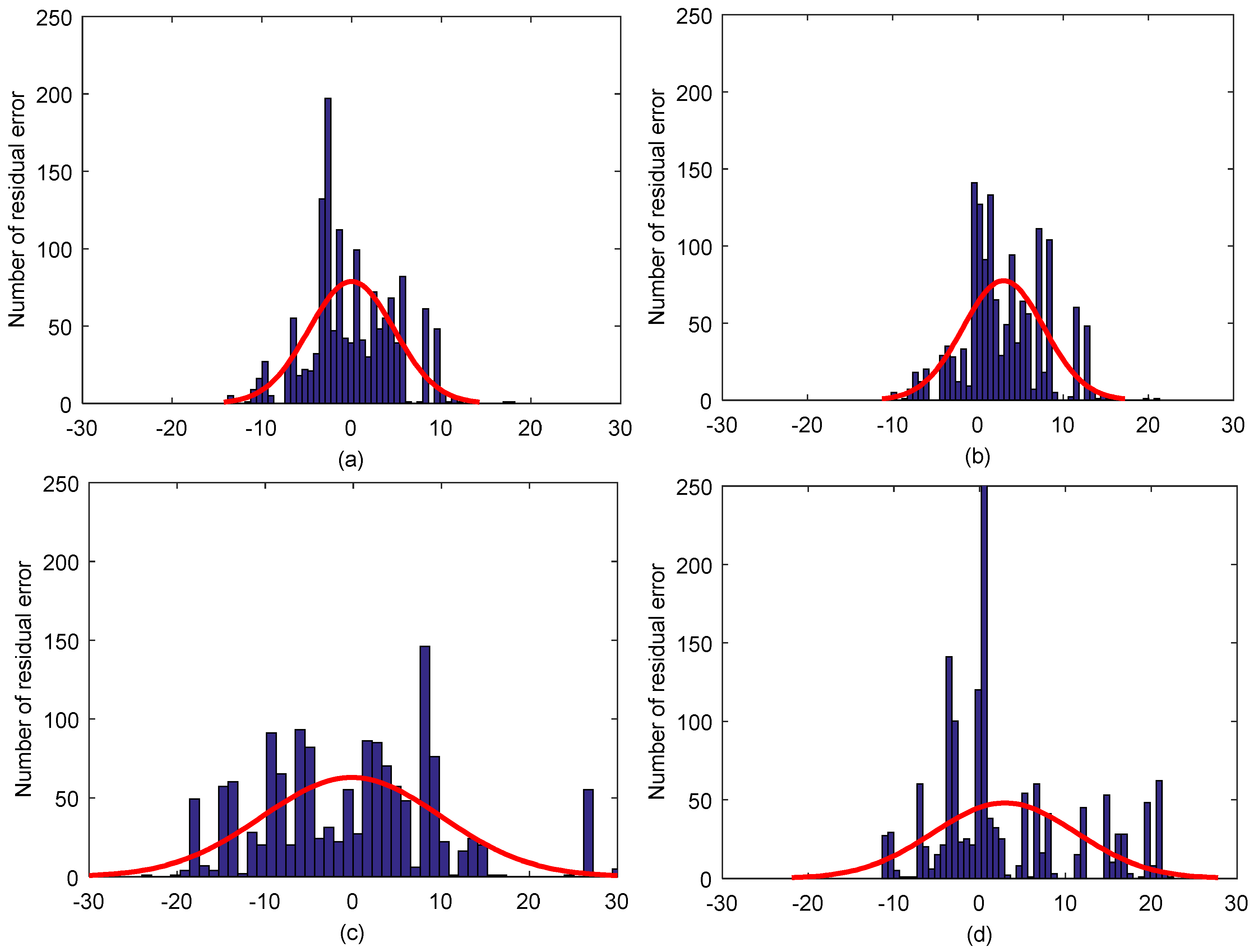
4.1.3. Experimental Results and Analysis
4.2. Electrical Load Forecasting of One Service Restaurant
4.2.1. Applied Dataset
4.2.2. Experimental Setting
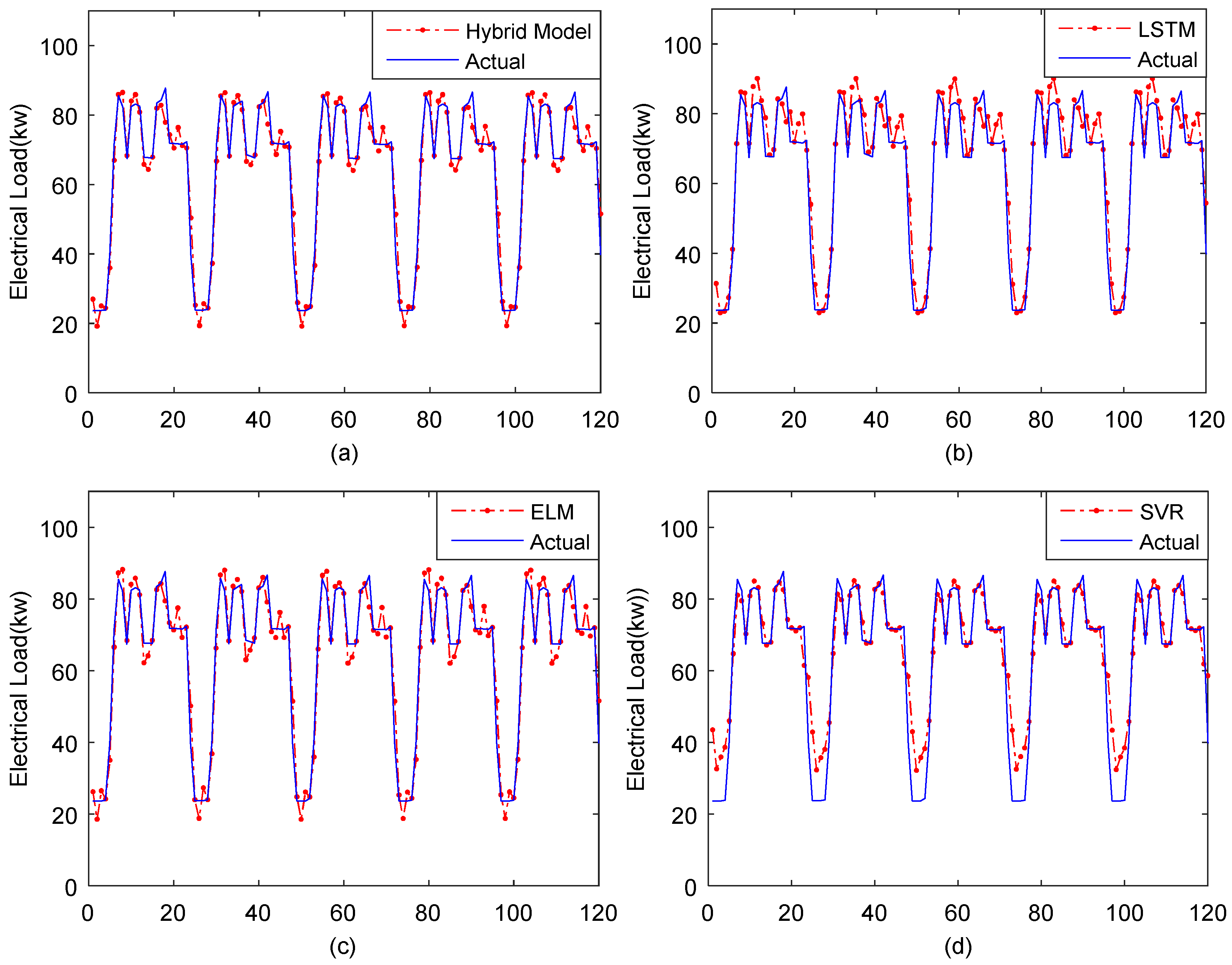
4.2.3. Experimental Results and Analysis
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Global Power Report. Available online: http://www.powerchina.cn/art/2016/9/20/art_26_186950.html (accessed on 5 May 2018).
- Pappas, S.S.; Ekonomou, L.; Karamousantas, D.C.; Chatzarakis, G.E. Electricity demand loads modeling using AutoRegressive Moving Average (ARMA) models. Energy 2008, 33, 1353–1360. [Google Scholar] [CrossRef]
- Im, K.M.; Lim, J.H. A design of short-term load forecasting structure based on ARIMA using load pattern classification. Commun. Comput. Inf. Sci. 2011, 185, 296–303. [Google Scholar]
- Huang, S.J.; Shih, K.R. Short-term load forecasting via ARMA model identification including non-Gaussian process considerations. IEEE Trans. Power Syst. 2003, 18, 673–679. [Google Scholar] [CrossRef]
- Papalexopoulos, A.D.; Hesterberg, T.C. A regression-based approach to short-term system load forecasting. IEEE Trans. Power Syst. 1990, 5, 1535–1547. [Google Scholar] [CrossRef]
- Hong, T.; Gui, M.; Baran, M.E.; Willis, H.L. Modeling and forecasting hourly electric load by multiple linear regression with interactions. In Proceedings of the IEEE Power and Energy Society General Meeting, Providence, RI, USA, 25–29 July 2010; pp. 1–8. [Google Scholar]
- Vamvakas, P.; Tsiropoulou, E.E.; Papavassiliou, S. Dynamic provider selection & power resource management in competitive wireless communication markets. Mob. Netw. Appl. 2017, 7, 1–14. [Google Scholar]
- Tsiropoulou, E.E.; Katsinis, G.K.; Filios, A.; Papavassiliou, S. On the problem of optimal cell selection and uplink power control in open access multi-service two-tier femtocell networks. In Proceedings of the International Conference on Ad-Hoc Networks and Wireless, Benidorm, Spain, 22–27 June 2014; pp. 114–127. [Google Scholar]
- Cordeschi, N.; Amendola, D.; Shojafar, M.; Baccarelli, E. Performance evaluation of primary-secondary reliable resource-management in vehicular networks. In Proceedings of the IEEE 25th Annual International Symposium on Personal, Indoor, and Mobile Radio Communication, Washington, DC, USA, 2–5 September 2014; pp. 959–964. [Google Scholar]
- Cordeschi, N.; Amendola, D.; Shojafar, M.; Naranjo, P.G.V.; Baccarelli, E. Memory and memoryless optimal time-window controllers for secondary users in vehicular networks. In Proceedings of the International Symposium on Performance Evaluation of Computer and Telecommunication Systems, Chicago, IL, USA, 26–29 July 2015; pp. 1–7. [Google Scholar]
- Espinoza, M. Fixed-size least squares support vector machines: A large scale application in electrical load forecasting. Comput. Manag. Sci. 2006, 3, 113–129. [Google Scholar] [CrossRef]
- Chen, Y.B.; Xu, P.; Chu, Y.Y.; Li, W.L.; Wu, Y.T.; Ni, L.Z.; Bao, Y.; Wang, K. Short-term electrical load forecasting using the Support Vector Regression (SVR) model to calculate the demand response baseline for office buildings. Appl. Energy 2017, 195, 659–670. [Google Scholar] [CrossRef]
- Duan, P.; Xie, K.G.; Guo, T. T.; Huang, X.G. Short-term load forecasting for electric power systems using the PSO-SVR and FCM clustering techniques. Energies 2011, 4, 173–184. [Google Scholar] [CrossRef]
- Agarwal, V.; Bougaev, A.; Tsoukalas, L. Kernel regression based short-term load forecasting. In Proceedings of the International Conference on Artificial Neural Networks, Athens, Greece, 10–14 September 2006; pp. 701–708. [Google Scholar]
- Mordjaoui, M.; Haddad, S.; Medoued, A.; Laouafi, A. Electric load forecasting by using dynamic neural network. Int. J. Hydrog. Energy 2017, 28, 17655–17663. [Google Scholar] [CrossRef]
- Pan, L.N.; Feng, X.S.; Sang, F.W.; Li, L.J.; Leng, M.W. An improved back propagation neural network based on complexity decomposition technology and modified flower pollination optimization for short-term load forecasting. Neural Comput. Appl. 2017, 13, 1–19. [Google Scholar] [CrossRef]
- Leme, R.C.; Souza, A.C.Z.D.; Moreira, E.M.; Pinheiro, C.A.M. A hierarchical neural model with time windows in long-term electrical load forecasting. Neural Comput. Appl. 2006, 16, 456–470. [Google Scholar]
- Li, H.Z.; Guo, S.; Li, C.J.; Sun, J.Q. A hybrid annual power load forecasting model based on generalized regression neural network with fruit fly optimization algorithm. Knowl. Based Syst. 2013, 37, 378–387. [Google Scholar] [CrossRef]
- Salkuti, S.R. Short-term electrical load forecasting using radial basis function neural networks considering weather factors. Electri. Eng. 2018, 5, 1–11. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: A new learning scheme of feedforward neural networks. In Proceedings of the IEEE International Joint Conference on Neural Networks, Budapest, Hungary, 25–29 July 2004; pp. 985–990. [Google Scholar]
- Zhu, Q.Y.; Qin, A.K.; Suganthan, P.N.; Huang, G.B. Rapid and brief communication: Evolutionary extreme learning machine. Pattern Recognit. 2005, 38, 1759–1763. [Google Scholar] [CrossRef]
- Ertugrul, O.F. Forecasting electricity load by a novel recurrent extreme learning machines approach. Int. J. Electr. Power Energy Syst. 2016, 78, 429–435. [Google Scholar] [CrossRef]
- Zhang, R.; Dong, Z.Y.; Xu, Y.; Meng, K.; Wong, K.P. Short-term load forecasting of Australian National Electricity Market by an ensemble model of extreme learning machine. IET Gener. Transm. Dis. 2013, 7, 391–397. [Google Scholar] [CrossRef]
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement learning: A survey. J. Artifi. Intell. Res. 1996, 4, 237–285. [Google Scholar]
- Boyan, J.A. Generalization in reinforcement learning: Safely approximating the value function. In Proceedings of the Neural Information Processings Systems, Denver, CO, USA, 27 November–2 December 1995; pp. 369–376. [Google Scholar]
- Xiong, R.; Cao, J.; Yu, Q. Reinforcement learning-based real-time power management for hybrid energy storage system in the plug-in hybrid electric vehicle. Appl. Energy 2018, 211, 538–548. [Google Scholar] [CrossRef]
- Li, C.D.; Ding, Z.X.; Zhao, D.B.; Yi, J.Q.; Zhang, G.Q. Building energy consumption prediction: An extreme deep learning approach. Energies 2017, 10, 1525. [Google Scholar] [CrossRef]
- Li, C.D.; Ding, Z.X.; Yi, J.Q.; Lv, Y.S.; Zhang, G.Q. Deep belief network based hybrid model for building energy consumption prediction. Energies 2018, 11, 242. [Google Scholar] [CrossRef]
- Dong, Y.; Liu, Y.; Lian, S.G. Automatic age estimation based on deep learning algorithm. Neurocomputing 2016, 187, 4–10. [Google Scholar] [CrossRef]
- Raveane, W.; Arrieta, M.A.G. Shared map convolutional neural networks for real-time mobile image recognition. In Distributed Computing and Artificial Intelligence, 11th International Conference; Springer International Publishing: Cham, Switzerland, 2014; pp. 485–492. [Google Scholar]
- Kumaran, N.; Vadivel, A.; Kumar, S.S. Recognition of human actions using CNN-GWO: A novel modeling of CNN for enhancement of classification performance. Multimed. Tools Appl. 2018, 1, 1–33. [Google Scholar] [CrossRef]
- Potluri, S.; Fasih, A.; Vutukuru, L.K.; Machot, F.A.; Kyamakya, K. CNN based high performance computing for real time image processing on GPU. In Proceedings of the Joint INDS'11 & ISTET'11, Klagenfurt, Austria, 25–27 July 2011; pp. 1–7. [Google Scholar]
- Ahmad, J.; Sajjad, M.; Rho, S.; Kwon, S.I.; Lee, M.Y.; Balk, S.W. Determining speaker attributes from stress-affected speech in emergency situations with hybrid SVM-DNN architecture. Multimed. Tools Appl. 2016, 1–25. [Google Scholar] [CrossRef]
- Wu, Z.Y.; Zhao, K.; Wu, X.X.; Lan, X.Y.; Meng, L. Acoustic to articulatory mapping with deep neural network. Multimed. Tools Appl. 2015, 74, 9889–9907. [Google Scholar] [CrossRef]
- Lv, Y.S.; Duan, Y.J.; Kang, W.W.; Li, Z.X.; Wang, F.Y. Traffic flow prediction with big data: A deep learning approach. IEEE T. Intell. Transp. Syst. 2015, 16, 865–873. [Google Scholar] [CrossRef]
- Ma, X.L.; Yu, H.Y.; Wang, Y.P.; Wang, Y.H. Large-scale transportation network congestion evolution prediction using deep learning theory. Plos One 2015, 10. [Google Scholar] [CrossRef] [PubMed]
- Yu, D.H.; Liu, Y.; Yu, X. A data grouping CNN algorithm for short-term traffic flow forecasting. In Asia-Pacific Web Conference; Springer: Cham, Switzerland, 2016; pp. 92–103. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Che, Z.; Purushotham, S.; Cho, K.; Sontag, D.; Liu, Y. Recurrent neural networks for multivariate time series with missing values. Sci. Rep. 2018, 8, 6085. [Google Scholar] [CrossRef] [PubMed]
- Lipton, Z.C.; Kale, D.C.; Wetzel, R. Modeling Missing Data in Clinical Time Series with RNNs. Available online: http://proceedings.mlr.press/v56/Lipton16.pdf (accessed on 5 July 2018).
- Ma, X.; Tao, Z.; Wang, Y.; Yu, H.; Wang, Y. Long short-term memory neural network for traffic speed prediction using remote microwave sensor data. Transp. Res. Part C 2015, 54, 187–197. [Google Scholar] [CrossRef]
- Karim, F.; Majumdar, S.; Darabi, H.; Chen, S. LSTM fully convolutional networks for time series classification. IEEE Access 2018, 6, 1662–1669. [Google Scholar] [CrossRef]
- AESO Electrical Load Data Set. Available online: https://www.aeso.ca. (accessed on 12 March 2018).
- Commercial and Residential Buildings’ Hourly Load Dataset. Available online: https://openei.org/datasets/dataset/commercial-and-residential-hourly-load-profiles-for-all-tmy3-locations-in-the-united-states. (accessed on 13 April 2018).
| Trial | Input | Cell | Averaged Indices | Trial | Input | Cell | Averaged Indices | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE | MRE(%) | RMSE | MAE | MRE(%) | RMSE | ||||||
| 1 | 5 | 20 | 116.9954 | 1.2601 | 152.1007 | 21 | 9 | 20 | 102.1704 | 1.0997 | 132.9284 |
| 2 | 5 | 40 | 97.2733 | 1.0570 | 129.7889 | 22 | 9 | 40 | 122.0178 | 1.3104 | 151.9188 |
| 3 | 5 | 60 | 84.5351 | 0.9317 | 116.7891 | 23 | 9 | 60 | 95.1910 | 1.0435 | 122.9191 |
| 4 | 5 | 80 | 89.2817 | 0.9798 | 121.4982 | 24 | 9 | 80 | 80.6772 | 0.8834 | 108.8855 |
| 5 | 5 | 100 | 86.1510 | 0.9516 | 117.5446 | 25 | 9 | 100 | 90.6934 | 0.9839 | 122.7209 |
| 6 | 6 | 20 | 84.5489 | 0.9283 | 116.2049 | 26 | 10 | 20 | 98.7483 | 1.0667 | 127.0956 |
| 7 | 6 | 40 | 85.0707 | 0.9425 | 117.9868 | 27 | 10 | 40 | 91.7649 | 0.9960 | 119.4111 |
| 8 | 6 | 60 | 97.7385 | 1.0591 | 129.7166 | 28 | 10 | 60 | 72.2753 | 0.7963 | 98.4589 |
| 9 | 6 | 80 | 115.2194 | 1.2475 | 146.6029 | 29 | 10 | 80 | 73.5594 | 0.8078 | 99.5021 |
| 10 | 6 | 100 | 84.7226 | 0.9298 | 118.0570 | 30 | 10 | 100 | 82.0465 | 0.8944 | 109.2512 |
| 11 | 7 | 20 | 91.4179 | 1.0080 | 120.6575 | 31 | 11 | 20 | 73.3172 | 0.8060 | 98.6403 |
| 12 | 7 | 40 | 82.4949 | 0.9090 | 112.7130 | 32 | 11 | 40 | 76.3391 | 0.8406 | 102.6357 |
| 13 | 7 | 60 | 86.2502 | 0.9427 | 116.7535 | 33 | 11 | 60 | 79.0162 | 0.8680 | 104.7912 |
| 14 | 7 | 80 | 98.2174 | 1.0788 | 126.8882 | 34 | 11 | 80 | 85.3047 | 0.9272 | 112.1438 |
| 15 | 7 | 100 | 82.4535 | 0.9047 | 114.1381 | 35 | 11 | 100 | 105.8272 | 1.1464 | 132.3876 |
| 16 | 8 | 20 | 125.2901 | 1.3474 | 161.0009 | 36 | 12 | 20 | 77.5761 | 0.8551 | 102.5785 |
| 17 | 8 | 40 | 81.4138 | 0.8948 | 110.8346 | 37 | 12 | 40 | 93.2179 | 1.0102 | 120.6827 |
| 18 | 8 | 60 | 84.5120 | 0.9297 | 114.3067 | 38 | 12 | 60 | 81.2607 | 0.8938 | 106.8901 |
| 19 | 8 | 80 | 106.8368 | 1.1719 | 138.6301 | 39 | 12 | 80 | 128.2620 | 1.3791 | 160.0733 |
| 20 | 8 | 100 | 113.2714 | 1.2239 | 144.1222 | 40 | 12 | 100 | 124.7561 | 1.3343 | 163.9346 |
| MAE | MRE(%) | RMSE | |
|---|---|---|---|
| Hybrid model | 68.7121 | 0.7565 | 93.2667 |
| LSTM | 72.0921 | 0.7924 | 98.6150 |
| ELM | 85.2096 | 0.9272 | 121.0129 |
| SVR | 81.3732 | 0.8884 | 115.8054 |
| Trial | Input | Cell | Averaged Indices | Trial | Input | Cell | Averaged iIndices | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE | MRE(%) | RMSE | MAE | MRE(%) | RMSE | ||||||
| 1 | 6 | 20 | 7.1771 | 12.9736 | 9.6727 | 21 | 10 | 20 | 7.7198 | 13.9318 | 9.9992 |
| 2 | 6 | 40 | 6.2598 | 12.5989 | 9.3245 | 22 | 10 | 40 | 7.0582 | 13.0492 | 9.6955 |
| 3 | 6 | 60 | 5.5457 | 10.8710 | 8.3062 | 23 | 10 | 60 | 5.5835 | 10.0200 | 8.0960 |
| 4 | 6 | 80 | 5.5134 | 10.6229 | 8.2383 | 24 | 10 | 80 | 6.4581 | 11.5403 | 9.0721 |
| 5 | 6 | 100 | 7.1821 | 12.4820 | 9.3755 | 25 | 10 | 100 | 5.9818 | 11.0428 | 8.6531 |
| 6 | 7 | 20 | 7.5924 | 14.3682 | 9.9352 | 26 | 11 | 20 | 7.0673 | 13.5552 | 9.7034 |
| 7 | 7 | 40 | 6.6790 | 13.1658 | 8.9878 | 27 | 11 | 40 | 6.6684 | 12.7804 | 9.4788 |
| 8 | 7 | 60 | 6.6408 | 13.2102 | 9.2235 | 28 | 11 | 60 | 6.8561 | 13.5773 | 9.3759 |
| 9 | 7 | 80 | 6.5768 | 12.0001 | 8.7904 | 29 | 11 | 80 | 4.8765 | 8.8409 | 7.1536 |
| 10 | 7 | 100 | 6.2907 | 11.0141 | 8.4172 | 30 | 11 | 100 | 5.2019 | 9.4162 | 6.9256 |
| 11 | 8 | 20 | 7.1725 | 14.1086 | 9.9249 | 31 | 12 | 20 | 6.9364 | 12.7357 | 9.1828 |
| 12 | 8 | 40 | 7.7985 | 15.1546 | 10.3129 | 32 | 12 | 40 | 6.9170 | 12.7038 | 9.1602 |
| 13 | 8 | 60 | 7.1521 | 13.3672 | 9.8928 | 33 | 12 | 60 | 7.5057 | 13.7293 | 9.5874 |
| 14 | 8 | 80 | 6.9347 | 14.0792 | 9.9348 | 34 | 12 | 80 | 5.2464 | 10.3753 | 7.2903 |
| 15 | 8 | 100 | 6.0706 | 11.9748 | 8.6654 | 35 | 12 | 100 | 4.2324 | 7.9345 | 5.7119 |
| 16 | 9 | 20 | 6.3518 | 12.7758 | 9.3983 | 36 | 13 | 20 | 6.3514 | 12.7800 | 8.8737 |
| 17 | 9 | 40 | 7.3086 | 14.3657 | 9.7797 | 37 | 13 | 40 | 6.3419 | 12.4733 | 9.0717 |
| 18 | 9 | 60 | 6.4742 | 12.0802 | 9.2994 | 38 | 13 | 60 | 5.3390 | 10.7757 | 7.1112 |
| 19 | 9 | 80 | 5.7523 | 11.1158 | 8.2278 | 39 | 13 | 80 | 5.2022 | 10.2410 | 6.5495 |
| 20 | 9 | 100 | 5.9189 | 10.8050 | 8.2184 | 40 | 13 | 100 | 5.3477 | 10.8264 | 6.9637 |
| MAE | MRE(%) | RMSE | |
| Hybrid Model | 2.8782 | 5.4335 | 3.6224 |
| LSTM | 4.2631 | 7.9125 | 5.6178 |
| ELM | 5.7569 | 10.5350 | 6.7282 |
| SVR | 5.9182 | 16.7053 | 8.5685 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Li, C.; Xie, X.; Zhang, G. Long-Short-Term Memory Network Based Hybrid Model for Short-Term Electrical Load Forecasting. Information 2018, 9, 165. https://doi.org/10.3390/info9070165
Xu L, Li C, Xie X, Zhang G. Long-Short-Term Memory Network Based Hybrid Model for Short-Term Electrical Load Forecasting. Information. 2018; 9(7):165. https://doi.org/10.3390/info9070165
Chicago/Turabian StyleXu, Liwen, Chengdong Li, Xiuying Xie, and Guiqing Zhang. 2018. "Long-Short-Term Memory Network Based Hybrid Model for Short-Term Electrical Load Forecasting" Information 9, no. 7: 165. https://doi.org/10.3390/info9070165
APA StyleXu, L., Li, C., Xie, X., & Zhang, G. (2018). Long-Short-Term Memory Network Based Hybrid Model for Short-Term Electrical Load Forecasting. Information, 9(7), 165. https://doi.org/10.3390/info9070165





