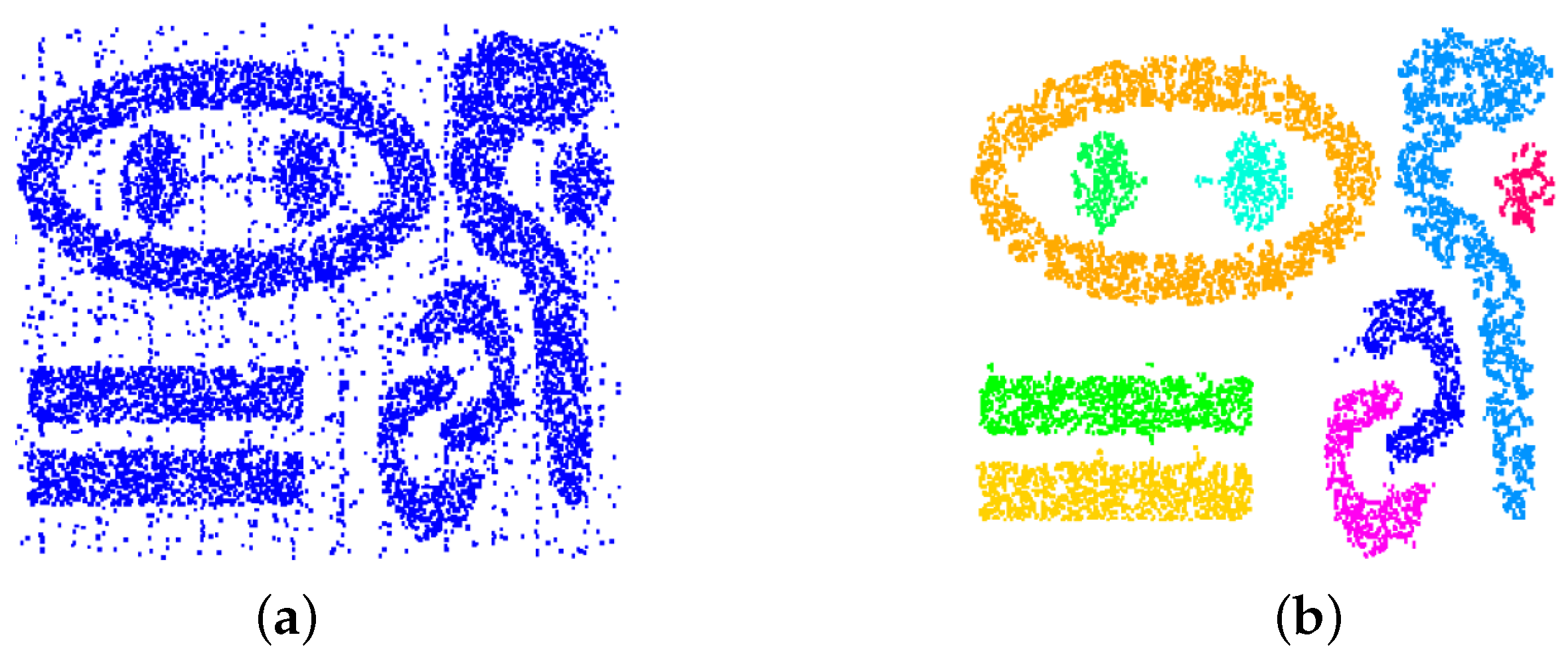1. Introduction
Visualization of multivariate volume data has become a common, yet still challenging task in scientific visualization. Datasets come from traditional scientific visualization applications such as numerical simulations, see VisContest 2008 [
1], or medical imaging, see VisContest 2010 [
2]. While looking into individual attributes can be of high interest, the full phenomena are often only captured when looking into all attributes simultaneously. Consequently, visualization methods shall allow for the investigation and analysis of the multidimensional attribute space. The attribute space may consist of measured and/or simulated attributes as well as derived attributes including statistical properties (e.g., means and variances) or vector and tensor field properties (e.g., divergence, finite time Lyupanov exponent, and diffusion tensor eigenvalues). Hence, we are facing a multidimensional data analysis task, where dimension here refers to the dimensionality of the attribute space.
Multidimensional data analysis typically requires some automatic components that need to be used to produce a visual encoding. Typical components are clustering approaches or projections from higher-dimensional spaces into 2D or 3D visual spaces. Often, clustering and projections are combined to produce a visualization of a clustering result. The clustering approach shall be applied first to produce high-dimensional clusters, which can be used as an input for an improved projection. Unfortunately, clustering in a high-dimensional space faces the problem that points belonging to the same cluster can be rather far apart in the high-dimensional space. This observation is due to the curse of dimensionality, a term coined by Bellman [
3]. It refers to the fact that there is an exponential increase of volume when adding additional dimensions.
The impact of the curse of dimensionality on practical issues when clustering high-dimensional data is as follows: Clustering approaches can be categorized as being based on distances between data points or being based on density estimates. However, only distance-based clustering algorithms can effectively detect clusters of arbitrary shape. Distance-based clustering approaches require local density estimates, which are typically based on space partitioning (e.g., over a regular or an adaptive grid) or on a kernel function. Both grid-based and kernel-based approaches require the choice of an appropriate size of locality for density estimation, namely, the grid cell size or the kernel size, respectively. Using a too large size leads to not properly resolving the clusters such that clusters may not be separated. Hence, a small size is required. However, due to the curse of dimensionality, clusters fall apart when using a too small size and one ends up with individual data points rather than clusters thereof.
Attribute spaces of multivariate volume data are a specific case of multidimensional data, as the unstructured data points in attribute space do have a structure when looking into the corresponding physical space. We propose to make use of this structure by applying interpolation between attribute-space data points whose corresponding representations in physical space exhibit a neighbor relationship. Thus, the objective of the paper is to develop a grid-based multifield clustering approach, which is robust to the grid cell size and is free of any density threshold.
The contributions of the paper include: generation of sufficiently high number of multifield data points to overcome the curse of dimensionality, applying a threshold-free grid-based technique for computing a hierarchical cluster tree, and visualizing the clustering results using coordinated views. The present paper extends our previous work [
4] by a detailed discussion of adaptive data upsampling in the presence of sharp material boundaries or missing values, which is a typical case in many applications, e.g., for geophysical datasets. We include a new case study using climate simulation data, demonstrate the effect of adaptive interpolation in the land–sea border regions, and properly handle the varying spatial grid cells’ areas.
The overall approach presented in this paper takes as input a multivariate volume dataset. First, it applies an interpolation scheme to upsample the attribute space, see
Section 4 for the main idea,
Section 5 for an improved computation scheme, and
Section 6 for an amendment to handle sharp material boundaries. The upsampled attribute space is then clustered using a hierarchical density-based clustering approach, see
Section 3. Based on the clustering result,
Section 7 describes how a combined visual exploration of physical and attribute space using coordinated views can be employed. The results of the approach are presented in
Section 8 and its properties are discussed in
Section 9. It is shown that our approach manages to produce high-quality clustering results without the necessity of tweaking the grid cell size or similar. We also document that comparable results cannot be obtained when clustering without the proposed interpolation step. The linked volume visualization, therefore, reflects the phenomena in the multivariate volume data more reliably.
3. Clustering
We present a hierarchical density cluster construction based on nonparametric density estimation using multivariate histograms. Clusters can be identified without any threshold parameter of density level sets. Let the domain of the attribute space be given in form of a
d-dimensional hypercube, i.e., a
d-dimensional bounding box. To derive the density function, we spatially subdivide the domain of the dataset into cells (or bins) of equal shape and size. Thus, the spatial subdivision is given in form of a
d-dimensional regular structured grid with equidistant
d-dimensional grid points, i.e., a
d-dimensional histogram. For each bin of the histogram, we count the number of sample points lying inside. The multivariate density function is estimated by the formula
for any
x within the cell, where
n is the overall number of data points,
is the number of data points inside the bin, and
is the area of the
d-dimensional bin. As the area
is equal for all bins, the density of each bin is proportional to the number
of data points lying inside the bin. Hence, it suffices to just operate with those numbers
.
To estimate all non-empty bins, we use a partitioning algorithm that iterates through all dimensions.
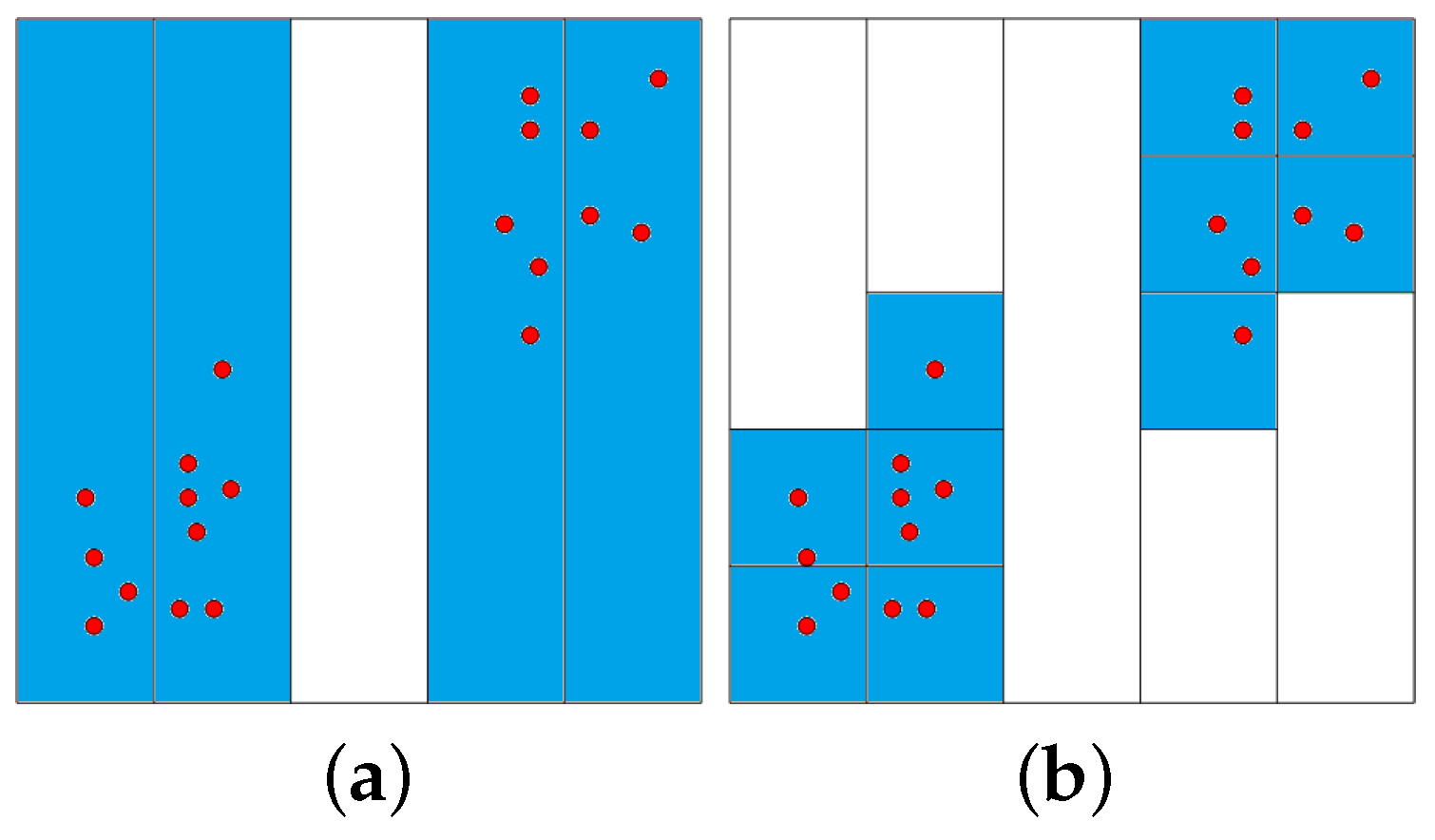
Figure 1 illustrates the partition process for a two-dimensional dataset: The first dimension is divided into 5 equally-sized intervals on the left-hand side of
Figure 1. Only four non-empty intervals are obtained. These intervals are subsequently divided into the second dimension, as shown on the right-hand side of
Figure 1. The time complexity for partitioning the data space is
, i.e., it can handle both datasets with many samples
n and datasets with high dimensionality
d.
Given the
d-dimensional histogram, clusters are defined as largest sets of neighboring non-empty bins, where neighboring refers to sharing a common vertex. To detect higher-density clusters within each cluster, we remove all cells containing the minimum number of points in this cluster and detect among the remaining cells, again, largest sets of neighboring cells. This step may lead to splitting of a cluster into multiple higher-density clusters. This process is iterated until no more clusters split. Recording the splitting information, we obtain a cluster hierarchy. Those clusters that do not split anymore represent local maxima and are referred to as mode clusters.
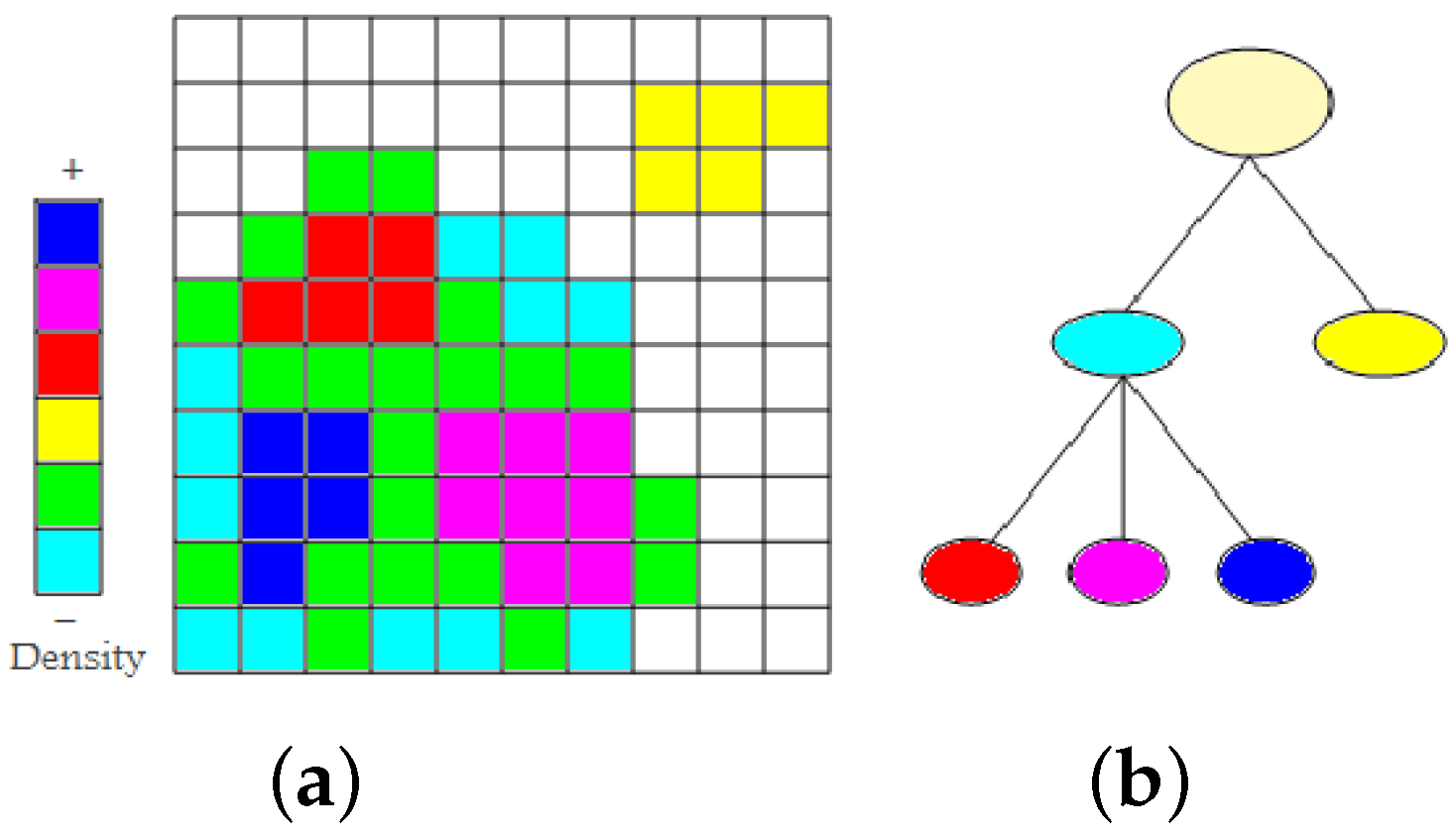
Figure 2a shows a set of non-empty cells with six different density levels in a two-dimensional space. First, we find the two low-density clusters as connected components of non-empty cells. They are represented in the cluster tree as immediate children nodes of the root node (cyan and yellow), see
Figure 2b. From the cluster colored cyan, we remove all minimum density level cells (cyan). The cluster remains connected. Then, we again remove the cells with minimum density level (green). The cluster splits into three higher-density clusters (red, magenta, and blue). They appear as children nodes of the cyan node in the cluster tree. As densities are given in form of counts of data points, they are always natural numbers. Consequently, we cannot miss any split of a density cluster when iterating over the natural numbers (from zero to the maximum density). The time complexity to create a hierarchical density cluster tree is
, where
m is the number of non-empty cells.
Figure 3 shows that the clustering approach is capable of handling clusters of any shape and that it is robust against changing cluster density and noise. Noise has been handled by removing all cells with a number of sample points smaller than a noise threshold. The dataset is a synthetic one [
31].
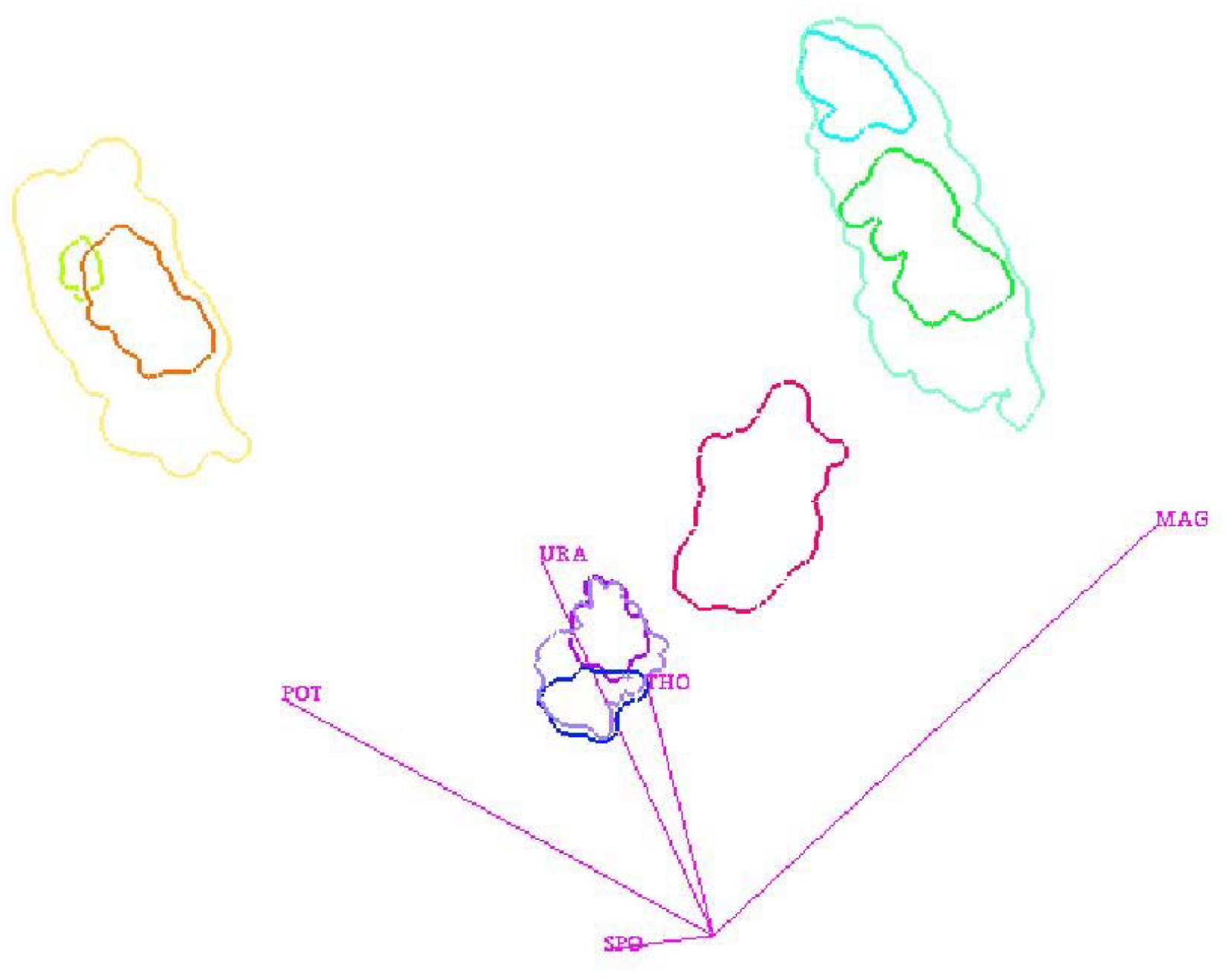
Figure 4 shows the visualization of a cluster hierarchy for the “out5d” dataset with 16,384 data points and five attributes, namely, spot (SPO), magnetics (MAG), potassium (POS), thorium (THO), and uranium (URA), using a projection in optimized 2D star coordinates [
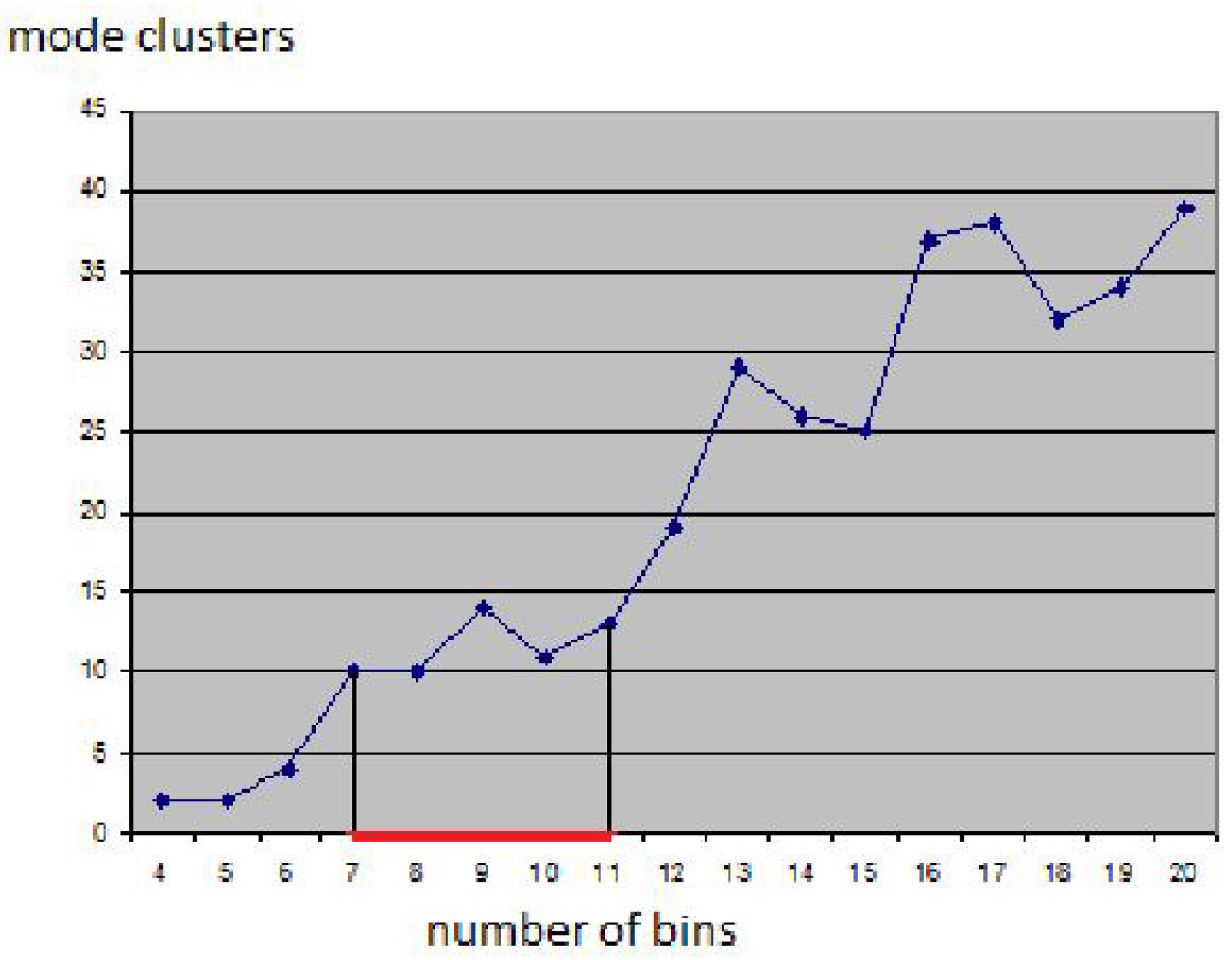
25]. The result seems feasible and all clusters were found without defining any density thresholds, but the choice of the bin size had to be determined empirically.
Figure 5 shows how sensitive the result is to the bin size: Using smaller bin sizes merges some clusters, while using larger sizes makes clusters fall apart. The result in
Figure 4 was obtained using the heuristic that cluster numbers only vary slowly close to the optimal bin size value (area marked red in
Figure 4). However, in practice, one would not generate results for the entire range of possible bin sizes for being able to apply this heuristic. Instead, one would rather use a trial-and-error approach, not knowing how reliable the result is.
4. Interpolation
Let the attribute values of the multivariate volume data be given at points
,
, in physical space. Moreover, let
,
, be the attribute values at
. Then, the points
exhibit some neighborhood relationship in physical space. Typically, this neighborhood information is given in the form of grid connectivity, but, even if no connectivity is given, meaningful neighborhood information can be derived in physical space by looking at distances (e.g., nearest neighbors or natural neighbors). Based on this neighborhood information, we can perform an interpolation to reconstruct a continuous multivariate field over the volumetric domain. In the following, we assume that the points
are given in structured form over a regular (i.e., rectangular) hexahedral grid. Thus, the reconstruction of a continuous multivariate field can be obtained by simple trilinear interpolation within each cuboid cell of the underlying grid. More precisely: Let
be a point inside a grid cell with corner points
,
, and let
be the local Cartesian coordinates of
within the cell. Then, we can compute the attribute values at
by
for all attributes (
). In attribute space, we obtain the point
, which lies within the convex hull of the set of points
,
.
Now, we want to use the interpolation scheme to overcome the curse of dimensionality when creating the d-dimensional density histogram. Using the trilinear interpolation scheme, we reconstruct the multivariate field within each single cell, which corresponds to a reconstructed area in attribute space. The portion by which the reconstructed area in attribute space falls into a bin of the d-dimensional density histogram defines the amount of density that should be added to the respective bin of the histogram. Under the assumption that each grid cell has volume , where c is the overall number of grid cells, one should add the density to the respective bin of the histogram. However, we propose to not compute r exactly for two reasons: First, the computation of the intersection of a transformed cuboid with a d-dimensional cell in a d-dimensional space can be rather cumbersome and expensive. Second, the resulting densities that are stored in the bins of the histogram would no longer be natural numbers. The second property would require us to choose density thresholds for the hierarchy generation. How to do this without missing cluster splits is an open question.
Our approach is to approximate the reconstructed multivariate field by upsampling the given dataset. This discrete approach is reasonable, as the output of the reconstruction/upsampling is, again, a discrete structure, namely a histogram. We just need to assure that the rate for upsampling is high enough such that the histogram of an individual grid cell has all non-empty bins connected. Thus, the upsampling rate depends on the size of the histogram’s bins. Moreover, if we use the same upsampling rate for all grid cells, density can still be measured in the form of the number of (upsampled) data points per bin. Hence, the generation of the density-based cluster hierarchy still works as before.
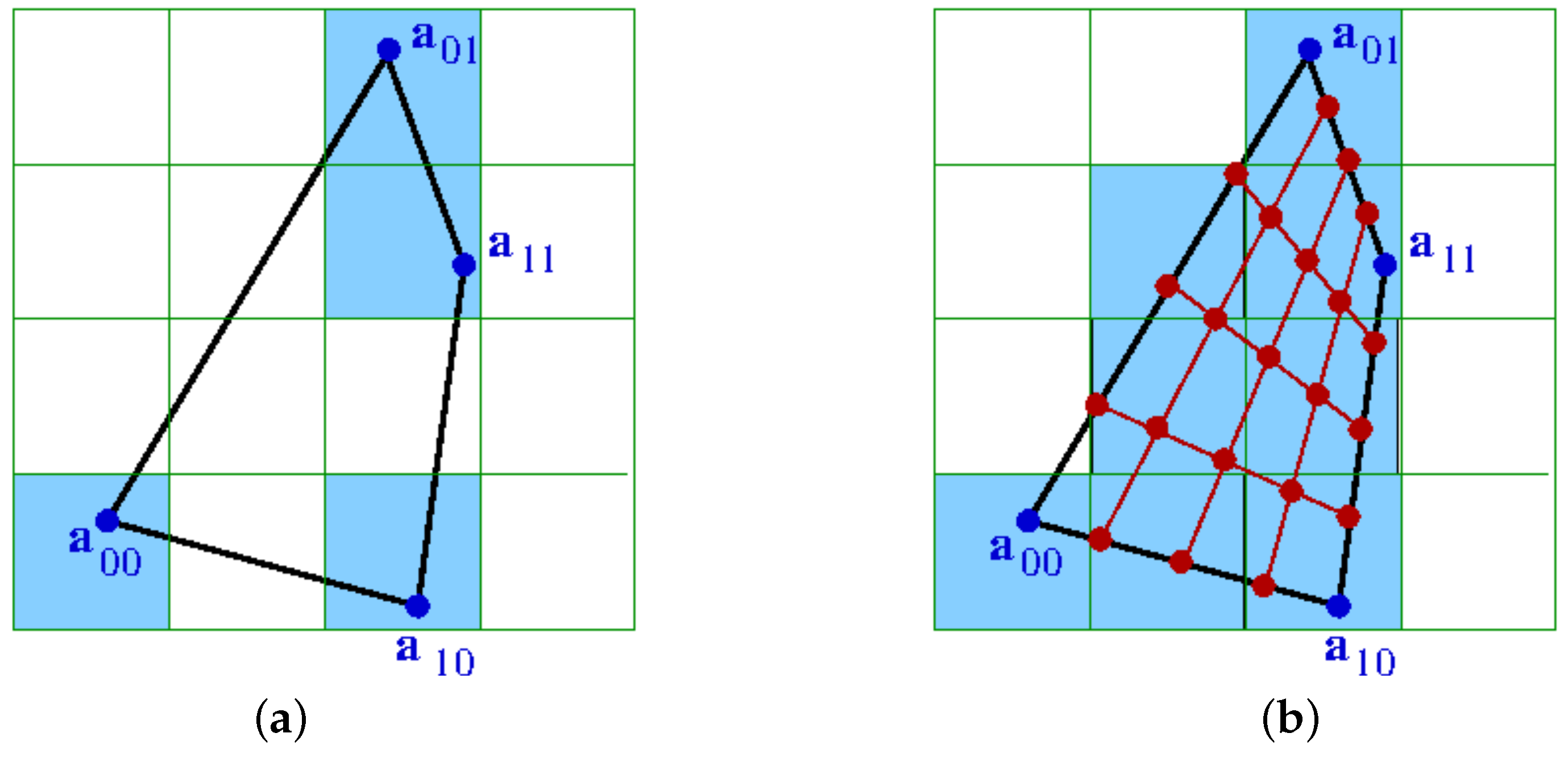
Figure 6 shows the impact of upsampling in the case of a 2D physical space and a 2D attribute space, i.e., for a transformed 2D cell with corners
,
, and a histogram with
dimensions. Without the upsampling, the non-empty bins of the histogram are not connected. After upsampling, the bins between the original non-empty bins have also been filled and the 2D cell represents a continuous region in the 2D attribute space.
When performing the upsampling for all cells of the volumetric grid, we end up with a histogram, where all non-empty cells are connected. Hence, we have overcome the curse of dimensionality. On such a histogram, we can generate the density-based cluster hierarchy without the effect of clusters falling apart.
8. Results
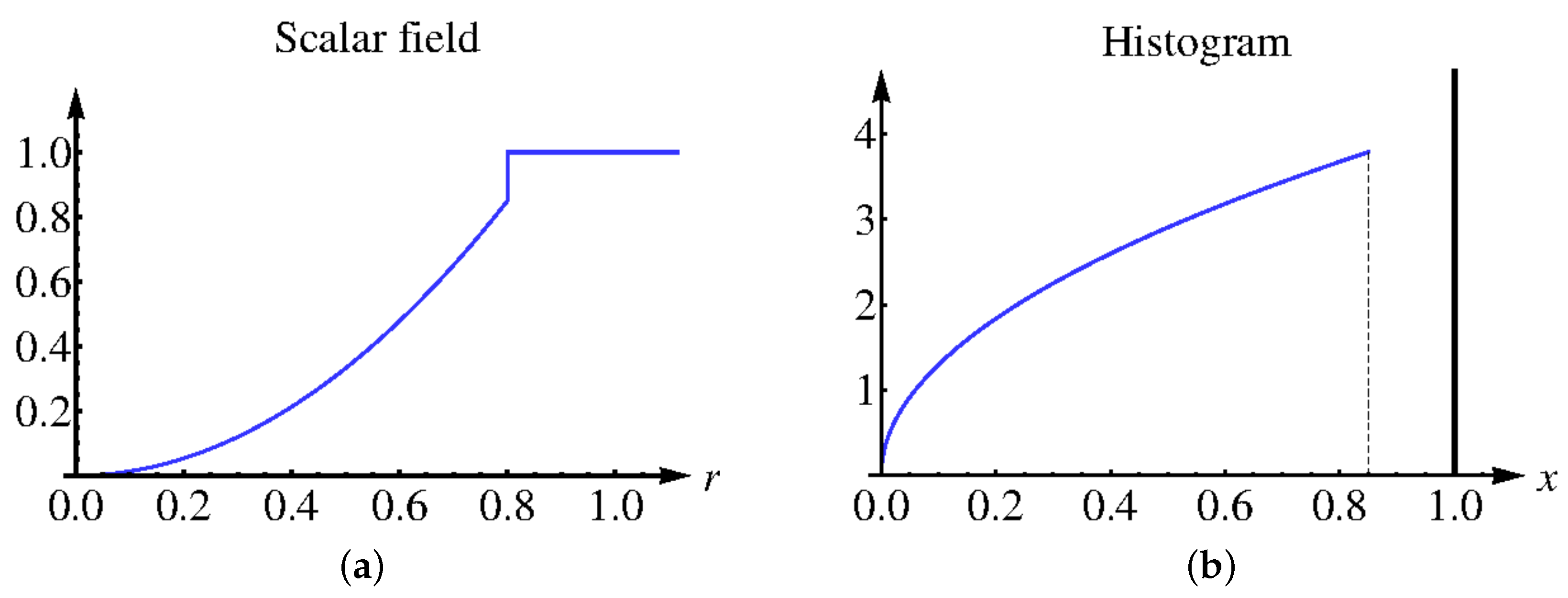
First, we demonstrate on a simple scalar field example how our approach works and show that the discrete histogram of interpolated data approaches the continuous analogon as the interpolation depth increases. Let scalar field
be defined as follows:
where
r stands for the Euclidean distance to the center of domain
, see
Figure 9a. The continuous histogram
can be computed using the relation
which leads to
The continuous histogram is plotted in
Figure 9b. The continuous data are clearly separated into two clusters, which represent the interior of a sphere and the background in physical space. However, when sampling the field at
regular samples in the physical domain. the use of 100 bins in the attribute space leads to the effect that the sphere cluster breaks into many small parts. In
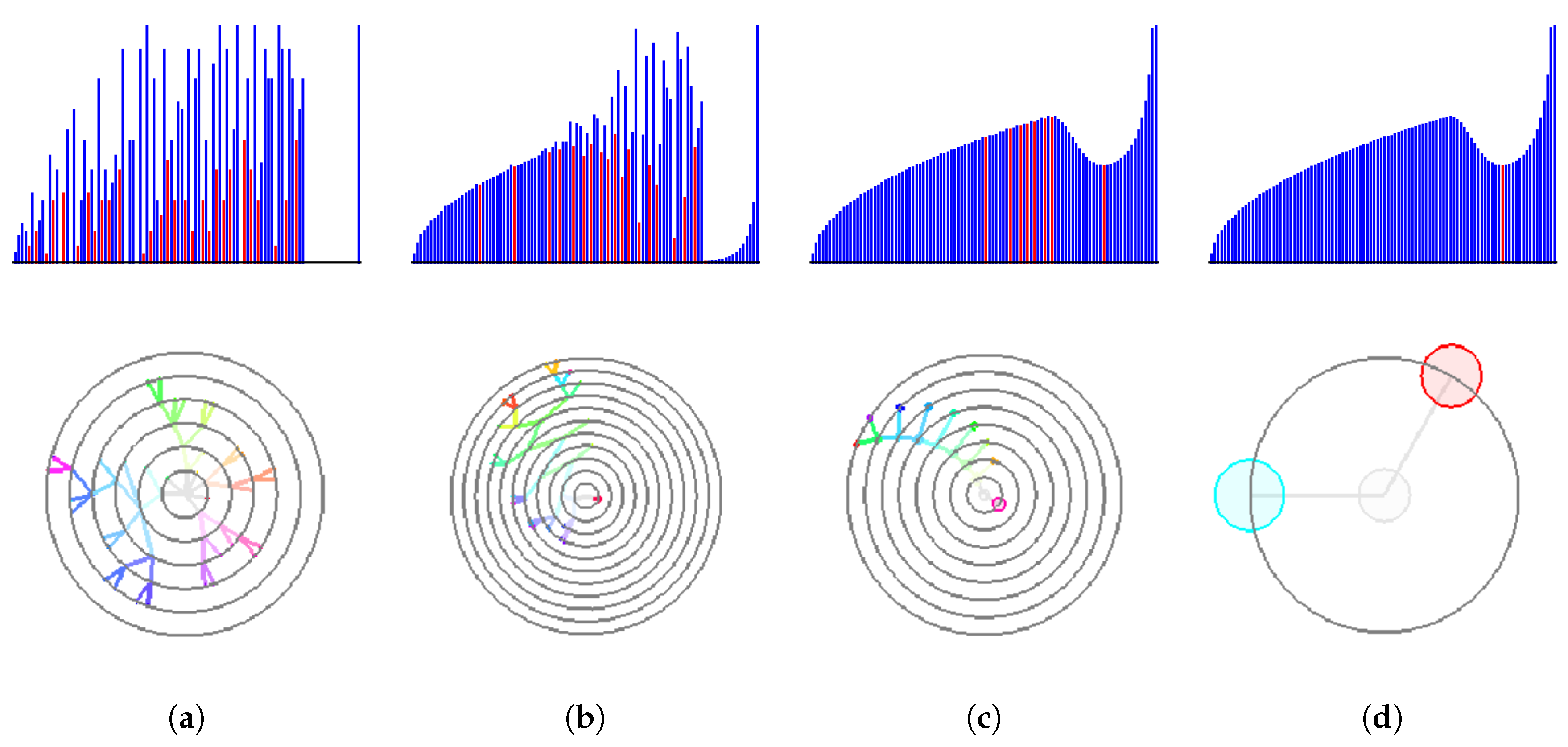
Figure 7, we demonstrate how our interpolation approach corrects the histogram (upper row) and the respective cluster tree (lower row). Without upsampling or with a low-rate upsampling (
), the corresponding histograms contain multiple local minima. Therefore, a non-vanishing density threshold is required for a correct identification of two analytically designed clusters. However, a reliable choice of such a threshold is difficult in a general set-up and thus should be avoided. As the upsampling depth grows, the resulting discrete histograms approach the shape of the continuous one. Depth
is needed to converge to the correct result of the two clusters without the need of any density threshold.
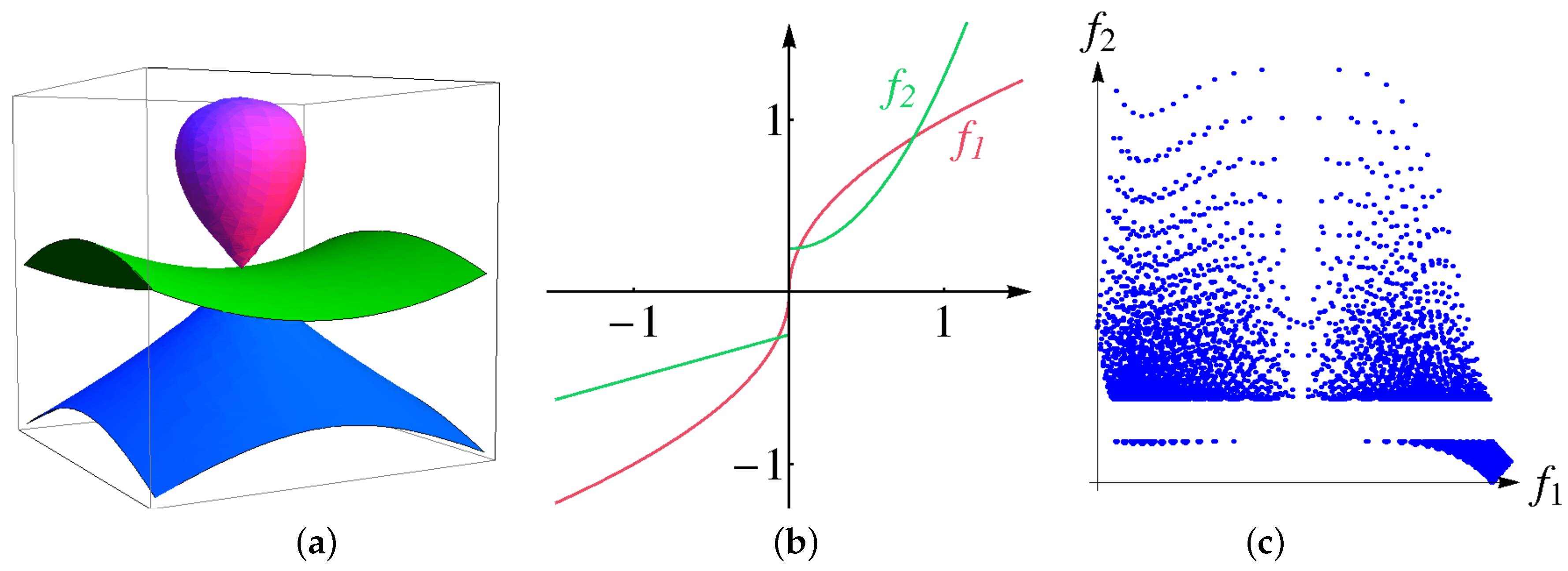
Second, we design a volumetric multi-attribute dataset, for which the ground truth is known, show how the size of bins affects the result of the clustering procedure and demonstrate that interpolation helps to resolve the issue. Given physical domain
, we use the following algebraic surfaces
see
Figure 10a. We construct the distributions of two attributes as functions of algebraic distances to the surfaces above, i.e.,
Functions
are chosen to have a discontinuity or a large derivative at the origin, respectively, see
Figure 10b. Thus, the surfaces
are cluster boundaries in the physical space. The distribution of the attribute values
is shown in a 2D scatterplot in
Figure 10c when sampling over a regular grid with
nodes. The data represent four clusters. Using 10 bins for each attribute to generate the histogram is not enough to separate all clusters resulting in a cluster tree with only two clusters as shown in
Figure 8 (upper row). A larger number of bins is necessary. When increasing the number of bins to 30 for each attribute clusters fall apart due to the curse of dimensionality, which leads to a noisy result with too many clusters, see
Figure 8 (middle row). However, applying four interpolation steps fixes the histogram. Then, the cluster tree has the desired four leaves and the boundary for all four clusters are correctly detected in physical space, see
Figure 8 (lower row).
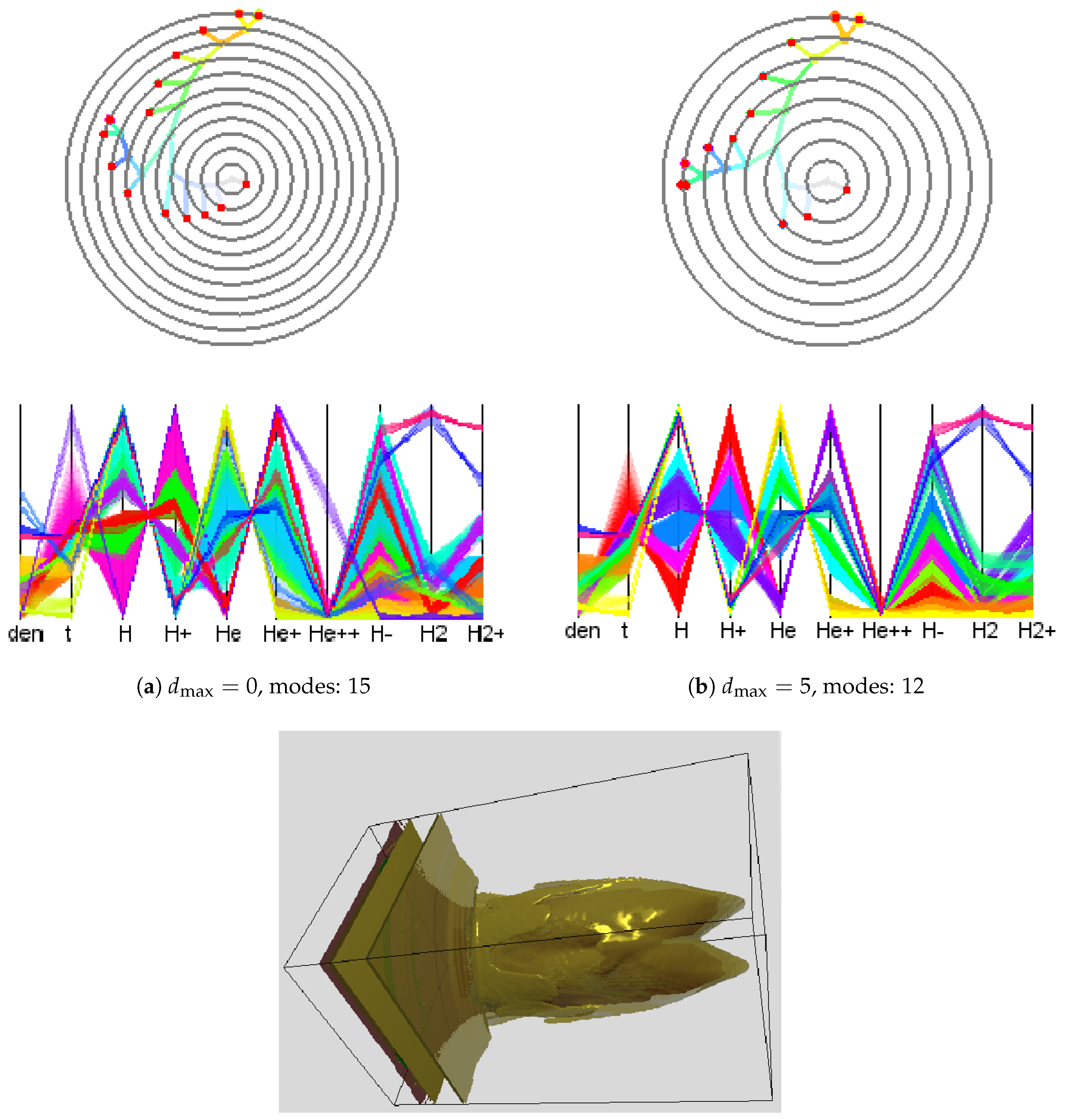
Next, we applied our methods to the simulation-based dataset provided in the 2008 IEEE Visualization Design Contest [
1] and quantified the gain of (modified) adaptive upsampling. We picked time slice 75 of this ionization front instability simulation. We considered the 10 scalar fields (mass density, temperature, and mass fractions of various chemical elements). What is of interest in this dataset are the different regions of the transition phases between atoms and ions of hydrogen (H) and helium (He). To reduce computational efforts, we used the symmetry of the data with respect to the
and the
planes and restricted consideration to data between
and
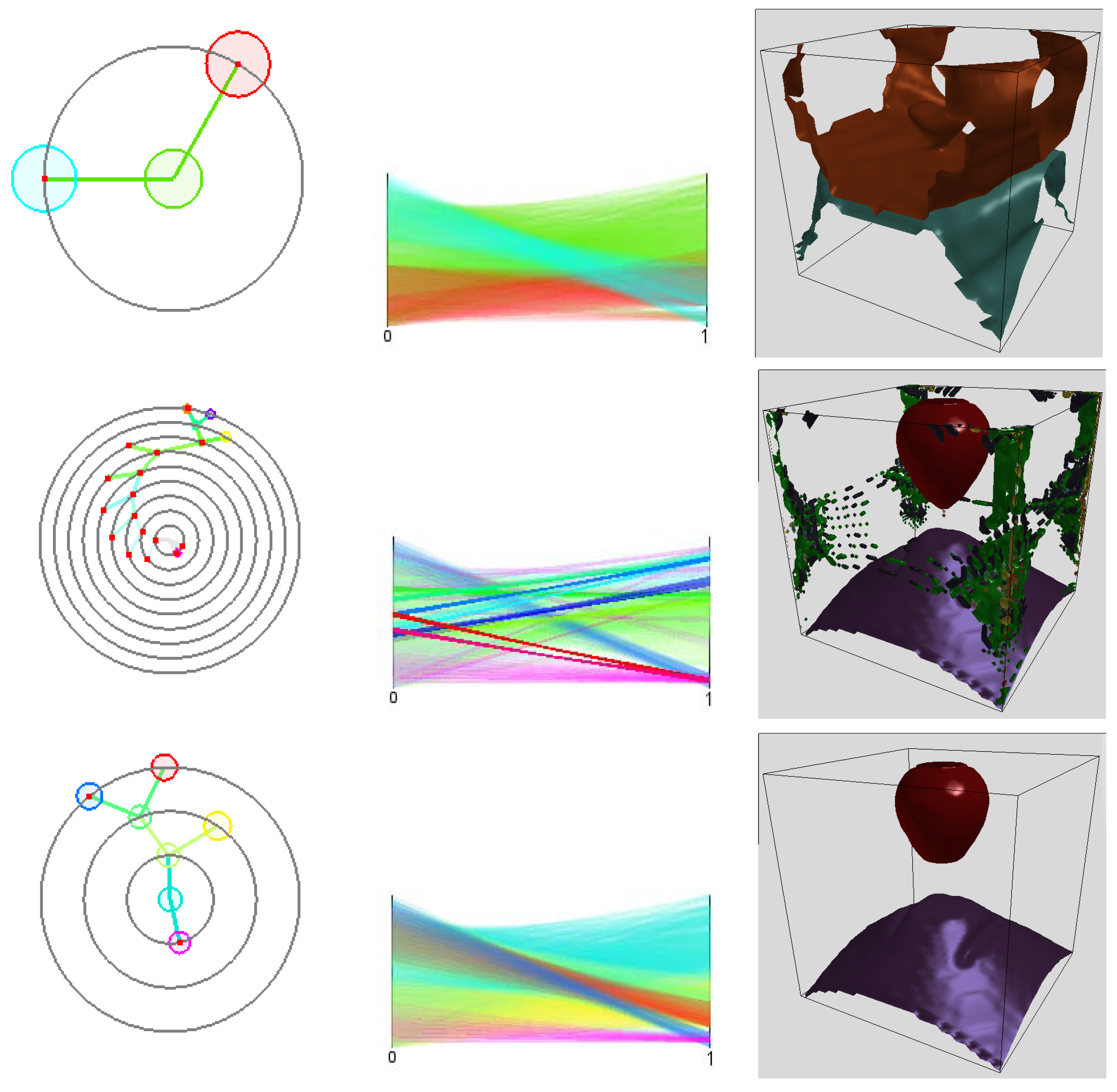
localizing the front. When applying the clustering approach to the original attribute space using a 10-dimensional histogram with 10 bins in each dimension, we obtained a cluster tree with 15 mode clusters. The cluster tree and the corresponding parallel coordinates plot are shown in
Figure 11a. Not all of the clusters are meaningful, since some of them appear as a result of data discretization or a sub-optimal choice of the histogram bin size. These mode clusters are not clearly separated when observing the parallel coordinates plot, see, for example, axis
in
Figure 11a. After applying our approach with
, such clusters were merged leading to 12 modes and a simplified cluster tree. Results are shown in
Figure 11b. The timings of adaptive and non-adaptive upsampling for different interpolation depths are given in
Table 1. “Modified adaptive” upsampling refers to the approach with no upsampling across sharp material boundaries, see
Section 6. The adaptive schemes lead to a significant speed up (up to one order of magnitude). All numerical tests presented in this section were performed on a PC with an Intel Xeon 3.20 GHz processor.
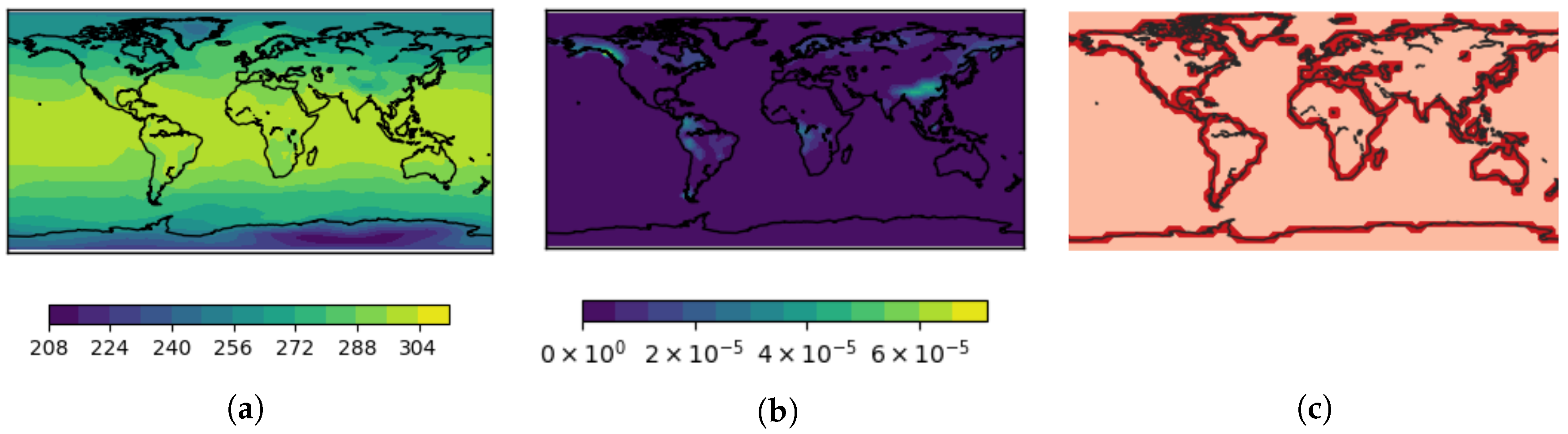
Skipping the voxels with sharp material boundaries or missing values is reasonable only if the fraction of such voxels is low. In our next experiment we used a dataset (courtesy of Max-Planck-Institute for Meteorology) representing a climate simulation which is a spin-up of a preindustrial climate state (approximately 1850 AD). It covers a period of 100 years storing monthly mean data values. The full dataset consists of
time steps at which many scalar fields either volumetric or at the Earth surface are recorded. We picked two 2D fields
surface temperature and
surface runoff and drainage sampled at a regular (longitude-latitude) grid of size
at a single time step. The field
surface temperature is globally defined and has values between 210.49 K and 306.26 K, see
Figure 12a. The field
surface runoff and drainage contains dimensionless values between 0 kg/m
s and
kg/m
s and has non-vanishing values only in the land regions, see
Figure 12b. Thus, the field has sharp boundaries along the cost line. Due to the low resolution of the spatial grid, about
of the grid cells contain a part of the land–sea border, see
Figure 12c. A smooth interpolation of the field
surface runoff and drainage within these cells does not correspond to the discontinuity observed in the real world. A nearest-neighbor interpolation a better and more natural choice for these grid cells. For the other grid cells, bi-linear interpolation is chosen. Moreover, the globally smooth field
surface temperature can be upsampled using a bi-linear interpolation scheme for all grid cells within the whole domain.
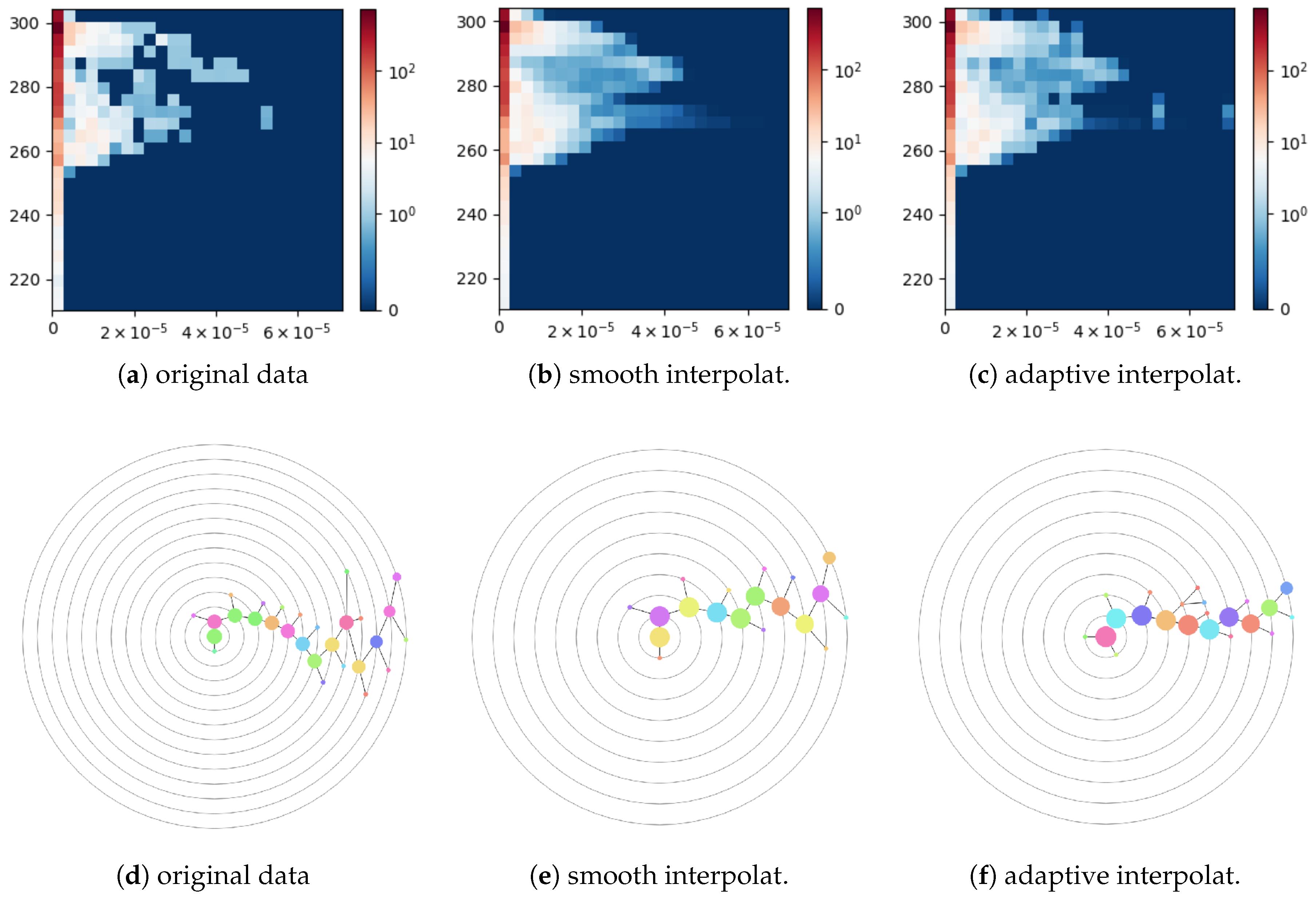
In this experiment, we used 25 bins in each dimension for all histograms. Due to the variation of the surface element area, we weighted the data samples by the cosine of their latitude when accumulating them in a histogram.
Figure 13a shows a 2D histogram computed for the original data, i.e., without upsampling. The first column of the histogram corresponds to the regions with vanishing surface runoff and drainage including oceans and ordinary and polar deserts. The histogram data are noisy, which is reflected in the corresponding cluster tree of depth 13 with 28 nodes shown in
Figure 13d. When applying a smooth bi-linear interpolation to both fields globally with the upsampling depth equal to four in each dimension, the resulting histogram shown in
Figure 13b becomes over-smoothed. In particular, the small separated cluster on the right-hand side in
Figure 13a has been merged with the main cluster in
Figure 13b and is not even anymore a local maximum. The cluster tree constructed for this histogram has depth 9 and contains 19 nodes, see
Figure 13e. A histogram for the data upsampled with the nearest-neighbor interpolation of field
surface runoff and drainage in the coastal region cells is shown in
Figure 13c. The corresponding cluster tree has depth 9 and contains 22 nodes. Thus, adaptive interpolation allows for reducing noise artifacts in the histogram data but avoids over-smoothing the data. Thus, the structure of the resulting cluster tree is simplified without losing important clusters.
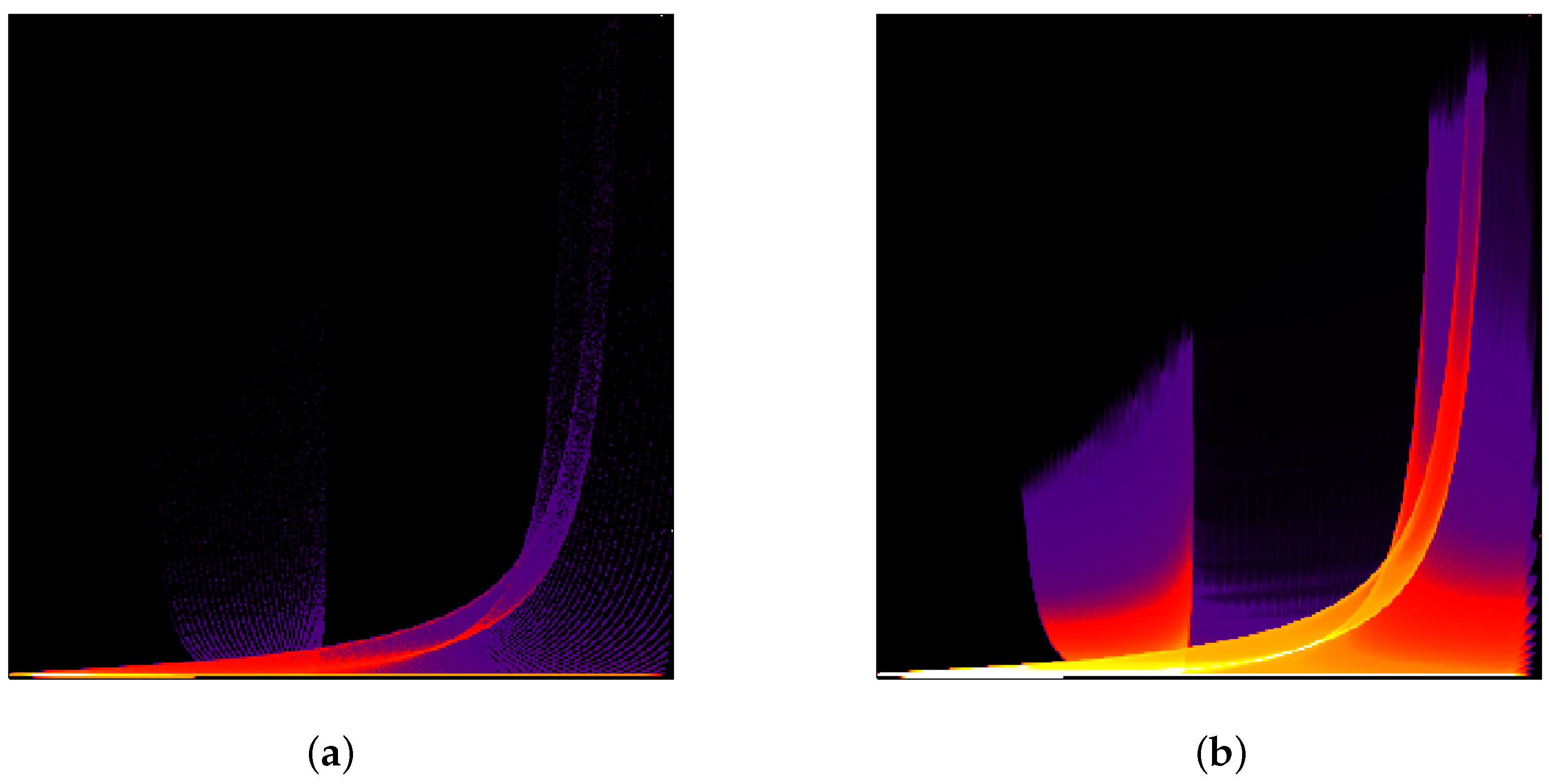
Finally, we demonstrate that scatterplots of upsampled data approach the quality of continuous scatterplots as presented by Bachthaler and Weiskopf [
26] and the follow-up papers. The “tornado” dataset [
32] was sampled on a uniform grid of resolution
. Similar to [
26], the magnitude of the velocity and the velocity in
z-direction were taken as two data dimensions. In
Figure 14, we show scatterplots of the original data and of the adaptively upsampled data with interpolation depth 5. The number of bins is 300 for each attribute. The quality of the upsampled scatterplot is similar to the continuous scatterplot presented in [
26]. We would like to note that, rigorously speaking, evaluation of vector magnitude and interpolation are not commutative operations. Thus, the upsampling with respect to the first chosen parameter could have significant errors in both the continuous and the discrete setting. However, we intentionally followed this way to be able to compare our results with results presented in [
26].