A Top-Down Interactive Visual Analysis Approach for Physical Simulation Ensembles at Different Aggregation Levels
Abstract
1. Introduction
2. Related Work
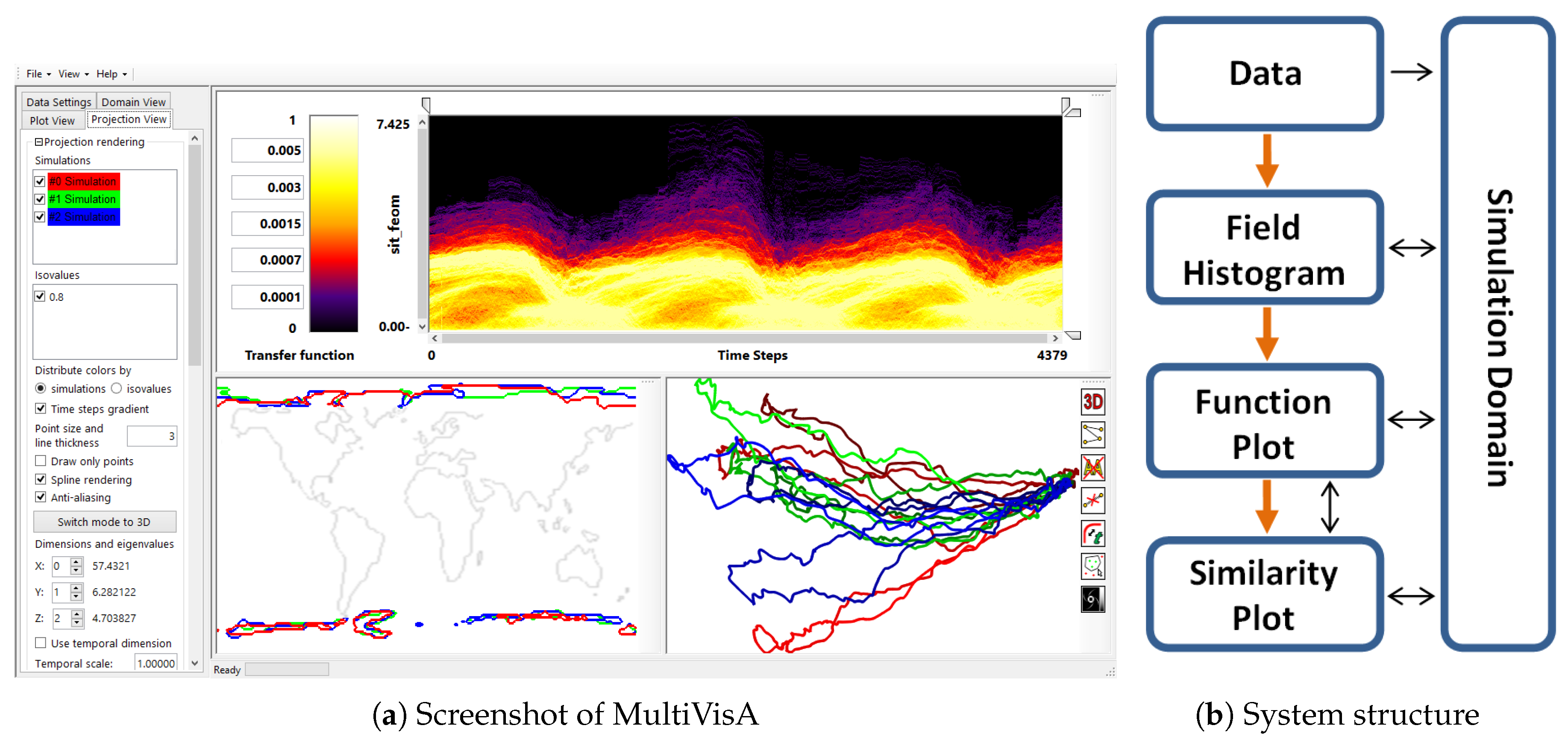
3. Visual Analysis of Multi-Run Simulation Data
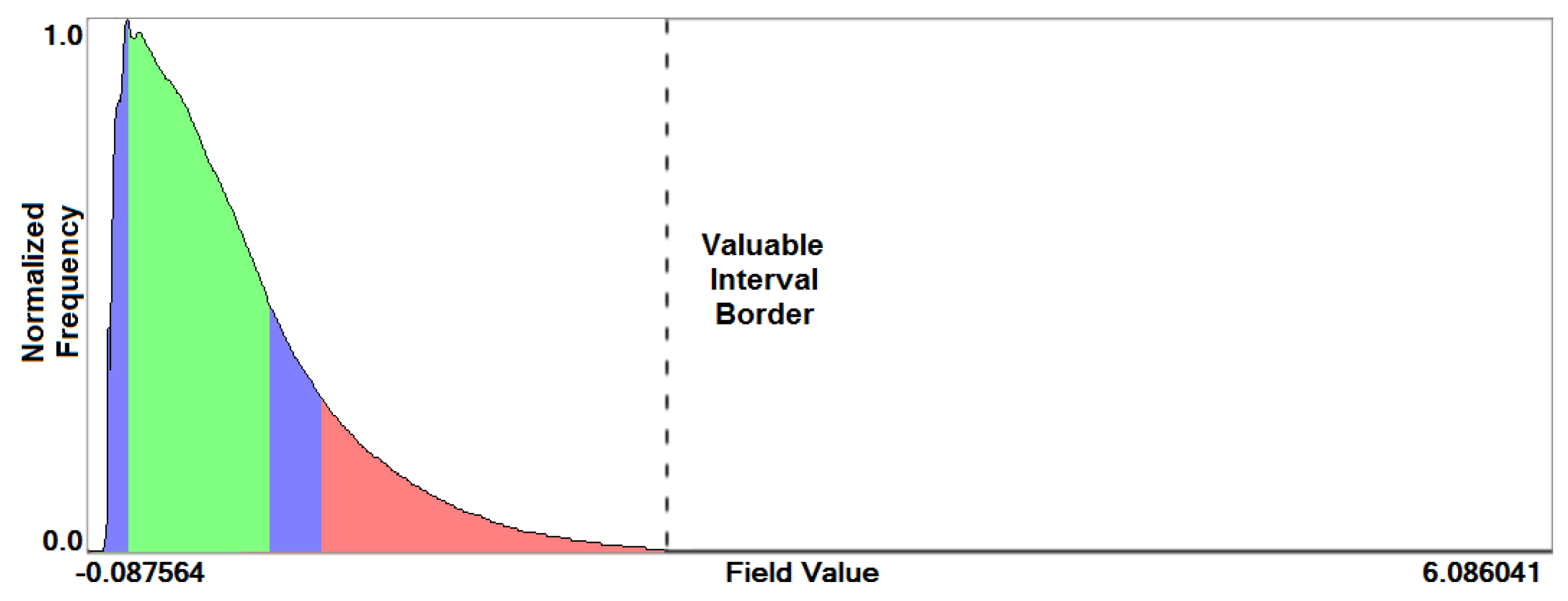
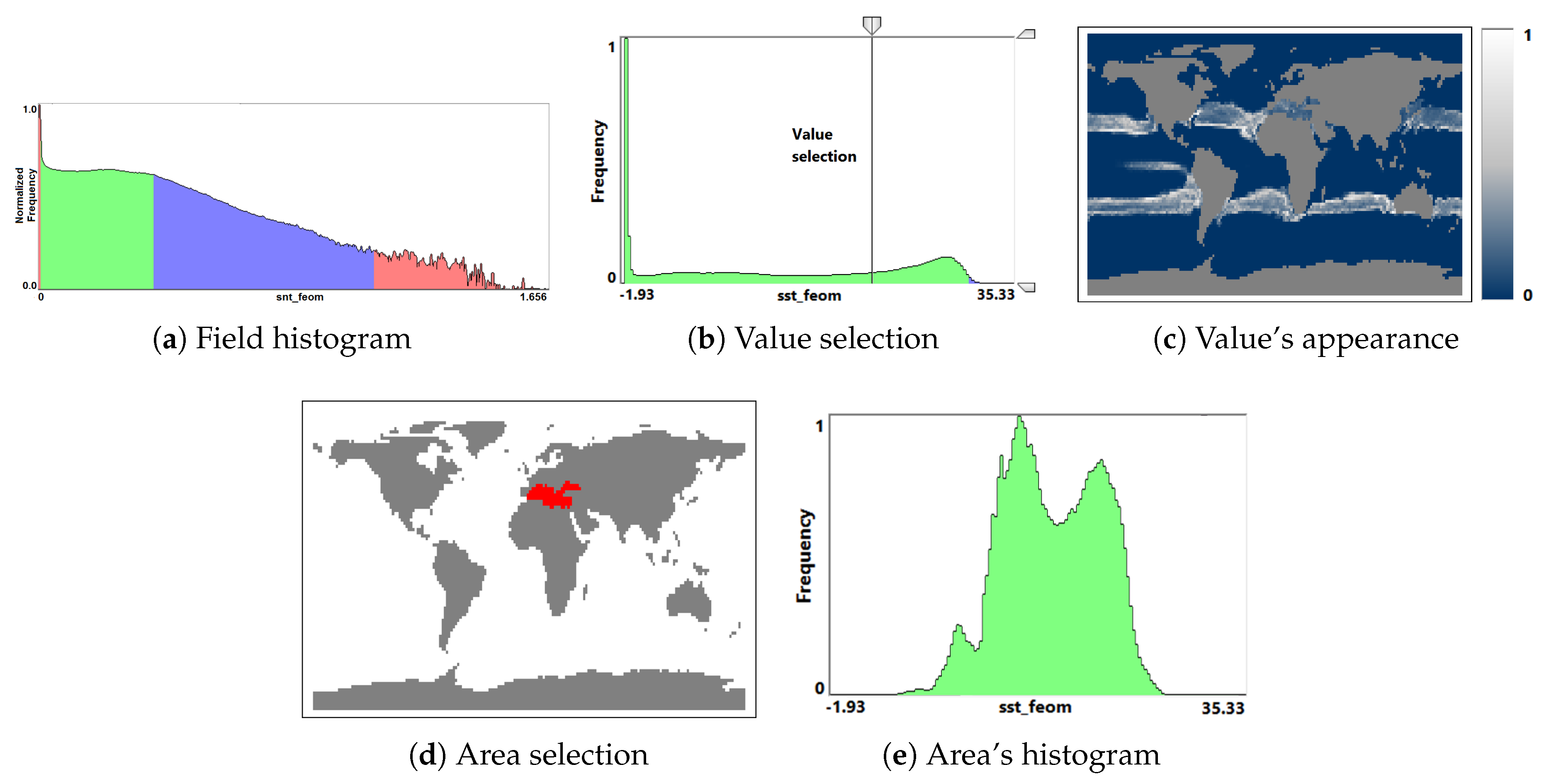
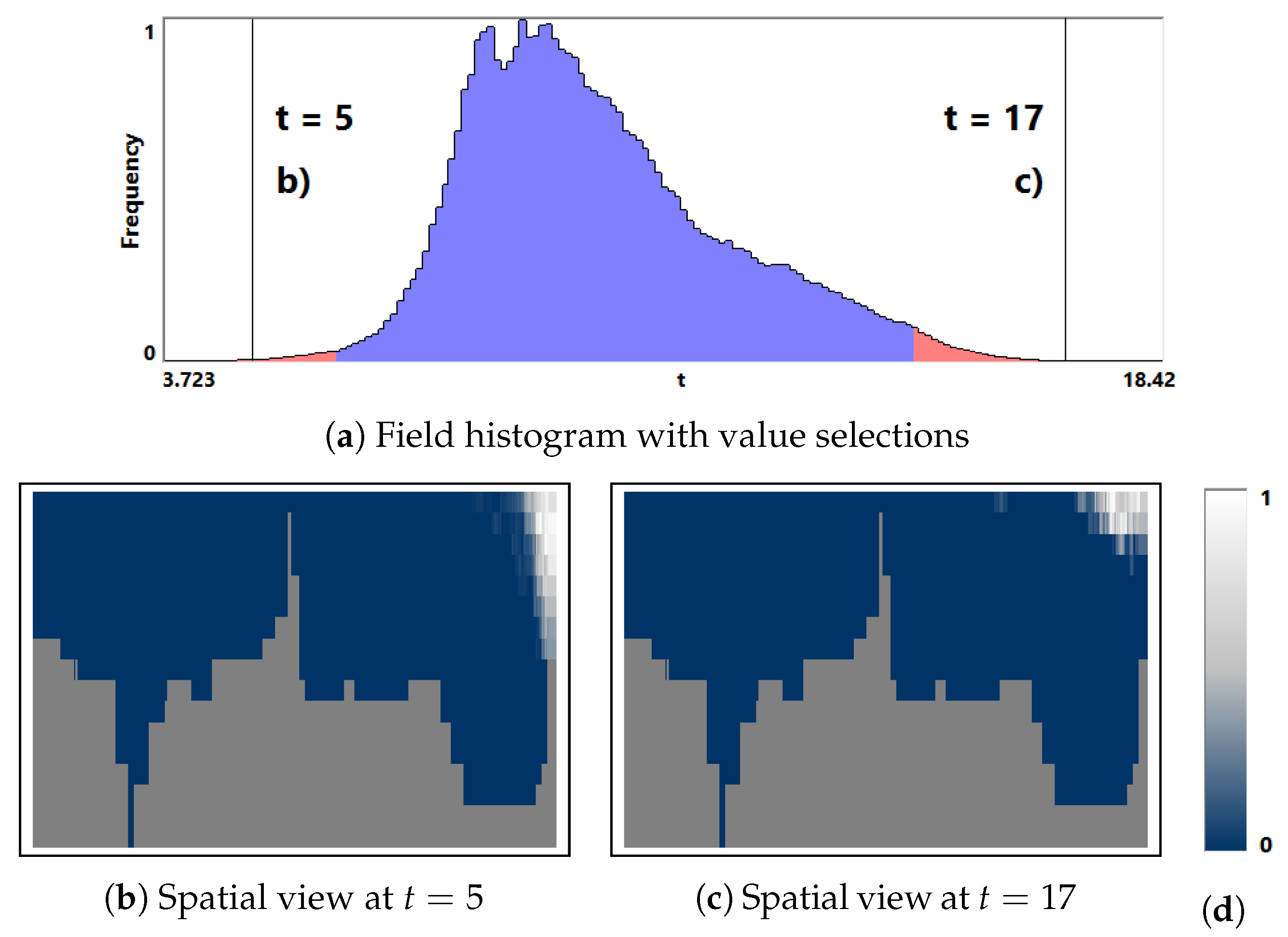
- Overview analysis of field range distribution. In a first stage, one is interested in getting an overview of the ensemble, which can be achieved by investigating the range of the considered data field and the distribution of field values within the simulation runs. Respective histograms allow for first conclusions and to narrow down the field range for subsequent analysis stages (see Section 3.1).
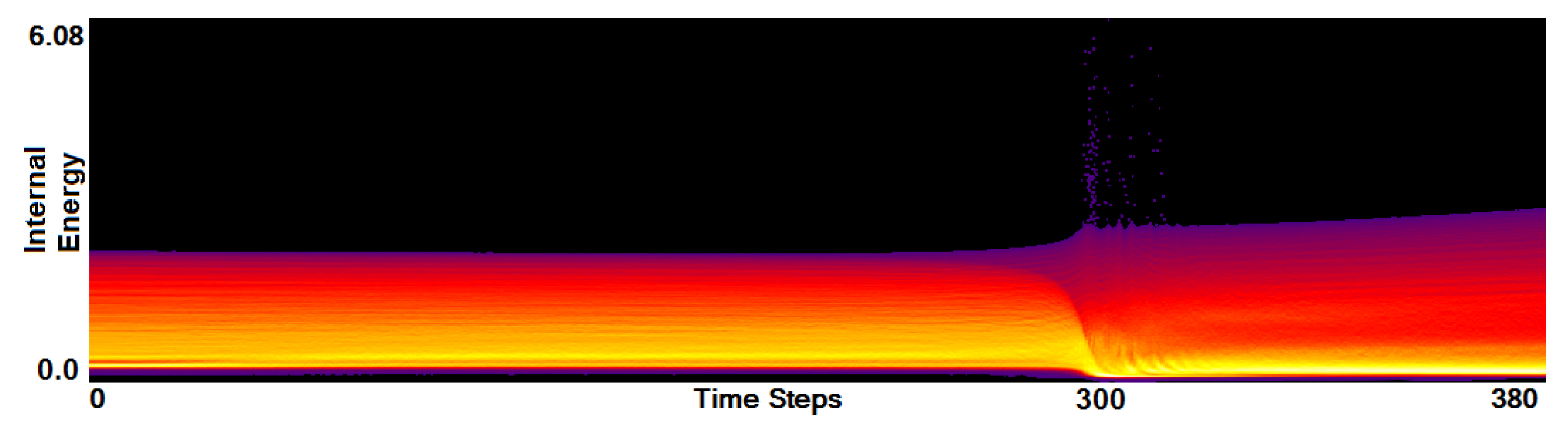
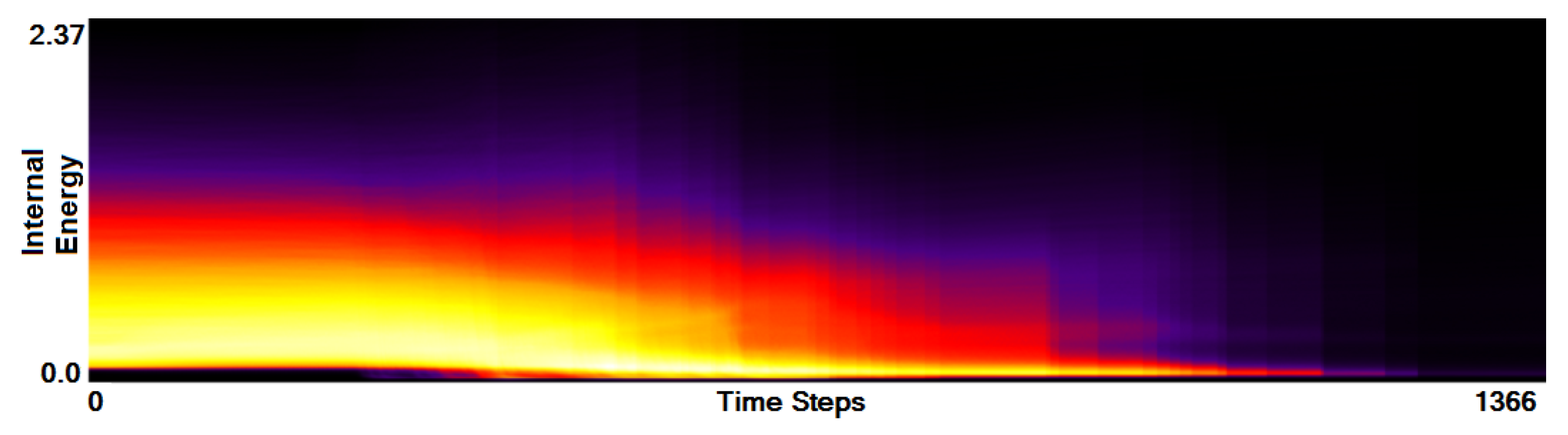
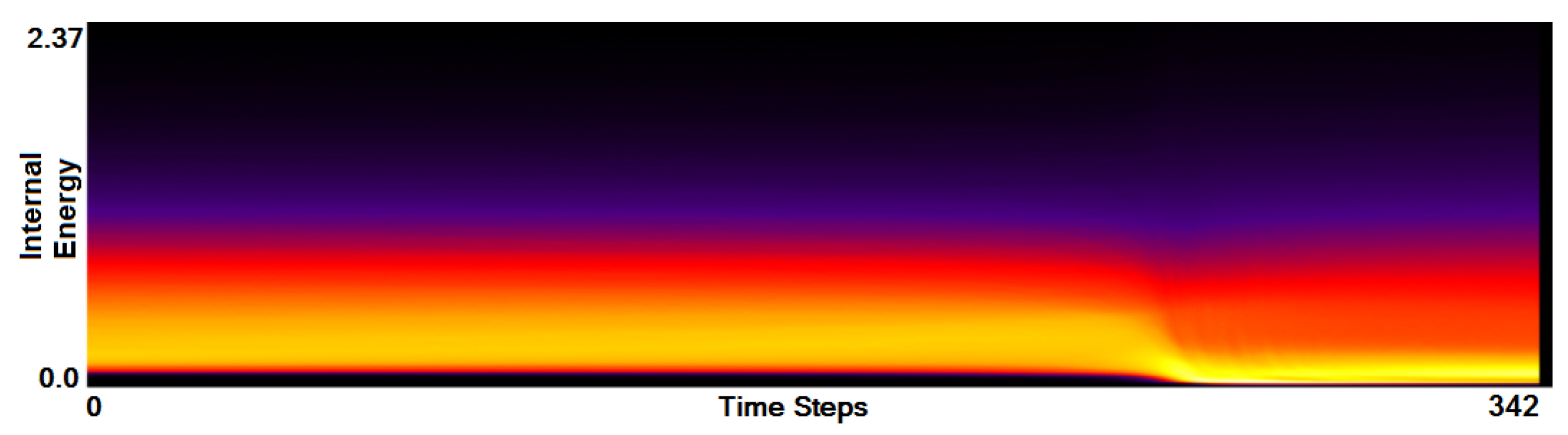
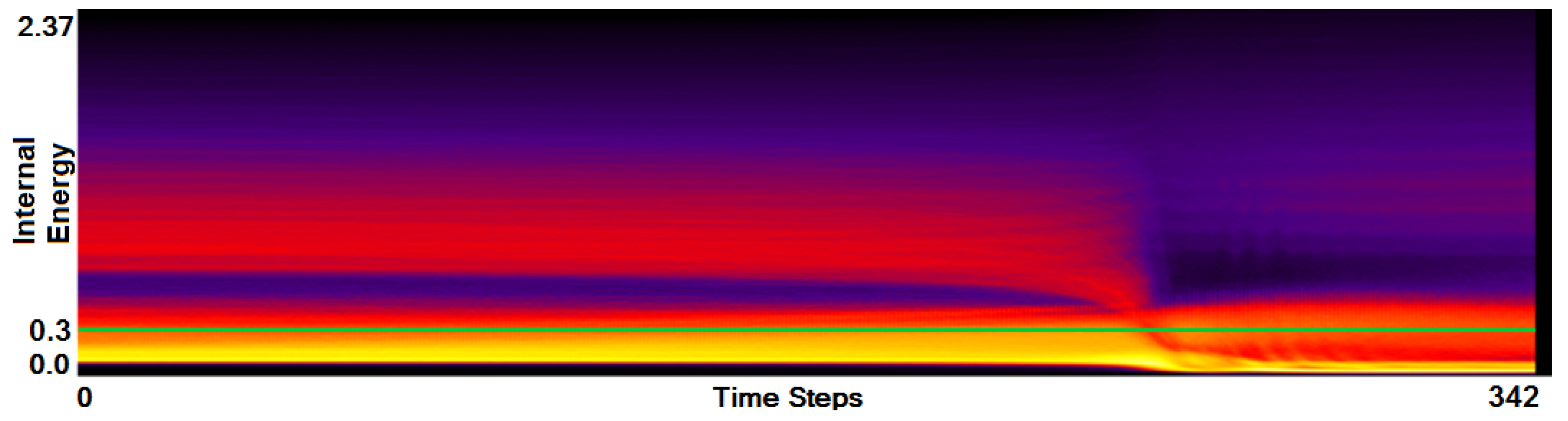
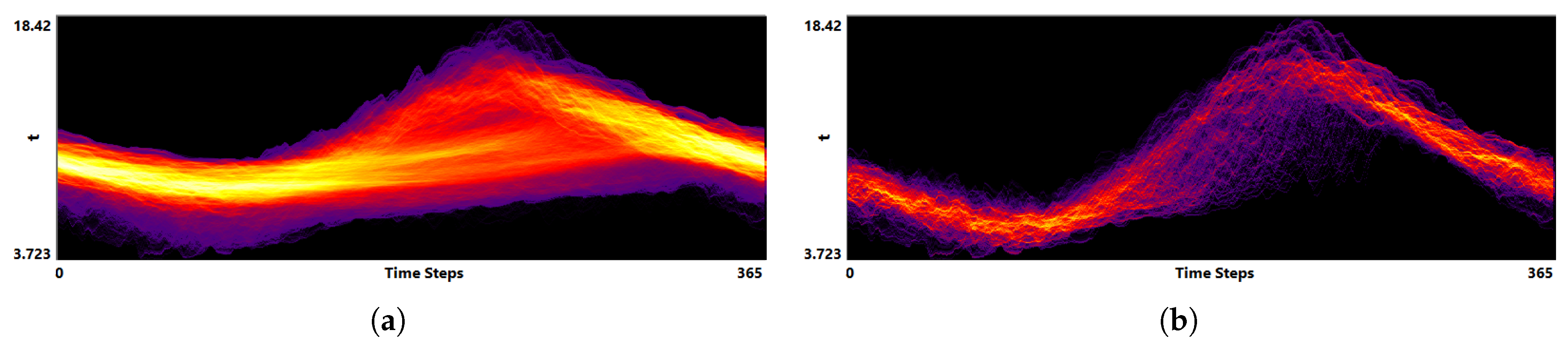
- Analysis of field distribution over time. In this stage, one would like to investigate the change within the simulation runs over time, which supports multiple important tasks. First, one can detect features and the time intervals they occur, which narrows down the time interval for further analysis steps. Second, one can identify individual field values of interest, which can be further examined, e.g., by choosing them as isovalues. Third, one can detect overall patterns in the ensemble as well as outliers. A run identified to be of interest can also be observed individually as well as in further analyses with physical domain visualizations. Finally, one can also compare and correlate different fields of a multi-field data set at this level (see Section 3.2).
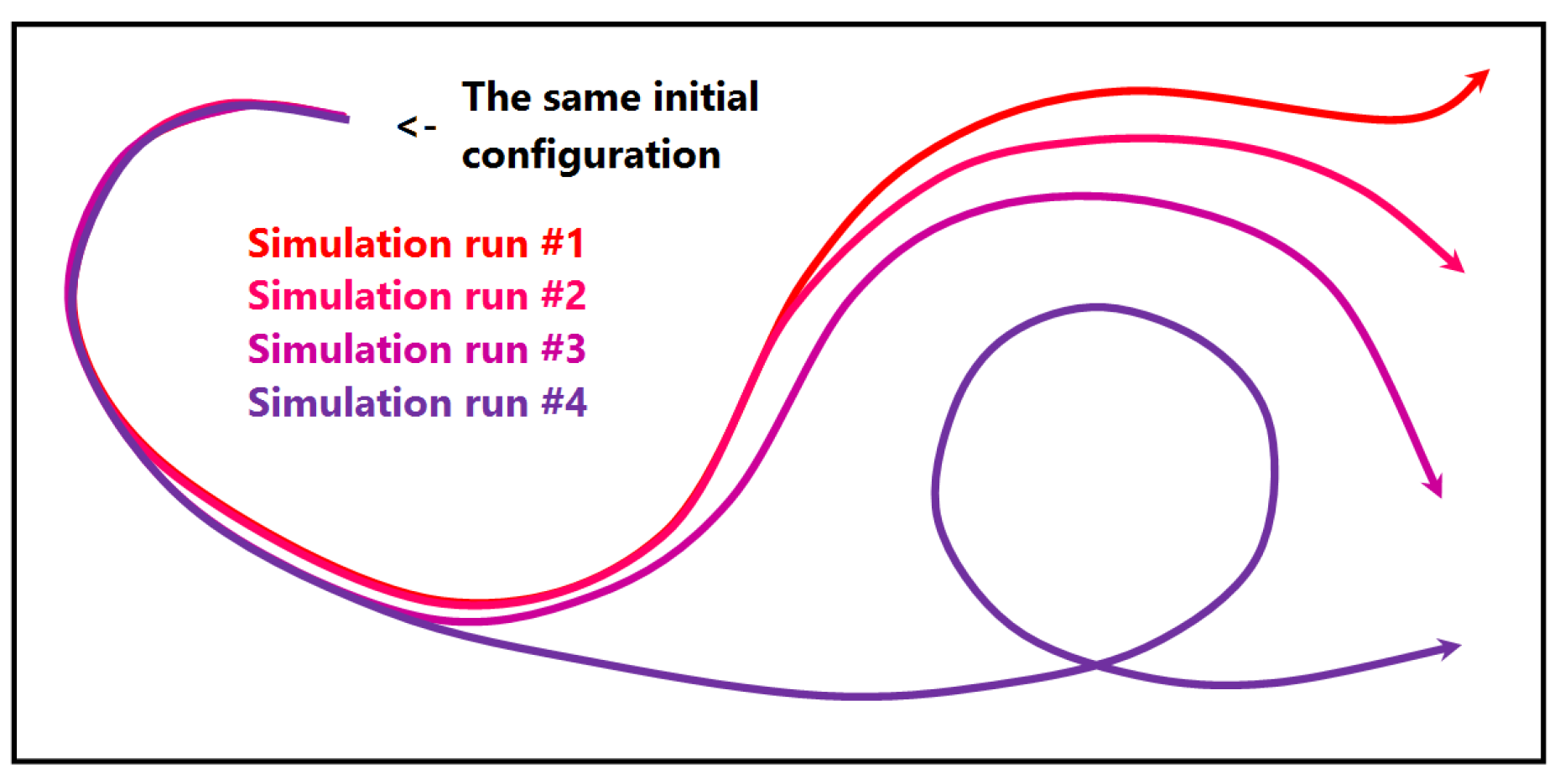
- Comparative analysis of individual runs. While the second stage was operating on an aggregation over multiple runs, this stage shall allow for a detailed understanding of the behavior of individual runs in a comparative view. Making appropriate selections in the preceding stage (i.e., identifying time interval and field value of interest) allows for an accurate and efficient analysis approach (see Section 3.3).
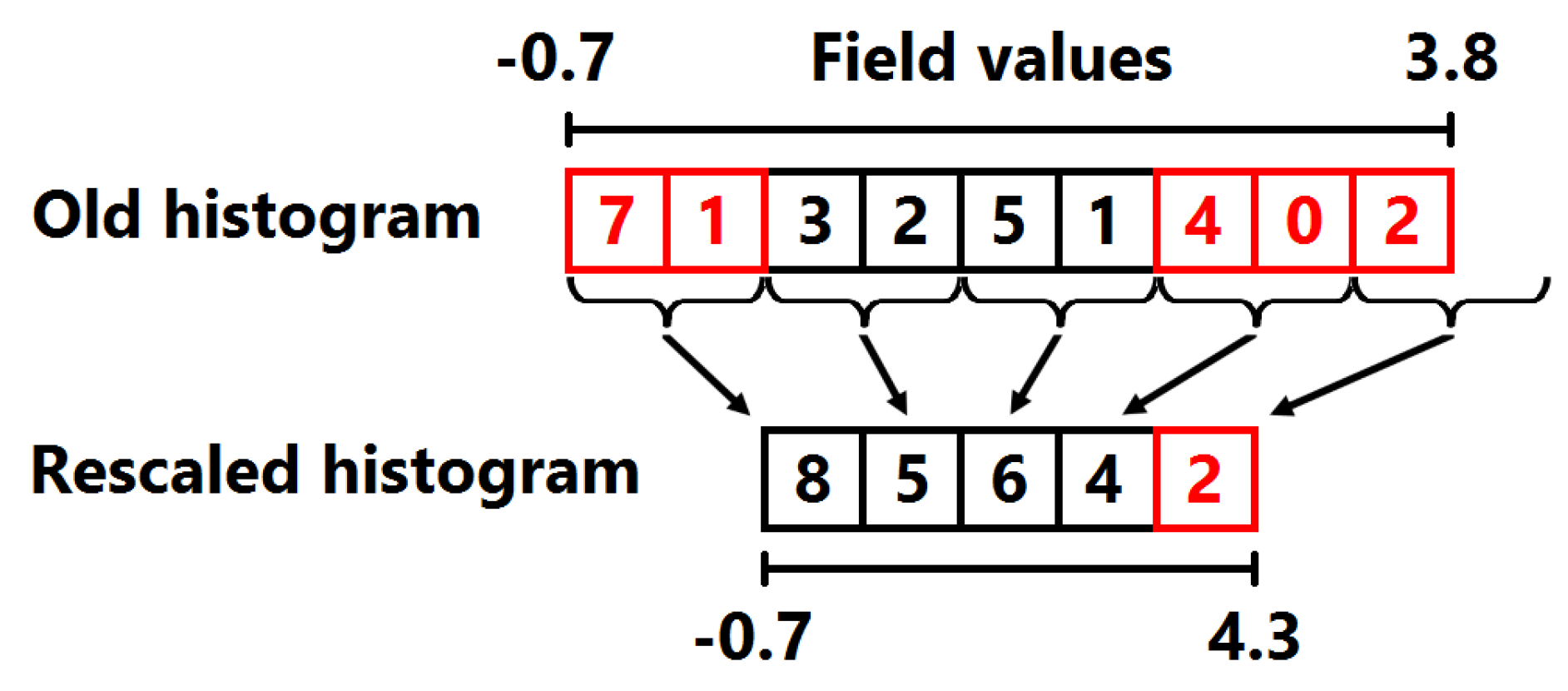
3.1. Field Distribution Histogram
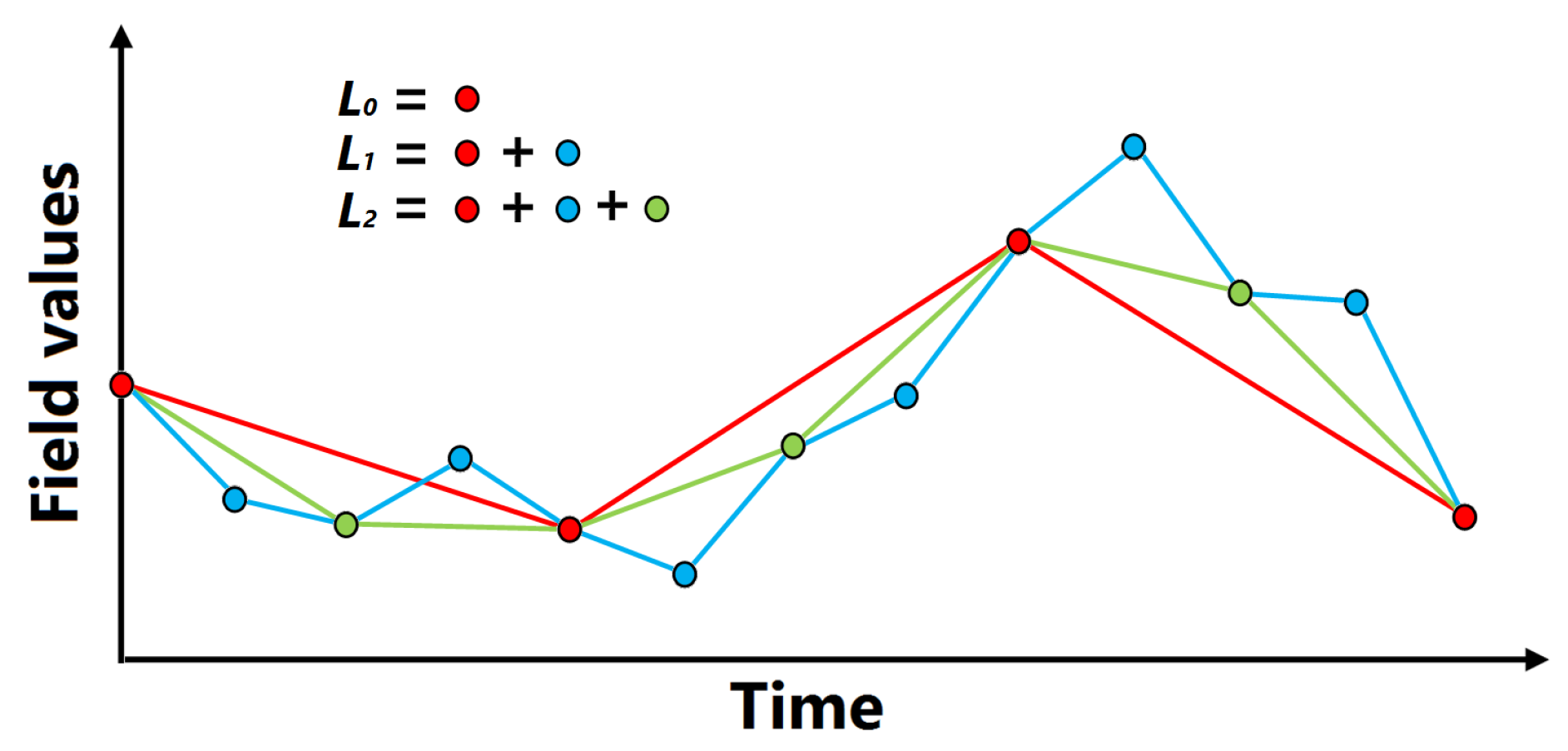
3.2. Function Plot
3.3. Similarity Plot
3.4. Top-Down Analysis
4. Implementation Features
4.1. Computation of Field Distribution Histogram for Interactive Use
4.2. Computation of Function Plot for Interactive Use
4.3. MDS for Similarity Plot Generation
- Set up matrix of squared distances .
- Apply double centering: , where , is the identity matrix, is the matrix with all entries being 1, and n is the number of samples.
- Extract the m largest positive eigenvalues of and the corresponding m eigenvectors .
- An m-dimensional spatial configuration of the n objects is derived from the coordinate matrix , where is the matrix of the m eigenvectors and is the diagonal matrix of the m eigenvalues of .
5. Case Studies
5.1. Astrophysical Simulations
- To identify simulation features within a whole ensemble, researchers are using their own scripts and subroutines, as even advanced applications such as SPLASH [21] do not provide enough functionality. With our tool a multi-run simulation analysis becomes easy to visualize and it allows for a faster data investigation.
- The task of time alignment is one of the most time consuming for the researchers. From expert’s experience to perform the alignment on an ensemble of 250 runs one needs to spend couple of weeks, while with our tool one can do it by a single click.
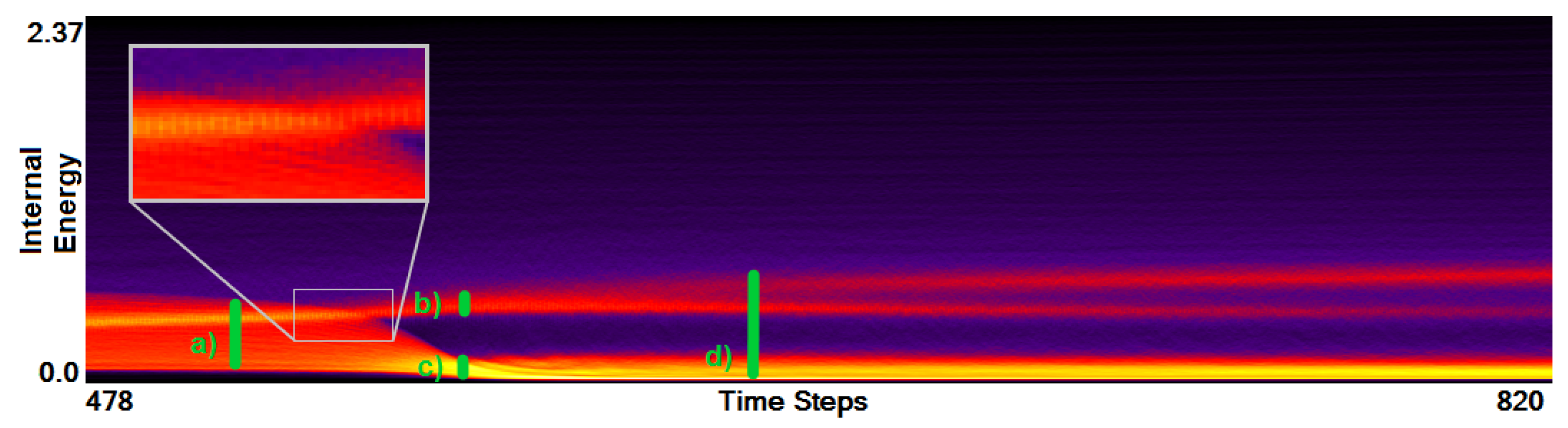
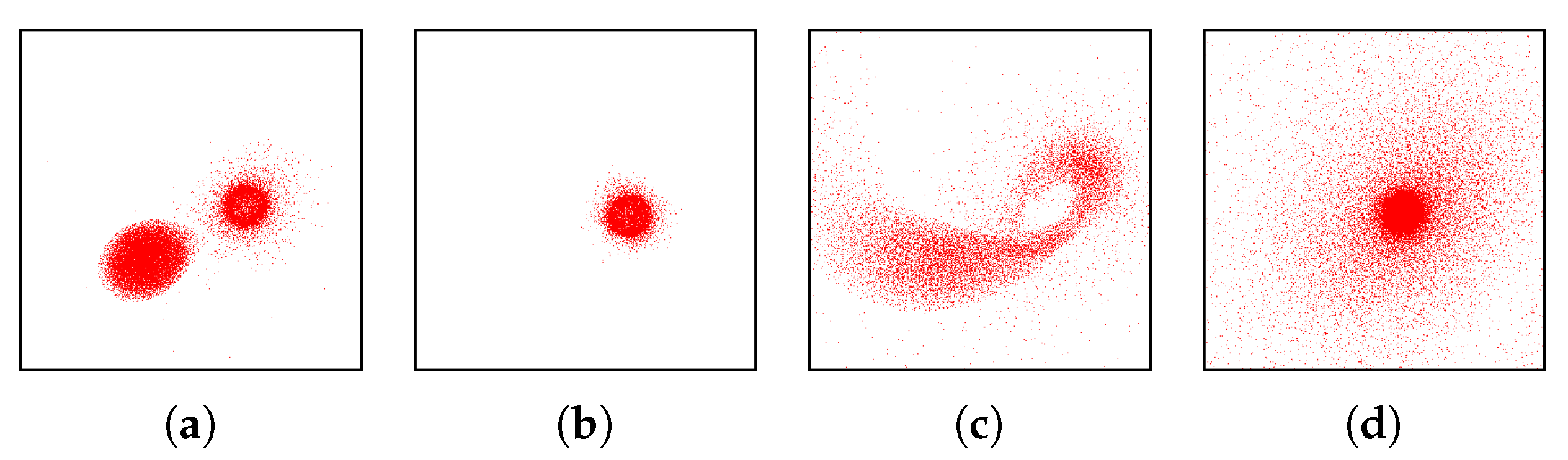
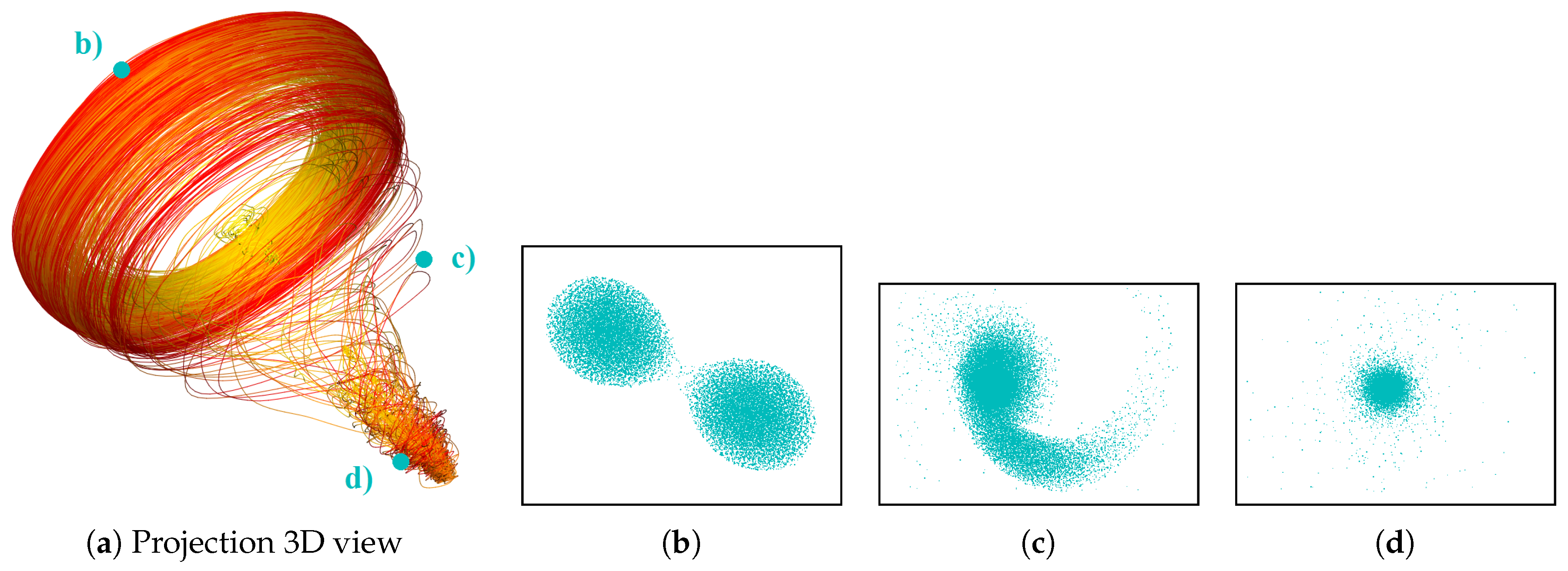
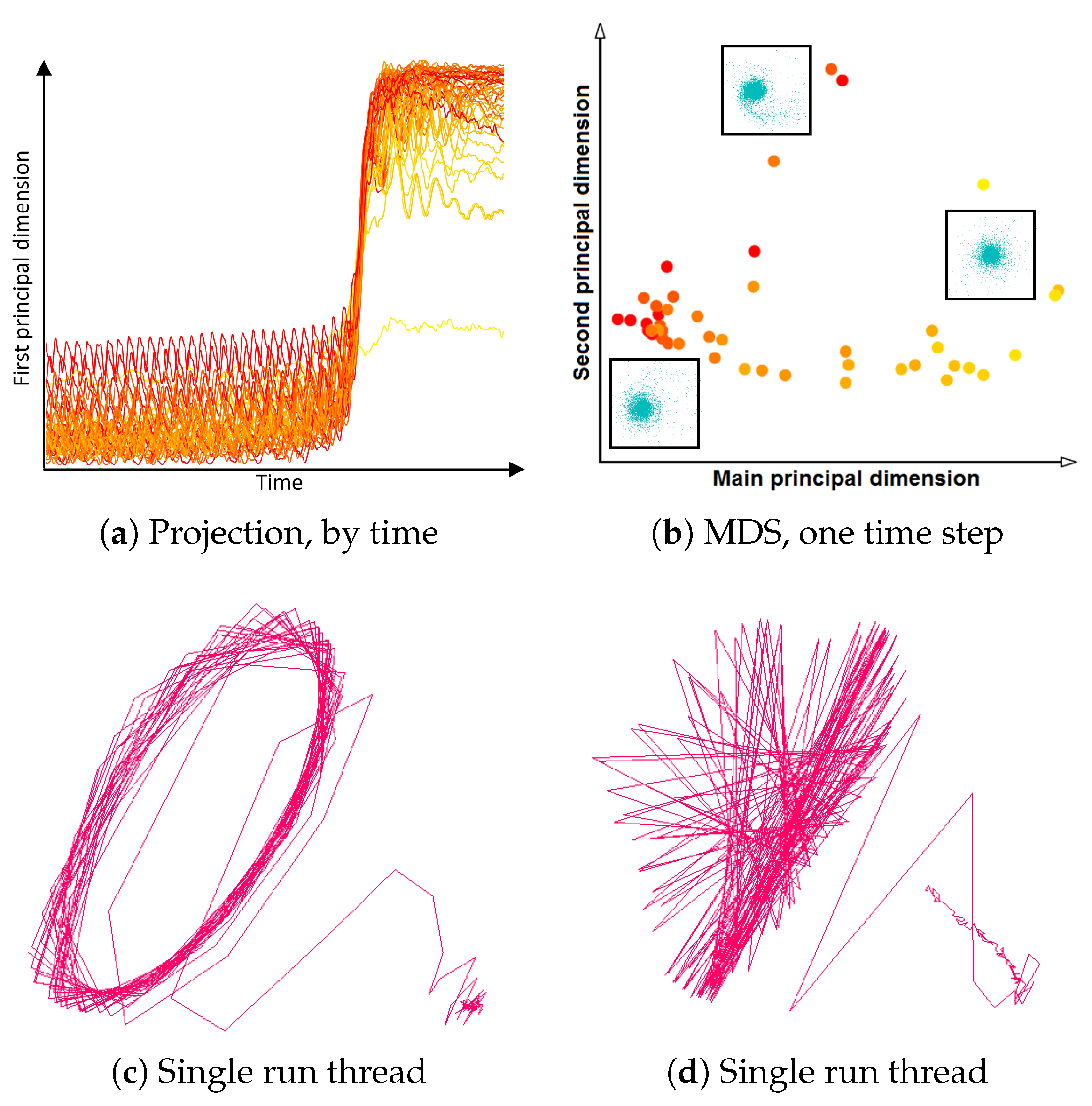
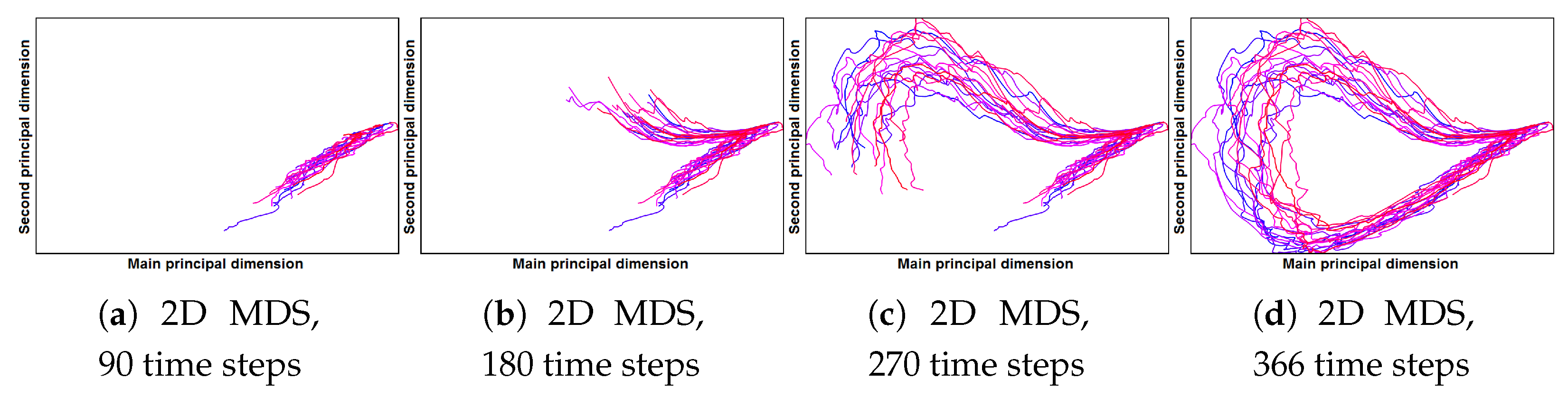
- Correct and precise time definition of the analyzed features leads to increased accuracy of the analysis steps. For example, one can significantly increase the quality of the MDS projection when narrowing down the time interval. Figure 13d shows the same similarity plot as in (c), where in (c) one could use all time steps within the shorter time interval, while in (d) one could only use every other time step of the full time series.
- The domain expert has been working on this data set for a long time and knows it very well. Using our tools he was able to recognize most of the known data features in one session. Moreover, he even identified some additional features for further investigation.
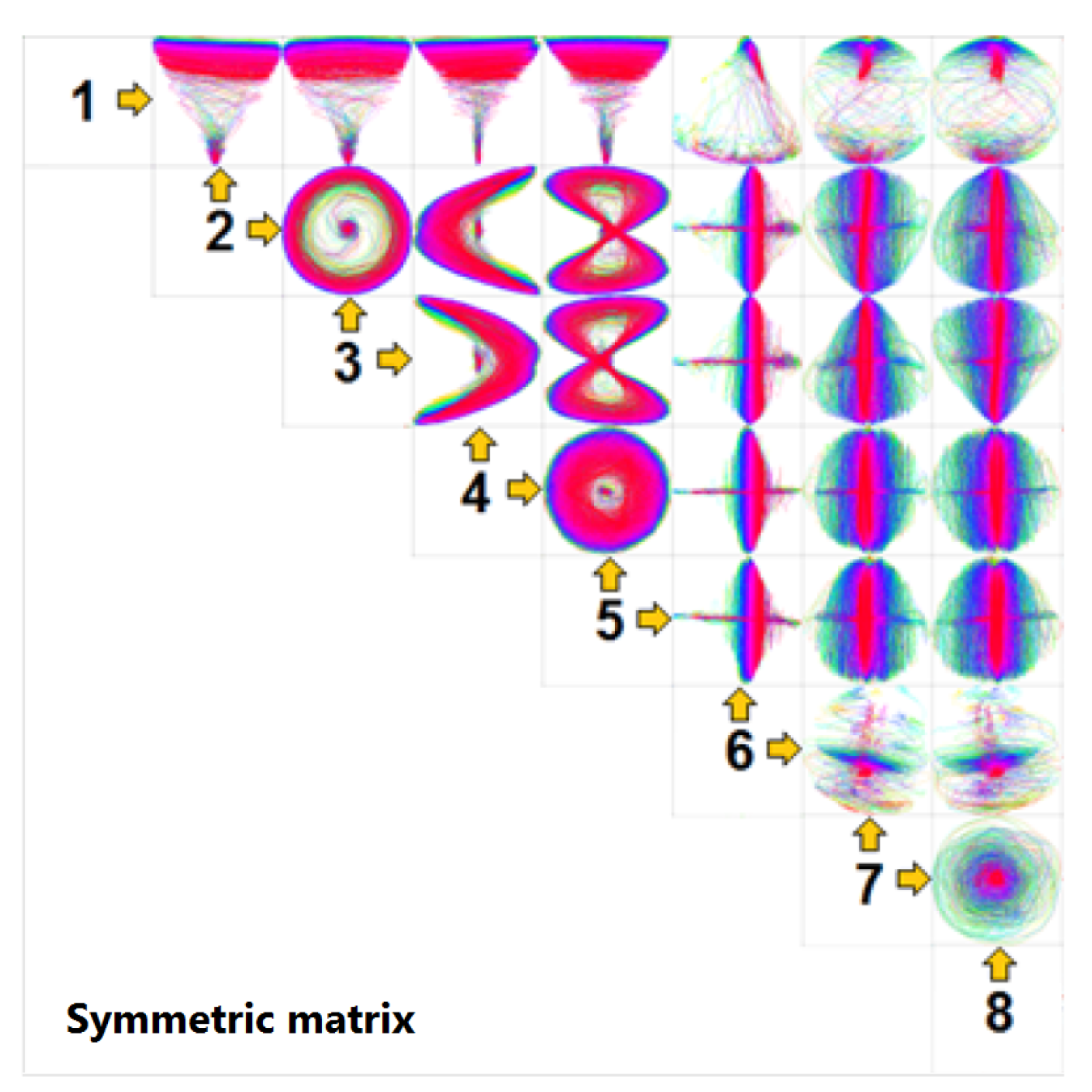
Investigating Projection Dimensions
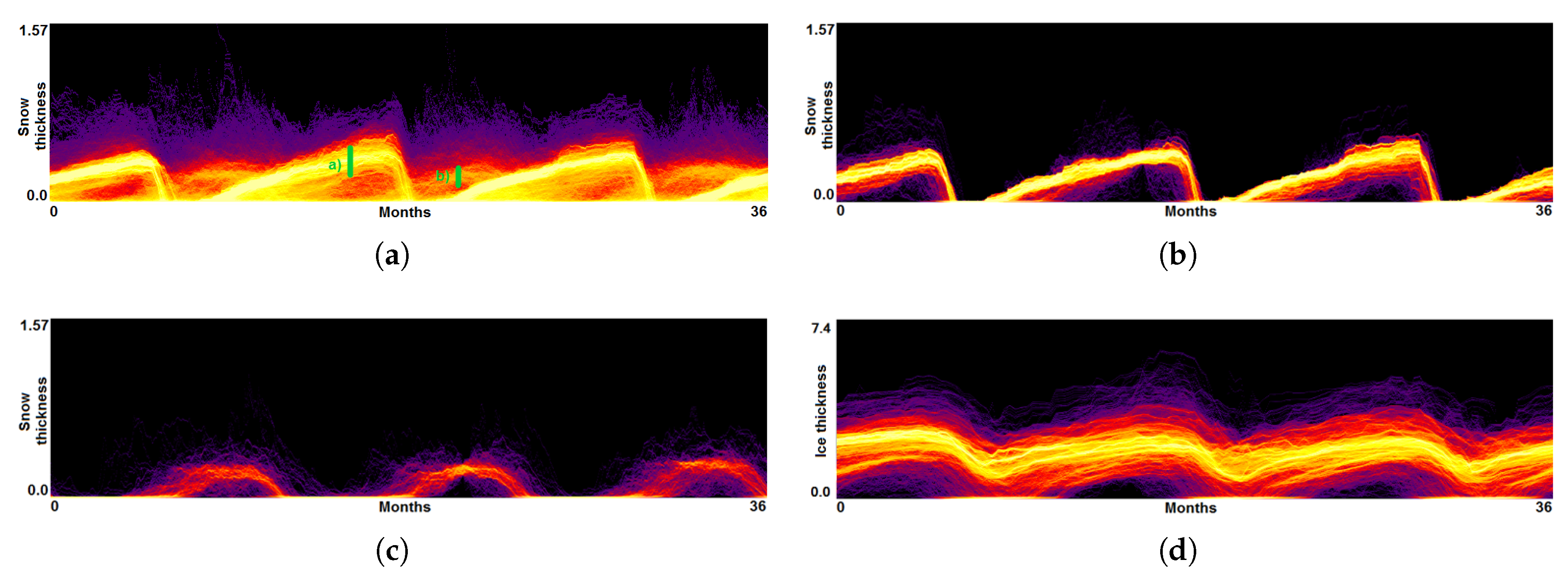
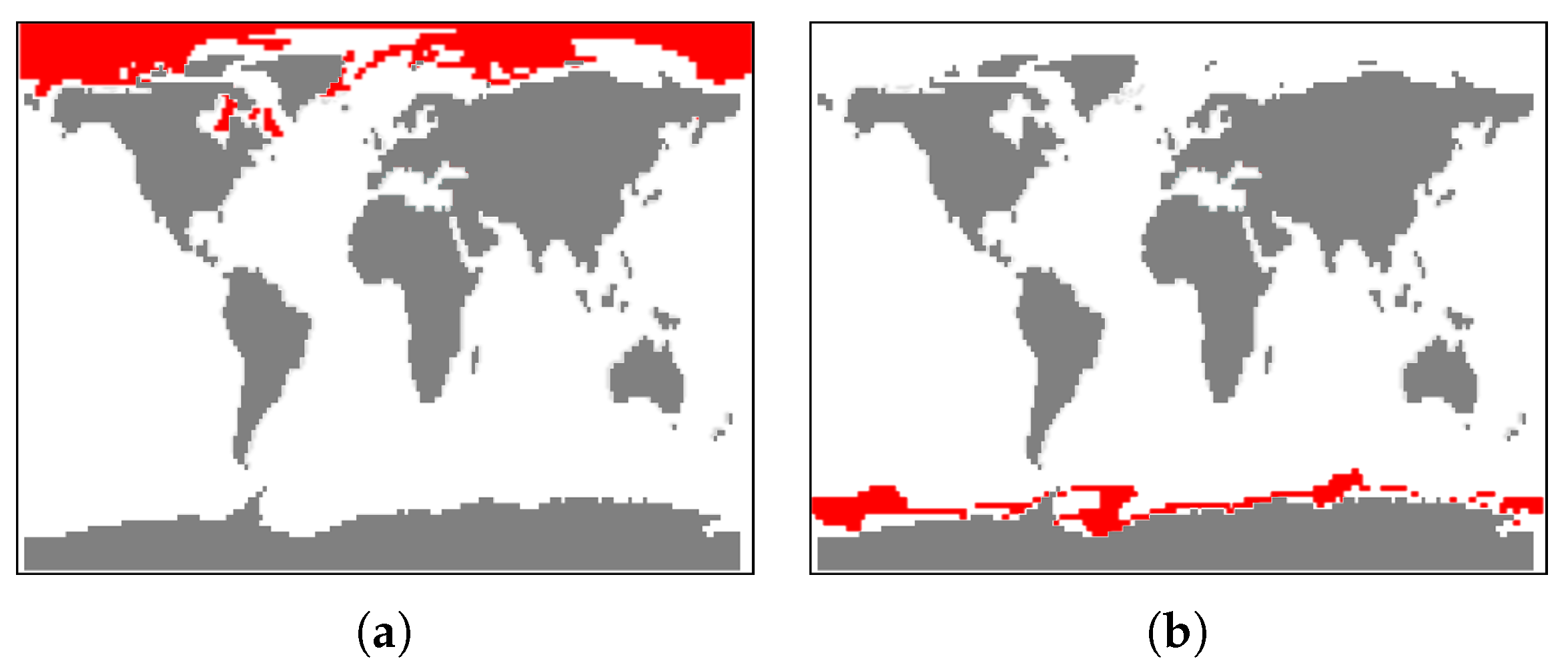
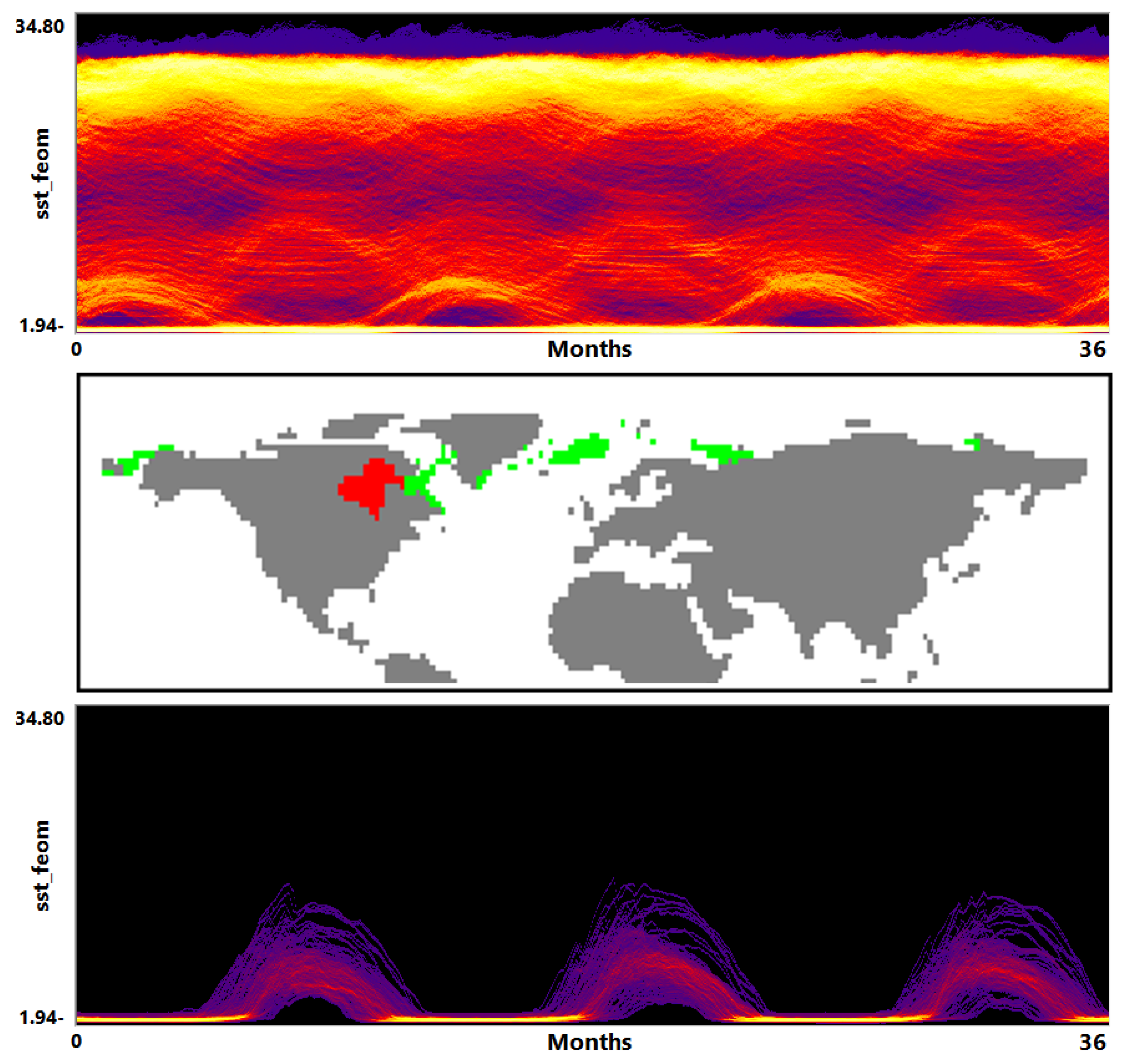
5.2. Global Climate Simulations
- Visualization of the entire ensemble at once allows for estimating the diversity of the simulations’ behavior and identifying patterns and outliers.
- A strong advantage is the option to easily estimate activities of subregions. Usually one would need to look at some physical domain visualization for some selected time steps. Our tools leads to increased accuracy of feature detection.
- Estimating the influence of initial conditions to the simulation result is usually performed in sensitivity studies. A large number of statistical descriptors needs to be used. While it is complicated to capture the behavioral differences with a single value descriptor, our approach captures them in a multidimensional fashion and allows for interaction and navigation.
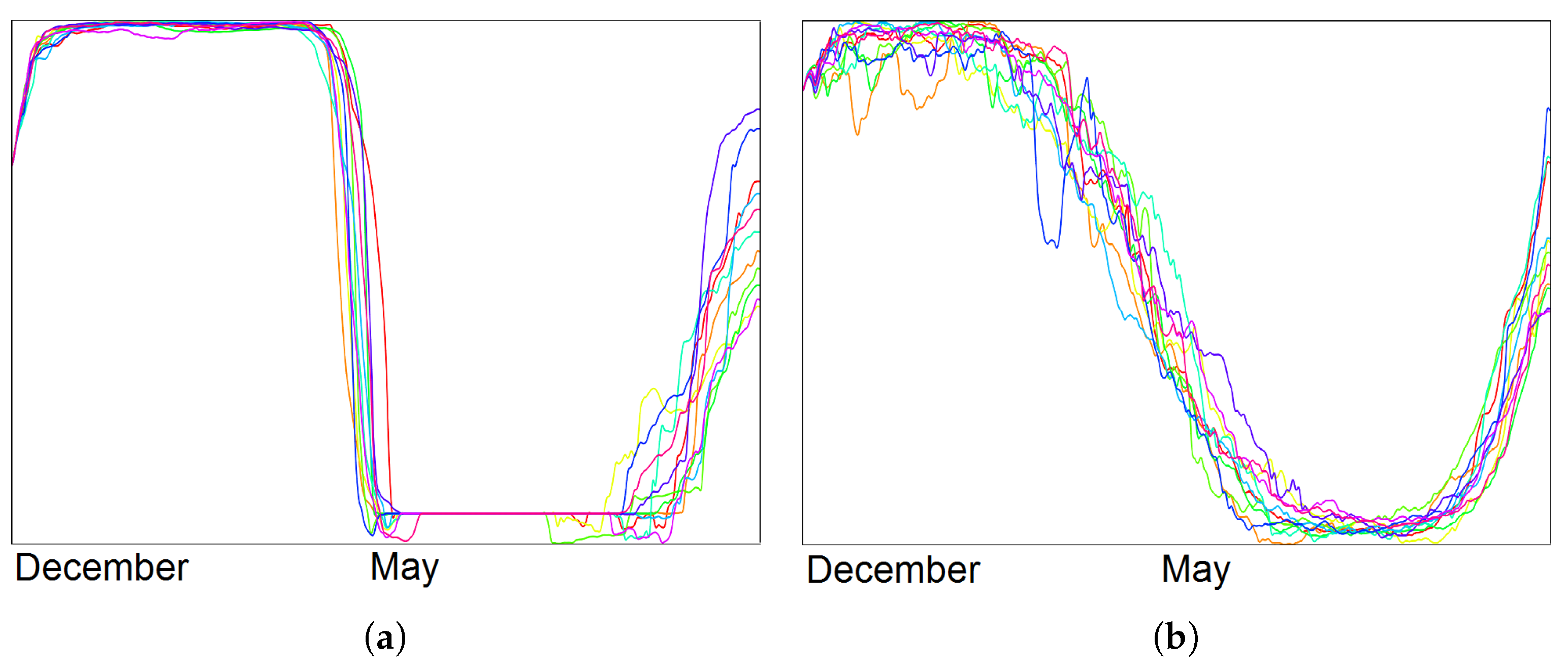
5.3. Local Climate Simulations
5.4. Computation Times
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Moere, A. Time-Varying Data Visualization Using Information Flocking Boids. In Proceedings of the IEEE Symposium on Information Visualization, Austin, TX, USA, 10–12 October 2004; pp. 97–104. [Google Scholar]
- Busking, S.; Botha, C.P.; Post, F.H. Dynamic multi-view exploration of shape spaces. In Proceedings of the 12th Eurographics/IEEE—VGTC Conference on Visualization, Bordeaux, France, 9–11 June 2010; pp. 973–982. [Google Scholar]
- Woodring, J.; Shen, H.W. Multi-variate, Time Varying, and Comparative Visualization with Contextual Cues. IEEE Trans. Vis. Comput. Graph. 2006, 12, 909–916. [Google Scholar] [CrossRef] [PubMed]
- Akiba, H.; Ma, K.L. A tri-space visualization interface for analyzing time-varying multivariate volume data. In Proceedings of the 9th Joint Eurographics/IEEE VGTC Conference on Visualization, Norrköping, Sweden, 23–25 May 2007; pp. 115–122. [Google Scholar]
- Lee, T.Y.; Shen, H.W. Visualization and Exploration of Temporal Trend Relationships in Multivariate Time-Varying Data. IEEE Trans. Vis. Comput. Graph. 2009, 15, 1359–1366. [Google Scholar] [PubMed]
- Phadke, M.N.; Pinto, L.; Alabi, O.; Harter, J.; Taylor, R.M.; Wu, X.; Petersen, H.; Bass, S.A.; Healey, C.G. Exploring ensemble visualization. Proc. SPIE 2012, 8294, 1–12. [Google Scholar]
- Pöthkow, K.; Weber, B.; Hege, H.C. Probabilistic Marching Cubes. Comput. Graph. Forum 2011, 30, 931–940. [Google Scholar] [CrossRef]
- Potter, K.; Wilson, A.; Bremer, P.T.; Williams, D.; Doutriaux, C.; Pascucci, V.; Johnson, C. Visualization of uncertainty and ensemble data: Exploration of climate modeling and weather forecast data with integrated ViSUS-CDAT systems. J. Phys. Conf. Ser. 2009, 180, 012089. [Google Scholar] [CrossRef]
- Potter, K.; Wilson, A.; Bremer, P.T.; Williams, D.; Doutriaux, C.; Pascucci, V.; Johnson, C. Ensemble-Vis: A Framework for the Statistical Visualization of Ensemble Data. In Proceedings of the 2009 IEEE International Conference on Data Mining Workshops, Miami, FL, USA, 6 December 2009; pp. 233–240. [Google Scholar]
- Sanyal, J.; Zhang, S.; Dyer, J.; Mercer, A.; Amburn, P.; Moorhead, R.J. Noodles: A Tool for Visualization of Numerical Weather Model Ensemble Uncertainty. IEEE Trans. Vis. Comput. Graph. 2010, 16, 1421–1430. [Google Scholar] [CrossRef] [PubMed]
- Preston, A.; Ghods, R.; Xie, J.; Sauer, F.; Leaf, N.; Ma, K.L.; Rangel, E.; Kovacs, E.; Heitmann, K.; Habib, S. An integrated visualization system for interactive analysis of large, heterogeneous cosmology data. In Proceedings of the 2016 IEEE Pacific Visualization Symposium (PacificVis), Taipei, Taiwan, 19–22 April 2016; pp. 48–55. [Google Scholar]
- Chen, H.; Zhang, S.; Chen, W.; Mei, H.; Zhang, J.; Mercer, A.; Liang, R.; Qu, H. Uncertainty-Aware Multidimensional Ensemble Data Visualization and Exploration. IEEE Trans. Vis. Comput. Graph. 2015, 21, 1072–1086. [Google Scholar] [CrossRef] [PubMed]
- Berger, W.; Piringer, H.; Filzmoser, P.; Gröller, E. Uncertainty-Aware Exploration of Continuous Parameter Spaces Using Multivariate Prediction. Comput. Graph. Forum 2011, 30, 911–920. [Google Scholar] [CrossRef]
- Konyha, Z.; Lež, A.; Matković, K.; Jelović, M.; Hauser, H. Interactive visual analysis of families of curves using data aggregation and derivation. In Proceedings of the 12th International Conference on Knowledge Management and Knowledge Technologies, Graz, Austria, 5–7 September 2012; pp. 24:1–24:8. [Google Scholar]
- Kehrer, J.; Hauser, H. Visualization and Visual Analysis of Multifaceted Scientific Data: A Survey. IEEE Trans. Vis. Comput. Graph. 2013, 19, 495–513. [Google Scholar] [CrossRef] [PubMed]
- Fofonov, A.; Molchanov, V.; Linsen, L. Visual Analysis of Multi-run Spatio-temporal Simulations Using Isocontour Similarity for Projected Views. IEEE Trans. Vis. Comput. Graph. 2016, 22, 2037–2050. [Google Scholar] [CrossRef] [PubMed]
- Akiba, H.; Fout, N.; Ma, K.L. Simultaneous Classification of Time-varying Volume Data Based on the Time Histogram. In Proceedings of the Eighth Joint Eurographics/IEEE VGTC Conference on Visualization, Lisbon, Portugal, 8–10 May 2006; pp. 171–178. [Google Scholar]
- Buono, P.; Aris, A.; Plaisant, C.; Khella, A.; Shneiderman, B. Interactive pattern search in time series. Proc. SPIE 2005, 5669, 175–186. [Google Scholar]
- Kehrer, J.; Member, S.; Ladstädter, F.; Doleisch, H.; Steiner, A.; Hauser, H. Hypothesis Generation in Climate Research with Interactive Visual Data Exploration. IEEE Trans. Vis. Comput. Graph. 2008, 14, 1579–1586. [Google Scholar] [CrossRef] [PubMed]
- Wickelmaier, F. An Introduction to MDS; Institut for Elektroniske Systemer, Afdeling for Kommunikationsteknologi, Aalborg Universitetscenter Rapport; Aalborg Universitetsforlag: Aalborg, Denmark, 2003. [Google Scholar]
- Price, D.J. SPLASH: An Interactive Visualisation Tool for Smoothed Particle Hydrodynamics Simulations. Publ. Astron. Soc. Aust. 2007, 24, 159–173. [Google Scholar] [CrossRef]
| Data | FH | FP | DM | MDS |
|---|---|---|---|---|
| Astrophysical data | 8743 | 7014 | 3107 | 679 |
| Global climate data | 1061 | 1037 | 214 | 70 |
| Local climate data | 117 | 100 | 103 | 189 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fofonov, A.; Linsen, L. A Top-Down Interactive Visual Analysis Approach for Physical Simulation Ensembles at Different Aggregation Levels. Information 2018, 9, 163. https://doi.org/10.3390/info9070163
Fofonov A, Linsen L. A Top-Down Interactive Visual Analysis Approach for Physical Simulation Ensembles at Different Aggregation Levels. Information. 2018; 9(7):163. https://doi.org/10.3390/info9070163
Chicago/Turabian StyleFofonov, Alexey, and Lars Linsen. 2018. "A Top-Down Interactive Visual Analysis Approach for Physical Simulation Ensembles at Different Aggregation Levels" Information 9, no. 7: 163. https://doi.org/10.3390/info9070163
APA StyleFofonov, A., & Linsen, L. (2018). A Top-Down Interactive Visual Analysis Approach for Physical Simulation Ensembles at Different Aggregation Levels. Information, 9(7), 163. https://doi.org/10.3390/info9070163




