Abstract
Aiming at a special type of ill-defined complicate multiple attributes group decision-making (MAGDM) problem, which exhibits hybrid complexity features of decision hesitancy, prioritized evaluative attributes, and unknown decision-makers’ weights, we investigate an effective approach in this paper. To accommodate decision hesitancy, we employ a compound expression tool of interval-valued dual hesitant fuzzy unbalanced linguistic set (IVDHFUBLS) to help decision-makers elicit their assessments more comprehensively and completely. To exploit prioritization relations among evaluating attributes, we develop a prioritized weighted aggregation operator for IVDHFUBLS-based decision-making scenarios and then analyze its properties and special cases. To objectively derive unknown decision-makers’ weighting vector, we next develop a hybrid model that simultaneously takes into account the overall accuracy measure of the individual decision matrix and maximizing deviation among all decision matrices. Furthermore, on the strength of the above methods, we construct an MAGDM approach and demonstrate its practicality and effectiveness using applied study on a green supplier selection problem.
1. Introduction
After decades of extension and exploitation research [1], multiple attributes decision-making (MADM) approaches have been widely applied to many practical problems in social and technical systems, such as supply chain management [2,3,4,5], business intelligence evaluation [6,7], emergency management [8,9,10], teaching evaluation [11], product design evaluation [12], energy management [13], and waste management [14], among others. Due to increasing complexity in socioeconomic scenarios, and limitedness and uncertainty in human cognition, a single decision-maker is quite often incompetent when confronted with complicated decision-making scenarios. Therefore, multiple attributes group decision-making (MAGDM) methodologies have been developed and deeply studied regarding the strength of fuzzy tools for preferences expression [15,16,17,18,19,20,21,22,23], such as fuzzy sets [24], intuitionistic fuzzy sets [25,26], hesitant fuzzy sets (HFS) [27,28], dual-hesitant fuzzy sets (DHFS) [29,30,31,32], etc. Especially, HFS and DHFS are capable of addressing the common phenomena of decision hesitancy, that is, decision-makers are often irresolute about possible membership degrees to a fuzzy set [27,28]; comparatively, DHFS manages to reflect decision hesitancy more completely than HFS by accommodating both membership degrees and non-membership degrees when depicting decision hesitancy [29].
Regarding ill-structured decision-making problems with higher complexity that cannot be quantified by the above-mentioned fuzzy tools, effective MAGDM approaches have also been put forward by employing the linguistic term set [33] to qualitatively express decision-makers’ opinions directly [34,35]. However, decision-makers quite often approximate the most-preferred linguistic label in a certain linguistic term set but still hesitate about possible membership degrees or non-membership degrees with regard to that linguistic label [36]. Consequently, by fusing the merits of both the linguistic term set and the hesitant fuzzy set, more effective and comprehensive expression tools have been further introduced and exploited to construct multiple attributes decision-making approaches, such as hesitant fuzzy linguistic set [37,38], interval-valued hesitant fuzzy linguistic set [36,39], dual-hesitant fuzzy linguistic set [40], interval-valued dual hesitant fuzzy linguistic set [41], etc. As can be seen, nearly all the above approaches drew on the presumption that linguistic labels must be distributed in a symmetrical and balanced manner [34,35]. However, practical investigations [42,43] have indicated that decision-makers preferred non-uniform or asymmetric linguistic term sets, i.e., the unbalanced linguistic term set (ULTS) [44], to express their complicate assessments more precisely and objectively. Most recent studies [45,46] also verified that ULTS attains better adaptability and flexibility. So, coherently, to tackle complex decision-making more effectively under ill-structured scenarios with decision hesitancy, there are actual needs to develop hybrid hesitant fuzzy linguistic expression tools that are capable of inheriting advantages of both ULTS and hesitant fuzzy sets. However, thus far, to the best of our knowledge, only Qi et al. [47] developed the interval-valued dual hesitant fuzzy unbalanced linguistic set (IVDHFUBLS) and its power aggregation operators. Although IVDHFUBLS manages to be more effective and flexible in depicting complicated assessments with interval values for both membership degrees and non-membership degrees to a designated unbalanced linguistic label, their MAGDM approaches were only developed to cope with the special type of decision-making problems with mutually supportive assessments in decision matrices. Obviously, it is still substantively necessary to investigate various hesitant fuzzy unbalanced linguistic expression tools and exploit their derivative multiple attributes decision-making approaches to resolve practical complex problems.
In fact, in determination of appropriate weights for attributes in MAGDM, decision-makers are generally required to reciprocally compare evaluating attributes so that AHP-like method can be used to derive attributes weights [48]. However, quite often, due to limited expertise on ill-structured problems, decision-makers need many iterations to achieve acceptable consistency or are even unwilling to fulfill the reciprocal comparisons, while on the contrary, for difficulties of high uncertainty, Delphi-like analytical processes provide decision-makers with ways of utilizing collective knowledge to approximate fairly accurate prioritization relations among evaluating attributes [49,50]. For instance, considering four indicators to select emergency response plans for chemical spills events: response efficiency (A1), environmental impact (A2), social impact (A3) and cost (A4). If the event location L1 was in districts with scarce any residence but freeways, decision-makers would naturally deduce the prioritization relation among the indicators as A1 A4 A3 A2, while if L1 was nearby a residence district, decision-makers would derive different prioritization as A1 A3 A2 A4. In viewing of the common existence of prioritization relations among assessing attributes in multiple attributes decision-making, ref. [49,51] introduced the prioritized average (PA) operator and the prioritized ordered weighted average (POWA) operator, which provide effective ways with which to consider decision information from both assessments under attributes and prioritization relation among the attributes. Since then, prioritized operators have been extended to complicated decision environments of high uncertainty, such as prioritized operators for decision-making under intuitionistic fuzzy environments [52,53,54,55], multi-granular uncertain linguistic environments [56], hesitant fuzzy environments [50], dual hesitant fuzzy environments [57], and hesitant fuzzy linguistic environments [58]. Nevertheless, there is still a lack of investigation on prioritized operators in hesitant fuzzy unbalanced linguistic environments. Therefore, aiming at resolving these types of practical multiple attributes decision-making problems with prioritization relation among evaluating attributes, on the basis of IVDHFUBLS [47], we focus on studying prioritized average operators for IVDHFUBLS and corresponding effective MAGDM approaches.
To do so, in this paper, we first propose a fundamental prioritized aggregation operator for fusing preferences in the form of IVDHFUBLS and simultaneously considering prioritization relation among evaluative attributes, i.e., the interval-valued dual hesitant fuzzy unbalanced linguistic prioritized weighted aggregation (IVDHFUBLPWA) operator. We then investigate its desirable properties and discuss its special cases. Further, to objectively determine decision-makers’ weights, which cannot be obtained up-front in complex problem scenarios, we develop a hybrid model that takes into account overall accuracy measure of the individual decision matrix and the maximizing deviation among all decision matrices. Subsequently, on the strength of the above-developed aggregation operator and decision-makers’ weighting model, an effective approach is constructed to tackle practical MAGDM problems that take features of decision-makers’ decision hesitancy, prioritization relationships among evaluative attributes, and unknown decision-makers’ weights.
The remainder of this paper unfolds as follows. Section 2 presents a literature review to discuss the limitations of existing approaches, thereby showing the motivation of this paper. In Section 3, necessary preliminaries for the interval-valued dual hesitant fuzzy unbalanced linguistic set (IVDHFUBLS) are detailed. In Section 4, we firstly define the interval-valued dual hesitant fuzzy unbalanced linguistic prioritized weighted aggregation (IVDHFUBLPWA) operator and discuss its properties, as well as special cases; next, the hybrid model is developed for determining unknown weights for decision-makers; then, an effective MAGDM approach based on the above methods is constructed in detail. In Section 5, an illustrative example of the green supplier selection problem is given to demonstrate the effectiveness and practicality of our proposed approach. Finally, conclusions and future research directions are given in Section 6.
2. Literature Review on Hesitant Fuzzy Linguistic MADM Approaches
With support of fuzzy set and its extensions, classic MADM methodologies have been successfully extended and enhanced to accommodate complicated decision-making environments in which decision-makers have imprecise, uncertain, or vague assessments [15], while for those decision scenarios of ill-structured definition, fuzzy expression tools cannot directly apply. Zadeh [59] thus suggested employing linguistic variables to facilitate expression of judgments. However, no matter whether assigning membership degrees to given fuzzy set or utilizing linguistic labels to depict decision-makers’ complicate judgments, there is a common phenomenon that decision-makers quite often hesitate among possible values [27,28]. Torra and Narukawa [27] and Torra [28] thus use hesitant fuzzy set (HFS) to describe the decision hesitancy. In viewing of same importance of membership degrees and non-membership degrees in depicturing decision hesitancy, Zhu et al. [29] further extended HFS to dual hesitant fuzzy set (DHFS).
Regarding linguistic decision-making scenarios, Rodríguez et al. [60] introduced the hesitant fuzzy linguistic term sets (HFLTSs) to allow decision-makers to directly express their uncertain opinions with possible linguistic labels, based on which the authors then developed a group decision-making model through comparative linguistic expressions [61]. Using HFLTSs, Beg and Rashid [62] endowed conventional TOPSIS with the ability to deal with decision hesitancy. From another perspective, when using linguistic variables to denote their judgments, decision-makers commonly are capable of efficiently determining the most approximate linguistic term while having decision hesitancy with regard to the one selected. Therefore, Lin et al. [37] proposed the effective compound expression tool of hesitant fuzzy linguistic set (HFLS) that employs hesitant fuzzy set to describe decision hesitancy with regard to the selected linguistic label. Wang et al. [36] then introduced the interval-valued hesitant fuzzy linguistic set (IVHFLS) to help decision-makers express their decision hesitancy with possible interval values, on the basis of which they developed a single-person MADM approach. Be aware that above hybrid linguistic expression tools only took into account possible membership degrees but neglected same importance of non-membership degrees; Yang and Ju [40] introduced the dual hesitant fuzzy linguistic set (DHFLS) by incorporating both possible membership degrees and possible non-membership degrees. However, in Yang and Ju [40], they also yet investigated a single-person MADM approach. Qi et al. [41] took a step further to study the interval-valued dual hesitant fuzzy linguistic set (IVDHFLS) and constructed a multiple attributes group decision-making approach based on a family of generalized power aggregation operators. Recently, researchers have started to extend classic MADM methodologies by utilizing the above compound hesitant fuzzy linguistic tools; for example, Wang et al. [63] developed a MADM approach based on TOPSIS and TODIM methods in which attribute values take the form of hesitant fuzzy linguistic numbers. As can be seen, recent studies have verified effectiveness of the compound hesitant fuzzy linguistic expression tools at eliciting complicate uncertain assessments under ill-structured decision situations.
Unfortunately, all the formerly discussed hesitant fuzzy linguistic decision-making models presumed that linguistic labels must be distributed in a symmetrical and balanced manner [34,35]. However, Herrera-Viedma and López-Herrera [42] revealed from their studies on information retrieval system that users (decision-makers) preferred more labels on the right side of a non-uniform or asymmetric linguistic scale, which further was verified by the experiments of olive sensory evaluation in Martínez et al. [43]. Herrera et al. [44] thus defined this special type of linguistic variable as the unbalanced linguistic term set (ULTS) and studied its operations. To a deeper extent, Meng and Pei [45] developed some weighted, unbalanced linguistic aggregation operators and applied them to a multiple attributes group decision-making problem; Dong, et al. [46] investigated group decision-making based on unbalanced linguistic preference relations and proposed a consistency reaching method. Generally speaking, ULTS attains better adaptability and flexibility than strictly symmetrical or balanced linguistic term set. However, till now, regarding MADM based on compound hesitant fuzzy linguistic expressions, only Qi et al. [47] introduced the expression tool of interval-valued dual hesitant fuzzy unbalanced linguistic set (IVDHFUBLS) and investigated its power aggregation operators. Despite merits of ULTS into IVDHFUBLS, the group decision-making approach in Qi et al. [47] only applies to decision scenarios with mutually supportive assessments in decision matrices; nevertheless, the weighting methods for both attributes and decision-makers were derived from and specific to the mutually supportive relations. For more clarity, representative hesitant fuzzy linguistic MADM methods from above discussion and their properties have been compared in Table 1.

Table 1.
Representative hesitant fuzzy linguistic MADM methods and their properties.
Furthermore, to determine unknown attributes’ weights in complex decision problems, analytical hierarchy process (AHP) generally exhibits an effective way with which to obtain relative importance among attributes [64]. However, AHP method requires precisely consistent judgments for reciprocal comparisons to proceed, which quite often cannot be guaranteed for complex problems and thus result in multiple rounds of adjustments or even failure in decision-making, that is, lack of efficiency to some extent, while, in fact, decision-makers are generally capable of obtaining rather accurate prioritization relations among evaluative attributes thanks to their group intelligence and expertise [49]. For example, suppose we choose the following eight attributes to evaluate alterative response solutions to specific emergency event: response time to start emergency response solution () [9,48], reasonable organizational structure and clear awareness of responsibilities () [9,48], economic cost () [65], operability of the response solution () [9,66], monitoring and forecasting potential hazards () [9,48], reconstruction ability () [9,48], social impact () [67], and environmental impact () [68,69]. Additionally, features of the target emergency event have already been identified as follows: (i) Located on an intersection of two highways in a sandstorm desert area where no residences are nearby; (ii) Truck drivers were injured; (iii) A large amount of highly corrosive fluid materials in both trucks are leaking; (iv) Accident trucks destroyed a critical sand control dam. Then, decision-makers will efficiently arrive at the prioritization relations among the eight evaluative attributes () () () () () () () (). Apparently, there is a practical need to further investigate IVDHFUBLS-based decision-making approaches that exploit the prioritization relations. Therefore, based on the prioritized average (PA) operator [49], in the following, we firstly develop PA operator for IVDHFUBLS to address prioritization relations among attributes. To gain more generality of decision-makers’ weighting method rather than the problem-specific limitedness of the one devised in Qi et al. [47], we then develop a deviation-maximizing method to objectively derive decision-makers’ weights. Finally, on the strength of these methods, we manage to construct a practical and effective IVDHFUBLS-based multiple attributes group decision-making approach.
3. Preliminaries for IVDHFUBLS
By fusing the merits of both unbalanced linguistic term set [44] and interval-valued dual hesitant fuzzy set (IVDHFS) [32], most recently, Qi et al. [47] introduced the effective hybrid expression tool called interval-valued dual hesitant fuzzy unbalanced linguistic set (IVDHFUBLS), as shown in following definition.
Definition 1
[47].Letbe a fixed set andbe a finite and continuous linguistic label set; then, an interval-valued dual hesitant fuzzy unbalanced linguistic set (IVDHFUBLS)onis defined as
in whichis an unbalanced linguistic variable from predefined unbalanced linguistic label set, which represents decision-makers’ judgments of an evaluated object;is a set of closed interval values in [0, 1], denoting possible membership degrees to whichbelongs to;is a set of closed interval values in [0, 1], denoting possible non-membership degrees to whichbelongs to. Inand,and, in whichandfor all.
Generally, is called an interval-valued dual hesitant fuzzy unbalanced linguistic number (IVDHFUBLN) and IVDHFUBLNs are all elements of IVDHFUBLS.
Definition 2
[47].Let,, andbe any three IVDHFUBLNs,; some operations on these IVDHFUBLNs are defined by
- (1)
- (2)
- (3)
- (4)
In Definition 2, , , are the corresponding levels of unbalanced linguistic terms , , in the linguistic hierarchy () [44], respectively; is the maximum level of , , in . Using the transformation function defined in following Definition 3, any 2-tuple linguistic representation format can be transformed into a term in .
Definition 3
[44].In linguistic hierarchies, whose linguistic term sets are represented by, the transformation function from a linguistic label in levelto a label in consecutive levelis defined as: , such that
In order to compare any two IVDHFUBLNs, following Definition 4 introduces comparison rules based on a score function and accuracy function. Taking a step further, Definition 5 defines a fundamental distance measure to calculate separation degree between any two IVDHFUBLNs.
Definition 4
[47].Letbe an IVDHFUBLN, and then a score functioncan be denoted as
and an accuracy functioncan be denoted as
Here, and are numbers of interval values in and , respectively, and is the corresponding level of unbalanced linguistic term in the ; is the maximum level of in . Subsequently, given any two and , based on and , we have following comparison rules:
- (1)
- If , then .
- (2)
- If , then
- (a)
- If , then ;
- (b)
- If , then .
Definition 5
[47].Let two IVDHFUBLNsand, , , , andare the lengths of, , , and, respectively, which represent number of elements in the sets of, , , and. Suppose, , in whicheandare the corresponding levels of unbalanced linguistic termsandin the linguistic hierarchy, andis the maximum level ofandin. Then, a distance measurebased on the normalized Euclidean distance can be defined as follows:
Situation 1. When and , then
Situation 2. When or , then
Example 1.
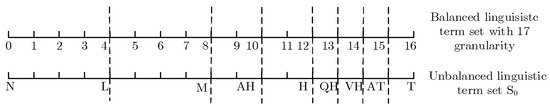
Suppose we utilize an unbalanced linguistic term setfor evaluation, in which. Figure 1 demonstratesand its mapping in a linguistic hierarchy. Then, we got two IVDHFUBLNsand. Let = (L,{[0.2,0.3],[0.4,0.5],[0.5,0.6]},{[0.1,0.2],[0.3,0.4]}) and= (VH,{[0.1,0.4],[0.5,0.6]},{[0.2,0.3]}).

Figure 1.
Unbalanced linguistic term set S0 and its mapping in linguistic hierarchy.
Then, by use of Definition 5, we can directly calculate the distance between and without adding any elements into , and we get .
4. Proposed Approach for MAGDM Based on IVDHFUBLS
When confronted with complicate practical MAGDM scenarios, decision-makers usually are inadequate in determining exact weighting information for evaluative attributes due to time limit or lack of domain knowledge, while they are capable of deriving relatively exact prioritization relation among evaluative attributes, such as the talent introduction decision-making problem [70], teaching quality evaluation problem [54], software selection problem [71], etc. In actuality, Yager [49] acutely noticed the real-world prioritization phenomena among assessing criteria and thus developed the prioritized average (PA) operator. PA operator has been verified as a fundamentally effective aggregation operator that enables classic multiple criteria decision-making methodologies to include prioritization relations among indicators as decision information in their mechanisms [54,70,71,72].
Therefore, firstly in this section, we develop the fundamental prioritized average aggregation operator for IVDHFUBLS and study its desirable properties. Next, considering that decision-makers’ weighting information also quite often cannot be subjectively obtained in advance under complex decision-making environments, we develop a programming model based on deviation maximizing method to objectively derive weighting vector for decision-makers. Furthermore, based on the developed prioritized average aggregation operator and the programming model, we propose an algorithm for MAGDM under IVDHFUBLS environment in which prioritization relation among evaluating attributes exists and decision-makers’ weighting vector is unknown.
4.1. Prioritized Average Aggregation Operator for IVDHFUBLS
Definition 6.
For a collection of IVDHFUBLNs, which are prioritized such that, the IVDHFUBLPWA operator is defined as follows:
in which,andis the accuracy value ofcalculated by Definition 4.
IVDHFUBLPWA operator also can be rewritten as following Theorem 1.
Theorem 1.
Letbe a collection of IVDHFUBLNs. By noticing that aggregation results obtained from Definition 6 have been transformed to the form of interval-valued dual hesitant fuzzy balanced linguistic numbers (IVDHFBLNs), we have
Proof.
- (1)
- When , obviously, it is right.
- (2)
- When ,So, when , Theorem 1 also is right.
- (3)
- Suppose that when , Theorem 1 is right; then, we haveThen, when ,So, when , Theorem 1 is right too.According to steps (1), (2), and (3), we get that Theorem 1 is right for all . ☐
Theorem 2.
IVDHFUBLPWA operator holds following properties:
- (1)
- Commutativity: Letbe any permutation of, then
- (2)
- Idempotency: Let, for all, then
- (3)
- Boundedness: the IVDHFUBLPWA operator lies between the max and min operators,
Proof.
- (1)
- Assume that is any permutation of ; then, for each , there exists one and only one , such that and vice versa. Additionally, also we have . Thus, based on Theorem 1, we have
- (2)
- Since for all , then
- (3)
- Suppose , , in whichObviously,Additionally, for all , we haveMeanwhile, we haveThenAccording to Definition 4 and Theorem 1, we havewhich completes the proof. ☐
Theorem 3.
For a collection of IVDHFUBLNs, if there is no prioritized relationship between theme, then IVDHFUBLPWA operator reduces to the interval-valued dual hesitant fuzzy unbalanced linguistic weighted average (IVDHFUBLWA) operator, in which
in whichis the weighting vector forwithand.
4.2. A Hybrid Model for Determining the Unknown Experts’ Weights
Generally, when the weighting information for decision-makers cannot be subjectively acquired in advance, decision matrices given by decision-makers should be taken into account to derive the unknown weighting vector objectively.
Basically, there are two indispensible aspects with which to exploit assessments in decision matrices objectively. On one side, the accuracy function for hesitant fuzzy elements [32] can be utilized to measure the overall fuzziness of individual decision matrix given by each decision-maker; hence, the less fuzziness there is in a decision matrix, the bigger the weight that should be configured to the corresponding decision-maker. On the other side, according to deviation maximizing methodology [73], the smaller the difference between the assessments offered by one specific decision-maker with those offered by the other decision-makers, the more precise the evaluation information given that specific decision-maker; a larger weight thus should be correspondingly assigned to the decision-maker.
Therefore, firstly, we apply the accuracy function in Definition 4 to indicate information fuzziness in IVDHFUBL individual decision matrix . There is less fuzzy information contained in individual decision matrix than other IVDHFUBL decision matrix, so the th decision-maker plays an important role in prioritization process and should be assigned a bigger weight. Then, specifically from this aspect, we naturally can obtain type of experts’ weights by
Secondly, we here take the divergence degree measure to calculate the deviation between IVDHFUBL decision matrix given by the th decision-maker and IVDHFUBL decision matrix given by the th decision-maker. If the overall divergence of appears to be larger than other decision matrices, then the th decision-maker should be assigned a smaller weight. On the contrary, overall divergence of evaluations in IVDHFUBL decision matrix comes to be smaller than other decision matrices; then, it can be seen that the th decision-maker should be assigned a larger weight. As a result, we establish the following programming model (M-1) for calculating the divergence-based weighting vector for decision-makers.
Because of , we rewrite the above model (M-1) to following model (M-2).
in which is applied according to Definition 5.
Regarding the model (M-2), we have following Theorems 4 and 5.
Theorem 4.
The optimal solution to (M-2) is
Proof.
To solve this model, we construct the Lagrange function as follows:
By differentiation on Equation (13) with respect to and , and setting these partial derivatives equal to zero, the following set of equations is obtained:
By solving Equation (14), we get a simple and exact formula for determining the weights of decision-makers, as follows:
Then, by normalizing be a unit, we have the optimal solution:
As can be seen, is the unique solution to (M-2) and applies to determine DMs’ weights for MAGDM under IVDHFUBLS environment, which completes the proof. □
Theorem 5.
If, then it is reasonable to assign the expertsthe same weight.
Proof.
If , then we have . By solving the programming model (M-2), we will obtain the experts weights , which completes the proof. □
Now, to simultaneously consider the fuzziness of individual decision matrix and deviation measures between decision matrices, based on Equations (11) and (16), we can get the overall experts’ weights according to a hybrid model, as follows:
in which , generally , or and depend on real decision situations.
4.3. Algorithm for MAGDM Based on IVDHFUBLS with Prioritization Relation among Evaluative Attributes and Unknown Decision-Makers’ Weights
Let be the set of response solutions, be the set of attributes, be the set of decision-makers. Suppose that, according to knowledge from decision contexts and Delphi method, decision-makers are capable of determining a prioritization relation, , among evaluative attributes, which means the attribute has a higher priority level than the attribute . Suppose constitutes the IVDHFUBL decision matrices given by all t decision-makers, among which denotes assessments presented by the th decision-maker based on an unbalanced linguistic term set with respect to alternative under attribute , and and take the form of IVDHFUBLNs. Then, on the strength of above-developed methods, we here construct the following Procedure I for MAGDM based on IVDHFUBLS with prioritization relation among evaluative attributes and unknown decision-makers’ weights.
Procedure I. MAGDM based on IVDHFUBLS with prioritization relation among evaluative attributes and unknown decision-makers’ weights.
- Step I-1.
- Compute the weight vector for decision-makers by applying Equation (17).
- Step I-2.
- According to the prioritization relation, , among attributes, transform each individual decision matrix to the prioritized individual decision matrix ,, in which , .
- Step I-3.
- Calculate prioritized levels in prioritized individual IVDHFUBL decision matrices: , .Calculate the score values of according to Equation (3) in Definition 4, then compute the numerical prioritized levels in each prioritized individual IVDHFUBL decision matrix, in which
- Step I-4.
- Obtain aggregated results in prioritized individual decision matrices, , , by applying operator IVDHFUBLPWA.Utilize the IVDHFUBLPWA operator described in Definition 6 to aggregate so that we get the decision-maker’s decision result on the alternative , in which
- Step I-5.
- Obtain collective results of all alternatives by applying decision-makers’ weighting vector.Given the weighting vector for decision-makers, which has been determined in Step 1, we now aggregate all the individual overall decision values into the overall group decision values by use of the IVDHFUBLWA operator described in Equation (10), in which
- Step I-6.
- According to Definition 4, calculate the score value of the group overall assessments to alternatives , then rank all the alternatives and select the most desirable one(s).
5. Illustrative Examples
5.1. Applied Case Study on Green Supplier Selection Problem
Due to increasing environmental concerns in socioeconomic activities, more and more companies have been urged to enhance their green images so as to maintain and improve competitiveness. As a result, leading enterprises like Dell, HP, and IBM have already turned to include green supply chains in their business processes. Obviously, in order to construct effective green supply chains, core companies generally are only willing to select suppliers who exhibit better practices regarding green supply chain management [2]. Therefore, to demonstrate the practicality and effectiveness of our proposed approach, we apply the Algorithm I to resolve the following example of green supplier selection problem.
Suppose we are evaluating three alternative suppliers, i.e., , , according to eight attributes : (1) —Economic performance, (2) —Regulation, (3) —Perceived stakeholders’ pressure, (4) —Green design, (5) —Environmental performance, (6) —Recovery and reuse of used products, (7) —Supplier/customer collaboration, and (8) —Green purchasing. A panel of decision-makers, i.e., , , have been already organized, and decision-makers also reached a consensus opinion on the prioritization relation, i.e., among the attributes.
Next, all three decision-makers were invited to provide their preferences in the form of interval-valued dual hesitant fuzzy unbalanced linguistic numbers. The corresponding linguistic variables are chosen from two unbalanced linguistic term sets and , in which and . The relationship between unbalanced linguistic term sets , , and linguistic hierarchies is shown in Figure 2. Decisionmakers and evaluate the three suppliers by the unbalanced linguistic term set , while utilizes the unbalanced linguistic term set . Then, three interval-valued dual hesitant fuzzy unbalanced linguistic (IVDHFUBL) decision matrices, i.e., , have been collected, as shown in Table 2, Table 3 and Table 4.
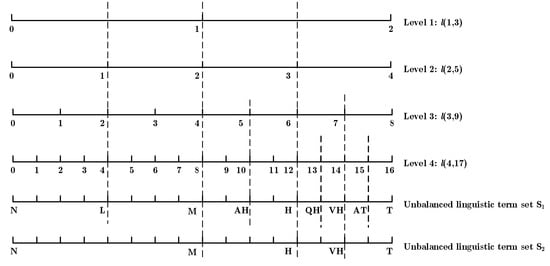
Figure 2.
Unbalanced linguistic term sets (S1 and S2) and their mapping in linguistic hierarchies.

Table 2.
The IVDHFUBL decision matrix provided by decision-maker .

Table 3.
The IVDHFUBL decision matrix provided by decision-maker .

Table 4.
The IVDHFUBL decision matrix provided by decision-maker .
Now, we apply the proposed Procedure I to solve the above green supplier selection problem. The following are details steps in Procedure I.
- Step I-1.
- Compute the weight vector for decision-makers. Firstly, by solving the programming model (M-2), we obtain deviation-based weighting vector asThen, by applying Equation (11), we get the accuracy-measure based experts’ weighting vector asFinally, according to Equation (17), we here suppose ; then, the hybrid experts’ weighting vector is obtained as
- Step I-2.
- Transform each individual IVDHFUBL decision matrix into the prioritized individual IVDHFUBL decision matrix according to the different priority levels of attributes, as listed in Table 5, Table 6 and Table 7.
 Table 5. The prioritized individual IVDHFUBL decision matrix .
Table 5. The prioritized individual IVDHFUBL decision matrix . Table 6. The prioritized individual IVDHFUBL decision matrix .
Table 6. The prioritized individual IVDHFUBL decision matrix . Table 7. The prioritized individual IVDHFUBL decision matrix .
Table 7. The prioritized individual IVDHFUBL decision matrix . - Step I-3.
- Calculate prioritized levels in each prioritized individual IVDHFUBL decision matrix by Equations (18) and (19), and then we have
- , ; , , , , , , ,
- , , , , , ; , , , , , , ,
- , , , , , , ; , , , , , , , ; , , , , ,
- Step I-4.
- Utilize the IVDHFUBLPWA operator described in Definition 6 to aggregate , so that we get the k th expert’s decision result on alternatives , in which
- = (,{[0.439,0.5428],[0.4392,0.5429],[0.4397,0.5438],[0.4399,0.5439]},{[0.1633,0.2744],[0.1633,0.2744],[0.1633,0.2745],[0.1633,0.2746],[0.1675,0.2744],[0.1675,0.2744],[0.1675,0.2745],[0.1675,0.2746],[0.2598,0.373],[0.2598,0.373],[0.2598,0.3731],[0.2598,0.3732],[0.2665,0.373],[0.2665,0.373],[0.2665,0.3731],[0.2665,0.3732]}});
- = (,{[0.5479,0.6638],[0.5483,0.6642],[0.5517,0.6676],[0.5521,0.6681],[0.5538,0.6676],[0.5542,0.668],[0.5576,0.6714],[0.558,0.6718],[0.5579,0.6728],[0.5583,0.6732],[0.5616,0.6766],[0.562,0.677],[0.5637,0.6765],[0.5641,0.677],[0.5673,0.6802],[0.5677,0.6806]},{[0.1152,0.2172],[0.1225,0.2252],[0.1152,0.225],[0.1225,0.2333]});
- = (,{[0.2778,0.383],[0.2789,0.3841],[0.2778,0.3927],[0.2789,0.3938],[0.3647,0.475],[0.3656,0.476],[0.3647,0.4832],[0.3656,0.4842]},{[0.2911,0.4718],[0.2948,0.4753],[0.3186,0.5093],[0.3227,0.5131]});
- = (,{[0.1186,0.3686],[0.1431,0.3885]},{[0.1649,0.2682],[0.165,0.2683],[0.2188,0.3278],[0.2189,0.3279]});
- = (,{[0.4817,0.6085],[0.483,0.6099]},{[0.1246,0.231],[0.1256,0.2326]});
- = (,{[0.4365,0.5779]},{[0.2377,0.3445],[0.2646,0.3745]});
- = (,{[0.4134,0.5925],[0.4139,0.5925]},{[0.235,0.3833],[0.2487,0.3997]});
- = (,{[0.4072,0.5418],[0.4106,0.5452],[0.4294,0.5685],[0.4327,0.5718],[0.4646,0.5954],[0.4676,0.5985],[0.4846,0.6191],[0.4876,0.6219]},{[0.1748,0.2911],[0.1777,0.2932]});
- = (,{[0.6027,0.7085]},{[0.1053,0.2225],[0.1284,0.2522]}).
- Step I-5.
- Aggregate all the individual overall decision values into the overall group decision values by use of the IVDHFUBLWA operator described in Equation (10) and experts’ weighting vector determined in Step 1. Taking as an example, we have
- ,{[0.4597,0.5809],[0.46,0.5811],[0.4597,0.583],[0.46,0.5833], [0.4815,0.6021],[0.4817,0.6023],[0.4815,0.6041],[0.4817,0.6043]},{[0.191,0.3273],[0.2047,0.3419],[0.1979,0.3364],[0.2121,0.3514],[0.1918,0.328],[0.2055,0.3427],[0.1987,0.3372],[0.2129,0.3522],[0.1966,0.3354],[0.2107,0.3504],[0.2037,0.3448],[0.2183,0.3601],[0.1974,0.3362],[0.2116,0.3512],[0.2046,0.3456],[0.2192,0.361]}}).
- Step I-6.
- Calculating scores of the alternatives , we haveAccordingly, then the ranking order of all the alternatives is determined asTherefore, solution is the most desirable green supplier.
5.2. Comparison with IVDHFUBLS-Based TOPSIS Method
Due to the fact that there are no directly related decision-making approaches based on IVDHFUBLS for comparison with our proposed Procedure I, in this section, we firstly develop a IVDHFUBLS-based TOPSIS method as shown in following Procedure II, in which conventional TOPSIS method is endowed the ability to address linguistic decision hesitancy and to accommodate group decision-making scenarios by use of the interval-valued dual hesitant fuzzy unbalanced linguistic weighted aggregation (IVDHFULWA) operator, which was defined in Section 3. We then apply the following Procedure II to solve the same problem adopted in Section 5.1 and discuss their ranking results.
Procedure II. IVDHFUBLS-based TOPSIS method for group decision-making.
- Step II-1.
- Obtaining individual decision matrices from decision-makers, we get .
- Step II-2.
- Aggregate individual decision matrices into individual overall evaluation values corresponding to each alternative according to IVDHFULWA operator. Here, assume , and
- Step II-3.
- Calculate separating measure from positive and negative ideal solutions.Determine positive ideal solution (PIS) and negative ideal solution (NIS) , in which , .Then, we calculate the separating measure from the PIS and NIS for each alternative according to the distance measure introduced in Equation (5), in whichNext, we can obtain
- Step II-4.
- Calculate the relative closeness to the ideal solution by
- Step II-5.
- Rank the green suppliers according to the descending order of ; then, we get the most desirable supplier.
Now we can apply Procedure II to the same problem adopted in Section 5.1 and compare their ranking results.
In Step II-1, we directly accept the decision matrices in Section 5.1. In Step II-2, we adopt . Then, according to Equations (23) and (24), in Step II-3, we calculate the separating measure from the PIS and NIS for each alternative, and we get , , , , , and . Subsequently, in Step II-4, according to Equation (24), we obtain the relative closeness to the ideal solution: = 0.5459, = 0.5638, and = 0.5986. Therefore, Step II-5 generates the ranking result of , which means the most desirable alternative is .
By comparing the ranking results obtained by Procedure I and Procedure II, we find out that the two algorithms unanimously identify that the supplier is the worst alternative. However, the permutation of suppliers and changes in the ranking results. The reasons are that Algorithm II takes equal weights for both attributes and decision-makers and obviously is incapable of more completely including decision information in complicated decision-making scenarios. Contrariwise, Procedure I manages to exploit prioritization relations among attributes and objectively deduce relative importance among decision-makers, thus producing a different result.
In sum, when tackling ill-structured MAGDM problems, our proposed Procedure I provides decision-makers with an effective expression tool with which to depict their complicated assessments more comprehensively. Using the developed prioritized aggregation operator, Procedure I manages to exploit more efficiently group opinions on prioritization relations among evaluative attributes, rather than multiple rounds adjustments in conventional AHP-based methodologies under decision-making environments of high complexity. Additionally, the maximizing deviation model help Procedure I achieves more generality and objectivity in deriving unknown weights for decision-makers. Therefore, the proposed Procedure I performs an effective and efficient approach to complicate decision-making problems.
6. Conclusions
Focusing on the special type of ill-structured complex multiple attributes group decision-making problems, which characterize facets of decision-makers’ decision hesitancy and prioritization relationships among evaluative attributes and unknown weighting information for decision-makers, we have developed an effective approach by employing IVDHFUBLS to elicit hesitant assessments more precisely and completely. To accommodate prioritization relationships among evaluative attributes, the proposed interval-valued dual hesitant fuzzy unbalanced linguistic prioritized weighted aggregation (IVDHFUBLPWA) operator is capable of simultaneously considering both assessments given by decision-makers and prioritization relationships. As for deducing unknown weights for decision-makers, the devised hybrid model succeeds in objectively determining rational decision-makers’ weights by exploiting the overall accuracy measure of the individual decision matrix and maximizing the deviation among all decision matrices. Applied study on a green supplier selection problem has demonstrated the effectiveness and practicality of our approach.
Although we have constructed an effective approach for MAGDM under IVDHFUBLS environments, the approach applies to only the homogeneous format of assessments in group decision-making scenarios. However, sophisticated MAGDM approaches for tackling more complex practical problems should allow decision-makers to denote their specific preferences with various expression tools so as to attain better flexibility and adaptability. Therefore, future research should be firstly directed to investigate heterogeneous MAGDM approaches under IVDHFUBLS environments to deep depth, and more application studies on real problems as well, such as sustainable supplier selection, risk evaluation, etc.
Author Contributions
X.-W.Q. contributed to theoretical analysis and writing the whole paper. J.-L.Z. carried out the case studies. C.-Y.L. provided overall instructions of this work.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank precious suggestions by all anonymous reviewers. The authors would also like to thank great joint-support by the National Natural Science Foundation of China (Nos. 71701181, 71771075, 71331002), the Social Science Foundation of Ministry of Education of China (No. 16YJC630094), and the Natural Science Foundation of Zhejiang Province of China (LQ17G010002, LY18G010010, and LQ18G030012).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zimmermann, H.J. Fuzzy Set Theory and Its Applications; Springer: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Lin, R.-J. Using fuzzy dematel to evaluate the green supply chain management practices. J. Clean. Prod. 2013, 40, 32–39. [Google Scholar] [CrossRef]
- Qin, J.; Liu, X. 2-tuple linguistic muirhead mean operators for multiple attribute group decision making and its application to supplier selection. Kybernetes 2016, 45, 2–29. [Google Scholar] [CrossRef]
- Junior, F.R.L.; Osiro, L.; Carpinetti, L.C.R. A comparison between fuzzy AHP and fuzzy TOPSIS methods to supplier selection. Appl. Soft Comput. 2014, 21, 194–209. [Google Scholar] [CrossRef]
- Qi, X.; Liang, C.; Zhang, J. Generalized cross-entropy based group decision making with unknown expert and attribute weights under interval-valued intuitionistic fuzzy environment. Comput. Ind. Eng. 2015, 79, 52–64. [Google Scholar] [CrossRef]
- Ghazanfari, M.; Rouhani, S.; Jafari, M. A fuzzy topsis model to evaluate the business intelligence competencies of port community systems. Pol. Marit. Res. 2014, 21, 86–96. [Google Scholar] [CrossRef]
- Rouhani, S.; Ghazanfari, M.; Jafari, M. Evaluation model of business intelligence for enterprise systems using fuzzy topsis. Expert Syst. Appl. 2012, 39, 3764–3771. [Google Scholar] [CrossRef]
- Zhang, J.; Hegde, G.; Shang, J.; Qi, X. Evaluating emergency response solutions for sustainable community development by using fuzzy multi-criteria group decision making approaches: Ivdhf-topsis and ivdhf-vikor. Sustainability 2016, 8, 291. [Google Scholar] [CrossRef]
- Ju, Y.B.; Wang, A.H.; You, T.H. Emergency alternative evaluation and selection based on ANP, DEMATEL, and TL-TOPSIS. Nat. Hazards 2015, 75, 347–379. [Google Scholar] [CrossRef]
- Ju, Y.; Wang, A.; Liu, X. Evaluating emergency response capacity by fuzzy AHP and 2-tuple fuzzy linguistic approach. Expert Syst. Appl. 2012, 39, 6972–6981. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.; Zhang, H.; Hu, J. A heterogeneous linguistic magdm framework to classroom teaching quality evaluation. Eurasia J. Math. Sci. Technol. Educ. 2017, 13, 4929–4956. [Google Scholar] [CrossRef]
- Xu, Y.P. Model for evaluating the mechanical product design quality with dual hesitant fuzzy information. J. Intell. Fuzzy Syst. 2016, 30, 1–6. [Google Scholar] [CrossRef]
- Başar, Ö.; Cengiz, K. Evaluation of renewable energy alternatives using hesitant fuzzy topsis and interval type-2 fuzzy AHP. In Soft Computing Applications for Renewable Energy and Energy Efficiency; Maria del Socorro García, C., Juan Miguel Sánchez, L., Antonio David Masegosa, A., Carlos Cruz, C., Eds.; IGI Global: Hershey, PA, USA, 2015; pp. 191–224. [Google Scholar]
- Liu, H.-C.; You, J.-X.; Lu, C.; Chen, Y.-Z. Evaluating health-care waste treatment technologies using a hybrid multi-criteria decision making model. Renew. Sustain. Energy Rev. 2015, 41, 932–942. [Google Scholar] [CrossRef]
- Mardani, A.; Jusoh, A.; Zavadskas, E.K. Fuzzy multiple criteria decision-making techniques and applications—Two decades review from 1994 to 2014. Expert Syst. Appl. 2015, 42, 4126–4148. [Google Scholar] [CrossRef]
- Kahraman, C.; Onar, S.C.; Oztaysi, B. Fuzzy multicriteria decision-making: A literature review. Int. J. Comput. Intell. Syst. 2015, 8, 637–666. [Google Scholar] [CrossRef]
- Montazer, G.A.; Saremi, H.Q.; Ramezani, M. Design a new mixed expert decision aiding system using fuzzy electre III method for vendor selection. Expert Syst. Appl. 2009, 36, 10837–10847. [Google Scholar] [CrossRef]
- Chen, T.-Y. An interval type-2 fuzzy promethee method using a likelihood-based outranking comparison approach. Inf. Fusion 2015, 25, 105–120. [Google Scholar] [CrossRef]
- Park, J.H.; Park, I.Y.; Kwun, Y.C.; Tan, X.G. Extension of the topsis method for decision making problems under interval-valued intuitionistic fuzzy environment. Appl. Math. Model. 2011, 35, 2544–2556. [Google Scholar] [CrossRef]
- Zhang, X.L.; Xu, Z.S. The todim analysis approach based on novel measured functions under hesitant fuzzy environment. Knowl.-Based Syst. 2014, 61, 48–58. [Google Scholar] [CrossRef]
- Zhang, X.L.; Xu, Z.S. Hesitant fuzzy qualiflex approach with a signed distance-based comparison method for multiple criteria decision analysis. Expert Syst. Appl. 2015, 42, 873–884. [Google Scholar] [CrossRef]
- Chen, N.; Xu, Z.S. Hesitant fuzzy electre II approach: A new way to handle multi-criteria decision making problems. Inf. Sci. 2015, 292, 175–197. [Google Scholar] [CrossRef]
- Peng, J.-J.; Wang, J.-Q.; Wang, J.; Yang, L.-J.; Chen, X.-H. An extension of electre to multi-criteria decision-making problems with multi-hesitant fuzzy sets. Inf. Sci. 2015, 307, 113–126. [Google Scholar] [CrossRef]
- Turksen, I.B. Interval valued fuzzy sets based on normal forms. Fuzzy Sets Syst. 1986, 20, 191–210. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Atanassov, K.T.; Gargov, G. Interval valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Torra, V.; Narukawa, Y. On hesitant fuzzy sets and decision. In Proceedings of the 18th IEEE International Conference on Fuzzy Systems, Jeju Island, Korea, 20–24 August 2009; pp. 1378–1382. [Google Scholar]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Zhu, B.; Xu, Z.S.; Xia, M.M. Dual hesitant fuzzy sets. J. Appl. Math. 2012, 2012. [Google Scholar] [CrossRef]
- Farhadinia, B. Correlation for dual hesitant fuzzy sets and dual interval-valued hesitant fuzzy sets. Int. J. Intell. Syst. 2014, 29, 184–205. [Google Scholar] [CrossRef]
- Zhu, B.; Xu, Z.S. Some results for dual hesitant fuzzy sets. J. Intell. Fuzzy Syst. 2014, 26, 1657–1668. [Google Scholar]
- Ju, Y.B.; Liu, X.Y.; Yang, S.H. Interval-valued dual hesitant fuzzy aggregation operators and their applications to multiple attribute decision making. J. Intell. Fuzzy Syst. 2014, 27, 1203–1218. [Google Scholar]
- Herrera, F.; Herrera-Viedma, E.; Martínez, L. A fusion approach for managing multi-granularity linguistic term sets in decision making. Fuzzy Sets Syst. 2000, 114, 43–58. [Google Scholar] [CrossRef]
- Tao, Z.; Liu, X.; Chen, H.; Zhou, L. Using new version of extended t-Norms and s-Norms for aggregating interval linguistic labels. IEEE Trans. Syst. Man Cybern. Syst. 2016, 47, 3284–3298. [Google Scholar] [CrossRef]
- Martínez, L.; Herrera, F. An overview on the 2-tuple linguistic model for computing with words in decision making: Extensions, applications and challenges. Inf. Sci. 2012, 207, 1–18. [Google Scholar] [CrossRef]
- Wang, J.Q.; Wu, J.T.; Wang, J.; Zhang, H.Y.; Chen, X.H. Interval-valued hesitant fuzzy linguistic sets and their applications in multi-criteria decision-making problems. Inf. Sci. 2014, 288, 55–72. [Google Scholar] [CrossRef]
- Lin, R.; Zhao, X.F.; Wang, H.J.; Wei, G.W. Hesitant fuzzy linguistic aggregation operators and their application to multiple attribute decision making. J. Intell. Fuzzy Syst. 2014, 27, 49–63. [Google Scholar]
- Zhang, N. Hesitant fuzzy linguistic information aggregation in decision making. Int. J. Oper. Res. 2014, 21, 489–507. [Google Scholar] [CrossRef]
- Zhang, W.; Ju, Y.; Liu, X. Multiple criteria decision analysis based on shapley fuzzy measures and interval-valued hesitant fuzzy linguistic numbers. Comput. Ind. Eng. 2017, 105, 28–38. [Google Scholar] [CrossRef]
- Yang, S.H.; Ju, Y.B. Dual hesitant fuzzy linguistic aggregation operators and their applications to multi-attribute decision making. J. Intell. Fuzzy Syst. 2014, 27, 1935–1947. [Google Scholar]
- Qi, X.; Liang, C.; Zhang, J. Multiple attribute group decision making based on generalized power aggregation operators under interval-valued dual hesitant fuzzy linguistic environment. Int. J. Mach. Learn. Cybern. 2016, 7, 1147–1193. [Google Scholar] [CrossRef]
- Herrera-Viedma, E.; López-Herrera, A.G. A model of an information retrieval system with unbalanced fuzzy linguistic information. Int. J. Intell. Syst. 2007, 22, 1197–1214. [Google Scholar] [CrossRef]
- Martínez, L.; Espinilla, M.; Liu, J.; Pérez, L.G.; Sánchez, P.J. An evaluation model with unbalanced linguistic information applied to olive oil sensory evaluation. J. Mult.-Valued Log. Soft Comput. 2009, 15, 229–251. [Google Scholar]
- Herrera, F.; Herrera-Viedma, E.; Martinez, L. A fuzzy linguistic methodology to deal with unbalanced linguistic term sets. IEEE Trans. Fuzzy Syst. 2008, 16, 354–370. [Google Scholar] [CrossRef]
- Meng, D.; Pei, Z. On weighted unbalanced linguistic aggregation operators in group decision making. Inf. Sci. 2013, 223, 31–41. [Google Scholar] [CrossRef]
- Dong, Y.; Li, C.C.; Herrera, F. An optimization-based approach to adjusting unbalanced linguistic preference relations to obtain a required consistency level. Inf. Sci. 2015, 292, 27–38. [Google Scholar] [CrossRef]
- Qi, X.; Zhang, J.; Liang, C. Multiple attributes group decision-making approaches based on interval-valued dual hesitant fuzzy unbalanced linguistic set and their applications. Complexity 2018, 2018. [Google Scholar] [CrossRef]
- Ju, Y.B.; Wang, A.H. Emergency alternative evaluation under group decision makers: A method of incorporating ds/ahp with extended topsis. Expert Syst. Appl. 2012, 39, 1315–1323. [Google Scholar] [CrossRef]
- Yager, R.R. Prioritized aggregation operators. Int. J. Approx. Reason. 2008, 48, 263–274. [Google Scholar] [CrossRef]
- Wei, G. Hesitant fuzzy prioritized operators and their application to multiple attribute decision making. Knowl.-Based Syst. 2012, 31, 176–182. [Google Scholar] [CrossRef]
- Yager, R.R. Prioritized owa aggregation. Fuzzy Optim. Decis Mak. 2009, 8, 245–262. [Google Scholar] [CrossRef]
- Yu, D.; Wu, Y.; Lu, T. Interval-valued intuitionistic fuzzy prioritized operators and their application in group decision making. Knowl.-Based Syst. 2012, 30, 57–66. [Google Scholar] [CrossRef]
- Yu, X.H.; Xu, Z.S. Prioritized intuitionistic fuzzy aggregation operators. Inf. Fusion 2013, 14, 108–116. [Google Scholar] [CrossRef]
- Yu, D.J. Prioritized information fusion method for triangular intuitionistic fuzzy set and its application to teaching quality evaluation. Int. J. Intell. Syst. 2013, 28, 411–435. [Google Scholar] [CrossRef]
- Zhao, Q.Y.; Chen, H.Y.; Zhou, L.G.; Tao, Z.F.; Liu, X. The properties of fuzzy number intuitionistic fuzzy prioritized operators and their applications to multi-criteria group decision making. J. Intell. Fuzzy Syst. 2015, 28, 1835–1848. [Google Scholar]
- Peng, D.H.; Wang, T.D.; Gao, C.Y.; Wang, H. Multigranular uncertain linguistic prioritized aggregation operators and their application to multiple criteria group decision making. J. Appl. Math. 2013, 2013. [Google Scholar] [CrossRef]
- Ren, Z.; Wei, C. A multi-attribute decision-making method with prioritization relationship and dual hesitant fuzzy decision information. Int. J. Mach. Learn. Cybern. 2017, 8, 755–763. [Google Scholar] [CrossRef]
- Wu, J.T.; Wang, J.Q.; Wang, J.; Zhang, H.Y.; Chen, X.H. Hesitant fuzzy linguistic multicriteria decision-making method based on generalized prioritized aggregation operator. Sci. World J. 2014. [Google Scholar] [CrossRef] [PubMed]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning-I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Rodríguez, R.M.; Martínez, L.; Herrera, F. Hesitant fuzzy linguistic term sets for decision making. IEEE Trans. Fuzzy Syst. 2012, 20, 109–119. [Google Scholar] [CrossRef]
- Rodríguez, R.M.; Martínez, L.; Herrera, F. A group decision making model dealing with comparative linguistic expressions based on hesitant fuzzy linguistic term sets. Inf. Sci. 2013, 241, 28–42. [Google Scholar] [CrossRef]
- Beg, I.; Rashid, T. Topsis for hesitant fuzzy linguistic term sets. Int. J. Intell. Syst. 2013, 28, 1162–1171. [Google Scholar] [CrossRef]
- Wang, J.-Q.; Wu, J.-T.; Wang, J.; Zhang, H.-Y.; Chen, X.-H. Multi-criteria decision-making methods based on the hausdorff distance of hesitant fuzzy linguistic numbers. Soft Comput. 2016, 20, 1621–1633. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Chinese Government. Regulations on Natural Disaster Rscue and Assistance; The-Ministry-of-Civil-Affairs, Chinese Government: Beijing, China, 2010. Available online: http://www.mca.gov.cn/article/zwgk/fvfg/jzjj/201008/20100800095101.shtml (accessed on 13 June 2018).
- Chinese Government. Emergency Plan for Natural Disaster Rescue, Modified ed.; The-Ministry-of-Civil-Affairs, Chinese Government: Beijing, China, 2011. Available online: http://www.mca.gov.cn/article/zwgk/fvfg/jzjj/201111/20111100191129.shtml (accessed on 13 June 2018).
- Momoh, J.A.; Zhang, Y.; Fanara, P.; Kurban, H.; Iwarere, L.J. Social impact based contingency screening and ranking. Int. J. Crit. Infrastruct. 2007, 3, 124–141. [Google Scholar] [CrossRef]
- Kelly, C. Quick Guide: Rapid Environmental Impact Assessment in Disaster; Benfield Hazard Research Centre, University College London and CARE International: London, UK, 2003; pp. 1–43. [Google Scholar]
- Kelly, C. Guidelines for Rapid Environmental Impact Assessment in Disasters; Benfield Greig Hazard Research Centre, University College London and CARE International: London, UK, 2005; pp. 1–86. [Google Scholar]
- Zhou, X.Q.; Li, Q.G. Generalized hesitant fuzzy prioritized einstein aggregation operators and their application in group decision making. Int. J. Fuzzy Syst. 2014, 16, 303–316. [Google Scholar]
- Ye, J. Prioritized aggregation operators of trapezoidal intuitionistic fuzzy sets and their application to multicriteria decision-making. Neural Comput. Appl. 2014, 25, 1447–1454. [Google Scholar] [CrossRef]
- Chen, L.; Xu, Z. A new prioritized multi-criteria outranking method: The prioritized promethee. J. Intell. Fuzzy Syst. 2015, 29, 2099–2110. [Google Scholar] [CrossRef]
- Wang, Y.M. Using the method of maximizing deviations to make decision for multi-indices. Syst. Eng. Electron. 1997, 8, 21–26. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).