1. Introduction
There have been theories of consciousness that make use of mathematics, e.g. mathematical models of patterns of activity in neural nets, but no theory of brain function or automated reasoning that I have encountered explains how brains enable great mathematical discoveries to be made, e.g. the discoveries in geometry and topology, reported many centuries ago in Euclid’s
Elements [
1], describing not just
observed regularities but
necessary connections or impossibilities, some of which, e.g. Pythagoras’ theorem, are still in regular use world-wide by scientists, engineers and architects. (For readers unfamiliar with Euclidean geometry, there is a very useful short (17 min) introduction, presented by Zsuzsanna Dancso, at
https://www.youtube.com/watch?v=6Lm9EHhbJAY.)
In 1964, Gelernter’s geometry prover [
2] discovered a proof not previously known to the developer, simply because of the combinatorial power built into the search for a proof. There have been several automated geometry theorem provers of increasing sophistication since then. Automated geometry theorem provers generally start with logic-based formulations of Euclid’s axioms, postulates, etc. (e.g. using David Hilbert’s axiomatization of geometry, [
3] and assuming the Cartesian coordinate representation of geometry). But that approach to mathematics was not developed until long after the original discoveries in geometry.
In contrast, [
4] Nathaniel Miller describes a package that operates on diagrams in a way that partly corresponds to the original proofs in Euclid’s elements. However he does not claim that its operation models the cognitive processes in ancient human mathematicians. For example, as far as I can tell, his system does not express anything about necessity or impossibility. It merely finds proofs using 2-D graphical structures rather than logical formulae, though it also uses logical and algebraic mechanisms. (I may have missed some features of the system.)
I am not aware of any theories or working models that explain convincingly how cognitive or neural mechanisms made discoveries in geometry and topology possible for ancient human mathematicians, as contrasted with discoveries of observed statistical regularities that are often used to infer approximate generalisations or to estimate probabilities.
Mechanisms for discovering
statistical regularities and
probabilities cannot explain or justify claims regarding
necessity or
impossibility, which are characteristic features of mathematical discoveries as Kant pointed out in 1781. Such claims about mathematics should not be confused with claims about discovering phenomena that happen to occur with 100% or 0% probability in certain contexts. Necessity and impossibility are not types of probability. (I am not relying on “possible world” semantics for these modal concepts, for reasons given below. [
5,
6]).
Since the 1960s, there have been AI geometry theorem provers, but, as remarked above, they usually start with logic-based formulations of Euclid’s axioms and postulates, usually enhanced with assumptions about numerical representations of geometry based on Cartesian coordinates. The latter were not used by Euclid, since Cartesian coordinates were not invented until much later.
Moreover, for ancient mathematicians the axioms and postulates were not freely
chosen starting points for logical derivations, as in modern uses of the axiomatic method to define a mathematical topic, e.g. Group theory, described in
https://en.wikipedia.org/wiki/Group_theory. In such cases, the axioms do not represent known deep mathematical truths, but are parts of implicit
definitions of particular mathematical (sub-)topics.
In contrast, Euclid’s axioms and postulates reported deep discoveries about spatial structures. They were selected as axioms or postulates because other interesting geometrical facts could be derived from them, even if some of those facts had originally been discovered independently. The axioms were not selected because they could be used to specify a new mathematical sub-field, then used as a basis for studying that field.
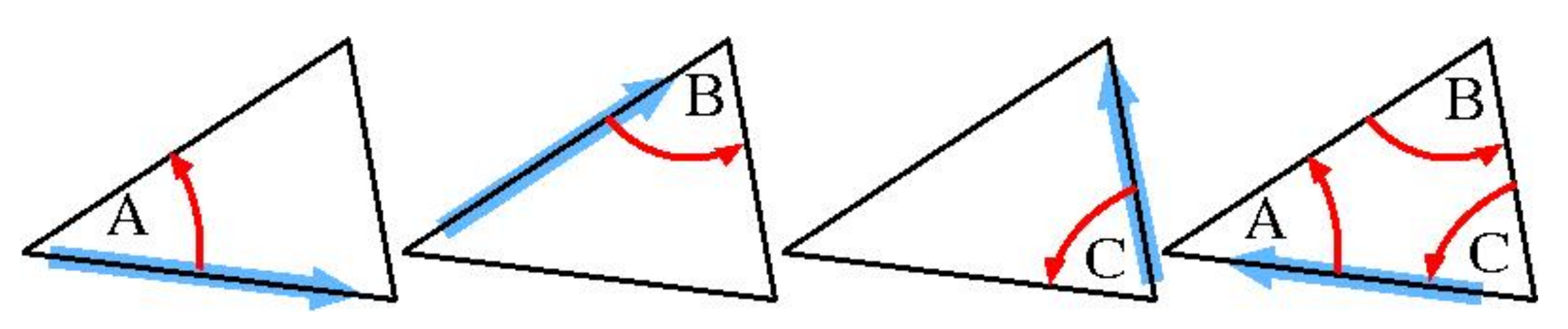
For example, Euclid showed how the parallel axiom could be used to prove the triangle sum theorem (
Internal angles of a planar triangle must always sum to half a rotation, i.e., 180°). But the same theorem could have been discovered independently of Euclid’s parallel axiom, and proved using a method that Mary Pardoe informed me she had discovered while teaching mathematics to school children (around 1970). Her proof, shown in
Figure 1, demonstrated the
necessary truth of the triangle sum theorem without any explicit reference to parallel lines.
What sorts of brain mechanisms allow such discoveries to be made, and understood, including understanding that some things do not merely report things frequently observed or never observed, but express necessary truths or falsehoods. As far as I know, there is nothing in current neuroscience that explains such capabilities, and no AI system that can make, or even understand, such discoveries about necessity or impossibility in spatial configurations, even if some of them understand necessary truths or impossibilities involving numbers or simpler relations.
On 26 March 2018, Tim Penttila (School of Mathematical Sciences, The University of Adelaide) wrote to me with very interesting information about the earlier history of the proof in
Figure 1 discovered by Mary Pardoe. This is what he wrote, demonstrating that the proof had previously been taken seriously by professional mathematicians:
The proof of the angle sum of a triangle that you attribute to Mary Pardoe was first published by Bernhard Friedrich Thibaut (1775–1832) in the second edition of his Grundriss der reinen Mathematik, published in Goettingen by Vandenhoek und Ruprecht in 1809 (see p. 363).
A neural model or deep learning system could discover an approximation to the triangle sum theorem by inspecting many planar triangles, measuring their angles and adding the sizes. But that would not prove that the theorem is a necessary truth regarding planar triangles, incapable of being refuted at some future time by a new planar triangle with a special combination of lengths and angles.
There are many geometrical discoveries that are not derivable from Euclid’s axioms. For example, possibilities for creating 3-D structures by repeated folds of a flat sheet of paper (Origami) can produce combinations of lines that cannot be achieved in Euclidean geometry, including trisection of an arbitrary angle (for more details see
https://en.wikipedia.org/wiki/Origami). Another example not derivable within Euclidean geometry is the
Neusis construction that was known to ancient mathematicians, but not included in Euclid’s
Elements. It involves use of a movable straight edge with two marks, and it allows arbitrary angles to be trisected easily, as explained in
http://www.cs.bham.ac.uk/research/projects/cogaff/misc/trisect.html. The discovery of non-euclidean geometries was another important example, famously used by Einstein in his General Theory of Relativity.
Although Euclidean geometry can be axiomatised using logic and algebra, as David Hilbert showed in 1899 [
3], it is clear that the original human ability to discover and understand truths of geometry did not depend on use of modern logical and algebraic reasoning. Those types of reasoning were unknown to ancient mathematicians, and developed only within the last few centuries.
Topological reasoning abilities, concerned with continuous deformation of shapes, and continuous routes on collections of lines and vertices, seem to be even more widespread among non-mathematicians, as discussed in [
7]. Young children who have never studied logic or algebra can tell that it is
impossible for two linked rings made of solid, impermeable matter to become unlinked without at least one of them changing shape (e.g. ceasing to be a ring). This can be seen in their responses to clever stage magicians who make it
look as if the impossible has been achieved. A closely related topological problem: if a length of string is passed through a ring, it can be removed from the ring by pulling either end of the string, while the ring is held fixed. Try persuading a child that the string will be removed (intact) twice as fast if both ends are held and pulled together. What brain mechanisms enable us to see that such things are impossible, even though many examples support the hypothesis that two forces pulling an object (e.g. a string) in a certain direction will cause it to move faster in that direction than use of one force—because they forget that in some contexts forces in the same direction can be in total conflict.
It is not obvious what we would have to add to current AI systems to give them such abilities. A current learning machine could be fooled (at least temporarily) by the evidence that usually two people pulling something manage to get it moving faster than one pulling alone, or that doubling a force applied will speed up movement produced. Apart from the AI systems based on logic, the AI learning systems known to me use statistical evidence to infer probabilities. They cannot even represent, let alone learn about impossibilities and necessary connections.
Some admirers of deep learning mechanisms believe that given appropriate training such a mechanism could make the same discoveries as ancient mathematicians, and human toddlers can. Likewise I suspect some neuroscientists believe that mathematical discoveries can be triggered by examples using the same mechanisms as lead to generalisations, such as “unsupported objects fall”. But those learning mechanisms are inherently statistics based and can only discover that certain generalisations have high, or low, probabilities. They cannot discover that something is
necessarily true or that something is
impossible: these are totally different from very high and very low probabilities—as Immanuel Kant understood when he pointed out [
8,
9] that Hume’s classification of types of knowledge was incomplete. He identified an important type of mathematical knowledge that is
non-empirical and about
necessary truths and
impossibilities (necessary falsehoods). Trainable neural nets, in which all information is based on nodes in graphs with weighted connections cannot even
express the idea of something being impossible, or necessarily the case. Without the
expressive power, animals or machines cannot have the
reasoning power to derive such conclusions.
Note, however, that modal operators, e.g. “necessary”, “impossible” should not be analysed using “possible world” semantics. In many contexts the space of possibilities under consideration is merely the space of possible variants of a local
part of the universe. Details are beyond the scope of this paper. See [
5,
6]. I do not believe there is any sense in which ordinary individuals can, or need to, refer to
complete alternative universes when making discoveries about geometrical or topological possibility, impossibility or necessity.
It is not clear what enables humans to understand concepts like necessity and impossibility: neural nets that merely record categories encountered so far and their relative frequencies cannot express these concepts, which, as Kant pointed out, characterise mathematical knowledge. That implies that human brains have mechanisms with powers beyond those of artificial neural nets, since humans (and perhaps some other animals) can understand and use those concepts, e.g. in recognizing that performing a certain action is a guaranteed way of achieving some goal, or in recognizing that no action could possibly achieve the goal. The fact that the number of vertices of a convex planar polygon, no matter what its size or shape, must equal the number of sides is not a statistical fact.
How can you decide whether there is a spatial configuration in which a planar triangle and a circle have exactly seven boundary points in common? You can work out which numbers of common points are possible, by doing mental experiments with imagined triangles and circles. As far as I know no current AI system can discover that impossibility without using something like Hilbert’s axiomatisation of geometry, using Cartesian coordinates, which children don’t need, and ancient mathematicians did not know about: Cartesian coordinates were not discovered until the 17th Century. (The discovery was crucial to Newton’s mechanics and the invention/discovery of differential and integral calculus, on which a great deal of modern science and engineering depends.)
2. Why Is Non-Empirical Knowledge of Non-Contingent Truths Important?
The kind of mathematical knowledge under discussion, knowledge of impossibilities, or exceptionless generalities, that can be identified without exhaustive testing in vast numbers of situations, is not just a philosophical oddity. It is of great practical importance to intelligent agents. For example, knowing that something is impossible makes it unnecessary to waste time to find out whether it can occur. Recognition of such “negative affordances” may be crucial to the intelligence of species such as squirrels, nest-building birds, elephants and many other animals. Likewise knowing that having some feature is a necessary consequence of having some other feature allows decisions to be taken and used with confidence that might otherwise have to be tested repeatedly and with caution, wasting time and energy. In these and other ways the modal features of mathematical knowledge are important for processes of scientific discovery and processes of engineering design.
Some examples are based on knowledge that visual information travels in straight lines except in special situations (e.g. crossing water/air boundaries). If you are looking at a partly obstructed portion of the environment which way should you move to see beyond the obstruction? In many cases the choice is whether to move your head more to the left or to the right, to see round an obstruction with a vertical edge on the left or on the right. We find it obvious that moving one way will make visible larger portions of remote surfaces, and sometimes previously obscured surfaces, whereas moving in the opposite direction will have the opposite effect, obscuring more distant surface parts. I suspect far more animals have that sort of mathematical competence than anyone has ever investigated, even if most don’t know they have it or why it works. In those cases, a solution to the problem of deriving new information may have been directly programmed by evolution, with no metacognitive ability to detect its presence or use. Most people never detect it, and only a subset of philosophers of mathematics seem to.
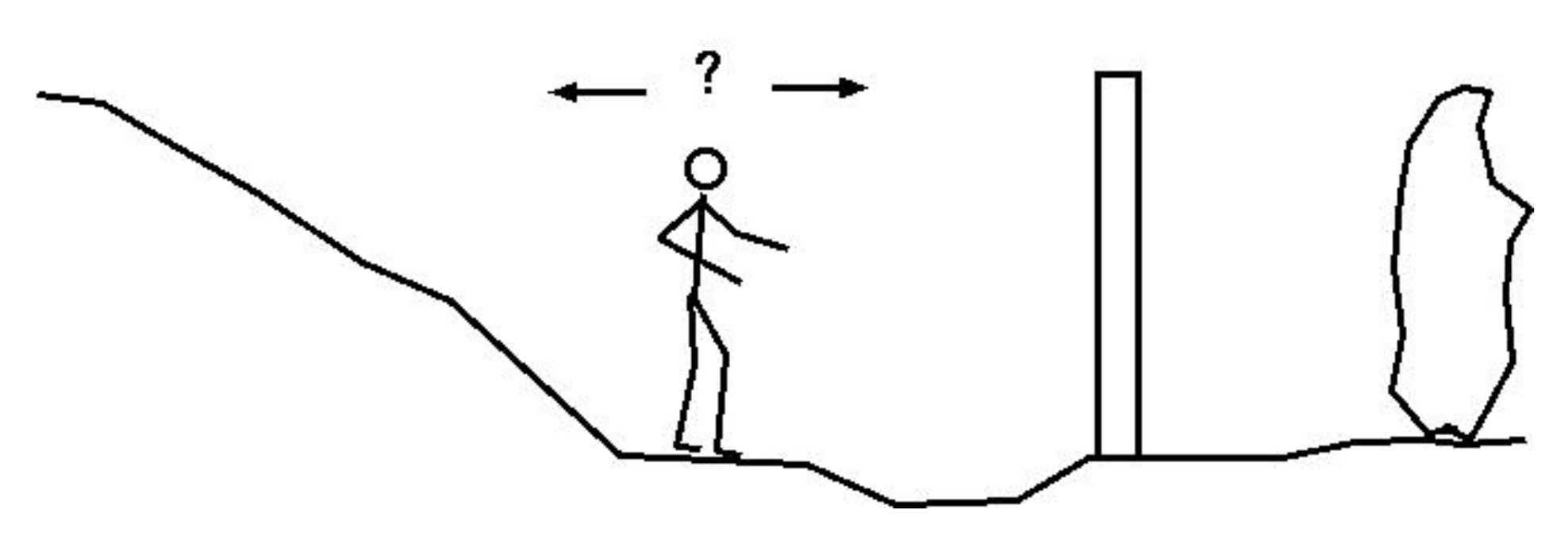
A simple example of use of such knowledge is presented in
Figure 2. If you know that the object you are seeking is nearly as tall as an obstructing wall, and it is either infeasible, or unhelpful to move left or right (e.g. the wall is too long), then, if you are in the situation depicted, you can work out that walking
away from the wall will raise your eye height to well above the height of the wall, whereas moving toward the wall will not. If you already know that the ground around you is firm, then you can work out which direction of motion must give you a view over the top of the wall—you must walk uphill to increase your head height. Of course the (mathematical) “must” here is relative to many assumptions about absence of malevolent influences, invisible step ladders etc. There are many practical problems, including engineering problems, where the mathematically best answer is the one to use even if there is no absolute guarantee that the rest of the environment will remain normal.
Not only humans can benefit from this kind of reasoning. Biological evolution has clearly made and used many mathematical discoveries in selecting physical and chemical structures capable of complex and varied behaviours, and in selecting control mechanisms for those structures. For example, negative feedback control is used in many “homeostatic” control mechanisms from the very simplest organisms to control of blood pressure, temperature, chemical balances and other features of complex organisms.
A more complex use of mathematical abstraction is the design of control mechanisms for muscles of organisms that vary in size, shape, weights, and moments of inertia of various body parts as they grow. The muscular forces exerted in a child need to be both task specific and in some cases also continually replaced by larger forces as that child grows bigger, heavier, and faster-moving. So evolution produces (a) physical structures with mathematical properties supporting a range of uses, (b) parametrised mechanisms to control those structures in accordance with requirements determined by task and context, (c) abstract versions of (a) and (b) that can be instantiated with different parameters as an individual changes in size, weight, strength, and needs or goals.
The combination of similarities and differences across species suggests that this diversity was made possible by evolution of “parametrised” generic construction kits that could be tailored to the specifics of particular species, using another level of mathematical abstraction.
Evolution makes and uses many profoundly important mathematical discoveries, in producing organisms or parts of organisms whose designs use mathematical concepts and techniques. A recurring example mentioned above is use of negative feedback for control of continuous change, i.e., homeostatic control, of temperature, pressure, direction, speed, etc. These are examples of “blindly used” mathematics. James Watt famously rediscovered the importance of such negative feedback control when he invented the Watt governer for steam engines. Many other past products of human ingenuity implicitly used the same principle, e.g. use of secondary vanes to control the direction in which force generating windmill vanes face, so as to obtain maximal energy from the wind. Many more complex examples are found in more recent applications of control engineering, including both discrete and continuous control on many spatial and temporal scales of magnitude. However, spectacular examples were produced by biological evolution and its products long before there were any human control engineers.
These examples illustrate the fact that the ability to discover and use mathematical facts does not presuppose the ability to recognize what has been achieved as a mathematical discovery that is independent of its practical applications. It also does not involve abilities to recognise necessity and impossibility. That explicit level of mathematical metacognition seems to have been achieved only by a subset of humans, probably long before Euclid, although implicit, unreflective forms of such metacognition seem to occur in other intelligent species and in intelligent humans who have not been taught mathematics. This may be based on more wide-spread abilities that insightful teachers can transform into mathematical competences, although initially the transformation must have occurred without such teachers.
In the last few centuries cultural evolution, including the development and spread of engineering and mathematical knowledge, has enormously expanded the variety of examples of mathematical cognition. (There are also some pre-mathematical pattern-recognition competences that are mistaken for mathematical/numerical competences by some psychologists and neuroscientists. But that’s a large topic to be discussed elsewhere.) For our purposes it is important that many of the mathematical competences have not yet been replicated in AI systems, despite the common view of computers as mathematical reasoners.
3. Toddler Theorems and Animal Intelligence
In [
11] I have a disorganised and still growing collection of examples of types of proto-mathematical spatial reasoning and discovery that can be observed in young children without any mathematical training, including pre-verbal children. I have labelled some of the examples “toddler theorems”, mentioned below. Piaget recorded many more examples, e.g. in his last two books [
12,
13] as well as earlier work.
There is also evidence for what could be called “proto-mathematical” reasoning about spatial structures in other intelligent species, e.g. squirrels, the planning and plan execution abilities of Portia spiders [
14], and the abilities of nest-building birds [
15]. The implicit (unconscious) grasp of mathematical necessities and impossibilities can enable an animal quickly to rule out actions that are incapable of achieving some goal, or to remove features of a situation that make the goal impossible to achieve, e.g. chopping a large tree into small pieces to make transport possible.
The variety of different spatial configurations that can arise during assembly of a nest from twigs and leaves is so huge that if birds had to learn from experience which configurations are useful which not, and which actions produce the useful configurations in various situations, very few might live long enough learn how to build even one nest reliably. Yet weaver birds manage to produce very complex knotted structures using a thousand or more knotted leaves, and it is not plausible to suggest that evolution has evolved innate reflex responses for every intermediate situation that can occur during the process of construction of a nest using hundreds or thousands of leaves.
Instead, it seems to have provided a kind of implicit mathematical reasoning ability that allows the birds to choose between good and bad options in a wide enough range of situations to enable successful nest construction in a fairly short time. For an online video showing some parts of the construction process see
https://www.youtube.com/watch?v=qbWM1QAVGzs.
I am not suggesting that the birds have the kind of mathematical understanding of what they are doing that an engineer does who uses mathematical reasoning to produce novel designs that are provably effective. That requires at least two distinct levels of competence: (a) the ability to reason mathematically in particular cases, and (b) meta- knowledge about how and why that form of mathematical reasoning (e.g. using physical or imagined diagrams) works. In very young humans, and in many intelligent non-human species, I suggest there are evolved spatial-mathematical abilities that allow information about appropriate actions to be derived from a range of intention/situation combinations without any (meta-cognitive) understanding of why those decisions work, or how to extend them to novel situations. At least in humans that can understanding can develop later, unless prevented by bad teaching of mathematics!.
There may also be some intelligent species that have mathematical (e.g. geometrical, topological) reasoning abilities that allow them to solve novel problems without wasting time on trial and error learning, but without knowing what they are doing or why it works—a description that also fits electronic calculators and many other useful software tools.
Young pre-verbal humans seem to have that kind of unwitting mathematical competence. Several examples of “toddler theorems” are presented in [
11], including reasoning about how to avoid jamming fingers when pushing drawers shut, and how to close a door after crawling through the doorway, by rolling over onto one’s back and using feet to push the door.
Deeper investigation might reveal several layers of mathematical and meta-mathematical development in young humans, combining genetic factors with information gained from the environment, e.g. the materials in the environment, including types of furniture, types of toy, and types of games played. I think I learnt a great deal from meccano sets. (Compare the processes of “representational redescription” postulated by Karmiloff-Smith [
16], also referred to below.)
A particular example of non-spatial mathematical intelligence in young humans is the ability to create subsuming generative grammars after many patterns of verbal communication have been found to work in the environment. This has the great benefit of allowing novel linguistic structures to be created, or to be understood, without being restricted to examples provided by more advanced language users.
This stage of extended competence is usually followed by a new level of competence in adjusting the mechanisms used to cope with exceptions to the rules in the child’s linguistic input and output mechanisms, since the initial collection of re-usable experienced grammatical structures has to be extended to deal with exceptions to the rules, found in human languages.
That is a rather messy kind of mathematical process, and the use of such abilities to derive a new linguistic utterance to communicate a novel thought is not guaranteed to be successful, because it depends on the competences and vagaries of other humans. I suspect that, at present, very little is known about the precise forms of representation used in young human brains during generation and comprehension of language, whether spoken, written or signed, since the details cannot always be inferred from perceived examples of language use: they need to be re-created.
5. Spatial Affordances
Perception and use of spatial affordances, by humans and other animals acting in natural environments, require abilities to perceive and reason about spatial structures and spatial relationships, including topological relationships such as containment and overlap, and partial orderings (nearer, wider, more curved, etc), rather than precise measures, though precise measures are required for some competences, including the trapeze artistry of spider monkeys.
I suspect animal brains use far more forms of mathematical reasoning, especially several types of topological and geometrical reasoning illustrated (with the help of some videos) in
http://www.cs.bham.ac.uk/research/projects/cogaff/misc/impossible.html and in [
22]. The Wikipedia entry on Spider monkeys suggests that their meta-cognitive abilities extend to reasoning about requirements for actions by their young offspring, e.g. reducing gaps between branches for them.
Moreover, as Kant pointed out, many humans also develop the ability to understand such reasoning as demonstrating necessary truths of falsehoods, though most need stimulation and help from other humans, e.g. teachers. But there must be brain mechanisms that make the recognition of such cases possible without a teacher, since the first teacher or teachers could not have had teachers. But that does not imply that the knowledge is innate: it may require general mathematical competences to be stimulated to develop in particular ways by aspects of the environment. (It is possible that there are some exceptional individuals who do not require such external stimulation, or need much less than most young mathematicians.)
There is strong counter-evidence to claims about innateness of number competences. In particular, the concepts of cardinality and ordinality presuppose the concept of one-to-one correspondence and an understanding that it is a transitive and symmetric relation (required for existence of an equivalence class for each number), and
necessarily so. Piaget’s work, e.g. [
23], suggests that the transitivity of one-to-one correspondence (sometimes loosely described as “conservation” of number) is not understood until a child’s fifth or sixth year. That suggests that the knowledge is not pre-programmed in the genome (could an evolutionary process achieve that?), but rather a product of interactions between some deeper, late developing innate mechanism, and products of prior experience, as is clearly the case with development of grammatical knowledge. The difference is that grammatical knowledge clearly develops partly under the influence of culture-specific linguistic practices that vary around the planet, whereas mathematical knowledge, e.g. knowledge of transitivity of one-to-one correspondence may depend on a late developing but innate mechanism for making topological discoveries about graph structures, as suggested in Chapter 8 of [
24]. That suggests that often cited empirical evidence for use of number concepts in very young children, or non-humans, is actually evidence for something different: the ability to use flexible pattern matching with simple templates to distinguish groups of one, two, or more items, may be innate but distinct from the mathematical concept of natural number, which is far deeper and more general than any finite collection of pattern concepts, and which I suspect requires one of the later layers of gene expression depicted in
Figure 3. So far no AI system that I know of has this kind of grasp of finite cardinals and ordinals. If it had, such a system might be able to re-discover Peano’s axioms for arithmetic, by reflecting on features of its numerical competences.
6. Back to Ancient Mathematical Reasoning and Discovery
Both the logic based AI mechanisms recommended by McCarthy and Hayes in [
19]) and the currently more fashionable allegedly “brain-inspired”, but quite un-brainlike neural net mechanisms (that usually ignore all the chemical complexity of brains), seem to be unable to replicate the kinds of mathematical reasoning that led to the deep, ancient discoveries assembled by Euclid.
By examining examples of the spatial (diagrammatic) reasoning involved in ancient mathematical discoveries we may hope to gain some insights into what is missing from current forms of computation. I’ll use an example below in
Section 7.1 that, as far as I know, has never been deemed worthy of note by mathematicians, but has a number of interesting features, including very easy comprehension by non-mathematicians who make a deep mathematical discovery as a result of thinking about the example.
This example is highly artificial, but similar points could be made about various stages of nest construction by birds, though details would be very different depending on the materials and construction processes used. For example, fetching lumps of mud and pressing them onto a surface where the new nest is being built, fetching twigs and weaving them into a stable structure on a tree branch as crows and magpies do, and fetching leaves and weaving them into hanging nests, as weaver birds do (as illustrated by the BBC here
https://www.youtube.com/watch?v=6svAIgEnFvw) all require a collection of abilities to perceive structures, select items to manipulate, possibly after moving them to new required locations, and then taking actions to enable the new items to be part of a growing stable structure providing support and shelter. Different cases involve very different physical and mathematical competences. Some pose far greater cognitive challenges than others.
Conjecture: Information processing mechanisms required for practical purposes in structured environments evolved in many species, using geometric and topological reasoning about spatial structures and relationships, but without precise metrical information. In humans, those mechanisms were later used in new ways, in conjunction with new meta-cognitive and meta-meta-cognitive mechanisms, that eventually made possible explicit mathematical reasoning, discussion, and teaching, especially reasoning about topological and geometrical aspects of structures and processes in the environment. These later stages must have been important contributors to social/cultural evolution, by-passing biological reproductive mechanisms.
It is often assumed that mathematical discovery and reasoning must be concerned with numerical values and relationships, but I suggest those came much later and in many cases are not needed because qualitative relationships, such as partial orderings, suffice and are more accessible to biological mechanisms, and adequate for many practical purposes.
In particular, as organisms evolve to cope with more complex structures and processes
in the environment, they use increasingly complex abilities to create and manipulate new
internal information structures, representing parts and relationships of external structures and processes, and supporting reasoning about consequences of possible actions, as hypothesised by Craik in 1943 [
25]. Initially those mechanisms and information structures must have been used for practical decision making and action control in many species, and in pre-verbal human toddlers, e.g. controlling grasping actions and controlling motion towards desired objects, including avoiding obstacles where necessary.
Later on, newly evolved meta-cognitive mechanisms, for reflecting on and comparing successes and failures of such reasoning processes, allowed new, mathematical, aspects of the structures and relationships to be discovered, thought about, and, in some cultures, communicated and used in explicit teaching and discussion.
Much later, via social and cultural processes for which I suspect historical records are not available, the materials came to be organised systematically, recorded in various external “documents”, such as Euclid’s Elements, and taught in specialised sub-communities—a form of cultural evolution.
7. Towards a Super-Turing Geometric Reasoner: Deforming Triangles
7.1. Mathematical Insight into Some Partial Orderings
Why talk about deforming triangles? Because I think there are deep, largely unnoticed, aspects of the ways human and non-human animal minds work that are closely connected with the mechanisms underlying important non-numerical mathematical discoveries by ancient mathematicians, i.e., topological and geometrical discoveries. It is not always remembered that for ancient mathematicians the axioms and postulates in Euclidean geometry were not arbitrarily chosen starting formulae from which conclusions could be derived using pure logic: the ancient axioms were all major discoveries, using mechanisms still available to us. And modern logic was unknown at that time. (As far as I know, Aristotle’s logic was not rich enough to express as much mathematics as the forms of logic developed in the 19th and 20th century.)
Consider mechanisms involved in thinking about what happens to angles of a triangle as it gets stretched by motion of one vertex relative to the other two. I suggest those mechanisms were available to ancient mathematicians, whether they thought of this example or not.
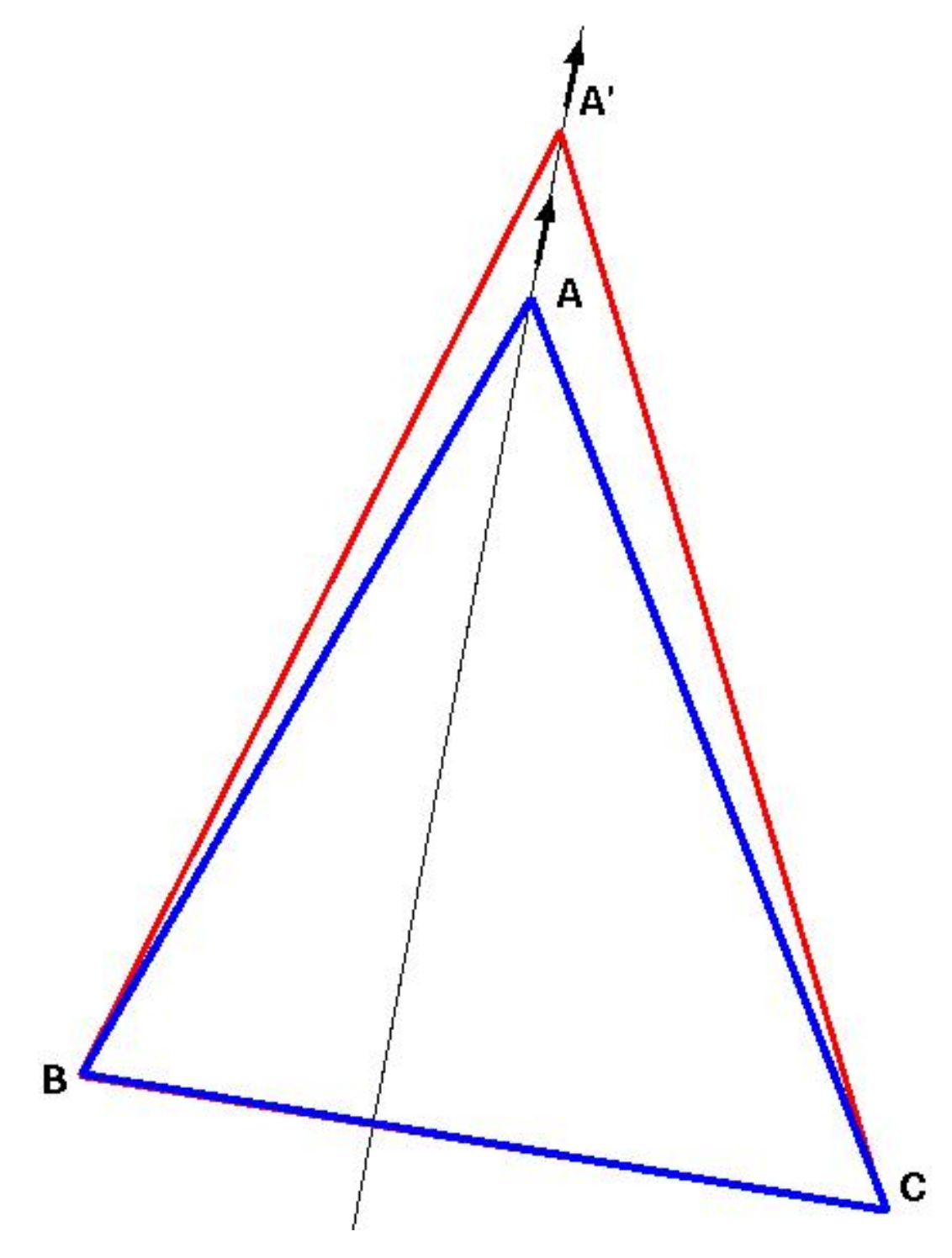
Imagine an arbitrary planar triangle ABC, such as the triangle depicted in
Figure 4, below. What will happen to the angle at A if it continually moves further from the opposite side, BC, along a line that intersects BC and passes through A, as illustrated in
Figure 4? I have informally given the problem to at least 40 people, most of them non-mathematicians, including many who have never studied Euclidean geometry, and they all (so far) seem to have been able to discover the same effect of moving the vertex further from BC along a line passing between B and C. Many cannot say
why such a relationship
must exist.
I have given this problem to a variety of non-mathematicians, and many who have never studied Euclidean geometry, and they all (so far) seem to have been able to discover the same effect of moving the vertex further from BC along a line passing between B and C, namely, as the point A moves further from BC the angle BAC will steadily decrease. Many cannot say why such a relationship must exist.
Despite being so obvious to non-mathematicians, this answer has surprising mathematical sophistication. First of all it involves two continua: there is the continuum of locations of the angle A, along the line—or distances of A from the line BC, and the continuum of sizes for the angle A. Second there is a systematic relationship between the two continua: as the distance increases the angle size decreases. This is a qualitative relationship that holds for a wide variety of shapes and sizes of the initial triangle, since no units of measurement for the length or the angle are specified, and the initial shape and size are not restricted by the question, especially if posed without a drawn triangle.
It is not obvious
exactly how the angle size at A, and the length are related, though it is obvious that as one increases the other decreases. This is not true if the line along which A moves does not intersect the line BC between B and C. The case where A moves along a line that intersects BC outside the triangle is discussed in another document, and some of the implications are surprisingly complex, e.g. the intricacies of the problem of finding where the angle size at A is maximal as it moves along a line meeting BC outside the triangle. For details see:
http://www.cs.bham.ac.uk/research/projects/cogaff/misc/apollonius.html.
For now, however, I merely want to raise a question arising from my informal investigations, which suggest that many adult humans find the answer to the question about angle change in the simple case (in
Figure 4) fairly obvious, either immediately or after a few minutes’ thought. The question is: what sort of reasoning mechanism would enable a future robot to find the answer obvious and present at least a partial explanation. (The exact proportion of humans that find it obvious is irrelevant to questions about what is
possible for human and non-human minds, and how it is possible, as I explained in Chapter 2 of [
24].)
A robot designed by a mathematician might answer the question by using trigonometry to compute a formula linking the angle size to the distance of A from a point on BC, e.g. the midpoint. But the question whose answer all my respondents found obvious was independent of the intersection point, because it was a qualitative answer, or, more precisely, an answer referring to partial orderings, namely as the distance between the point A and the line BC increases, the size of the angle BAC decreases, though normal humans cannot specify an exact rate of decrease or a formula relating angle size to distance along the line of motion.
What sort of spatial reasoning system could we give a future robot that would enable it to find the answer as obvious as humans seem to, and independently of the precise point at which the line of motion of A intersects BC?
We can ask this sort of question, about required mechanisms, for all aspects of human spatial reasoning, mathematical and non-mathematical. I think the answers will be different for professional mathematicians who already have various previously known relevant geometric or trigonometric formulae readily at hand. But I am more interested in the non-mathematicians: what kind of mechanism enables them to find the answer above so obvious?
My tentative conjecture is that there is something brains can do that is not explained by current neural net mechanisms nor by current AI models of spatial reasoning using logic or logic plus algebra, trigonometry etc., but which allows discovery of necessary truths and impossibilities (i.e., necessary falsehoods) and which makes sophisticated use of perceived or imagined spatial structures and relationships.