Tag-Driven Online Novel Recommendation with Collaborative Item Modeling
Abstract
1. Introduction
- There are many more users than novels according to user behavior analysis in the 3G literary community, therefore, item-based algorithm is more appropriate than user-based algorithm for practical application considering data sparsity.
- There are few novels that have been read by one user in a certain period, leading to a sparse rating matrix and low accuracy of similarity calculation for a user-based algorithm. Therefore, it is difficult to find groups with similar interests. In contrast, the rating matrix of an item-based algorithm is denser than that of a user-based algorithm, leading to more accurate similarity calculation.
- A user’s interest in a short term remains stable according to user behavior analysis. In other words, every user has his special preference. In consideration of individualization, novel tag is regarded as an important determinant and an item-based collaborative filtering algorithm is more feasible.
2. Related Works
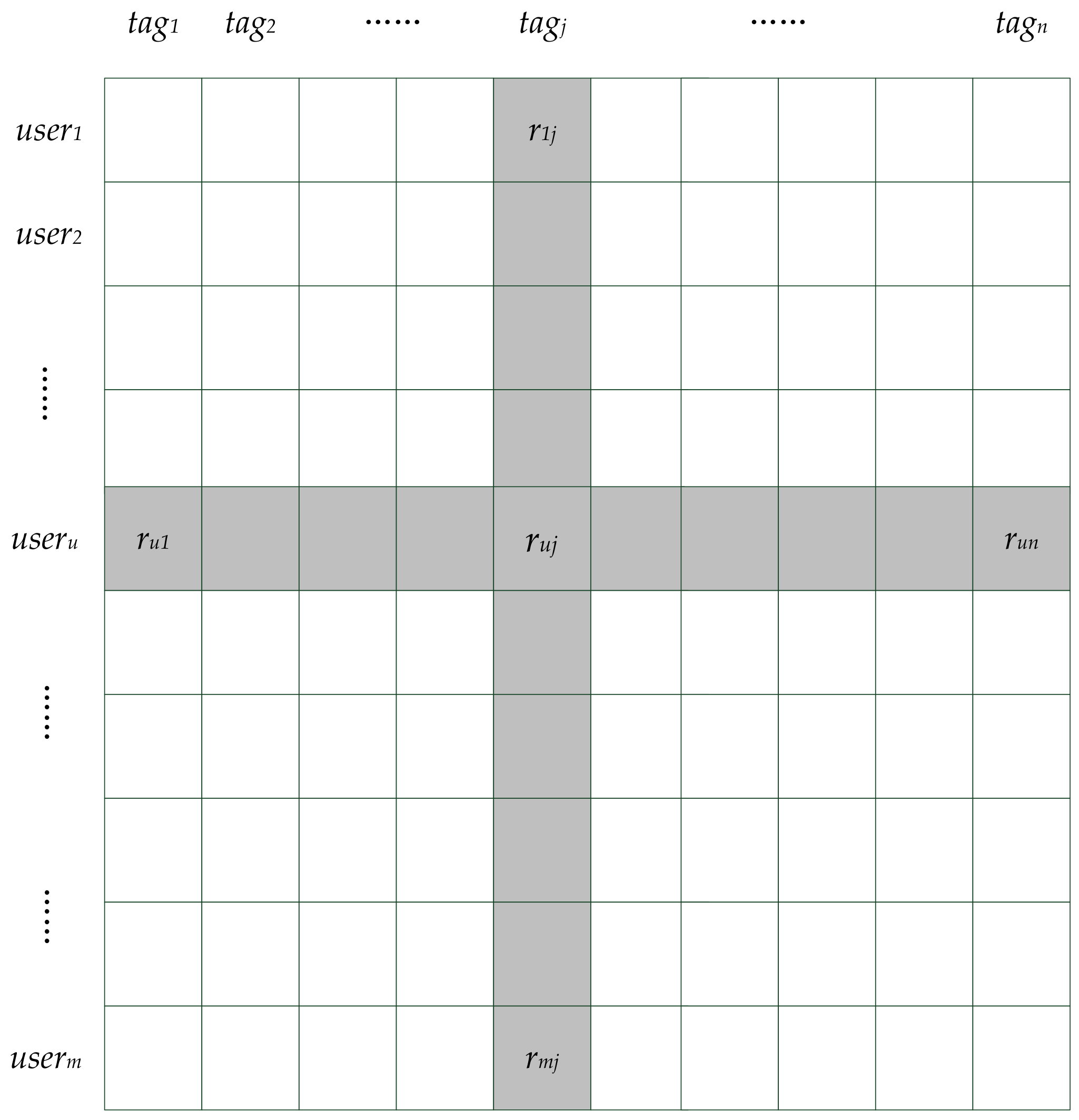
3. Latent Preference Rating
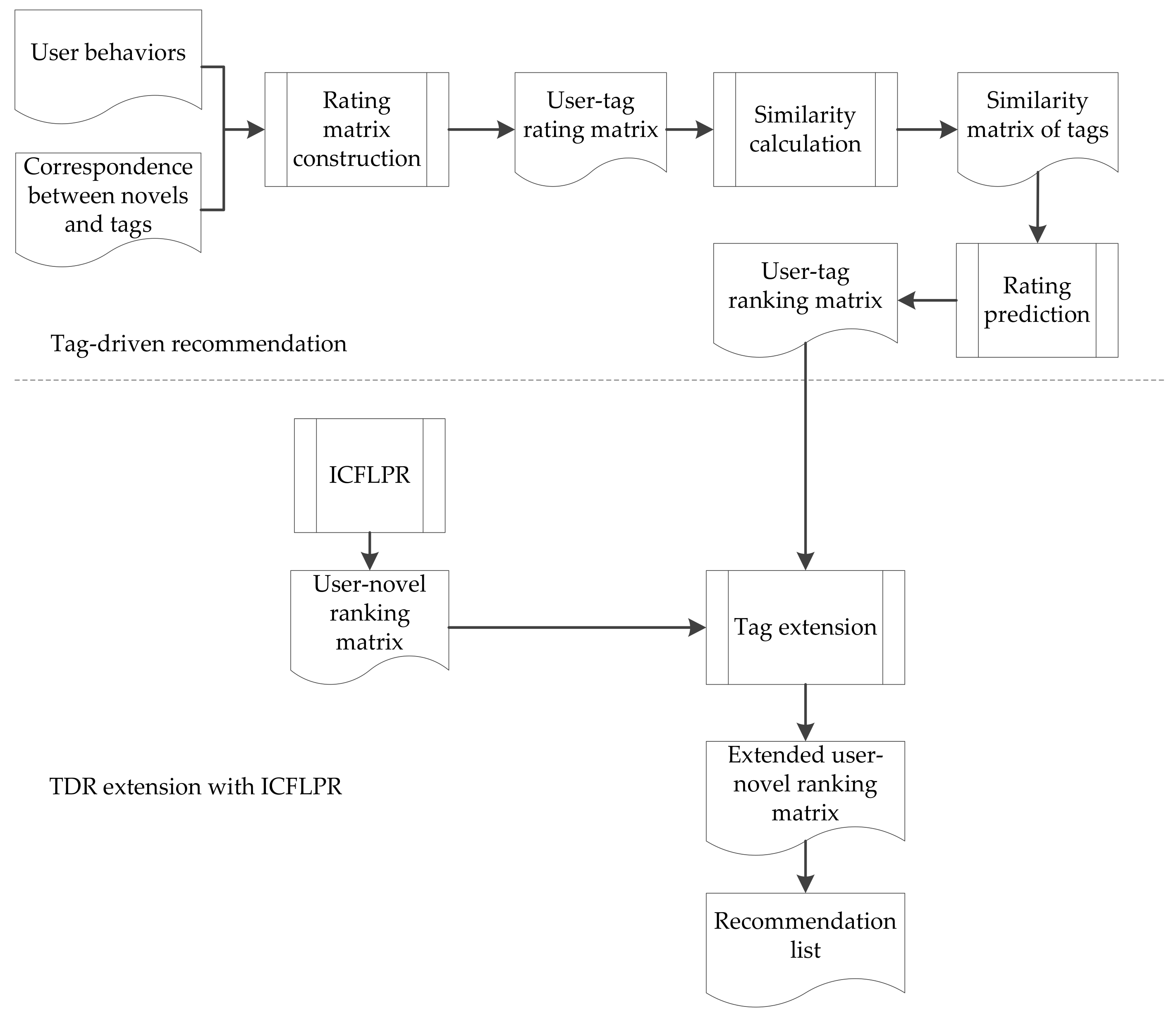
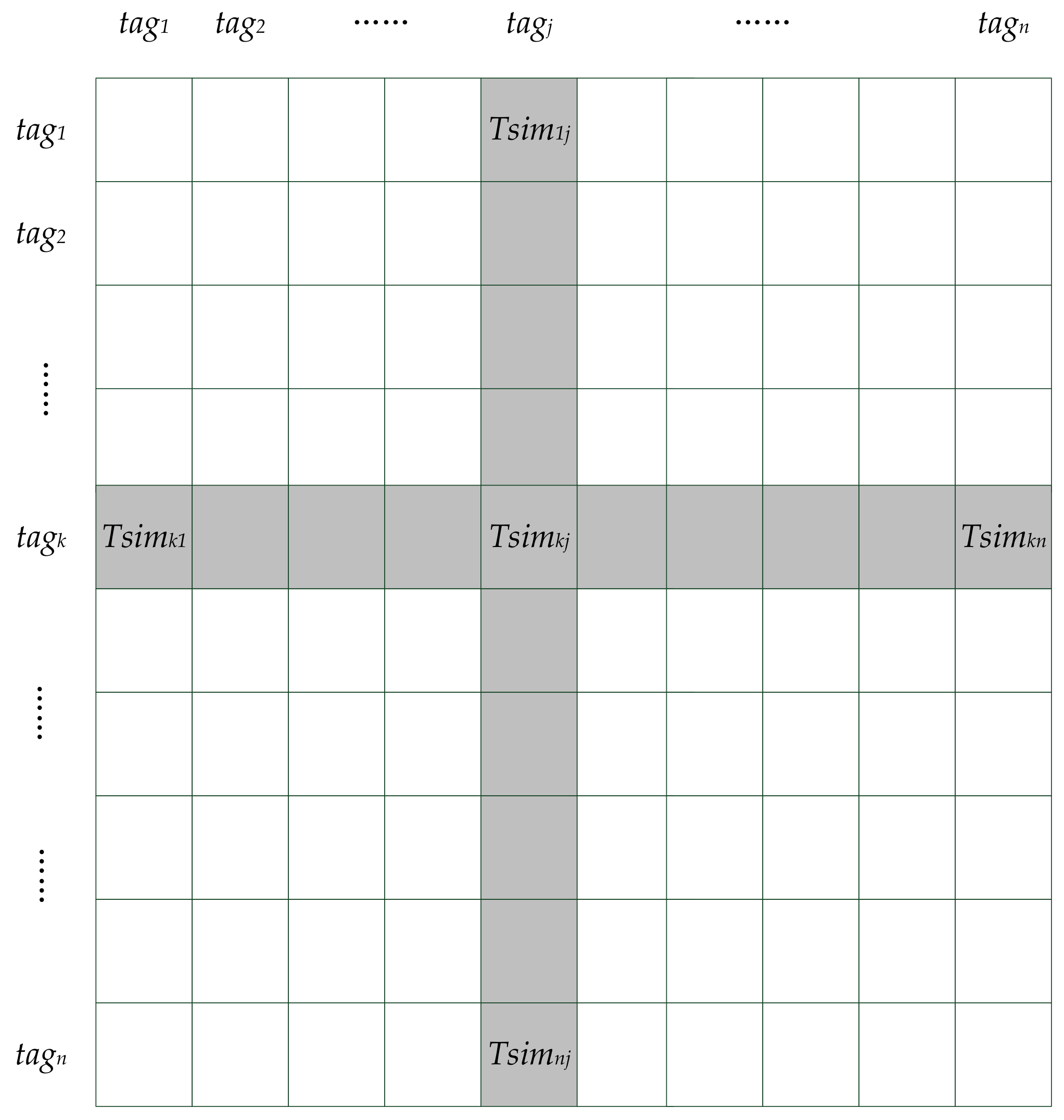
4. Tag-Driven Recommendation with Collaborative Item Modeling
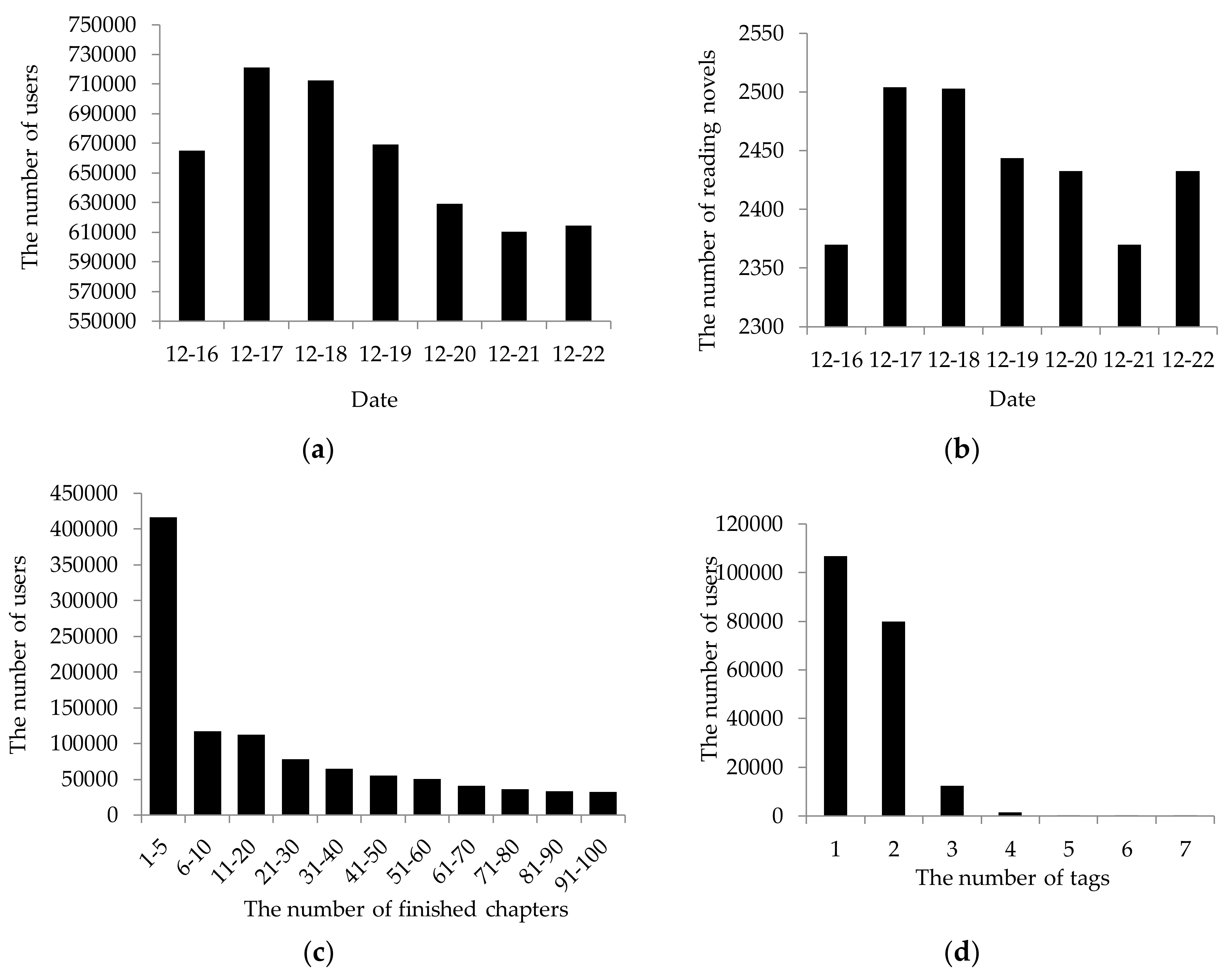
5. Experiments and Discussions
5.1. Experimental Setup
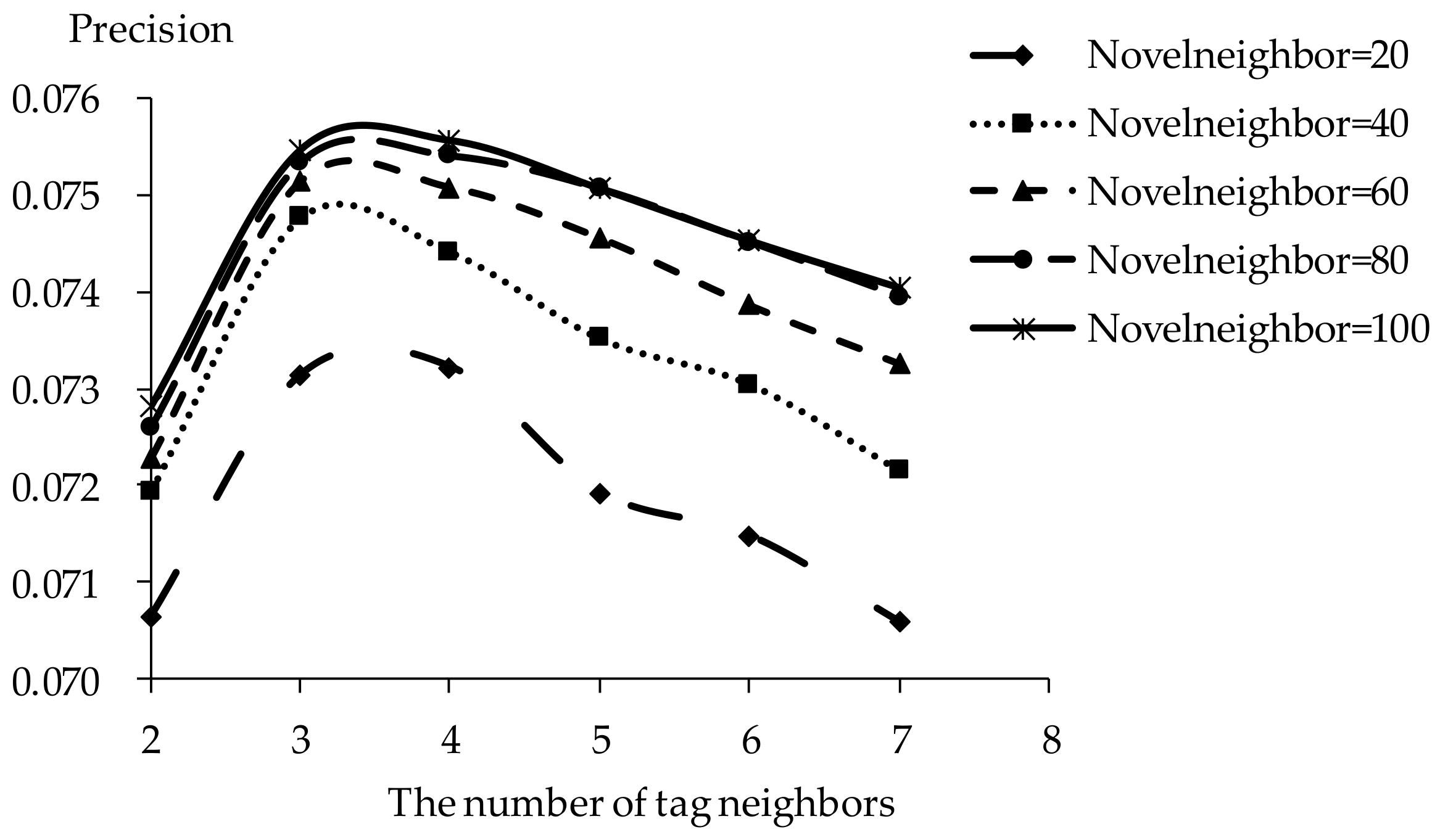
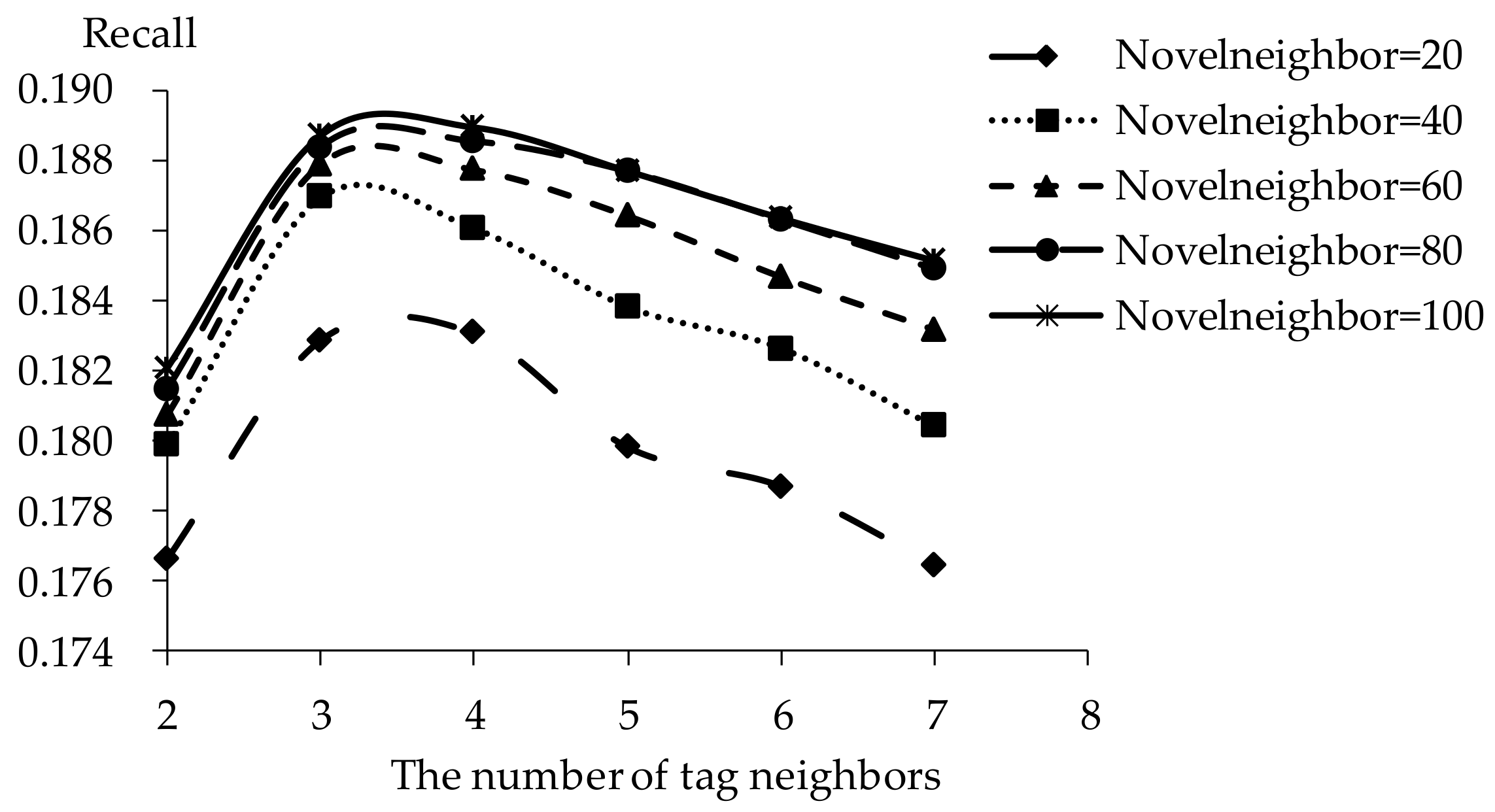
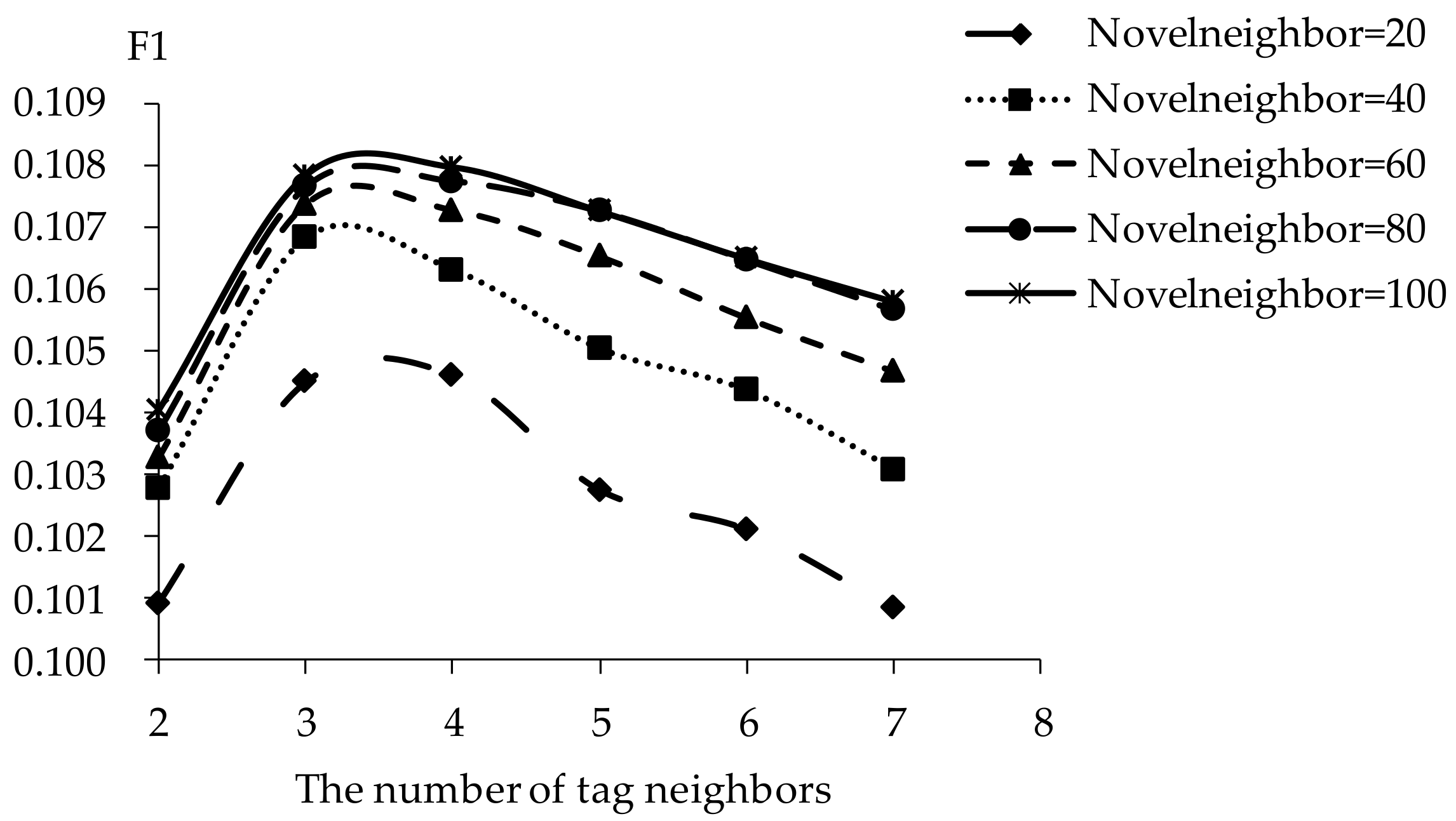
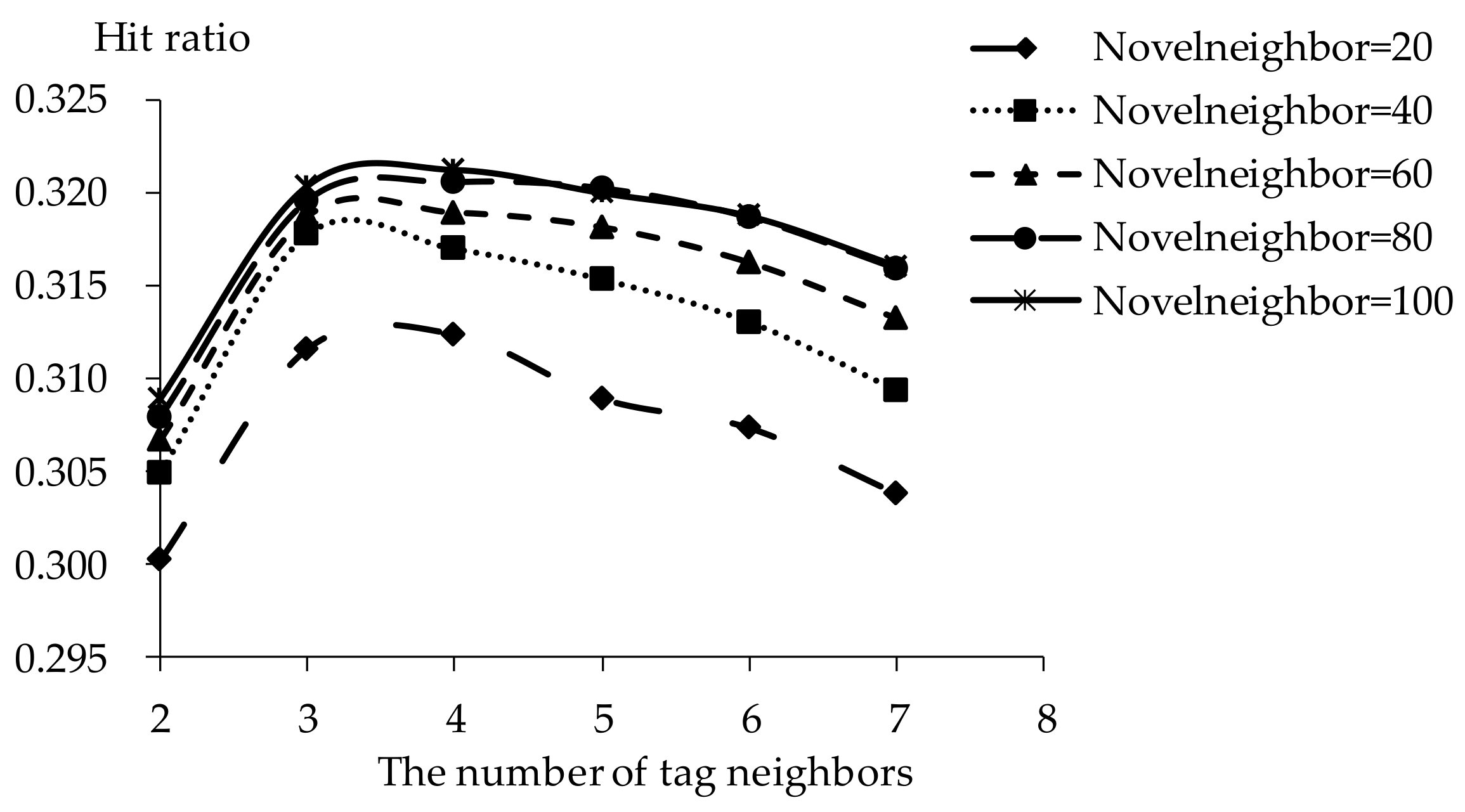
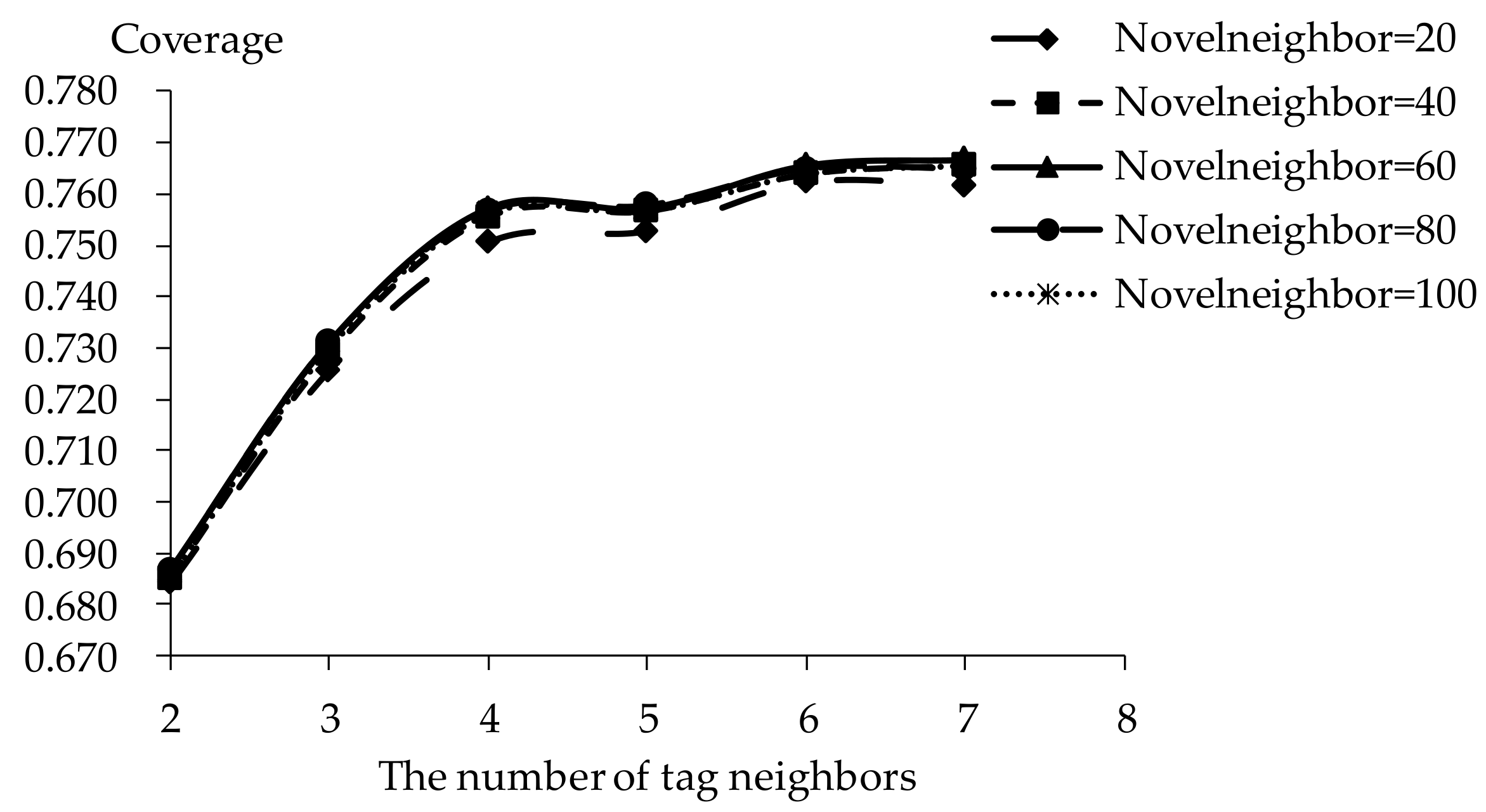
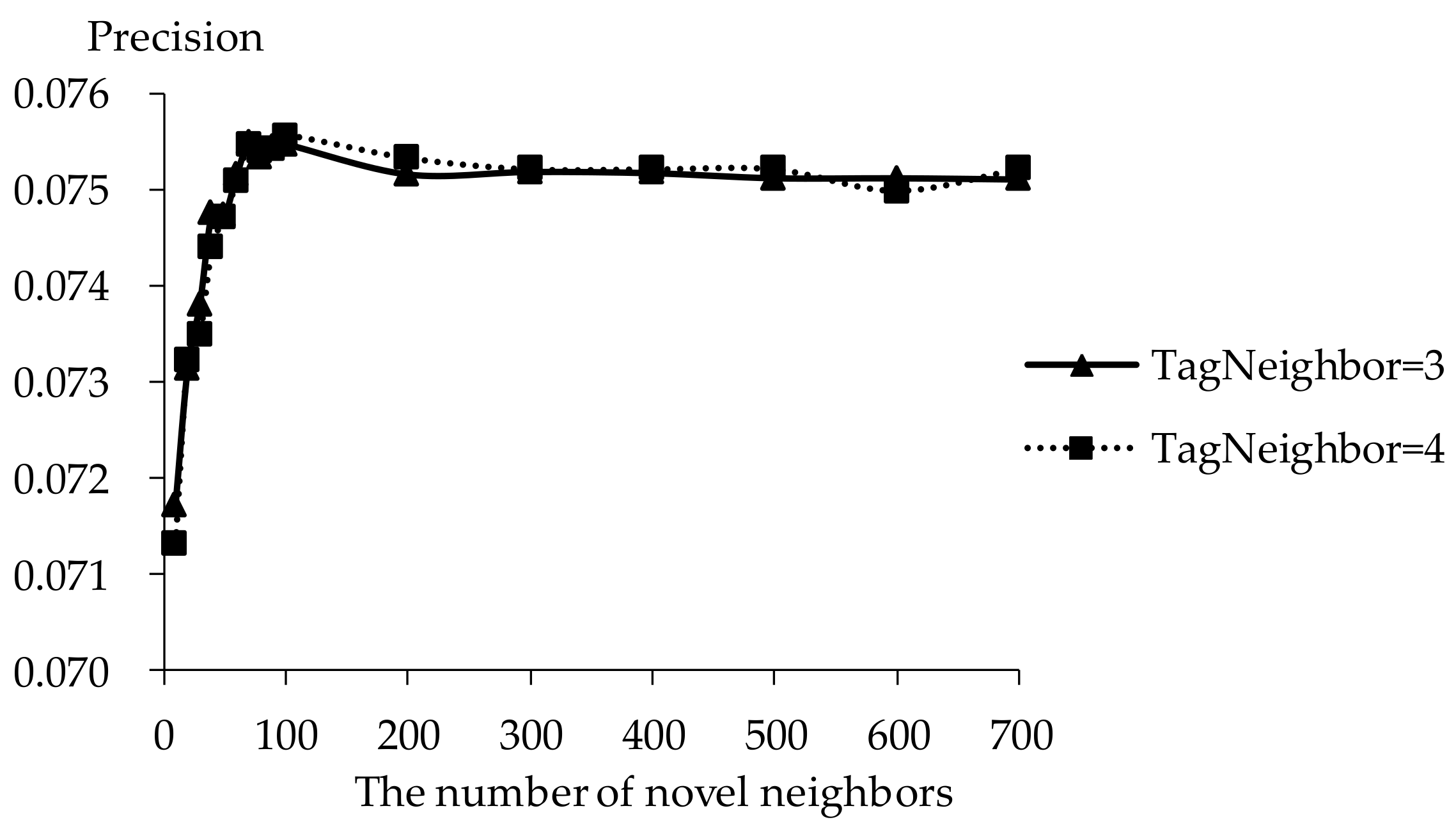
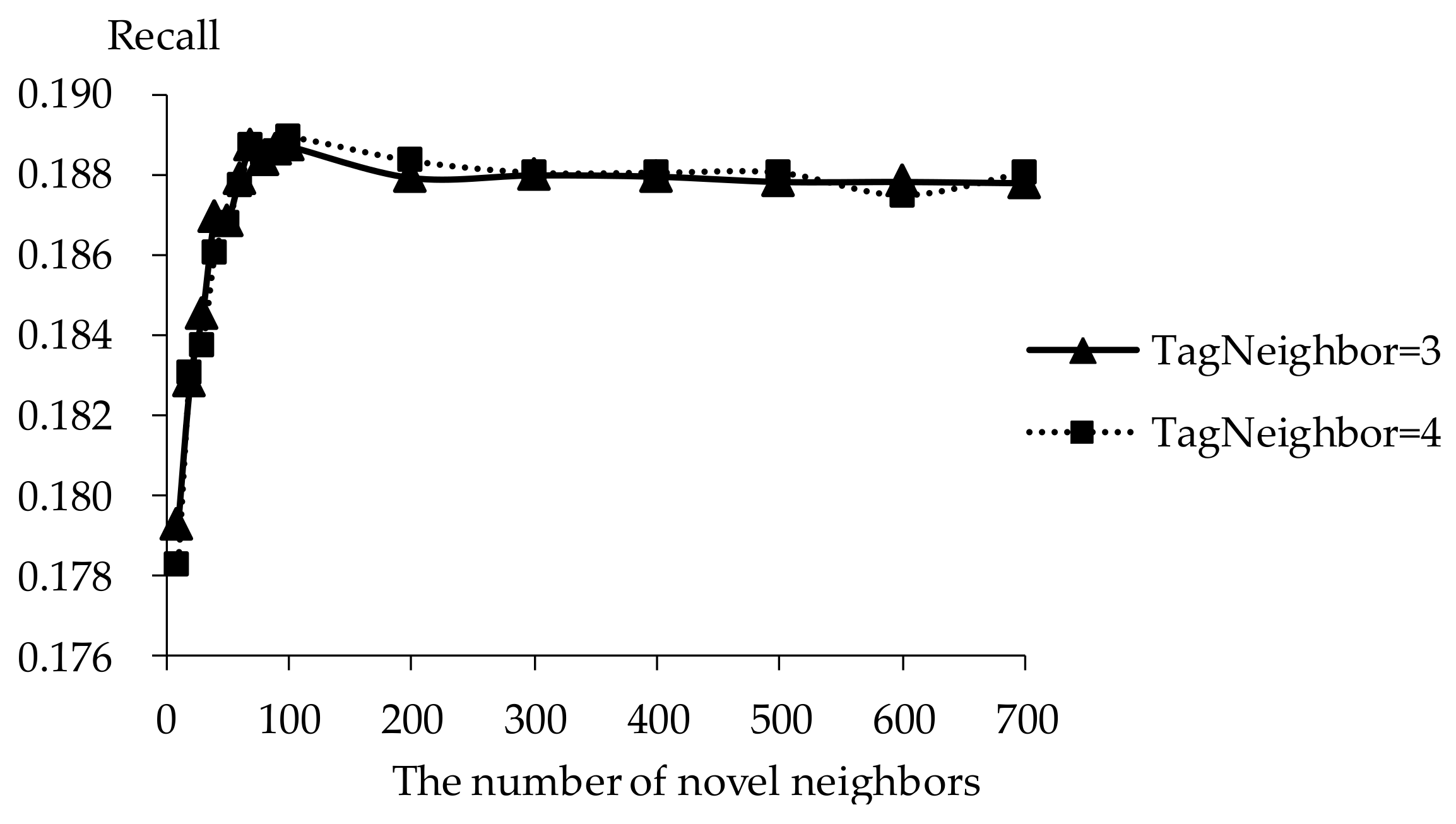
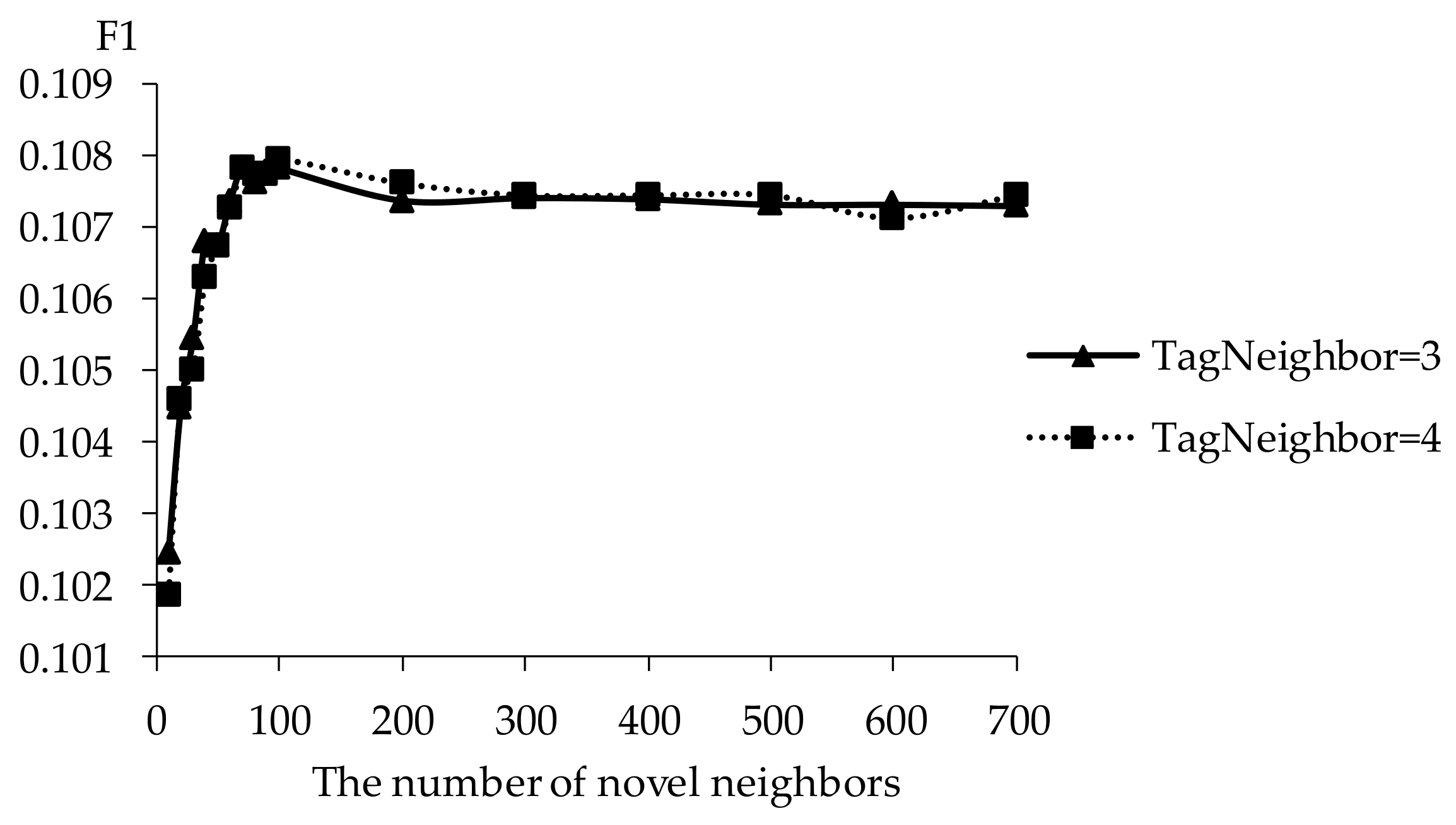
5.2. Impact of Tag Neighbors
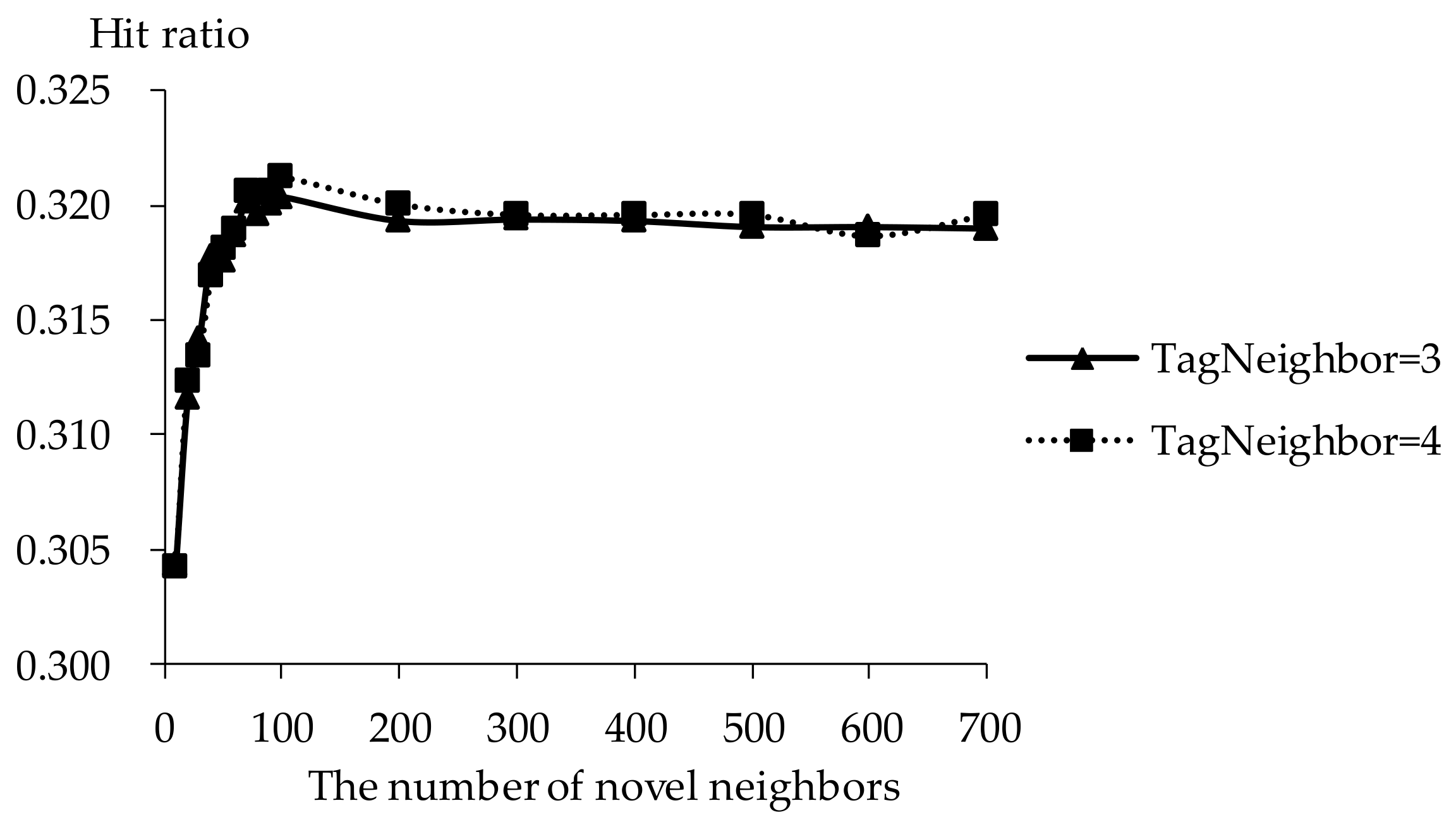
5.3. Impact of Novel Neighbors
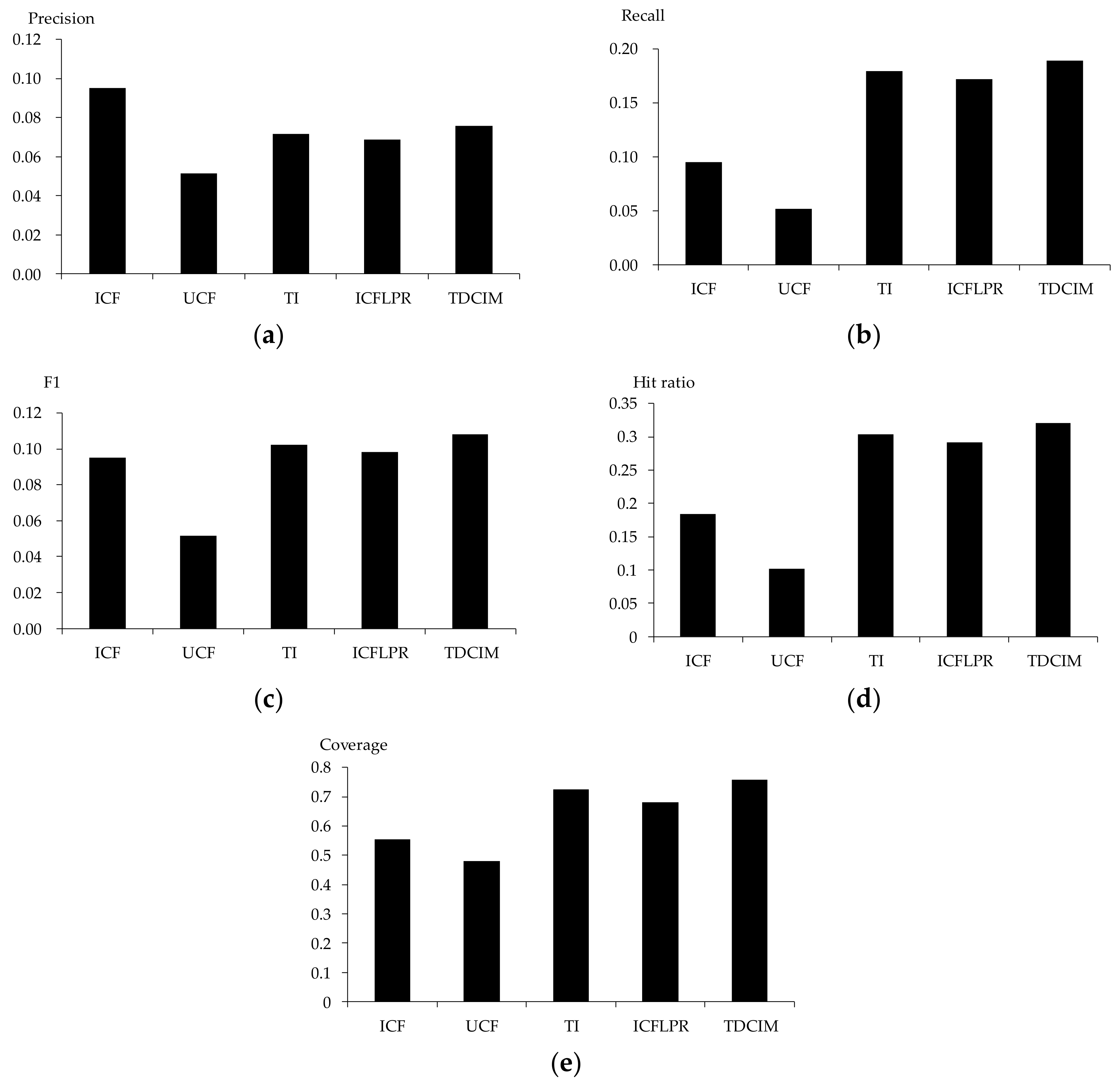
5.4. Effectiveness
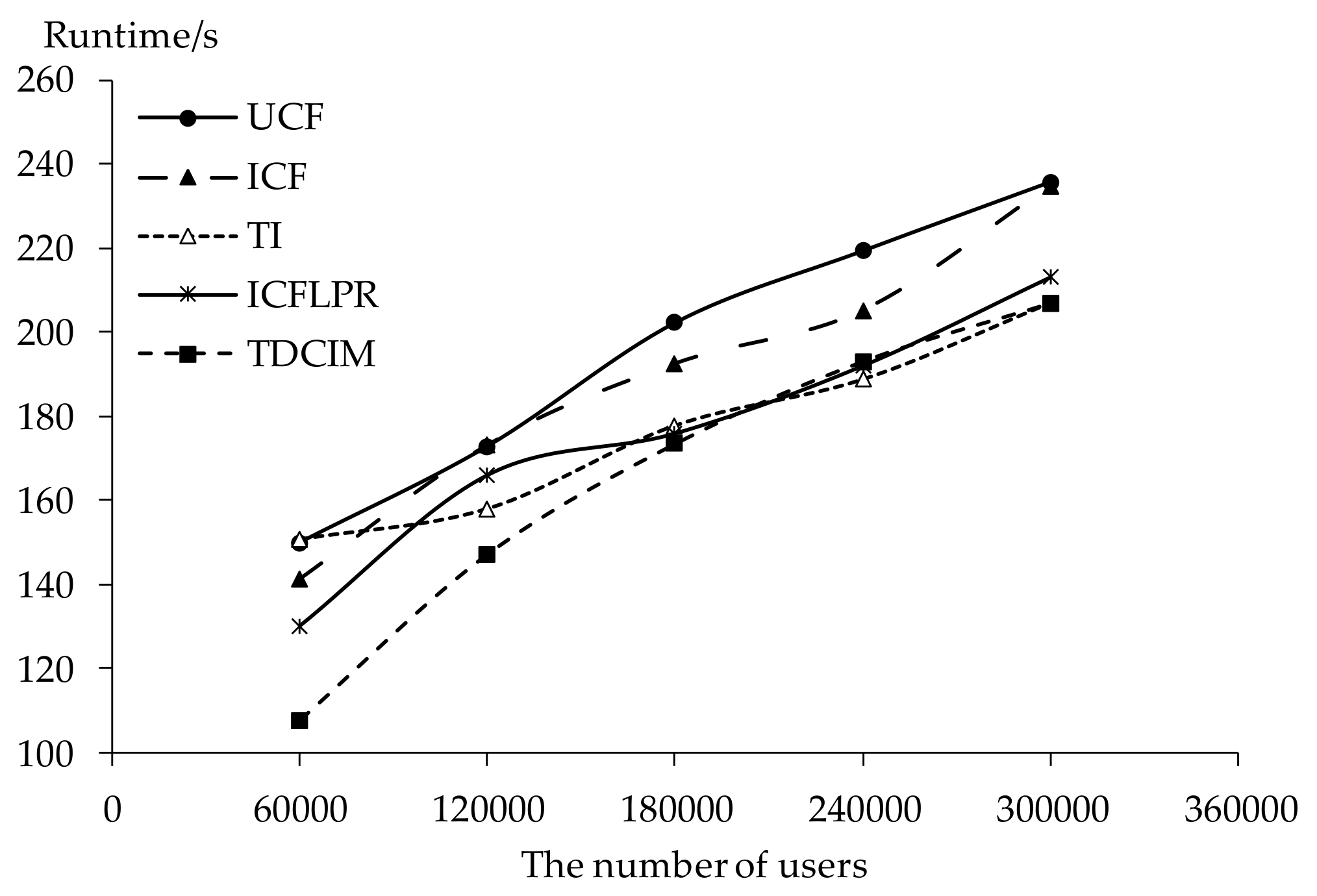
5.5. Time Complexity
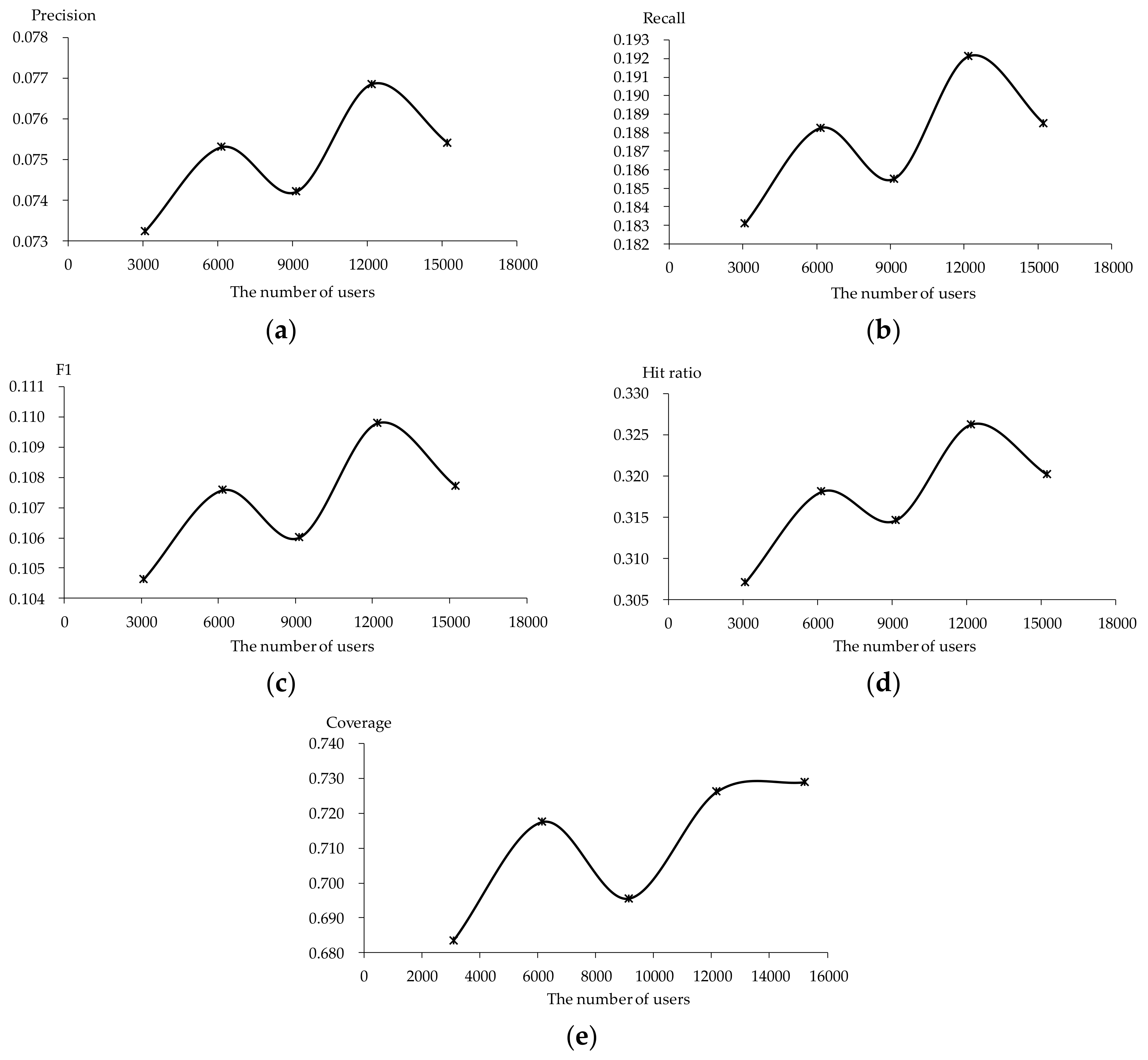
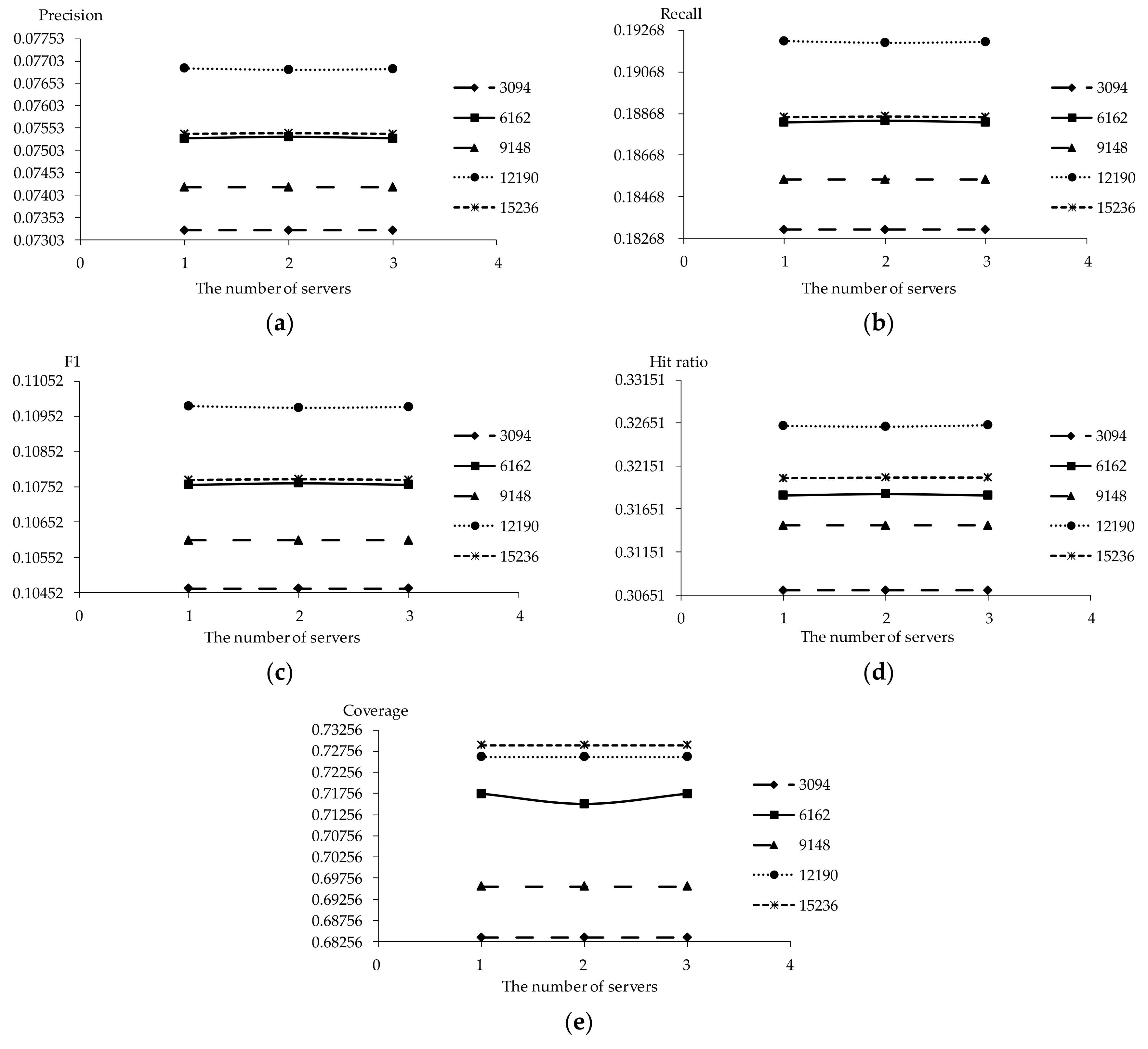
5.6. Scalability
6. Conclusions and Future Works
- Data sparsity and recommendation personalization are considered in an item-based approach, which is more effective than a user-based approach for online novel recommendation.
- Inaccurate preference rating and the lack of preference degree are solved by latent preference rating according to the difference between online novel reading and traditional book marketing.
- A punishment mechanism based on novel popularity is considered, ameliorating the Matthew effect and the long tail effect for online novel recommendation.
- A user’s interest remains stable over the short term and can be reflected adequately by novel tags. Consequently, performance is greatly improved by the tag-driven algorithm with collaborative item modeling.
- The proposed algorithm contributes to the performance of online novel recommendation not only with regards to recommendation quality but also to scalability.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tan, S.L.; Bu, J.J.; Chen, C.; Xu, B.; Wang, C.; He, X.F. Using rich social media information for music recommendation via hypergraph model. ACM Trans. Multimed. Comput. Commun. Appl. 2011. [Google Scholar] [CrossRef]
- Carrer, N.W.; Hernández, A.M.L.; Valencia, G.R.; Francisco, G.S. Social knowledge-based recommender system. Application to the movies domain. Expert Syst. Appl. 2012, 39, 10990–11000. [Google Scholar] [CrossRef]
- Barragáns, M.A.B.; Costa, M.E.; Burguillo, J.C.; Marta, R.L.; Fernando, A.M.F.; Ana, P. A hybrid content-based and item-based collaborative filtering approach to recommend TV programs enhanced with singular value decomposition. Inf. Sci. 2010, 180, 4290–4311. [Google Scholar] [CrossRef]
- Crespo, R.G.; Martínez, O.S.; Lovelle, J.M.C.; Bustelo, B.C.P.G.; Gayo, J.E.L.; Patricia, O.D.P. Recommendation system based on user interaction data applied to intelligent electronic books. Comput. Hum. Behav. 2011, 27, 1445–1449. [Google Scholar] [CrossRef]
- Vaz, P.C.; David, M.D.M.; Martins, B.; Calado, P. Improving a hybrid literary book recommendation system through author ranking. In Proceedings of the 12th ACM/IEEE-CS Joint Conference on Digital Libraries, Washington, DC, USA, 10–14 June 2012; pp. 387–388. [Google Scholar]
- Tewari, A.S.; Kumar, A.; Barman, A.G. Book recommendation system based on combine features of content based filtering, collaborative filtering and association rule mining. In Proceedings of the IEEE International Advance Computing Conference, Gurgaon, India, 21–22 February 2014; pp. 500–503. [Google Scholar]
- Núñez-Valdéz, E.R.; Lovelle, J.M.C.; Martínez, O.S.; Vicente, G.D.; Patricia, O.D.P.; Carlos, E.M.M. Implicit feedback techniques on recommender systems applied to electronic books. Comput. Hum. Behav. 2012, 28, 1186–1193. [Google Scholar] [CrossRef]
- Choi, K.; Yoo, D.; Kim, G.; Suh, Y. A hybrid online-product recommendation system: Combining implicit rating-based collaborative filtering and sequential pattern analysis. Electron. Commer. Res. Appl. 2012, 11, 309–317. [Google Scholar] [CrossRef]
- Unger, M.; Bar, A.; Shapira, B.; Rokach, L. Towards latent context-aware recommendation systems. Knowl. Based Syst. 2016, 104, 165–178. [Google Scholar] [CrossRef]
- Birtolo, C.; Ronca, D. Advances in clustering collaborative filtering by means of fuzzy c-means and trust. Expert Syst. Appl. 2013, 40, 6997–7009. [Google Scholar] [CrossRef]
- Park, Y.K.; Park, S.C.; Lee, S.G.; Jung, W. Fast collaborative filtering with a k-nearest neighbor graph. In Proceedings of the International Conference on Big Data and Smart Computing, Bangkok, Thailand, 15–17 January 2014; pp. 92–95. [Google Scholar]
- Ricci, F.; Rokach, L.; Shapira, B.; Kantor, P.B. Recommender Systems Handbook; Springer: Boston, MA, USA, 2011; pp. 73–105. [Google Scholar]
- Park, D.H.; Kim, H.K.; Choi, I.Y.; Kim, J.K. A literature review and classification of recommender systems research. Expert Syst. Appl. 2012, 39, 10059–10072. [Google Scholar] [CrossRef]
- Mandl, M.; Felfernig, A.; Teppan, E.; Schubert, M. Consumer decision making in knowledge-based recommendation. J. Intell. Inf. Syst. 2011, 37, 1–22. [Google Scholar] [CrossRef]
- Cakir, O.; Aras, M.E. A recommendation engine by using association rules. Procedia Soc. Behav. Sci. 2012, 62, 452–456. [Google Scholar] [CrossRef][Green Version]
- Albanese, M.; Acierno, A.D.; Moscato, V.; Persia, F.; Picariello, A. A multimedia recommender system. ACM Trans. Internet Technol. 2013, 13. [Google Scholar] [CrossRef]
- Reena, P.; Shalmali, A.P. Study of collaborative filtering recommendation algorithm-Scalability issue. Int. J. Comput. Appl. 2013, 67, 10–15. [Google Scholar]
- Fang, Y.N.; Guo, Y.F.; Hu, H.C.; Lan, J.L. Improved collaborative filtering recommender algorithm based on sigmoid function. Appl. Res. Comput. 2013, 30, 1688–1691. [Google Scholar]
- Salehi, M.; Kmalabadi, I.N. A hybrid attribute-based recommender system for e-learning material recommendation. IERI Procedia 2012, 2, 565–570. [Google Scholar] [CrossRef][Green Version]
- Ullah, F.; Sarwar, G.; Lee, S.C.; Yun, K.P.; Moon, K.D.; Kim, J.T. Hybrid recommender system with temporal information. In Proceedings of the International Conference on Information Networking, Bali, Indonesia, 1–3 February 2012; pp. 421–425. [Google Scholar]
- Ghazanfar, M.A.; Prugel, B.A. Building switching hybrid recommender system using machine learning classifiers and collaborative filtering. IAENG Int. J. Comput. Sci. 2010, 37, 272–287. [Google Scholar]
- Amato, F.; Moscato, V.; Picariello, A.; Piccialli, F. SOS: A multimedia recommender system for online social networks. Futur. Gener. Comput. Syst. 2017. [Google Scholar] [CrossRef]
- Yu, Y.; Yu, H.T.; Huang, R.Y. Collaborative filtering recommendation algorithm based on entropy optimization nearest-neighbor selection. Appl. Res. Comput. 2017, 34, 2618–2623. [Google Scholar]
- Zhang, J.; Peng, Q.K.; Sun, S.Q.; Liu, C. Collaborative filtering recommendation algorithm based on user preference derived from item domain features. Physica A 2014, 396, 66–76. [Google Scholar] [CrossRef]
- San, Y.H.; Chin, P.W.; Yi, F.L. Coauthorship networks and academic literature recommendation. Electron. Commer. Res. Appl. 2010, 9, 323–334. [Google Scholar]
- Colace, F.; Santo, M.D.; Greco, L.; Moscato, V.; Picariello, A. A collaborative user-centered framework for recommending items in online social networks. Comput. Hum. Behav. 2015, 51, 694–704. [Google Scholar] [CrossRef]
- Jadhav, S.D.; Channe, H.P. Efficient recommendation system using decision tree classifier and collaborative filtering. Int. Res. J. Eng. Technol. 2016, 3, 2113–2118. [Google Scholar]
- Kim, H.N.; Alkhaldi, A.; Saddik, A.E.; Jo, G.S. Collaborative user modeling with user-generated tags for social recommender systems. Expert Syst. Appl. 2011, 38, 8488–8496. [Google Scholar] [CrossRef]
- Ma, H.F.; Jia, M.H.Z.; Zhang, D.; Lin, X.H. Combining tag correlation and user social relation for microblog recommendation. Inf. Sci. 2017, 385–386, 325–337. [Google Scholar] [CrossRef]
- Ghazarian, S.; Nematbakhsh, M.A. Enhancing memory-based collaborative filtering for group recommender systems. Expert Syst. Appl. 2015, 42, 3801–3812. [Google Scholar] [CrossRef]
- Park, Y.K.; Park, S.C.; Jung, W.S.; Lee, S.G. Reversed CF: A fast collaborative filtering algorithm using k-nearest neighbor graph. Expert Syst. Appl. 2015, 42, 4022–4028. [Google Scholar] [CrossRef]
- Mou, B.H.; Zhang, Z.H.; Zhang, L.; Min, F. Comparison study of collaborative filtering algorithms based on quadripartite graph. J. Front. Comput. Sci. Technol. 2017, 11, 875–886. [Google Scholar]

| Task | User-Based CF | Item-Based CF |
|---|---|---|
| preprocessing | similarity matrix construction between users | similarity matrix construction between items |
| recommendation | top k users selection that have rated the item and all rating predictions | top k items selection that have been rated by an active user and all rating predictions |
| personalization | dependent on the group with similar interests and inclined to socialization | dependent on user’s historical preference and inclined to individualization |
| adaptability | time-consuming with a great number of users and effective with relatively few users | time-consuming with a great number of items and effective with relatively few items |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Lin, Z.; Wang, Z. Tag-Driven Online Novel Recommendation with Collaborative Item Modeling. Information 2018, 9, 77. https://doi.org/10.3390/info9040077
Li F, Lin Z, Wang Z. Tag-Driven Online Novel Recommendation with Collaborative Item Modeling. Information. 2018; 9(4):77. https://doi.org/10.3390/info9040077
Chicago/Turabian StyleLi, Fenghuan, Zhaosheng Lin, and Zhenyu Wang. 2018. "Tag-Driven Online Novel Recommendation with Collaborative Item Modeling" Information 9, no. 4: 77. https://doi.org/10.3390/info9040077
APA StyleLi, F., Lin, Z., & Wang, Z. (2018). Tag-Driven Online Novel Recommendation with Collaborative Item Modeling. Information, 9(4), 77. https://doi.org/10.3390/info9040077




