2. Related Work
In this section, we briefly review the recent aircraft detection models [
9,
10,
11] and the related technologies [
3,
4,
5,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21] in the literature on object detection.
Compared with other detection task, such as lane detection [
22], license plate detection [
23], and face detection [
1], aircraft detection faces more challenging problems, like various weather conditions, occlusion, cluttered scenes, and illumination changes. In addition, our system requires fast detection speed which significantly supports the aircraft tracking and guidance. Recently, a great many aircraft detection models have been designed. Wu et al. [
9] proposed a detection model which applied a similarity measure for aircraft type recognition. However, this model is not suitable for the aircraft in cluttered scenes and varied postures. Rastegar et al. [
10] proposed a model which combined wavelets with SVM, and it was applied to detect the aircraft in the original video and images. However, the procedure of training is time-consuming. Liu et al. [
11] proposed an efficient approach for feature extraction in high-resolution optical remote sensing images. A rotation invariant feature combined sparse coding and radial gradient transform was presented and showed high performance. However, this model is inefficient for our images obtained from optoelectronic cameras.
In the last decade, object detection technologies have achieved great success. Dalal et al. [
3] proposed a discriminative detection model which combined linear SVM with HOG (histogram of oriented gradient) and obtained great success in pedestrian detection. Due to its discriminative power, the HOG feature was adopted widely in object detection. Felzenszwalb et al. [
4] proposed a detection model based on a mixture of multiscale deformable part models and made further improvement on original HOG feature. Although it obtained favorable performance on detection accuracy (especially for the object with pose changing), it is costly. These kinds of models always search for an image pyramid space and match the location of the object. Once the objects were occluded partially, or truncated, it was difficult to detect. Malisiewicz et al. [
5] discard the partial models in [
4] and trained a model called exemplar-SVMs, which included a set of holistic templates (exemplars) for a specific category and which handled the inner-categories detection problem (objects in one specific category have great differences) and accelerated the detection. However, it was still based on a sliding window fashion. With the increase of exemplars, the computational cost grew as well. In order to speed up detection, Song et al. [
18,
19,
20] improved the DPM models [
4] and proposed the sparselet models which use the shared intermediate representations and reconstruction sparsity to accelerate the multi-class object detection. The sparselet models not only achieve the favorable accuracy, but also reduce the time cost greatly. Cheng et al. [
21] improved the previous work and proposed coarse-to-fine sparselets, which combines coarse and fine sparselets and outperforms the sparselets baseline work.
Moreover, some works were proposed to reduce the searching space by extracting the candidate regions. The works [
13,
14] proposed the rough segmentation method to reduce the search spaces for category-specific detectors. However, these methods are still computationally expensive, and which cost minutes per image. Uijlings et al. [
12] proposed a method named selective search which generates several candidate regions for detecting, and the number of candidate regions is much less than the searching space of the sliding window method. However, the detection results are object-like things rather than category-specific objects. Therefore, several category-specific detectors [
15,
16] were developed based on this method; however, the hierarchies of these detectors are complicated.
In all cases, occlusions always cause a significant decrease in performance. Actually, the above studies have not focused on such problems. Shu et al. [
24] proposed a part-based model for pedestrian detection. Tian et al. [
25] also applied part information to detect vehicles. These models always handle the part information of a specific object before training.
Therefore, the consideration of our work refers to two aspects: (1) developing an efficient and accurate aircraft detection model; and (2) this model is robust for partially occlusion.
Acknowledgments
This work was supported by Youth Innovation Promotion Association, CAS (Grant No. 2016336). The authors would appreciate the anonymous reviewers for their valuable comments and suggestions for improving this paper.
Author Contributions
J.Z. proposed the original idea and wrote this paper; T.L. gave many valuable suggestions and revised the paper; and G.Y. and P.J. designed a part of the experiments and revised the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Viola, P.; Jones, M. Robust real-time object detection. Comput. Vis. 2004, 57, 137–154. [Google Scholar] [CrossRef]
- Li, F.; Fergus, R.; Perona, P. Learning generative visual models from few training examples: An incremental Bayesian approach tested on 101 object categories. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 27 July–2 June 2004; pp. 178–189. [Google Scholar]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–25 June 2005; pp. 886–893. [Google Scholar]
- Felzenszwalb, P.; Girshick, R.; McAllester, D.; Ramanan, D. Object detection with discriminatively trained part based models. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1627–1645. [Google Scholar] [CrossRef] [PubMed]
- Malisiewicz, T.; Gupta, A.; Efros, A.A. Ensemble of exemplar-SVMs for object detection and beyond. In Proceedings of the International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 89–96. [Google Scholar]
- Baraniuk, R. Compressive sensing. IEEE Signal Process. Mag. 2007, 24, 118–121. [Google Scholar] [CrossRef]
- Candes, E.; Tao, T. Near-optimal signal recovery from random projections: Universal encoding strategies? IEEE Trans. Inf. Theory 2006, 52, 5406–5425. [Google Scholar] [CrossRef]
- Donoho, D. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Wu, Q.; Sun, H.; Sun, X.; Zhang, D.; Fu, K.; Wang, H. Aircraft Recognition in High Resolution Optical Satellite Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2015, 12, 112–116. [Google Scholar]
- Rastegar, S.; Babaeian, A.; Bandarabadi, M.; Toopchi, Y. Airplane Detection and Tracking Using Wavelet Features and SVM Classifier. In Proceedings of the 41st Southeastern Symposium on System Theory, Tullahoma, TN, USA, 15–17 March 2009; pp. 64–67. [Google Scholar]
- Liu, L.; Shi, Z. Airplane detection based on rotation invariant and sparse coding in remote sensing images. Optik 2014, 125, 5327–5333. [Google Scholar] [CrossRef]
- Uijlings, J.; Van de Sande, K.; Gevers, T.; Smeulders, A. Selective search for object recognition. Int. J. Comput. Vis. 2013, 104, 154–171. [Google Scholar] [CrossRef]
- Carreira, J.; Sminchisescu, C. CPMC: Automatic object segmentation using constrained parametric min-cuts. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1312–1328. [Google Scholar] [CrossRef] [PubMed]
- Endres, I.; Hoiem, D. Category independent object proposals. In Proceedings of the 11th European Conference on Computer Vision, Heraklion, Crete, Greece, 5–11 September 2010; pp. 575–588. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Wang, C.; Ren, W.; Huang, K.; Tan, T. Weakly Supervised Object Localization with Latent Category Learning. In Proceedings of the 13th European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 431–445. [Google Scholar]
- Lin, Y.; Liu, T.; Fuh, C. Fast Object Detection with Occlusions. In Proceedings of the 8th European Conference on Computer Vision, Prague, Czech Republic, 11–14 May 2004; pp. 402–413. [Google Scholar]
- Song, H.; Girshick, R.; Zickler, S.; Geyer, C. Generalized Sparselet Models for Real-Time Multiclass Object Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1001–1012. [Google Scholar] [CrossRef] [PubMed]
- Song, H.; Zickler, S.; Althoff, T.; Girshick, R.; Fritz, M.; Geyer, C.; Felzenszwalb, P.; Darrell, T. Sparselet models for efficient multiclass object detection. In Proceedings of the European conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 802–815. [Google Scholar]
- Girshick, R.; Song, H.; Darrell, T. Discriminatively activated sparselets. In Proceedings of the 30th International Conference on International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 196–204. [Google Scholar]
- Cheng, G.; Han, J.; Lei, G.; Liu, T. Learning coarse-to-fine sparselets for efficient object detection and scene classification. In Proceedings of the IEEE Conference Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1173–1181. [Google Scholar]
- You, F.; Zhang, R.; Zhong, L.; Wang, H.; Xu, J. Lane Detection Algorithm for Night-time Digital Image Based on Distribution Feature of Boundary Pixels. J. Opt. Soc. Korea 2013, 17, 188–199. [Google Scholar] [CrossRef]
- Lee, D.; Choi, J. Precise Detection of Car License Plates by Locating Main Characters. J. Opt. Soc. Korea 2010, 14, 376–382. [Google Scholar] [CrossRef]
- Shu, G.; Dehghan, A.; Oreifej, O.; Hand, E.; Shah, M. Part-based Multiple-Person Tracking with Partial Occlusion Handling. In Proceedings of the 8th European Conference on Computer Vision, Providence, RI, USA, 16–21 June 2012; pp. 1815–1821. [Google Scholar]
- Tian, B.; Tang, M.; Wang, F. Vehicle detection grammars with partial occlusion handling for traffic surveillance. Transp. Res. Part C Emerg. Technol. 2015, 56, 80–93. [Google Scholar] [CrossRef]
- Agarwal, S.; Roth, D. Learning a sparse representation for object detection. In Proceedings of the 7th European Conference on Computer Vision, Copenhagen, Denmark, 28–31 May 2002; pp. 113–130. [Google Scholar]
- Weber, M.; Welling, M.; Perona, P. Unsupervised learning of models for recognition. In Proceedings of the 6th European Conference on Computer Vision, Dublin, Ireland, 28 June–1 July 2000; pp. 18–32. [Google Scholar]
- Vidal-Naquet, M.; Ullman, S. Object Recognition with Informative Features and Linear Classification. In Proceedings of the IEEE International Conference on Computer Vision, Nice, France, 13–16 October 2003; pp. 281–289. [Google Scholar]
- Leibe, B.; Leonardis, A. Schiele, B. An Implicit Shape Model for Combined Object Categorization and Segmentation. Lect. Notes Comput. Sci. 2006, 4170, 508–524. [Google Scholar]
- Torralba, A.; Murphy, K.P.; Freeman, W.T. Sharing Visual Features for Multiclass and Multiview Object Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 854–869. [Google Scholar] [CrossRef] [PubMed]
- Neubeck, A.; Van Gool, L. Efficient Non-Maximum Suppression. In Proceedings of the International Conference on Pattern Recognition, Hong Kong, China, 20–24 August 2006; pp. 850–855. [Google Scholar]
- Achlioptas, D. Database-friendly random projections: Johnson-Lindenstrauss with binary coins. J. Comput. Syst. Sci. 2003, 66, 671–687. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, L.; Yang, M. Real-time Compressive Tracking. In Proceedings of the 12th European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 864–877. [Google Scholar]
- Dasgupta, S.; Gupta, A. An Elementary Proof of a Theorem of Johnson and Lindenstrauss. Random Struct. Algorithms 2003, 22, 60–65. [Google Scholar] [CrossRef]
- Liu, L.; Fieguth, P. Texture Classification from Random Features. IEEE Trans. Pattern Anal. Mach. Learn. 2012, 34, 574–586. [Google Scholar] [CrossRef] [PubMed]
- Baraniuk, R.; Davenport, M.; DeVore, R.; Wakin, M. A simple proof of the restricted isometry property for random matrices. Constr. Approx. 2008, 28, 253–263. [Google Scholar] [CrossRef]
- Li, P.; Hastie, T.; Church, K. Very sparse random projections. In Proceedings of the International Conference on Knowledge Discovery and Data Mining, Philadelphia, PA, USA, 20–23 August 2006; pp. 287–296. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive logistic regression: A statistical view of boosting. Ann. Stat. 2000, 28, 337–374. [Google Scholar] [CrossRef]
- Mei, K.; Zhang, J.; Li, G.; Xi, B.; Zheng, N. Training more discriminative multi-class classifiers for hand detection. Pattern Recognit. 2015, 48, 785–797. [Google Scholar] [CrossRef]
- Torralba, A.; Murphy, K.; Freeman, W. Sharing features: Efficient boosting procedures for multiclass object detection. In Proceedings of the IEEE Conference Computer Vision and Pattern Recognition, Washington, DC, USA, 27 June–2 July 2004; pp. 762–769. [Google Scholar]
- Yan, G.; Yu, M.; Yu, Y.; Fan, L. Real-time vehicle detection using histograms of oriented gradients and AdaBoost classification. Optik 2016, 127, 7941–7951. [Google Scholar] [CrossRef]
- Jolliffe, I. Principal Component Analysis, 2nd ed.; Springer: New York, NY, USA, 2002; pp. 21–26. [Google Scholar]
- Boutsidis, C.; Mahoney, M.; Drineas, P. Unsupervised Feature Selection for Principal Components Analysis. In Proceedings of the International Conference on Knowledge Discovery and Data Mining, Las Vegas, NV, USA, 24–27August 2008; pp. 61–69. [Google Scholar]
- Klema, V.; Laub, A. The singular value decomposition: Its computation and some applications. IEEE Trans. Autom. Control 1980, 25, 164–176. [Google Scholar] [CrossRef]
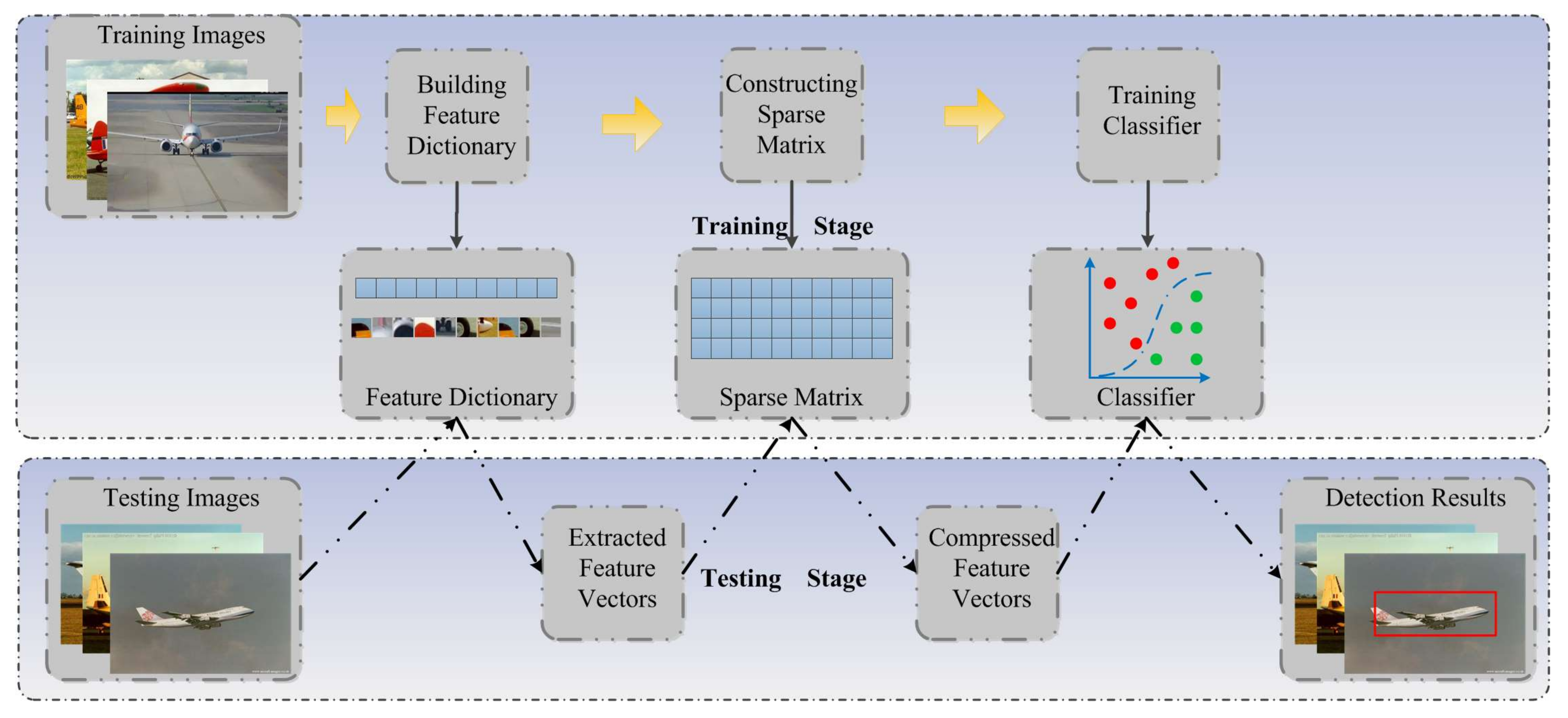
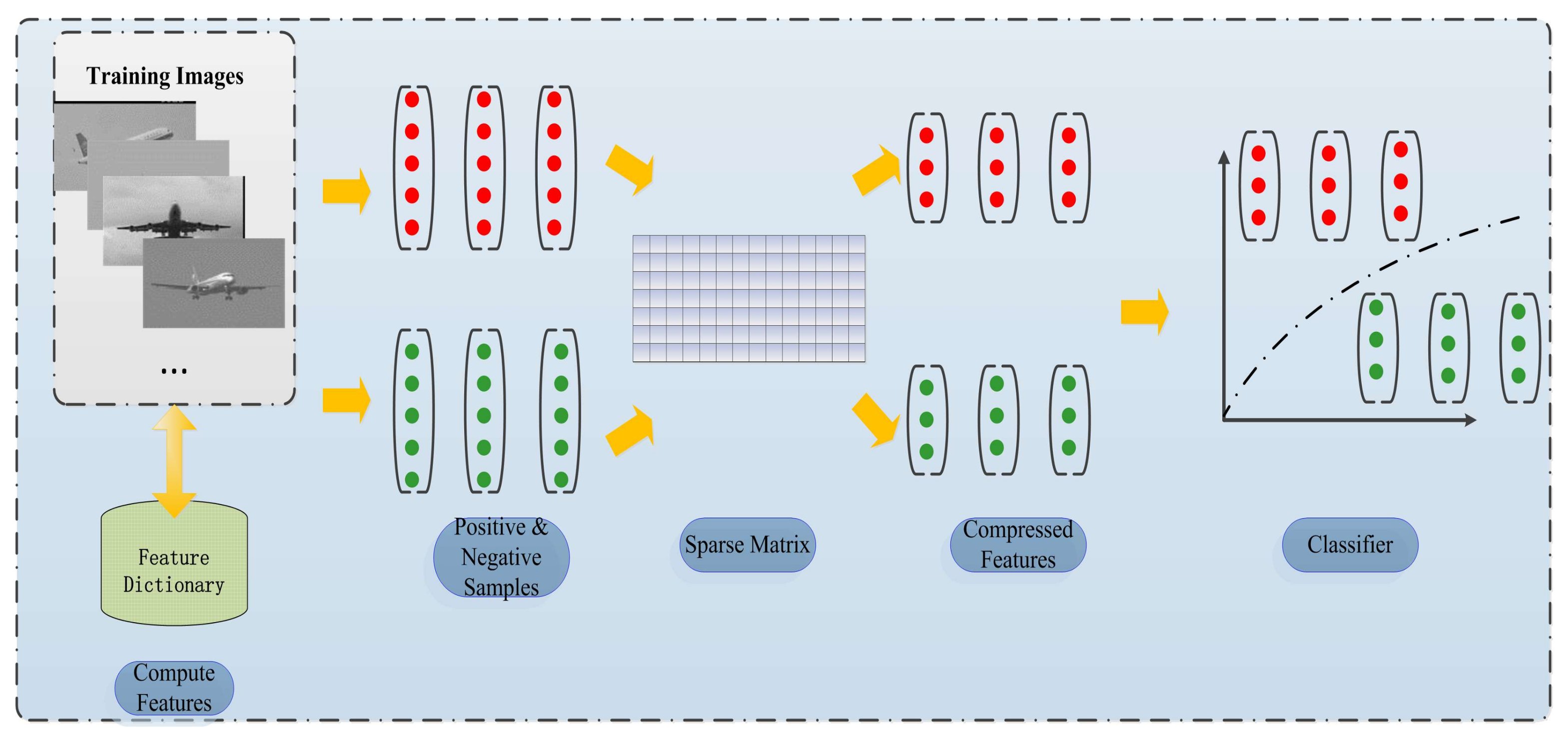
Figure 1.
Framework of the proposed model.
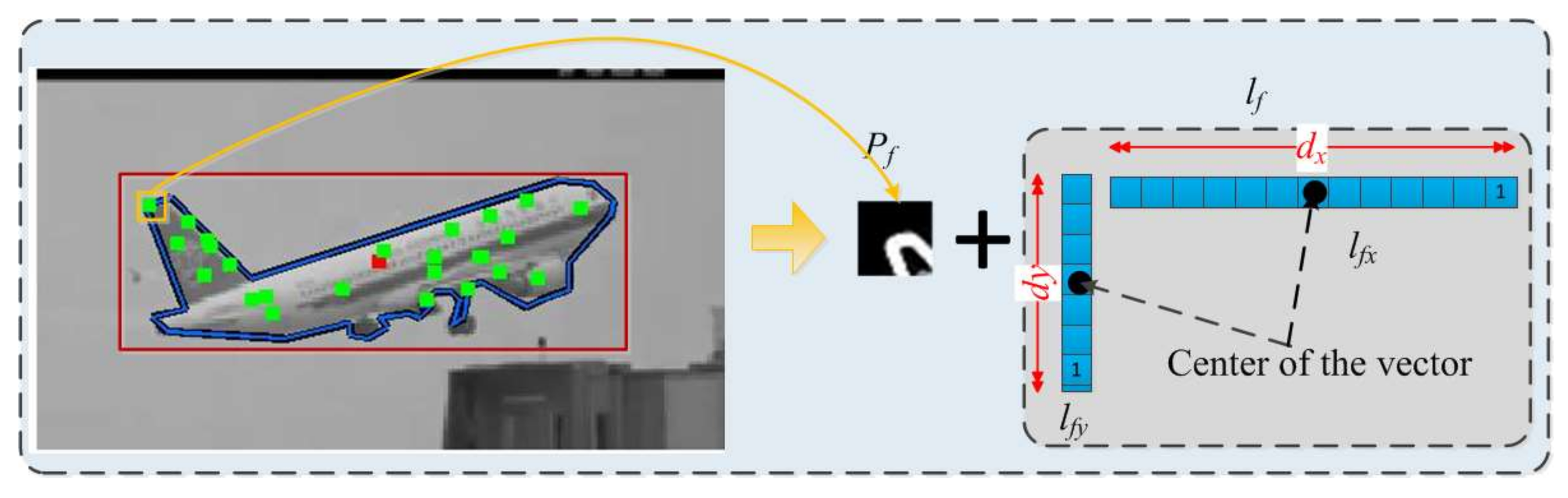
Figure 2.
The designed feature is combined an informative patch and two sparse vectors.
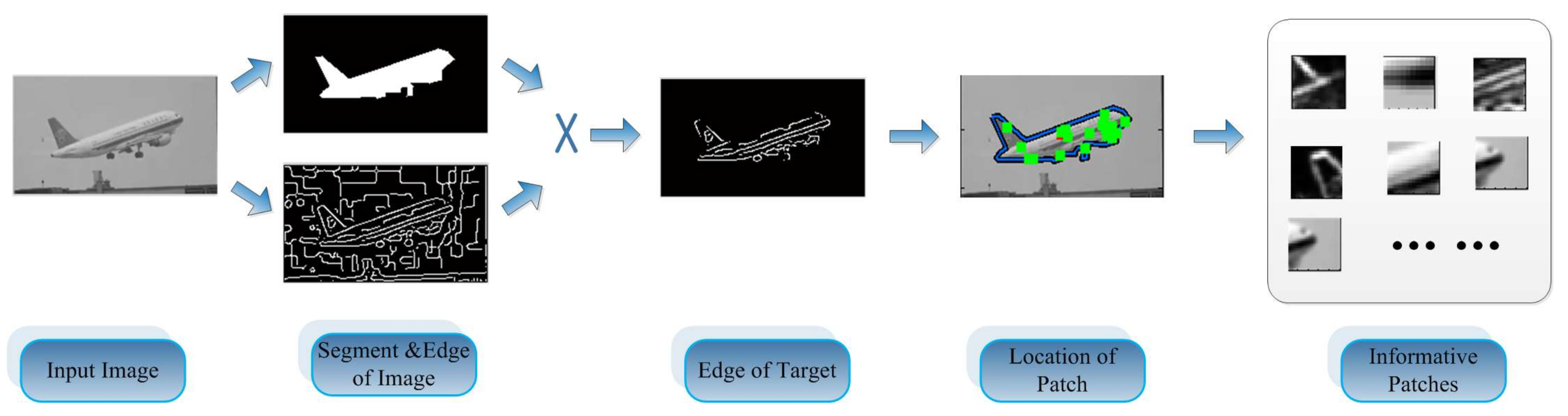
Figure 3.
The informative patches were extracted from the location which includes rich edge information.
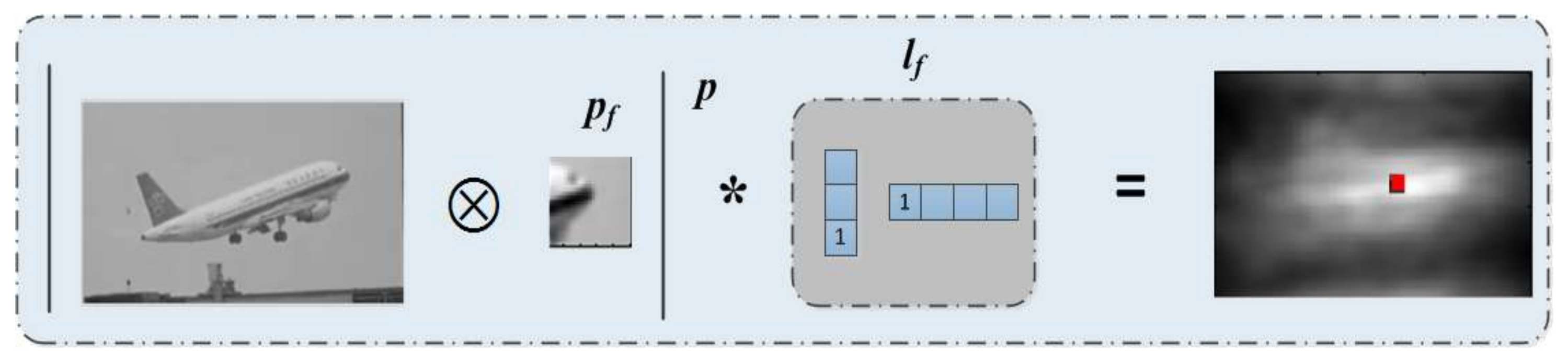
Figure 4.
A local informative patch is employed to construct feature vectors, from the picture in right column, object area has higher response than backgrounds.
Figure 5.
All of the feature vectors were compressed by a sparse matrix, and the compressed feature vectors were adopted to build the classifier.
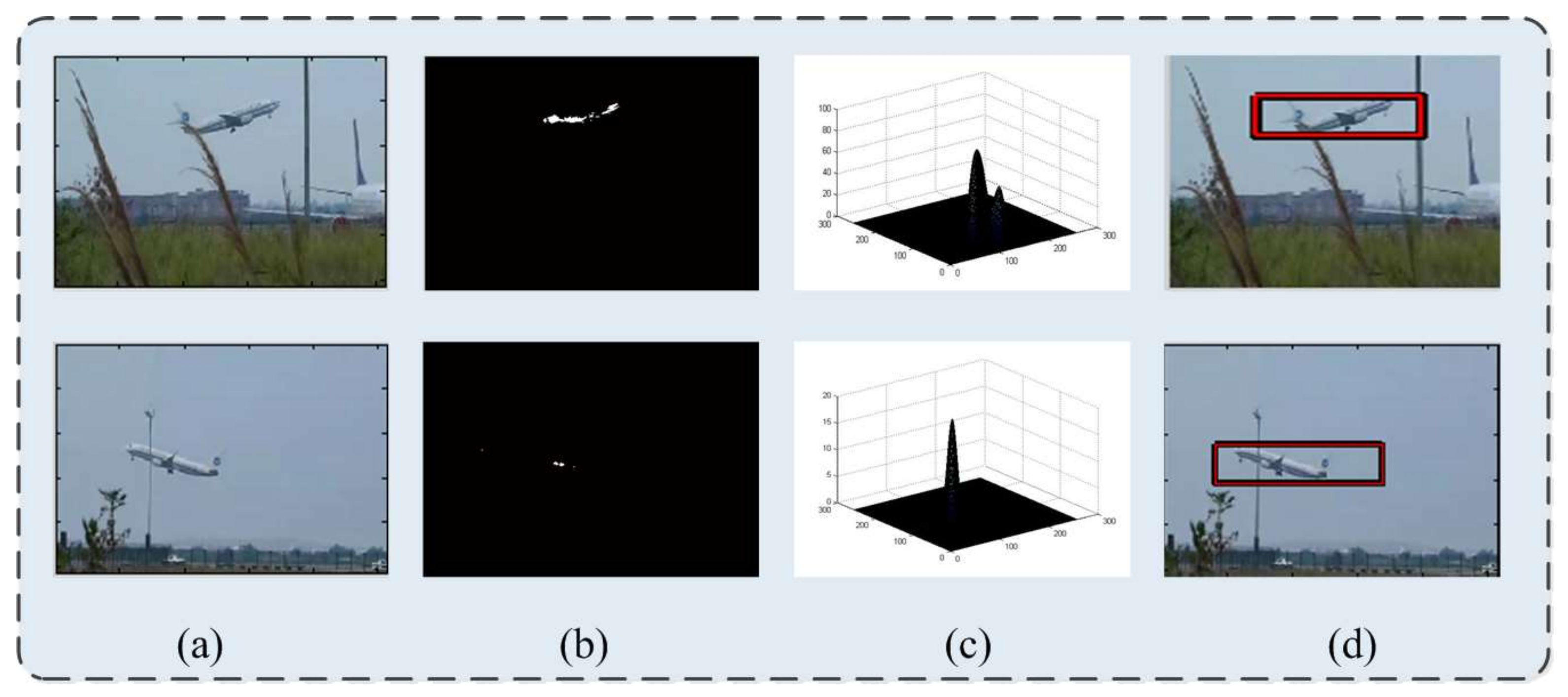
Figure 6.
(a) Testing image; (b) the score map calculated by classifier; (c) illustration of the distribution of the regional maxima; and (d) detection results.
Figure 7.
Examples from our moving aircraft database, the aircrafts appear in different scenes.
Figure 8.
(a) Illustration of the detection accuracy between our trained detectors (detector 1–4) and other models (DPM and exemplar-SVMs); and (b) the precision-recall curve.
Figure 9.
(a) Detection results of partially-occluded aircrafts in original images; and (b) detection results of the aircrafts with manual occlusion in different parts (nose, body, and tail).
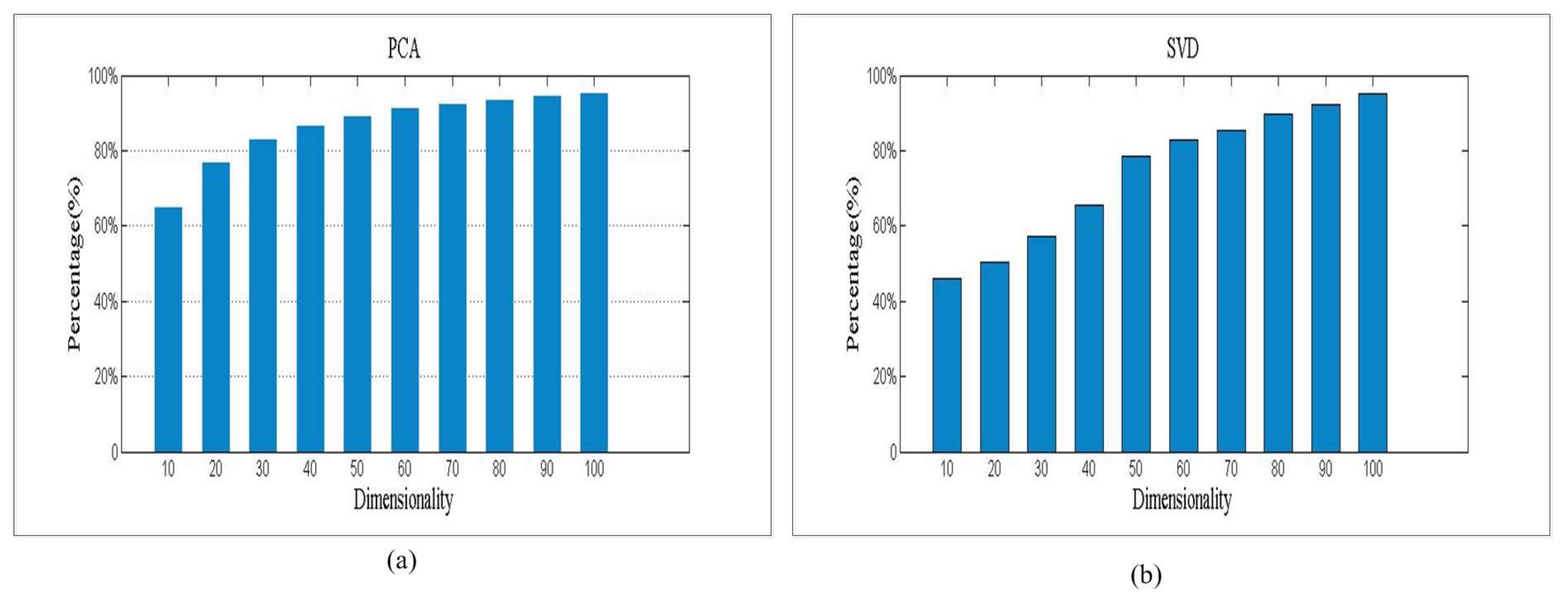
Figure 10.
Information preservation percentages of (a) PCA, and (b) SVD.
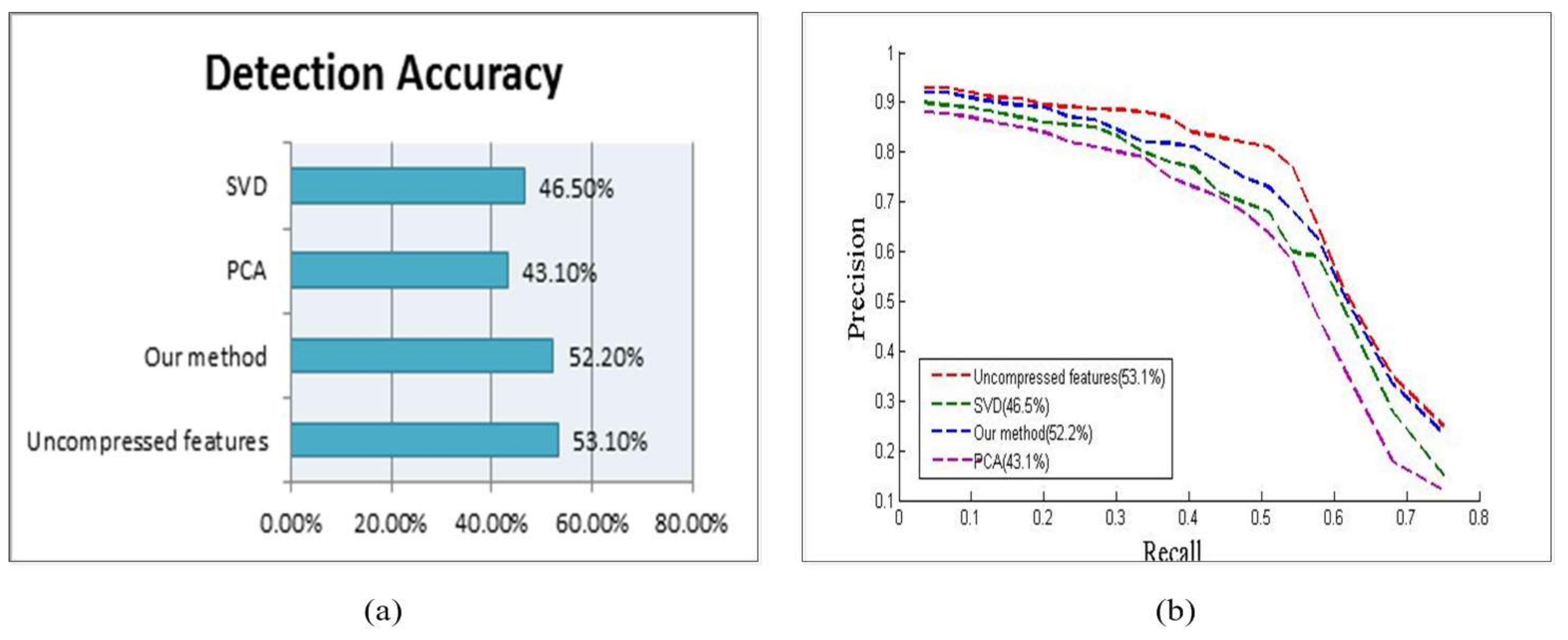
Figure 11.
(a) Illustration of the detection accuracy of four kinds of features; and (b) the precision-recall curve.
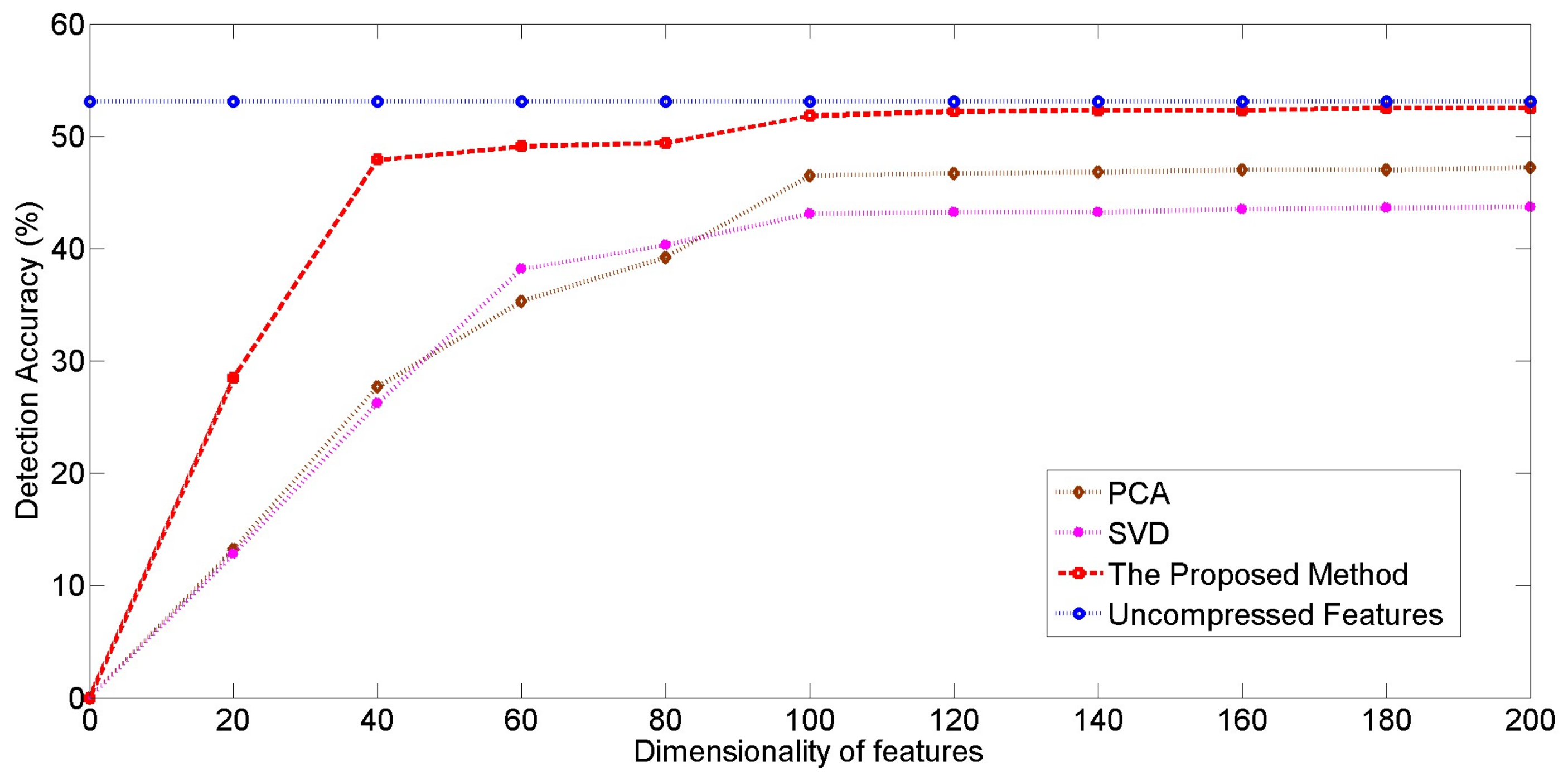
Figure 12.
Illustration of the relationship between compressed dimensionality and detection accuracy.
Figure 13.
Time consumption of three kinds of features.
Table 1.
The process of building the informative feature dictionary.
| Step 1: Segmenting the object with the background and calculating the centroid (cx, cy) of the object. |
| Step 2: Obtaining the image’s edge information by two 1-Dimensional masks [–1, 0, 1] and [–1, 0, 1]Transpose. |
| Step 3: Using the results of step 1 and step 2 to obtain the edge information of the object. |
| Step 4: Extracting the candidate patch (pf) at each location (lf) where holds an edge value calculated in step 3, and each extracted patch has a fixed size of 15 × 15 pixels. |
| Step 5: Adopting Non-Maximum Suppression (NMS) [31] to reduce the number of candidate patches. |
| Step 6: Performing k-means for the rest candidate patches. |
| Step 7: Selecting the clusters as the element of the informative patch dictionary. |
Table 2.
The process of collecting training samples.
| Step 1: Scaling the another subset of training images in order to make the objects fit into the bounding box (of size 40 × 120 pixels); |
| Step 2: Cropping images in uniform size (e.g., 120 × 200 pixels); |
| Step 3: Performing normalized cross correlation between each patches and training images; |
| Step 4: Performing element-wise exponentiation of the result from step 3 with exponent p = 3; |
| Step 5: Convolving the result of step 4 with the patch’s location; |
| Step 6: Features at object’s centroid and background were represented as positive and negative samples, respectively. |
Table 3.
Comparison of three methods in partially-occluded object detection (%).
| 1 D1 (N = 50) | D2 (N = 100) | D3 (N = 150) | D4 (N = 200) | DPM [4] | Exemplar-SVMs [5] |
|---|
| 26.8 | 28.3 | 31.2 | 32.7 | 27.2 | 20.3 |
Table 4.
Experiments on Caltech 101 database (aircraft sub-category) (%).
| D1 (N = 50) | D2 (N = 100) | D3 (N = 150) | D4 (N = 200) | DPM | Exemplar-SVMs |
|---|
| Original images | 35.8 | 39.8 | 42.7 | 43.9 | 32.8 | 45.8 |
| Occluded images | 29.7 | 33.1 | 35.9 | 36.5 | 19.6 | 32.3 |
Table 5.
Per image detection time of each detector (seconds).
| D1 (N = 50) | D2 (N = 100) | D3 (N = 150) | D4 (N = 200) | DPM | Exemplar-SVMs |
|---|
| Detection time | 2.01 | 3.66 | 5.69 | 6.57 | 27.53 | 19.87 |
Table 6.
Feature compression with three methods (milliseconds).
| Time Consumption | Our Method | PCA | SVD |
|---|
| 100 D | 18.7 | 656.3 | 535.2 |
| 200 D | 20.2 | 667.1 | 551.8 |
| 400 D | 26.9 | 695.6 | 567.5 |
| 800 D | 45.6 | 702.3 | 579.7 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).