Forecasting Monthly Electricity Demands by Wavelet Neuro-Fuzzy System Optimized by Heuristic Algorithms
Abstract
:1. Introduction
2. Literature Review
3. Preliminaries
3.1. Neuro-Fuzzy System
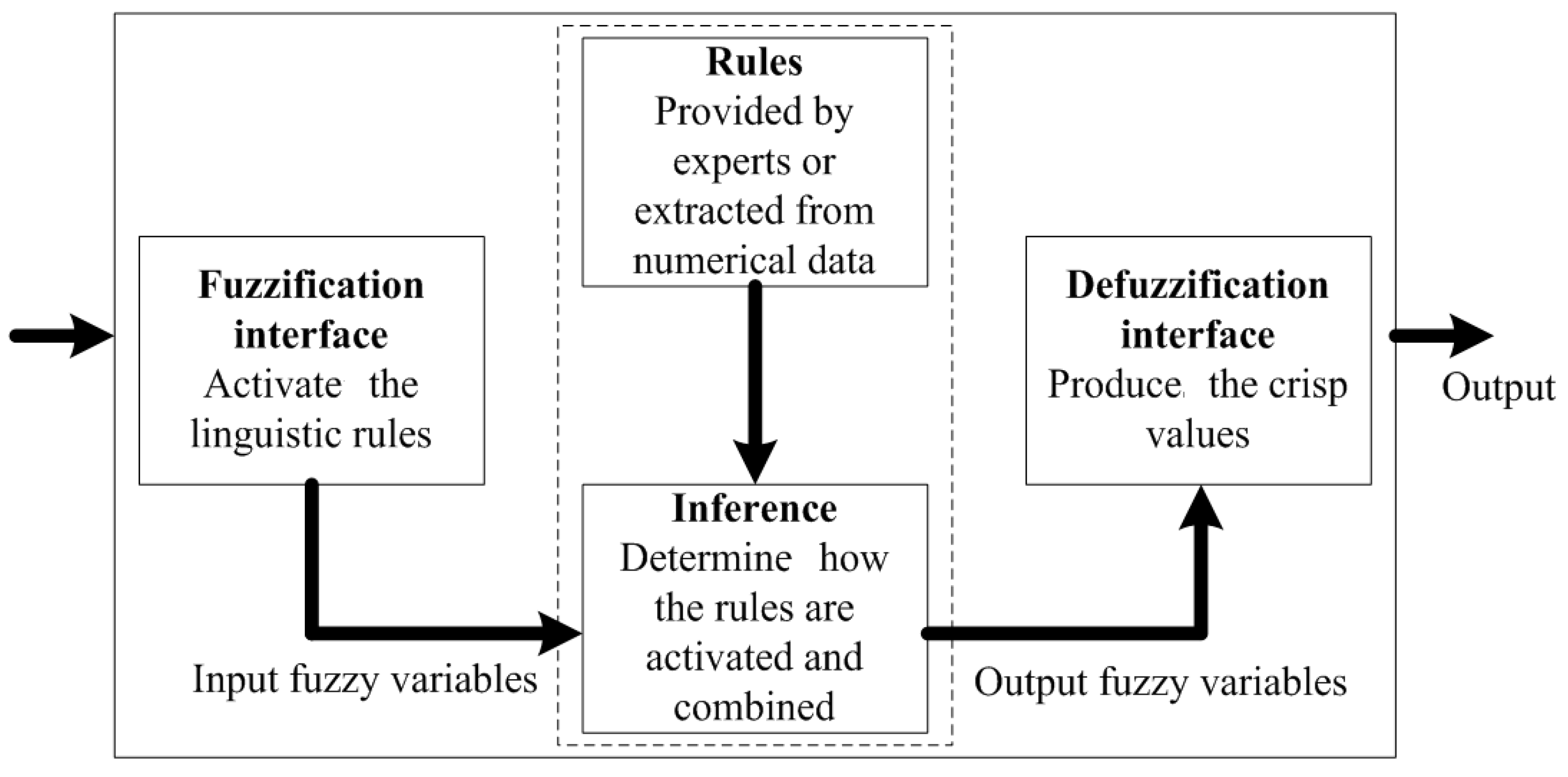
3.1.1. Fuzzy Inference System
- The fuzzification interface transforms each crisp input variable into a membership grade based on the membership functions defined.
- The inference engine then conducts the fuzzy reasoning process by applying the appropriate fuzzy operators in order to obtain the fuzzy set to be accumulated in the output variable.
- The defuzzification interface transforms the fuzzy output into a crisp output by applying a specific defuzzification method
- Mamdani fuzzy model
- Takagi-Sugeno fuzzy model
- Tsukamoto Model fuzzy model
- Step 1:
- Setting the fuzzy rules: Fuzzy rules are the conditional statements that define the relationship between the input membership functions and output membership functions. For example, if input 1 is low and input 2 is high then output is high. Here the values of low, medium and high to the inputs are called linguistic variables or the membership functions. Expert Knowledge is used for this purpose
- Step 2:
- Fuzzification: It is the process of converting crisp data into fuzzy data. The input data is classified into input membership functions which can be linguistic variables such as low, medium, etc. This is usually done on the basis of expert human knowledge.
- Step 3:
- Combining the fuzzified inputs according to the fuzzy rules to establish rule strength.
- Step 4:
- Finding the consequence of the rules by combining the rule strength and the output membership function.
- Step 5:
- The outputs of all the fuzzy rules are calculated and combined to get an output distribution.
- Step 6:
- Defuzzification: Usually a crisp output is required in most of the applications. Defuzzification is the process of converting fuzzy data (Output distribution) to crisp data (single value). There are many methods which can be used for this purpose. Some of the commonly used methods are Center of Mass, Mean of the Maximum etc.
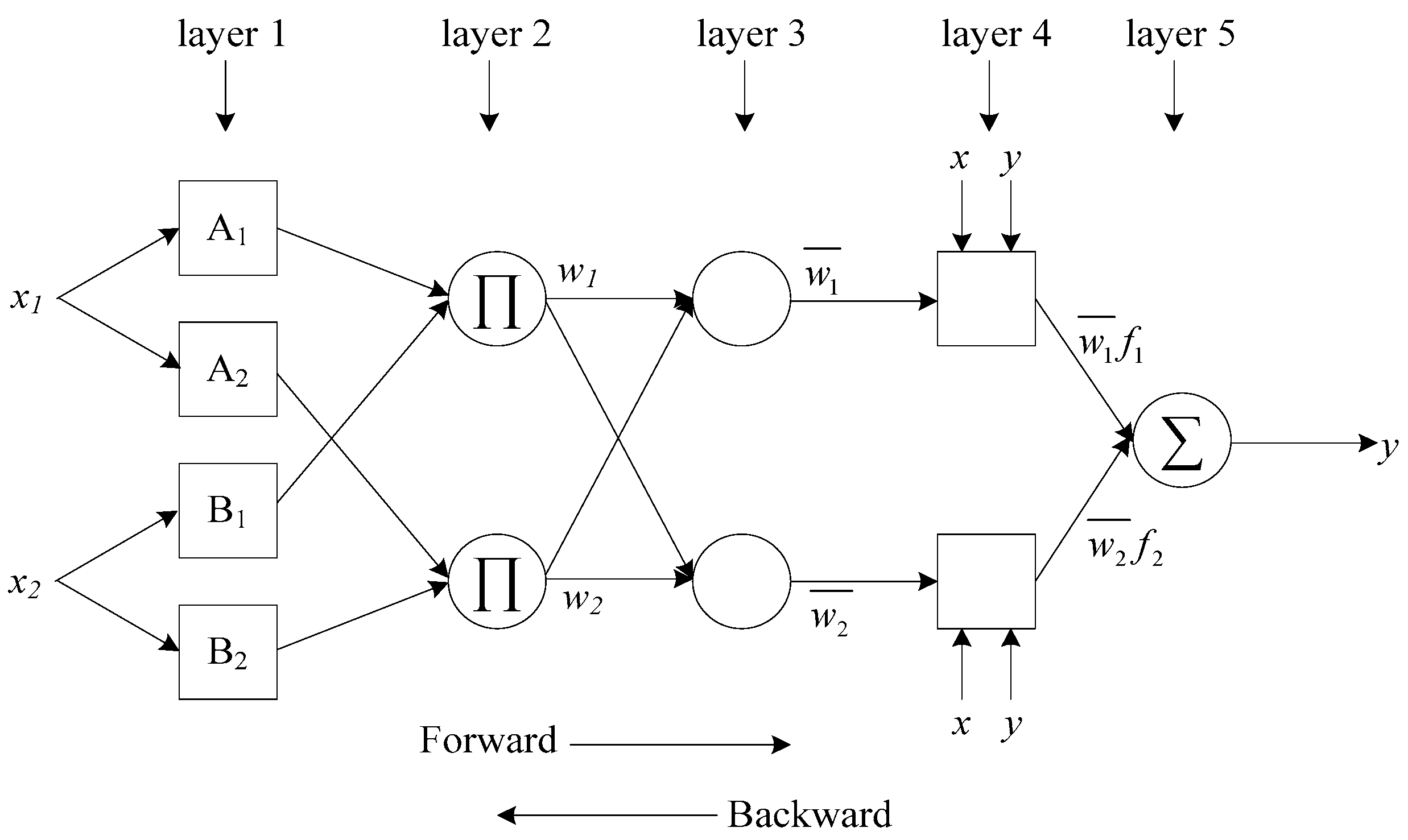
3.1.2. Adaptive Neuro-Fuzzy Inference System (ANFIS)
- Cooperative Neuro-Fuzzy System: The neural network is used at the initial phase to determine the fuzzy set and/or fuzzy rules, and then the fuzzy system is fully utilized for execution.
- Concurrent Neuro-Fuzzy System: Neural networks are used to provide input for a fuzzy system, or to change the output of the fuzzy system. In this case, the parameters of the fuzzy system are not changed by the learning process.
- Hybrid Neuro-Fuzzy System: A fuzzy system uses a learning algorithm inspired by the neural networks to determine its parameters through pattern processing.
Rule 2: If x1 is A2 and x2 is B2 then y2 = p2x1 + q2x2 + r2,
Rule 2: If x1 is A2 and x2 is B2 then y2 = C2,
O1,i= µBi−2(x2) for i = 3, 4,
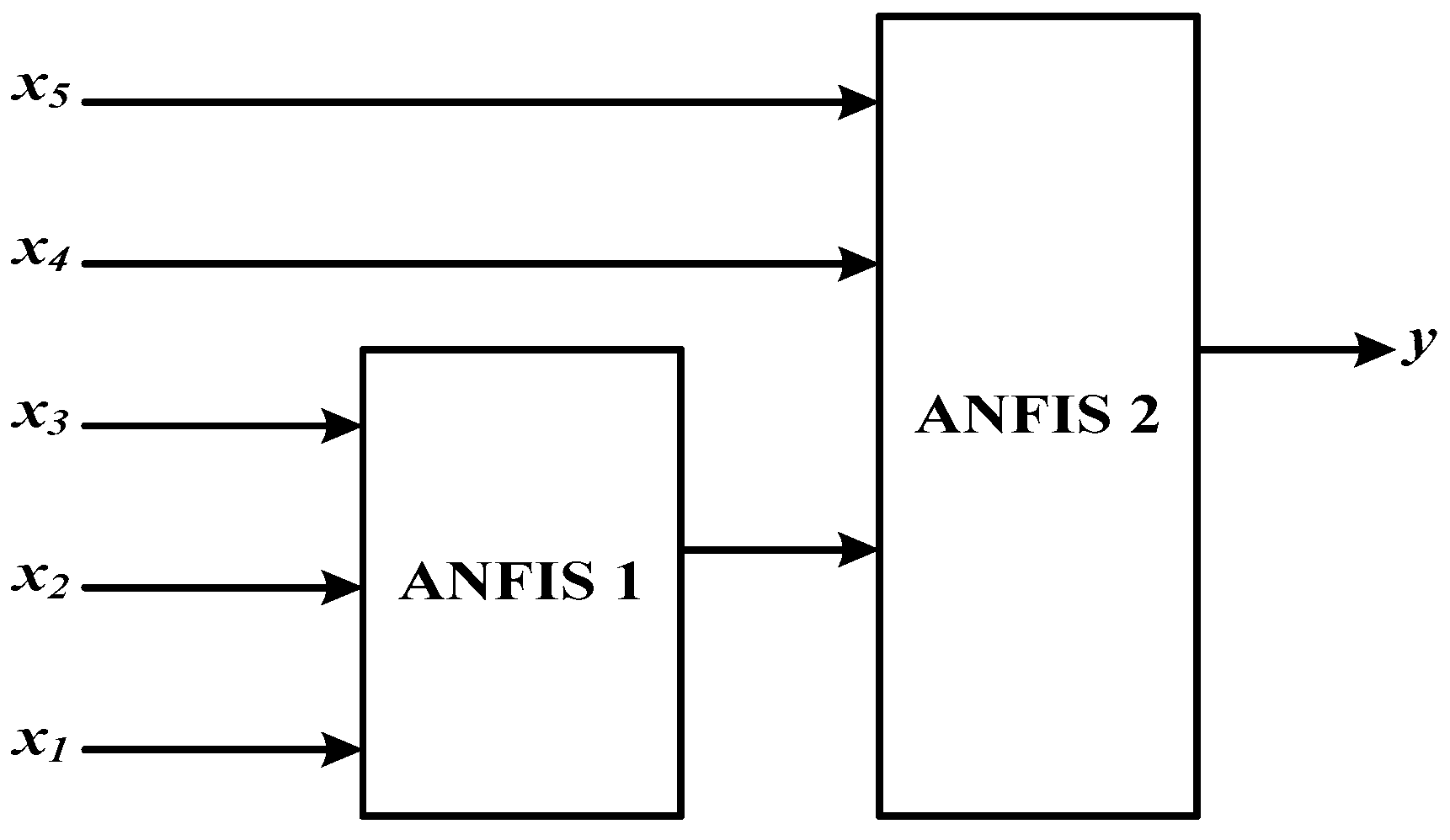
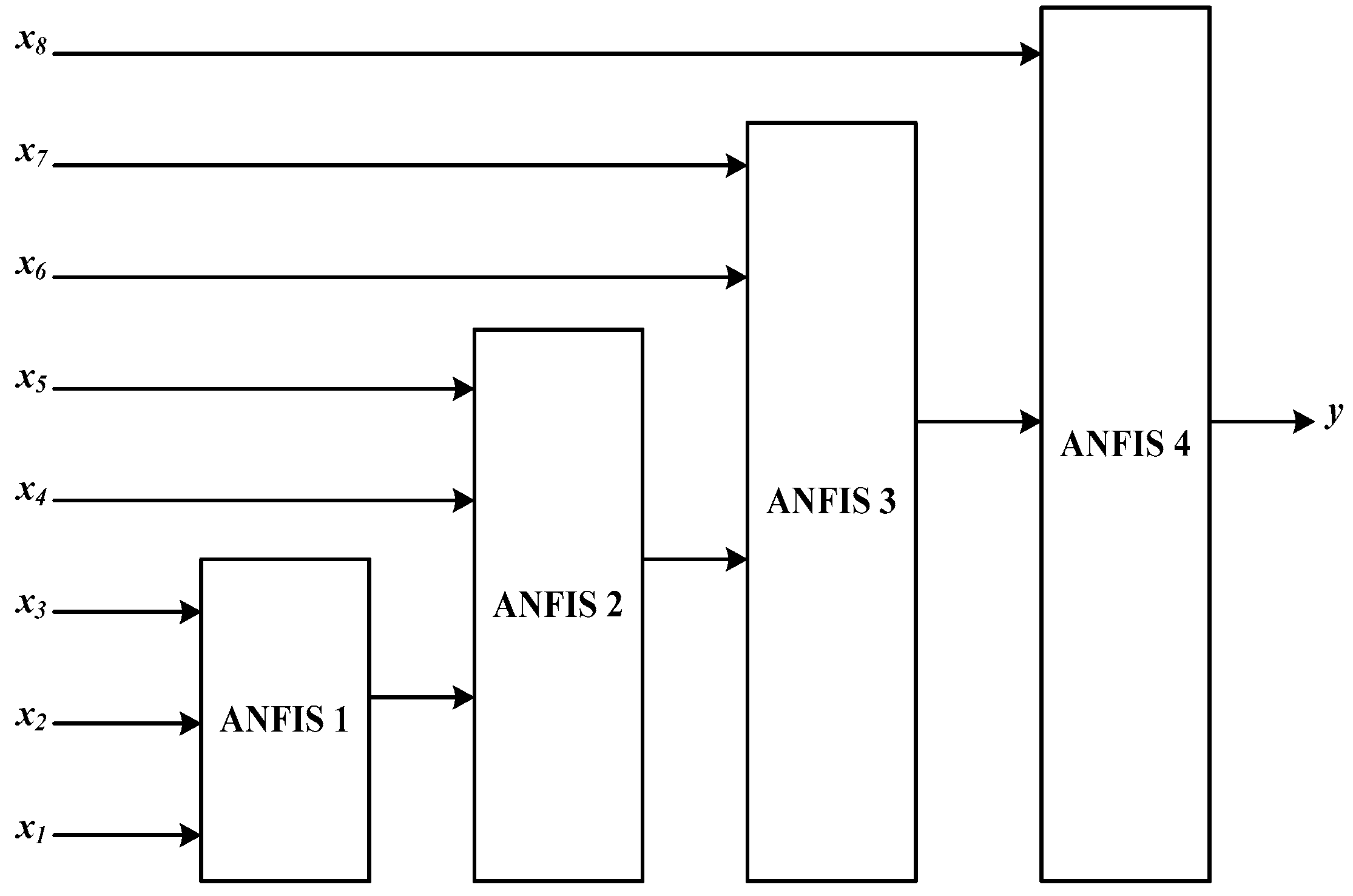
3.1.3. Rule Selection for Adaptive Neuro-Fuzzy Inference System (ANFIS)
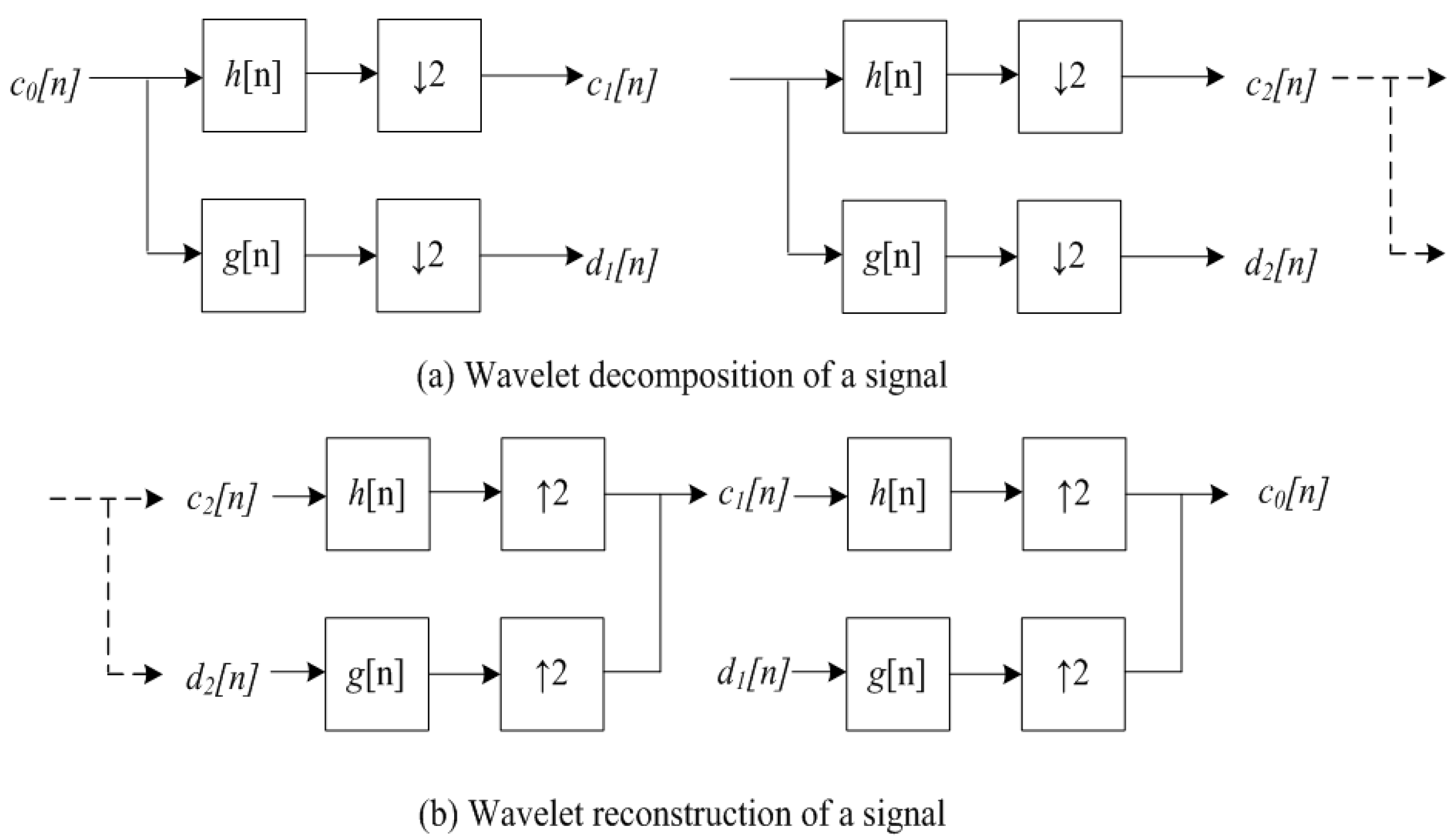
3.2. Wavelet Transform
3.3. Heuristic Algorithms
3.3.1. Gravitational Search Algorithm
3.3.2. Cuckoo Optimization Algorithm
3.3.3. Cuckoo Search Algorithm
4. Research Design
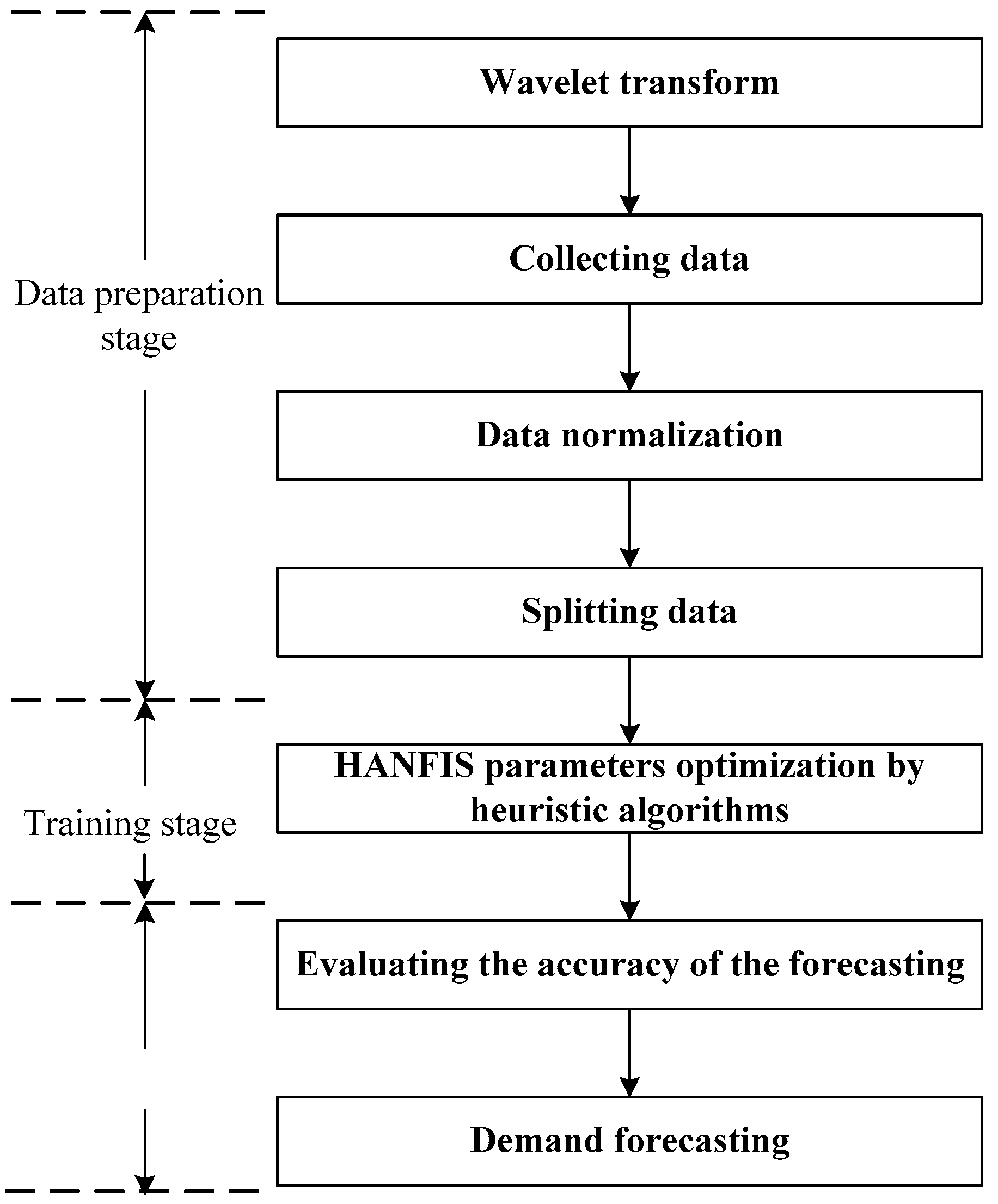
4.1. Methodology
4.2. Data Preparation
4.2.1. Data Collection
4.2.2. Noise Filtering Using Wavelet Transform
4.2.3. Collecting Data
4.2.4. Data Normalization
4.2.5. Splitting Data
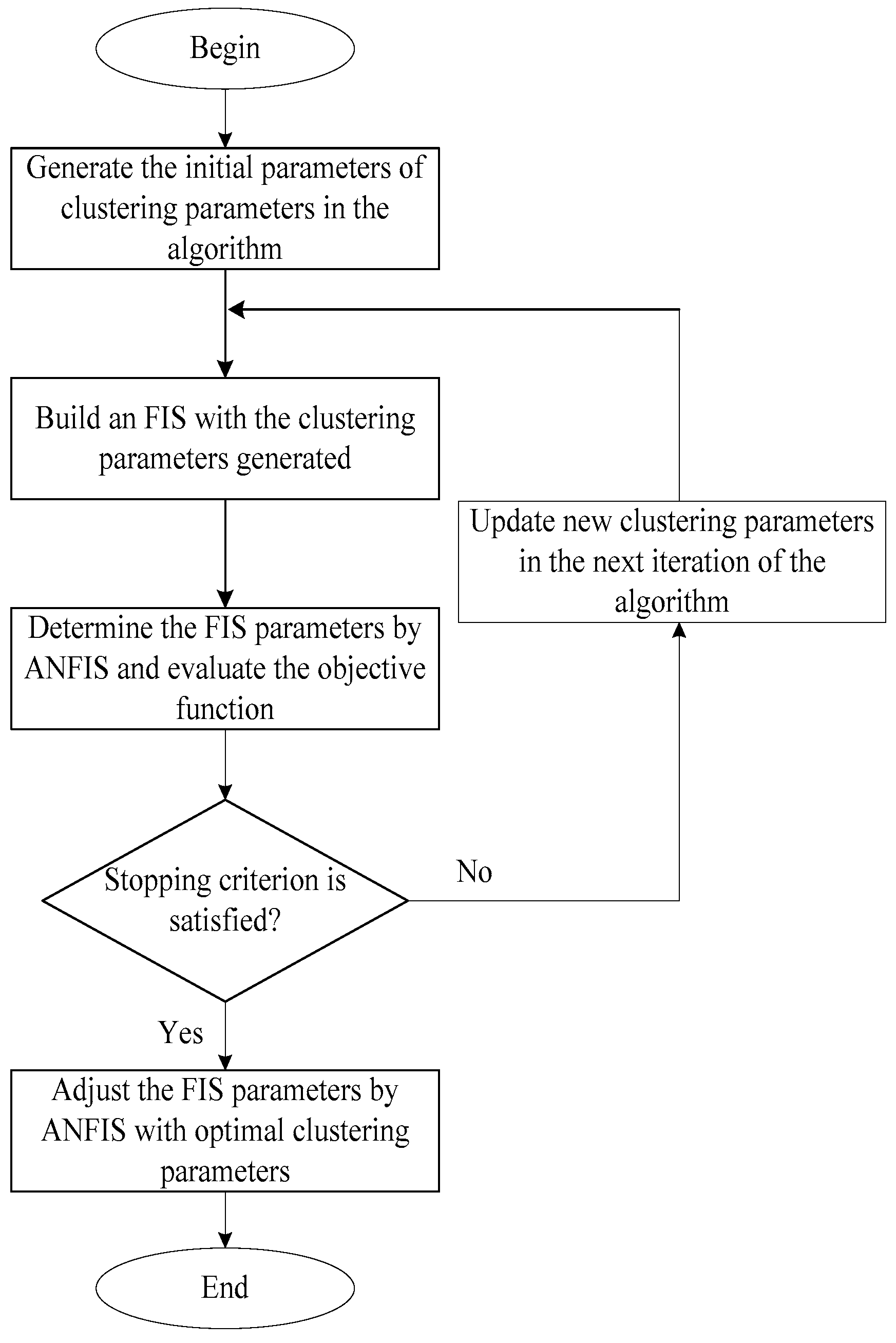
4.3. Training Adaptive Neuro Fuzzy Inference System (ANFIS)
4.4. ANFIS-based Forecasting Models
4.5. Evaluation Criteria
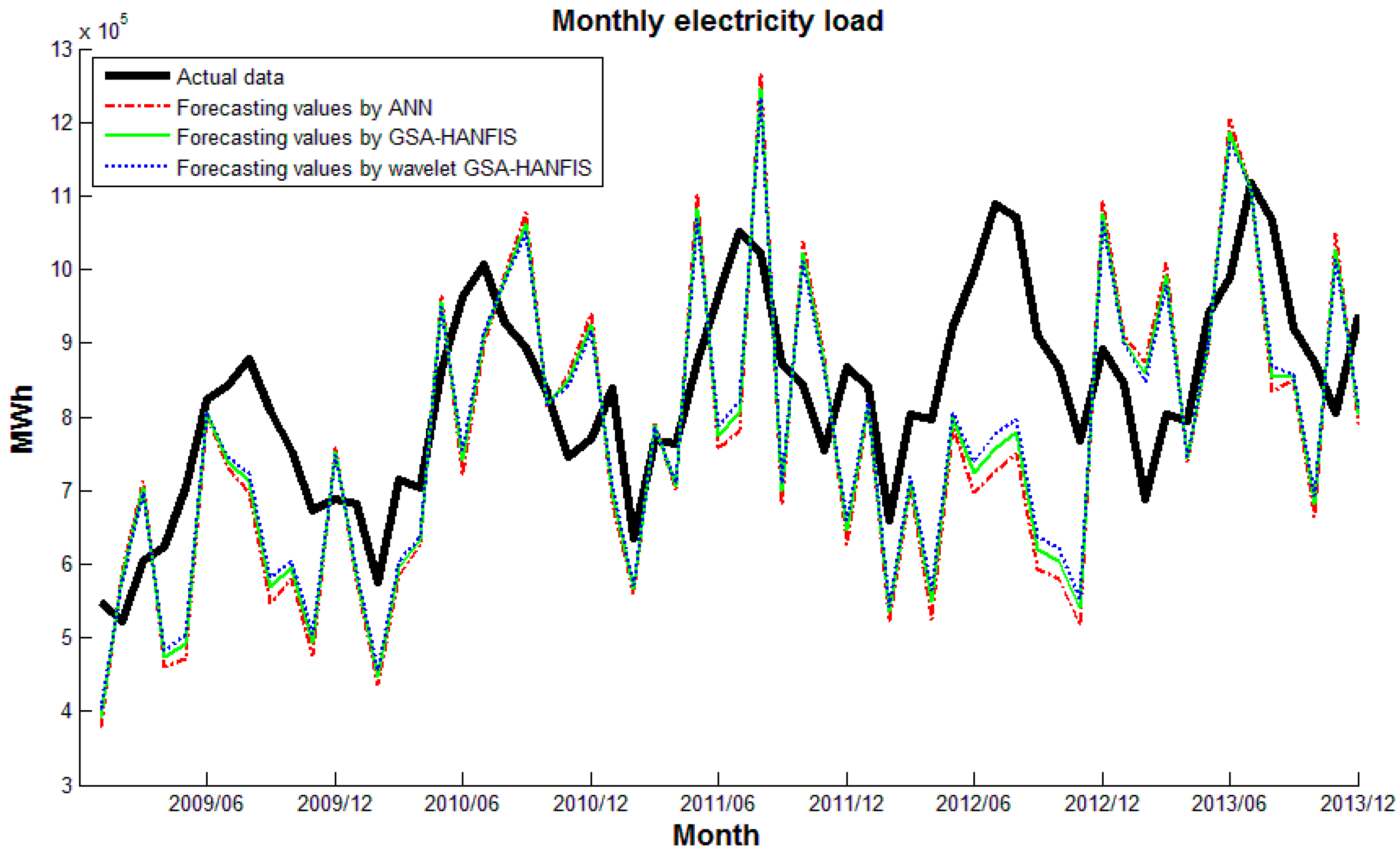
5. Experimental Results and Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Suganthia, L.; Samuelb, A.A. Electricity models for demand forecasting—A review. Renew. Sustain. Electr. Rev. 2012, 16, 1223–1240. [Google Scholar] [CrossRef]
- Dogan, E.; Akgungor, A. Forecasting highway casualties under the effect of railway development policy in Turkey using artificial neural networks. Neural Comput. Appl. 2013, 22, 869–877. [Google Scholar] [CrossRef]
- Erzin, Y.; Oktay Gul, T. The use of neural networks for the prediction of the settlement of one-way footings on cohesionless soils based on standard penetration test. Neural Comput. Appl. 2014, 24, 891–900. [Google Scholar] [CrossRef]
- Bhattacharya, U.; Chaudhuri, B. Handwritten Numeral Databases of Indian Scripts and Multistage Recognition of Mixed Numerals. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 444–457. [Google Scholar] [CrossRef] [PubMed]
- Kandananond, K. Forecasting Electricity Demand in Thailand with an Artificial Neural Network Approach. Energies 2011, 4, 1246–1257. [Google Scholar] [CrossRef]
- Chang, P.C.; Fan, C.Y.; Lin, J.J. Monthly electricity demand forecasting based on a weighted evolving fuzzy neural network approach. Int. J. Electr. Power Electr. Syst. 2011, 33, 17–27. [Google Scholar] [CrossRef]
- Amjady, N.; Keynia, F. A New Neural Network Approach to Short Term Load Forecasting of Electrical Power Systems. Energies 2011, 4, 488–503. [Google Scholar] [CrossRef]
- Santana, Á.L.; Conde, G.B.; Rego, L.P.; Rocha, C.A.; Cardoso, D.L.; Costa, J.C.W.; Bezerra, U.H.; Francês, C.R.L. PREDICT—Decision support system for load forecasting and inference: A new undertaking for Brazilian power suppliers. Int. J. Electr. Power Electr. Syst. 2012, 38, 33–45. [Google Scholar] [CrossRef]
- Azadeh, A.; Ghaderi, S.F.; Sohrabkhani, S. Forecasting electrical consumption by integration of Neural Network, time series and ANOVA. Appl. Math. Comput. 2007, 186, 1753–1761. [Google Scholar] [CrossRef]
- Azadeh, A.; Saberi, M.; Anvari, M.; Azaron, A.; Mohammadi, M. An adaptive network based fuzzy inference system-genetic algorithm clustering ensemble algorithm for performance assessment and improvement of conventional power plants. Expert Syst. Appl. 2011, 38, 2224–2234. [Google Scholar] [CrossRef]
- Buragohain, M.; Mahanta, C. A novel approach for ANFIS modeling based on full factorial design. Appl. Soft Comput. 2008, 8, 609–625. [Google Scholar] [CrossRef]
- Metin, E.H.; Murat, H. Comparative analysis of an evaporative condenser using artificial neural network and adaptive neuro-fuzzy inference system. Int. J. Refrig. 2008, 31, 1426–1436. [Google Scholar] [CrossRef]
- Iranmanesh, H.; Abdollahzade, M.; Miranian, A. Mid-Term Energy Demand Forecasting by Hybrid Neuro-Fuzzy Models. Energies 2012, 5, 1–21. [Google Scholar] [CrossRef]
- Zahedi, G.; Azizi, S.; Bahadori, A.; Elkamel, A.; Wan Alwi, S.R. Electricity demand estimation using an adaptive neuro-fuzzy network: A case study from the Ontario province Canada. Electricity 2013, 49, 323–328. [Google Scholar] [CrossRef]
- Yao, S.J.; Song, Y.H.; Zhang, L.Z.; Cheng, X.Y. Wavelet transform and neural networks for short-term electrical load forecasting. Electr. Convers. Manag. 2000, 41, 1975–1988. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Duman, S.; Güvenç, U.; Yörükeren, N. Gravitational Search Algorithm for Economic Dispatch with Valve-Point Effects. Int. Rev. Electr. Eng. 2010, 5, 2890–2895. [Google Scholar]
- Yang, X.S.; Deb, S. Engineering Optimisation by Cuckoo Search. Int. J. Math. Model. Numer. Optim. 2010, 1, 330–343. [Google Scholar] [CrossRef]
- Kawam, A.A.L.; Mansour, N. Metaheuristic Optimization Algorithms for Training Artificial Neural Networks. Int. J. Comput. Inf. Technol. 2012, 1, 156–161. [Google Scholar]
- Valian, E.; Mohanna, S.; Tavakoli, S. Improved Cuckoo Search Algorithm for Feedforward Neural Network Training. Int. J. Artif. Intell. Appl. 2011, 2, 36–43. [Google Scholar]
- Zhou, Y.; Zheng, H. A novel complex valued Cuckoo Search algorithm. Sci. World J. 2013, 2013. [Google Scholar] [CrossRef] [PubMed]
- Rajabioun, R. Cuckoo optimization algorithm. Appl. Soft Comput. 2011, 11, 5508–5518. [Google Scholar] [CrossRef]
- Balochian, S.; Ebrahimi, E. Parameter Optimization via Cuckoo Optimization Algorithm of Fuzzy Controller for Liquid Level Control. J. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Kazemi, S.M.R.; Seied Hoseini, M.M.; Abbasian-Naghneh, S.; Seyed Habib, A.R. An evolutionary-based adaptive neuro-fuzzy inference system for intelligent short-term load forecasting. Int. Trans. Oper. Res. 2014, 21, 311–326. [Google Scholar] [CrossRef]
- Chaturvedi, D.K.; Premdayal, S.A.; Chandiok, A. Short Term Load Forecasting using Neuro-fuzzy-Wavelet Approach. Int. J. Comput. Acad. Res. 2013, 2, 36–48. [Google Scholar]
- Akdemir, B.; Çetinkaya, N. Long-term load forecasting based on adaptive neural fuzzy inference system using real energy data. Electr. Procedia 2012, 14, 794–799. [Google Scholar] [CrossRef]
- Zhao, H.; Guo, S.; Xue, W. Urban Saturated Power Load Analysis Based on a Novel Combined Forecasting Model. Information 2015, 6, 69–88. [Google Scholar] [CrossRef]
- Chen, J.-F.; Lo, S.-K.; Do, Q.H. Forecasting Monthly Electricity Demands: An Application of Neural Networks Trained by Heuristic Algorithms. Information 2017, 8, 31. [Google Scholar] [CrossRef]
- Liang, J.; Liang, Y. Analysis and Modeling for China’s Electricity Demand Forecasting Based on a New Mathematical Hybrid Method. Information 2017, 8, 33. [Google Scholar] [CrossRef]
- Ghiassi, M.; Zimbra, D.K.; Saidane, H. Medium term system load forecasting with a dynamic artificial neural network model. Electr. Power Syst. Res. 2006, 76, 302–316. [Google Scholar] [CrossRef]
- Alamaniotis, M.; Ikonomopoulos, A.; Tsoukalas, L.H. Monthly load forecasting using kernel based Gaussian process regression. In Proceedings of the 9th Mediterranean Conference on Power Generation, Transmission Distribution and Energy Conversion (MEDPOWER 2014), Athens, Greece, 2–5 November 2012. [Google Scholar]
- Alamaniotis, M.; Bargiotas, D.; Tsoukalas, L.H. Towards smart energy systems: Application of kernel machine regression for medium term electricity load forecasting. SpringerPlus 2016, 5, 58. [Google Scholar] [CrossRef] [PubMed]
- Moreno-Chaparro, C.; Salcedo-Lagos, J.; Rivas, E.; Orjuela Canon, A. A method for the monthly electricity demand forecasting in Colombia based on wavelet analysis and a nonlinear autoregressive model. Ingeniería 2011, 16, 94–106. [Google Scholar]
- Gao, R.; Tsoukalas, L.H. Neural-wavelet Methodology for Load Forecasting. J. Intell. Robot. Syst. 2001, 31, 149. [Google Scholar] [CrossRef]
- Negnevitsky, M. Artificial Intelligence: A Guide to Intelligent Systems; Pearson Education Limited: Essex, UK, 2005. [Google Scholar]
- Mamdani, E.H.; Assilian, S. An experiment in linguistic synthesis with a fuzzy logic controller. Int. J. Man-Mach. Stud. 1975, 7, 1–13. [Google Scholar] [CrossRef]
- Sugeno, M. Industrial Applications of Fuzzy Control; Elsevier, Science: Amsterdam, The Netherlands, 1985; pp. 63–68. [Google Scholar]
- Norazah, Y.; Nor, B.A.; Mohd, S.O.; Yeap, C.N. A Concise Fuzzy Rule Base to Reason Student Performance Based on Rough-Fuzzy Approach. In Fuzzy Inference System—Theory and Applications; InTech Publisher: London, UK, 2010; pp. 63–82. [Google Scholar]
- Ata, R.; Kocyigit, Y. An adaptive neuro-fuzzy inference system approach for prediction of tip speed ratio in wind turbines. Expert Syst. Appl. 2010, 37, 5454–5460. [Google Scholar] [CrossRef]
- Mamdani, E.H. Application of fuzzy logic to approximate reasoning using linguistic synthesis. IEEE Trans. Comput. 1977, 26, 196–202. [Google Scholar] [CrossRef]
- Tsukamoto, Y. An Approach to Fuzzy Reasoning Method. In Advances in Fuzzy Set Theory and Applications; Gupta, M.M., Ragade, R.K., Yager, R.R., Eds.; North-Holland Publishing Company: Holland, The Netherlands, 1979; pp. 137–149. [Google Scholar]
- Jang, J.S.R.; Sun, C.T.; Mizutani, E. Neuro-fuzzy and soft computing: A computational approach to learning and machine intelligence. In Matlab Curriculum Series; Prentice Hall: Upper Saddle River, NJ, USA, 1997; pp. 142–148. [Google Scholar]
- Jang, J.S.R. ANFIS: Adaptive-network-based fuzzy inference. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Pal, K.S.; Mitra, S. Neuro-Fuzzy Pattern Recognition: Methods in Soft Computing; Wiley: New York, NY, USA, 1999; pp. 107–145. [Google Scholar]
- Nauck, F.K.; Kruse, R. Foundation of Neuro-Fuzzy Systems; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 1997; pp. 35–38. [Google Scholar]
- Singh, R.; Kainthola, R.; Singh, T.N. Estimation of elastic constant of rocks using an ANFIS approach. Appl. Soft Comput. 2012, 12, 40–45. [Google Scholar] [CrossRef]
- Takagi, H.; Hayashi, I. NN-driven fuzzy reasoning. Int. J. Approx. Reason. 1991, 5, 191–212. [Google Scholar] [CrossRef]
- Vieira, J.; Morgado Dias, F.; Mota, A. Neuro-fuzzy systems: A survey. In Proceedings of the 5th WSEAS NNA International Conference on Neural Networks and Applications, Udine, Italy, 25–27 March 2004. [Google Scholar]
- Takagi, T.; Sugeno, M. Derivation of fuzzy control rules from human operator’s control actions. Proc. IFAC Symp. Fuzzy Inf. Knowl. Represent. Decis. Anal. 1983, 16, 55–60. [Google Scholar] [CrossRef]
- Wei, M.; Bai, B.; Sung, A.H.; Liu, Q.; Wang, J.; Cather, M.E. Predicting injection profiles using ANFIS. Inf. Sci. 2007, 177, 4445–4461. [Google Scholar] [CrossRef]
- Singh, T.N.; Kanchan, R.; Verma, A.K.; Saigal, K. A comparative study of ANN and neuro-fuzzy for the prediction of dynamic constant of rockmass. J. Earth Syst. Sci. 2005, 114, 75–86. [Google Scholar] [CrossRef]
- Güneri, A.F.; Ertay, T.; Yücel, A. An approach based on ANFIS input selection and modeling for supplier selection problem. Expert Syst. Appl. 2011, 38, 14907–14917. [Google Scholar] [CrossRef]
- Brown, M.; Bossley, K.; Mills, D.; Harris, C. High dimensional neuro-fuzzy systems: Overcoming the curse of dimensionality. In Proceedings of the International Joint Conference of the Fourth IEEE International Conference on Fuzzy Systems and the Second International Fuzzy Engineering Symposium, Yokohama, Japan, 20–24 March 1995; pp. 2139–2146. [Google Scholar]
- Abonyia, J.; Andersenb, H.; Nagya, L.; Szeiferta, F. Inverse fuzzy-process-model based direct adaptive control. Math. Comput. Simul. 1999, 51, 119–132. [Google Scholar] [CrossRef]
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithm; Plenum Press: New York, NY, USA, 1981. [Google Scholar]
- Li, K.; Sua, H. Forecasting building electricity consumption with hybrid genetic algorithm-hierarchical adaptive network-based fuzzy inference system. Electr. Build. 2010, 42, 2070–2076. [Google Scholar]
- Chiu, S.L. Fuzzy Model Identification Based on Cluster Estimation. J. Intell. Fuzzy Syst. 1994, 2, 267–278. [Google Scholar]
- Yager, R.R.; Filev, D.P. Generation of Fuzzy Rules by Mountain Clustering. J. Intell. Fuzzy Syst. 1994, 2, 209–219. [Google Scholar]
- Amjady, N.; Keynia, F. Short-term load forecasting of power systems by combination of wavelet transform and neuro-evolutionary algorithm. Energy 2009, 34, 46–57. [Google Scholar] [CrossRef]
- Alexandridis, A.K.; Achilleas, D.Z. Wavelet neural networks: A practical guide. Neural Netw. 2013, 42, 1–27. [Google Scholar] [CrossRef] [PubMed]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Russell, S.J.; Norvig, P. Artificial Intelligence a Modern Approach; Prentice Hall: Upper Saddle River, NJ, USA, 1995. [Google Scholar]



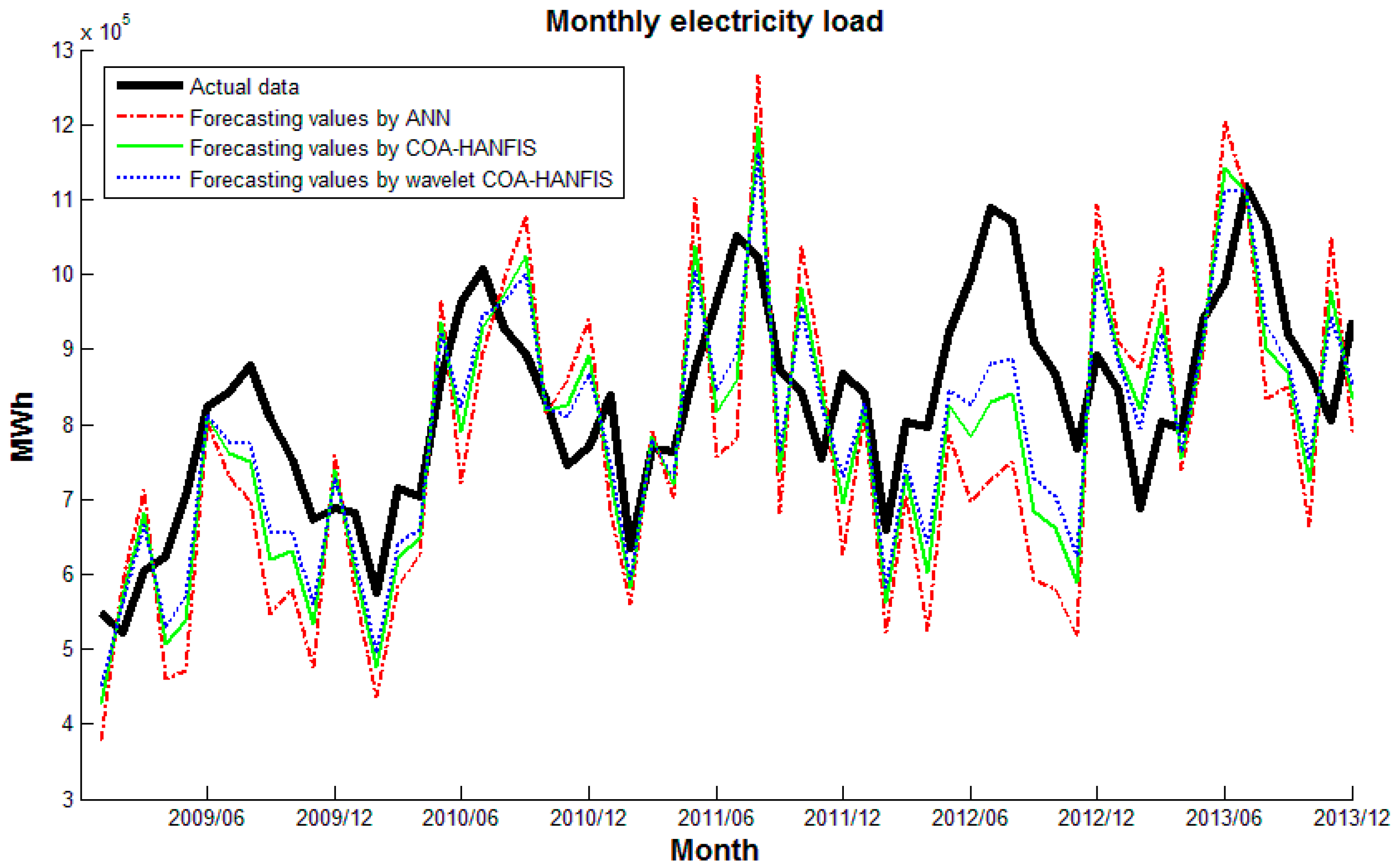
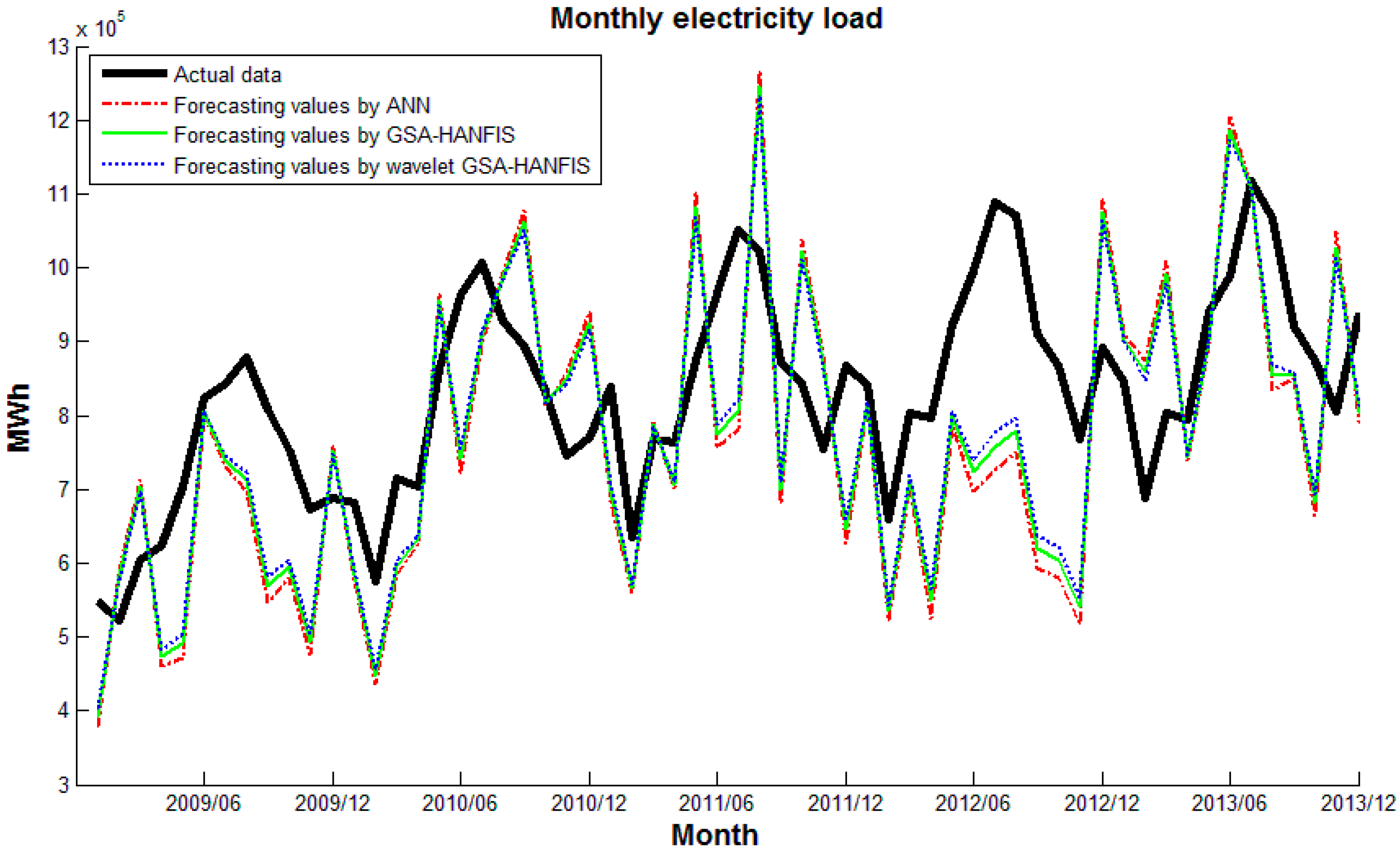
| Factor | |
|---|---|
| X1 | Month index |
| X2 | Average air pressure |
| X3 | Average temperature |
| X4 | Average wind velocity |
| X5 | Rainfall |
| X6 | Rainy time |
| X7 | Average relative humidity |
| X8 | Daylight time |
| Model | MAPE | RMSE | MAE | R |
|---|---|---|---|---|
| ANN | 0.3953 | 197,234 | 152,084 | 0.5634 |
| GSA-HANFIS | 0.2843 | 183,118 | 123,108 | 0.6142 |
| Wavelet GSA-HANFIS | 0.2023 | 134,126 | 101,321 | 0.7409 |
| COA-HANFIS | 0.0947 | 75,148 | 67,100 | 0.8700 |
| Wavelet COA-HANFIS | 0.0764 | 54,123 | 66,267 | 0.8779 |
| CS-HANFIS | 0.0577 | 47,210 | 60,129 | 0,8934 |
| Wavelet CS-HANFIS | 0.0433 | 39,073 | 49,238 | 0.9287 |
| Method | MAPE | RMSE | MAE | R |
|---|---|---|---|---|
| MLR | 0.1702 | 160,540 | 141,870 | 0.6331 |
| ARIMA (2,1,1) | 0.1693 | 152,070 | 136,253 | 0.7146 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.-F.; Do, Q.H.; Nguyen, T.V.A.; Doan, T.T.H. Forecasting Monthly Electricity Demands by Wavelet Neuro-Fuzzy System Optimized by Heuristic Algorithms. Information 2018, 9, 51. https://doi.org/10.3390/info9030051
Chen J-F, Do QH, Nguyen TVA, Doan TTH. Forecasting Monthly Electricity Demands by Wavelet Neuro-Fuzzy System Optimized by Heuristic Algorithms. Information. 2018; 9(3):51. https://doi.org/10.3390/info9030051
Chicago/Turabian StyleChen, Jeng-Fung, Quang Hung Do, Thi Van Anh Nguyen, and Thi Thanh Hang Doan. 2018. "Forecasting Monthly Electricity Demands by Wavelet Neuro-Fuzzy System Optimized by Heuristic Algorithms" Information 9, no. 3: 51. https://doi.org/10.3390/info9030051
APA StyleChen, J.-F., Do, Q. H., Nguyen, T. V. A., & Doan, T. T. H. (2018). Forecasting Monthly Electricity Demands by Wavelet Neuro-Fuzzy System Optimized by Heuristic Algorithms. Information, 9(3), 51. https://doi.org/10.3390/info9030051




