Tradeoff Analysis between Spectral and Energy Efficiency Based on Sub-Channel Activity Index in Wireless Cognitive Radio Networks

Abstract

In recent years, there has been a rapid evolution of wireless technologies that has led to the challenge of high demand for spectral resources. To overcome this challenge, good spectrum management is required that calls for more efficient use of the spectrum. In this paper, we present a general system, which makes a tradeoff between the spectral efficiency (SE) and energy efficiency (EE) in the cellular cognitive radio networks (CCRN) with their respective limits. We have analyzed the system taking into account the different types of power used in the CCRN, namely the spectrum detection power (Z_s) and the relay power (Z_r). Optimal policy for emission power allocation formulated in the function of sub-channel activity index (SAI) as an optimization problem in order to maximize spectrum utilization and minimize the energy consumption in the base station of the secondary system energy consumption, is subject to different constraints of the main user system. We also evaluate the collaborative activity index of the sub-channel describing the activity of the primary users in the CCRN. The theoretical analyses and simulation results sufficiently demonstrate that the SE and EE relationship in the CCRN is not contrary and thus the achievement of optimal tradeoff between SE and EE. By making a rapprochement with a cognitive cellular network where SBSs adopts an equal power allocation strategy for sub-channels, the results of our proposed scheme indicate a significant improvement. Therefore, the model proposed in this paper offers a better tradeoff between SE and EE.

1. Introduction

The concept of cognitive radio contributes to the establishment of a new generation network, it provides radio equipment with intelligent learning and decision-making capabilities so that it is aware of the state of its environment and to adjust its operating parameters to that state [1,2]. The most widespread application in the literature of intelligent radio is that it can dynamically access to spectrum radio. In view of the increase in the number of users and the scarcity of spectral resources set by the Federal Communications Commission (FCC) [3,4], this concept gives the opportunity to unlicensed terminal users to use them, by adjusting their parameters to the new frequency bands. Cognitive radio technology allows unlicensed users (secondary users, SUs) to transmit in licensed frequency bands without disrupting the quality of service (QoS) of licensed users (primary users, PUs) transmission in order to make efficient use of the spectral band [5,6].

1.1. Motivation

The increase in energy demand, the environmental concerns which result in high levels of emissions of greenhouse gases, high prices of energy, and high operating costs have resulted in more in-depth research efforts in energy efficiency (EE) communication systems. Efficient exploitation and optimum utilization of energy resources are of paramount importance for cognitive radio networks (CRNs) in order to effectively exploit the power of limited issuance of cognitive radios powered by a battery and to bear the complementary requirements in the field of signal processing such as the detection of the spectrum. Many of the existing research deals with the conception of optimal resource allocation in order to maximize the spectrum efficiency (SE) and EE for secondary users. In [7], the authors calculated the optimal duration of detection and control of power in order to maximize the capacity of ergodic systems in cognitive radio, operating on multiple narrowband channels in two different transmission systems, namely opportunistic spectrum access and spectrum sharing based on the detection. In [8], the authors characterized the optimal power control strategy and the actual capacity of cognitive users in the presence of errors in detection. In [9], the authors concentrated primarily on the decision threshold of detection and the duration of optimal detection in order to maximize the weighted sum of SE and EE. In [10], the authors have discussed the duration of optimal detection that maximizes the EE of cognitive users subject to a constraint on the probability of detection. In [11], the optimal allocation of the subcarrier and the assignment of power have been proposed to maximize the EE means of secondary users in an Orthogonal Frequency Division Multiplexing (OFDM) based cognitive radio networks or to maximize the worst case of EE. In [12], the authors have analyzed the optimal power control system that maximizes the sum of the cognitive user’s EE for 5G communication systems. In [13], the authors have innovated control algorithms of energy efficient power for cognitive users in a cellular network. In our work, we suggest that the primary users transmit in a timed manner, meaning that, the activity of primary users rests the same.

Spectral band reuse is the essential objective of CNRs to enhance spectral efficiency. This reuse of the spectral band is implemented through a coordination mechanism, which is completed by the principal functions of the CRNs such as spectrum detection, the dynamic spectrum access (DSA) and the spectrum jumps. These functions are generally regarded as operations for consumer’s energy, which certainly increases the consumption of energy in CCRNs and reduces the EE [3,6]. The energy and spectral effectiveness of the secondary system is also important for the increased use of low bandwidth and emission power limitation. Furthermore, there is still a tradeoff between SE and EE in CCRNs regardless of the channel access mode of secondary users. Accordingly, the compromise could be reached and this compromise was discussed in [14].

In this work, the optimal power distribution is expressed in such a way that the total utility of the secondary base stations (SBSs) is maximized, in terms of SE, and this subject to the total emission power at the constraints of the probability of collision between SUs and PUs. Then, under the same settings for the system, we make an optimal distribution of the power supply in the goal of maximizing the total usefulness of the SUs, with respect to energy efficiency, linked to the same constraints. The feature and model of the sub-channel activity index are obtained through the cooperation between the base stations in order to integrate the activities related to the communication system of the PUs in the allocation of emission power suboptimal. The cellular cognitive radio networks (CCRN) of sub-channel allocation and transmission power in the SUs is expressed to allow maximization of the total utility function of the SUs focused on EE and SE. We discover that the proposed strategy for the tradeoff between SAI, EE and SE is more convenient and efficient compared to the conventional system of the tradeoff between SE and EE.

To deal with the problems mentioned above, we retain the following plan: Section 2 describes the concept of spectral and energy efficiency in the CCRN. Primary and secondary user activity model is discussed in Section 3. Section 4 presents the cellular cognitive radio networks (CCRN) model. Section 5 discusses the collaborative SE and EE tradeoff. In Section 6, tradeoff analysis of energy and spectral efficiency. Section 7 gives the simulation results and analyses. The last section presents the conclusion.

1.2. Main Contribution

Our main contribution in this paper is summarized as follows:

• The paper makes a more specific and in-depth description of the problems related to the trade-off between SE and EE for CCRNs. It is proved that despite additional energy consumption for the implementation of cognitive radio functions there is no inverse trade-off between SE and EE.
• In this paper, an optimal transmission power allocation strategy is formulated according to SAI in the form of an optimization problem in order to maximize the total utilization rate and minimize energy consumption in CCRNS.
• SAI is evaluated to describe primary user activities in CCRNs. And a sub-channel power allocation scheme is proposed in the SBSs to maximize the utility function of the SU.

2. The Notion of Spectral and Energy Efficiency in the Context of CCRNs

2.1. Energy Efficiency

Energy efficiency as a whole is assumed to be a considerable constraint thus limiting the exploitation, implementation, and design of most wireless networks component battery devices. In CRNs, this constraint becomes more complex where the energy can be totally non-renewable. Considering a CRN that consists essentially of base stations (BSs), cognitive radio nodes, and basic networks, the lifespan of the network depends on the energy consumption of BSs and the use of energy by the cognitive radio nodes. Consequently, the energy consumed for the transmission, reception, and the other objectives related to cognitive is the main element which affects the duration of network existence [15,16].

Given that energy is regarded as a resource of major constraint for the CRNs, the lifespan of the network is regarded as a significant measure of performance because of its relation to the energy used in the processing and the transmission of data, and also the dissipated energy to various levels and network components. Taking these factors into account, EE should be considered an important element in the design of cognitive radio and in all aspects of the operation, not exclusively for essential parts of the network, but likewise for the entire communication network [17,18]. Low energy consumption in CRNs demands appropriate technologies and solutions and also requires a lot of attention in order to improve the EE of the network. The idea of CR has been developed in order to address problems of spectrum shortage, but because of its integrated properties that promote high energy consumption, this is an essential aspect of research in the field of green communications. CR is essentially characterized by a system of adaptive radio and autonomous, designed by a smart progressive functionality that relates to its exploitation environment and to draw lessons from its experiences and observations into the plan, decide and reason on future activities to deal with the different needs [19,20]. These features cause a considerable increase in the spectral and energy efficiency of the network but still contribute to increased energy consumption in the network.

CRs generally detects the spectrum band vacant for communication to the assistance of a technique for spectrum detection and they do so intermittently with the aim of avoiding interference with a primary user. Thus, each structure is divided into different sections, one of which is used in the context of transmission and in the context of detection. The more time used to detect, the greater the precision of the detection is high, more energy consumption is high and the longer the duration of transmission is short. Energy efficiency is high when transmission and detection programming is carried out in a way to ensure a balance between the effectiveness of transmission and the accuracy of detection, as well as a better EE [21,22]. Optimizing EE in the framework of CRNs constitutes a vital step to guarantee a higher QoS of the network [23]. The optimization concerning EE will fall not only the overall cost of the network of terminals to base stations but also will decrease its environmental impacts and will also participate to make the communication much more practical and affordable in a ubiquitous framework [24].

2.2. Spectral Efficiency

The allocation of spectral resources in wireless communication systems focused on the OFDM model is one of the very important topics that has been researched for more than a decade. Radio resources are costly and limited. Therefore, they must be used effectively to make the system economically feasible [25]. SE is defined as the ratio between the band occupied by the transmitted signal and the useful throughput, it is part of a highly accepted criterion for optimizing a wireless network. SE of the system is usually measured in (bit/s)/Hz. This measure is influenced not only by the single-user transmission system but also by multiple access schemes and radio resource management techniques. SE can be greatly enhanced by radio resources management techniques such as efficient dynamic or static channel allocation, link adaptation, and power control to reduce interference. SE is characterized by the optimized utilization of the bandwidth or of the spectrum so that the maximum data transmitted on this medium is less affected by transmission errors [26,27]. The evolution of data services is characterized by a growing number of users with requests for the bandwidth increasing more and more to the extent that the market of wireless data increases. This makes deployment of wireless technologies with high spectral efficiency to be of paramount importance.

3. Primary and Secondary User Activity Model

For efficient use of the spectrum, the network CR must be able to know the statistics of the traffic of the primary networks in every spectrum, generally called PU activity [28].

3.1. Activity Model of the Primary User

Consider that in the system there is only one channel exploited by one or more main users. We estimate that the channel may be in the idle position (OFF) or in the active position (ON). The appropriate duration of the OFF and ON periods is based initially on the user’s attitudes (e.g., the PU data transfer process) [29,30]. In addition, this is based on the type of data transfer (e.g., short VoIP data compared to long file data). Such information may not be inferred or known by the SU. To take account of the maximum quantity of generality and while keeping the analytical traceability, we thus develop the OFF-ON activity model of the PUs as both the alternative renewal process [31,32]:$\left(P_{OFF}^n,P_{ON}^n\right)$, $n\ge 1$, where $n$ indicates the number of renewal OFF-ON evacuated up to the instant $t$. The duration of the entire OFF ($P_{OFF}^n$) period or the ON $\left(P_{ON}^n\right)$ period, is designated as a random variable that is distributed according to a probability density function and is autonomous compared to other OFF or ON periods [33]. This model of PU activity is much more flexible than that of simple models.

3.2. Activity Model of the Secondary User

In this model, we assume that SUs can access a channel if and only if the PU has no activity on the channel. In other words, during the OFF periods of the channel. For that, the data of SU is transmitted with success on the channel the duration of the period off and the duration of these data must be taken into account [34]. We estimate that when a PU starts transmitting this data on the channel before the SU data is fully transmitted over the channel, the SU data is assumed to be lost under the collision effect and will be retransmitted when the channel will be again inactive. We also estimate that the spectrum detection capability of SUs is normal. In other words, there is the absence of false alarms and that of missing detections. These kinds of scenarios are supposed to be orthogonal to our analysis and our model and can be assimilated in the PU OFF–ON process, if possible.

In reality, an SU has the ability to access several channels. Different protocols and architectures have been suggested in order to discover and facilitate access to these channels [31]. In order not to introduce architectural details that can all time restrict the generality of the results and make our analysis complicated, we decide to keep the only stochastic process ON–OFF. When the process is in the active state, it means that the SU does not have the ability to emit new queued data or a new given on the channel. This ON period can look like between others to: (1) the SU is waiting on an active channel until this channel is unoccupied again, in the case where the mobility of the spectrum is costly or not likely to give the best performance and (2) a period of scanning at the time the SU attempts to regain or gain one (or several) channel(s) inactive(s).

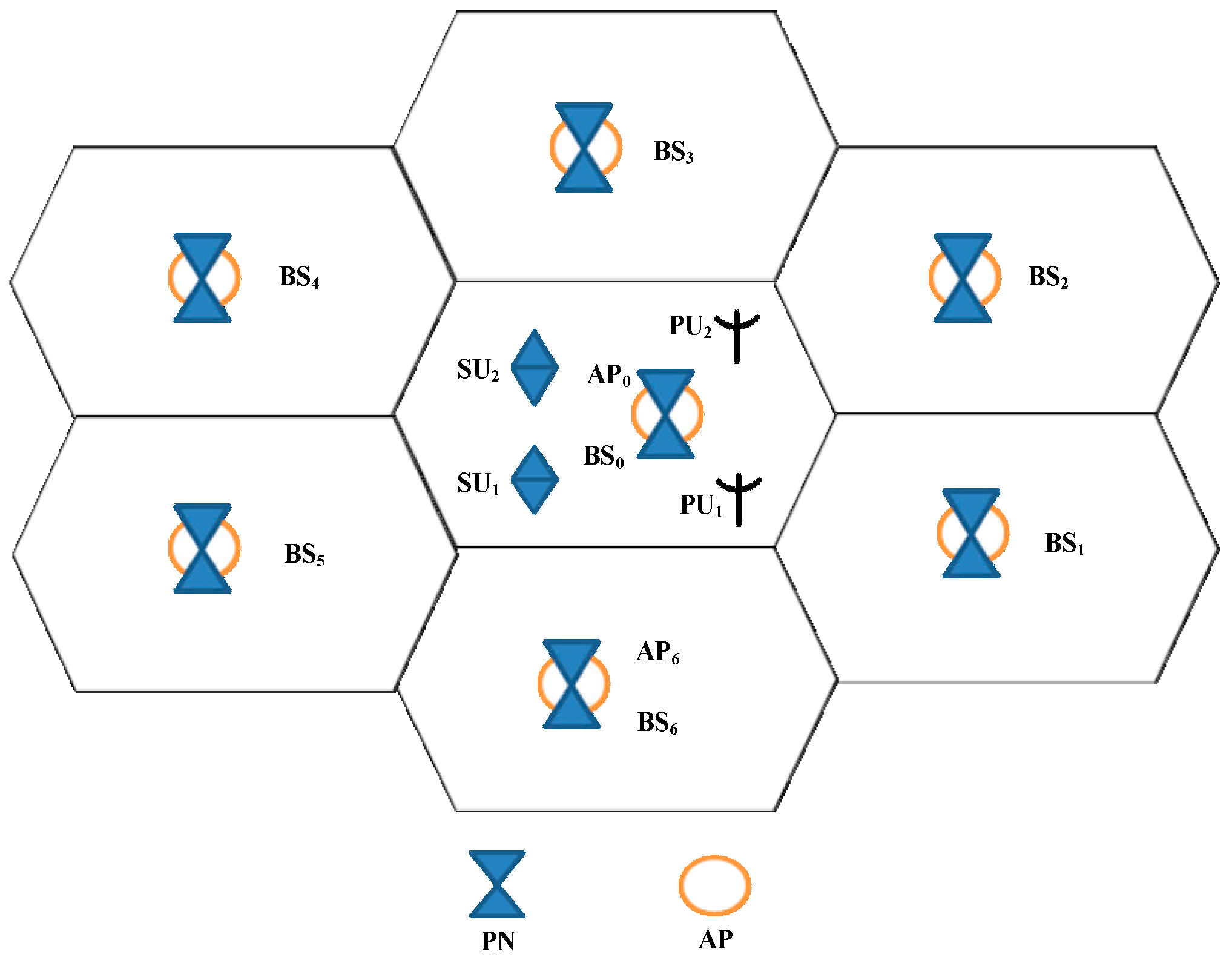
4. Network Model

We consider a cellular cognitive radio network (CCRN) that coexists with an existing primary cellular network. Inside each primary network cell (PN), there are several PUs and a base station (BS) or relay. However, inside each cell of the CCRN, there are several SUs and an access point (AP). Each cell of the CCRN is co-located with a PN cell as shown in Figure 1. The coverage of microcells overlaps with the coverage of existing networks. Microcell base stations can provide high-speed wireless transmission in indoor and access point scenarios [35].

For their activities, every PU is allowed to use a $k^{\prime }\in \left\{1,\dots ,K^{\prime }\right\}$ frequency band with B Hz bandwidth. The cognitive network has several cells with N SBSs. The SBSs are exploited by the SUs and are indexed by SUl, $l\in \left\{1,\dots ,L\right\}$. The cognitive network uses OFDMA and the radio frequency is subdivided into M sub-channels $W_k=B/M$ Hz, $k\in \left\{1,\dots ,M\right\}$. Here, the SE of SUl, access to the sub-channel k is formulated by $d_{lk}={\log }_2\left(1+z_{lk}{h}_{lk}\right)$ bps/Hz, where $z_{lk}$ designates the emission power allocated on the sub-channel k to the BSS corresponding to SU_l and $h_{lk}$ represents the channel gain of the SUl. We also specify $d_l={\left[d_{l1}\dots d_{lk}\dots d_{lM}\right]}^T$ as the frequency vector for SU_l, where T designates the transposition operator. The optimal emission power $z_k^{*}$ is closely linked to the main activity of the communication network on the kth sub-channel.

5. SE and EE Collaboration Technique

For a sub-channel k in a secondary base station (SBS) with neighboring (N − 1) SBS, the sub-channel activity index (SAI) is formulated as follows: $\stackrel{\wedge }{S_k}=\frac{1}{N}{\displaystyle \sum _{n=1}^N\left(S_{n,k}\right)},{\forall }_k$. For a given SBS, the activity index vector is formulated as follows: $\stackrel{\wedge }{S}=\left[\stackrel{\wedge }{S_1}\dots ,{\stackrel{\wedge }{S}}_M\right]$ where $0\le {\stackrel{\wedge }{S}}_k\le 1,{\forall }_k$.

Obtaining an SAI for each SBS is done through 1-bit information per sub-channel that is necessary for neighboring SBSs to transmit to back. As part of the strategy proposed in this paper, each SBS broadcasts its S at the beginning of each time slot recognized and received by all other neighboring SBS. Therefore, to get an SAI for all the M sub-channels in an SBS with (N-1) neighbor cells require (N − 1) × M bits back. The accessibility of a sub-channel in an SBS depends on the value of signal-to-noise ratio (SNR) and the SBS decides the access method on each sub-channel according to its activity index.

5.1. Analysis Related to Spectral Efficiency

Improved spectral efficiency requires a good spectrum allocation strategy. The new problem of optimizing the allocation of resources is related to the reuse of spectra. The secondary system SE is maximized for a proposed power allocation method. The transmission collision between the primary system and the secondary system can occur only when the interference created by the secondary system exceeds a predefined threshold ${\alpha }_{k^{\prime }k}$. To avoid the transmission collision between the primary system and the secondary system while guaranteeing the QoS, the allocation of spectral resources is made so that the probability of collision (Pc) in the primary system does not exceed ${\mu }_{k^{\prime }k}$. The constraint presented in (2) shows that the transmission power in the SBS must not exceed maximum transmission power. In addition, the collision probability for the primary systems must not also exceed ${\mu }_{k^{\prime }k}$ as indicated in (3). The optimal allocation of spectrum resources is expressed as follows:

$$B_1:\underset{Z}{\max }{\displaystyle \sum _{k=1}^M\frac{1}{\stackrel{\wedge }{S_k}}\sum _{l\in L}{\log }_2}\left(1+\frac{{\left|h_{lk}\right|}^2{z}_{lk}\left({\stackrel{\wedge }{S}}_k\right)}{N_0+I_{zk}}\right),$$

(1)

$$s.t.{\displaystyle \sum _{l=1}^L{\displaystyle \sum _{k=1}^M{z}_{lk}\le Z_t}},$$

(2)

$${\mathrm{P}}_c\left\{{\displaystyle \sum _{l=1}^L{Z}_{lk}}{\left|h_{k^{\prime }k}\right|}^2>{\alpha }_{k^{\prime }k}\right\}\le {\mu }_{k^{\prime }k},\forall k^{\prime },k,$$

(3)

where $z_{lk}$ designates the emission power allocated on the kth sub-channel, z is the L×M matrix, $z=\left[z_1|\dots z_L|\right]$ and $z_l={\left[z_{l1},\dots ,z_{lM}\right]}^T$. N₀ designates the spectral density of the noise. $I_{zk}$ denotes the interference caused by the simultaneous transmission of the PUs. $Z_t$ denotes the total transmission power. $h_{lk}$ indicates the channel gain of the SUl. $h_{k^{\prime }k}$ represents the channel gain of the PUk′. ${\alpha }_{k^{\prime }k}$ denotes the predefined threshold of interference created by the secondary system. ${\mu }_{k^{\prime }k}$ is the predefined threshold of collision probability for the primary systems. ${\stackrel{\wedge }{S}}_k$ is the sub-channel activity index. For every sub-channel, the assignment of optimal power that maximizes total usefulness in the SBS is regarded as a classic question of water filling, thereby:

$$z_{lk}^{*}={\left[\frac{1/\ln 2}{{\stackrel{\wedge }{S}}_k\left(\gamma +{\displaystyle {\sum }_k{\eta }_k}\right)}-\frac{N_0+I_{zk}}{{\left|h_{lk}\right|}^2}\right]}^{+}$$

(4)

$\gamma$ is the Lagrangian multiplier associated with the constraint and ${\eta }_k$ is the Lagrangian vector associated with the constraint.

5.2. Analysis Related to Energy Efficiency

In this section, the technique of efficient allocation of transmission power is presented from the point of view of EE. The objective of this optimization is to maximize the utility of total SBS and the total capacity of SBS in terms of EE under transmission power constraint. The EE system of the proposed network with respect to the spectrum sharing is analyzed through the SAI parameter, $\stackrel{\wedge }{S}$. As evoked in the case of spectral efficiency, we consider the same constraints for the case of the energy efficiency in order to guarantee the minimum QoS to the PUs. The best possible EE based on SAI is obtained thanks to the following optimization problem:

$$B_1:\underset{Z}{\max }\frac{{\displaystyle \sum _{k=1}^M\frac{1}{\stackrel{\wedge }{S_k}}{\displaystyle \sum _{l\in L}{\log }_2}\left(1+\frac{{\left|h_{lk}\right|}^2{z}_{lk}\left(\stackrel{\wedge }{S_k}\right)}{N_0+I_{zk}}\right)}}{b_1+b_2{\displaystyle \sum _{k=1}^M{\displaystyle \sum _{l=1}^L{z}_{lk}\left(\stackrel{\wedge }{S_k}\right)}}},$$

(5)

$$s.t.{\displaystyle \sum _{l=1}^L{z}_{lk}{\left|h_{kl}\right|}^2}\le {\alpha }_{k^{\prime }k},$$

(6)

$$z_{lk}\ge 0,\forall l,k,$$

(7)

where b₁ and b₂, respectively, represent the constants of the power amplifier and the energy consumption of the circuit. By making the mathematical manipulations direct and pursuing the concept of Charnes–Cooper Transformation, we get the optimum transmission power as follows:

$$z_{lk}^{*}=\min \left\{{\left[\frac{1/\ln 2}{\stackrel{\wedge }{S_k}\left({\displaystyle {\sum }_k{\gamma }_k}{\left|h_{k^{\prime }k}\right|}^2+\eta \right)}-\frac{N_0+I_{zk}}{{\left|h_{lk}\right|}^2}\right]}^{+},Z_t\right\}.$$

(8)

We exploit the theorem of Dinkenlbach [36] in order to adjust the transmission power and the energy efficiency.

6. Tradeoff Analysis of Spectral Efficiency and Energy Efficiency

6.1. General Relationship between SE and EE

Before proving the relationship between SE and EE, it is essential to introduce some key concepts. The data rate $q_{lk}$ for the SUl on kth sub-channel is determined as follows:

$$q_{lk}=W{\log }_2\left(1+\frac{z_{lk}{h}_{lk}}{N_{0}W+\delta \left({\displaystyle \sum _{k^{\prime }\in K^{\prime },k^{\prime }\ne l}{z}_{k^{\prime }k}{h}_{k^{\prime }k}+{\displaystyle \sum _k{z}_{kk}{h}_{kk}}}\right)}\right),$$

(9)

where N₀ refers to the spectral density of noise. $\delta$ represents the factor of interference, $\delta =1$ or $\delta =0$ indicates if the interferences of others PUs or SUs are taken into consideration. $z_{lk}$, $z_{k^{\prime }k}$, and $z_{kk}$ represents the transmission powers of the SUl, the SUk, and PUk′. $h_{lk}$, $h_{kk}$, and $h_{k^{\prime }k}$ designates the corresponding channel gains. $W$ is the sub-channels bandwidth.

To determine the data rate of the SUl, the transmission powers of the PUs and of the other SUs are considered to be interferences. Given all SUs in all available sub-channels, the CCRNs throughput is calculated as follows:

$$D={\displaystyle \sum _{l\in L}{\displaystyle \sum _{k\in K}{q}_{lk}}},$$

(10)

The total transmission power of the CCRNs is determined as:

$$Z_t={\displaystyle \sum _{l\in L}{\displaystyle \sum _{k\in K}{z}_{lk}}},$$

(11)

The total bandwidth available for the CCRNs is calculated as:

$$B={\displaystyle \sum _{l\in L}{\displaystyle \sum _{k\in K}{W}_{lk}}},$$

(12)

where $W_{lk}$ indicates that the kth sub-channel is used by SUl.

In a perfect wireless transmission system, if only the power of emission is taken into account, the general relationship between SE and EE is expressed as follows [37]:

$$EE=\frac{SE}{\left(2^{SE}-1\right)N_0/h_t}.$$

(13)

This expression is deduced through the following equations [37]:

$$D=W{\log }_2\left(1+\frac{Z_t{h}_t}{W{N}_0}\right),$$

(14)

$$SE=\frac{D}{W},$$

(15)

$$EE=\frac{D}{Z_t},$$

(16)

where $h_t$ refers to the total gain of the channel, D designates the throughput of CCRN and Z_t denotes the total transmission power of CCRN. Nonetheless, it is important to emphasize that, in (13), it is assumed that only the transmission power is taken into account. In a communication network, apart from the transmission power Z_t, we note the existence of other types of power consumed which makes it possible to maintain the whole network. In this part, we refer to temporarily the other types of power that is the power of the circuit Z_c. If the power of the circuit Z_c is taken into account, the general relationship between SE and EE indicated in (13) is rewritten as follows:

$$EE=\frac{SE}{Z_c/W+\left(2^{SE}-1\right)N_0/h_t},$$

(17)

where Z_c is averaged by the sub-channel bandwidth B. The expression mentioned above is deducted by the modified formula of the EE, which is:

$$EE=\frac{D}{Z_t{h}_t+Z_c},$$

(18)

With reference to (13) and (17), we note that Z_c which represents the power of the circuit should surely decrease the EE system.

In the CCRNs, certain specific powers are required in order to allow the networks to carry out specific operations. To obtain a lot of spectrum, the CCRNs require the presence of the Z_r relay power to facilitate the transmission of PU data, and the CCRNs also require the presence of Z_s spectrum detection power to obtain available spectrum holes. In addition, we report the presence of specific limits on the emission power in the CCRNs. The total transmission power Z_t in the CCRNs must be lower than the threshold set by the PU network systems and Z_c must also be superior to QoS requirements set by the CCRNs. Therefore, given the constraints, the total power transmission (Z) consumed by the CCRN is composed of transmission power (Z_t), spectrum detection power (Z_s), relay power (Z_r), and power of the circuit (Z_c). It is calculated as follows:

$$Z=Z_c+Z_t+Z_r+Z_s,$$

(19)

$$I_I\le Z_t\le I_s.$$

(20)

The lower limit of Z_t imposed by the QoS of the CCRNs is indicated by $I_I$ and the superior limit of Z_t required by the primary network interference limit is designated by $I_S$. In this condition, the EE in the CCRNs is defined as follows:

$$EE=\frac{D}{Z},$$

(21)

and the SE in the CCRNs is defined as follows:

$$SE=\frac{D}{B}.$$

(22)

6.2. Optimal Tradeoff Between SE and EE

Using the general relationship between EE and SE presented in (17), the problems related to optimization for SE and EE in CCRNs are mentioned in part. Optimal solutions of tradeoff SE-EE for the CCRNs are deducted from the optimal SE and the optimal EE. To highlight the key points and facilitate the analyses, we retain the following hypotheses.

-

We assume there is an only pair of SUs (a receiver and a transmitter) in the CRNs and also only pair of PUs (a receiver and a transmitter) with a sub-channel number set to K = 1.

-

The transmission power (Z_t), the transmission relay (Z_r), power detection (Z_s), and the circuit power (Z_c) are relative to time t.

-

The CCRN period $P_{t,i}=t_{t,i}+t_s$ is determined, we consider that the time of inactivity (OFF) and the transmission time (ON) for the CRNs are similar.

6.2.1. General Optimization in Case the Energy Efficiency (EE)

The maximum of the general EE is obtained following to the optimization problem formulated below. The objective of this optimization is to maximize EE while considering the constraints presented above.

$$\{\begin{array}{c}\underset{t_t,z}{\max }EE\left(t_t,z,P_{fa},P_d\right)=\frac{D\left(t_t,z,P_{fa},P_d\right)}{Z\left(t_t,z,P_{fa},P_d\right)}\\ s.t.t_t\le P\\ I_I\le Z_t\le I_S\\ \rho \ge P_{fa}\\ \sigma \le P_d\end{array},$$

(23)

where t_t refers to the transmission time, the total transmission power Z_t must satisfy the required condition of QoS $I_I$ and the interference constraint $I_s$, the detection probability $P_d$ must be greater than $\sigma$, and the false alarm probability $P_{fa}$ must be inferior to $\rho$. The intrinsic values of $\sigma$ and $\rho$ are determined and required by the primary user network systems. It is important to stress that the constraints mentioned here are not imposed in a specific CCRN.

6.2.2. General Optimization in Case the Spectral Efficiency (SE)

As in the case of EE, we consider the same constraints in order to guarantee the minimum QoS to the PUs. The optimal SE is formulated as follows:

$$\begin{array}{c}\underset{t_t,z}{\max }SE\left(t_t,z,P_{fa},P_d\right)=\frac{D\left(t_t,z,P_{fa},P_d\right)}{B\left(t_t,z,P_{fa},P_d\right)}\\ s.t.t_t\le P\\ I_I\le Z_t\le I_S\\ \rho \ge P_{fa}\\ \sigma \le P_d\end{array},$$

(24)

where $B\left(t_t,z,P_{fa},P_d\right)$ designates the available spectral bands, which are found from the PU network systems.

6.3. Tradeoff between SE and EE in the CCRN

In this section, we analyze the compromise between SE and EE when the different powers are taken into account in the CCRN and this is done according to the general relationship SE-EE studied above.

6.3.1. Tradeoff between SE and EE when relay power is taken into account in the CCRNs

Power Limit When Relay Power (Z_r) Is Taken into Account in the CCRNs

CCRNs must transmit PU data in order to gain spectral resources for their transmissions. Then, the total flow rate D is composed of two parts: D_t denotes the flow rate of its own transmission and the other flow rate D_r represents the flow rate for the transmission relay system of the primary user network systems. Thus, the total flow rate is formulated as follows:

$$D=D_t+D_r.$$

(25)

The power $Z$ consumed by the CCRNs is composed of three parts namely: the circuit power $Z_c$, the transmission power $Z_t$, and the relay station power $Z_r$. It is formulated as follows:

$$Z=Z_c+Z_t+Z_r.$$

(26)

We assume that for PU systems the power is not limited, the transmitting power $Z_t$ must obey the requirement of QoS $I_s$ and the relay power $Z_r$ must also obey the QoS $I_s$ requirements of PU. Thus, the power limits of the relay and of the transmission power are expressed as follows:

$$Z_t\ge I_S,$$

(27)

$$Z_r\ge I_I.$$

(28)

Theorem 1.

The optimal EE for the CCRNs with $\phi$ as the relay factor, where $\phi$ represents the ratio of transmission time $t_t$ to relay time $t_r$, in other words, $\phi =\raisebox{1ex}{$t_r$}\!\left/ \!\raisebox{-1ex}{$t_t$}\right.$. We assume that the relay power $Z_r$ and the transmit power $\phi$ follow this relationship, $Z_r=Z_t\phi$. In the SE interval, there is an optimal EE. The relationship between EE and SE when the relay power is taken into account in the CCRN is formulated as follows:

$$EE=\frac{SE}{\raisebox{1ex}{$Z_c$}\!\left/ \!\raisebox{-1ex}{$W$}\right.+\left(2^{SE}-1\right)\left(1+\phi \right)N_0{h}_t},$$

(29)

where the upper and the lower limit are determined by the relay required condition of the PU network systems and required condition QoS of the CCRNs.

Proof. 

In this case, optimal EE when relay power is taken into account in the CCRN is rewritten as follows:

$$\begin{array}{c}\underset{P,z}{\max }EE\left(P,z\right)=\frac{D\left(P,z\right)}{Z\left(P,z\right)}=\frac{D_t\left(t_t,z\right)}{Z_c+Z_t+Z_r}\\ s.t.t_t\le \frac{P}{1+\phi }\\ I_I\le Z_t\le \raisebox{1ex}{$Z_r$}\!\left/ \!\raisebox{-1ex}{$\phi $}\right.\end{array},$$

(30)

where the total power emission $Z\left(P,z\right)=Z_c+Z_t+Z_r$. The constraints are: the power of the relay divided by $\phi$ should be greater than the transmission power Z_t and P/(1 + $\phi$) should be greater than the transmission time $t_t$. The flow rate of the system $D\left(P,z\right)$ is composed of two parts, namely the relay flow rate $D_r\left(t_r,z\right)$ and the transmission flow rate $D_t\left(t_t,z\right)$, in other terms:

$$D\left(P,z\right)=D_t\left(t_t,z\right)+D_r\left(t_r,z\right),$$

(31)

where P is the total period of the network system $P=t_t+t_r$. $\phi$ is required by PU network systems, it is assumed to be the exchange rate between the spectrum obtained from PU network systems and the data packet transmitted to PU network systems. It is important to emphasize that this rate is constantly controlled by PU network systems. It does not require detection of the presence of PU therefore, the probability of detection and the probability of false alarm do not occur. The Optimal SE is rewritten as follows:

$$\{\begin{array}{c}\underset{P,z}{\max }SE\left(P,z\right)=\frac{R\left(P,z\right)}{B\left(P,z\right)}=\frac{D_t\left(t_t,z\right)}{W}\\ s.t.t_t\le \frac{P}{1+\phi }\\ I_I\le Z_t\le \raisebox{1ex}{$Z_r$}\!\left/ \!\raisebox{-1ex}{$\phi $}\right.\end{array},$$

(32)

where W is equal to B. It admits that CCRNs gain a portion of the W spectrum through PU network systems while transmitting PU data and that the network cohabitation model focuses on a time division mode. By considering the flow rate of the system $D=W{\log }_2\left[1+\left(Z_t{h}_t/W{N}_0\right)\right]$, the relationship between Z_t and Z_r and power system, EE is calculated in function of SE as present (29). For CCRNs, SE increases with Z_t; For Z_c and Z_c there is an interval for SE. The upper limit of SE is dictated by the factor $\phi$, in other words, the CCRNs must exhaust the power necessary to relay the packets of PU data in order to gain the bandwidth. In the SE interval and taking account of the SE-EE relationship, an optimal EE is possible. □

6.3.2. Tradeoff between SE and EE when spectrum detection power is taken into Account in the CCRNs

Power Limit When Spectrum Detection (Z_s) Is Taken into Account in the CCRNs

In this section, we identify the existence of two types of periods, namely the inactive period P_i (P_OFF) and the transmission period P_t (P_ON). These two types of periods are formulated as follows:

$$\{\begin{array}{c}{P}_i=t_s+t_i\\ P_t=t_s+t_t\end{array},$$

(33)

where t_i, t_s, and t_t indicate the inactive time, the spectrum detection time, and the transmit time, respectively. To simplify the work t_i and t_t are considered as similar. The detection time of the spectrum t_s is essentially determined through the detection capability of the CCRNs and the limited level of interference of PU network systems. When t_s is estimated at a great value, the sensing performance (detection probability (P_d)) is convincing and interference prejudicial to PU network systems are limited. Nevertheless, a lot of spectrum detection (SD) power Z_s is consumed, and the data rate of flow is reduced because transmission time is lower. The compromise between the system flow rate and the SD time has been studied in [38], where the total flow rate is enhanced by taking an optimal detection time. The main objective of this paper is to implement the compromise between SE and EE in CCRNs, considering that the optimal t_s is chosen. When the detected target channel is busy, the CRNs carry out a new detection after the idle time t_i. And when the detected target frequency is unoccupied, the CCRNs begin transmission in the transmission time t_t. t_i, and t_r are essentially decided through the interference limits of the PU systems and the QoS requirements of the CCRNs. We define t_i = t_t to simplify our analysis. Thus, we use P to indicate the inactive period (P_i) and the inactive period (P_t) of the channel in the CCRNs. Thus, the transmission power Z_t of the CCRNs is lower a threshold required by the PU network systems and the total power consumed Z in the CCRNs is expressed as follows.

$$Z=Z_c+Z_t+Z_s,$$

(34)

$$I_I\le Z_t\le I_S,$$

(35)

where Z_t, Z_c, and Z_s designate the transmission power, the circuit power, and the detection power, respectively. $I_I$ and $I_s$ denote the interference level limitation related to PU network systems and the power limits required by the QoS imposed of the CCRNs.

Lemma 1.

An optimal t_s in the CCRNs for the maximum flow rate of the system D: for the CCRNs, there exists an optimal t_s to beget the maximum flow rate of the system D. The formulation of the optimization is: [38]

$$\{\begin{array}{c}\underset{t_s}{\max }D\left(P\right)=D_0\left(P-t_s\right)+D_1\left(P-t_s\right)\\ P_{fa}\le \rho \\ P_d\ge \sigma \end{array},$$

(36)

where D₀ and D₁ represent the flow rate of CCRNs under two hypotheses: hypothesis indicating the absence of PU signal and hypothesis indicating present of PU signal; P_fa and P_d must obey different constraints $\rho$ and $\sigma$. Through these constraints $\rho$ and $\sigma$, an optimal t_s is determined by the maximum flow rate of the system. The total period P = t_s + t_r is associated with the transmission time t_t and the detection time t_s.

Proof. 

Given the system flow rate D and the CCRNs mechanism, an optimal t_s can be achieved. This notion was developed in [38], this notion has been developed in [38], in which the compromise between system flow rate and spectrum detection has also been studied. Focusing on the mechanism of the CCRNs and the optimal t_s presented in Lemma above, we retain the theorem below. □

Theorem 2.

Sub-optimal spectral Efficiency (EE) for CCRNs with the probability of access P_a. For CCRNs, P_a refers to the access probability that estimates the likelihood that CCRNs can reach the selected frequency band W. For an optimal t_s, the relationship between EE and SE when the spectrum detection power is taken into account in the CCRN is formulated as follows:

$$EE=\frac{SE}{\frac{Z_c+Z_s}{W}+\left(2^{\frac{SE}{P_a}}-1\right)\raisebox{1ex}{$N_0$}\!\left/ \!\raisebox{-1ex}{$h_t$}\right.},$$

(37)

where the probability of access P_a can be determined as follows

$$P_a=P_{H_0}{P}_d+P_{H_1}\left(1-P_d\right).$$

(38)

As mentioned in (38), $P_d$, $P_{H_1}$, and $P_{H_0}$ refer to the probability of detection by CCRNs, presence probability of the primary user, and absence probability of the primary user respectively.

Proof. 

Optimizations for SE in (23) and EE in (24) can still exploit in this case. As a constraint, the transmission time must be less than or equal to the total time minus the spectrum detection time and the transmission power must be greater than or equal to the interference limit level. Given the optimal t_s and the Lemma 1, the optimal EE is reformulated as follows:

$$\begin{array}{c}\underset{t_t,z}{\max }EE\left(t_t,z,P_{fa},P_d\right)=\frac{D\left(t_t,z,P_{fa},P_d\right)}{Z\left(P,z,P_{fa},P_d\right)}\\ s.t.t_t\le P-t_s\\ I_I\le Z_t\\ P_{fa}\le \rho \\ P_d\ge \sigma \end{array},$$

(39)

where the t_t can be determined as follows:

$$\{\begin{array}{c}{t}_t=\left(P-t_s\right)\left[P_{H_0}{P}_d+P_{H_1}\left(1-P_{fa}\right)\right]\\ t_t=\left(P-t_s\right)P_a\end{array},$$

(40)

the total power of the system is $Z\left(P,z,P_{fa},P_d\right)=Z_c+Z_t+Z_s$. □

In a similar way, the optimal SE is reformulated as follows:

$$\{\begin{array}{c}\underset{t_t,z}{\max }SE\left(t_t,z,P_{fa},P_d\right)=\frac{D\left(t_t,z,P_{fa},P_d\right)}{W}\\ s.t.t_t\le P-t_s\\ P_{fa}\le \rho \\ P_d\ge \sigma \end{array},$$

(41)

where the flow rate of the system is expressed as follows:

$$D\left(t_t,z,P_{fa},P_d\right)=W{P}_a{\log }_2\left(1+\frac{Z_t{h}_t}{N_{0}W}\right).$$

(42)

Focusing on (39), (41), and (42), the suboptimal EE is deduced in (37) and ultimately expressed as a function of the access probability P_a and SE. The suboptimal EE can only be estimated numerically to vary P_a and SE. Focusing on (42) and (39), the CCRNs EE is expressed as:

$$EE=\frac{W{P}_a{\log }_2\left(1+\frac{Z_t{h}_t}{N_{0}W}\right)}{Z_c+Z_t\left(1+\theta \right)},$$

(43)

where $\theta$ represents the detection factor and is calculated as the ratio of the detection power of the spectrum Z_s to the transmission power Z_t, in other words, $\theta =\raisebox{1ex}{$Z_s$}\!\left/ \!\raisebox{-1ex}{$Z_t$}\right.$. Through (42), it can already be observed that the EE in the CCRNs decreases when the emission power Z_t increases. In the CCRNs, considering that the circuit power Z_c and the total power consumed Z are all constant, the relationship between P_a and the SE can be expressed as follows:

$$SE=P_a{\log }_2\left(1+\frac{\left(Z-Z_c\right)h_t}{\left(1+\theta \right)P_a{N}_{o}W}\right).$$

(44)

Through this expression, it can be observed that, if the detection capacity of the CCRNs is better (the detection factor $\theta$ is smaller), the corresponding SE is better.

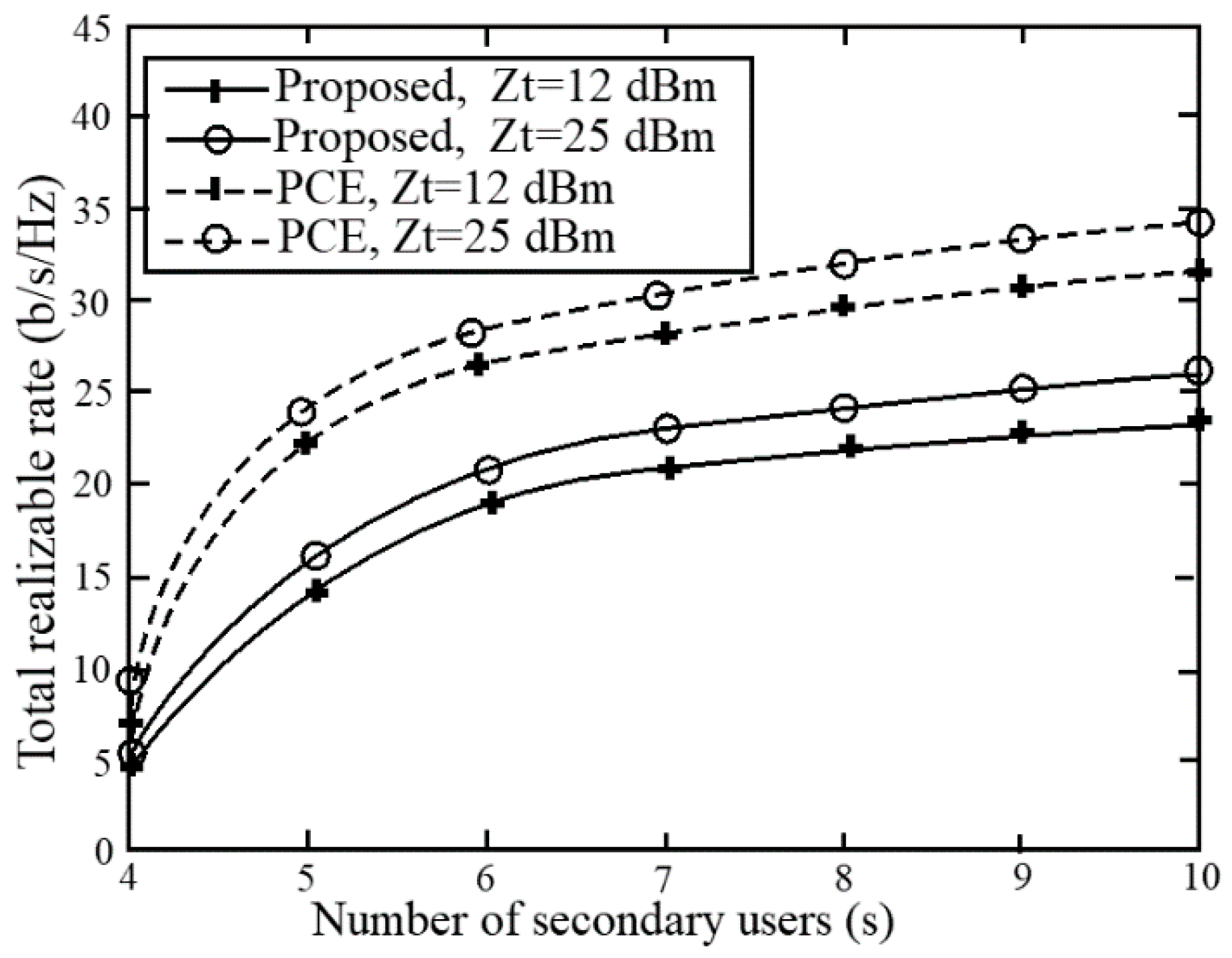
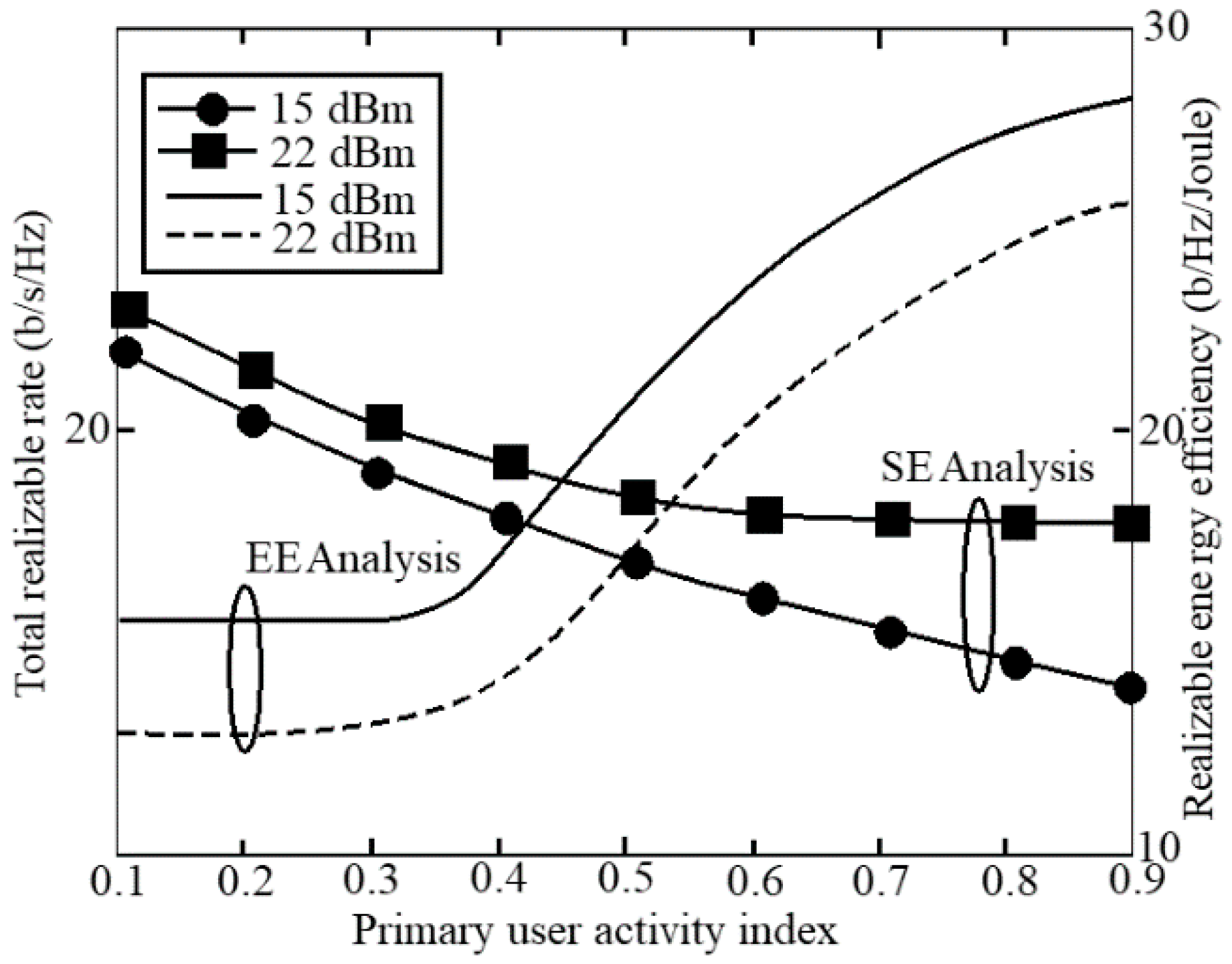
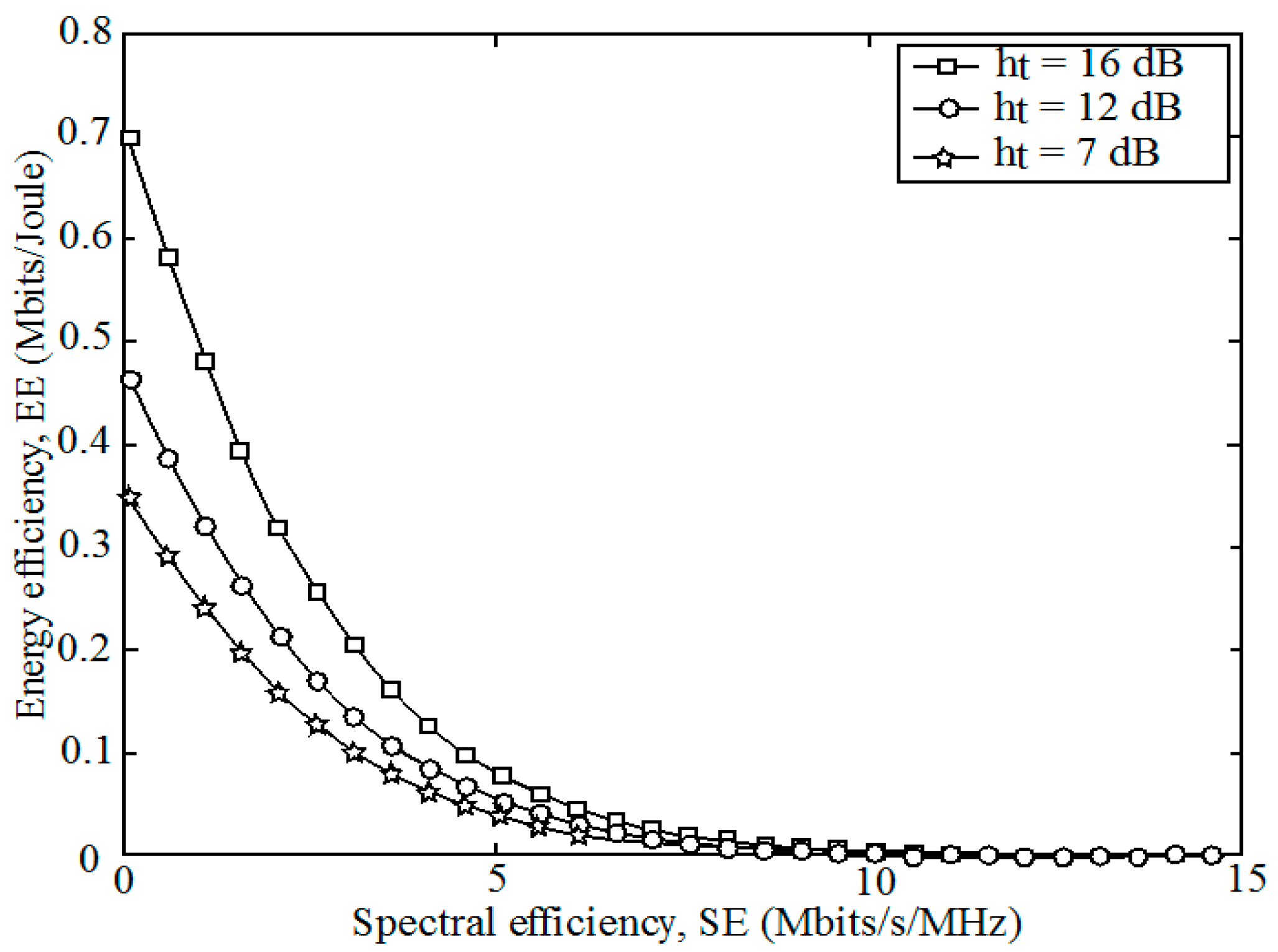
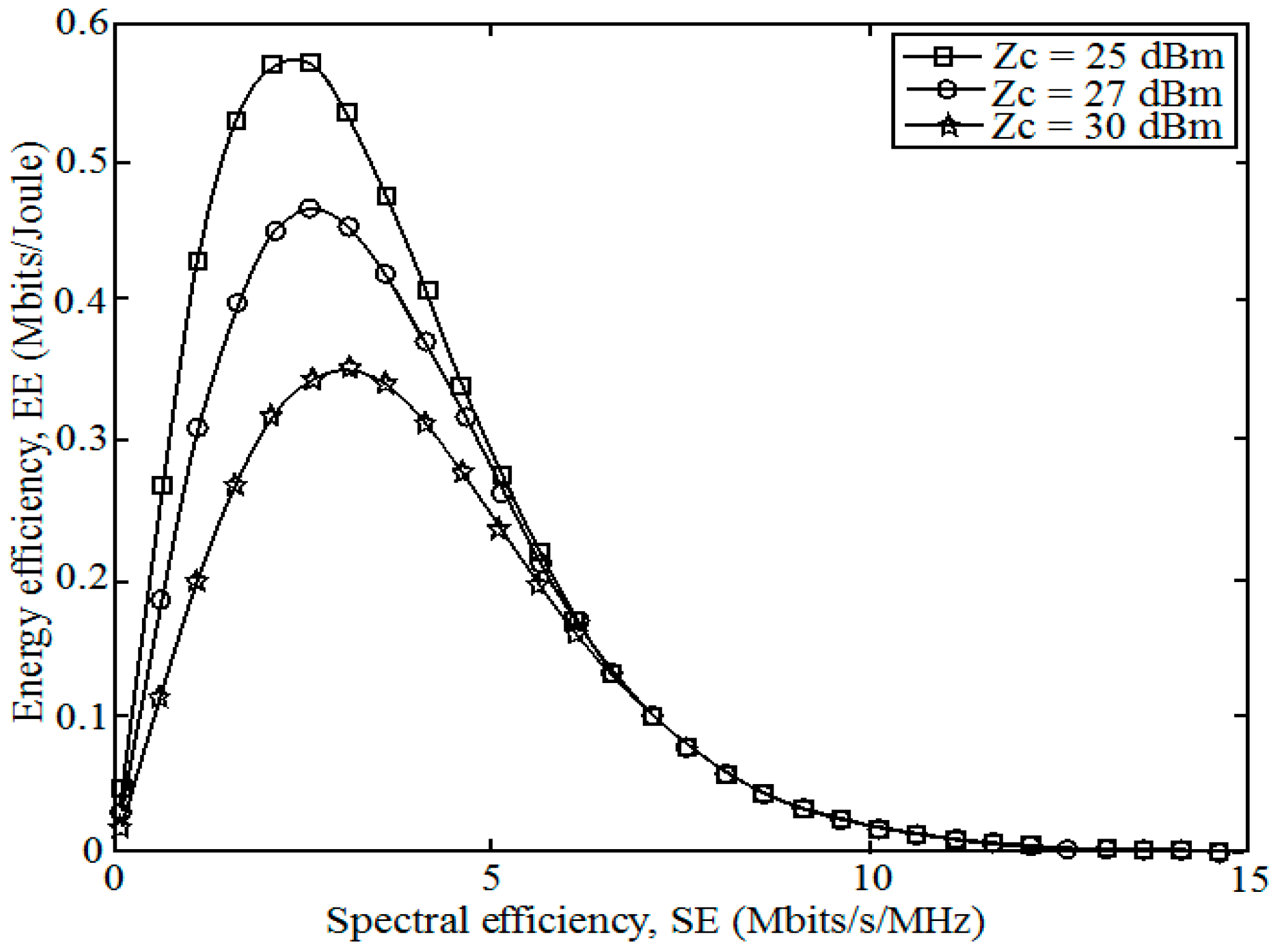
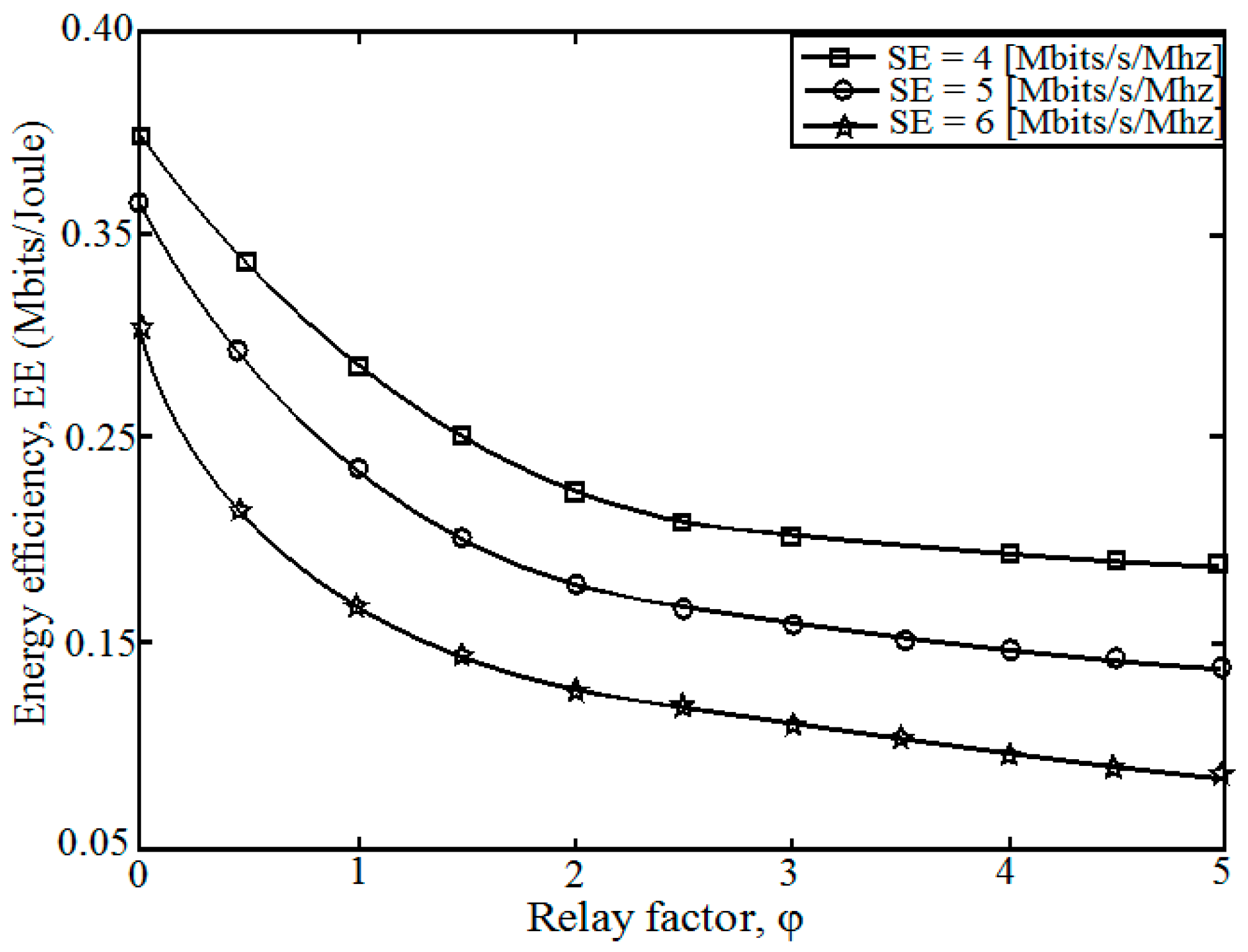
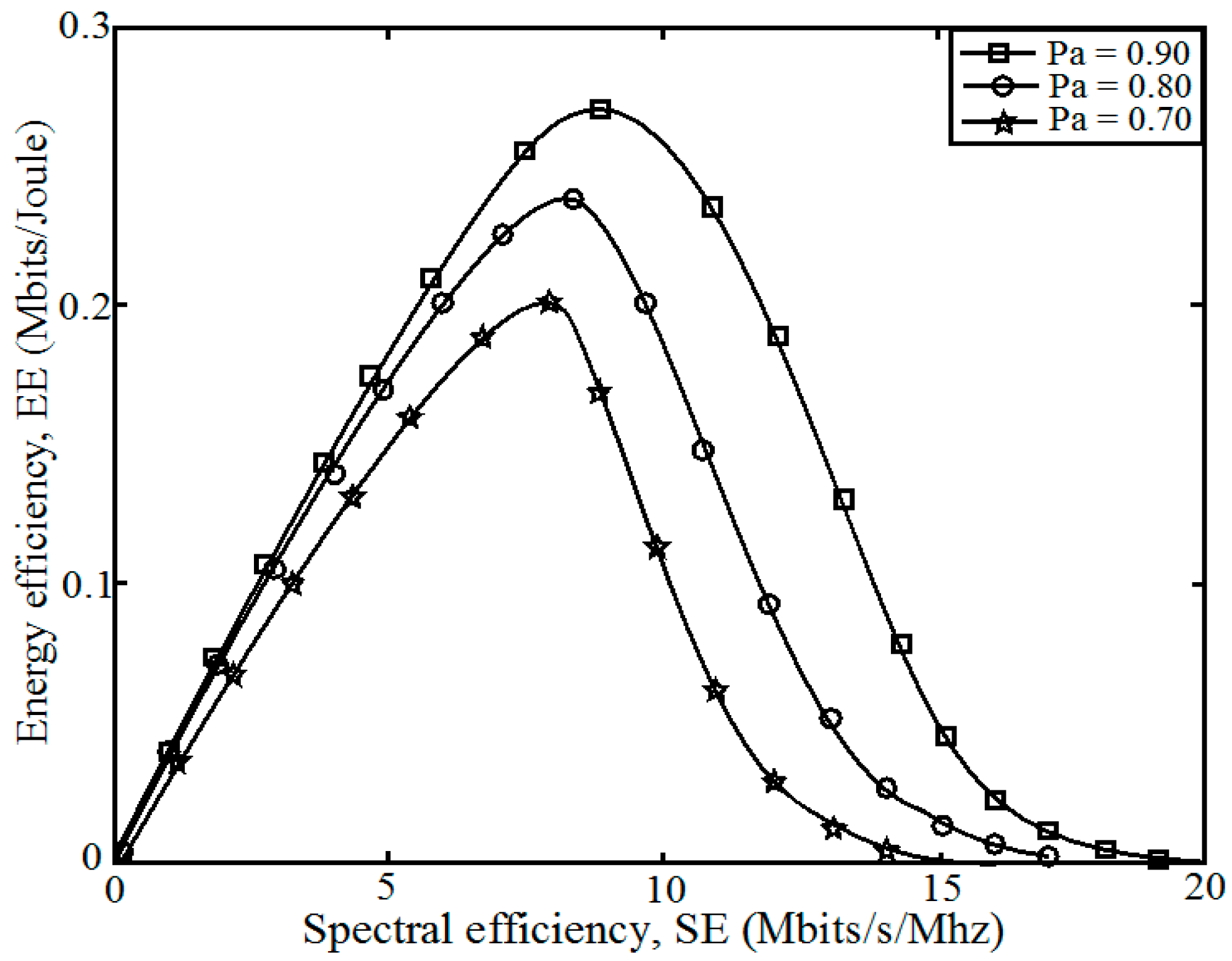
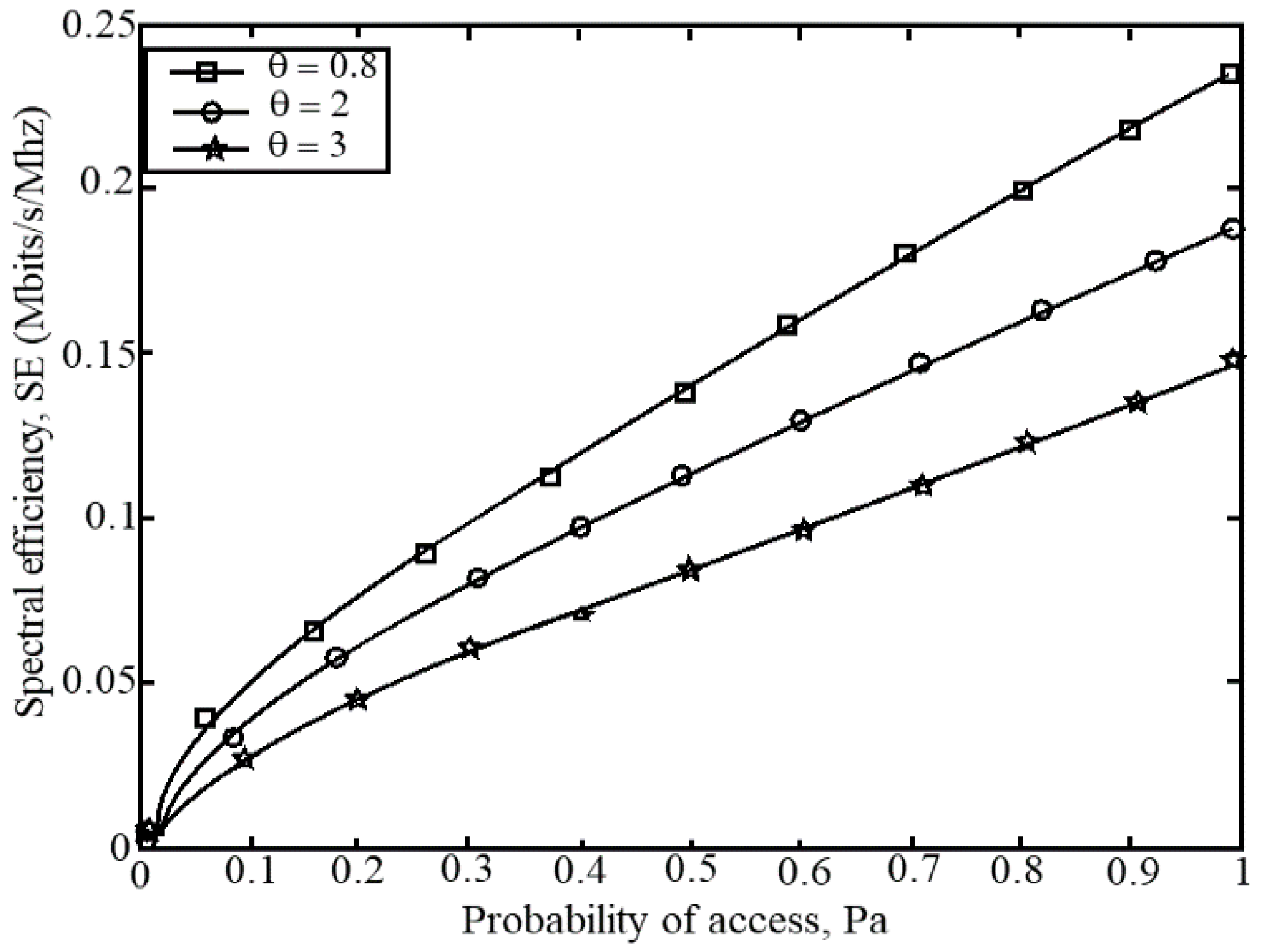
7. Simulation Results

We consider a cognitive radio network made up of several cells and by focusing on OFDMA multiplexing technique. Cognitive and primary users are randomly distributed in a cell. In every time interval, SAI, in other words, $0<\stackrel{\wedge }{S_k}\le 1,{\forall }_k\in \left[1\dots M\right]$, is evaluated through a probability ratio test. We consider the following scenarios. Firstly, equal power allocation which is the scenario in which an autonomous SBS without signaling among adjacent SBSs is considered. Thereby, the BS has no knowledge of the SAI that forces equal power allocation across all sub-channels. Secondly, perfect channel exploitation (PCE) which is considered a second reference scenario for comparison purposes. This ideal scenario is the reference, which in practice is not generally available. The PCE is a scenario in which an ideal spectrum sharing system is considered, in which spectrum detection information is accurate and a perfect interference channel state is available on the secondary system. The main objective of the PCE is to optimize the use of sub-channels. The PCE uses the underlying spectrum sharing method for underutilized sub-channels and overlapping spectrum sharing for available sub-channels. The parameters selected for the simulation are shown in the following

Table 1. Parameters selected for the simulation.

Parameter	Value
Bandwidth	124 kHz
Threshold of collision probability $(\overline{\mu })$	[0.2 to 0.7]
Inactive channel probability	0.6
Period (P)	0.01 s
Probability of false alarm (Pfa)	0.01
Probability of detection (Pd)	92%
Interference threshold selected	0.17
Maximum transmission power (Zt) related to SBS	27 dBm
Number of SUs	7
Number of subchannels	32
Channel model	Okumura-Hata

.

Figure 2 shows the comparison of the network parameters referred to as PCE with different transmission power values (Z_t = 12 dBm and Z_t = 25 dBm) and the realizable rate of the suggested system. PCE system is such that the channel is used in sub-layer mode or in overlay mode as a function of the parameter SAI. We note through the Figure 2 that the PCE gives a better exploitation of sub-channels. In addition, we find that the suggested system follows closely the perfect access to the sub-channels, in another term the PCE, with a rate somewhat lower, but a much lower overhead of signaling between the secondary systems.

We analyze optimal spectral and energy efficiency as a consolidated model for the real-time estimation of the SAI ($\stackrel{\wedge }{S}$). Such a common analysis is feasible through the proposed assignment of resources. Figure 3 presents the analysis of the spectral and energy efficiency as a function of the activity index of the primary users under different total power constraints. We notice that when $\stackrel{\wedge }{S_k},k\in \left[1\dots M\right]$ is between 0.36 and 0.46, the optimal designing of the energy efficiency and that of the spectral efficiency is carried out simultaneously. Nonetheless, when the sub-channel activity index is lower (corresponding to inactive PUs) or higher (corresponding to PUs active), it is solely one of the two parameters which can be optimized. In a classical SE and EE optimization, the compromise between SE and EE is found in function of the emission power studied in [14], or supplementing the objectives SE and EE through the weight [9]. However, in our proposed model, by squeezing or relaxing detection parameters, a smaller or larger number of channels are available to secondary users, so that $\stackrel{\wedge }{S_k}$ advances slightly towards the lower or upper range. Consequently, according to the required conditions, SE or EE are optimized by adjusting the parameters of the system without degrading the quality of service of the primary user in the system proposed.

The relationship between SE and EE in this condition is presented in Figure 4, in which the transmission power maximum Z_t is 20 dBm, the noise spectral density N₀ is −105 dBm/MHz, The power gain of the channel $h_t$ is determined on the basis of the model Okumura-Hata [37]. The power gain of the standardized channel and taking into account the distance effect is fixed at 16 dB, 12 dB, and 7 dB, we can the note in the simulation results. From Figure 4 and (13), we can note that the SE increases with EE reducing and the relationship between SE and EE seems to be contradictory. This kind of relationship proves that the system will face high costs of energy in order to improve the SE and conversely. In a scenario as easy, it is difficult to obtain an optimal tradeoff between SE and EE.

The relationship between SE and EE indicated in (17) is represented in Figure 5, in which a system of communication using the same settings as the one in Figure 4 is displayed. In our simulation, we retain 12 dB as the channel gain $h_t$ and the power of the circuit Z_c is adjusted to 25, 27 and 30 dBm. In Figure 5, we find that the optimal EE is obtained in every line i.e., the relationship between SE and EE is not contradictory in contrast to that of Figure 4 and that the optimality compromise is obtained. In short, CCRNs must cost a lot of energy in order to gain additional spectrum for transmission and the tradeoff between SE and EE is difficult and attractive.

Figure 6 presents the relationship between SE and EE in the CCRNs when the relay power is taken into account with the different relay factors. By comparing the maximum EE of $\phi =0.2$ with the other relay factor values $\phi =2$ and $\phi =2.8$, there is sensibly 25% and 38% attenuation for different SE. This is justified by the simple fact that CCRNs consume a lot of power to allow them to transmit PU data. The energy efficiency of the CCRNs for the relay factor value $\phi =0.2$ can reach sensibly 3.8 Mb/J, when the spectral efficiency value is at 4 Mb/s/Hz. It can have a tradeoff between SE and EE for CCRNs, when the relay factor is designed and determined by PU systems.

Figure 7 shows the effect of the relay factor $\phi$ through the different SE values in the CCRNs. We find that when the relay factor θ increases, the CCRNs consume a lot of energy to allow them to transmit PU data. It is important to emphasize that the numerical results presented in Figure 6 and Figure 7 are focused on the hypothesis that SE and EE only take into account the D_t transmission flow rate of CCRNs, the D_r flow rate of CCRNs relayed PU systems is not considered. The expressions (30) and (31) designate this hypothesis.

Figure 8 shows the relationship between SE and EE in the CCRNs when the detection power is taken into account with the different access probability. It is noticed that the EE increments when the access probability P_a is high. We exploit P_a to indicate the possibility of access to the selected spectral bands. It is also seen from this figure that there is a gain of 0.28 Mb/J for energy efficiency in the CCRNs when P_a increases by 8%. The SE that corresponds to the optimal EE increments sensibly to 0.99 Mb/s/MHz when the P_a is improved. At the point when the SE is under 6 Mb/s/MHz, the EE for various P_a is practically indistinguishable. This result demonstrates that an ideal compromise between SE and EE can be accomplished for different values of P_a.

Figure 9 presents the EE in the CCRNs when the detection power is taken into account at different detection factors with the access probability P_a varying from 0 to 1 when the detection time is considered to be an optimum value. It is noted that EE in the CCRNs increments when P_a also increments. This justifies that the CCRNs have the possibility of achieving a better EE when the networks proceed more spectrum. Moreover, when the detection factor $\theta$ is greater (the CCRNs consume a lot of energy during the spectrum detection), leading to the degradation of the EE. This figure further demonstrates that energy saving is possible when the detection capacity of CCRNs is improved.

Focusing on (44), the relation between the P_a and the SE with the different detection factors $\theta$ in the CCRNs is shown in Figure 10. The total power Z consumed is decided at 30 dBm. In this figure, it is noticed that CCRNs with better detection capability can get better SE. The gain of SE is approximately at 0.28 Mb/s/MHz for P_a = 0.95 and when the detection factor φ leaves from 2 to 0.8.

8. Conclusions

This paper presented the tradeoff between SE and EE for CCRNs. We propose a general scheme in order to assess the tradeoff between SE and EE. We estimate the collaborative activity index of the sub-channel in order to describe the activity of the primary users in CCRNs. Taking into account the spectral and energy efficiencies the sub-optimal power assignment in the SBS of SAI function was obtained. The proposed system was analyzed by considering the different power types used in the CCRN with practical system parameters. The theoretical analyses and simulation result sufficiently demonstrate that the relationship between SE and EE in CCRNs is not contrary, meaning that, the optimal tradeoff between SE and EE can be achieved. By making a rapprochement with a cognitive cellular network where SBSs adopts an equal power allocation strategy for sub-channels, the results of our proposed scheme indicate a significant improvement. Therefore, the method proposed in this paper offers a better tradeoff between SE and EE in CCRNs.

The future research topic will focus on spectral and energy efficiency trade-offs for a small cell in cognitive radio networks.