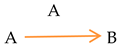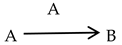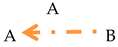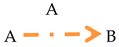2. Elements of Named Set Theory
As it is demonstrated in [
12], fundamental triads, which are also called named sets, have different types and categories. We use two names for the same structure to emphasize different properties of this structure. Calling this structure a named set, we explicate its propensity towards its inner structure. Identifying this structure as a fundamental triad, we illuminate its unity. Here we consider three primary types of named sets and fundamental triads—basic, bidirectional and cyclic fundamental triads (named sets).
Definition 1. A basic fundamental triad or a basic named set is a triad X = (X, f, N) with the following visual (graphic) representation: In this triad X = (X, f, N), components X and N are two objects and f is a correspondence (e.g., a binary relation) from X to N. With respect to X, X is called the support of X, N is called the component of names (reflector) or set of names of X, and f is called the naming correspondence (reflection) of X. Note that here, X and N are not automatically sets, while f is not necessarily a mapping or a function even if X and N are sets. For instance, X and N are sets of words and f is an algorithm.
The standard example is a basic named set (basic fundamental triad), in which
X consists of people,
N consists of their names and
f is the correspondence between people and their names. Another example is a basic named set (fundamental triad), in which
X consists of things,
N consists of their names and
f is the correspondence between things and their names [
22].
Many mathematical systems are particular cases of named sets or fundamental triads: functions, operators, variables, binary relations, vectors, vector fields, tensor fields, homomorphisms, homeomorphisms, morphism in categories [
23], graphs and hypergraphs [
24], Boolean valued sets [
25], topological and fiber bundles [
26], fuzzy sets [
27] and multisets [
28]. Moreover, any ordinary set, as a matter of fact, is some named set, and namely, a singlenamed set, i.e., such a named set in which all elements have the same name. Besides, it is demonstrated that named sets form unified foundations of mathematics comprising set theory, category theory, theory of algorithms and logic [
29].
Named set or fundamental triad is also the most fundamental structure in physics situated at the root of all other physical structures. In fact, one of the founders of quantum theory in general and quantum mechanics in particular, Werner von Heisenberg wrote that all forms of matter derive both from energy and from a simple yet profound mathematical structure because “all the other relations, which we thus know in various fields of physics as laws of nature, should derive from this unique structure” [
30].
At the same time, it is proved [
12] that all physical structures are or are formed from named sets. Taking this into account, we can conclude that all forms of matter derive both from energy and named sets. This explicates and at the same time, supports the insightful prediction of Heisenberg.
Interestingly, this role of fundamental triads or named sets in the material world and beyond is also maintained in the classical Chinese philosophy by the famous Lao Tse, who writes:
| Dao creates one; | |
| one produces two; | |
| two produces three; | |
| and three generates the whole world. | |
| Lao Tse, Tao TeChing [31] |
Knowing the role of fundamental triad in the world, we can interpret these words in the following way:
| Dao creates the whole, |
| the whole is divided into a dyad, |
| while connections between parts of the dyad form fundamental triad, |
| which is a building structural block of every thing. |
It is not incidental that the bridge between the modern quantum theory and the classical Chinese philosophy is made by mathematics in the realm of the World of Structures.
In addition, fundamental triad reflects the essence of physical measurement suggesting a solution to the problem of infinities appearing in physics. On the one hand, theoretical calculations often bring physicists to diverging series and integrals in quantum mechanics and quantum electrodynamics (cf., for example, [
32]), as well as in quantum statistics and thermodynamics (cf., for example, [
33]), in hydrodynamics, astrophysics and cosmology (cf., for example, [
34]). On the other hand, physicists never encounter infinite values in measurement and observation. A tentative explanation is that the measured value is the difference between the potential of measured physical system and the potential of measuring instrument. As the theory of hypernumbers and extrafunctions explains, it is possible that both potential are infinite while the difference is finite [
35,
36]. The structure of two potentials with the difference between them is a fundamental triad, in which the difference is the naming correspondence (reflection).
It is necessary to make a distinction between triples and triads. A
triple is any set with three elements, while a
triad is a system of three connected elements (components). It is worthy of note that mathematicians introduced the concept of a triple in an abstract category [
37]. In essence, such a triple is a triad that consists of three fundamental triads and thus is a triad of the second order [
12]. Understanding of the complex nature of the
categorical triple compelled to mathematicians to change the name of this structure and now it is always called a
monad [
38]. Interestingly, this shows connection between fundamental triads and Leibniz monads. However, in this case, a monad consists of triads and not the other way around.
Named sets (fundamental triads) play an important role in information theory because different models of information are based on the concept of operator, while an operator is a kind of a named set (fundamental triad). For instance, cognitive information is modeled by operators in knowledge spaces, which is also a named set [
39]. Moreover, the categorical approach to information theory characterizes information as a special type of morphism or functors, which are, in essence, named sets [
40].
Definition 2. A bidirectional fundamental triad or a bidirectional named set is a triad D = (X, f, Z) with the following visual (graphic) representation and in which the naming correspondence f goes in two directions: To understand the difference between basic and bidirectional named sets, let us consider set-theoretical named sets, in which the reflection
f is a binary relation [
12]. A
directed binary relation between sets
X and
Y is a set of pairs, in which the first element is for
X and the second from
Y, while an
undirected binary relation between sets
X and
Y is a set of pairs, in which either the first element is for
X and the second from
Y or the first element is for
Y and the second from
X. The same difference exists between general graphs and directed graphs [
24]. Thus, a basic named set has a directed binary relation as its reflection. In contrast to this, a bidirectional named set has an undirected binary relation as its reflection.
Often binary relations are treated as subsets of a Cartesian product of two sets. However, in their super-formalized treatise on mathematics, Boubaki define a binary relation as a set-theoretical named set. Namely, a binary relation R is defined as an ordered triple (
X,
G,
Y) where
X and
Y are arbitrary sets (or classes), and
G is a subset of the Cartesian product
X ×
Y [
41]. It means that a binary relation is a basic set-theoretical named set.
A bidirectional set-theoretical named set has a reflection, which consists of two binary relations. As one of these binary relations can be empty, any basic set-theoretical named set is a particular case of a bidirectional set-theoretical named set. At the same time, as we will see, any bidirectional set-theoretical named set can be composed of two basic set-theoretical named sets.
We have an example of a bidirectional named set when two people are exchanging messages, e.g., by e-mails, messaging or talking to one to another. In this case, X and Z are people while f and g are messages that go from one person to another.
Note that when mathematicians or computer scientists use connections without directions such as, for example, edges in general graphs or multigraphs [
24], these connections actually have both directions and are more explicitly represented by bidirectional named sets allowing a representation as the union of directed connections
h and
g.
There is one more important class of named sets.
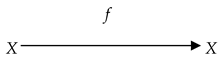
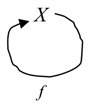
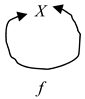
Definition 3. A cyclic fundamental triad or a cyclic named set is a fundamental triad or named set X = (X, f, X).
A cyclic named set can be basic. Then it has the following form:
The following graphic form can also describe it:
An example of a basic cyclic named set is a subatomic particle, such as an electron, which acts on itself (cf., for example, [
32]).
A cyclic named set can be also bidirectional. Then it has the following form:
The following graphic form can also describe it:
An example of a bidirectional cyclic named set is a computer network. In it, X consists of computers and f contains all connections between them.
Let us obtain some properties of named sets related to their compositions. Sequential composition of named sets is an important operation [
12]. For set-theoretical named sets, their sequential composition is defined as follows [
12]:
Definition 4. If X= (X, r, I) and Y= (Y, q, J) are named sets, then their sequential composition X∘Y is the named set X∘Y = (X, roqo, J) where ro = r ∩ (X × (I ∩ Y)) and qo = q ∩ ((I ∩ Y) × J).
Example 1. Superposition of functions is the sequential composition of the corresponding named sets in the case when I = Y.
Example 2. Composition of morphisms in categories is the sequential composition of the corresponding named sets.
Example 3. Derivation of partitions in languages is the sequential composition of the corresponding named sets [
42,
43,
44].
Example 4. Composition of binary relations is the sequential composition of the corresponding named sets.
However, sequential composition of named sets is more general than the sequential composition of binary relations because it does not demand any additional properties of the naming correspondences of the composed named sets.
The considered classes of named sets are closed with respect to sequential composition as following result states.
Proposition 1. - (a)
The sequential composition of basic named sets is a basic named set.
- (b)
The sequential composition of bidirectional named sets is a bidirectional named set.
- (c)
The sequential composition of cyclic named sets is a cyclic named set.
- (d)
The sequential composition of a cyclic named set with a bidirectional named set is a bidirectional named set.
- (e)
The sequential composition of a cyclic named set with a basic named set is a basic named set.
- (f)
The sequential composition of a bidirectional named set with a cyclic named set is a bidirectional named set.
- (g)
The sequential composition of a basic named set with a cyclic named set is a basic named set.
Corollary 1. - (a)
The class of all basic named sets is closed with respect to sequential composition.
- (b)
The class of all bidirectional named sets is closed with respect to sequential composition.
- (c)
The class of all cyclic named sets is closed with respect to sequential composition.
There are also other compositions of named sets. For instance, the parallel composition of two set-theoretical named sets is defined as follows (Burgin, 2011).
Definition 5. If X = (X, r, I) and Y = (Y, q, J) are named sets, then their parallel composition X⊕Y is Proposition 2. - (a)
The parallel composition of basic set-theoretical named sets is a basic set-theoretical named set.
- (b)
The parallel composition of bidirectional set-theoretical named sets is a set-theoretical bidirectional named set.
- (c)
The parallel composition of cyclic set-theoretical named sets is a cyclic set-theoretical named set.
In many cases, a bidirectional named set can be represented as a composition of two basic named sets. This property determines a special class of bidirectional named sets.
Definition 6. A bidirectional named set D = (X, f, Y) is called decomposable if its naming correspondence (reflection) is the inverse composition of two basic named sets.
A decomposable bidirectional named set
D = (
X,
f,
Y) is equivalent to the following diagram, which is a decomposition of Diagram (7).
Here the correspondence f = [h, g] or f = h∪g. Thus, a decomposed bidirectional named set D is denoted by D = (X, [h, g], Z) and has two components, which are basic named sets:
The direct component X = (X, f, Z)
The inverse component Y = (Z, g, X)
Proposition 3. Any set-theoretical bidirectional named set D is equal to the inverse composition of its components X and Y.
For instance, the set-theoretical bidirectional named set
with the naming correspondence (a binary relation in this case)
is decomposable the inverse composition of the direct component
Z = (
X,
h,
Z) and inverse component
Y = (
Z,
g,
X) where
and
We see that in this case, f = h∪g.
This shows how it is possible to construct bidirectional named sets using inverse composition of basic named sets [
12].
Inverse composition of basic set-theoretical named sets (
X,
f,
I) and (
Y,
g,
J) is defined as
It is possible to define inverse composition of basic set-theoretical named sets using sequential composition and involution of basic set-theoretical named sets [
12].
Definition 7. If X = (X, r, I) is a set-theoretical named set, then its involution is the named set Y= (I, r−1, X).
This concept allows better description of inverse composition.
Proposition 4. The inverse composition of basic set-theoretical named sets X and Y is equal to the sequential composition of X and the involution Y° of Y, i.e., Although any bidirectional named set is the inverse composition of basic named sets, it is a fundamental structure such as a set, graph, category, fuzzy set or multiset. In more detail, relations between basic and bidirectional named sets are studied elsewhere.
Proposition 5. The sequential composition of decomposable bidirectional named sets is a decomposable bidirectional named set.
Properties of standard named sets studied in the named set theory [
12] determine the following types (classes) of bidirectional named sets.
A bidirectional named set D = X≬Y is called:
- (a)
Left functional if X is a functional basic named set
- (b)
Right functional if Y is a functional basic named set
- (c)
Bifunctional if X and Y are functional basic named sets
- (d)
Left cofunctional if X is a cofunctional basic named set
- (e)
Right cofunctional if Y is a cofunctional basic named set
- (f)
Bicofunctional if X and Y are cofunctional basic named sets
- (g)
Functional if X is a functional basic named set and Y is a cofunctional basic named set
- (h)
Cofunctional if X is a cofunctional basic named set and Y is a functional basic named set
Properties of functions allow proving the following result.
Proposition 6. All classes of bidirectional named sets are closed with respect to sequential composition.
An important special case of inverse composition is cyclic composition of named sets.
If
X= (
X,
r,
Y) and
Y = (
Y,
q,
X) are two named sets, in which the support of
X coincides with the reflector of
Y and the support of
Y coincides with the reflector of
X, then their
cyclic composition has the form
Proposition 7. If X = (X, r, Y) and Y = (U, q, Z) are bidirectional named sets, then their cyclic composition is a bidirectional cyclic named set.
If
X= (
X,
r,
Y) and
Y = (
U,
q,
Z) are two named sets such that
U∩
Z ≠ ⊘, then their
chain composition is a named set chain, which has the form [
12]
Chain compositions of named sets are used for describing threads in communication as well as for studying compositions of information operators.
3. Interpersonal Communication
Any system has three basic levels of descriptions/models [
21]:
Static descriptions/models
Functional descriptions/models
Process descriptions/models
The latter two types are dynamic system descriptions/models. Here we develop communication modeling on all three levels starting with static descriptions/models, which represent the invariable structure of the system where communication takes place.
People understand communication either as a process of information exchange or as a result of such a process. In addition, communication can include exchange of ideas, thoughts and/or opinions. However, everything that is transmitted in communication comes through information exchange. As a result, it is natural to treat communication as a system of information transmissions, which can be organized in a sequence or go concurrently. The action of information transmission has the structure of a basic named set, in which its support and reflector have the roles of a sender and receiver.
Communication as a pure exchange of information in the form of messages has the structure presented in Diagram (9) of a decomposed bidirectional named set, in which the naming relation represents messaging.
Here each participant of communication acquires the two-folded role of a Sender/Receiver.
Note that both the Sender and Receiver can be not only human beings but also groups of human beings, societies, organizations, technical devices such as computers, birds, animals and other living beings.
Connections t, f and g between the Sender and the Receiver have three components, which compose the static structure of interpersonal communication:
- −
Communication space, e.g., a channel or a system of channels, is the medium, in which communication goes and which allows sending messages from the sender to the receiver
- −
A system of messages, e.g., one message, where a message is the object sent (transmitted)
- −
Context consists of conditions (environment) in which communication goes
Messages are carriers of information and usually have three components:
- −
The physical component, e.g., electrical signals or piece of paper with some text.
- −
The structural component, e.g., text or picture
- −
The mental component, e.g., the meaning of a text
Contexts usually have one of the following three types:
- −
Individual context
- −
Group context
- −
General context
The context determines how information is transmitted and also has three components:
- −
The physical component of the context, e.g., conditions, in which information is sent and received
- −
The structural component of the context, e.g., language of the message
- −
The mental component of the context, e.g., knowledge of the participants of communication
All these structures give us the static structure of interpersonal communication.
In addition to interpersonal communication, there is such a phenomenon as self-communication, which in essence is intrapersonal communication. Self-communication is communication self-directed in the elaboration and sending of the message, self-selected in the reception of the message, and self-defined in terms of the formation of the communication space. Self-communication is special case of intrapersonal communication.
Self-communication is represented by the following cyclic named set, in which
X is both the Sender and the Receiver.
Another important case of intrapersonal communication represented by a cyclic named set is communication in networks, such as the Internet, where each node can be both a receiver and sender. This process is also naturally modeled by a cyclic named set, in which X is the whole network.
A combination of network communication and self-communication is called mass self-communication.
Enhanced communication as an exchange of information with inclusion of information processing, which includes information organization, is the sequential composition of two cyclic and one bidirectional named sets, which is often decomposable as it is shown in the following diagram.
According to the general theory of information, information for a system R is a capacity to change an infological system IF(R) of the system R.
There are three basic forms of information organization:
Quantization by determining units of information and then measuring or counting these units
Qualification, in which information is represented in an explicit form pertinent to the problem or situation, e.g., by modeling or describing
Categorization, e.g., classification or clustering
All considered above types and schemas represented
direct communication.
Mediated communication has the structure of a chain of bidirectional named sets (fundamental triads) represented in the following diagram:
For instance, Shannon describes communication or more exactly, information transmission in technical systems as follows [
45]:
- 1
The information source (or more exactly, the message source) produces messages or parts of messages intended for a particular destination.
- 2
On the basis of the produced message, the transmitter codes the message generating a sequence of signals such that are transmitted over a channel.
- 3
The channel is a medium used to transmit signals from transmitter to receiver. During transmission the signals may be perturbed and distorted by noise coming from some source. A channel is a particular case of the communication space introduced and studied in [
46].
- 4
The receiver usually performs the reverse operation to the transmitter, reconstructing if possible the original message from the signals.
- 5
The destination is the addressee of the message and can be either a person or a thing. It requires a priori knowledge about the information source that enables it to understand the message transmitted. In particular, the destination must know the set of signs available to the information source.
This description of a static communication structure is represented by the following chain of basic named sets (fundamental triads):
A more developed model includes a communication space and has the following structure on the first level of detailization [
46].
All components of this model have multidimensional structure formed by different components.
Information Sender includes (combines) information source, coder and transmitter.
Information Receiver includes (combines) information destination, decoder and receptor/receiver.
Communication Space has three components:
The technical component, which includes the channel of communication
The linguistic component, which includes the messages of communication
The context component, which represents the environment of communication
In turn, the linguistic component also has three dimensions:
syntactic dimension
semantic dimension
pragmatic dimension
The context component too has three dimensions:
physical component
mental component
structural component
The technical component can contain several components, for example, when the channel of communication is the Internet. Components can be positive, such as routers and servers, or negative, such as interceptors and disruptors.
A subjective perspective on communication reflects comprehension of an individual participant. To explicate the functional (goal) structure of communication, we categorize goals and functions of communication and use fundamental triads (named sets) to represent them in an explicit visual form.
Analyzing communication, we can see that in general case, it has not only informative goals and functions. Thus, goals and functions of communication are naturally divided into three groups:
For instance, the primary goal in an interview is informative. In a public speech of a politician, the primary goal is impact. When a painter communicates with other people through his or her paintings, the primary goal is expressive.
There are following instances of informative goals/functions in communication:
Getting information
Giving information
Information exchange
For instance, the primary goal of a writer is giving information to other people. A journalist at first has the goal of getting interesting information and then the goal of giving this information to other people. Negotiations, as a rule include exchange of information.
Analyzing informative goals and functions, it is necessary to take into account existence of three types of information [
21]:
Cognitive information
Affective information
Effective information
Sometimes people give cognitive information to get affective (emotional) or effective (instructional) information. For instance, when a person coming to a new city informs that she is lost to somebody, this person tries to instructional information where to go.
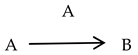
Getting information is structurally represented by the following basic fundamental triad labeled by the name of the focal participant A:
Giving information is structurally represented by the following basic fundamental triad labeled by the name of the focal participant A:
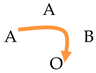
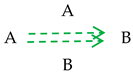
Information exchange is structurally represented by the following bidirectional fundamental triad labeled by the name of the focal participant A:
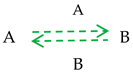
For instance, interviewing is communication, in which one participant, say A, is only giving information while the other participant, say B, is only receiving information. It is represented by the following diagram
A communication monitoring system can display the information diagram of the interview. When instead of Diagram (12), the interviewer B sees Diagram (13), which indicates that she does not receive information, the interviewer knows that it is necessary to change something in the interview to make it efficient.
Intensity is an important parameter of communication and is represented by the thickness of the corresponding diagram:
![Information 09 00283 i019]()
displays (informs about) high intensity of the process
![Information 09 00283 i020]()
displays (informs about) moderate intensity of the process
![Information 09 00283 i021]()
displays (informs about) low intensity of the process
Note that intensity of communication can change in the process and it is possible to express this change in the diagram of communication.
Modality is an important characteristic of communication goals and functions and is represented by the color of the corresponding diagram:
![Information 09 00283 i022]()
displays (informs about) a positive process
![Information 09 00283 i023]()
displays (informs about) a neutral process
![Information 09 00283 i024]()
displays (informs about) a negative process
There are following instances of impact goals/functions:
Influence on the other participant of communication is represented by the following basic fundamental triad labeled by the name of the focal participant A:
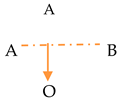
Self-influence is represented by the following cyclic fundamental triad labeled by the name of the focal participant A:
Influence on others outside communication is represented by the following basic fundamental triad labeled by the name of the focal participant A:
For instance, persuasion is communication, in which one participant, say A, is trying to influence the other participant, say B. When it is represented by Diagram (14), the process goes in a positive way.
At the same time, Diagram (15) shows that the goal is not achieved, while Diagram (16) indicates that the process is negative and instead of persuasion A dissuades B.
There are following instances of expressive goals/functions:
Understanding another participant of communication, i.e., comprehension of what the other participant wishes to express
Self-expression
Understanding the context of communication as expression of the environment
Here understanding means getting expression of another participant of communication, i.e., what this participant tries to express in the communication, or of the context of communication. For instance, writers and artists try to express themselves in their communication through their creations. Note that communication can be not verbal but for example, by means of a painting.
Understanding of another participant of communication is represented by the following basic fundamental triad labeled by the name of the focal participant A:
Self-expression is represented by the following basic fundamental triad labeled by the name of the focal participant A:
Understanding of the context of communication is represented by the following basic fundamental triad labeled by the name of the focal participant A:
Process description/model f communication represents the flow of messages, changes of goals and functions of participates and interaction of communication system with its environment. Taking into account different features of communication processes, researchers decide on formation of communication typology.
In a sequential communication, all messages are linearly ordered in time and transmission of each of them does not intersect in time with transmission of another one.
There are different types of messages in communication:
- −
The starting message m0 is the first message in communication.
- −
The concluding message mf is the last message in communication.
- −
A feedback message is an outcoming message caused by some incoming message.
- −
A direct feedback message is an outcoming message caused by the previous incoming message.
- −
An initializing message is a message that is not a feedback message.
There are three types of feedback messages:
- −
A causal feedback message to a message m is a message caused by m
- −
A topical feedback message to a message m is a message, which has the same topic as m and is caused by m
- −
A semantic or meaningful feedback message to a message m is a message, which is caused by m and the meaning of which is directly related to the meaning of m
Let us informally determine structural components of communication, which is understood as exchange of information between systems via sending messages.
Definition 8. A set of interrelated messages in communication is called a communication instance.
Messages allow delineation of characteristic structures in communication.
Definition 9. Communication thread L consists of an initializing message called the root of L and a sequence of direct feedback messages, in which the first message is the feedback to the initializing message and each next message is the direct feedback to the preceding message.
However, it might be useful to skip some direct feedbacks when communication threads are elucidated and analyzed. This brings us to the concept of a communication leaping thread.
Definition 10. Communication leaping thread H consists of an initializing message called the root of H and a sequence of feedback messages, in which the first message is the feedback to the initializing message and each next message is the feedback to the preceding message but not necessarily direct feedback.
Note that a communication thread is also a communication leaping thread.
The types of feedback messages determine types of communication threads giving three pure and four mixed communication threads.
Pure communication threads are divided into the following classes:
- −
Causal communication threads or cc-threads, which consist of causal feedback messages
- −
Topical communication threads or tc-threads, which consist of topical feedback messages
- −
Semantic communication threads or sc-threads, which consist of semantic feedback messages
Mixed communication threads are divided into the following classes:
- −
ctc-threads, which consist of causal and topical feedback messages
- −
csc-threads, which consist of causal and semantic feedback messages
- −
st-threads, which consist of semantic and topical feedback messages
- −
ctsc-threads, which consist of causal, topical and semantic feedback messages
Threads are used to form communication structures of higher order. One of these structures unite threads with the common origin.
Definition 11. Communication multithread is the union of communication threads with a common root.
When we also employ leaping communication threads, we come to the concept of a communication leaping multithread.
Definition 12. Communication leaping multithread is the union of communication threads, which have a common root and some of them can be leaping.
Note that a communication thread is also a communication multithread and a communication multithread is also a communication leaping multithread.
Another of dynamic structure unites arbitrary threads.
Definition 13. Communication hyperthread is the union of arbitrary communication threads.
When we also employ leaping communication threads, we come to the concept of a communication leaping hyperthread.
Definition 14. Communication leaping hyperthread is the union of arbitrary communication threads, some of which can be leaping.
This gives us different types of communication.
- −
Communication is linear if it consists of a single communication thread.
- −
Communication is branching if it contains, at least, one communication multithread.
- −
The most general is concurrent communication, which can be represented as a hyperthread.
Two communication threads are disjoint if each of them does not have a feedback message to a message from another one.
Communication is disjoint if it consists of disjoint communication threads.
Explication of structural peculiarities of communication is aimed at better organization of interpersonal communication in both human society and networks of artificial devices such as cell phone networks or the Internet. Computation and especially networking have been intensively studied as systems of communicating processes (cf., for example, [
47,
48,
49,
50,
51,
52]). Description of structural characteristics of such communication helps improving organization and increasing efficiency of these processes.
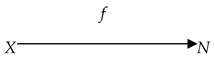
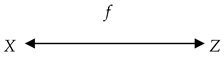

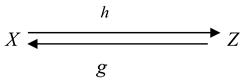
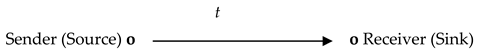
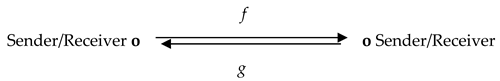
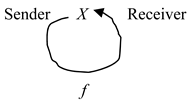

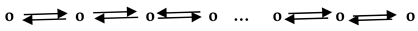




displays (informs about) high intensity of the process
displays (informs about) moderate intensity of the process
displays (informs about) low intensity of the process
displays (informs about) a positive process
displays (informs about) a neutral process
displays (informs about) a negative process