A Theory of Physically Embodied and Causally Effective Agency

Abstract

Causality is fundamental to agency. Intelligent agents learn about causal relationships by interacting with their environments and use their causal knowledge to choose actions intended to bring about desired outcomes. This paper considers a causal question that is central to the very meaning of agency, that of how a physically embodied agent effects intentional action in the world. The prevailing assumption is that both biological and computer agents are automatons whose decisions are determined by the physical processes operating in their information processing apparatus. As an alternative hypothesis, this paper presents a mathematical model of causally efficacious agency. The model is based on Stapp’s theory of efficacious choice in physically embodied agents. Stapp’s theory builds on a realistic interpretation of von Neumann’s mathematical formalization of quantum theory. Because it is consistent with the well-established precepts of quantum theory, Stapp’s theory has been dismissed as metaphysical and unfalsifiable. However, if taken seriously as a model of efficacious choice in biological agents, the theory does have empirically testable implications. This paper formulates Stapp’s theory as an interventionist causal theory in which interventions are ascribed to agents and can have macroscopically distinguishable effects in the world. Empirically testable implications of the theory are discussed and a path toward scientific evaluation is proposed. Implications for artificial intelligence are considered.

1. Introduction

A defining feature of intelligence is the ability to use knowledge of causal relationships to choose actions intended to bring about desirable results. Accompanying the impressive successes of model-free learning methods is a growing concern about their inherent limitations [1,2]. The inability to distinguish correlation from causation, itself listed in [2] as a fundamental limitation of purely associational learning, also contributes to other limitations, including poor generalizability to environments that differ from the training data, inability to explain results, lack of adaptability to a changing world, and susceptibility to being spoofed. Endowing computer agents with causal reasoning capability can, it is argued, address many limitations of associational learning approaches [3].

Automating causal reasoning requires formal language and mathematical models to represent and reason about causal relationships and to distinguish causation from statistical association. Until recently, science lacked such a formal framework. Students were exhorted against confusing correlation with causation, but were provided no tools beyond unaided intuition for the causal judgments required to use statistics to make causal inferences. In the past few decades, a sea change has occurred. Powerful new theories, models, and tools have emerged for reasoning about causality and learning causal relationships [4,5,6]. Artificial intelligence has both inspired and benefited from this causal revolution. Many applications of probabilistic causal models have appeared in the literature (e.g., [7,8,9]). Researchers and practitioners in a variety of fields have embraced new methods and tools for addressing causal questions. As stated by Peterson and van der Laan [10], “A formal causal framework can help in designing a statistical analysis that comes as close as possible to answering the motivating causal question, while making clear what assumptions are required to endow the resulting estimates with a causal interpretation.” Pearl and Mackenzie [11] posit causal reasoning capability as a necessary enabler to endow computers with human-level intelligence.

This paper focuses on a different but related causal question, that of what it means for a physically embodied agent to choose an action and cause it to be effected. Russell and Norvig [12] define an agent as “anything that can be viewed as perceiving its environment through sensors and acting on that environment through actuators” (italics in original). They cite humans, robots, and software agents as examples of agents. Even a device as simple as a thermostat is an agent by this definition, because it can sense the room temperature and use the sensor reading to control the heating and cooling system. Increasingly, artificial agents are being developed that approach or exceed human performance on certain narrowly defined tasks. Robotic agents can do hazardous or monotonous manufacturing work, perform household chores, provide household assistance for the ill or elderly, and drive autonomous vehicles [13]. Computer agents have beaten human experts at tasks like chess and recognizing and sorting images [14,15].

Our choice of language often reflects a view of agency akin to this definition. We might say a credit-scoring system “decided” to reject a given applicant, that an image understanding system “decided” that a given object was a tree, or that a robot “chose” to take a given route to its destination. This way of speaking is useful as a cognitive-level description of behavior we know is implemented at the micro level as a computer program. Similarly, treating mental processes as cognitive-level descriptions of complex underlying brain processes has proven useful to neuroscience and psychology. Neuroscientists have identified neural correlates of a wide range of mental and behavioral phenomena. Psychologists have formulated and validated cognitive-level theories of mental processes expressed as computer programs. These insights have led to advances in fields such as medicine, education, and decision support systems.

Alongside the unquestioned successes of these computational theories of agency is an unshakeable feeling that our own choices are not pre-programmed. We have a strong sense that there are multiple alternatives open to us, each leading to different outcomes in the world. After we have made a choice, we have the definite impression that it would have been possible to have chosen differently, and if we had, the world would have been different. Although our human-engineered agents are designed as automatons, we do not experience ourselves as automatons.

What is the reality behind this experience? Do we really have different physically possible options open to us? Is there truth to our sense that we could have chosen other than we did? The mainstream view in artificial intelligence, and in science as a whole, is that the answer is no. The history of science is replete with examples in which strong intuitions turned out to be wrong. Mainstream science views our thoughts and behavior as manifestations of the operation of the laws of physics in our brains and bodies. As with the computer program that decides to accept a credit applicant, the mainstream view is that our feeling of having multiple allowable choices is a high-level encoding of complex, low-level electrochemical processes unfolding according to effectively deterministic laws of physics. Pearl and Mackenzie suggest that this “illusion of free will” gives evolutionary advantage through the ability to encode complex causal relationships compactly and to support efficient learning. As an example, they explain a coach’s admonishment, “You should have passed the ball to Charlie,” as a shorthand for conveying a set of complex instructions for reweighting priorities among different goals and reassessing predictions “so that ‘pass to Charlie’ becomes the preferred action.” Such a compact encoding gives social agents survival advantage: “No matter how technically proficient the individual robots are their team’s performance will improve if they can speak to each other as if they are not preprogrammed robots but autonomous agents believing they have options” ([11], p. 365–366).

In addition to facilitating efficient communication, believing we have free will may be important in fostering socially adaptive behavior. Studies have found a positive correlation between belief in free will and pro-social and ethical attitudes and behaviors [16,17]. The association between free will and moral judgment appears to be robust across different cultures and societies, although moderated by variation in countries’ institutional integrity [17]. Experimental manipulations that decrease belief in free have been found to cause increases in anti-social and unethical behavior (see [16] for a review). Although a recent series of studies failed to find a statistically significant effect of general abstract belief in free will on judgments of moral responsibility, they did find a strong effect of perceived choice capacity [18]. This finding is consistent with studies of the lay concept of free will [19,20], which suggest that people define free will in terms of the ability to make reasoned choices in absence of or in spite of external constraints. Although more research is needed to unpack the influence of different factors surrounding free will, the literature suggests the possibility of negative social consequences if belief that free will is an illusion becomes widespread in the general public.

Most discussion of free will in scientific circles takes as a given that human behavior is entirely generated by biological and chemical processes in the brain. Arguments center on whether free will and moral responsibility can be reconciled with the notion that our behavior is a deterministic function of the prior state of our bodies and the inputs from our environment. Incompatibilists view free will and moral responsibility as inconsistent with a mechanistic model of behavior. Compatibilists say any perceived conflict is only apparent, and is due to conflating different levels of description. Social scientists worry that popularizing neurobiological models of behavior will undermine society’s belief in free will, resulting in socially undesirable consequences. In these debates, the fundamental assumption of mechanistic reductionism is rarely questioned.

This paper presents an alternative to the mechanistic reductionism presupposed by most mainstream scientists. The theory of efficacious free choice proposed by Stapp [21,22,23] has its theoretical basis in a realistic interpretation of von Neumann’s [24] orthodox formulation of quantum theory. Stapp’s theory is formalized as an interventionist causal theory in which interventions are ascribed to agents. Causal Markov processes are introduced as a mathematical model of agents’ choices and their effects on the physical world. Agents are modeled as causal Markov processes in which states are density operators and agents take action by initiating quantum state reductions. These choices influence the macroscopic world by exploiting a phenomenon called the quantum Zeno effect (QZE), in which a rapid sequence of reductions can affect the macroscopic behavior of a quantum system. Stapp has shown that QZE can have macroscopically distinguishable effects at energies and physical dimensions consistent with human brains ([23], Appendix F). Stapp argues that his theory of efficacious free choice in physically embodied agents provides a scientifically well-founded alternative to the mechanistic model of human decision-making most scientists take as given.

Because the predictions of Stapp’s theory are entirely consistent with orthodox quantum theory, it has been dismissed as metaphysical and not susceptible to scientific inquiry. This paper argues the contrary, that it can indeed generate empirically testable predictions. Furthermore, evidence in its favor would have far-reaching implications for theories of agency and the future of artificial intelligence. If biological agents actually do make choices that are free in a way that those of computer programs are not, then today’s AI systems are in an important sense only simulations of intelligence. If so, achieving true engineered intelligence would hinge on developing a fundamental, physically grounded theory of the kinds of systems that are capable of making their own choices. Just as banishing causality from formal scientific discourse has until recently hindered progress in science, the lack of a language and mathematical tools for discussing physically embodied agency may be hindering progress in artificial intelligence and cognitive science. If Stapp is correct, then developing such a theory and operationalizing it as an engineering discipline could make the difference between simulated and true engineered intelligence.

Whether Stapp’s theory of agency proves correct or turns out to be a scientific dead end, its profound implications argue for taking it seriously enough to devise and conduct tests of its plausibility. The remainder of this paper presents Stapp’s theory of efficacious choice, sketches a path to evaluating it scientifically, and discusses its implications for artificial intelligence.

2. Background

This section introduces notation, theory, and background that will be useful in the remainder of the paper. Section 2.1 introduces structural causal models, a formal mathematical theory for representing and reasoning about cause and effect relationships. Section 2.2 introduces the causal Markov process, a mathematical structure for representing dynamically evolving systems whose state transition is influenced by an exogenous control. Section 2.3 gives a brief introduction to the basic mathematical formulation of quantum theory.

2.1. Structural Causal Models

A causal model represents more than just associations between variables. As Pearl and Verma [25] put it:

Causal claims are much bolder than those made by probability statements; not only do they summarize relationships that hold [in the data generating process], but they also predict relationships that should hold when the [process] undergoes changes a stable dependence between X and Y that cannot be attributed to some prior cause common to both [and is] preserved when an exogenous control is applied to X.

Until recently, researchers and scientists lacked the formal mathematical foundation to address causal questions with the same degree of rigor as questions of statistical associations. Over the past several decades, a unifying mathematical formalism has been developed to fill this gap. Pearl defines a structural causal model as follows [4]:

Definition 1.

A structural causal model (SCM) is a tuple $M=\langle U, V, E, P\rangle$, where $U$ is a set of exogenous variables determined from outside the model, $V$ is a set of endogenous variables whose values are determined by the model, $E$ is a set of structural equations that determine the value of each variable in $V$ as a function of values of other variables in $U$ and $V$, and $P$ is a joint probability distribution over the variables in $U$.

The equations in a SCM are assumed to be deterministic, so the joint probability distribution $P$ over the exogenous variables $U$ induces a joint probability distribution over all the variables in the model. This distribution represents undisturbed evolution of the system. Interventions are represented by the do-operator. An intervention to set an endogenous variable $X$ to a specific value x, denoted by $do\left(X=x\right)$, is accomplished by modifying $E$ to remove the equation that specifies $X$ as a function of the other variables in the model, setting $X$ directly to the value $x$. The resulting model, denoted $M_{X=x}$, represents a local intervention that sets $X$ equal to x without disturbing any of the other causal relationships in the model. In particular, any variables influenced by $X$ will use the value x in their defining equations, while the equations relating the other variables remain undisturbed.

Structural causal models provide a formal mathematical framework for answering queries about causal relationships. Pearl and Mackenzie [11] distinguish three levels of causal query: queries about association between variables in the unperturbed model, queries about the effects of interventions, and counterfactual queries. Associational queries do not distinguish between causal associations (e.g., smoking and cancer are associated because smoking causes cancer) or spurious associations (e.g., deaths by drowning and ice cream sales are not causally related, but vary together because both increase with temperature increases). Queries about the effects of interventions capture causal relationships (e.g., intervening to decrease smoking will reduce the incidence of cancer, but intervening to reduce drowning deaths will not affect ice cream sales). Counterfactual queries allow inferences about what would have happened had the world been different (e.g., would George still be alive had he not been a smoker?). Structural causal models provide a mathematical framework for determining which queries can be answered given available information, together with methods for answering those queries the model is capable of answering [4].

2.2. Causal Markov Processes

Causal Markov processes generalize stochastic processes to allow event probabilities to depend not only on past events, but also on an exogenous control. For the purpose of this paper, the exogenous control represents choices made by agents. These choices have causal influence in the sense of Pearl [4]. A causal Markov process is a family of stochastic processes on a given state space, indexed by a set of allowable actions. Any deterministic or stochastic rule for choosing actions gives rise to one of the processes in the family.

Definition 2.

A (time-invariant, first-order, discrete) causal Markov process is a family of stochastic processes specified by the 3-tuple (S, A, π), where S is a state space, A is an action space, and π is a transition distribution, such that the following conditions are satisfied:

• For each s, s’ ∈ S and a ∈ A, the function π (· | s’; a) is a discrete probability measure on S.
• Given an initial state $s_0$ and conditional distributions $\theta \left(a_k|h_{k-1}\right), k=1,\dots ,n$ for selecting actions conditional on the past history $h_k=\left(a_1,a_2,\dots ,a_{k-1},s_0,s_1,s_2,\dots ,s_{k-1}\right)$ of actions and states, the joint distribution for the sequence $\left(a_1,a_2,\dots ,a_n,s_1,s_2,\dots ,s_n\right)$ of actions and states satisfies:

  $$\mathrm{P}(a_1,a_2,\dots ,a_n,s_1,s_2,\dots ,s_n|s_0)={\displaystyle \prod _{k=1}^n}\theta \left(a_k|h_k\right)\pi \left(s_k|s_{k-1},a_k\right).$$

  (1)

Equation (1) is called the causal Markov condition. For a given action distribution, system states evolve in a way that depends on the past history only through the most recent past state and the current action. If a system is evolving according to (1), an intervention $do\left(a_k=a^{*}\right)$ corresponds to replacing the distribution $\theta \left(a_k|h_k\right)$ with the distribution $1_{\left[a_k=a^{*}\right]}$ that assigns probability 1 to the state $a^{*}$. Such an intervention satisfies a locality condition: the joint distribution for the first k-1 states remains unchanged, and the conditional distribution for future states given the chosen action $a^{*}$ also remains unchanged. That is, an intervention to replace $\theta \left(a_k|h_{k-1}\right)$ with $1_{\left[a_k=a^{*}\right]}$ changes the joint distribution to:

$$\mathrm{P}(a_1,a_2,\dots ,a_{n-1},s_1,s_2,\dots ,s_{n-1})=\pi (s_k|s_{k-1},a^{*})1_{[a_k=a^{*}]}{\displaystyle \prod _{j\ne \mathrm{k}}^n}\theta (a_j|h_j,)\pi (s_j|s_{j-1},a_j).$$

(2)

As described in Section 2.1, the intervention $do\left(a_k=a^{*}\right)$ disconnects $a_k$ from the past history, sets $a_k$ equal to $a^{*}$, and leaves all other causal mechanisms unchanged [4]. Therefore, the evolution of the system is affected only by changing the likelihood of the kth action from $\theta \left(a_k|h_k\right)$ to $1_{\left[a_k=a^{*}\right]}$, the distribution placing probability 1 on $a_k=a^{*}$.

Causal Markov processes are widely applied as models of temporally evolving systems. Augmenting a causal Markov process with a reward $r\left(s_{k-1},s_k\right)$ for the transition from $s_{k-1}$ to $s_k$ results in a Markov decision process [26]. Markov decision processes are a common representation for problems of decision-making over time in uncertain environments. A mapping $\theta \left(a_k|s_{k-1}\right)$ from the most recent state $s_{k-1}$ to a probability distribution on the next action $a_k$ is called a policy. A decision-making agent seeks a policy that maximizes the discounted sequence ${\sum }_k{\delta }^{k}r\left(s_{k-1},s_k\right)$ of rewards, where $0<\delta <1$ is a discount factor. In problems of any complexity, finding an optimal policy is generally intractable. Approximating solutions to Markov decision problems is an active area of research. Some of the most exciting success stories of artificial intelligence have employed Markov decision processes.

2.3. Quantum Theory Basics

Early in the twentieth century, classical physics was overturned by a new fundamental physical theory. Quantum theory differs in several important respects from its classical predecessor. First, quantum theory replaces the determinism of classical physics with an intrinsically stochastic element. Quantum theory can make only probabilistic predictions of the outcomes of measurements taken on a system. Second, the theory is non-local. Measurements taken at different spacelike separated locations may be correlated in a manner that cannot be accounted for by hidden variable theories. Third, measurements on a quantum system are in general non-commutative. That is, different results are obtained depending on the order in which measurements are taken. Thus, measuring a quantum system cannot be treated as observing and recording pre-existing facts; rather, the facts come into being with the measurement. Finally, quantum theory is dynamically incomplete in that the theory specifies a probability distribution for the outcome of a measurement conditional on the time of measurement and the type of event being measured, but does not specify when measurements occur or what is measured. The empirical predictions of quantum theory have been verified to exceptional accuracy, but its drastic departures from the previously accepted picture of the physical world has caused consternation among scientists and philosophers, and has generated controversy over how the theory should be interpreted.

The formal mathematical foundation for quantum theory was developed by von Neumann [24] in the 1930s. While the interpretation of the mathematics remains controversial, von Neumann’s formalism remains the standard textbook presentation of quantum theory (e.g., [27,28]).

With each quantum system is associated a characteristic Hilbert space $\mathcal{H}$. A Hilbert space is a complex inner product space that is complete with respect to the norm induced by the inner product. In addition to their fundamental role in quantum theory, Hilbert spaces are important in many areas of mathematics, physics, and information theory.

A quantum state can be represented by a vector in $\mathcal{H}$ (called a ket), or equivalently, by a density operator on $\mathcal{H}$. This paper adopts the density operator representation because it is more natural when treating open systems such as occur in biological systems. Commonly denoted by the Greek letter $\rho ,$ a density operator on a $\mathcal{H}$ is a self-adjoint, positive semidefinite operator with unit trace, i.e., $Tr\left(\rho \right)=1$. Density operators of rank 1 are in one-to-one correspondence with kets, and represent pure states, or states that are known exactly. Density operators of rank greater than 1 represent statistical ensembles of pure states and/or subsystems of a composite quantum system. The advantage of the density operator formalism is its ability to represent statistical ensembles and subsystems in the same notation as pure states.

In the von Neumann formalization, a quantum system undergoes two distinct kinds of evolution. The first is deterministic mechanical evolution in the absence of interventions. The second is an instantaneous, discontinuous, stochastic transformation to one of a set of possible states.

Mechanical evolution is represented mathematically by the action of a completely positive trace-preserving (CPTP) map on $\mathcal{H}$ [27].

Definition 3.

A completely positive trace-preserving (CPTP) map $\mathcal{A}$ satisfies the following properties:

• Tr($\mathcal{A}\rho$) = Tr(ρ);
• $\mathcal{A}\rho$ is a positive operator; and
• If τ is a density operator on the tensor product space $\mathcal{H}\otimes \mathcal{G}$ and $I_{\mathcal{G}}$ is the identity operator on $\mathcal{G}$, then ($\mathcal{A}\otimes I_{\mathcal{G}}$)τ is also a positive operator.

Evolution for d units of time, represented by the CPTP map ${\mathcal{A}}_d$, transforms the state $\rho$ to the state ${\mathcal{A}}_d\rho$. Evolution is continuous in time, and ${\mathcal{A}}_0=\underset{d\to 0}{\lim }{\mathcal{A}}_d$ = $I_{\mathcal{H}}$. Further, if evolution is time-invariant, then ${\mathcal{A}}_{d_1+d_2}\rho ={\mathcal{A}}_{d_1}{\mathcal{A}}_{d_2}$.

An important special case is a unitary transformation ${\mathcal{A}}_d\rho =\exp \left\{-\frac{iHd}{\hslash }\right\}\rho \exp \left\{\frac{iHd}{\hslash }\right\}$, where H is a self-adjoint operator known as the Hamiltonian, and $\hslash$ is Planck’s constant divided by 2π. A quantum system evolving in isolation from its environment undergoes a unitary transformation. Evolution of a non-isolated quantum system can be represented as the action of a unitary operator on a larger system consisting of the system coupled to its environment. In this case, it can be shown that the subsystem considered alone transforms according to a CPTP map [27]. The general case of mechanical evolution of a quantum system can thus be represented as unitary evolution of a supersystem consisting of the system coupled to its environment.

The second type of evolution of a quantum system is a stochastic transition called reduction, projective measurement or collapse. The state $\rho$ instantaneously transforms to one of a set of mutually orthogonal post-reduction states. Mathematically, reduction is represented by application of a reduction operator. The set of allowable reduction operators forms a mathematical structure called a von Neumann algebra [29]. Von Neumann algebras have broad applicability in mathematics, the physical sciences, information theory, and engineering (e.g., [27,30]).

Definition 4.

A von Neumann algebra is a self-adjoint algebra of bounded operators on $\mathcal{H}$ that is closed with respect to the weak operator topology.

When a reduction operator R is applied to a state $\rho$, the state instantaneously transforms to one of the possible post-reduction states. The possible post-reduction states and their probabilities are determined as follows. The spectral decomposition theorem implies that $R$ can be decomposed as the sum $R={\sum }_{r}r{P}_r$, where the r are numbers and the $P_r$ are mutually orthogonal projection operators summing to the identity, i.e.,

• $P_r^2=P_r$ for each r;
• $P_r{P}_s=0$ for r ≠ s; and
• ${\sum }_r{P}_r=I_{\mathcal{H}}$.

Because R is self-adjoint, the values r, called eigenvalues, are all real. Each eigenvalue r corresponds to a possible value of some observable associated with the quantum system (e.g., position, momentum, spin, etc.), and reduction corresponds to measuring the observable. The probability of observing the value r is $q_r=Tr\left(P_r\rho P_r\right)$. If the value r is observed, the state changes suddenly and discontinuously to the density operator $\frac{1}{q_r}{P}_r\rho P_r$. The rule for calculating the probability is called the Born rule. It is straightforward to show that the probabilities for the different values of r sum to 1. It is also straightforward to show that if reduction operator $R$ is applied, outcome $\frac{1}{q_r}{P}_r\rho P_r$ occurs, and the operator $R$ is applied again immediately afterward, the outcome will again be $\frac{1}{q_r}{P}_r\rho P_r$ with probability 1. This is an immediate consequence of the property $P_r^2=P_r$ of projection operators.

Because von Neumann algebras are in general non-commutative, the result of applying reduction operator $R$ followed by $S$ may be different from first applying $S$ and then $R$. In this case, it is said that the operators R and S do not commute. There is a fundamental limit in the precision to which observations from two non-commuting operators can be simultaneously predicted. In particular, the Heisenberg uncertainty principle implies that if the observed value from applying R to state $\rho$ can be predicted very precisely, then the observed value from applying S state $\rho$ must be highly imprecise. Mathematically, this is expressed as an inequality bounding the product of the standard deviations of observations from non-commuting operators strictly away from zero.

To summarize, a quantum system changes in time according to two distinct processes:

• Mechanical evolution (von Neumann’s Process 2): A state $\rho$ evolving mechanically for d time units transforms to ${\mathcal{A}}_d\rho$, where ${\mathcal{A}}_d$ is a CPTP map satisfying ${\mathcal{A}}_0\rho =\rho$ and, in the case of time-invariant evolution, ${\mathcal{A}}_{d_1+d_2}\rho ={\mathcal{A}}_{d_1}{\mathcal{A}}_{d_2}\rho$.
• Reduction (von Neumann’s Process 1): The state $\rho$ undergoes an instantaneous and discontinuous transformation to $\frac{1}{q_r}{P}_r\rho P_r$, where r is one of the eigenvalues of the reduction operator $R$, and $P_r$ is the associated projection operator in the spectral decomposition, and $q_r=Tr\left(P_r\rho P_r\right)$ is the probability of the outcome associated with eigenvalue r. The allowable reduction operators form a von Neumann algebra.

Quantum theory provides a precise mathematical rule for the result ${\mathcal{A}}_d\rho$ of mechanical evolution, and a precise rule for calculating the probabilities $q_r$ for the outcomes $\frac{1}{q_r}{P}_r\rho P_r$ from applying the reduction operator $\mathcal{R}$. However, there is no theory for when reductions will occur or which reduction operator will be applied. This fundamental gap in quantum theory has generated intense debate over the ontological status of reductions. The many-worlds interpretation asserts that there are no reductions. Each outcome actually occurs in its own world with its own observers. The question of why we observe only one outcome in our world has not been answered satisfactorily. Realistic interpretations assert that reductions do occur. There are different proposals for filling the explanatory gap for how and when reductions occur, none of which has gained broad acceptance or achieved empirical confirmation. The Copenhagen interpretation eschews ontological claims, focusing instead on pragmatic rules for predicting the outcome of experiments. This paper focuses on one specific realistic interpretation, due to Stapp [22,23]. Stapp argues that his interpretation provides an opening for a theory of agents possessing efficacious free will. While acknowledged to be provisional, the theory is consistent with the well validated precepts and rules of quantum theory. Further, as discussed in Section 4 below, recent advances in neuroscience and computation make it feasible to devise and conduct tests of the theory.

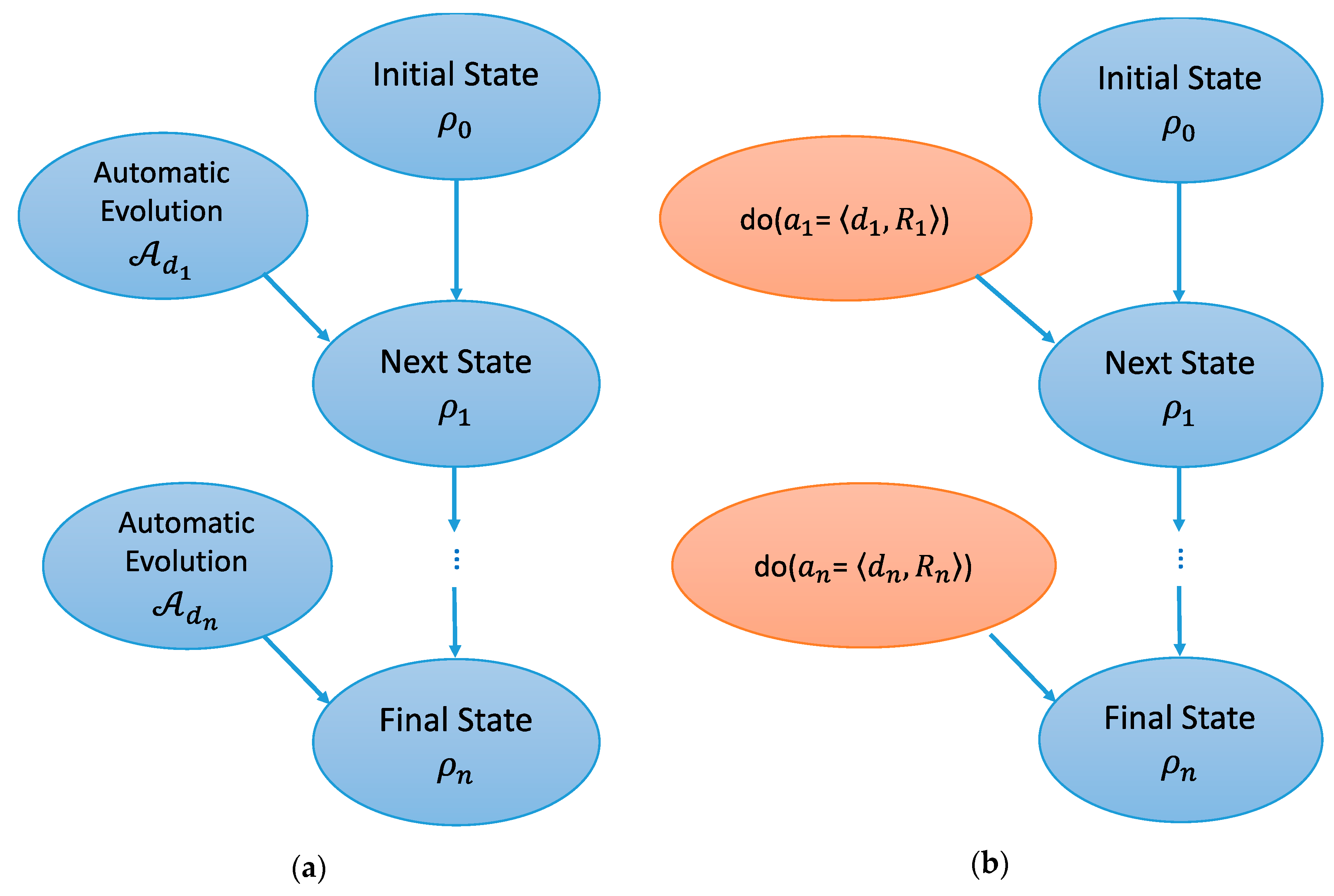
3. A Causal Model of Physically Embodied Agents

Our experience of having free will is undeniable. When facing a decision between two options, we have a strong sense that choosing either option is physically possible, and it is our decision that determines which option is effected in the world. After making and implementing a choice, we have the distinct feeling that we could have chosen otherwise, and if so, the outcomes in the world would have been different. In other words, we experience our choices as having a causal impact on the world, and we experience ourselves as the cause of the choices we make.

What does it actually mean to say we cause our choices? Does this experience of causing our choices have any basis in reality? It has been argued (e.g., [11]) that this experience is a cognitive-level representation of processes that are effectively deterministic at the micro level. Our brains examine the options, predict their consequences, assess the desirability of each option, and select the option that comes out best. The underlying micro-level processes are deterministic, except perhaps for a bit of quantum-level randomness. We have no scientific language for discussing the alternatives to this micro-mechanistic reductionist narrative. Thus, any suggestion that there may be something more to our feeling of free will is dismissed as deus ex machina.

But what if our lack of vocabulary and formal tools is preventing us from formulating and examining a genuine alternative to mechanistic reductionism? If there is more to the cognitive level than a compact description of micro-level automatic processes, if there is a fundamental property that biological agents possess but thermostats and robots do not, then fleshing out and investigating a non-reductionist scientific theory of agency is a vitally important endeavor. This endeavor is possible only if formal language and mathematical tools exist for formulating theories, deriving their implications, and testing the implications empirically. Artificial intelligence today can represent, formulate, and implement theories of deterministic and stochastic phenomena. In the past two decades, a set of powerful new tools has emerged for representing and reasoning with causal phenomena. Mathematical decision theory can represent decision problems, analyze and predict the consequences of different options, and calculate the value to an agent of each available option. But artificial intelligence has no fundamental, formal, mathematically rigorous, physically grounded theory of agency.

This paper proposes a candidate theory of agency. As with any scientific theory, it must be viewed with skepticism and subjected to empirical test. The remainder of this section presents the theory. Section 3 below lays out a path to testing it empirically.

3.1. Properties a Theory of Efficacious Free Choice Must Satisfy

A theory of efficacious free choice by physically embodied agents should satisfy the following properties (modified from [31]; see also the properties proposed by [32]):

P1

Freedom. The theory contains a construct to represent free choices made by agents. That is, there are occasions, called choice points, at which there are multiple possibilities for the agent’s future behavior.

P2

Attribution. The determination of which alternative is enacted at a given choice point is ascribed to the agent’s choice.

P3

Efficaciousness. The elements representing free choices should be efficacious in the sense that they cause effects in the physical world that depend on the choices made by agents.

P4

Physicality. The theory should be consistent with the laws of physics.

It is commonly assumed that these properties are not mutually consistent. P4 would seem to require either deterministic or behavior or quantum randomness. Deterministic choices violate P1. Random choices violate P2. Compatibilists argue that P1 and P2 should be understood not as actual physical properties, but as cognitive level experience of these properties.

This paper argues that P1–P4 are in fact mutually consistent. Specifically, Stapp’s [23,33] realistic interpretation of von Neumann’s [24] formulation of quantum theory is a rationally coherent theory satisfying all four properties. Stapp’s interpretation contains constructs explicitly representing choices made by agents. These choices can have macroscopically distinguishable causal impacts on the physical world. Section 3.2 below shows that von Neumann’s formalization of quantum theory has a natural formalization in terms of causal Markov processes on a state space consisting of density operators. Section 3.3 demonstrates that the choice of reductions can have a macroscopically observable impact on the evolution of a quantum system. Section 3.4 ties the previous sections together into a theory of causally effective agency, and shows that the theory satisfies properties P1–P4.

3.2. Quantum Theory as a Causal Markov Process

Bohm [34] said the quantum state has been called a wave of probability, but it is more accurately described as a “wave from which many related probabilities can be calculated.” That is, a quantum state predicts not what will occur, nor a single probability distribution for what will occur, but rather a family of probability distributions, one for each possible policy for applying reduction operators. Each reduction results in a stochastic transformation from the pre-reduction state to one of the allowable post-reduction states. Formally, quantum theory can be viewed as an interventionist causal theory [35] and formalized as a causal Markov process. To arrive at this representation, we need to specify the state space, the action space, and the transition distribution. Each of these is considered in turn below.

• State space: The states of a quantum causal Markov process are density operators on the Hilbert space $\mathcal{H}$ of the quantum system.
• Action space: The allowable actions in a quantum causal Markov process are the tuples $\langle d,R,\rangle$ where d is a positive real number representing the time until the next reduction and R is a reduction operator. The allowable reduction operators form a von Neumann algebra over $\mathcal{H}$.
• Transition distribution. According to Definition 1, the transition distribution for a causal Markov process is a set of probability measures on states, one for each combination of previous state and current action. Let ρ be the state just after the previous reduction, d the time until the next reduction, ${\mathcal{A}}_d$ the CPTP map representing mechanical evolution, and R the reduction operator applied after d time units. The initial state ρ evolves mechanically to ${\mathcal{A}}_d\rho$, at which point the state transitions abruptly to the outcome associated with one of the eigenvalues r. The probability of observing eigenvalue r is given by $q_r=\mathrm{Tr}\left(P_r{\mathcal{A}}_d\rho P_r\right)$. The post-reduction state if r is observed is ${\rho }_r=\frac{1}{q_r}{P}_r{\mathcal{A}}_d\rho P_r$. The possible outcomes ${\rho }_r$ are mutually orthogonal.

Although the possible actions $\langle d,R\rangle$ range over an uncountable set, the set of possible outcomes of any given action is finite or countably infinite. Thus, the distribution of outcomes conditional on a particular action is always discrete.

A causal Markov process for evolution of a given quantum system is given as follows. The state the system at a given initial time $t_0$ is represented as a density operator ${\rho }_0$. A policy is a rule for selecting, as a function of the current state, a time at which to initiate the next reduction and an operator to apply. For any finite set of positive time steps $d_1,d_2,\dots ,d_{n-1}$, undisturbed evolution of the system for time $d_1+d_2+\dots +d_n$ is given by a deterministic transition in which the state ${\rho }_k$ at time $t_k=d_1+d_2+\dots +d_k$ is ${\mathcal{A}}_{t_k}\rho$ = ${\mathcal{A}}_{d_1}{\mathcal{A}}_{d_2}\cdots {\mathcal{A}}_{d_k}{\rho }_0$. (This formulation assumes that the CPTP map representing mechanical evolution is time-invariant; with appropriate modifications, the analysis can be extended to the case of a time-varying evolution process.) This is the same state that would occur if the sequence of no-intervention actions $\langle d_1,I_{\mathcal{H}}\rangle , \dots , \langle d_n,I_{\mathcal{H}}\rangle$ had been applied to the initial state ${\rho }_0$. Any of these non-intervention actions can be replaced by an intervention do($a_k$ = $\langle d_k, R_k\rangle$), where $d_k$ is a time step and $R_k$ is a reduction operator. The action do($a_k$ = $\langle d_k, R_k\rangle$) results in a stochastic transition, where the previous state ${\rho }_{k-1}$ transforms into $\frac{1}{q_r}{P}_r{\mathcal{A}}_{d_k}{\rho }_{k-1}{P}_r$ with probability $q_r=\mathrm{Tr}\left(P_r{\mathcal{A}}_{d_k}{\rho }_{k-1}{P}_r\right)$.

Figure 1 is a graphical representation of this causal Markov process. The left-hand side shows the deterministic transition corresponding to automatic evolution of the system. The right-hand side depicts the stochastic result of applying a series of interventions with their resulting stochastic transitions.

It was noted in Section 2.3 that quantum theory specifies the process of deterministic evolution in the absence of reductions and the rule for calculating probabilities of the outcomes of reductions, but provides no theory for when reductions occur or what operations are applied. That is, quantum theory predicts the transition distribution $\pi \left({\rho }_k|{\rho }_{k-1},a_k\right)$ for each state ${\rho }_k$ conditional on the prior state ${\rho }_{k-1}$ and the action $a_k=\left(d_k,R_k\right)$, but provides no theory for how the actions are selected.

3.3. Quantum Theory Ontology

Although the mathematics of quantum theory is undisputed, there is vigorous argument over how that mathematics should be interpreted, and especially over the ontological status of reductions. Phenomenologically, reductions are associated with measurements taken by scientists to observe the system. For this reason, the lack of a fundamental theory for reductions has been called the measurement problem.

The standard textbook interpretation of quantum theory, called the Copenhagen interpretation, treats quantum theory strictly as a recipe for computing the results of measurements. Measurement occurs when a quantum system interacts with a classically described measurement device, producing an irreversible stochastic transition to one of the possible outcomes. It is considered meaningless to speculate about what is really going on with a quantum system when it is not being measured. The process of carrying out a measurement is described entirely pragmatically in the classical language of measurement devices and processes. The Copenhagen interpretation has been summarized as a “shut up and calculate” approach [36] that eschews ontology to focus entirely on describing and predicting observations.

Some scientists have attempted to resolve the measurement problem by doing away with reductions altogether, formulating quantum theory entirely in terms of the automatic evolution of a system coupled to its environment. A quantum system interacting with its environment loses the characteristic quantum property of interference and behaves to close approximation like a probability mixture of classical-like states. Some claim that this phenomenon, called environmental decoherence [37], removes the need for reductions. However, decoherence does not solve the problem of why we experience a single definite macroscopic world rather than a probability mixture of possible worlds [38]. The many-worlds interpretation resolves this problem by asserting that all these possible worlds actually do exist. According to this interpretation, the universe is constantly splitting into classical-like worlds, each with its own observers seeing their own classical-like states. We see only one world, with its classical-seeming states, but observers in other worlds see different worlds with different classical-seeming states.

Realistic interpretations view both the quantum state and the reduction process as ontologically real. In other words, a realistic interpretation treats the quantum state $\rho$ as representing a real entity in the natural world; application of a reduction operator R as representing a real phenomenon in nature that generates an instantaneous, discontinuous, stochastic transition from $\rho$ to $\frac{1}{q_r}{P}_r{\mathcal{A}}_{d_k}\rho P_r$; and the Born rule probabilities $q_r=\mathrm{Tr}\left(P_r{\mathcal{A}}_{d_k}{\rho }_{k-1}{P}_r\right)$ as real propensities for their respective outcomes to occur. Because standard quantum theory supplies no mechanism for when and how reductions occur, realistic interpretations posit that new laws will be required to fill this gap. Some such proposals (e.g., [39,40]) make changes to the dynamical equations of quantum theory, and are thus more properly termed alternative theories rather than interpretations of the standard theory. They make different empirical predictions from the standard theory, although these differences cannot be detected with present-day experiments. Stapp’s realistic interpretation makes no changes to the existing von Neumann formalization [33]. Instead, it augments the existing formalism by postulating new ontologically real entities, agents, that are capable of initiating reductions.

In the language of the causal Markov model, all interpretations consistent with the standard mathematics of quantum theory agree that ${\rho }_k$ will take value $\frac{1}{q_r}{P}_r{\mathcal{A}}_{d_k}{\rho }_{k-1}{P}_r$ with probability $q_r=\mathrm{Tr}\left(P_r{\mathcal{A}}_{d_k}{\rho }_{k-1}{P}_r\right)$ if reduction operator do($a_k$ = $\langle d_k, R_k\rangle$) is applied. Interpretations disagree on the ontological status of the intervention do($a_k$ = $\langle d_k, R_k\rangle$). The Copenhagen interpretation regards talk of intervention as convenient informal language for the formal mathematical tools used to calculate the results of outcomes experienced by observers, but declines to speculate about what is actually going on in the quantum world. Measurements are described in classical language. Although the laws of physics are presumed to be applicable to macroscopic systems, the Copenhagen interpretation makes no formal connection of the quantum level to the classical level. The many-words interpretation asserts that there are no actual interventions and no actual reductions. All outcomes actually occur, and observers experience only the outcomes occurring in their own worlds. Stapp’s realistic interpretation asserts that interventions and reductions are real phenomena. As discussed in detail below, Stapp hypothesizes that at least some do($a_k$ = $\langle d_k, R_k\rangle$) interventions are caused by agents exerting free will. He has shown mathematically that interventions can cause observable effects in the macroscopic world.

Absent empirical evidence to distinguish among interpretations, the scientific attitude recommends exploring multiple interpretations with the aim of identifying testable implications of each. Any particular interpretation may legitimately be adopted as a working hypothesis, but until disconfirmed by evidence, other interpretations should be recognized as valid alternative hypotheses. Scientific progress occurs through deriving implications of different working hypotheses and subjecting these implications to empirical evaluation. In other words, replacing “shut up and calculate” with “think deeply about the testable implications of your preferred ontological stance” might produce practical advances that would not otherwise be possible. In that spirit, this paper offers a path toward identifying empirically testable implications of Stapp’s realistic ontology and theory of agency.

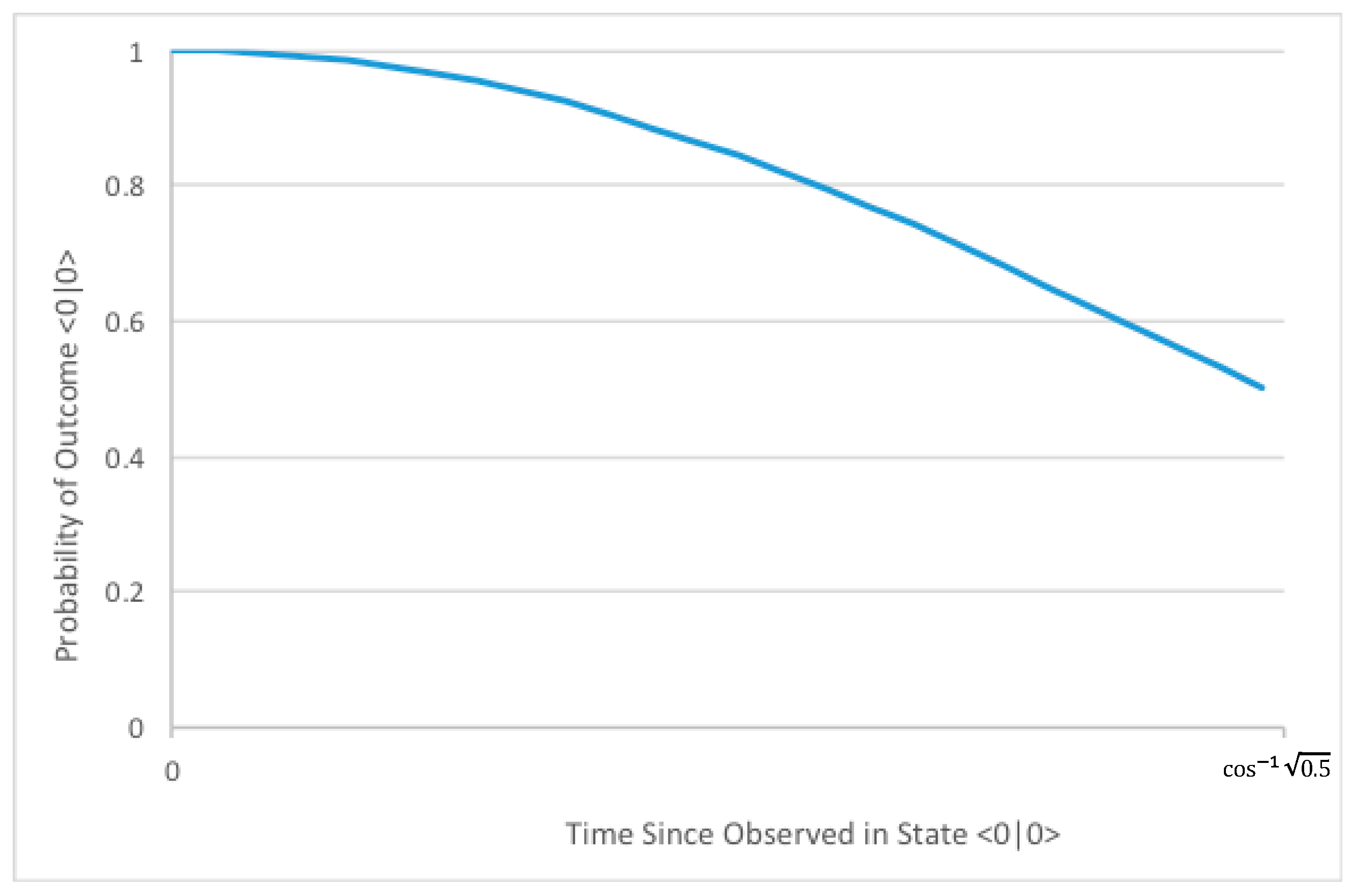
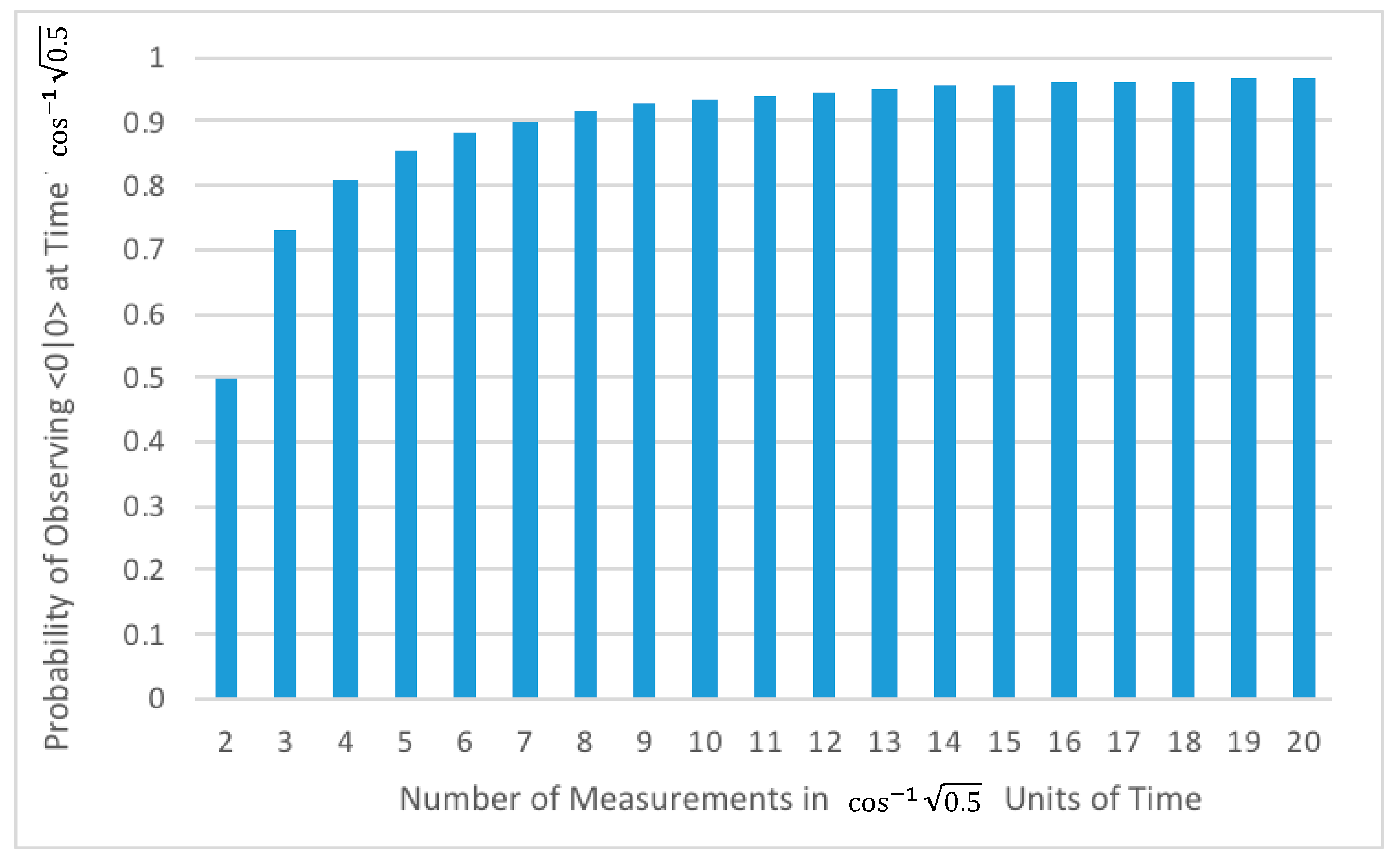
3.4. Quantum Zeno Effect

Stapp’s realistic interpretation of quantum theory posits that the world contains systems, which might be called reducing agents, that can cause reductions to some parts of their own physical states. A reducing agent can choose a policy for initiating reductions intended to bring about desired outcomes. Formally, a policy is a rule for choosing an intervention do($a_k$ = $\langle d_k, R_k\rangle$) as a function of the previous state ${\rho }_{k-1}$.

Stapp hypothesizes that reducing agents act efficaciously in the world by exploiting a phenomenon called the quantum Zeno effect (QZE), whereby rapid repeated reductions applied to a quantum system change its observable behavior [41]. This section explains how QZE works; the next section presents Stapp’s reducing agent hypothesis (RAH).

Consider an example in which repeated reductions are applied to a single quantum bit (qubit). The state space for a qubit is represented as a density operator on a 2-dimensional Hilbert space. Possible states of a qubit can be represented as 2-dimensional self-adjoint positive semidefinite matrices of trace 1. The quantum states corresponding to the classical states 0 and 1 are commonly denoted by <0|0> and <1|1>, with respective matrix representations given by:

$$<0|0>=\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]\mathrm{and}<1|1>=\left[\begin{array}{cc}0& 0\\ 0& 1\end{array}\right]$$

The evolution operator for our example is the unitary operator that transforms the state $\rho$ into the state

$${\mathcal{A}}_d\left(\rho \right)=\left[\begin{array}{cc}\cos d& -i\sin d\\ -i\sin d & \cos d\end{array}\right] \rho \left[\begin{array}{cc}\cos d& i\sin d\\ i\sin d& \cos d\end{array}\right]$$

If the system starts out in state <0|0> and evolves undisturbed for a period d, the state will be:

$${\mathcal{A}}_d\left(<0|0>\right)=\left[\begin{array}{cc}{\cos }^{2}d& i\sin d\cos d\\ -i\sin d\cos d& {\sin }^{2}d\end{array}\right]$$

(3)

Suppose a reduction with projection operators {<0|0>, <1|1>} is applied at time d. By the Born rule, the probability is ${\cos }^{2}d$ that the post-reduction state will be <0|0> and ${\sin }^{2}d$ that the post-reduction state will be <1|1>. As shown in Figure 2, when d is near zero, the probability is near 100% that the reduction result will be <0|0>. The probability of obtaining <0|0> decreases as d increases, reaching 50% at $d={\cos }^{-1}\sqrt{0.5}$. The rate of decrease is slow at first, and increases with increasing d. It is this nonlinearity that gives rise to the quantum Zeno effect.

To see how QZE works, consider a sequence of N evenly spaced reductions, in which the first reduction occurs at time 0 and the Nth reduction occurs at time ${\cos }^{-1}\sqrt{0.5}$. Between reductions, the system evolves according to (3). As N grows larger, the time between reductions becomes shorter. If the initial reduction at time 0 resulted in <0|0>, the second reduction at time ${\cos }^{-1}\sqrt{0.5}/N$ has a probability near 100% of the outcome <0|0>. If so, the process resets with a very high and slowly decreasing probability of outcome <0|0> at the next reduction. The third reduction, occurring at time 2${\cos }^{-1}\sqrt{0.5}$/N, will again yield outcome <0|0> with very high probability. As before, the process resets with a very high and slowly decreasing probability of obtaining <0|0> with the next measurement. The more rapidly the reductions occur, the higher the probability that the system will still be in state <0|0> after the last reduction.

Figure 3 illustrates how a rapid sequence of reductions tends to hold the state of a quantum system in place. The graph shows, for different values of N, the probability of observing <0|0> at the end of the sequence of reductions if the system is observed initially in state <0|0> and N evenly spaced reductions occur between time 0 and time ${\cos }^{-1}\sqrt{0.5}$. Figure 1 corresponds to the case N =2, with measurements taken at 0 and ${\cos }^{-1}\sqrt{0.5}$, and a 50% probability of observing <0|0>. As the number of reductions increases, the probability of outcome <0|0> at time ${\cos }^{-1}\sqrt{0.5}$ increases to near 100%. That is, rapid measurement “freezes” the system at outcome <0|0>.

Rapid measurement can also drive a quantum system to a desired state ([24], Chapter V.2). Instead of using repeated applications of the same measurement operator to hold a quantum system in place, the inverse quantum Zeno effect [42] applies a slowly changing sequence of measurement operators with outcomes along a path from the initial to the intended outcome. Applying this sequence of operators in rapid succession drives the system along the intended path with high probability. In what follows, the term QZE will be used to refer both to the standard quantum Zeno effect in which the same operator is repeated rapidly to freeze a system, and to the inverse quantum Zeno effect in which a sequence of operators is applied rapidly to drive a system to an intended state.

3.5. A Model of Efficacious Physically Embodied Agency in Humans

As discussed above, the reducing agent hypothesis (RAH) postulates that free will operates via application of state reductions. Specifically, RAH posits that there are quantum systems possessing the ability to initiate reductions to some part of their own physical state. These reducing agents exert free will by choosing which of their available reduction operators to apply at what times. Reducing agents (RAs) include humans and other life forms, and possibly other kinds of systems in the natural world. In the specific case of human free will, RAH postulates that human agents make free choices by initiating reductions to some part of their own bodies. Because the cerebral cortex appears to be responsible for cognition and decision-making, it is natural to hypothesize that human reducing agents are able to initiate reductions in the cerebral cortex.

The idea that humans might initiate reductions in their own brains and bodies differs substantially from textbook accounts of reductions. Quantum theory textbooks describe reductions as interactions between inanimate microscopic quantum systems and inanimate measuring devices to produce measurements that are observed by scientists. While the founders of quantum theory stressed that the decision of when to initiate a measurement and what measurement to take should be assigned to the free choice of the scientist, they did not consider how such a free choice might be formulated and then executed by the scientist’s brain and body. In the mathematical formalism of quantum theory, the choice of measurement is free in the specific sense that the theory provides no rules for how the choice is made. Stapp makes the bold suggestion that this gap could be filled by considering the human brain as a quantum system and postulating that human decision-making might be implemented in the brain via quantum state reductions.

The hypothesis that agents exert free will through the initiation of reductions satisfies the four properties identified in Section 3.1. To summarize:

P1

Freedom. As currently understood, the laws of physics specify how a quantum system evolves when not subjected to reductions and the probability distribution of outcomes given the time since the last reduction and the operator set. That is, quantum theory specifies the following dynamic laws:

• $\rho \to {\mathcal{A}}_d\rho$ via mechanical evolution for d time units; and
• $\rho \to$ ($\frac{1}{q_r}{P}_r{\mathcal{A}}_d\rho P_r$) with probability $q_r=\mathrm{Tr}\left(P_r{\mathcal{A}}_d\rho P_r\right)$ if reduction operator R with spectral decomposition $R={\sum }_{r}r{P}_r$ is applied after undisturbed evolution for d time units.
  The known laws of physics place no constraints on the choice of time interval d or reduction operator R. Modulo as yet undiscovered limits on d and R, there are multiple allowable choices of action $\langle d,R\rangle .$ Therefore, there are multiple possible options at each choice point.

P2

Attribution. RAH attributes the choice of action $\langle d,R\rangle$ to the reducing agent.

P3

Efficaciousness. The analysis of Section 3.4, as illustrated in Figure 3, demonstrates that the choice of action has empirically distinguishable effects in the physical world.

P4

Physicality. RAH is fully consistent with the known laws of physics as formalized by von Neumann [24].

By virtue of satisfying P1–P4, RAH qualifies as a viable candidate theory of efficacious choice by physically embodied agents. But the reducing agent hypothesis goes beyond this claim, making the much stronger claims that humans are reducing agents and that QZE is the mechanism by which humans take volitional action. These assertions place demands on any theory of reducing agents that it be consistent with the neurobiology of volitional action in humans. Specifically, a physically grounded theory of free choice in humans should demand that human reducing agents be physical symbol systems in the sense of Newell and Simon [43]. The following additional properties (modified from [31]) address this requirement:

P5

Representation. Human reducing agents must be able, in a manner consistent with neurobiology, to form representations of the world. They must be able to manipulate these representations to predict the effects of the available options and compare the desirability of different options.

P6

Implementation. There must be a way, consistent with human neurobiology and physiology, for human reducing agents to enact their choices to cause their bodies to behave as intended.

The prevailing view in science is that cognition and decision-making can be modeled satisfactorily without explicit use of quantum theory. While it is acknowledged that quantum theory applies to all physical systems, the full machinery of quantum theory is considered necessary only for microscopic systems kept in strict isolation from their environments. Systems coupled to their environments rapidly lose their distinctly quantum properties because of environmental decoherence. Because the human brain is a macroscopic object embedded in and strongly coupled to its environment, it is believed that the classical approximation is fully adequate for modeling cognition and decision-making. Recently, to the surprise of many, quantum effects have been found to play an important role in biological phenomena such as photosynthesis and avian navigation [44]. These discoveries open the door to a potentially broader role for the application of quantum theory to biology. Furthermore, Stapp’s proposed mechanism for volitional action, the quantum Zeno effect, survives decoherence [33].

The model presented here for volitional action in humans draws from [31] and builds on the work of Stapp [21,23,33]. Stapp agrees that classical physics is indeed adequate for modeling many aspects of volitional action. Specifically, the brain can be modeled to close approximation as a probability mixture of classically described possibilities. Thus, classical neural networks work well for modeling many aspects of learning, cognition, and motor control. However, Stapp postulates that quantum theory plays a fundamental role in volitional control of the motor system.

Just prior to taking volitional action, Stapp proposes, a person’s brain retrieves a pattern of neurological activity he calls a template for action. A template for action is a learned pattern of activity that the brain executes to send a sequence of nerve signals to the muscles, causing the body to behave in a certain way. During execution of one of these templates, the senses provide input to the brain, allowing the brain to adjust the signals it sends to the muscles. This feedback and control process allows sensory inputs to guide execution of motor outputs. Templates for action are refined with practice until they can be executed smoothly with little conscious attention. Templates for action can be described to close approximation using spreading activation models like those used widely in neuroscience (e.g., [45]), robotic control (e.g., [46,47]), and computer vision (e.g., [48]).

Where quantum theory enters, Stapp proposes, is through the use of the quantum Zeno effect to keep a given template in operation longer than it would through purely automatic evolution. Stapp views QZE as a physical model of what psychologist William James calls “effort of attention.” According to James [49], “The essential achievement of the will … is to attend to a difficult object and hold it fast before the mind... Effort of attention is thus the essential phenomenon of will.” Stapp argues that effort of attention, implemented through QZE, holds an action template in place long enough for the brain to control the body in executing a sequence of desired actions. The success of standard neural network models at modeling many aspects of perception, cognition and behavior is due to the fact that action templates can be closely approximated by classical stochastic processes. The quantum Zeno effect comes into play, argues Stapp, for fine-tuned feedback and control via effort of attention as an action template is executed.

4. Evaluating the Theory

Section 3.5 established that the reducing agent hypothesis satisfies the four proposed necessary conditions for a theory of efficacious free choice. Freedom (P1) is satisfied because the laws of physics permit multiple qualitatively different reduction policies. Responsibility (P2) is satisfied because the choice of reductions is ascribed to the reducing agent. Efficaciousness (P3) is satisfied because, as demonstrated by Figure 3, different reduction policies can cause different physical effects. Physicality (P4) is satisfied because RAH is based on and fully consistent with the von Neumann formalization of quantum theory.

These four conditions establish the potential of RAH as a theory of efficacious free choice, but additional conditions are needed to support a theory of agency in humans and other animals. The fundamental challenge is to develop and evaluate a concrete model of how reductions are employed in brains to effect purposive behaviors. Stapp has proposed templates for action as the brain’s representation (P5) of intended behavior, and the quantum Zeno effect as the physical correlate of the focused attention employed by a biological agent to implement (P6) purposive behavior. To evaluate Stapp’s hypothesis that agents use QZE to hold desired action templates in place, a specific biological model for action templates must be developed and tested.

4.1. Simulating a Reducing Agent

Synchronous oscillations of activity in the brain’s neural network appear to play an important role in cognitive processes [50,51,52]. Synchronicity has been hypothesized as a mechanism for how the brain binds component features into representations of composite objects. For example, in vivo studies in behaving animals have found that neurons responding to individual features begin firing synchronously when the animal recognizes that the features form a coherent object [53]. Synchronous oscillations also appear to play an important role in motor control [54], preparation for motor activity [55], sensory motor coordination, and focused attention [51]. These findings suggest that templates for action may be characterized by periods of synchronous oscillation in areas of the brain associated with the action to be executed.

Other research suggests a feedback relationship between neural activity and the brain’s electrical field [56,57]. Externally applied electromagnetic fields have been found in laboratory studies to affect neural activity, and are used in a clinical setting to diagnose and treat a range of neural disorders. Fröhlich and McCormick [56] studied the brain’s endogenously generated electric field in a series of in vivo experiments and in a computational simulation. Their findings provide evidence of a feedback process in which endogenous electric fields act in a feedback process in which synchronous oscillations increase the strength of the brain’s electric field, which in turn reinforces synchronicity of oscillations. Several authors have suggested the brain’s electric field as the locus for consciousness (e.g., [22,58,59,60]). Although the EM field hypothesis is controversial, its proponents argue that it explains how information distributed among millions of neurons is unified into coherent precepts. Regardless of the role played by the electric field in consciousness, its role in entraining synchronicity in neural activity appears to be important.

In light of the important role played by oscillations in the brain’s electric field, Stapp ([23], Appendix F) developed a simple model of the use of QZE to control the strength of the electric field. His model employed a single frequency quantum oscillator at 20 Hz. The choice of frequency was based on an experimental study that found beta range (15–30 Hz) oscillations in the motor cortex of trained monkeys approximately 100 ms after the monkeys were instructed to move [61]. He also noted that beta oscillations in cortical minicolumns are at the quantum scale [62], thus suggesting the possible relevance of quantum effects. His single frequency oscillator model can be solved exactly, being a natural extension of the classical simple harmonic oscillator. His analysis demonstrated that the inverse quantum Zeno effect can be applied to increase the amplitude of the quantum oscillator. He calculated the rate required to have a high probability of increasing the amplitude and concluded that the time scale was reasonable for the neuroscience domain. The amplitude of oscillation corresponds to the strength of the electric field. Thus, Stapp’s stylized model demonstrates that the inverse quantum Zeno effect can be applied to increase the strength of the electric field, which in turn would enhance synchronicity in oscillations in the brain’s neural network.

Stapp’s model considered the oscillating electric field in isolation, without considering how it affects and is affected by synchronicity in neural firing. His model, while suggestive that the QZE could be employed in scenarios consistent with known neuroscience, needs to be extended to a more realistic neurodynamic model.

One potential avenue of approach would be through a model that explicitly considers the interaction between the electric field and the spreading activation process in the neural network. The Fröhlich and McCormick model [56] does just this. The model contains some stochastic elements, but is not quantum. Adding quantum effects to this or a similar model could yield a concrete, biologically plausible model that could be used to investigate Stapp’s theory of how efficacious choice is implemented in brains. Such a model could be used to examine whether rapid reductions could generate macroscopically distinguishable effects on synchronicity of neural activity at biologically realistic parameter settings. The rate of application of state reductions could be included in the model as an adjustable parameter. Reductions could be employed to nudge the brain toward synchronous firing of neurons associated with an action template the organism intends to effect, or to disrupt synchronous firing and thus interrupt an action template the organism intends to discontinue.

Once such a model was developed, it could be implemented on a computer and systematic experimentation could be performed to investigate whether the rate of reduction can be adjusted to entrain or disrupt synchronicity of neural firing. Once neurons are firing synchronously, are there rates of reduction, i.e., “attention density settings,” that either reinforce or disrupt synchronous firing? If neurons are not firing synchronously, can “attention density” be employed to generate synchronicity? These and other pertinent questions could be addressed through computational experiments.

It should be noted that the kind of simulation envisioned here should be of the same order of computational complexity as models commonly used in neuroscience. Because environmental decoherence suppresses quantum interference, the quantum neurodynamic model could be approximated as a probability mixture of near-classical possibilities. In other words, extending the approach taken by Stapp in Appendix F of [23], it should be possible to model QZE by modifying a standard stochastic neural network model. This approach avoids the computational difficulties of representing and simulating high-dimensional density operators.

If computational experiments demonstrated that different “attention density settings” produced clearly distinguishable differences in synchronicity using biologically realistic parameter settings, it would lend support to the reducing agent model of efficacious choice.

4.2. Laboratory Studies

Previous sections have articulated a set of hypotheses about how reducing agents may influence the world through the application of QZE. Specifically, synchronous oscillations in neural firing, in a mutually reinforcing feedback relationship with endogenous electric fields, appear to play a fundamental role in neural information processing. It is reasonable to hypothesize that the templates for action that guide automatic processing involve waves of synchronous oscillation of relevant parts of the brain’s neural network in a feedback relationship with the brain’s endogenous electric field. Stapp hypothesizes that Jamesian attention density is used to hold desired action templates in place and fine-tune guidance of their execution. He further hypothesizes that Jamesian attention density operates through the quantum Zeno effect and/or inverse quantum Zeno effect. The rapidly repeated reductions occur in parts of the brain associated with intentional action, and act to increase synchronous firing of neurons associated with action templates the agent intends to implement.

Section 3.1 proposed that concrete mathematical models be developed for how QZE influences synchronous firing in neural networks. Such modeling should be informed by laboratory research on the structure and behavior of biological neural networks. Computational experiments with the resulting models could be used to examine the biological plausibility of the hypothesis that efficacious choice operates via the quantum Zeno effect. If successful, these computational experiments should give rise to predictions about the biological mechanisms underlying volition, attention and motor control. These predictions could be tested in laboratory experiments on animals. Results from the laboratory could then be used to refine the computational models and generate additional predictions for further laboratory experiments. The resulting feedback cycle would increase our understanding of the neurobiological processes underlying volitional action.

4.3. Hardware Implementation

Intelligent agents form representations of the world around them, learn better representations through environmental feedback, manipulate their representations to predict the consequences of different actions, and use these predictions to take intentional action. These representations are formed and manipulated in a physical substrate. Artificial intelligence has taken the computational metaphor as a given and assumed that the physical substrate of digital computers is sufficient for intelligent behavior. AI has thus pursued the objective of building artificially intelligent agents executing on digital computers. If the reducing agent hypothesis is correct, then the best that can be hoped for with digital computer systems is a simulation of intelligence. These simulations have performed extremely well on some tasks and less well on others. The reducing agent hypothesis suggests that at least some of the failures may be due to intrinsic limitations of digital computers. Under the reducing agent hypothesis, achieving true engineered intelligence would require a physical substrate capable of supporting efficacious action through the employment of reductions. That is, an agent’s cognitive and motor architecture must be instantiated in a physical structure that can produce macroscopically distinguishable behaviors from different policies for applying reduction operators. The agent must also have a sensory apparatus to convey the real-world results of behavior to a learning system capable of refining the agent’s world representation in response to environmental feedback.

A demonstration that efficacious choice can be achieved by reducing agents in biologically plausible simulations would both lend plausibility to the reducing agent hypothesis and support the development of a fundamental theory of physically embodied agency. As simulations are refined and compared against laboratory experiments, they could point the way to hardware implementations. If successful, such systems might move beyond simulated intelligence to achieve true engineered intelligence.

5. Conclusions

A science of physically embodied agency requires a theory of what kind of systems can be agents and the physical conditions enabling efficacious choice by agents. Such a theory should provide scientific laws describing how physically embodied agents make choices to act in physical world to bring about desired effects. This paper proposes such a theory of efficacious free choice by agents. The theory is based on the reducing agent hypothesis, which postulates that physically embodied agents act efficaciously in the world by choosing and applying sequences of quantum state reductions acting on some part of their physical states. It was shown that this theory satisfies the four necessary conditions of freedom, attribution, efficaciousness and physicality. These reducing agents are hypothesized to include humans, other life forms, and possibly other natural systems. Two additional conditions of representation and implementation are postulated for intelligent biological agents. That is, intelligent agents must be physical symbol systems capable of forming and manipulating representations to predict the consequences of their actions, and implementing these actions to bring about desired consequences in the external world.

The reducing agent hypothesis was formalized as an interventionist causal theory. A reducing agent acts in the world by applying quantum state reduction, which is formalized as a do operator to intervene to bring about intended bodily motions and thereby effect desired effects in the external world.

The reducing agent hypothesis takes a realistic interpretation of von Neumann’s mathematical formulation of quantum theory. Both the quantum state and state reductions are viewed as real phenomena in nature. The reducing agent hypothesis adds a new ontological category of the reducing agent to the ontology of science. Reducing agents are able to select and implement state reductions to effect behavior intended to bring about desired states.

Although some have argued that controversies over interpretations of quantum theory are purely metaphysical debates with no empirically verifiable consequences, the reducing agent hypothesis has important real-world implications and is amenable to empirical evaluation. Section 3 presented avenues of empirical evaluation through computer simulation, laboratory experimentation on biological systems, and ultimately physical implementation in hardware. Each of these avenues of evaluation could provide empirical data to evaluate the plausibility of the reducing agent hypothesis. If the tests suggested in Section 3 are successful, lending plausibility to RAH, they would also yield insights into the physical conditions supporting the emergence of reducing agents, and ultimately pave the way to engineered intelligence that is more than a simulation.

6. Discussion

The mainstream view in artificial intelligence is that it is unnecessary to employ quantum theory explicitly in models of mind, cognition, and behavior. Although all physical systems are quantum systems, the classical approximation is adequate for a large range of macroscopic phenomenon. The classical theory of computing is generally thought to be sufficient as a foundation for artificial intelligence. While acknowledging that the reducing agent hypothesis is speculative at this stage, this paper argues that it is consistent with well-established physics and has profound implications for the future of artificial intelligence. If human choices are fundamentally free in a way that choices by computer agents are not, then today’s AI systems are at best simulations of intelligence. The reducing agent hypothesis represents a novel research path for artificial intelligence. Under the reducing agent hypothesis, intelligent agents require a physical substrate that supports the ability to represent the world, formulate choices, and take volitional action. Designing intelligent physically embodied agents therefore requires a fundamental, physically grounded theory of agency. Just as the lack of a formal mathematical theory of causation has until recently hindered progress in many fields of science, the lack of formal language and mathematical tools for representing physically embodied agency may be hindering progress in artificial intelligence and cognitive science. If Stapp’s theory is correct, then the prospects for true engineered intelligence depend on developing such a foundational theory. This paper proposes a research path toward evaluating Stapp’s theory. If successful, the research program could lead to the needed foundational theory and ultimately to true engineered intelligence.