Abstract
Many optimization problems can be found in scientific and engineering fields. It is a challenge for researchers to design efficient algorithms to solve these optimization problems. The Particle swarm optimization (PSO) algorithm, which is inspired by the social behavior of bird flocks, is a global stochastic method. However, a monotonic and static learning model, which is applied for all particles, limits the exploration ability of PSO. To overcome the shortcomings, we propose an improving particle swarm optimization algorithm based on neighborhood and historical memory (PSONHM). In the proposed algorithm, every particle takes into account the experience of its neighbors and its competitors when updating its position. The crossover operation is employed to enhance the diversity of the population. Furthermore, a historical memory Mw is used to generate new inertia weight with a parameter adaptation mechanism. To verify the effectiveness of the proposed algorithm, experiments are conducted with CEC2014 test problems on 30 dimensions. Finally, two classification problems are employed to investigate the efficiencies of PSONHM in training Multi-Layer Perceptron (MLP). The experimental results indicate that the proposed PSONHM can effectively solve the global optimization problems.
1. Introduction
Artificial Neural Networks (ANN) is one of the more significant inventions in the field of soft computing [1]. There are different types of ANNs in which the Feedforward Neural Network (FNN) has been widely used. There are two types of FNN: Single-Layer Perceptron (SLP) [2] and Multi-Layer Perceptron (MLP) [3]. MLP can solve nonlinear problems because it has more than one perceptron. The ANN training process is an optimization process with the aim of finding a set of weights to minimize an error measure [4]. Then, some conventional gradient descent algorithms, such as the Back Propagation (BP) algorithm [5], are used to solve the problem. However, the BP algorithm is prone to getting trapped in local minima because it is highly dependent on the initial values of weights and biases.
To search for the optimal weights of the network, various heuristic optimization methods have been utilized to train FNNs, such as Particle swarm optimization (PSO) [6], Differential evolution (DE) [7], Genetic algorithms (GAs) [8], Ant colony algorithm [9], etc. These evolutionary algorithms (EAs) have been recognized to be effective and efficient for tackling the optimization problems. They have been successfully applied in various scientific and engineering fields, such as optimization, engineering design, neural network training, scheduling, large-scale, constrained, economic problems, multi-objective, forecasting, and clustering [10,11,12,13,14,15,16,17]. However, the EAs are often stuck in a local optimum because of the possible occurrence of premature convergence. It is necessary for the EAs to address the issue of exploration–exploitation of the search space. To achieve a proper balance between exploration and exploitation during the optimization process, many heuristic algorithms that imitate biological or physical phenomena are proposed. These heuristic algorithms include the derandomized Evolution Strategy with Covariance Matrix Adaptation (CMA-ES) [18], the Simulated Annealing (SA) [19,20], Biogeography-Based Optimizer (BBO) [21], Chemical Reaction Optimization (CRO) [22], Brain Storm Optimization (BSO) [23] and so on. CMA-ES, proposed by Hansen and Ostermeier, adapts the complete covariance matrix of the normal mutation distribution to solve optimization problems. SA, proposed by Kirkpatrick et al., mimics the way that metals cool and anneal. In order to solve the premature convergence, two partial re-initializing solutions strategies are proposed to improve the population diversity in BSO. Inspired by a correspondence between optimization and chemical reaction, CRO is proposed by mimicking what happens to molecules in chemical reactions.
PSO, proposed by Kennedy and Eberhart in 1995 [24], is a simple yet powerful optimization algorithm that imitates the flying and the foraging behavior of birds. The concept of PSO is based on the movement of particles and their personal and best individual experiences [24]. In classical PSO, each particle is attracted by its previous best position (pbest) and the global best position (gbest). That is to say, the particles adjust their speed and position dynamically by sharing information and experiences of the best particles. Then, the algorithm can converge quickly by using the best solution information in the evolutionary process. However, the information sharing strategy reduces the diversity of the particle swarm, because all particles except itself only share the optimal particle information while ignoring other particles’ information. Therefore, the algorithm is prone to premature convergence because of losing diversity too rapidly during the evolutionary process. To improve the performance of PSO, researchers have studied and proposed many improvement strategies based on classical PSO [25,26,27,28,29,30,31]. M. Clerc and J. Kennedy proposed PSO with constriction factor (PSOcf) [26] by studying a particle’s trajectory as it moves in discrete time. Mendes proposed the fully informed particle swarm (PSOwFIPS) [32], in which the particle uses information from all its neighbors, rather than just the best one. J. J. Liang et al. present the comprehensive learning particle swarm optimizer (CLPSO) utilizing a new learning strategy [33]. T. Krzeszowski et al. propose a modified fuzzy particle swarm optimization method, in which the Takagi–Sugeno fuzzy system is utilized to change the parameters [27]. A. Alfi et al. present an improved fuzzy particle swarm optimization (IFPSO) that uses a fuzzy inertia weight to balance the global and local exploitation abilities [28]. Fuzzy self-turning PSO (FST-PSO), proposed by M. S. Nobile et al. [34], is a novel self-tuning algorithm that exploits fuzzy logic (FL) to calculate the control parameters for each particle. Therefore, FST-PSO realizes a complete settings-free version of PSO.
Obviously, it is impossible to find an algorithm that can solve all the problems. In fact, to develop a new optimization method that can effectively deal with the exploration–exploitation dilemma in some problems during the optimization process remains an important and significant research work.
An innovative element of this work is to propose an improved PSO based on neighborhood and historical memory (PSONHM). Differently from the former PSO, each particle uses the information about the neighborhood and the competitor to update its velocity and position in PSONHM. The inferior particle is recorded as the competitor in the proposed algorithm. Moreover, instead of the same elite (gbest) in the former PSO, multiple elites (good solutions) are employed to guide the population toward a promising area. Furthermore, to solve premature convergence, a crossover operator is introduced to make the population disperse. Overall, the main contributions of PSONHM can be described as follows.
- (1)
- Local neighborhood exploration method is introduced to enhance the local exploration ability. With the local neighborhood exploration method, each particle updates its velocity and position with the information of the neighborhood and competitor instead of its own previous information. The method can effectively increase population diversity.
- (2)
- The crossover operator is employed to generate new promising particles and explore new areas of the search space. The multiple elites are employed to guide the evolution of the population instead of gbest, and thus avoid the local optima.
- (3)
- Successful parameter settings can reduce the likelihood of being misled and make the particles evolve towards more promising areas. Then, a historical memory Mw, which stores the parameters from previous generations, is used to generate new inertia weights with a parameter adaptation mechanism.
- (4)
- The last contribution of PSONHM is to design a PSONHM-based trainer for MLPs. Classic learning methods, such as Back Propagation (BP), may lead MLPs to local minima rather than the global minimum. Neighborhood method, crossover operator and historical memory can enhance the exploitation and exploration capability of PSONHM. Then, it can help PSONHM find the optimal choice of weights and biases in the ANN and achieve the optimal result.
The remainder of this paper is organized as follows. In Section 2, PSO and its variants are reviewed. Section 3 presents an improving particle swarm optimization based on neighborhood and historical memory (PSONHM). Section 4 reports the experimental results compared with eight well-known EAs on the latest 30 standard benchmark problems listed in the CEC2014 contest. In Section 5, two classification problems are employed to investigate the efficiencies of PSONHM in training MLP. Section 6 gives the conclusions and possible future research.
2. Related Work
PSO is a population-based optimization algorithm that uses interaction between particles to find the optimal solution. In the following, a brief account of basics and improvements of PSO will be given.
2.1. PSO Framework
PSO algorithm, which is inspired by the behaviors of flocks of birds, is a population-based optimization algorithm. Firstly, a randomly population of NP particles are generated in a D-dimension search space. Each particle is a potential solution. To restrict the change of velocities and control the scope of search, Shi and Eberhart introduced an inertia weight in PSO [35], the corresponding velocity vi,G and the position xi,G are updated as follows:
where is the position of the ith particle at generation G. is the velocity of particle i. c1 and c2 are acceleration coefficients. are random numbers generated in the interval [0, 1]. is the historical best position for ith particle. is the best swarm historical position found so far.
The performance of PSO can be greatly improved by adjusting the inertia weight . Shi and Eberhart [36] designed a linearly decreasing inertia weight, which is computed as follows:
where and are usually fixed as 0.9 and 0.4. G is the current generation. MaxGen is the maximum generation.
2.2. Improved PSO Based on Neighborhood
To get a proper trade-off between exploration and exploitation, neighborhood, which is an important and efficient method, is widely used in evolutionary algorithms. For example, Das et al. [37] propose two kinds of neighborhood models for DE, namely the local neighborhood model and the global mutation model that can facilitate the exploration and the exploitation of the search space. Omran et al. [38] employ the index-based neighborhood to enhance the DE mutation scheme. The fully informed PSO, proposed by Mendes [32], uses an index-based neighborhood as the basic structure. The contribution of each neighbor was weighted by the goodness of its previous best. A PSO with a neighborhood operator, proposed by Suganthan, gradually increases the local neighborhood size in the search process [39]. Nasir et al. proposed a dynamic neighborhood learning particle swarm optimizer (DNLPSO) [40]. In DNLPSO, the exemplar particle is selected from a neighborhood and the learner particle can learn from the historical information of its neighborhood. The winner’s personal best is used as the exemplar. Each particle in the swarm is known as learner particle. Ouyang et al. proposed an improved global-best-guided particle swarm optimization with learning operation (IGPSO) for solving global optimization problems [41]. In IGPSO, the personal best neighborhood learning strategy is employed to effectively enhance the communication among the historical best swarm.
3. Proposed Modified Optimization Algorithm PSONHM
In this section, the details of the proposed algorithm are described. First, the motivations of this paper are given. Then, the neighborhood exploration strategy, the property of stagnation and the inertia weight assignments based on historical memory are presented. Finally, the pseudo-code of the proposed algorithm is shown.
3.1. Motivations
In the canonical PSO, a particle depends on its personal best and the global best to establish a trajectory along the search space. The global best particle guides the swarm to exploit in the search process. Therefore, similar to other population based algorithms, the algorithm experiences premature convergence because of poor diversity. In PSO, all the particles are attracted by gbest, so it is possible that the particles will be easily misguided into unpromising areas. In addition, little attention has been paid to utilize the competitor information, which is helpful for maintaining diversity. To overcome the weakness of PSO, we attempt to use the neighborhood model to prevent the population from getting trapped in local minima. With the neighborhood model, each particle can learn from its neighbors and competitor. In this manner, the possibility of misguidance by the elite may be decreased. Then, the crossover operation is introduced to generate new promising particles. Furthermore, it is widely believed that the inertia weight can significantly influence the performance of PSO. However, there is not much work devoted to discussing or using history information to design the inertia weight. We attempt to use historical memory to guide the selection of future inertia weight.
3.2. Neighborhood Exploration Strategy
It is well known that the traditional PSO includes two types of behaviors: cognitive and social. Generally, gbest, which represents the best position, is used in social behaviors. However, the algorithm is easy to drop into the local optimum if gbest is not near the global optimum. A main issue in the application of PSO is to implement effective exploration and exploitation. In general, the task of exploration is to find the search space where better solutions are existed. On the other hand, the task of exploitation is to realize a fast convergence to the optimum solution.
Next, we investigate the impact of neighborhood mechanism and archive method, which are used in traditional PSO. They are PSO, PSOwFIPS [32] and PSO_Archive, respectively. In PSOwFIPS, the particle uses information from all its neighbors. In PSO_Archive, the inferior particles are added to the archive at each generation. If the archive size exceeds the population size, then some particles are randomly removed from the archive. Then, we employ as a case study benchmark problem f4 and f17 selected from CEC2014 contest benchmark problems. f4 is a simple multimodal problem, while f17 is a hybrid problem. Each problem is executed for 30 runs. The maximal number of function evaluations (FES) for all of the compared algorithms is set to D × 10,000 with D = 30. To evaluate the performance of each algorithm, the minimum value of the solution error measure, which is defined as f(x) − f(x*) is recorded, where f(x) is the best fitness value found by an algorithm in a run, and f(x*) is the real global optimization value of a tested problem.
Figure 1 shows that the neighborhood information can effectively enhance PSO performance because the informed individuals can find better solutions with a higher probability. Hence, we come up with the idea that the neighborhood and the competitor should be utilized when stagnation is happening to PSO.
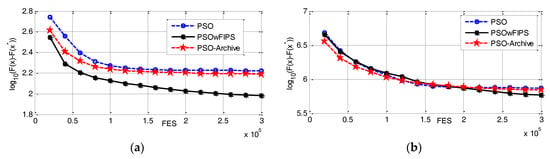
Figure 1.
The mean function error values versus the number of FES on test problems. (a) f4; (b) f17.
Various neighborhood topologies have been proposed in [26], such as star, wheel, circular, pyramid and 4-clusters. In the proposed algorithm, the ring topology is used because it has better performance compared to other neighborhood topologies. The population is assumed to be organized on a ring topology in connection with their indices. For example, the neighbors of xi,G are xi+1,G and xi−1,G. The ring topology used in PSONHM is illustrated in Figure 2.
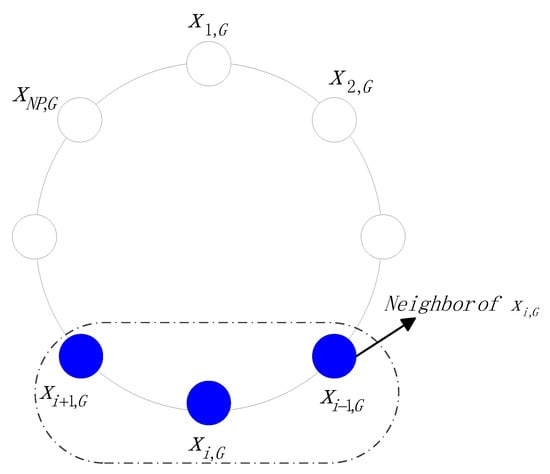
Figure 2.
Ring topology of H-neighborhood in PSONHM.
In traditional PSO, all the particles are attracted by gbest and the swarm has the tendency to fast converge to the current globally best position. Then, the algorithm may stagnate in the local optimum area because of the rapid convergence. The competitive particles, which may contain some useful information, may be closer to the global minimum. Hence, the difference vector between the personal best position and the competitive particle can be seen as a good direction for exploration. To lessen the influence of gbest on the whole population, multiple elites, similar to the better individuals used in DE/current-to-pbest [42], are selected to replace gbest and instruct updating. In addition, the information of all the neighbors is taken into consideration. The difference vector between the multiple elites and the neighbors can be seen as a good direction for exploitation. Consequently, each particle receives information from its neighbors and competitor, which can increase the probabilities of generating successful solutions and decreases the probability of premature convergence. The neighborhood exploration strategy is designed as follows:
where is the competitor of pbesti,G. pbesti,G denotes the best previously visited position of the ith particle. At G generation, the objective values of ith particle is compared with pbesti,G, The winner is denoted as pbesti,G+1, while the loser, namely the competitor, is denoted as . xn(j,i),G denotes the jth neighbor of the particle i at generation G. Each particle has H neighbors. which is used in Label (1) may result in fast convergence. However, it may also cause premature convergence due to the reduced population diversity. Therefore, , which is randomly chosen as one of the top 100p% particles in the current population, is used instead of . mean(•) denotes the arithmetic mean value function.
After neighborhood exploration, a binomial crossover operation is employed to enhance the diversity of the population. is updated as follows:
The crossover factor CR is calculated as follows:
where D is the dimension. rand denotes a uniformly selected random number from [0, 1]. denotes natural logarithm function. c1 is the acceleration coefficient.
3.3. Property of Stagnation
It is called stagnation when the algorithm cannot find any better solutions. The property of stagnation can be shown in PSONHM by the ti,G at generation G, which is evaluated to estimate whether the algorithm cannot generate any successful solutions. The ti,G is updated as follows:
where f(*) is the objective function. NP is the population size.
The initial values ti,1 are set to zero. It indicates that the algorithm cannot generate any successful solutions for the ith particle if ti,G increases continually. In this moment, it is thought that stagnation happens to the algorithm. In PSONHM, the neighborhood exploration strategy is employed to increase the probabilities of generating successful solutions when ti,G exceeds a fixed threshold value, namely, T.
3.4. Inertia Weight Assignments Based on Historical Memory
The inertia weight is helpful to balance the local and global search during the evolutionary process [35]. Instead of solely depending on a linearly decreasing inertia weight, the historical memory Mw, which stores a set of inertia weight values that performed well in the past, is used to generate new inertia weight with a parameter adaptation mechanism. PSONHM keeps a historical memory with k entries for inertia weight w. At first, the value of historical memory Mw with k entries at the first generation is all initialized as follows. c0 is set to 0.5. The index determines the inertia weight wq that is to update in the memory:
where Norm(•) is Gaussian distribution.
In each generation, the inertia weight wr used by each particle is generated with a random index r within the range [1, k]. The wr used by successful particle is recorded in Sw. At the end of the generation, the memory is updated as follows:
At first, q is initialized to 1. When a new inertia weight w is inserted into the memory, q is increased. If q > k, q is reset to 1. If the population fails to generate a promising particle, which is better than the parent, the memory is not updated. Otherwise, the qth inertia weight in the memory is updated. c0 is set to 0.5. MaxFES is the maximum number of fitness evaluations. The weighted Lehmer mean meanw (Sw) is computed as follows, which is proposed in [43]:
where Δfk = |f(xk,G) − f(xk,G-1)| is the amount of fitness improvement, which is used to influence the parameter adaptation.
The pseudo-code of PSONHM is illustrated in Algorithm 1. NP is the population size. H, which is the number of neighbors, is set to 5. k is the number of inertia weight values in the memory and is set to 5. T, which is the stagnation tolerance value, is set to 3. CR is the crossover factor.
| Algorithm 1. PSONHM Algorithm. |
| 1: Initialize D(number of dimensions), NP, H, k, T, c0, c1 and c2 2: Initialize population randomly 3: Initialize position xi, velocity vi, personal best position pbesti, competitor of pbesti and global best position gbest of the NP particles (i = 1, 2, …, NP) 4: Initialize Mw,q according to Equation (8) 5: Index counter q = 1 6: while the termination criteria are not met do 7: Sw = ϕ 8: for i = 1 to NP do 9: r = Select from [1, k] randomly 10: w = Mw,r 11: if ti > = T 12: Compute velocity vi with neighborhood strategy according to Equation (4) 13: Update velocity vi by crossover operation according to Equations (5) and (6) 14: else 15: Compute velocity vi according to Equation (1) 16: end if 17: Update position xi according to Equation (2) 18: Calculate objective function value f(xi) 19: Calculate ti for next generation according to Equation (7) 20: end for 21: Update pbesti, gbest, and the competitor of pbesti (i = 1, 2, …, NP) 22: Update Mw,q based on Sw according to Equation (9) 23: q = q + 1 24: if q > k, q is set to 1 25: end while Output: the particle with the smallest objective function value in the population. |
4. Experiments and Discussion
In this section, CEC2014 contest benchmark problems, which are widely adopted in numerical optimizaiton methods, are used to verify the performance of the PSONHM algorithm. The general experimental setting is explained in Section 4.1. The experimental results and comparison with other algorithms are explained in Section 4.2.
4.1. General Experimental Setting
(1) Test Problems and Dimension Setting: To verify the performance of PSONHM, CEC2014 [44] contest benchmark problems are used. According to their diverse characteristics, these test problems can be divided into four kinds of optimization problems [44]:
- unimodal problems f1–f3,
- simple multimodal problems f4–f16,
- hybrid problems f17–f22, and
- composite problems f23–f30.
The search space is [−100, 100]D for the optimization problems. D denotes the dimension and is set to 30 in this paper.
(2) Experimental Platform and Termination Criterion: All the experiments are run on a PC with a Celeron 3.40 GHz CPU (City, US State abbrev. if applicable, Country) and 4 GB memory. Each problem is executed for 30 runs with the maximal number of function evaluations (FES) D × 10,000.
(3) Performance Metrics: The metrics, such as Fmean (mean value), SD (standard deviation), Max (maximum value) and Min (minimum value) of the solution error measure [45], are used to appraise the performance of each algorithm. The solution error measure is defined as f(x) − f(x*). f(x) is the best fitness value and f(x*) is the real global optimization value. The error will be recorded as 0 when the value f(x) − f(x*) is less than 10−8. In view of statistics, the Wilcoxon signed-rank test [46] at the 5% significance level is used to compare PSONHM with other compared algorithms. “≈”, “+” and “−” are applied to express the performance of PSONHM is similar to, worse than, and better than that of the compared algorithm, respectively.
(4) Control parameters: PSONHM is compared with PSO, PSOcf, TLBO (Teaching-Learning-Based Optimization) [47], Jaya [48], GSA (Gravitational Search Algorithm) [49], BBO, CoDE (Differential evolution with composite trial vector generation strategies and control parameters) [46] and FPSO (Fuzzy Adaptive Particle Swarm Optimization) [50]. Default parameters settings for these algorithms are given in Table 1.

Table 1.
Default parameters settings.
For most intelligent algorithms, the size of the population plays a significant role in controlling the convergence rate. Small population sizes may result in faster convergence, but increases the risk of premature convergence. On the contrary, large population sizes tend to explore widely, but reduce the rate of convergence. There are many studies on the population size of the optimization algorithms. Different population size of the same algorithm may result in different performance. Therefore, without loss of generality, the settings used for the competing algorithms are selected on the basis of the original papers. For PSONHM, we make experiments to study the influence of different population size N. The experimental results show that both smaller population size and larger population size are not the best choice for PSONHM. Therefore, the population size of PSONHM is recommended to set as the value 100, which is based on the result of the experiments.
4.2. Comparison with Nine Optimization Algorithms on 30 Dimensions
The statistical results, in terms of Fmean, SD, Max and Min obtained in 30 independent runs by each algorithm, are reported in Table 2.

Table 2.
Experimental results of PSO, PSOcf, TLBO, Jaya, GSA, BBO, CoDE, FPSO and PSONHM on f1–f3.
(1) Unimodal problems f1–f3
From the statistical results of Table 2, we can see that PSONHM performs well on f1–f3 for 30 dimensions. For f1–f3, PSONHM works better than PSO, PSOcf, TLBO, Jaya, GSA, BBO, CoDE and FPSO on 3, 3, 2, 3, 3, 3, 1, 3 test problems, respectively. The overall ranking sequences for the test problems are PSONHM, CoDE, PSO, TLBO, FPSO, BBO, PSOcf (GSA) and Jaya in a descending direction. The average rank of PSOcf is the same as that of GSA. For unimodal problems f1–f3, the results indicate that the inertia weight, which is updated adaptively, is helpful for PSONHM to find the area where the potential optimal solution existed and converge to the optimal solution quickly.
(2) Simple multimodal problems f4–f16
Considering the simple multimodal problems f4–f16 in Table 3, PSONHM outperforms other algorithms on f5, f6, f7, f9, f12, f13 and f15. CoDE performs well on f4. BBO performs well on f8, f10, f11 and f16. TLBO performs well on and f14. PSONHM performs better PSO, PSOcf, TLBO, Jaya, GSA, BBO, CoDE and FPSO on 12, 12, 11, 13, 13, 6, 11 and 12 test problems, respectively. The overall ranking sequences for the test problems are PSONHM, BBO, PSO, CoDE (FPSO), TLBO, PSOcf, Jaya and GSA in a descending direction. The average rank of CoDE is the same as that of FPSO. The results indicate that PSONHM generally offered better performance in most of the simple multimodal problems, though it worked slightly worse on several problems. Due to the neighborhood mechanism, the population makes full use of the information from its neighbors and the competitor, and guides the evolution process successfully toward more promising solutions.

Table 3.
Experimental results of PSO, PSOcf, TLBO, Jaya, GSA, BBO, CoDE, FPSO and PSONHM on f4–f16.
(3) Hybrid problems f17–f22
The results in Table 4 show that PSONHM performs better than other compared algorithms except CoDE. The overall ranking sequences for the test problems are CoDE, PSONHM, TLBO, PSO, FPSO, BBO, PSOcf, GSA and Jaya in a descending direction. Because of the crossover operation, which is utilized to enhance the potential diversity of the population, PSONHM can avoid premature convergence with a higher probability and show better performance than most compared algorithms on these hybrid problems.

Table 4.
Experimental results of PSO, PSOcf, TLBO, Jaya, GSA, BBO, CoDE, FPSO and PSONHM on f17–f22.
(4) Composite problems f23–f30
The composite problems are very complex and time-consuming because they combine multiple test problems into a complex landscape. Thus, it is difficult for optimization algorithms to achieve better solutions. Table 5 shows that the overall ranking sequences for the test problems are GSA, PSONHM, CoDE (TLBO), BBO, PSO, FPSO, Jaya and PSOcf in a descending direction. The average rank of CoDE is the same as that of TLBO. The results indicate that the neighborhood mechanism can not effectively solve the composite problems.

Table 5.
Experimental results of PSO, PSOcf, TLBO, Jaya, GSA, BBO, CoDE, FPSO and PSONHM on f23–f30.
All in all, PSONHM performs better than the compared algorithms when considering f1–f30 on 30 dimensions. Table 6 indicates PSONHM is competitive on CEC2014 test problems. PSONHM outperforms other algorithms on f2, f5, f6, f7, f9, f12, f13, f15, f19, f22 and f26. CoDE performs well on f1, f3, f4, f17, f18, f20 and f21. BBO performs well on f8, f10, f11 and f16. TLBO performs well on and f14, f24 and f25. GSA outperforms other algorithms on f23, f27, f28, f29 and f30. The total ranking orders on 30 test problems are PSONHM, CoDE, TLBO, PSO, BBO, FPSO, GSA, PSOcf and Jaya in a descending direction. Figure 3 shows the convergence curves for sixteen of the 30-dimensional CEC2014 benchmark problems. The curves illustrate mean errors (in logarithmic scale) in 30 independent simulations of PSO, PSOcf, TLBO, Jaya, GSA, BBO, CoDE, FPSO and PSONHM. As mentioned above, the curves indicate that, in most problems, PSONHM either achieves a fast convergence or behaves similarly to it.

Table 6.
Comparison of PSONHM with PSO, PSOcf, TLBO, Jaya, GSA, BBO, CoDE and FPSO on the CEC2014 benchmarks (D = 30 dimensions).
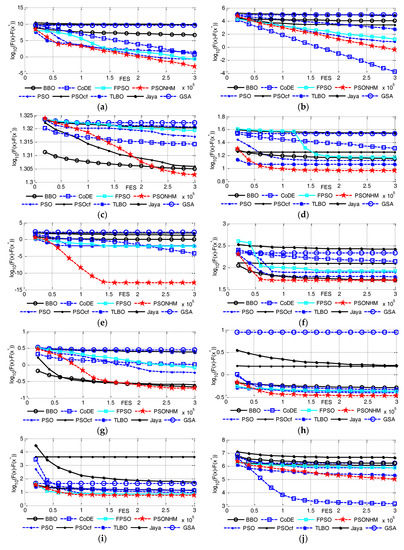
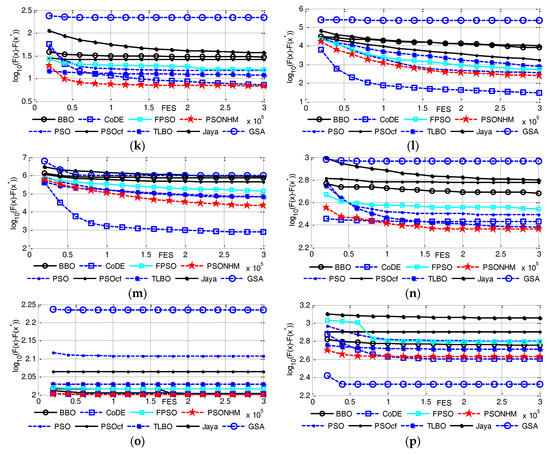
Figure 3.
Evolution of the mean function error values derived from PSO, PSOcf, TLBO, Jaya, GSA, BBO, CoDE, FPSO and PSONHM versus the number of FES on sixteen test problems with D = 30. (a) f2; (b) f3; (c) f5; (d) f6; (e) f7; (f) f9; (g) f12; (h) f13; (i) f15; (j) f17; (k) f19; (l) f20; (m) f21; (n) f22; (o) f26; (p) f27.
The experiment results reveal that PSONHM can work well for most test problems because of the use of neighborhood mechanism and the adaptive inertia weight assignments based on historical memory. With the interaction of the best particles, the neighborhood particles and the competitors, the neighborhood exploration mechanism is designed to guide the search better in the next generation. It is helpful for PSONHM to explore and find the area where the potential optimal solution is existed. The risk of premature convergence is decreased as much as possible. After neighborhood exploration, PSONHM utilizes the crossover operation to enhance the potential diversity of the population. The convergence rate of algorithm is obviously improved because of learning from previous experience. In addition, the inertia weight is adaptively adjusted based on the historical memory, where the better inertia weight preserved in each generation. Then, the probability of finding better solutions is greater and this is helpful for improving the performance of the proposed algorithm. Thus, the exploration and exploitation are done during the optimization process. Accordingly, PSONHM can not only improve the convergence rate of algorithm but can also decrease the risk of premature convergence as much as possible.
5. PSONHM for Training an MLP
In this section, the proposed PSONHM algorithm is applied to solve two classification problems by training an MLP. The basic structure of the proposed scheme is depicted in Figure 4.
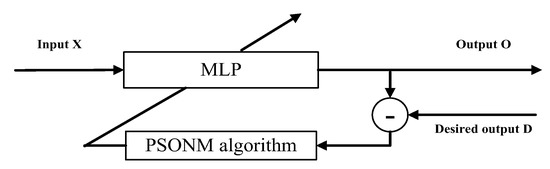
Figure 4.
PSONHM-based MLP.
5.1. Multi-Layer Perceptron
In this section, the proposed algorithm is used for training MLPs. There are three layers in MLP: input layer, hidden layer and output layer. Figure 5 shows a multi-layer perceptron for neural network architecture. These layers are interconnected by links called weights. The outputs of hidden nodes (Sj, j = 1, …, H) are calculated by an activation function, which is defined as follows:
where n is the number of the input nodes, Wij is the connection weight from the ith node in the input layer to the jth node in the hidden layer. Xi shows the ith input node. denotes the threshold.
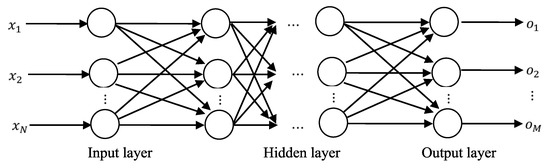
Figure 5.
Multi-layer perceptron for neural network architecture.
After calculating the outputs of hidden nodes, the final outputs (Ok, k = 1, …, m) are calculated by applying a sigmoid function:
where denotes the threshold of the kth output node. Wjk is the connection weight from the jth node in the hidden layer to the kth node in the output layer.
The aim of training MLPs is to find a set of weights with the smallest error measure. The objective function is the mean sum of squared errors (MSE) over all training patterns, which is shown as follows:
where Q is the number of training data set, K is the number of output units, dij is desired output and oij is actual output of the ith input node.
Finally, the objective function uses MSE to evaluate the fitness of the individuals in each optimization algorithm. The fitness of the ith training sample is calculated by:
Fitness (Xi) = MSE (Xi).
5.2. Classification Problems
In this section, PSONHM is evaluated on the classification datasets Iris and Balloon, and the two datasets are obtained from the University of California at Irvine (UCI) Machine Learning Repository [51]. The metrics, such as MSEmean (mean value), MSEstd (standard deviation), MSEmax (maximum value) MSEmin (minimum value) of MSE, and Classification rate are used to appraise the performance of each algorithm.
To provide a fair comparison, all algorithms were terminated when a maximum number of fitness evaluations (MaxFES = 50,000) were reached. The mean trained MLP with 10 runs is chosen and used to classify the test set. The performance of the different algorithms for Iris problem and Balloon problem is presented in Table 7 and Table 8.

Table 7.
Experimental results for the Iris dataset.

Table 8.
Experimental results for the Balloon dataset.
5.2.1. Iris Flower Classification
The Iris flower classification is a three-class problem with 150 samples. Each sample consists of four features, namely sepal length, sepal width, petal length, and petal width. Iris flower classification was solved using MLPs with four inputs, nine hidden nodes and three output nodes. The experimental results are shown in Table 7 and Figure 6.
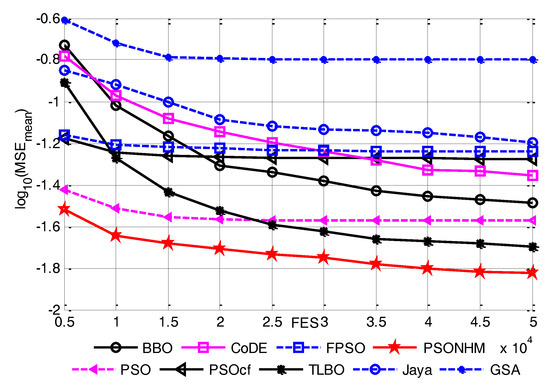
Figure 6.
Convergence curves of nine algorithms for the Iris dataset.
The MSE results show that PSONHM manages to solve the Iris flower classification with high accuracy compared PSO, PSOcf, TLBO, Jaya, GSA, BBO, CoDE and FPSO. The overall ranking sequences for MSEmean are PSONHM, TLBO, PSO, BBO, CoDE, PSOcf, FPSO, Jaya and GSA in a descending direction. The overall ranking sequences for classification rate are PSONHM, TLBO, PSOcf, PSO, FPSO, BBO, Jaya, CoDE and GSA in a descending direction. The classification rate is 93.40% for PSONHM, more than all the other algorithms. Figure 6 shows the convergence curves of nine algorithms. It can be seen that the convergence rate of PSONHM is much faster than all other algorithms.
5.2.2. Balloon Classification
The Balloon dataset has 16 samples that are divided into two classes: inflated or not. All samples have four attributes such as color, size, act, and age. This dataset is solved by employing MLP with four input nodes, nine hidden nodes, and one output node. The experimental results are shown in Table 8 and Figure 7.
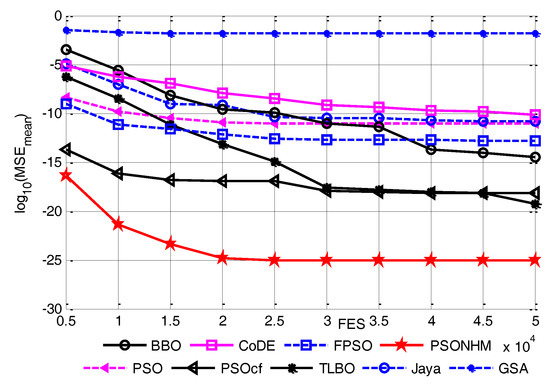
Figure 7.
Convergence curves of nine algorithms for the Balloon dataset.
The MSE results show that the classification rate is 100% for all the algorithms except GSA. The classification rate of GSA is 49.50%. As shown in Table 8, the overall ranking sequences for MSEmean are PSONHM, TLBO, PSOcf, BBO, FPSO, PSO, Jaya, CoDE and GSA in a descending direction. PSONHM achieves the minimum error on the balloon classification problem. In addition, it can be seen that the convergence of PSONHM is faster than other compared algorithms.
6. Conclusions
PSO shows better performance in exploitation but worse performance in exploration. It is difficult for the particles to jump out of the local optimal region because all the particles are attracted by the same global best particle, which limits the exploration ability of PSO. In this paper, we proposed an improving particle swarm optimization algorithm based on neighborhood and historical memory (PSONHM). In the proposed algorithm, the experience of its neighbors and its competitors is considered to decrease the risk of premature convergence as much as possible. Furthermore, the several best particles are selected instead of gbest to guide the swarm towards a new better space in the search process. Finally, the parameter adaptation mechanism is designed to generate new inertia weight. By comparing the experimental results with those from other algorithms on CEC2014 test problems and two benchmark datasets (Iris and Balloon), it can be concluded that the PSONHM algorithm significantly improves the performance of the original PSO algorithm.
In the future, the efficiency of PSONHM in training other types of ANN is worthy of study (e.g., Radia basis function networks, Kohonen networks, etc.). In addition, employing PSONHM to design an evolutionary neural network method is worth investigating. Finally, PSONHM will be expected to solve the multi-objective optimization problems and constrained optimization problems.
Acknowledgments
This research is supported by the support of the Doctoral Foundation of Xi’an University of Technology (112-451116017), and the National Natural Science Foundation of China under Project Code (61773314).
Conflicts of Interest
The author declares no conflict of interest.
References
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Let A Biogeography-Based Optimizer Train Your Multi-Layer Perceptron. Inf. Sci. 2014, 268, 188–209. [Google Scholar] [CrossRef]
- Rosenblatt, F. The Perceptron, a Perceiving and Recognizing Automaton Project Para; Cornell Aeronautical Laboratory: Buffalo, NY, USA, 1957. [Google Scholar]
- Werbos, P. Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. Ph.D. Thesis, Harvard University, Cambridge, MA, USA, 1974. [Google Scholar]
- Askarzadeh, A.; Rezazadeh, A. Artificial neural network training using a new efficient optimization algorithm. Appl. Soft Comput. 2013, 13, 1206–1213. [Google Scholar] [CrossRef]
- Gori, M.; Tesi, A. On the problem of local minima in backpropagation. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 76–86. [Google Scholar] [CrossRef]
- Mendes, R.; Cortez, P.; Rocha, M.; Neves, J. Particle swarms for feedforward neural network training. In Proceedings of the 2002 International Joint Conference on Neural Networks, Honolulu, HI, USA, 12–17 May 2002; pp. 1895–1899. [Google Scholar]
- Demertzis, K.; Iliadis, L. Adaptive Elitist Differential Evolution Extreme Learning Machines on Big Data: Intelligent Recognition of Invasive Species. Adv. Intell. Syst. Comput. 2017, 529, 1–13. [Google Scholar]
- Seiffert, U. Multiple layer perceptron training using genetic algorithms. In Proceedings of the European Symposium on Artificial Neural Networks, Bruges, Belgium, 25–27 April 2001; pp. 159–164. [Google Scholar]
- Blum, C.; Socha, K. Training feed-forward neural networks with ant colony optimization: An application to pattern classification. In Proceedings of the International Conference on Hybrid Intelligent System, Rio de Janeiro, Brazil, 6–9 December 2005; pp. 233–238. [Google Scholar]
- Tian, G.D.; Ren, Y.P.; Zhou, M.C. Dual-Objective Scheduling of Rescue Vehicles to Distinguish Forest Fires via Differential Evolution and Particle Swarm Optimization Combined Algorithm. IEEE Trans. Intell. Transp. Syst. 2016, 99, 1–13. [Google Scholar] [CrossRef]
- Guedria, N.B. Improved accelerated PSO algorithm for mechanical engineering optimization problems. Appl. Soft Comput. 2016, 40, 455–467. [Google Scholar] [CrossRef]
- Segura, C.; CoelloCoello, C.A.; Hernández-Díaz, A.G. Improving the vector generation strategy of Differential Evolution for large-scale optimization. Inf. Sci. 2015, 323, 106–129. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, Q.F.; Fernandez, F.V.; Gielen, G.G.E. An Efficient Evolutionary Algorithm for Chance-Constrained Bi-Objective Stochastic Optimization. IEEE Trans. Evol. Comput. 2013, 17, 786–796. [Google Scholar] [CrossRef]
- Zaman, M.F.; Elsayed, S.M.; Ray, T.; Sarker, R.A. Evolutionary Algorithms for Dynamic Economic Dispatch Problems. IEEE Trans. Power Syst. 2016, 31, 1486–1495. [Google Scholar] [CrossRef]
- CarrenoJara, E. Multi-Objective Optimization by Using Evolutionary Algorithms: The p-Optimality Criteria. IEEE Trans. Evol. Comput. 2014, 18, 167–179. [Google Scholar]
- Cheng, S.H.; Chen, S.M.; Jian, W.S. Fuzzy time series forecasting based on fuzzy logical relationships and similarity measures. Inf. Sci. 2016, 327, 272–287. [Google Scholar] [CrossRef]
- Das, S.; Abraham, A.; Konar, A. Automatic clustering using an improved differential evolution algorithm. IEEE Trans. Syst. Man Cybern. Part A 2008, 38, 218–236. [Google Scholar] [CrossRef]
- Hansen, N.; Kern, S. Evaluating the CMA evolution strategy on multimodal test functions. In Parallel Problem Solving from Nature (PPSN), Proceedings of the 8th International Conference, Birmingham, UK, 18–22 September 2004; Springer International Publishing: Basel, Switzerland, 2004; pp. 282–291. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Černý, V. Thermo dynamical approach to the traveling salesman problem: An efficient simulation algorithm. J. Optim. Theory Appl. 1985, 45, 41–51. [Google Scholar] [CrossRef]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Lam, A.Y.S.; Li, V.O.K. Chemical-Reaction-Inspired Metaheuristic for Optimization. IEEE Trans. Evol. Comput. 2010, 14, 381–399. [Google Scholar] [CrossRef]
- Shi, Y.H. Brain Storm Optimization Algorithm; Advances in Swarm Intelligence, Series Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6728, pp. 303–309. [Google Scholar]
- Kennedy, J.; Eberhart, K. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Bergh, F.V.D. An Analysis of Particle Swarm Optimizers. Ph.D. Thesis, University of Pretoria, Pretoria, South Africa, 2002. [Google Scholar]
- Clerc, M.; Kennedy, J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Krzeszowski, T.; Wiktorowicz, K. Evaluation of selected fuzzy particle swarm optimization algorithms. In Proceedings of the Federated Conference on Computer Science and Information Systems (FedCSIS), Gdansk, Poland, 11–14 September 2016; pp. 571–575. [Google Scholar]
- Alfi, A.; Fateh, M.M. Intelligent identification and control using improved fuzzy particle swarm optimization. Expert Syst. Appl. 2011, 38, 12312–12317. [Google Scholar] [CrossRef]
- Kwolek, B.; Krzeszowski, T.; Gagalowicz, A.; Wojciechowski, K.; Josinski, H. Real-Time Multi-view Human Motion Tracking Using Particle Swarm Optimization with Resampling. In Articulated Motion and Deformable Objects; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7378, pp. 92–101. [Google Scholar]
- Sharifi, A.; Harati, A.; Vahedian, A. Marker-based human pose tracking using adaptive annealed particle swarm optimization with search space partitioning. Image Vis. Comput. 2017, 62, 28–38. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yun, G.J.; Yang, X.S.; Talatahari, S. Chaos-enhanced accelerated particle swarm optimization. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 327–340. [Google Scholar] [CrossRef]
- Mendes, R.; Kennedy, J.; Neves, J. The fully informed particle swarm simpler, maybe better. IEEE Trans. Evol. Comput. 2004, 8, 204–210. [Google Scholar] [CrossRef]
- Liang, J.J.; Qin, A.K.; Suganthan, P.N.; Baskar, S. Comprehensive Learning Particle Swarm Optimizer for Global Optimization of Multimodal Functions. IEEE Trans. Evol. Comput. 2006, 10, 281–295. [Google Scholar] [CrossRef]
- Nobile, M.S.; Cazzaniga, P.; Besozzi, D.; Colombo, R. Fuzzy self-turning PSO: A settings-free algorithm for global optimization. Swarm Evol. Comput. 2017. [Google Scholar] [CrossRef]
- Shi, Y.H.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the IEEE World Congress on Computational Intelligence, Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Shi, Y.H.; Eberhart, R.C. Empirical study of particle swarm optimizaiton. In Proceedings of the IEEE Congress on Evolutionary Computation, Washington, DC, USA, 6–9 July 1999; pp. 1950–1955. [Google Scholar]
- Das, S.; Abraham, A.; Chakraborty, U.K.; Konar, A. Differential evolution using a neighborhood-based mutation operator. IEEE Trans. Evol. Comput. 2009, 13, 526–553. [Google Scholar] [CrossRef]
- Omran, M.G.; Engelbrecht, A.P.; Salman, A. Bare bones differential evolution. Eur. J. Oper. Res. 2009, 196, 128–139. [Google Scholar] [CrossRef]
- Suganthan, P.N. Particle swarm optimiser with neighbourhood operator. In Proceedings of the IEEE Congress on Evolutionary Computation, Washington, DC, USA, 6–9 July 1999; Volume 3, pp. 1958–1962. [Google Scholar]
- Nasir, M.; Das, S.; Maity, D.; Sengupta, S.; Halder, U. A dynamic neighborhood learning based particle swarm optimizer for global numerical optimization. Inf. Sci. 2012, 209, 16–36. [Google Scholar] [CrossRef]
- Ouyang, H.B.; Gao, L.Q.; Li, S.; Kong, X.Y. Improved global-best-guided particle swarm optimization with learning operation for global optimization problems. Appl. Soft Comput. 2017, 52, 987–1008. [Google Scholar] [CrossRef]
- Zhang, J.Q.; Sanderson, A.C. JADE: Adaptive Differential Evolution with Optional External Archive. IEEE Trans. Evol. Comput. 2009, 13, 945–957. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunaga, A. Success-history based parameter adaptation for differential evolution. In Proceedings of the IEEE Congress on Evolutionary Computation, Cancún, Mexico, 20–23 June 2013; pp. 71–78. [Google Scholar]
- Liang, J.J.; Qu, B.Y.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for the CEC 2014 Special Session and Competition on Single Objective Real-Parameter Numerical Optimization; Technical Report; Zhengzhou University and Nanyang Technological University: Singapore, 2013. [Google Scholar]
- Suganthan, P.N.; Hansen, N.; Liang, J.J.; Deb, K.; Chen, Y.P.; Auger, A.; Tiwari, S. Problem Definitions and Evaluation Criteria for the CEC2005 Special Session on Real-Parameter Optimization. 2005. Available online: http://www.ntu.edu.sg/home/EPNSugan (accessed on 9 January 2017).
- Wang, Y.; Cai, Z.X.; Zhang, Q.F. Differential evolution with composite trial vector generation strategies and control parameters. IEEE Trans. Evol. Comput. 2011, 15, 55–66. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching-learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Rao, R.V. Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. Int. J. Ind. Eng. Comput. 2016, 7, 19–34. [Google Scholar]
- Rashedi, E.; Nezamabadi, S.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Shi, Y.H.; Eberhart, R.C. Fuzzy adaptive particle swarm optimization. In Proceedings of the Congress on Evolutionary Computation, Seoul, Korea, 27–30 May 2001; Volume 1, pp. 101–106. [Google Scholar]
- Bache, K.; Lichman, M. UCI Machine Learning Repository. 2013. Available online: http://archive.ics.uci.edu/ml (accessed on 9 January 2017).
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).