Abstract
Lightweight cryptographic solutions are required to guarantee the security of Internet of Things (IoT) pervasiveness. Cryptographic primitives mandate a non-linear operation. The design of a lightweight, secure, non-linear 4 × 4 substitution box (S-box) suited to Internet of Things (IoT) applications is proposed in this work. The structure of the 4 × 4 S-box is devised in the finite fields GF (24) and GF ((22)2). The finite field S-box is realized by multiplicative inversion followed by an affine transformation. The multiplicative inverse architecture employs Euclidean algorithm for inversion in the composite field GF ((22)2). The affine transformation is carried out in the field GF (24). The isomorphic mapping between the fields GF (24) and GF ((22)2) is based on the primitive element in the higher order field GF (24). The recommended finite field S-box architecture is combinational and enables sub-pipelining. The linear and differential cryptanalysis validates that the proposed S-box is within the maximal security bound. It is observed that there is 86.5% lesser gate count for the realization of sub field operations in the composite field GF ((22)2) compared to the GF (24) field. In the PRESENT lightweight cipher structure with the basic loop architecture, the proposed S-box demonstrates 5% reduction in the gate equivalent area over the look-up-table-based S-box with TSMC 180 nm technology.
1. Introduction
Cryptography paves the way for the realization of security in the information technology era. Lightweight cryptographic algorithms are in immense demand in the present decade for Internet of Things (IoT) applications. Industrial IoT systems are ubiquitous in nature and have widespread access through smart devices. They are strictly resource-constrained, and lightweight security solutions are the most suitable option for the security of such systems. The traditional security algorithms, such as Advanced Encryption Standard (AES), are not suitable for IoT devices due to their intense mathematical operations, which are computationally expensive. IoT physical security concerns emphasize the resource constraints and the level of security to be addressed by the lightweight cryptographic algorithms and lightweight cryptographic primitives [1,2,3,4,5,6]. The necessity of lightweight ciphers with compact implementation of the non-linear S-box to realize the practical IoT is addressed in [7,8,9]. The optimal linear and differential cryptanalysis resistance of the lightweight S-box is also analyzed as a major factor. Trends in the lightweight cipher design for IoT are based on two factors: the choice of the non-linear operation and the key schedule [10]. The non-linear operation is mandatory in any cryptographic primitive. The primary non-linear operation in the cryptographic algorithms is the S-box. This work contributes to the finite field hardware design of the combinational, lightweight, optimal S-box suited to IoT devices. An S-box in a finite field is an inversion followed by affine transformation.
The proposed S-box is lightweight in terms of having a smaller number of gates and has adequate security properties, as discussed in the latter sections. The combinational design of the proposed lightweight S-box offers hardware advantages—namely compactness in terms of a smaller number of gates—enables sub-pipelining to improve performance optimization and also enables masking mechanisms to counteract side channel attacks [11]. Hardware implementations of the symmetric cryptographic algorithms have been widely explored in the literature [12,13,14,15,16,17]. However, they report the bare minimal focus on the architectural design of the different symmetric lightweight security ciphers. All the lightweight ciphers defined so far have only look-up table-based S-boxes, which have their own limitations in hardware [18,19,20,21,22,23,24,25].
Sufficient background on the derivation of the hardware structures in the finite fields is given in [26,27,28,29,30]. The finite field design involves the design of the operations in varied sub fields. The isomorphism between the fields and the methods for those transformations has been explained in [31,32,33]. Reference [34] discusses the properties of affine equivalence in AES. Literature to date on lightweight cipher algorithm implementations has concentrated on the gate equivalents in ASIC implementations and RAM-based Field Programmable Gate Array (FPGA) implementations [35,36,37,38,39]. A Boolean S-box using the Karnaugh map and the factorization technique has been designed to achieve a maximum throughput of 51.32 Mbps for the PRESENT cipher architecture for an 8-bit data path [40]. To the best of the knowledge of the authors, this work is the first attempt at the construction of a finite field hardware style for the 4 × 4 S-box.
The rest of the paper is organized as follows: Section 2 reiterates the properties of the optimal S-box. Section 3 explains the design methodology of the proposed work. Section 4 elaborates the construction of the fields, followed by the multiplicative inversion derivation in the composite field in Section 5. Section 6 focuses on the isomorphism between the fields GF (24) and GF ((22)2), and the description of the involved affine transformation is given in Section 7. The proposed hardware structure for the S-box and its implementation are shown in Section 8 and Section 9, respectively. The security analyses of the proposed S-box are presented in Section 10. Section 11 concludes the paper.
2. Properties of the Optimal S-Box
The security of IoT devices needs lightweight cryptographic primitives and they deploy 4 × 4 S-boxes in their cipher definition. The selection of the S-box in the lightweight block ciphers plays an important role in characterizing its security–performance trade-off. The choice of the 4 × 4 S-box for the lightweight constructions results in compact hardware, unlike the 8 × 8 S-box used in the AES. A high volume of the lightweight ciphers and hash functions, namely, PRESENT, RECTANGLE, SPONGENT, ICEBERG, SERPENT, NOEKEON, PRINT and PRINCE, have the 4 × 4 S-box in their structure [41]. The improved hardware performance with fixed level of security margin is attained by the optimal S-box constructions. Let the 4 × 4 bijective S-box be denoted by S in the field . The conditions to be satisfied for the S-box to be optimal are
- (1)
- Bijective, i.e., for any .
- (2)
- Let the difference XOR propagation between the input XOR values (ΔI) and the output XOR values (ΔO) be given by NDs (ΔI, ΔO) = #{x |S(x) ⊕ S (x ⊕ ΔI) = ΔO}; it should be ≤4.
- (3)
- The differential uniformity: i.e., the diffusion of the S-box is given by the .
- (4)
- Let the linear imbalance of the S-box be denoted by Imbs (ΓI, ΓO) = #{x |ΓI .x = ΓO. S(x)} − 8|: it should be ≤4, where ΓI and ΓO are the input and output masks of the S-box linear approximation and “.” is the inner product on .
- (5)
- The linearity of the S-box is given by the
- (6)
- No fixed point, i.e., for any .
S-boxes that satisfy these values are said to be optimal S-boxes [42,43,44]. The smaller the value of diffusion of the S-box, the more secure the S-box is against differential cryptanalysis. Similarly, the smaller the value of linearity of the S-box, the more secure the S-box is against linear cryptanalysis. For an S-box, the number of times that a 1-bit input difference causes a 1-bit output difference and the number of times that a 1-bit input selection pattern causes a 1-bit output selection pattern also determines the differential and linear cryptanalysis resistance of the 4-bit S-boxes.
3. Design Methodology
The finite field theory specifies the mathematical operations in terms of logic gates. The design methodology employs the finite fields in a polynomial basis for the hardware definition of the 4 × 4 S-box. The multiplicative inverse is derived in the composite field, resulting in less hardware complexity. The steps involved in the S-box design are elucidated as follows and are shown in Figure 1.
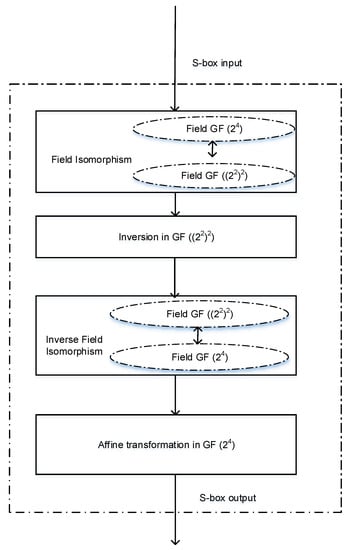
Figure 1.
Design methodology.
- (1)
- The construction of the field GF (2nm=4) in the polynomial basis using the irreducible primitive polynomial of degree 4.
- (2)
- The construction of the composite field GF ((2n=2)m=2) in the polynomial basis using the respective bases.
- (3)
- Derivation of the multiplicative inverse structure in the composite field GF ((2n=2)m=2) using the Euclidean algorithm. The multiplicative inversion involves the subfields GF (2), GF ((2n=2)m=2) and GF (2nm=4).
- (4)
- The isomorphic transformation of the sub fields based on the primitive element of the higher order field.
- (5)
- The affine transformation in the field GF (2nm=4).
- (6)
- Validation of the proposed S-box structure through the physical implementation of the proposed S-box in the one of the lightweight cipher algorithms, PRESENT, and estimation of its hardware performance.
- (7)
- Security analysis of the proposed S-box structure to prove its security strength.
4. Construction of the Fields
The field GF (24) is constructed with the irreducible polynomial of degree 4 in the polynomial basis. There are three irreducible polynomials of degree 4:
A primitive irreducible polynomial generates all the unique 24 = 16 elements of the field GF (24). However, the non-primitive polynomial will not generate all the 16 unique elements. Both the primitive polynomials and are applicable for the GF (24) field generation. The polynomial is a non-primitive polynomial. The proposed work generates the field based on the polynomial . The composite field GF ((2n=2)m=2) is also constructed using the polynomial basis. The process involved in the construction of the composite field GF ((22)2) for the realization of the 4 × 4 S-box employs the following three polynomial bases: B1, B2 and B3.
- B1: The binary extension field employed is the GF (24), and is defined over the prime field GF (2). If is a root of , then the set forms the basis for the field GF (24). Any element A in can be expressed as , where i for i = 0 to 3. The row vector () is called the representation of the element A in the basis B1. This is the polynomial basis for the representation of the field GF (24) over GF (2).
- B2: The irreducible polynomial of degree defined over GF (22) has root . Then, the set is the basis of GF ((22)2). Any element in the basis B2 can be expressed as , where for i = 0, 1. The row vector (, is called the composite field representation of the element A in the basis B2. The coefficients in the composite field representation are in the ground field GF (22).
- B3: The irreducible polynomial of degree over GF (2) constructs the ground field GF (22) with a root and the basis B3. Therefore, any element GF (22) can be written as , where . The row vector ( represents the element GF (22), in the basis B3.
The representations of the different bases involved in the composite field construction are expressed below.
The field has only one irreducible polynomial of degree 2. The field is irreducible with the polynomial of the form with the possible value of in GF (2). The derivation of the multiplicative inverse structure in the composite field is detailed in the next section.
5. Multiplicative Inverse in the Composite Field
The multiplicative inversion and its efficient hardware implementation are the key elements in the structural realization of the S-box. The inversion is calculated using the extended Euclidean algorithm. The multiplicative inverse in the higher order field domain is more complex, and hence the lower order composite field is preferred, with all the arithmetic operations performed in the lower domain. The composite field GF ((22)2) with the suitable values of n = 2 and m = 2, for k = 2 × 2 = 4, is generated based on the respective degree field polynomials.
The multiplicative inverse in the composite field is realized by the following steps:
- (1)
- Isomorphic transformation from the higher order field representation to the lower order composite field representation .
- (2)
- Multiplicative inversion in the composite field using the Euclidean theorem.
- (3)
- Inverse isomorphic transformation of the result obtained by the multiplicative inverse, to the higher order field .
6. Isomorphism and Field Polynomials
The calculation of the multiplicative inverse in the lower field offers an advantage as discussed in Section 3. The computation of inverse in the composite field cannot be applied directly in . Therefore, every element needs to be mapped to its composite field representation via isomorphic mapping and vice versa. Such an isomorphism provides the conversion of the field representations. The derivations of the conversion matrix to establish the isomorphism between the fields is evaluated through any one of the two mechanisms mentioned below:
- (1)
- Construction of the conversion matrix between and , where the generation polynomials are known a priori through an exhaustive search method.
- (2)
- Construction of the conversion matrix, in which the generator polynomial is not known a priori nor fixed. In this field conversion, the isomorphism between the fields is derived based on the primitive or the non-primitive polynomials. The primitive elements of the irreducible polynomials are the key for the isomorphic transformations in this technique.
This work employs the primitive element method for its isomorphism. The manipulations involved for the base representations, the minimal polynomials involved and the conversion mechanism are explained in the following sub sections.
6.1. Minimal Polynomials for the Composite Field Conversion
The two different fields, namely over over , have the following minimal polynomials:
- (1)
- With and the composite field is constructed with as the ground field. The minimal polynomial of for the composite field construction is given asThe polynomial is an irreducible polynomial of degree 2 with coefficients in . The subfield is . The operation in the field is performed in over .
- (2)
- The minimal polynomial of for the field over construction is given asThe polynomial is an irreducible polynomial of degree 4 with coefficients in . The primitive polynomial used for the field construction is a polynomial of degree whose coefficients are in .
6.2. Evaluation of the Conversion Matrix
The conversion from the composite field representation to the binary representation based on the primitive elements is explained below. The primitive polynomial involved in the construction of with root is given by and is a primitive element in . The elements A in in basis B1 is given by
The primitive element for the composite field construction is expressed in the ground field . The irreducible polynomial used to construct over is given by as and it is of degree 2 with the coefficients from the ground field .
The reduction of the polynomial as evaluate to the form as given below.
where is in .
The elements of A in the field in basis 2 can be written as , where . Using as the primitive element, the can be expressed as .
Substituting this expression for , the elements of A are arrived at as given below.
Reducing this using , the element can now be expressed as
Comparison of the elements on the basis B1 and B2, the following equations relating the coefficients can be derived as follows:
Based on relations (13) to (16) cited above, the conversion matrix from the binary field to the composite field and vice versa are shown below.
Conversion matrix from to
Conversion matrix from
The discussions made so far pertained to the processes involved in finding the multiplicative inverse and the necessary isomorphic transformations between the different fields. The affine transformation chosen for the S-box is explained in Section 7.
7. Affine Transformation
The affine transformation resists interpolation attacks and wraps algebraic manipulations so that it is less vulnerable to such attacks. An appropriate affine transform resists the interpolation attacks without causing damage to the resistance of the linear and differential cryptanalysis properties of the multiplicative inverse operation. The affine transformation is a scaling operation followed by addition with an affine constant. The affine and inverse transformations are given by
where ‘a’ and ‘’ are 4 × 4 matrices and ‘b’ is a 4 × 1 matrix.
The expression for the affine transformation and the inverse affine transformation are represented in Equations (21) and (22) respectively.
The hardware structures of the affine transformation are also implemented based on the finite field arithmetic. All the related composite field arithmetic operations and the hardware realization of the individual substructures for implementation of inversion in the field are discussed in Section 8.
8. Overall S-Box Structure and Substructures
This section presents the overall structure of the proposed 4 × 4 S-box. Figure 2 depicts the overall structure in the field derived using the Euclidean approach. The structure of the sub operations in the field are shown in Figure 3, Figure 4 and Figure 5. Note that, in the finite field, all the arithmetic operations are expressed in terms of the AND and XOR gates. Table 1 lists the symbols employed for each of these operation involved in the structure.
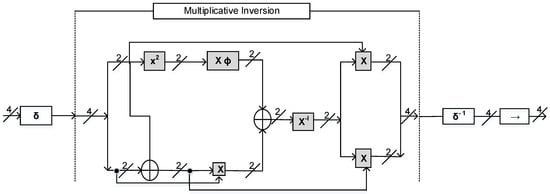
Figure 2.
Proposed S-box structure in finite fields. The affine and the inverse transformations are carried out in the field and the multiplicative inversion is carried out in the composite field .
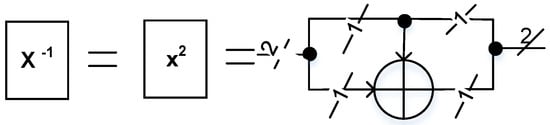
Figure 3.
Squarer/Fermat inversion in the composite field . Fermat’s inversion and the squarer have a similar structure in and employ only a single XOR gate.
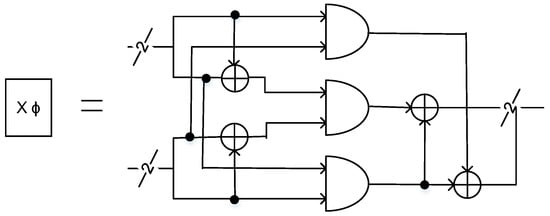
Figure 4.
Multiplier in the composite field . The 2 × 2 multiplier in the employs three XOR gates and three AND gates.
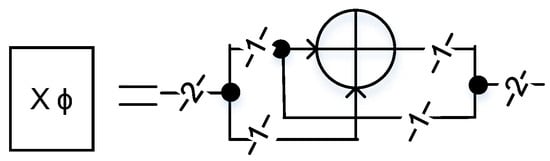
Figure 5.
Multiply with constant The constant multiplier employs only a single XOR gate in .

Table 1.
Symbolic representation of the substructures.
9. Hardware Performance in Block Ciphers
The proposed S-box is depicted in Table 2. The gate counts required for the individual sub operations in the composite field and are shown in Table 3. To demonstrate the efficiency of the proposed S-box in the block cipher hardware, the same is replaced in the substitution operation of the PRESENT cipher definition, and the performance results are given in Table 4. Performance estimation is done in terms of comparison of the gate equivalent (GE) area with the existing lightweight cipher ASIC implementations. It can be observed that the structure with the proposed S-box exhibits a smaller GE area compared to the look-up-table-based S-box implementation in the PRESENT cipher.

Table 2.
Proposed S-box.

Table 3.
Individual gate counts of the substructures in and .

Table 4.
Comparisons of the related works.
Note that the proposed S-box is applicable to any of the ciphers which employ a 4-bit substitution definition. The non-look-up-table-based S-box structure has the added advantage of further sub pipelining mechanisms to improve the throughput. The PRESENT basic loop architecture with the proposed S-box is specified in the VERILOG HDL and is implemented using the TSMC 0.18 µm standard cell library. The Cadence® nclaunch simulator has been used for the functional simulation. The PRESENT cipher with a block length of 64 bits and key length of 80 bits were chosen for the implementation. Reduction of gate count for the sub field operations is observed to be 86.5% in the composite field compared to the field A 5% lesser gate equivalent area is arrived at with the proposed S-box in the PRESENT lightweight cipher loop architecture in comparison with the look-up-table-based S-box in the same architecture. The security analysis of the impact of the S-box in the lightweight block ciphers has displayed satisfactory performance results and is explained as pertaining to security analysis in the following section.
10. Security Analysis
The characteristics of the S-box should resist linear and differential cryptanalysis. The linearity and the diffusion of the S-box reflect its strength with respect to the linear and differential cryptanalysis. The proposed substitution has the security characteristics that resist both the linear and differential cryptanalysis.
10.1. Linear Cryptanalysis
Linear cryptanalysis is a chosen plaintext attack that captures the highly probable linear relationship between the input plain texts and the resultant cipher texts. The proposed optimal S-box has a linearity of 4, as noted from the linear approximation structure in Table 5.

Table 5.
Linear approximation table of the proposed S-box.
The high probability linear approximation over the number of rounds will exploit the secret information without any knowledge of the intermediate values. The linear approximation of the only non-linear component in the cipher structure, i.e., the S-box over the rounds, will be concatenated using the pilling-up lemma in order to calculate the upper bound of linearity. The maximal bound is proportional to the number of active S-boxes in each of the rounds. The more the number of active S-boxes in each round, the better is the linear cryptanalysis resistance. In order to determine the maximal bound, the worst scenario of one active S-box in each round is taken into consideration. The r − 1 linear approximation probability is given as follows:
Here, || represents the maximum linear approximation probability bias of the S-box and is 2−2 for the proposed optimal S-box. The value of r = 32 is the number of rounds of the cipher. The number of plain texts required to perform the linear cryptanalysis is proportional to . Hence, 264 plaintexts are required, which is not practically possible. Note that the analysis has been done for the upper bound of one active S-box per round as indicated above, and hence the proposed S-box in the cipher provides better linear cryptanalysis resistance as the S-box in the existing lightweight block ciphers.
10.2. Differential Cryptanalysis
Differential cryptanalysis is also a chosen plain text attack, which focuses the high differential probability between the plain texts and cipher texts. The difference distribution table shows the XOR profile of the S-boxes which demands diffusion in its distribution of the input XOR profile, with respect to the output XOR profile. The proposed optimal S-box has a diffusion of 4 as seen from the difference distribution table in Table 6.

Table 6.
Difference distribution table of the proposed S-box.
In addition to the linearity property and the linear cryptanalysis resistance, the diffusion and the differential cryptanalysis resistance of the S-box in the cipher needs to be to known to estimate the security margin. The maximal differential bound is estimated by the high differential characteristic probability and the number of active S-boxes involved in each round of the cipher. The maximal differential characteristic probability of the proposed optimal S-box is 2−2. The upper bound on the complexity of the attack is evaluated by considering one active S-box in each round. With one active S-box per round, the expression for the differential characteristic of the cipher with the number of rounds r = 32 are given by
|2−2|r−1 = 2−62
The complexity of the attack is inversely proportional to the differential characteristic probability and is equal to 262. Such a value offers a reasonable limit on the upper bound of the differential characteristic. Hence, the proposed S-box in the cipher offers a sufficient margin of differential cryptanalysis resistance.
11. Conclusions
The primary objective of this work is to design a lightweight, secure optimal S-box that suits IoT applications. The combinational architecture in the finite field for the hardware implementation of the 4 × 4 S-box is presented. The motive for the combinational S-box design is to pave the way for additional optimization mechanisms, namely sub pipelining in the S-box structure. Such hardware optimization is infeasible with the traditional look-up-table-based S-box structure. The choice of the finite field for the hardware design yields all operations: namely multiplication, addition, multiplication with a constant, affine transformation and isomorphic mapping in terms of the logical AND and XOR gates. The hardware structure for the realization of the 4 × 4 S-box has been carried out through extensive mathematical derivations and exploitation of the linear algebra and the finite field theory. The validation of the derived structure is done through the incorporation of the S-box structure in the PRESENT block cipher with the TSMC 0.18 µm technology. The composite field GF ((22)2) based architecture shows less hardware complexity and a reduced gate count compared to its counterpart GF (24). Furthermore, the security analysis of the designed S-box proves its resistance to the linear and differential cryptanalysis.
The research presented in the paper provides further scope for improving the S-box architecture based on the requirements, the implementation choices, the optimization mechanisms and the algorithms employed.
Acknowledgments
The authors thank the management of VIT for the research fecilities provided in the School of Electronics Engineering in the VIT Chennai Campus. Author Contributions: A. Prathiba conceived and designed the work and V. S. Kanchana Bhaaskaran contributed to the analysis and use of tools. Both the authors contributed in prodcuing the paper in the present form.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Singh, S.; Sharma, P.K.; Moon, S.Y.; Park, J.H. Advanced lightweight encryption algorithms for IoT devices: Survey, challenges and solutions. J. Ambient Intell. Hum. Comput. 2017, 1–18. [Google Scholar] [CrossRef]
- Katagi, M.; Moriai, S. Lightweight cryptography for the internet of things. Sony Corp. 2008, 7–10. [Google Scholar]
- Xu, T.; Wendt, J.B.; Potkonjak, M. Security of IoT systems: Design challenges and opportunities. In Proceedings of the 2014 IEEE/ACM International Conference on Computer-Aided Design, San Jose, CA, USA, 2–6 November 2014; pp. 417–423. [Google Scholar]
- Daniel, D.; Le Corre, Y.; Khovratovich, D.; Perrin, L.; Grobschadl, J.; Biryukov, A. Triathlon of Lightweight Block Ciphers for the Internet of Things. 2015. Available online: http://orbilu.uni.lu/bitstream/10993/25565/1/209.pdf (accessed on 1 January 2018).
- McKay, K.A.; Bassham, L.; Turan, M.S.; Mouha, N. Report on Lightweight Cryptography; NIST DRAFT NISTIR 8114; National Institute of Standards and Technology (NIST): Gaithersburg, MD, USA, 2016. [Google Scholar]
- Batra, I.; Luhach, A.K.; Pathak, N. Research and Analysis of Lightweight Cryptographic Solutions for Internet of Things. In Proceedings of the Second International Conference on Information and Communication Technology for Competitive Strategies, Udaipur, India, 4–5 March 2016; p. 23. [Google Scholar]
- Patil, A.; Bansod, G.; Pisharoty, N. Hybrid Lightweight and Robust Encryption Design for Security in IoT. Int. J. Secur. Its Appl. 2015, 9, 85–98. [Google Scholar] [CrossRef]
- Lightweight Cryptography for the IoE. Available online: http://semiengineering.com/lightweight-cryptography-for-the-ioe/ (accessed on 10 January 2016).
- Shamir, A.; Biryukov, A.; Perrin, L.P. Summary of an Open Discussion on IoT and Lightweight Cryptography. In Proceedings of Early Symmetric Crypto Workshop; University of Luxembourg: Luxembourg, 2017. [Google Scholar]
- Biryukov, A.; Perrin, L. State of the Art in Lightweight Symmetric Cryptography; International Association for Cryptologic Research: Esch-sur-Alzette, Luxembourg, 2017. [Google Scholar]
- Wang, Y.; Ha, Y. FPGA-based 40.9-Gbits/s masked AES with area optimization for storage area network. IEEE Trans. Circuits Syst. II Express Briefs 2013, 60, 36–40. [Google Scholar] [CrossRef]
- McLoone, M.; McCanny, J.V. Rijndael FPGA implementations utilising look-up tables. J. VLSI Signal Process. Syst. Signal Image Video Technol. 2003, 34, 261–275. [Google Scholar] [CrossRef]
- Liu, F.; Ji, W.; Hu, L.; Ding, J.; Lv, S.; Pyshkin, A.; Weinmann, R.-P. Analysis of the SMS4 block cipher. ACISP 2007, 4586, 158–170. [Google Scholar]
- Lee, S.W.; Moon, S.-J.; Kim, J.N. High-Speed Hardware Architectures for ARIA with Composite Field Arithmetic and Area-Throughput Trade-Offs. ETRI J. 2008, 30, 707–717. [Google Scholar] [CrossRef]
- Bansod, G.; Raval, N.; Pisharoty, N. Implementation of a new lightweight encryption design for embedded security. IEEE Trans. Inf. Forensics Secur. 2015, 10, 142–151. [Google Scholar] [CrossRef]
- Kitsos, P.; Sklavos, N.; Parousi, M.; Skodras, A.N. A comparative study of hardware architectures for lightweight block ciphers. Comput. Electr. Eng. 2012, 38, 148–160. [Google Scholar] [CrossRef]
- Standaert, F.-X.; Piret, G.; Rouvroy, G.; Quisquater, J.-J. FPGA implementations of the ICEBERG block cipher. Integr. VLSI J. 2007, 40, 20–27. [Google Scholar]
- Li, Z.-R.; Zhuang, Y.-Q.; Zhang, C.; Gang, J.I.N. Low-power and area-optimized VLSI implementation of AES coprocessor for Zigbee system. J. China Univ. Posts Telecommun. 2009, 16, 89–94. [Google Scholar] [CrossRef]
- Good, T.; Benaissa, M. 692-nW Advanced Encryption Standard (AES) on a 0.13-µm CMOS. IEEE Trans. Very Large Scale Integr. Syst. 2010, 18, 1753–1757. [Google Scholar] [CrossRef]
- Wong, M.M.; Wong, M.L.D.; Nandi, A.K.; Hijazin, I. Construction of optimum composite field architecture for compact high-throughput aes s-boxes. IEEE Trans. Very Large Scale Integr. Syst. 2012, 20, 1151–1155. [Google Scholar] [CrossRef]
- Zhang, X.; Parhi, K.K. High-speed VLSI architectures for the AES algorithm. IEEE Trans. Very Large Scale Integr. Syst. 2004, 12, 957–967. [Google Scholar] [CrossRef]
- Satoh, A.; Morioka, S.; Takano, K.; Munetoh, S. A compact Rijndael hardware architecture with S-box optimization. Asiacrypt 2001, 2248, 239–254. [Google Scholar]
- Rudra, A.; Dubey, P.K.; Jutla, C.S.; Kumar, V.; Rao, J.R.; Rohatgi, P. Efficient Rijndael encryption implementation with composite field arithmetic. CHES 2001, 2162, 171–184. [Google Scholar]
- Canright, D. A very compact S-box for AES. In International Workshop on Cryptographic Hardware and Embedded Systems; Springer: Berlin/Heidelberg, Germany, 2005; pp. 441–455. [Google Scholar]
- Wong, M.M.; Wong, M.L.D.; Nandi, A.K.; Hijazin, I. Composite field GF (((22)2)2) Advanced Encryption Standard (AES) S-box with algebraic normal form representation in the subfield inversion. IET Circuits Dev. Syst. 2011, 5, 471–476. [Google Scholar] [CrossRef]
- Savas, E.; Koç, Ç.K. Finite field arithmetic for cryptography. IEEE Circuits Syst. Mag. 2010, 10, 40–56. [Google Scholar] [CrossRef]
- Deschamps, J.-P.; Imaña, J.L.; Sutter, G.D. Hardware Implementation of Finite-Field Arithmetic; McGraw-Hill: New York, NY, USA, 2009. [Google Scholar]
- Baktir, S.; Sunar, B. Optimal tower fields. IEEE Trans. Comput. 2004, 53, 1231–1243. [Google Scholar] [CrossRef]
- Bailey, D.V.; Paar, C. Efficient arithmetic in finite field extensions with application in elliptic curve cryptography. J. Cryptol. 2001, 14, 153–176. [Google Scholar] [CrossRef]
- Olofsson, M. VLSI Aspects on Inversion in Finite Fields; Department of Electrical Engineering, Linköpings Universitet: Linköpings, Sweden, 2002. [Google Scholar]
- Guajardo, J.; Paar, C. Itoh-Tsujii inversion in standard basis and its application in cryptography and codes. Des. Codes Cryptogr. 2002, 25, 207–216. [Google Scholar] [CrossRef]
- Sunar, B.; Savas, E.; Koç, Ç.K. Constructing composite field representations for efficient conversion. IEEE Trans. Comput. 2003, 52, 1391–1398. [Google Scholar] [CrossRef]
- Lv, J.; Kalla, P.; Enescu, F. Efficient gröbner basis reductions for formal verification of Galois field multipliers. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 12–16 March 2012; pp. 899–904. [Google Scholar]
- Youssef, A.M.; Tavares, S.E. Affine equivalence in the AES round function. Discrete Appl. Math. 2005, 148, 161–170. [Google Scholar] [CrossRef]
- El-Sheikh, H.M.; El-Mohsen, O.A.; Elgarf, S.T.; Zekry, A. A new approach for designing key-dependent S-box defined over GF (24) in AES. Int. J. Comput. Theory Eng. 2012, 4, 158. [Google Scholar] [CrossRef]
- Kong, J.H.; Ang, L.-M.; Seng, K.P. A comprehensive survey of modern symmetric cryptographic solutions for resource constrained environments. J. Netw. Comput. Appl. 2015, 49, 15–50. [Google Scholar] [CrossRef]
- Eisenbarth, T.; Kumar, S. A survey of lightweight-cryptography implementations. IEEE Des. Test Comput. 2007, 24, 522–533. [Google Scholar] [CrossRef]
- Sbeiti, M.; Silbermann, M.; Poschmann, A.; Paar, C. Design space exploration of present implementations for FPGAs. In Proceedings of the 5th Southern Conference on Programmable Logic, Sao Carlos, Brazil, 1–3 April 2009; pp. 141–145. [Google Scholar]
- Guo, X.; Chen, Z.; Schaumont, P. Energy and performance evaluation of an FPGA-based SoC platform with AES and PRESENT coprocessors. Lect. Notes Comput. Sci. 2008, 5114, 106–115. [Google Scholar]
- Tay, J.J.; Wong, M.L.D.; Wong, M.M.; Zhang, C.; Hijazin, I. Compact FPGA implementation of PRESENT with Boolean S-Box. In Proceedings of the 6th Asia Symposium on Quality Electronic Design (ASQED), Kula Lumpur, Malaysia, 4–9 August 2015; pp. 144–148. [Google Scholar]
- Bogdanov, A.; Knudsen, L.R.; Leander, G.; Paar, C.; Poschmann, A.; Robshaw, M.J.B.; Seurin, Y.; Vikkelsoe, C. PRESENT: An ultra-lightweight block cipher. CHES 2007, 4727, 450–466. [Google Scholar]
- Leander, G.; Poschmann, A. On the classification of 4 bit S-boxes. In Proceedings of the 1st international Workshop on Arithmetic of Finite Fields, Madrid, Spain, 21–22 June 2007; pp. 159–176. [Google Scholar]
- Zhang, W.; Bao, Z.; Rijmen, V.; Liu, M. A New Classification of 4-bit Optimal S-boxes and its Application to PRESENT, RECTANGLE and SPONGENT. In International Workshop on Fast Software Encryption; Springer: Berlin/Heidelberg, Germany, 2015; pp. 494–515. [Google Scholar]
- Zhang, W.; Bao, Z.; Lin, D.; Rijmen, V.; Yang, B.; Verbauwhede, I. RECTANGLE: A bit-slice lightweight block cipher suitable for multiple platforms. Sci. China Inf. Sci. 2015, 58, 1–15. [Google Scholar] [CrossRef]
- Poschmann, A.Y. Lightweight Cryptography: Cryptographic Engineering for a Pervasive World. Ph.D. Thesis, Ruhr University Bochum, Germany, 2009. [Google Scholar]
- Satoh, A.; Morioka, S. Hardware-focused performance comparison for the standard block ciphers AES, CAMELIA, and Triple-DES. In International Conference on Information Security; Springer: Berlin/Heidelberg, Germany, 2003; pp. 252–266. [Google Scholar]
- Shirai, T.; Shibutani, K.; Akishita, T.; Moriai, S.; Iwata, T. The 128-bit blockcipher CLEFIA. In Proceedings of the 14th International Workshop on Fast Software Encryption—FSE’07, Luxembourg, 26–28 March 2007; pp. 181–195. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).