Efficient Data Collection by Mobile Sink to Detect Phenomena in Internet of Things
Abstract
:1. Introduction
- A distributed energy-efficient algorithm, called Hilbert-order data collection strategy (HCS), to collect environmental data and detect possible phenomena. HCS method uses Hilbert-order method to compute the data collection path of the mobile sink.
- Two data collection optimization techniques, namely Phenomena-aware Collection Technique (PCT) and Lazy Update Technique (LUT), to reduce the data loss and overall energy cost of the network.
- An energy model for the proposed mobile wireless sensor network.
2. Related Work
2.1. Detecting Environmental Phenomena
2.2. Mobile Sinks in WSN
3. HCS Design Issues
3.1. Problem Formulation
3.2. Solution Outline
3.2.1. Sensor Mobility
3.2.2. Time Window
- Group Formation: mobile sensors associate themselves to the nearest GH.
- Local Phenomena Reporting: mobile sensors of each group report the observed phenomena data as well as their status information (remaining battery power, speed and direction) to their GH.
- GHs Election for Next Window: new set of GHs are elected for the next window based on their status and phenomena information.
- Data Collection by Mobile Sink: MS aggregates the collected local phenomena data to form a global phenomenon and computes the new data collection path for the next window.
3.2.3. Data Collection Path
4. Phenomena Detection Using mWSN and MS
- The mobile sensors have prior knowledge of the normal range of values (non-phenomena values).
- The mobile sensors are homogenous; that is they have the same processing power, initial battery life, storage, and communication range.
- Individual mobile sensors may have different speeds and direction.
- The mobile sensors are all distributed on the ground of the monitored field, while the MS flies over at about equal height from GHs.
- GHs are normal mobile sensors.
4.1. HCS for Phenomena Detection
4.2. HCS Algorithm
| Algorithm 1: HCS |
| Input: poi, ssi // poi is Phenomena observation, ssi is Sensor status. |
| Output: GP, DataCollPath // GP is global phenomena; DataCollPath is the computed data collection path for the next window. |
| 1: for each GHi in GHs do |
| 2: broadcastID(GHs) |
| 3: end for |
| 4: for each si in S do |
| 5: if s ∉ GHs |
| 6: AssociateWithClosestGH (GHs) |
| 7: end if |
| 8: end for |
| 9: for each si in S do |
| 10: if si sensed phenomenon |
| 11: reportObservationToGH (po, GH) |
| 12: reportStatusToGH (ss, GH) |
| 13: end if |
| 14: end for |
| 15: for each GHi in GHs do |
| 16: if GHi detected local phenomena |
| 17: LPi = computeLocalPhenomena (all poj) |
| 18: GHinew = electNewGHusingDGH (all ssj, LPi) |
| 19: end if |
| 20: end for |
| 21: for each GHi in GHs do |
| 22: reportLocalPhenomenaToSink (LPi, MS) |
| 23: reportNewGHsToSink (GHinew, MS) |
| 24: end for |
| 25: GP = computeGlobalPhenomena (all LPi) |
| 26: DataCollPath = computeDataCollectionPath (all GHinew) |
| 27: Return GP |
4.3. Optimizations of HCS
4.3.1. PCT
4.3.2. LUT
5. Energy Cost Model
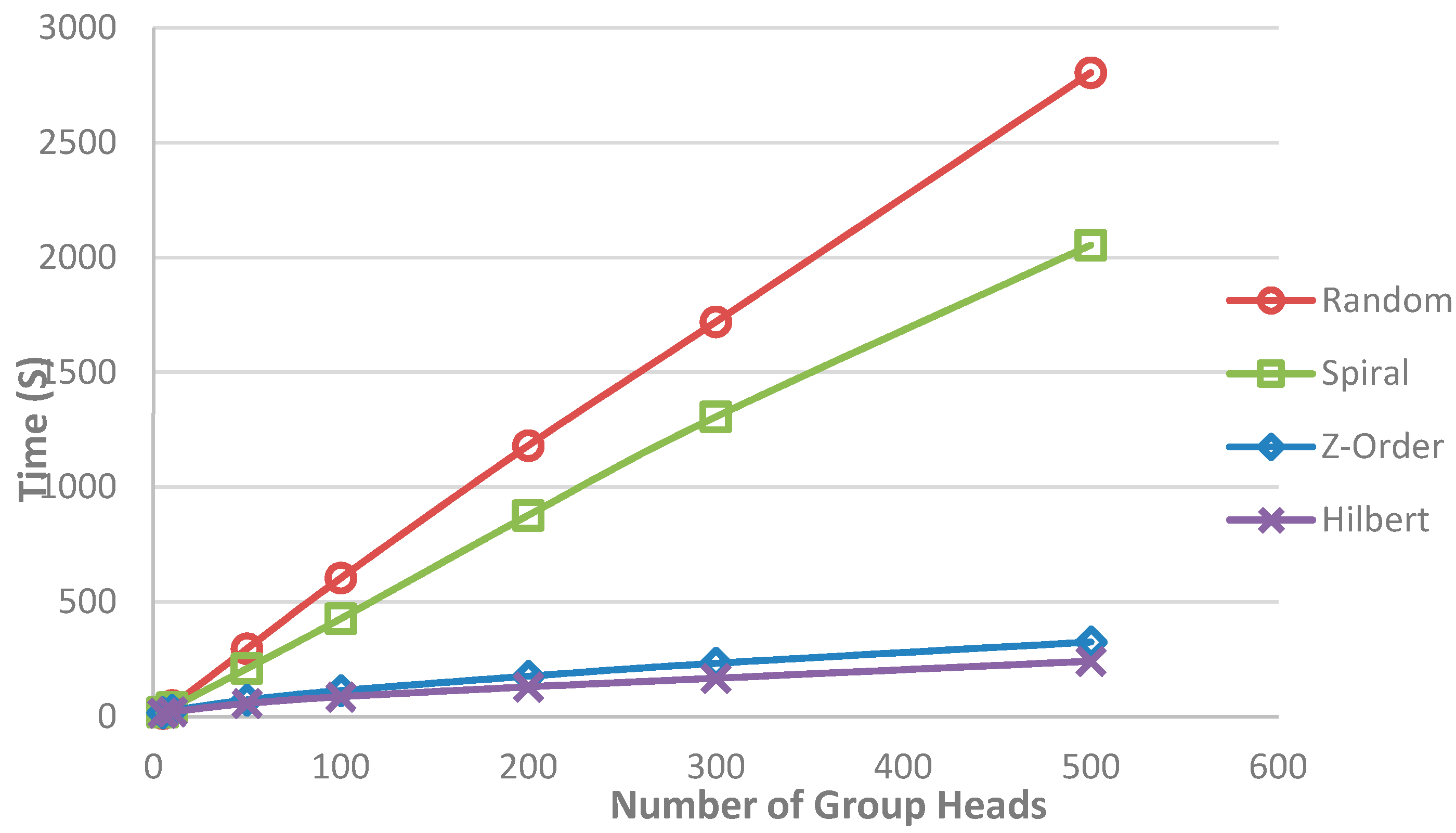
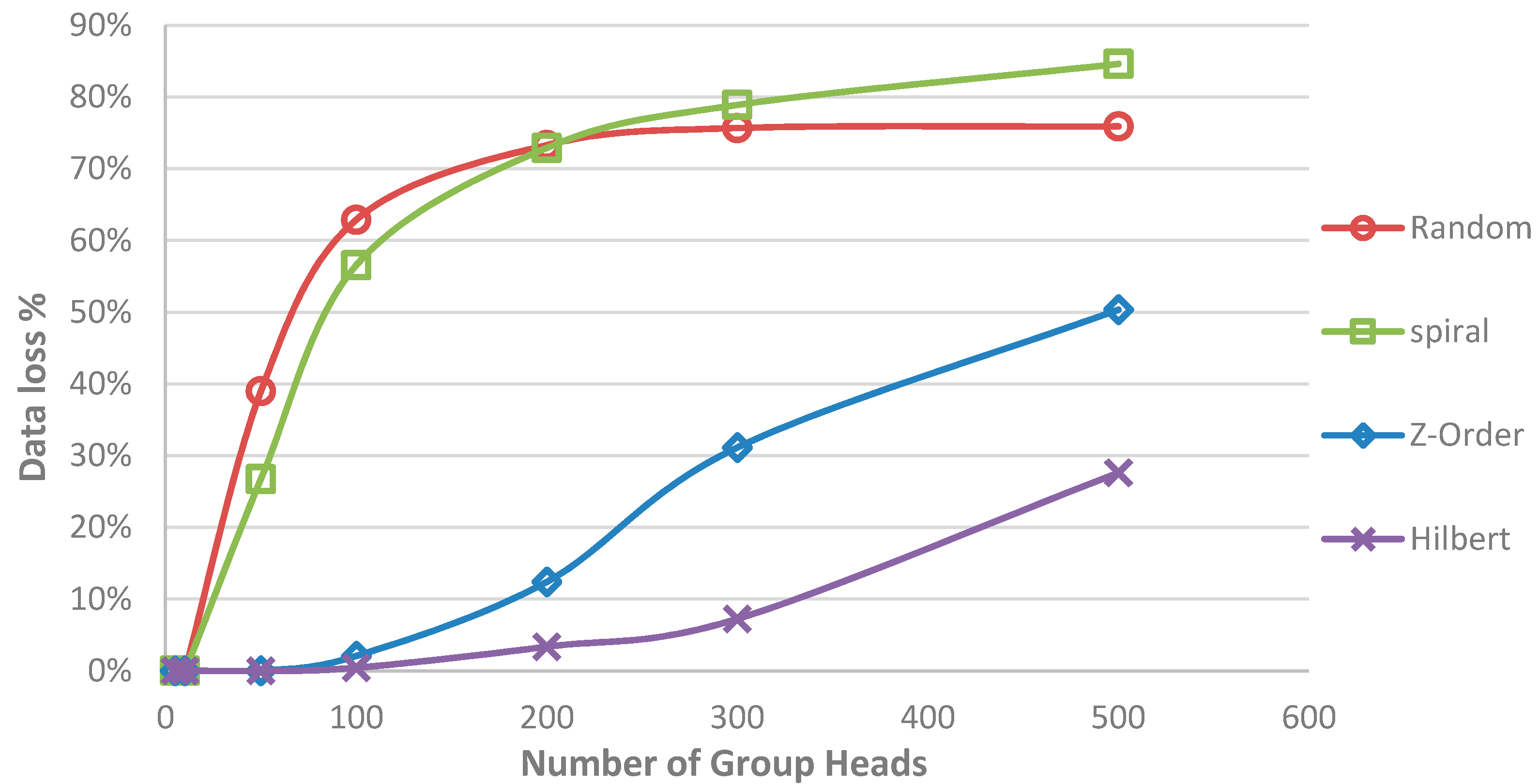
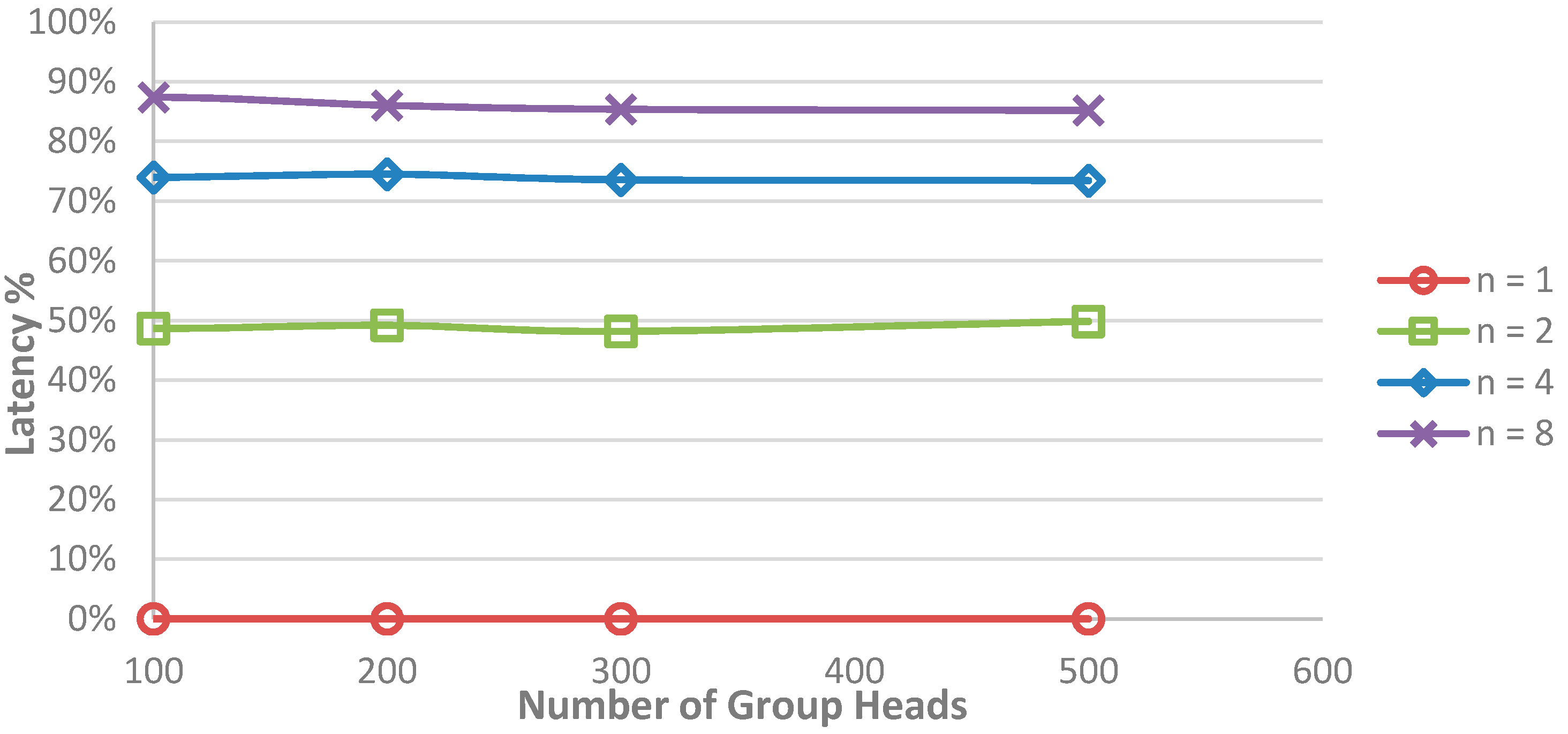
6. Experimental Results
6.1. Evaluation of the Data Collection Strategy
6.2. Evaluation of the Optimization Techniques
6.2.1. Effect of PCT
6.2.2. Effect of LUT
7. Conclusions
Author Contributions
Conflicts of Interest
References
- Zhang, D.; Yang, L.T.; Chen, M.; Zhao, S.; Guo, M.; Zhang, Y. Real-Time Locating Systems Using Active RFID for Internet of Things. IEEE Sens. J. 2016, 10, 1226–1235. [Google Scholar] [CrossRef]
- Al Aghbari, Z.; Kamel, I.; Elbaruni, W. Energy-efficient distributed wireless sensor network scheme for cluster detection. Int. J. Parallel Emerg. Distrib. Syst. 2012, 28, 1–28. [Google Scholar] [CrossRef]
- Safia, A.A.; Al Aghbari, Z.; Kamel, I. Phenomena Detection in Mobile Wireless Sensor Networks. Int. J. Netw. Syst. Manag. 2016, 24, 92–115. [Google Scholar]
- Doolin, D.M.; Sitar, N. Wireless sensors for wildfire monitoring. In Proceedings of the International Society for Optics and Photonicson Smart Structures and Materials, London, UK, 30–31 October 2005; pp. 477–484. [Google Scholar]
- Wichmann, A.; Korkmaz, T. Smooth path construction and adjustment for multiple mobile sinks in wireless sensor networks. Comput. Commun. 2015, 72, 93–106. [Google Scholar] [CrossRef]
- Rajesh, B.; Saravanan, K.A. An Improvised Effective Oceanography Monitoring Using Large Area Underwater Sensor Networks. In Geostatistical and Geospatial Approaches for the Characterization of Natural Resources in the Environment; Janardhana Raju, N., Ed.; Springer: New York, NY, USA, 2016; pp. 691–699. [Google Scholar]
- Bokareva, T.; Hu, W.; Kanhere, S.; Ristic, B.; Gordon, N.; Bessellet, T.; Rutten, M.; Jha, S. Wireless sensor networks for battlefield surveillance. In Proceedings of the Land Warfare Conference, Brisbane, Australia, 24–27 October 2006. [Google Scholar]
- Valverde, J.; Rosello, V.; Mujica, G.; Portilla, J.; Uriarte, A.; Riesgo, T. Wireless sensor network for environmental monitoring: Application in a coffee factory. Int. J. Distrib. Sens. Netw. 2012, 2012, 1–18. [Google Scholar] [CrossRef]
- Hao, X.; Jin, P.; Yue, L. Efficient Storage of Multi-Sensor Object- Tracking Data. IEEE Trans. Parallel Distrib. Syst. 2016, 27, 2881–2894. [Google Scholar] [CrossRef]
- Rao, J.; Biswas, S. Analyzing multi-hop routing feasibility for sensor data harvesting using mobile sinks. J. Parallel Distrib. Comput. 2012, 72, 764–777. [Google Scholar] [CrossRef]
- Zhang, Y.; Meratnia, N.; Havinga, P. Outlier detection techniques for wireless sensor networks: A survey. IEEE Commun. Surv. Tutor. 2010, 12, 159–170. [Google Scholar] [CrossRef]
- Rajasegarar, S.; Leckie, C.; Palaniswami, M.; Bezdek, J.C. Distributed anomaly detection in wireless sensor networks. In Proceedings of the IEEE Singapore International Conference on Communication Systems, Singapore, 30 October–2 November 2006; pp. 1–5. [Google Scholar]
- Kamel, I.; Al Aghbari, Z.; Awad, T. MG-join: Detecting phenomena and their correlation in high dimensional data streams. Distrib. Parallel Databases 2010, 28, 67–92. [Google Scholar] [CrossRef]
- Wittenburg, G.; Dziengel, N.; Wartenburger, C.; Schiller, J. A system for distributed event detection in wireless sensor networks. In Proceedings of the 9th ACM/IEEE International Conference on Information Processing in Sensor Networks, Stockholm, Sweden, 12–15 April 2010; pp. 94–104. [Google Scholar]
- Martincic, F.; Schwiebert, L. Distributed event detection in sensor networks. In Proceedings of the International Conference on Systems and Networks Communications, Tahiti, France, 29 October–3 November 2006; p. 43. [Google Scholar]
- Sheng, B.; Li, Q.; Mao, W.; Jin, W. Outlier detection in sensor networks. In Proceedings of the 8th ACM International Symposium on Mobile Ad Hoc Networking and Computing, Montreal, QC, Canada, 9–14 September 2007; pp. 219–228. [Google Scholar]
- Branch, J.W.; Giannella, C.; Szymanski, B.; Wolff, R.; Kargupta, H. In-network outlier detection in wireless sensor networks. Knowl. Inf. Syst. 2013, 34, 23–54. [Google Scholar] [CrossRef]
- Liu, C.M.; Lee, C.H.; Wang, L.C. Distributed clustering algorithms for data-gathering in wireless mobile sensor networks. Parallel Distrib. Comput. 2007, 67, 1187–1200. [Google Scholar] [CrossRef]
- Liu, C.M.; Lee, C.H. Power efficient communication protocols for data gathering on mobile sensor networks. In Proceedings of the 60th IEEE Vehicular Technology Conference, Los Angeles, CA, USA, 26–29 September 2004; pp. 4635–4639. [Google Scholar]
- Liu, C.M.; Lee, C.H.; Wang, L.C. Power-efficient communication algorithms for wireless mobile sensor networks. In Proceedings of the 1st ACM International Workshop on Performance Evaluation of Wireless Ad Hoc, Sensor, and Ubiquitous Networks, Venezia, Italy, 4–7 October 2004; pp. 121–122. [Google Scholar]
- Davies, V.A. Evaluating Mobility Models within an Ad Hoc Network. Ph.D. Thesis, Department of Mathematical and Computer Sciences, Colorado School of Mines, Golden, CO, USA, 2000. [Google Scholar]
- Royer, M.; Melliar-Smith, P.M.; Moser, L.E. An analysis of the optimum node density for ad hoc mobile networks. In Proceedings of the IEEE International Conference on Communications, Helsinki, Finland, 11–14 June 2001; Volume 3, pp. 857–861. [Google Scholar]
- Zhao, H.; Guo, S.; Wang, X.; Wang, F. Energy-efficient topology control algorithm for maximizing network lifetime in wireless sensor networks with mobile sink. Appl. Soft Comput. 2015, 34, 539–550. [Google Scholar] [CrossRef]
- Tunca, C.; Isik, S.; Donmez, M.Y.; Ersoy, C. Ring routing: An energy-efficient routing protocol for wireless sensor networks with a mobile sink. IEEE Trans. Mob. Comput. 2015, 14, 1947–1960. [Google Scholar] [CrossRef]
- Zhu, C.; Han, G.; Zhang, H. A honeycomb structure based data gathering scheme with a mobile sink for wireless sensor networks. Peer-to-Peer Netw. Appl. 2017, 10, 484–499. [Google Scholar] [CrossRef]
- Wang, W.; Shi, H.; Wu, D.; Huang, P.; Gao, B.; Wu, F.; Xu, D.; Chen, X. VD-PSO: An efficient mobile sink routing algorithm in wireless sensor networks. Peer-to-Peer Netw. Appl. 2017, 10, 537–546. [Google Scholar] [CrossRef]
- Tang, X.; Xie, L. Data Collection Strategy in Low Duty Cycle Wireless Sensor Networks with Mobile Sink. Int. J. Commun. Netw. Syst. Sci. 2017, 10, 227–239. [Google Scholar] [CrossRef]
- Chen, Y.; Lv, X.; Lu, S.; Ren, T. A Lifetime Optimization Algorithm Limited by Data Transmission Delay and Hops for Mobile Sink-Based Wireless Sensor Networks. J. Sens. 2017, 2017, 7507625. [Google Scholar] [CrossRef]
- Nayak, S.P.; Rai, S.C.; Pradhan, S. A Multi-clustering Approach to Achieve Energy Efficiency Using Mobile Sink in WSN. In Proceedings of the 3rd International Conference on Computational Intelligence in Data Mining, Singapore, 10–11 December 2016; pp. 793–801. [Google Scholar]
- Shekhar, S.; Chawla, S. Spatial Databases: A Tour; Prentice Hall: Upper Saddle River, NJ, USA, 2003. [Google Scholar]
- Shi, L.; Johansson, K.H.; Murray, M. Estimation over wireless sensor networks: Tradeoff between communication, computation and estimation qualities. In Proceedings of the 17th IFAC World Congress, Seoul, Korea, 6–11 July 2008; pp. 605–611. [Google Scholar]
- Mathur, G.; Desnoyers, P.; Chukiu, P.; Ganesan, D.; Shenoy, P. Ultra-low power data storage for sensor networks. ACM Trans. Sens. Netw. 2009, 5, 1–34. [Google Scholar] [CrossRef]
- Chu, Y.; Kosunalp, S.; Mitchell, P.D.; Grace, D.; Clarke, T. Application of reinforcement learning to medium access control for wireless sensor networks. Eng. Appl. Artif. Intell. 2015, 46, 23–32. [Google Scholar] [CrossRef]
- Chu, Y.; Mitchell, P.D.; Grace, D.; Clarke, T. Use of Q-learning approaches for practical medium access control in wireless sensor networks. Eng. Appl. Artif. Intell. 2016, 55, 146–154. [Google Scholar]
- Dimitriou, G.; Kikiras, P.K.; Stamoulis, G.I.; Avaritsiotis, I.N. A tool for calculating energy consumption in wireless sensor networks. In Proceedings of the 10th Panhellenic Conference on Informatics, Volos, Greece, 11–13 November 2005; pp. 611–621. [Google Scholar]




| Symbol | Definition |
|---|---|
| GH | Sensor elected as a group head |
| NS | The number of mobile sensors |
| MS | The mobile sink |
| τ | the trip time (see Definition 2) |
| w | Window time (see Definition 1) |
| NGH | The number of elected group heads |
| NGM | The number of sensors in a group |
| NPM | The number of sensors which detected phenomena inside a group |
| ET | Energy cost by the sensor’s transmitter |
| ER | Energy cost by the sensor’s receiver |
| MSP-430 Instruction Computation | CC2420 Radio Transmission | CC2420 Radio Receiving | |
|---|---|---|---|
| Energy (μJ/byte) | 0.0008 | 1.8 | 2.1 |
| Ratio | 1 | 2250 | 2600 |
| Variable | Value |
|---|---|
| ET | 1.8 μJ/byte |
| ER | 2.1 μJ/byte |
| NS | 1000 mobile sensors |
| NGH | 5, 10, 50, 100, 200, 300, 500 |
| K | 5 bytes |
| Sensor Speed | Range 0–5 m/s |
| α | 2 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Safia, A.A.; Aghbari, Z.A.; Kamel, I. Efficient Data Collection by Mobile Sink to Detect Phenomena in Internet of Things. Information 2017, 8, 123. https://doi.org/10.3390/info8040123
Safia AA, Aghbari ZA, Kamel I. Efficient Data Collection by Mobile Sink to Detect Phenomena in Internet of Things. Information. 2017; 8(4):123. https://doi.org/10.3390/info8040123
Chicago/Turabian StyleSafia, Amany Abu, Zaher Al Aghbari, and Ibrahim Kamel. 2017. "Efficient Data Collection by Mobile Sink to Detect Phenomena in Internet of Things" Information 8, no. 4: 123. https://doi.org/10.3390/info8040123
APA StyleSafia, A. A., Aghbari, Z. A., & Kamel, I. (2017). Efficient Data Collection by Mobile Sink to Detect Phenomena in Internet of Things. Information, 8(4), 123. https://doi.org/10.3390/info8040123




