1. Introduction
According to the Digital Agenda for Europe (DAE), by 2020, all Europeans should access the Internet at speeds greater than 30 Mbit/s, and not less than 50% of European households should be able to subscribe to contracts at speeds over 100 Mbit/s. The technology originally assumed as a baseline for the latter target of the DAE was considered to be Fiber-to-the-Home (FttH). This turned out to be a reasonable solution only in green-field deployments, where it can be delivered at a reasonable cost, but in Europe, telecommunication operators have to deal mostly with brown-field deployments in built-up, often dense urban areas. In particular, pervasive FttH deployment should have replaced copper for supporting novel ultra-broadband (UBB) services and network back-hauling. However, the very high costs (per home) of the FttH network have discouraged telecommunication operators to fully invest in FttH due to a non-favorable return of investments [
1,
2]. Thus, the need of UBB (such as for 4 K TV and cloud computing-based services) to their subscribers, as well as to provide back-hauling for actual and (possibly) future 5G radio access networks has led to a renewed interest in copper-based access technologies and in the related access network architectures to fully exploit their potentials. To improve achievable performance of copper, two main strategies can be followed. The first consists of the deployment of access network architectures capable of reducing the length of the copper wire to subscribers. The second focuses on the performance improvement of digital subscriber line (DSL) transmission technologies obtained with an increase of the transmission band and the adoption of techniques to reduce crosstalk.
In the last few years, the main approach toward UBB developed by most European telecommunication operators involved a careful evolutionary migration path from the presently ubiquitously deployed all-copper DSL access networks to all-optical access networks based on passive optical networks (PONs) [
3]. The evolutionary strategy is implemented case-by-case using one of the possible intermediate hybrid fiber–copper access solutions, including fiber-to-the-cabinet (FttC), fiber-to-the-distribution point (FTTDp) and fiber-to-the-building (FttB), which progressively reduce the wire lengths to the subscribers. The International Telecommunication Union (ITU) has recently finalized the standardization activity for the G.fast solution [
4] to be used in (future) FttDp architectures [
5]. Thanks to the reduction in copper wire length for FttDp (e.g., the typical distance between the Dp and the customer premises equipment (CPE) is about 100 m), the G.fast solution will allow the use of frequency ranges up to hundreds of MHz. Depending on the cable quality, the standard will presumably exploit the twisted pair’s spectrum up to about 100 or 200 MHz, thus achieving the maximum theoretical transmission capacity greater than 1 Gbit/s [
6]. However, even though the costs for FttDp deployment are lower than the costs for FttH, they can be still considerably high due to the large number of Dp’s to be deployed and connected by fiber to the back-haul/core network. Up to now, this fact limits the rapid and pervasive deployment of G.fast technology.
Very high-speed DSL type 2 (VDSL2, ITU-T G.993.2 [
7]) technology in the FttC architectures is currently the (only) solution adopted by telecommunication operators to provide UBB services. Thus, during the last few years, there has been a resurgent interest by standardization organizations and by the main manufacturers to find solutions to improve VDSL2 performance. In particular, recent VDSL2 systems allow very high bit rates to be achieved, thanks to the usage of vectoring [
8], which reduces the far-end crosstalk (FEXT), and/or extending the transmission band up to 35 MHz (e.g., V-plus) [
9], and/or adopting advanced coding techniques to improve transmission over copper (e.g., Huawei’s SuperVector [
10]). ITU has recently approved the VDSL profile 35b [
11] to accommodate these new technologies.
Performance of VDLS2 is commonly expressed in terms of the statistics (i.e., mean and percentiles) of the achievable bit rate per user. Their evaluations require the knowledge of the access network geometry, the models of propagation environment, and FEXT. Simulation tools including these models are typically used by telecommunication operators to assess performance. Proper FEXT characterization is an important issue to obtain realistic results. Direct propagation channel models depend on the cabinet-to-user distance and on the copper-pair propagation characteristics. These are described by the primary and secondary constants of the cable as a function of frequency [
12]. Concerning FEXT, several models (mostly based on experimental data) have been proposed by ITU [
11] and other organizations/institutions, such as in [
13]. The document in [
11] reports the attenuation model and the FEXT model based on the 99th percentile of FEXT measurements in the cable, i.e., only
of all pairs in all cables experience more crosstalk than the model value at the considered distance. Nevertheless, as indicated in [
14], the
worst-case assumption is acceptable for designing DSL system power spectral density (PSD) masks in order to limit the “impact” onto neighboring DSL services [
15]. However, in most of the cases, this does not correspond to realistic situations, and could negatively bias any performance gain inherent to technologies aimed at avoiding and/or mitigating FEXT-dominant crosstalk. In general, these FEXT models do not reflect the wide field variation of FEXT strengths throughout the channel, and they do not account for the variation in FEXT coupling dispersion throughout the cable.
To compensate for the limitations of the
worst-case assumption, FEXT models adding FEXT coupling dispersion with respect to the
model have been presented in the literature. Two important examples are reported in [
13,
14], where FEXT dispersion (in dB) has been modeled using beta and normal distributions. Both models in [
13,
14] allow accounting for inter-binder interference by adding an additional attenuation factor (in dB) to FEXT fluctuations, whose value depends on the relative positions of the binders in the cable.
To further include frequency selectivity in existing FEXT models, authors in [
16,
17] have proposed two distinct parametric stochastic models for FEXT frequency fluctuations. Then, the overall FEXT model is obtained by multiplying the
model, including dispersion, by the selectivity term at a frequency
evaluated in accordance with the models in [
16] or [
17]. Finally, in [
18], FEXT fluctuations have been modeled by the gamma distribution. This channel model is limited to
MHz and so it is not considered in the following.
The adoption of a simulation-based approach for preliminary planning of the access network can be time consuming. To overcome this inconvenience, in this paper, we propose an analytical framework based on two approximated stochastic models for the user bit rate that can be easily implemented on any calculator. In particular, differently from [
19], we introduce a novel normal stochastic model of the bit rate per user accounting for the bit-loading limitation per sub-carrier and for vectoring. A bit-loading limitation per sub-carrier is imposed by the VDSL2 standard, i.e., the number of bits per sub-carrier cannot exceed
, and cannot be lower than
. Moreover, we also present a closed-form expression for the maximum sub-carrier frequency
transmitting up to
bits. This formula evidences the dependence of
on the FEXT statistics, on the pair-coupling characteristics, on the distance of the reference user from the cabinet, on the geometry of the interference scenario, and on vectoring. Models have been obtained starting from log-normal approximations of the signal-to-interference-plus-noise ratio (SINR) per sub-carrier introduced in [
20] and further validated in [
19] and these are not discussed further. The presented analytical framework facilitates the preliminary design and performance assessment of current and enhanced VDSL2 systems and other technologies, such as ADSL and G.fast (ITU G.9701). The formulas presented in this paper are valid for the downstream (DS) transmission direction only, but can be re-adapted to upstream (US). The validity of the bit rate models presented in this paper has been assessed by computer calculations. A very good agreement with the bit rate values obtained from exact calculations has been observed for variable access network topologies, interference scenarios, and for distances which are of interest for practical VDSL2 deployment.
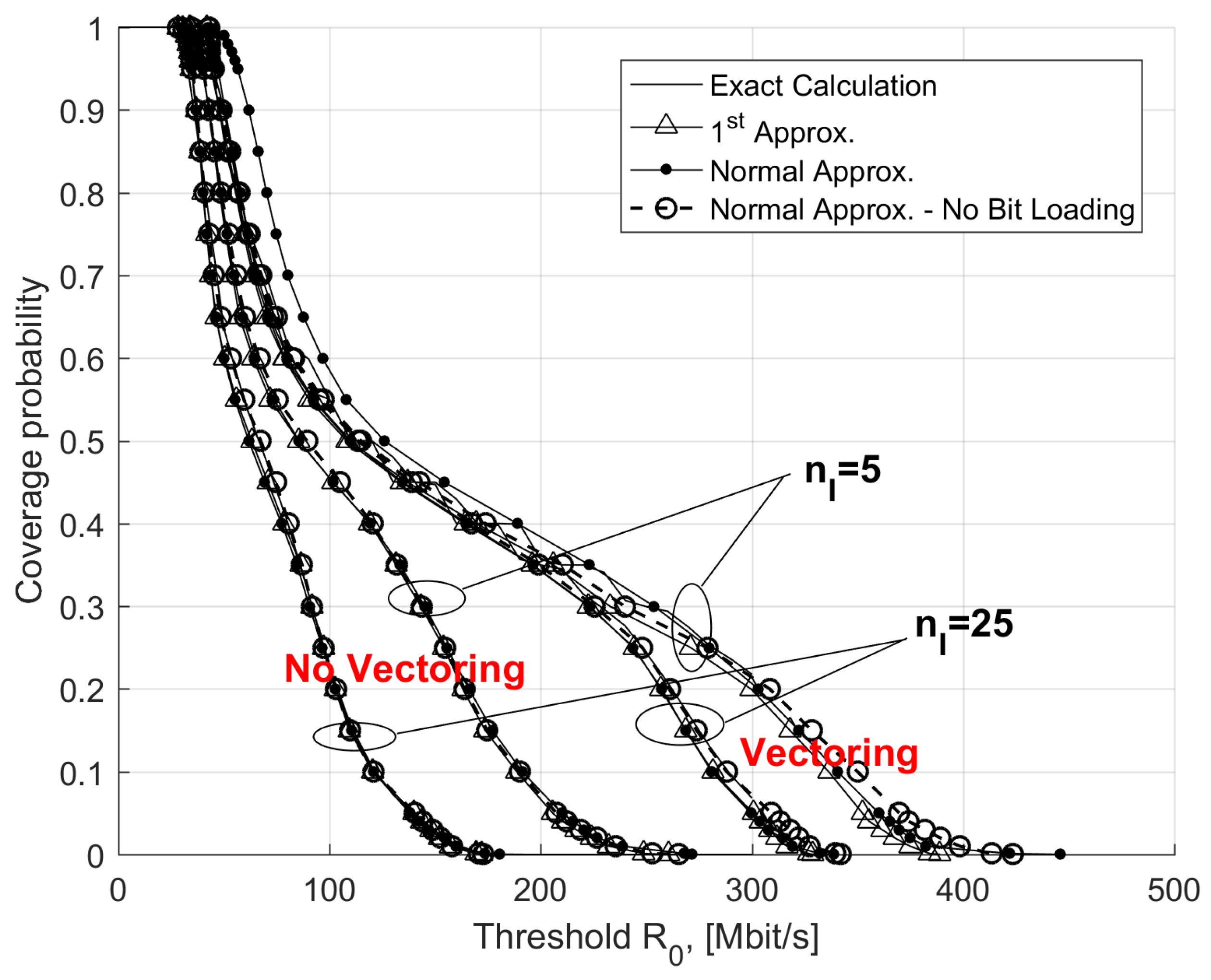
The bit rate coverage for fixed VDSL2 networks is introduced and evaluated in this paper. It is defined as the probability the bit rate per user is greater than a reference bit rate value. Coverage is obtained after saturating over all possible positions of interferers in the access network, and over all the distances of the reference user from the cabinet. By definition, the bit rate coverage provides an indication of the percentage of users that can be served with an assigned bit rate level for the given access network configuration and cable load (i.e., the number of active copper lines), independently of the position of terminals with respect to the cabinet(s). In a practical setting, VDSL2 coverage can be evaluated by first collecting bit rate measurements from a set of VDSL2 active lines from one cabinet in the area, and then evaluating the cumulative distribution of these measurements. When more cabinets are considered, the bit rate coverage can be calculated for each cabinet separately. This means we take into account the specific propagation and interference conditions of the single cabinet, and then combine results from all the cabinets in some way (for example, by averaging). Coverage results obtained from exact calculations are compared with those obtained using the bit rate approximations presented in this paper. A very good agreement between exact and approximated results was obtained.
The paper is organized as follows. In
Section 2, we describe the typical access network architecture for VDSL2 deployment, and we define the expression of the SINR per sub-carrier. The log-normal approximation of the SINR is introduced in
Section 3. In
Section 4, we derive the bit rate approximations, including the bit-loading limitations. The validity of the proposed models is discussed in
Section 5 under variable interference scenarios. Some applications of the proposed formulation, including VDSL2 coverage, are illustrated in
Section 6. Finally, conclusions are drawn.
2. Access Scenario and Performance Parameter Definition
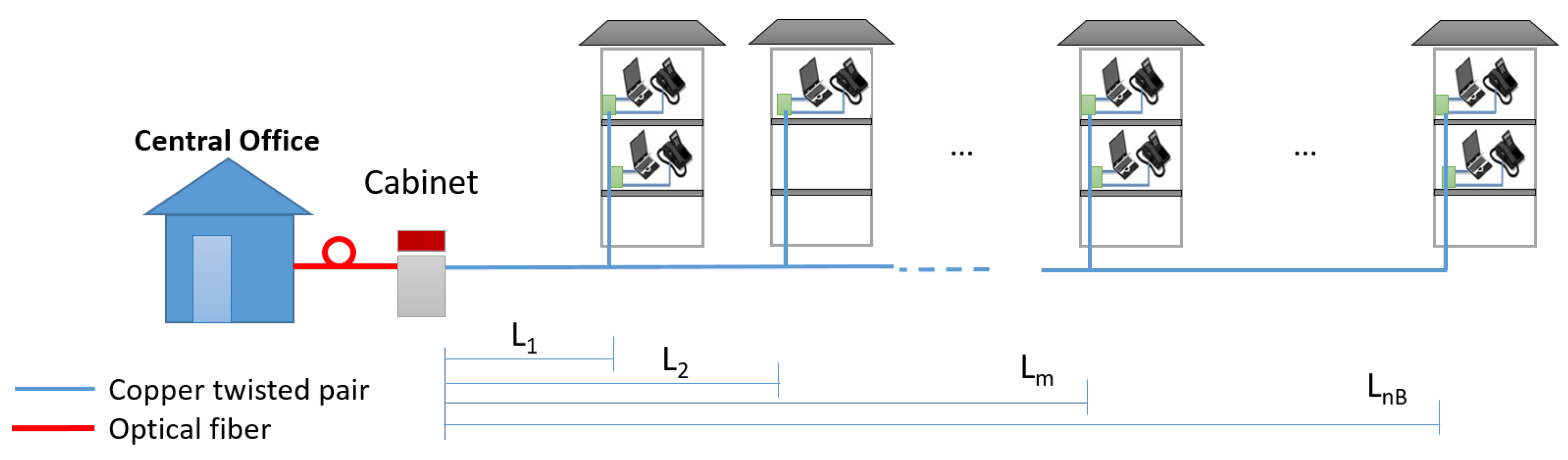
The typical geometry of FttC access networks is depicted in
Figure 1.
Interferers are inside the
buildings served by the same cable. The
ith building contains
active interferers using copper pairs in the same or in other binders inside the same cable. The typical number of copper pairs in each binder varies from 25 up to 50; the cable from the cabinet typically contains four or eight binders. As shown in
Figure 1, buildings are at distances
,
, from the cabinet. Active users in the same building can be randomly located on the floors. The main VDSL2 performance parameter is the bit rate achieved by a single user at distance
d from the cabinet. It is defined as:
In Equation (1),
is the set of sub-carrier indices assigned to DS transmission,
is the symbol rate,
is the number of bits that can be allocated on the
kth sub-carrier in accordance with the following criterion:
where
and
are the minimum and maximum number of bits, respectively, that can be allocated per sub-carrier, and
in Equation (1) is:
and
is the performance gap [
8]. The term
is the SINR of the
kth sub-carrier at frequency
for the reference user at distance
d from the cabinet and it is defined as:
In Equation (4),
is the direct-channel transfer function at frequency
,
is the background noise power, and
is the power transmitted by the reference user on the
kth sub-carrier. We assume DS users in the same cable use the same transmission power. This avoids harmful FEXT of high-power users on low-power users. The term
accounts for the (possible) FEXT reduction due to vectoring [
8], i.e.,
in the no vectoring case, and otherwise
. The exact values of
depend on the selected vectoring algorithm, and on its specific implementation in the DSL Access Multiplexer (DSLAM). Considering the typical vectoring algorithm indicated in [
21], we have observed that
increases with the frequency up to about
dB at 35 MHz. Finally,
is the FEXT power:
where
is the number of interferers on the reference receiver (r);
is the FEXT transfer function at distance
d accounting for the interference of the
pth user; and
, on the
kth sub-carrier of the reference user. To keep notation simple, the dependence of
on the corresponding coupling length has been omitted. For DS transmissions, we have [
14]:
where
is the coupling length between the
pth interfering user and the reference user, and
is the FEXT coupling coefficient. For assigned reference, distance
d,
can be easily obtained from the access network geometry in
Figure 1. The term
(in dB) is a random variable accounting for FEXT fluctuations with respect to the
FEXT condition [
14]. The term
is assumed to be normal (in dB), and its mean
and variance
do not depend on
d. Furthermore, we consider that the
do not vary with frequency, and are statistically independent and identically distributed (i.i.d.). From Equation (5) to Equation (6), the
in Equation (4) is
where
is the signal-to-background noise ratio and the random variables
are i.i.d., having a mean of
and standard deviation
.
3. Log-Normal Approximation of SINR
From the
Appendix,
in Equation (7) can be approximated as
where
is the equivalent number of interfering users. This can be easily seen in the case of co-located interferers (i.e.,
for each
p) where we obtain
. In general,
explicitly accounts for the positions of interfering users with respect to the reference user expressed by the coupling lengths
. In the case of the cable with
binders, indicated with
,
, the coupling coefficient among binders [
13], assuming the copper line associated to the reference user is in the first binder,
in Equation (9) is:
where
is the number of interferes in the
pth binder and
is the coupling length of the
pth active user in the
qth binder. The second term in Equation (10) is a sort of equivalent number of interferers due to active lines residing in the adjacent binders. This fact can be again evidenced in the co-located interferers case, yielding
From Equation (11), it is observed that thanks to the separation of binders in the cable, the total number of interferers is lower than the number of active users in the cable.
The normal random variable
in Equation (8) has a mean
and standard deviation
, which depend on
d, and
is a normal random variable
. When applying Wilkinson’s method [
22],
and
can be calculated as (see the
Appendix):
and
The
and
terms are two geometrical parameters accounting for the given access network geometry characteristics. It can be shown
is monotonically increasing with
d, and its minimum is
. Thus, when
increases (infinitely in the limit), the FEXT fluctuation in
tends to reduce. Extension of the proposed and more complex scenarios have been discussed in [
20].
Due to log-normality of the denominator in Equation (8), each argument of the logarithms in Equation (1) can be approximated as
where
is normal with a mean
and standard deviation
. Similarly,
is normal with a mean
and standard deviation
. The normal
random variable
in Equation (14) is the same as in
, and it accounts for the specific FEXT coupling situation (see
Appendix). The moments of the normal random variables
,
and
have been obtained using Wilkinson’s method without neglecting the 1 term in Equation (14) and in the denominator of Equation (8). Results have been reported in the following formulas starting with the moments of
. By repeated application of Wilkinson’s method, we obtain (for simplicity we omit the dependence on the distance
d in the following formulas):
where
and
with
and
and
are the mean and the standard deviation of the normal random variable associated to the log-normal approximation of the denominator in Equation (8). Finally,
and
for
, and
and
are in Equation (12). Equations (15)–(18) evidence the dependence of the bit rate statistics on the FEXT parameters
and
, and on the scenario geometry with
and
. To overcome the limitations of Wilkinson’s approach [
22], other methods to evaluate the log-normal parameters can be considered [
23]. However, in some cases, it may be not possible to obtain closed-form expressions for the parameters of the log-normal random variable approximating the sum.
On the Suitability of Log-Normal Sum Assumption
In [
20], authors discussed the suitability of log-normal sum approximation when the FEXT fluctuations were distributed in accordance with the beta distribution [
13]. Assuming the parameters of the log-normal FEXT are calculated, in order to have the same mean and variance of the exponentially beta-distributed FEXT, authors have proved in [
20] (by computer calculations) that the log-normal sum assumption still provides accurate results even in the beta-distributed FEXT case. This fact can be further confirmed considering the following two results presented in the literature. From [
14], we can observe that Kullback–Leibler distances evaluated with normal and beta exponent assumptions are close. Furthermore, in [
24], authors affirm that a log-normal distribution provides a good approximation for the sum of positive random variables under general conditions. Reasoning presented in [
24] seems to be correct, despite that we believe that results in [
24] should be considered as a conjecture/intuition rather than a formal proof. In fact, the paper indicates some desirable properties for a random variable to properly approximate the sum of positive random variables. The log-normal distribution owns these, but it is not clear if it is the unique distribution possessing these properties. However, the conjecture in [
24] enforces the validity of the log-normal sum assumption considered in this paper. In addition, in [
20], it was observed that the log-normal sum approximation of the sum of exponential beta random variables improves with the number of the summed random variables. It is out of the scope of this paper to further investigate this topic.
5. On the Validity of the Bit Rate Approximations
The effectiveness of the bit rate approximation in Equation (19) has been assessed in [
19], and the results are not repeated here. In this section, we discuss on the validity of Equations (21) and (26) in terms of the cumulative distribution function (CDF) of the bit rate under variable interference scenarios and FEXT conditions in the non-vectored case. Vectoring is discussed in the next subsection. Results have been obtained considering co-located and uniformly distributed interferers between 50 m and 1000 m along the cable. In accordance with VDLS2 Profile 35b (998E35 [
7]), we set the maximum VDSL2 frequency to
MHz, the symbol rate is
ksymbol/s,
kHz,
,
and
. Moreover, the overall transmission power was
dBm and a flat transmitter power spectrum was assumed. The FEXT coupling coefficient was
[
25]. For validation purposes, the exact value of
is not important. FEXT statistics are assumed to be normal, having a mean
(dB) and standard deviation
(dB) [
14]. We further assumed
and/or
were variable, so as to assess the validity and the limitations of the considered model under different FEXT conditions.
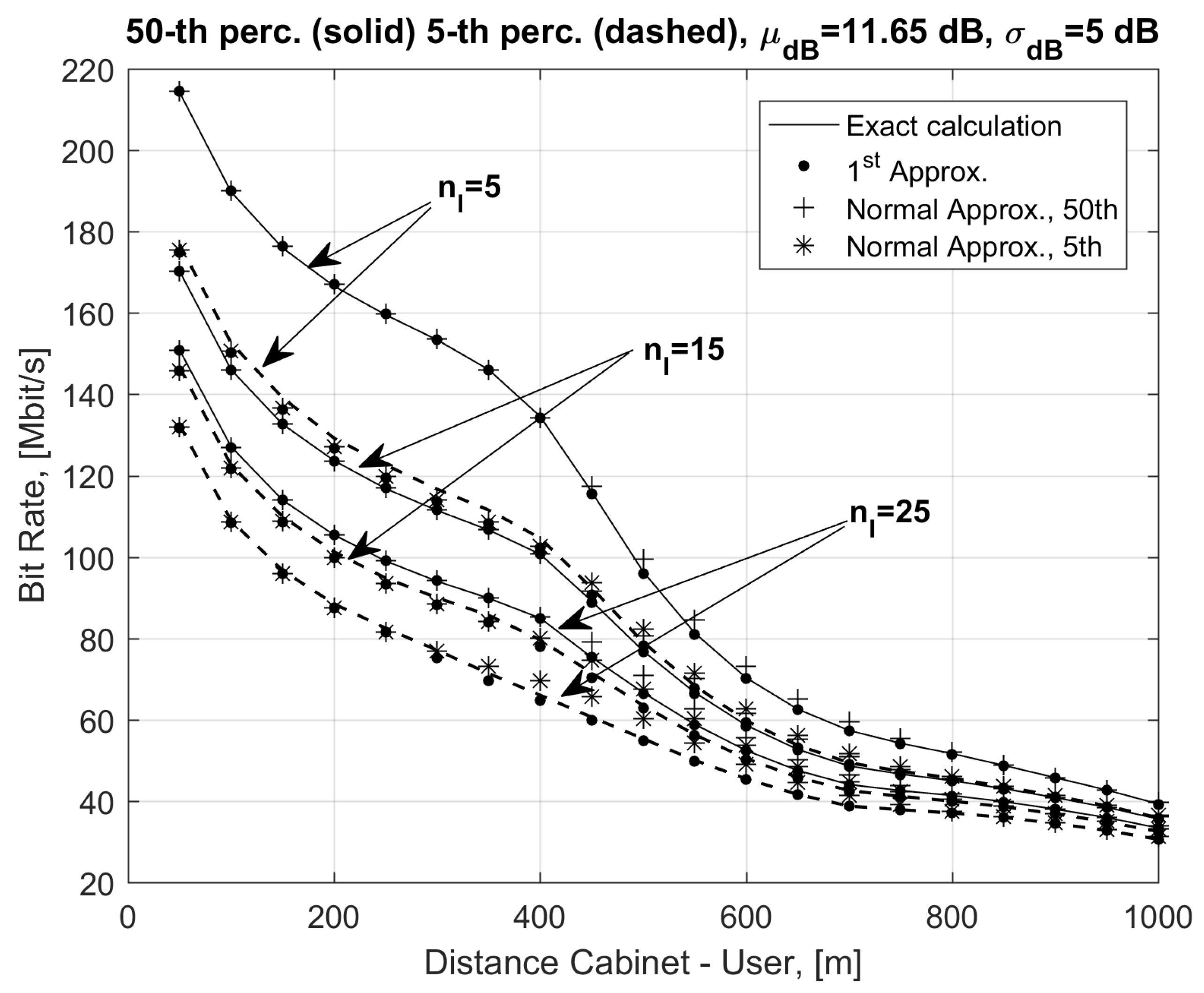
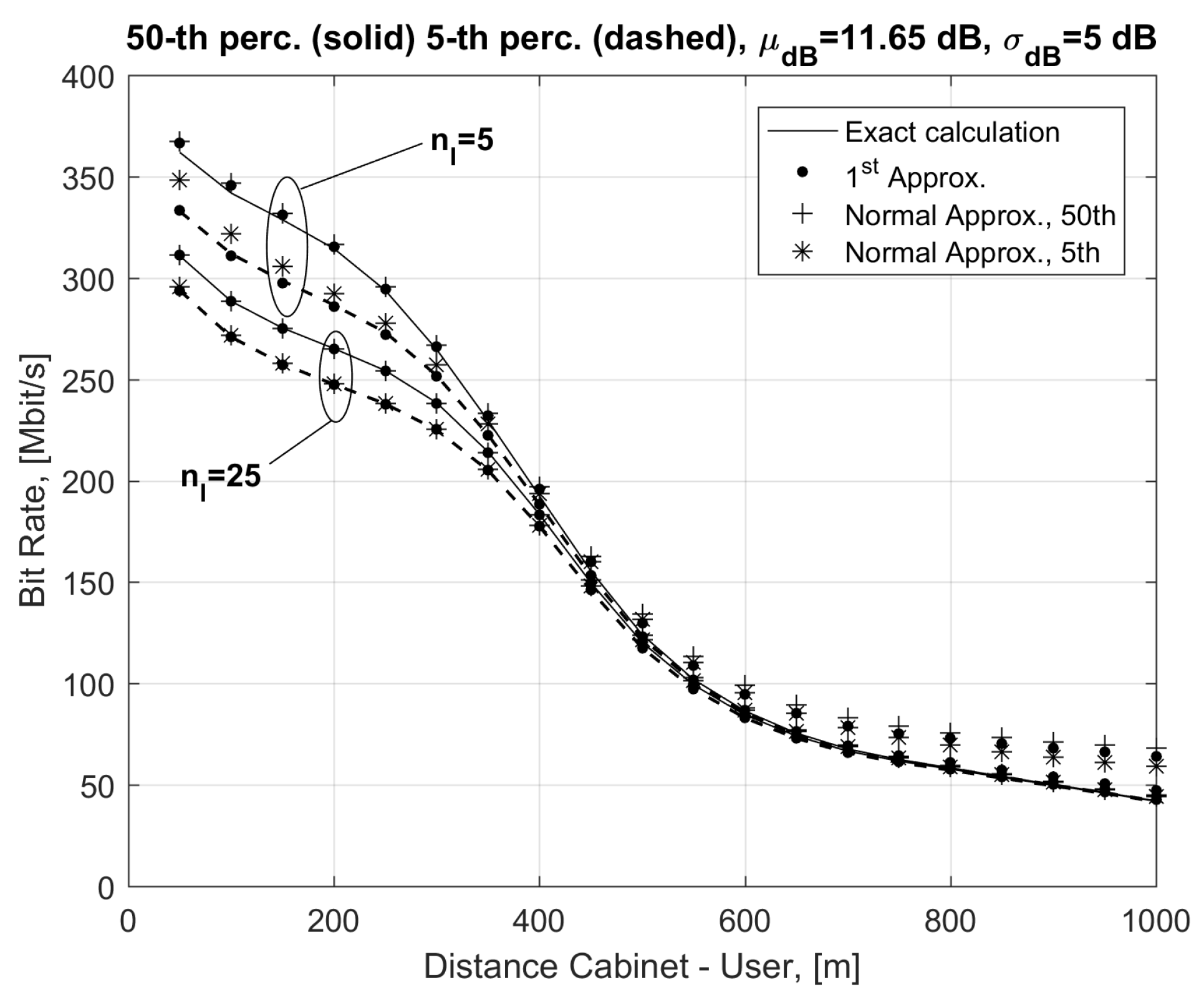
In
Figure 2 we report the 5th and the 50th percentile of the bit rate as a function of the distance
d of the reference user from the cabinet for variable numbers of interferers
, 15, 25 and a uniform distribution of the interfering users along the cable. Similar considerations applied to the co-located interferers case. Curves in
Figure 2 were obtained using exact formulas in Equation (1) with the SINR in Equation (4) and FEXT as in Equation (5) (without the log-normal approximation; solid lines for the 50th and dashed lines for the 5th percentile) and the bit rate approximations in Equations (21) (with dots) and (26) (with + marks for the 50th and * marks for the 5th percentile). Results in
Figure 2 show the very good agreement between the exact and approximated bit rate in Equation (21) at every distance
d. Instead, the normal approximation in Equation (26) overestimates the exact results (see for example the points marked with * in
Figure 2) and provides very accurate results for distances lower than 400 m and
.
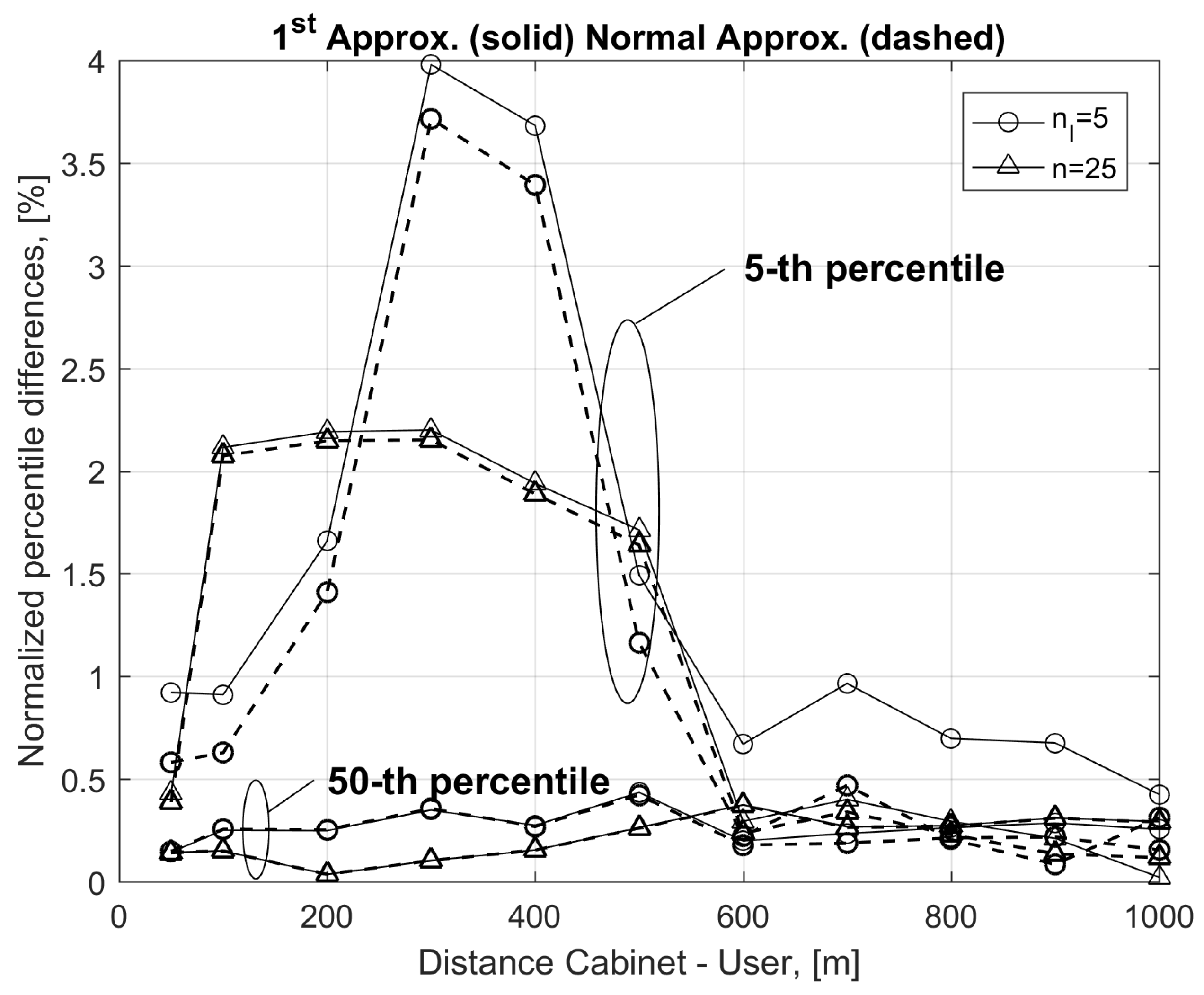
Differences between approximated bit rates are not clearly distinguishable in
Figure 2. For this reason, in
Figure 3, we plot the differences between the exact and the approximated values of the 50th and 5th percentiles obtained from Equations (21) (solid lines) and (26) (dashed lines). Differences have been normalized with respect to the corresponding bit rate values obtained using the exact formula in Equation (7). Differences in
Figure 3 are in the order of a few percent of the bit rate, and this further confirms the validity of the considered approximations. Furthermore, results obtained with Equation (26) are closer to the exact values, as they are greater than those provided by Equation (21) for low percentiles.
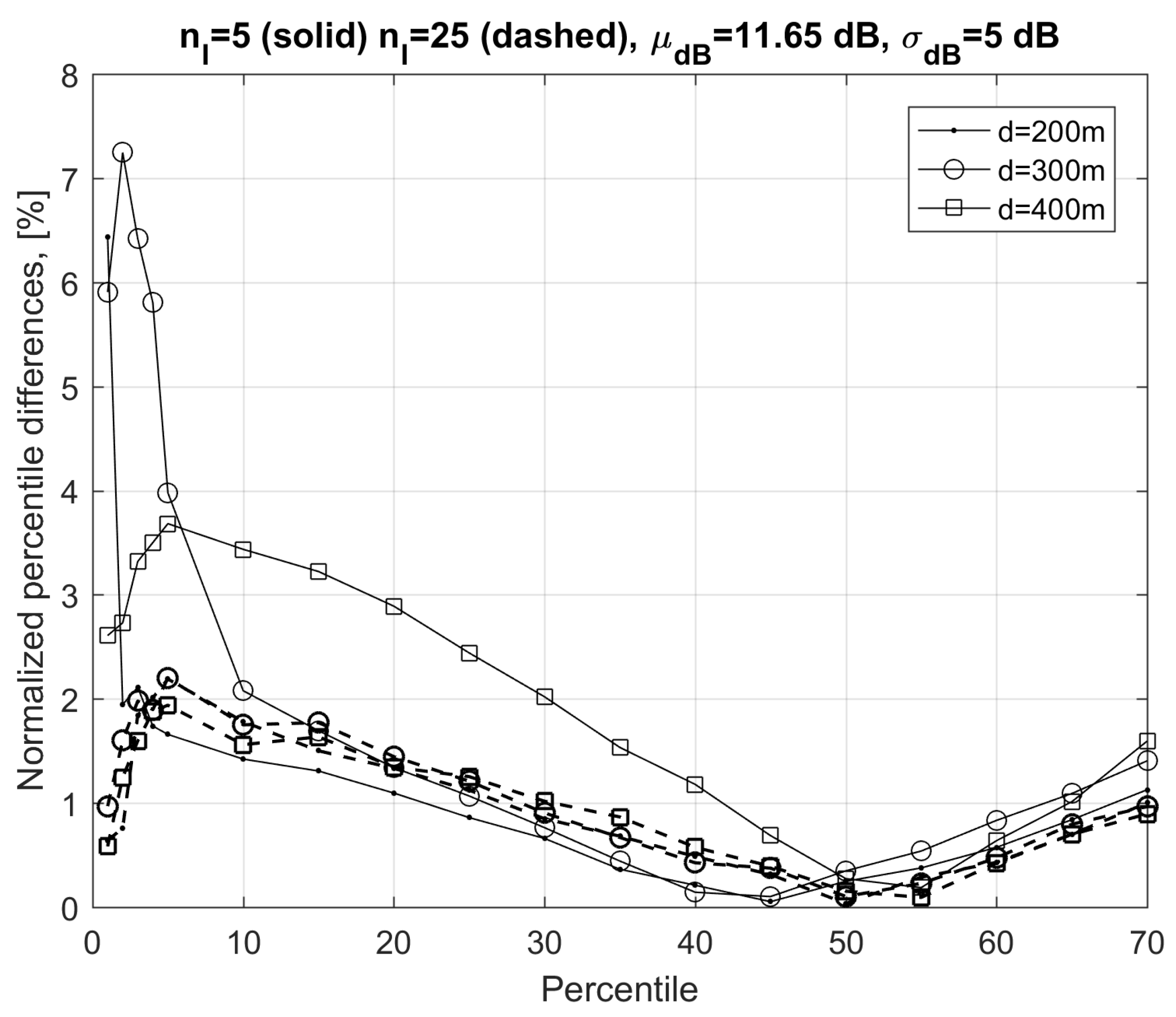
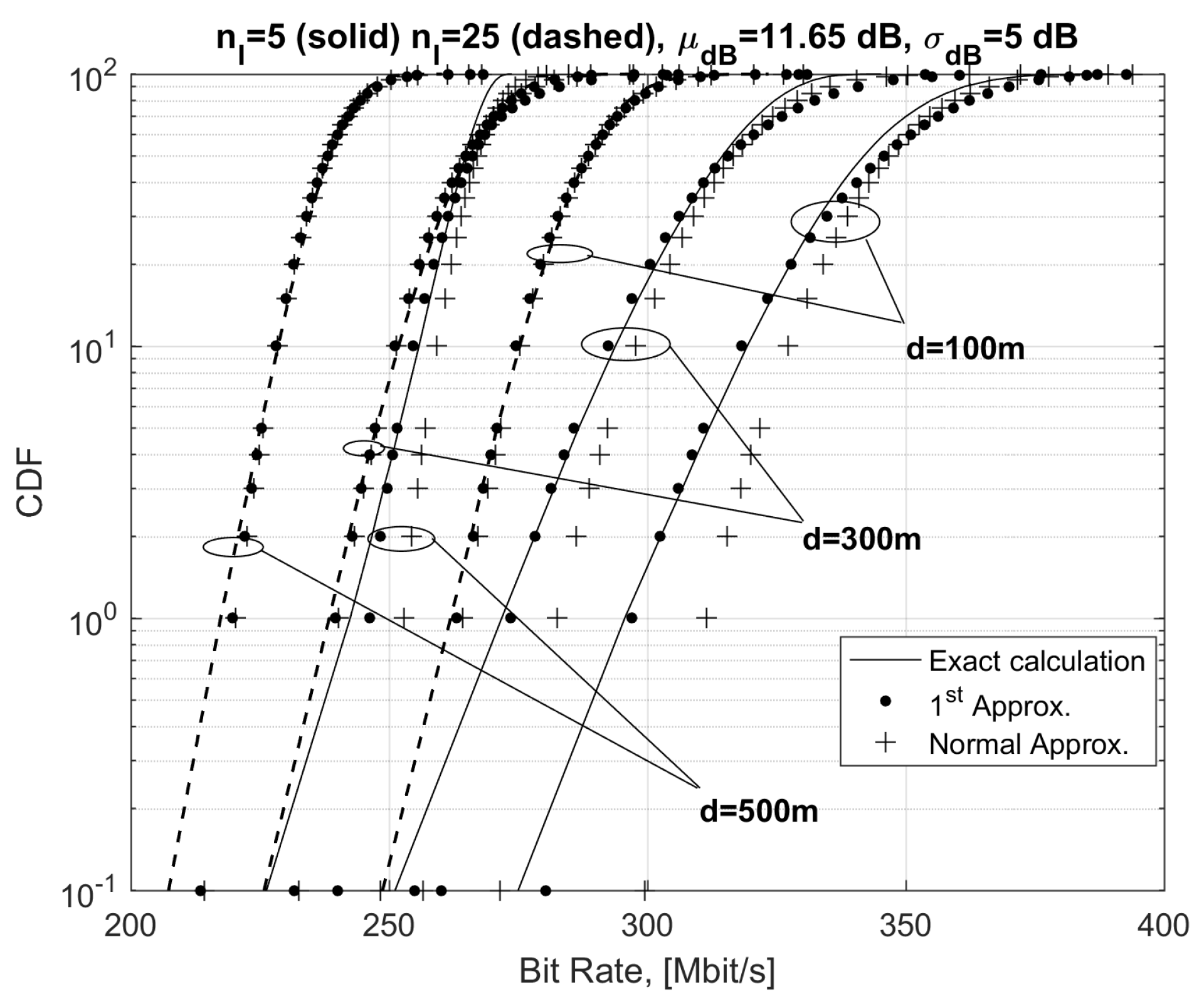
The effectiveness of Equations (21) and (26) are further confirmed by results in
Figure 4 concerning the CDFs of the exact and approximate bit rates in Equations (21) and (26) for variable distance
d and for
, 25. From
Figure 4, exact and approximated CDFs are practically superimposed in all cases. As expected, the differences between Equations (21) and (26) are more evident at distances greater than 400 m, where bit rates were relatively small and the addition of an (unrealistic) term due to sub-carriers with the number of bits per symbol lower than 1 was not negligible. Finally, by increasing distance
d, the CDFs corresponding to Equation (21) tended to be closer to the exact the CDF obtained with exact calculation because FEXT becomes gradually negligible with respect to background noise. This effect is visible for distances greater than 700 m (not shown to avoid an overcrowded graph). To evidence the differences between the CDFs obtained with the exact and approximated calculations in
Figure 4, in
Figure 5, we plot the normalized differences among the percentiles. Differences were mostly below
and this further confirms the validity of the proposed approximations.
The applicability of Wilkinson’s method for obtaining the statistics of the log-normal sum approximation is mainly related to the values of
[
23]. To further investigate the effectiveness of the proposed approximations, we have re-calculated the CDFs of the bit rate using Equations (21) and (26), for
dB and variable
(dB) for some distances
d and
. All results have been summarized in
Table 1, reporting the normalized differences between the 5th percentiles of the exact and approximated bit rates. Normalization of the difference was taken with respect to the corresponding exact bit rate. The results are for the variable distance
d, for
ranging from 4 dB up to 7 dB, and for
. From the results in
Table 1, it is observed that the differences increased with
, and they were more than
for
at distances of about 300 m, for both approximations in Equations (21) and (26). This may render the two approximations unusable. The reduction of the normalized difference with the distance
m for any
was due to the FEXT decrease with the distance. In general, it has been observed that for
dB, the approximations in Equations (21) and (26) provide accurate results, which are in very good agreement with the exact CDFs at any practical distance envisaged for VDSL2 deployment. In fact, the normalized difference of percentiles is always below
for both Equations (21) and (26) at any distance. This also confirms results concerning the applicability of Wilkinson’s method in [
23], which are accurate when
dB. For
dB, only the estimate of percentiles below
are accurate enough. Thus, the proposed formulation based on Wilkinson’s approach can even be used to assess percentiles of CDFs ranging from
up to
, when
dB. Discrepancies are due to the inability of Wilkinson’s approach to provide a good approximation for the distribution tails. In these cases, alternative methods (such as those in [
23]) should be considered to evaluate the parameters of the log-normal random variable approximating the sum. Instead, for
, the proposed bit rate approximations in Equations (21) and (26) provide results that are in very good agreement with the exact CDFs at any practical distance (see, for example, results in
Figure 4).