A Lightweight RFID Grouping-Proof Protocol Based on Parallel Mode and DHCP Mechanism

Abstract

A Radio Frequency Identification (RFID) grouping-proof protocol is to generate an evidence of the simultaneous existence of a group of tags and it has been applied to many different fields. For current grouping-proof protocols, there still exist some flaws such as low grouping-proof efficiency, being vulnerable to trace attack and information leakage. To improve the secure performance and efficiency, we propose a lightweight RFID grouping-proof protocol based on parallel mode and DHCP (Dynamic Host Configuration Protocol) mechanism. Our protocol involves multiple readers and multiple tag groups. During the grouping-proof period, one reader and one tag group are chosen by the verifier by means of DHCP mechanism. When only a part of the tags of the chosen group exist, the protocol can also give the evidence of their co-existence. Our protocol utilizes parallel communication mode between reader and tags so as to ensure its grouping-proof efficiency. It only uses Hash function to complete the mutual authentication among verifier, readers and tags. It can preserve the privacy of the RFID system and resist the attacks such as eavesdropping, replay, trace and impersonation. Therefore the protocol is secure, flexible and efficient. It only uses some lightweight operations such as Hash function and a pseudorandom number generator. Therefore it is very suitable to some low-cost RFID systems.

1. Introduction

With the wide application of Internet of Things (IoTs), Radio Frequency Identification (RFID) technique gets the broad attention. RFID is a pervasive technology deployed in daily life in order to identify objects using radio-waves, without visible light and physical contact. It is thought as a replacement technique for barcode. Today, RFID systems have been successfully applied to mobile payment, healthcare, manufacturing, supply chain management, agriculture, transportation and other fields [1]. In general, a tag is usually used to identify an object. However, under many circumstances, several tags are combined into a group and they are respectively used to identify different parts of an object. Or, for an object with large size, multiple tags are usually attached to different position of the object to ensure the object can be detected. Under these cases, it is necessary for a reader to read several tags simultaneously and to prove the co-existences of these tags, which is called grouping proof for RFID systems. For example, A. Juels [2] supposed a requirement for a certain medication to be dispensed together with a leaflet, which describes its side-effects. One RFID tag might be embedded in the container for the medication, while another is embedded in the accompanying leaflet. A grouping proof will provide evidence that each container of the medication is dispensed with a leaflet. Another example is that a manufacturer of aircraft equipment wishes to certify that a certain part always leaves its factories with a safety cap. Given RFID tags in both the part and the cap, a grouping proof can provide verifiable evidence to third-party. Under these circumstances, each tag is not only to be authenticated but also to be proved whether they exist simultaneously. In order to prove the co-existence of multiple tags, many grouping proof protocols have been proposed. Due to the hardware resource limitation of the built-in chips on the tag, the grouping-proof protocols usually use some lightweight encryption functions like the authentication protocols for FRID systems. However, many of them cannot protect the privacy of the tags [3,4,5]. Some grouping-proof protocols usually use the response from a tag as the input of next tag so that they need more response time to prove the co-existence of multiple tags. In order to overcome the flaws above, we propose an enhanced grouping-proof protocol. This protocol utilizes the parallel communication mode, DHCP (Dynamic Host Configuration Protocol) and broadcast mechanism to effectively complete the grouping proof.

Our main contribution in this paper is to present a lightweight RFID grouping-proof protocol. This protocol involves multiple readers and multiple tag groups. It flexibly utilizes the DHCP and broadcast mechanism to choose a reader and a tag group. It completes the mutual authentication among the verifier, readers and tags. It can flexibly authenticate all tags of a special group or a part of the group. During the entire grouping-proof process, any secret information about the tags is not leaked to the reader. The protocol protects the privacy and security of the RFID system.

The rest of this paper is organized as follows. In Section 2 we briefly review some typical grouping-proof protocols and analyze their security vulnerabilities. In Section 3, we describe the RFID system under the grouping-proof mode and propose its security model. In Section 4, we propose a new grouping-proof protocol by utilizing parallel communication mode and DHCP mechanism. We give two modes for our proposed grouping-proof protocol: active mode and passive mode. We describe the working process of the protocol with passive mode. In Section 5, security and performance analysis of our proposed protocol are addressed and compared with other typical grouping-proof protocols. Finally, we give the concluding remarks in Section 6.

2. The Related Grouping-Proof Protocols for RFID Systems

The first grouping-proof protocol only involves two tags and it is proposed by A. Juels [2], which is called the Yoking-proofs protocol for RFID Tags. “Yoking” means the co-existence of two tags. The protocol gives a proof that a pair of RFID tags has been scanned simultaneously in the range of a reader. It utilizes a timeout mechanism to guarantee the validity of co-existence proofs. The protocol assumes that tags have ability to perform basic cryptographic operations such as Hash operation, $\mathrm{MAC}$ functions and pseudorandom number generator. The Yoking-proofs protocol involves two tags ${\mathrm{T}}_{\mathrm{A}}$ and ${\mathrm{T}}_{\mathrm{B}}$. These tags are identified by their identifiers $\mathrm{A}$ and $\mathrm{B}$ respectively. Their secret keys are ${\mathrm{k}}_{\mathrm{A}}$ and ${\mathrm{k}}_{\mathrm{B}}$. The minimalist version of the “Yoking-proofs” protocol is described as follows.

(1) The reader sends the message $“\mathrm{left}\mathrm{proof}”$ to ${\mathrm{T}}_{\mathrm{A}}$.

(2) ${\mathrm{T}}_{\mathrm{A}}$ generates a random nouce ${\mathrm{r}}_{\mathrm{A}}$ and sends the message $\mathrm{a}=\left(\mathrm{A},{\mathrm{r}}_{\mathrm{A}}\right)$ to the reader.

(3) The reader sends $\left(“\mathrm{right}\mathrm{proof}”,{\mathrm{r}}_{\mathrm{A}}\right)$ to ${\mathrm{T}}_{\mathrm{B}}$.

(4) ${\mathrm{T}}_{\mathrm{B}}$ uses $\mathrm{MAC}$ function and its secret key ${\mathrm{k}}_{\mathrm{B}}$ to sign ${\mathrm{r}}_{\mathrm{A}}$. It gets ${\mathrm{m}}_{\mathrm{B}}={\mathrm{MAC}}_{{\mathrm{k}}_{\mathrm{B}}}\left[{\mathrm{r}}_{\mathrm{A}}\right]$. Then it generates a random nouce ${\mathrm{r}}_{\mathrm{B}}$ and sends $\mathrm{b}=(\mathrm{B},{\mathrm{r}}_{\mathrm{B}},{\mathrm{m}}_{\mathrm{B}})$ to the reader. The reader sends ${\mathrm{r}}_{\mathrm{B}}$ to ${\mathrm{T}}_{\mathrm{A}}$.

(5) ${\mathrm{T}}_{\mathrm{A}}$ signs ${\mathrm{r}}_{\mathrm{B}}$ with its secret key ${\mathrm{k}}_{\mathrm{A}}$ and calculates ${\mathrm{m}}_{\mathrm{A}}={\mathrm{MAC}}_{{\mathrm{k}}_{\mathrm{A}}}\left[{\mathrm{r}}_{\mathrm{B}}\right]$ and sends ${\mathrm{m}}_{\mathrm{A}}$ to the reader.

(6) The reader generates ${\mathrm{P}}_{\mathrm{AB}}=\left(\mathrm{A},\mathrm{B},{\mathrm{m}}_{\mathrm{A}},{\mathrm{m}}_{\mathrm{B}}\right)$ as the evidence and sends ${\mathrm{P}}_{\mathrm{AB}}$ to the verifier.

(7) The verifier judges the validity of co-existence proof ${\mathrm{P}}_{\mathrm{AB}}$. If ${\mathrm{P}}_{\mathrm{AB}}$ is generated within a reasonable and pre-defined time period it is valid. Otherwise, the protocol will be terminated and the generated proof is viewed as an invalid one.

As described above, the identifiers of the tags $\mathrm{A}$ and $\mathrm{B}$ is transferred with plaintext. So the Yoking-proofs protocol is not anonymous. J. Saito and K. Sakurai [6] analyzed the Yoking proofs protocol and they indicated the yoking-proofs protocol is not immune to replay attack because a malicious attacker can separately gather proof elements $\left(\mathrm{A},{\mathrm{m}}_{\mathrm{A}}\right)$ and $\left(\mathrm{B},{\mathrm{m}}_{\mathrm{B}}\right)$ within different proof sessions and combine them later to form a counterfeit proof. This vulnerability is caused by the independent generating process of ${\mathrm{m}}_{\mathrm{A}}$ and ${\mathrm{m}}_{\mathrm{B}}$ in the Yoking-proofs protocol [5]. Mike Burmester et al. [3] also analyzed the Yoking-proofs protocol and they pointed out other several weaknesses. The first is the Yoking-proofs protocol does not check each other’s computation result so that some unrelated tags can participate in a joking session. Sometimes, some proofs generated by the reader are meaningless. However, these proofs are still transferred to the verifier. The grouping-proof failure is finally detected by the verifier. This will result in a late response time. Another weakness is that the proof ${\mathrm{P}}_{\mathrm{AB}}$ cannot state two tags are scanned simultaneously, especially in the presence of a rogue reader. A corrupted tag can impersonate a legal tag (${\mathrm{T}}_{\mathrm{A}}$ or ${\mathrm{T}}_{\mathrm{B}}$) to generate and replay ${\mathrm{P}}_{\mathrm{AB}}$.

Huang and Ku [7] proposed an online grouping-proof protocol for Class-1 Gen-2 standard tags. Their protocol is used to check the accuracy of the association of drug and patient information so as to enhance medication safety. The protocol only uses a cyclic redundancy check (CRC) function and a pseudorandom number generator (PRNG). P. Peris-Lopez et al. [4] analyzed the protocol. They found that an attacker can exploit the linearity property of CRC function and the tag’s EPC transferred by plaintext to get the private information related to the objective tag. Then it can impersonate this tag in the future grouping-proof. So the protocol proposed by Huang and Ku cannot resist forgery attack. Otherwise, P. Peris-Lopez et al., pointed out that the protocol proposed by Huang H-H et al., cannot resist de-synchronization attack and replay attack.

HY Chien et al. [8] proposed two grouping-proof protocols conforming to the EPC Class-1 Gen-2 standard to enhance medication safety for two different scenarios: online and offline. For these protocols, the operations on the tags are very simple, which are limited to 16-bit PRNG and bitwise XOR operation. Peris-Lopez et al. [4] analyzed the online protocol. They found the protocol cannot resist forgery attack and subset replay attack. If an adversary detects that the random numbers generated by the tag and the reader are equal, he can use XOR operation to generate a fixed session message unrelated with the random numbers. Later he can use the message to impersonate a target tag to generate some false grouping proofs. Otherwise, the protocol assumed the reader is trusted and the tags have to store the secret keys of the readers so as to consume more storage resource of the tags.

Peris-Lopez et al., proposed an RFID-based grouping-proof scheme to enhance inpatient medication safety [9]. They use some low-cost RFID tags which can only perform PRNG function and bitwise XOR operation. Their scheme automatically finishes the matching operation between the unit-dose packages and the inpatient to avoid human error. In addition, digital evidence generated by their scheme can be used for medication tracking and auditing. Their scheme assumes that a physician utilizes a Personal Digital Assistant (PDA) equipped with an RFID reader to issue prescriptions and a nurse utilizes a PDA with an RFID reader to verify drugs for inpatients. Every inpatient wears a wristband with an RFID tag. Every unit-dose drug package is labeled with an RFID tag. After these tags are justified to be the same group, the unit-dose drug package can be dispatched to the inpatient. Yen et al. [10] found that the digital evidence generated by the scheme is only signed by the nurse, not including the inpatient’s signature. If a medication dispute occurs, the hospital can re-generate counterfeit evidence without inpatient’s awareness to cover up their medication errors. In order to overcome the shortcoming described above, Yi-Chung Yen et al. [10] proposed an online solution and an offline solution to secure medication administration, which are suitable to areas in a hospital environment where wireless communication is available or not. Their protocol involves four entities: the backend server, nurse’s PDA, the inpatient’s wristband with a tag and unit-dose drug packages. Nurse’s PDA and inpatient’s tag have the computing ability to complete digital signatures. Each unit-dose package is attached with a low-cost tag which only has a PRNG function. By analyzing, we found that for each grouping-proof protocol proposed by Yi-Chung Yen et al., if the inpatient and unit-dose tags receive the challenge $\left\{request,r_b\right\}$ from the nurse’s PDA many times, the inpatient will return the same response messages $PRNG\left(i{d}_{pi}\oplus r_b\oplus K_{pi}\right)$, and the unit-dose tags will return the same messages $PRNG\left(i{d}_{uj}\oplus r_b\right)$ and $PRNG\left(K_{uj}\oplus r_b\right)$ to the nurse’s PDA. An adversary can locate the inpatient and his/her unit-dose package by repeatedly sending the same message $\left\{request,r_b\right\}$ to inpatients and unit-dose packages. Therefore, the adversary can acquire the relationship of the inpatient with unit-dose package and he can find which unit-dose packages belong to the same group. So the grouping-proof protocol cannot resist tracing attack and it is easy to leak the privacy information of the inpatient and his/her unit-dose packages. The keys of the inpatient wristband’s tag and the unit-dose package’s tags are fixed and the protocol cannot provide forward security.

Hong Liu et al. [11] found that some previous protocols only involves the single reader and the single tag group, which limits the diverse application of RFID systems. Then they proposed a grouping-proof protocol which adopts the distributed authentication mode with independent subgrouping proofs. They claimed that their protocol can resist major attacks such as replay, forgery, tracking and denial of proof. Later, Jian Shen et al. [12] proposed an enhanced grouping-proof protocol for multiple readers and tag groups, which involves the mutual authentication and grouping proof between multiple readers and multiple tag groups. They claimed that their protocol can resist information leakage and replay attack. However, we found that their protocol use the plaintext of the tag’s identifier $I{D}_i$, the tag group’s identifier $GI{D}_i$ and the reader’s identifier $I{D}_{Ri}$ to communicate. Moreover, these identifiers are fixed during the period of grouping proof. So their protocol seriously exposes the privacy information of the RFID system and it cannot resist tracing attack. Their protocol involves multiple readers. However, it does not describe how to authorize a reader to finish grouping proof.

Daisuke Moriyama [13] analyzed some previous grouping-proof protocols and found that their communication complexity increase rapidly with the number of the tags. Then he proposed a provably secure two-round grouping-proof protocol. His protocol is a parallel protocol and it only uses two-round communication so that the number of the sessions for the protocol is independent of the number of the tags. However, his protocol can only resist impersonation attack. Otherwise, the transferred sessions include the redundant information, e.g., the random nonce $\mathrm{r}$. Moreover, the verifier cannot judge the validness of the grouping-proof evidences because the timestamp is generated by the reader.

Ping Huang and Haibing Mu [14] proposed a high-security RFID grouping-proof protocol. Their protocol introduces a new method of the key distribution by means of distributing the points on straight lines to different entities. The protocol attempts to complete two important targets for RFID grouping proof: the dependency between tags and the scalability of the RFID system. In order to reduce computing cost, the protocol does not use the Hash function to encrypt the sessions. However, the protocol makes a big mistake, which is that a tag updates its secret key twice during the authentication process. After a tag completes the first updating of its secret key ${\mathrm{c}}_{\mathrm{i}}$, the reader uses the previous ${\mathrm{c}}_{\mathrm{i}}$ to generate $|{\mathrm{c}}_{\mathrm{i}}-{\mathrm{a}}_{\mathrm{i}}+{\mathrm{r}}_{\mathrm{Ti}}|$ and send the result to the tag, which will make the tag not to authenticate the reader because of their different ${\mathrm{c}}_{\mathrm{i}}$. Hence DoS attack occurs. So the protocol cannot resist de-synchronization attack.

Jian Shen et al. [15] proposed a practical grouping authentication protocol. The protocol is divided into four phases: initialization, tag acquisition, main authentication and verification. The protocol only uses some simple operations, not Hash function. It uses the serial signature method to generate the grouping proof. So it costs more time to finish the entire grouping proof. Otherwise, the protocol seriously leaks the privacy of the RFID system. For the tag acquisition phase, an adversary can deduce the group’s key ${\mathrm{S}}_{\mathrm{g}}$ and the tag’s sequence number ${\mathrm{e}}_{\mathrm{i}}$ by eavesdropping the sessions between reader and tags. An adversary can eavesdrop the sessions ${\mathrm{M}}_{\mathrm{g}}=\left({\mathrm{GID}}_{\mathrm{g}}\oplus {\mathrm{ID}}_{\mathrm{Rm}}\right)+\left({\mathrm{S}}_{\mathrm{g}}\vee {\mathrm{r}}_{\mathrm{Rm}}\right)$ and $\left({\mathrm{ID}}_{\mathrm{Rm}},{\mathrm{M}}_{\mathrm{g}},{\mathrm{r}}_{\mathrm{Rm}}\right)$ from the reader, the sessions ${\mathrm{N}}_{\mathrm{Ti}}=\left[{\mathrm{M}}_{\mathrm{g}}-\left({\mathrm{GID}}_{\mathrm{g}}\oplus {\mathrm{ID}}_{\mathrm{Rm}}\right)\right]\vee {\mathrm{r}}_{\mathrm{Ti}}$, ${\mathrm{Q}}_{\mathrm{Ti}}={\mathrm{e}}_{\mathrm{i}}\oplus \left({\mathrm{S}}_{\mathrm{g}}\vee {\mathrm{r}}_{\mathrm{Ti}}\right)$ and $\left({\mathrm{N}}_{\mathrm{Ti}},{\mathrm{Q}}_{\mathrm{Ti}},{\mathrm{r}}_{\mathrm{Ti}}\right)$. from tags. Then an adversary can deduce ${\mathrm{M}}_{\mathrm{g}}-\left({\mathrm{GID}}_{\mathrm{g}}\oplus {\mathrm{ID}}_{\mathrm{Rm}}\right)$ from ${\mathrm{N}}_{\mathrm{Ti}}=\left[{\mathrm{M}}_{\mathrm{g}}-\left({\mathrm{GID}}_{\mathrm{g}}\oplus {\mathrm{ID}}_{\mathrm{Rm}}\right)\right]\vee {\mathrm{r}}_{\mathrm{Ti}}$ and ${\mathrm{r}}_{\mathrm{Ti}}$. Secondly, he can deduce $\left({\mathrm{S}}_{\mathrm{g}}\oplus {\mathrm{r}}_{\mathrm{Rm}}\right)$ from ${\mathrm{M}}_{\mathrm{g}}=\left({\mathrm{GID}}_{\mathrm{g}}\oplus {\mathrm{ID}}_{\mathrm{Rm}}\right)+\left({\mathrm{S}}_{\mathrm{g}}\vee {\mathrm{r}}_{\mathrm{Rm}}\right)$. Because ${\mathrm{r}}_{\mathrm{Rm}}$ is known, he can get the group’s key ${\mathrm{S}}_{\mathrm{g}}$. Finally he easily deduces the tag’s sequence number ${\mathrm{e}}_{\mathrm{i}}$ from ${\mathrm{Q}}_{\mathrm{Ti}}={\mathrm{e}}_{\mathrm{i}}\oplus \left({\mathrm{S}}_{\mathrm{g}}\vee {\mathrm{r}}_{\mathrm{Ti}}\right)$, where ${\mathrm{r}}_{\mathrm{Ti}}$ is known and it is from the ith tag. Moreover, the protocol cannot provide forward security because the secret information of the RFID system is not updated after each authentication.

Bianqing Yuan and Jiqiang Liu [16] proposed a universally composable secure grouping-proof protocol for RFID systems with anonymity, privacy preserving, mutual authorized access and anti-replay attack. In general, readers and tags are assumed to be some untrusted entities. They can be impersonated by an adversary. So a reader should not know more information about tags. However, the protocol proposed by Bianqing Yuan and Jiqiang Liu sends the identifier of the tag group to the reader. Thence the reader can know which group it searches. Otherwise, their protocol cannot state how to authenticate between a verifier and readers.

Hongyan Kang [17] analyzed the grouping-proof protocol proposed by L. Batina et al. [18] and he found the protocol proposed by L. Batina et al., cannot resist tracking attack and impersonation attack for tags. Then he proposed an improved grouping-proof protocol. However, his protocol still uses ECC mechanism and the computation of EC points means a high overload for low-cost tags. After the initialization of the protocol, its secret information is fixed and it cannot provide forward security. Otherwise, the protocol is a serial protocol and it can only complete grouping-proof for two tags. So it is not suitable for grouping proof of multiple tags.

As analyzed above, many grouping-proof protocols only involve a reader and a tag group, not multiple readers and multiple tag groups. The verifier does not know whether the reader is trusted during grouping proof. Many grouping-proof protocols use the serial approach to query each tag and to generate the grouping-proof evidence, which results in the low efficiency of grouping proof. When there exist many tag groups near the reader the verifier does not sense their co-existence. Especially, some grouping-proof protocols are vulnerable to information leakage and some common attacks.

3. The RFID System Under Grouping Proof and Its Secure Model

An RFID system consists of three components: Radio Frequency (RF) tags, RF readers and a backend server (simply called verifier), as shown in Figure 1. A tag is basically a silicon chip with antenna and a small memory that stores its unique identifier known as EPC (Electronic Product Code). A tag is usually used to identify an object. Tags are divided into active tags and passive tags. The active tags have their own internal power source. They provide large memory and complicated processing capabilities. The passive tags have no internal power source. When these tags communicate with the readers they are powered with their on-chip antenna coil activated by the RF signal from the reader. Thus, their computation and communication capabilities are very limited. However, the passive tags are very cheap. So they have become the most popular tags. The reader is a device capable of sending and receiving data in the form of radio frequency signal. This device is used to read EPC from the tag and to send it to the verifier. The verifier is used to store the information related to the tagged objects and cooperates with readers to finish authenticating, indexing and displaying the information.

Under many circumstances, two or multiple tags are sometimes utilized to identify an object together. A grouping-proof protocol is to give the evidence that there exist two or more RFID tags simultaneously within the reader’s broadcast range. According to the role of the verifier during grouping-proof period, the grouping-proof protocols are divided into two different modes: online or offline. For the first mode, the verifier can send and receive messages from specific tags (via the reader) throughout the protocol execution. In contrast, for offline mode, the verifier can only send challenges to the reader and it does not need the persistent presence during grouping-proof period. Many current grouping-proof protocols use offline mode. According to the sequence for tags to complete their signature during grouping-proof period, the grouping-proof protocols are divided into two other types: serial mode and parallel mode. For the first mode, after one tag finishes its signature another tag begins to sign for generating the grouping-proof evidence. For parallel mode, all tags finish their signatures to generate the grouping proof almost at the same time. So the grouping-proof protocols under parallel mode are more efficient than under serial mode.

For an RFID System under the grouping-proof mode, tags are usually divided into different groups. Each group is identified by its group identifier and its secret key. Each tag has its identifier and its secret key. We assume that any two tags cannot directly communicate each other. When a tag wants to send messages to another tag it first sends the messages to a reader. Then the reader transfers the messages to another tag. A reader can communicate directly with tags or verifier. There may be many readers for an RFID system. However, only the reader authorized by the verifier can scan tags, generate a grouping proof and provide the grouping proof to the verifier. During the grouping proof process, it is assumed that the verifier is a unique trusted entity and it shares some secret information with tags such as cryptographic keys. The readers are some potential untrusted entities and they are used to interrogate tags to generate the evidence of the co-existence of a tag group. The computing and storage resources of verifier and readers are abundant and they can use some complicated cryptographic functions. So we can assume that the channel between verifier and reader is secure. Moreover, the computing and storage resources of tags are very limited and they only use some simple cryptographic functions such as hash function and pseudorandom number generator. So we think that the channel between reader and tags is not secure. For an RFID system under the grouping proof mode, it should ensure anonymity and confidentiality. It can effectively resist information leakage, eavesdropping, trace, replay, de-synchronization, and impersonation attack [5].

4. The Grouping-Proof Protocol Based on Parallel Mode and DHCP Mechanism

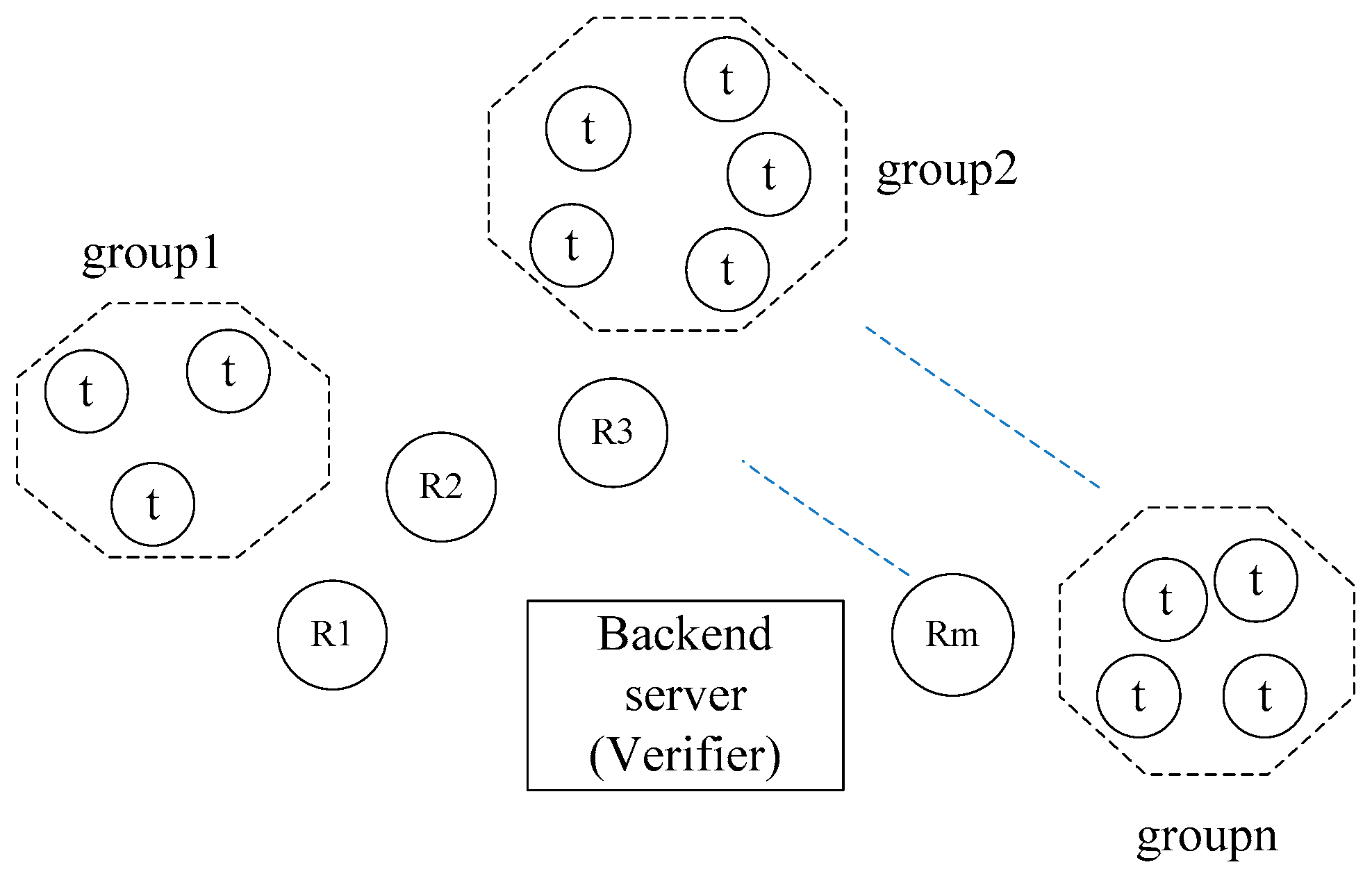
For an RFID System under the grouping proof mode, there are four kinds of entities: verifier, reader, tag and adversary. We assume that there are multiple readers and multiple tag groups for an RFID system. Therefore readers may be represented by $\left\{{\mathrm{R}}_{\mathrm{i}}\right|\mathrm{i}\in \left\{1,2,\dots \dots \mathrm{m}\}\right\}$. Tags are also represented by $\left\{{\mathrm{t}}_{\mathrm{ij}}\right|\mathrm{i}\in \left\{1,2,\dots \dots \mathrm{p}\right\},\mathrm{j}\in \left\{1,2,\dots \dots \mathrm{q}\}\right\}$, where ${\mathrm{t}}_{\mathrm{ij}}$ represents a tag which is the jth tag of the ith group. It is usually assumed that the verifier is a unique trusted entity and the readers are some untrusted entities. The communication channels between verifier and readers are secure and the communication channels between readers and tags are not secure. Before a reader is responsible for grouping proof, it must be authenticated and authorized by the verifier. It is also assumed that an adversary is probabilistic polynomial time algorithm and he can control all communication channels between readers and tags. He can eavesdrop, intercept, tamper, counterfeit and replay each session message transferred between reader and tag. His main attack goal is to counterfeit a grouping-proof evidence which is verified to be valid by the verifier or to obtain the private information of the RFID system, such as the secret keys and identifiers of tags.

For an RFID system under the grouping-proof model, there may be many readers and tag’s groups to be queried simultaneously. They almost give their responses at the same time. Which is chosen? DHCP gives a good approach. Now we utilize DHCP and broadcast mechanism from Internet to propose a novel grouping-proof protocol. Our protocol works under parallel mode and it is independent of reading order to tags. So it is very efficient. It concerns multiple readers and multiple tag groups. Each reader stores its identifier $\mathrm{ridi}$ and its secret key $\mathrm{rki}$. Each tag stores its secret key $\mathrm{tkj}$ and its group identifier $\mathrm{gid}$. The verifier stores the secret key and identifier $\left\{\mathrm{rki},\mathrm{ridi}\right\}$ of each reader and the secret information $\left\{\mathrm{tkj},\mathrm{gid}\right\}$ of each tag. L is the length of the secret information. The symbols used in our protocol are shown in

Table 1. The symbols used in our proposed protocol.

Notation	Description
gid	the identifier of a tag group
tkj	The secret key of the jth tag
rki	the secret key of the ith reader
ridi	the identifier of the ith reader
Hash ( )	a secure cryptographic Hash function
PRNG ()	a pseudorandom number generator
r1, r2, r3, r4	some random numbers generated by the different entities
t	the timestamp of the verifier
t1	The timer which the reader starts
⊕	bitwise XOR operation

.

For our protocol, two modes are involved: active mode and passive mode. Under active mode, the verifier knows the identifier of the tag group which it wants to search. When the protocol begins, the verifier sends the identifier of the tag group to the authorized reader. The reader collects the grouping-proof evidence and returns the evidence to the verifier. Under passive mode, the verifier does not know which tag group it wants to search. There may be many tag groups at this time. When the protocol begins, the authorized reader broadcasts the challenge to all tag groups. After tags receive the challenge from the reader, they return their randomized group identifiers to the reader. Then the reader transfers these group identifiers to the verifier. The verifier chooses a tag group by means of DHCP rule and returns the group identifier to the reader. The reader broadcasts the group identifier to all tags and activates the chosen tag group. It is obvious that the protocol under active mode is simpler than under passive mode. So we only describe the grouping-proof protocol under passive mode.

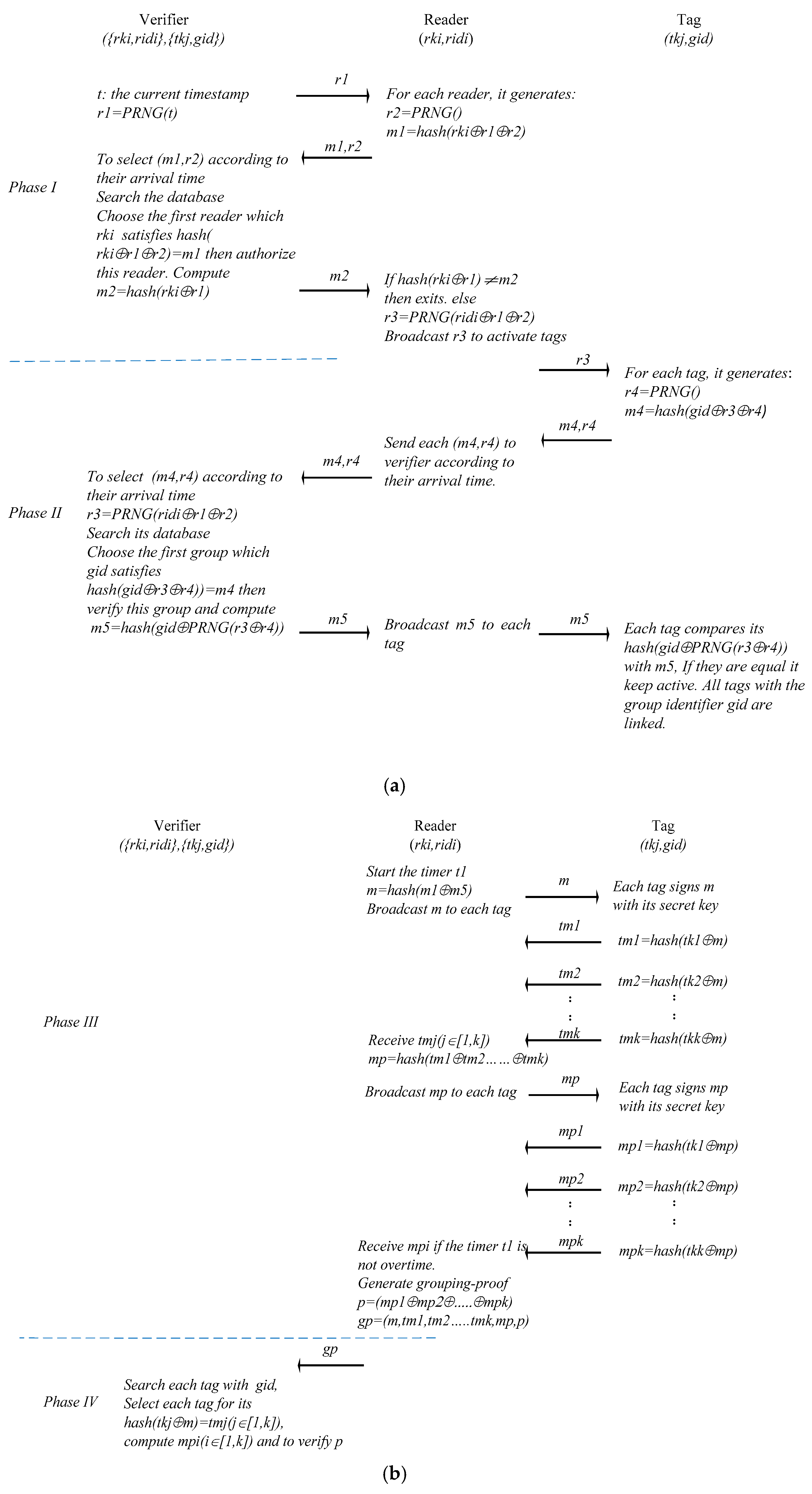
The protocol includes four phases: to authorize a reader, to choose a tag group, to generate a grouping-proof evidence and to verify the grouping-proof evidence, as shown in Figure 2.

Phase I: to authorize a reader

(1.1) The verifier uses its current timestamp $\mathrm{t}$ to generate a pseudorandom number $\mathrm{r}1=\mathrm{PRNG}\left(\mathrm{t}\right)$. Then it broadcasts $\mathrm{r}1$ to all readers.

(1.2) After a reader receives $\mathrm{r}1$, it generates a pseudorandom number $\mathrm{r}2=\mathrm{PRNG}()$ and $\mathrm{m}1=\mathrm{hash}\left(\mathrm{rki}\oplus \mathrm{r}1\oplus \mathrm{r}2\right)$.

(1.3) each reader sends its $\left(\mathrm{m}1,\mathrm{r}2\right)$ to the verifier respectively.

(1.4) The verifier chooses a reader according to the arrival time of each $\left(\mathrm{m}1,\mathrm{r}2\right)$. Then the verifier searches its database and finds the reader with $\mathrm{rki}$ which $\mathrm{hash}\left(\mathrm{rki}\oplus \mathrm{r}1\oplus \mathrm{r}2\right)=\mathrm{m}1$ holds. The verifier authenticates the reader. It computes $\mathrm{m}2=\mathrm{hash}\left(\mathrm{rki}\oplus \mathrm{r}1\right)$ and broadcasts $\mathrm{m}2$ to all readers. Each reader receives $\mathrm{m}2$ and uses its $\mathrm{rki}$ to judge whether $\mathrm{m}2$ equals $\mathrm{hash}\left(\mathrm{rki}\oplus \mathrm{r}1\right)$. If a reader finds that they are equal, it is authorized for the grouping proof.

(1.5) The authorized reader computes $\mathrm{r}3=\mathrm{PRNG}\left(\mathrm{ridi}\oplus \mathrm{r}1\oplus \mathrm{r}2\right)$ and sends $\mathrm{r}3$ to each tag.

Phase II: to choose a tag group

(2.1) After each tag receives $\mathrm{r}3$, it generates a pseudorandom number $\mathrm{r}4=\mathrm{PRNG}()$ and computes $\mathrm{m}4=\mathrm{hash}\left(\mathrm{gid}\oplus \mathrm{r}3\oplus \mathrm{r}4\right)$. Then they send $\left(\mathrm{m}4,\mathrm{r}4\right)$ to the reader respectively.

(2.2) The reader receives each $\left(\mathrm{m}4,\mathrm{r}4\right)$ and transfers them to the verifier according to their arrival time.

(2.3) The verifier chooses $\left(\mathrm{m}4,\mathrm{r}4\right)$ according to their arrival time and searches its database to find $\mathrm{gid}$ which $\mathrm{m}4=\mathrm{hash}\left(\mathrm{gid}\oplus \mathrm{r}3\oplus \mathrm{r}4\right)$ holds. Then the verifier computes $\mathrm{m}5=\mathrm{hash}\left(\mathrm{gid}\oplus \mathrm{PRNG}\left(\mathrm{r}3\oplus \mathrm{r}4\right)\right)$ and sends $\mathrm{m}5$ to the reader.

(2.4) The reader receives $\mathrm{m}5$ and broadcasts $\mathrm{m}5$ to all tags.

(2.5) After each tag receives $\mathrm{m}5$, it uses its $\mathrm{gid}$ to compute $\mathrm{hash}\left(\mathrm{gid}\oplus \mathrm{PRNG}\left(\mathrm{r}3\oplus \mathrm{r}4\right)\right)$. If the result equals $\mathrm{m}5$, it keeps active. Or it becomes silent. The tags with the same $\mathrm{gid}$ are linked.

Phase III: to generate a grouping-proof evidence

(3.1) The reader starts its timer $\mathrm{t}1$ and computes $\mathrm{m}=\mathrm{hash}\left(\mathrm{m}1\oplus \mathrm{m}5\right)$. It broadcasts $\mathrm{m}$ to all objective tags.

(3.2) Each objective tag signs $\mathrm{m}$ with its secret key respectively and sends the signed result to the reader. For the ith tag ($1\le \mathrm{i}\le \mathrm{k},\mathrm{k}\le \mathrm{n}$), it signs $\mathrm{m}$ with its secret key tki, gets $\mathrm{tmi}=\mathrm{hash}\left(\mathrm{tki}\oplus \mathrm{m}\right)$ and sends $\mathrm{tmi}$ to the reader.

(3.3) After the reader receives each $\mathrm{tmi}$, it computes $\mathrm{mp}=\mathrm{hash}\left(\mathrm{tm}1\oplus \mathrm{tm}2\oplus \dots \dots \oplus \mathrm{tmk}\right)$, $\mathrm{k}\le \mathrm{n}$. Then the reader broadcasts $\mathrm{mp}$ to all objective tags.

(3.5) After each objective tag receives $\mathrm{mp}$, it signs $\mathrm{mp}$ with its secret key respectively and sends the signed result to the reader. For the ith tag, it signs $\mathrm{mp}$, gets $\mathrm{mpi}=\mathrm{hash}\left(\mathrm{tki}\oplus \mathrm{mp}\right)$ and sends $\mathrm{mpi}$ to the reader.

(3.6) The reader receives each $\mathrm{mpi}$ until the timer $\mathrm{t}1$ is overtime. Then it computes $\mathrm{p}=\mathrm{hash}\left(\mathrm{mp}1\oplus \mathrm{mp}2\oplus \dots \dots \oplus \mathrm{mpk}\right)$, $\mathrm{k}\le \mathrm{n}$. The reader generates the grouping-proof evidence $\mathrm{gp}=\left(\mathrm{m},\mathrm{tm}1,\mathrm{tm}2\dots \dots \mathrm{tmk},\mathrm{mp},\mathrm{p}\right)$ and sends $\mathrm{gp}$ to the verifier.

Phase IV: to verify the grouping-proof evidence

The verifier receives $\mathrm{gp}$. If the timer $\mathrm{t}$ is not overtime, the verifier searches its database and gets $\mathrm{tki}$ which $\mathrm{tmi}=\mathrm{hash}\left(\mathrm{tki}\oplus \mathrm{m}\right)$ holds. Then it uses $\mathrm{tki}$ and $\mathrm{mp}$ to compute $\mathrm{mpi}$. Finally it can verify the validity of $\mathrm{p}$.

5. The Efficient and Secure Analysis of the Proposed Protocol

Our proposed protocol works under parallel mode and it is independent of reading order to tags. Each tag signs m and mp almost simultaneously, and return the response to the reader. So our protocol is very efficient. When tags sign, the collision probably happens. However, we assume that the collision among tags is avoided by the low-level protocol. Multi-level timer is taken by the verifier and the readers to control the proof time. For the current grouping-proof protocols, the reader collects the grouping-proof evidence and sends it to the verifier, whether the evidence is valid or not. The verifier finally judges whether it is overtime and the evidence is valid. For our protocol, the reader can judge whether it is overtime and it can find the invalid evidence in time. So our protocol is very efficient. For the computation and storage requirement for tag, our protocol is compared with other protocols, which is shown in

Table 2. The computation and storage requirements of the different protocols for tag.

Protocol	Computation	Storage	Mode	Efficiency
Mike Burmester’s protocol [3]	3 PRNG	6 L	Serial	low
Huang H-H’s protocol [7]	1 CRC + 2 PRNG	2 L	Serial	low
HY Chien’s protocol [8]	4 PRNG	2 L	Serial	low
Jian Shen’s protocol [12]	2 MAC + 1 PRNG	3 L	parallel	low
Our proposed protocol	4 hash + 2 PRNG	2 L	parallel	high

. It is obvious that our protocol does not require more computation resources than other protocols.

For the security of an RFID system under the grouping-proof mode, an adversary aims at counterfeiting a valid grouping-proof evidence or revealing the secret information of the RFID system. In order to resist the attacks described above, our protocol uses Hash function to encrypt all sessions transferred among verifier, readers and tags. Because Hash function is a one-way function, an adversary cannot reveal any secret information from the eavesdropped sessions. Therefore the confidentiality and privacy of the RFID system are protected. For different grouping-proof process, all sessions are randomized by different random numbers and the freshness of the sessions is ensured. An adversary cannot trace a tag or a tag group. As an untrusted party, the reader can receive the sessions from the verifier and tags. However, all sessions which the reader receives are encrypted by Hash function and it cannot acquire any secret information about the verifier and tags. So our proposed protocol can ensure the privacy and confidentiality of the RFID system, and it can prevent eavesdropping attack, tracing attack, replay attack and impersonation attack. Now we analyze the security of the proposed protocol as follows.

♦ Eavesdropping: During the grouping-proof period, all session messages transferred between tags and readers are encrypted by Hash function. None of the plaintext messages about the secrecy of the RFID system is transferred. An adversary can intercept all sessions between tags and readers. However, he cannot get any useful information about the tag and the tag group from the intercepted data. Eavesdropping to the communication channel between tags and readers is invalid. The privacy of the RFID system is preserved.

♦ Tracing attack: If a tag or a tag group is traced their privacy may be encroached upon. To resist this type of attack, a pseudorandom number generator is used to ensure that each session between tags and readers is variable so as to make attackers not to distinguish which tag or group sends their received information. For our protocol, an adversary can intercept $\mathrm{r}3$ and $\mathrm{m}4$ in phase II. Then he can repeat to send $\mathrm{r}3$ to tags many times. After the tag receives $\mathrm{r}3$ it will generate a different pseudorandom number $\mathrm{r}4$ to randomize its group identifier $\mathrm{gid}$. The randomized result is hashed to generate $\mathrm{m}4$. It is obvious that $\mathrm{m}4$ is different for each different $\mathrm{r}3$. Our protocol utilizes the parallel mode and all tags send their responses almost at the same time as soon as they receive the challenge from the reader. So it is very difficult for an adversary to distinguish and trace a tag.

♦ Replay attack: This type of attack means that an adversary can compromise an RFID system by replaying sessions intercepted by eavesdropping. In order to prevent replay attack, some pseudorandom number generators and timestamp are utilized. During the grouping-proof period, some pseudorandom numbers $\mathrm{r}1$, $\mathrm{r}2$, $\mathrm{r}3$ and $\mathrm{r}4$ are separately generated by the verifier, the reader and the tags. $\mathrm{r}1$ and $\mathrm{r}3$ are dependent on the current time of the verifier. These pseudorandom numbers are utilized to randomize the sessions between tags and readers. The current time of the verifier is not transferred among the system’s components and it is not possible for an adversary to acquire or predict it. If an attacker replays the intercepted session messages in the late grouping-proof period, these messages have not any meanings because a new grouping-proof process uses some new timestamp and pseudorandom numbers.

♦ De-synchronization: In order to reduce the computation and storage load on tags, our protocol does not update the tag’s secrecy, which may result in potential safety hazard to forward security. However, our protocol only reserves the current secrecy of each tag and it saves the time for updating the secrecy. So our protocol can resists de-synchronization attack. It completes the compromise between its secure level and its resource consumption.

♦ Impersonation: The protocol ensures user’s anonymity and privacy by using Hash function to encrypt all sessions transferred between readers and tags. Because Hash function is a one-way function an attacker cannot get the secrecy and identity information of tags or readers, so it cannot impersonate a valid tag or reader to cheat the RFID system.

♦ Counterfeiting attack: Because the communication channel between the verifier and the reader is assumed to be secure, an adversary cannot acquire any secrecy of the RFID system from this channel. Although the communication channel between tags and reader is assumed to be insecure, all sessions transferred between tags and readers are encrypted by Hash function. An adversary cannot also use his intercepted sessions to acquire any secrecy of the RFID system. Therefore he cannot counterfeit any valid grouping-proof. Otherwise, an adversary can abstract some parts of the evidences from the previous grouping-proof period and combine them to generate some new evidences to cheat the RFID system. However, these evidences are dependent on the timestamp of the verifier and different pseudorandom numbers. So it is impossible for the adversary to use these new combined evidences to cheat the RFID system. Counterfeiting attack is resisted by our protocol.

The comparison of our proposed protocol with some typical grouping-proof protocols is shown as

Table 3. The security comparison of the different grouping-proof protocols.

Protocol	Eavesdrop	Trace	Replay	Impersonation	Counterfeit
Yoking-proofs [2]	x	x	x	x	x
Mike Burmester’s protocol [3]	√	√	√	x	x
H.-H. Huang’s protocol [7]	√	√	x	x	x
H.Y. Chien’s protocol [8]	√	x	x	x	x
Jian Shen’s protocol [12]	x	x	√	x	x
L. Batina’ protocol [18]	√	x	√	x	x
Our proposed protocol	√	√	√	√	√

.

6. Conclusions

For many application circumstances, it is necessary for multiple tags to be attached to different part of an object so as to identify the whole object. So it is important to acquire the co-existence evidence of these tags. However, RFID systems are some typical resource-constrained devices and their computing and memory resources are very limited. In order to meet the special requirements of the RFID systems, we propose a lightweight grouping-proof protocol. This protocol involves multiple readers and multiple tag groups. It uses DHCP and broadcast mechanism to flexibly choose a reader and a tag group. It completes the mutual authentication of the verifier, readers and tags. It can flexibly authenticate all tags or one part of a special group. During the entire grouping-proof period, any secret information about the tags is not leaked to the reader. Although there exist some rogue readers the RFID system is still secure. Our protocol only utilizes Hash function and pseudorandom number generator to encrypt all sessions transferred between tags and readers. This ensures the confidentiality and privacy of the RFID system. Meanwhile, our proposed protocol uses random numbers to randomize each session transferred between tags and readers so as to resist tracing attack. So our proposed protocol can resist eavesdropping, tracing attack, replay attack, impersonation and de-synchronization attack. An adversary cannot counterfeit a valid grouping-proof to cheat the verifier. Our protocol is feasible for a low-cost RFID system to complete the secure and efficient grouping-proof function.