Expression and Analysis of Joint Roughness Coefficient Using Neutrosophic Number Functions
Abstract
:1. Introduction
2. Some Basic Concepts and Operations of NNs
3. JRC Data Obtained from an Actual Case
4. NN Functions for Describing the Anisotropic Characteristics of JRC
4.1. NN Functions of JRC in All Orientations
4.2. Anisotropic Parameter
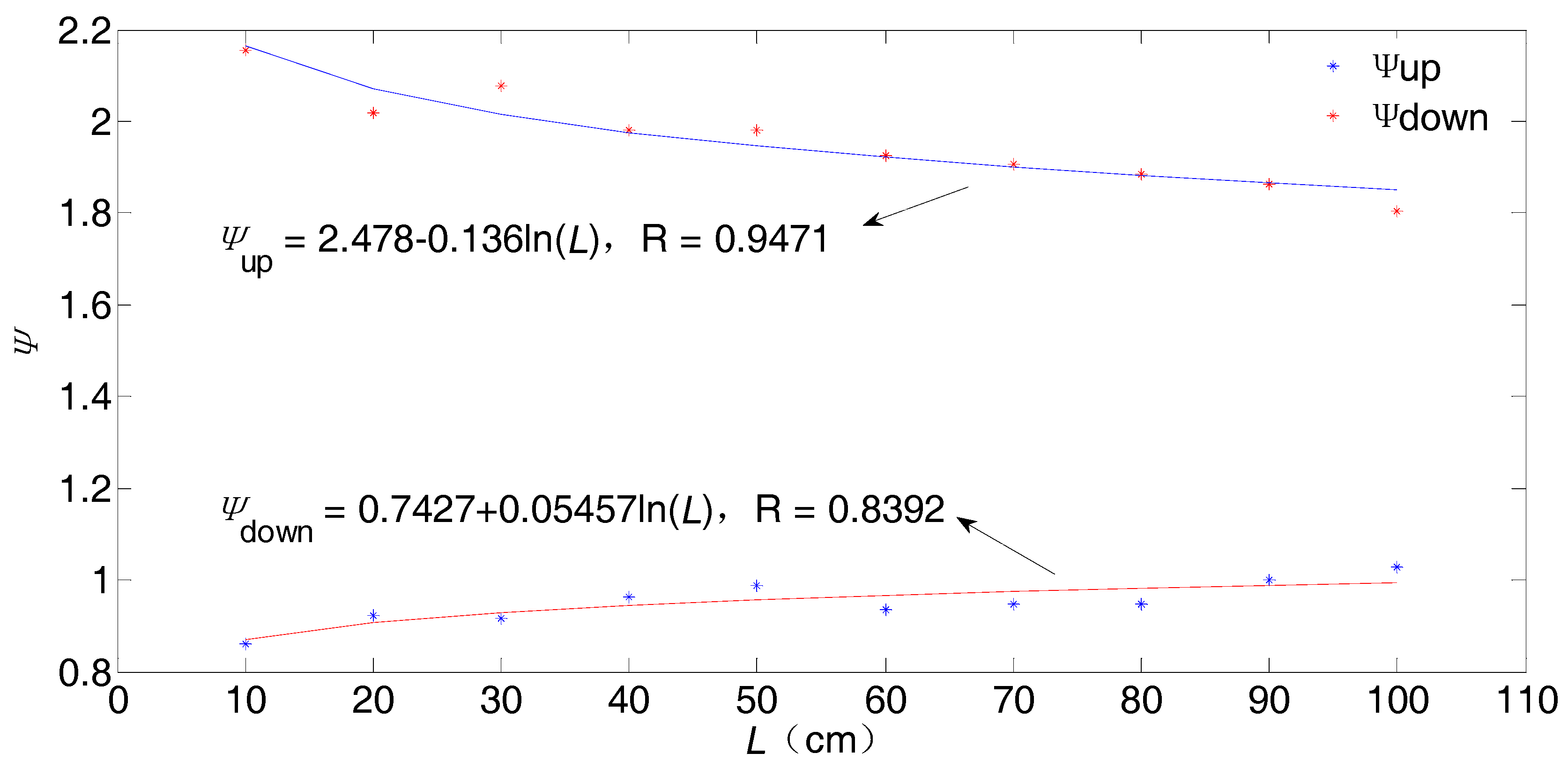
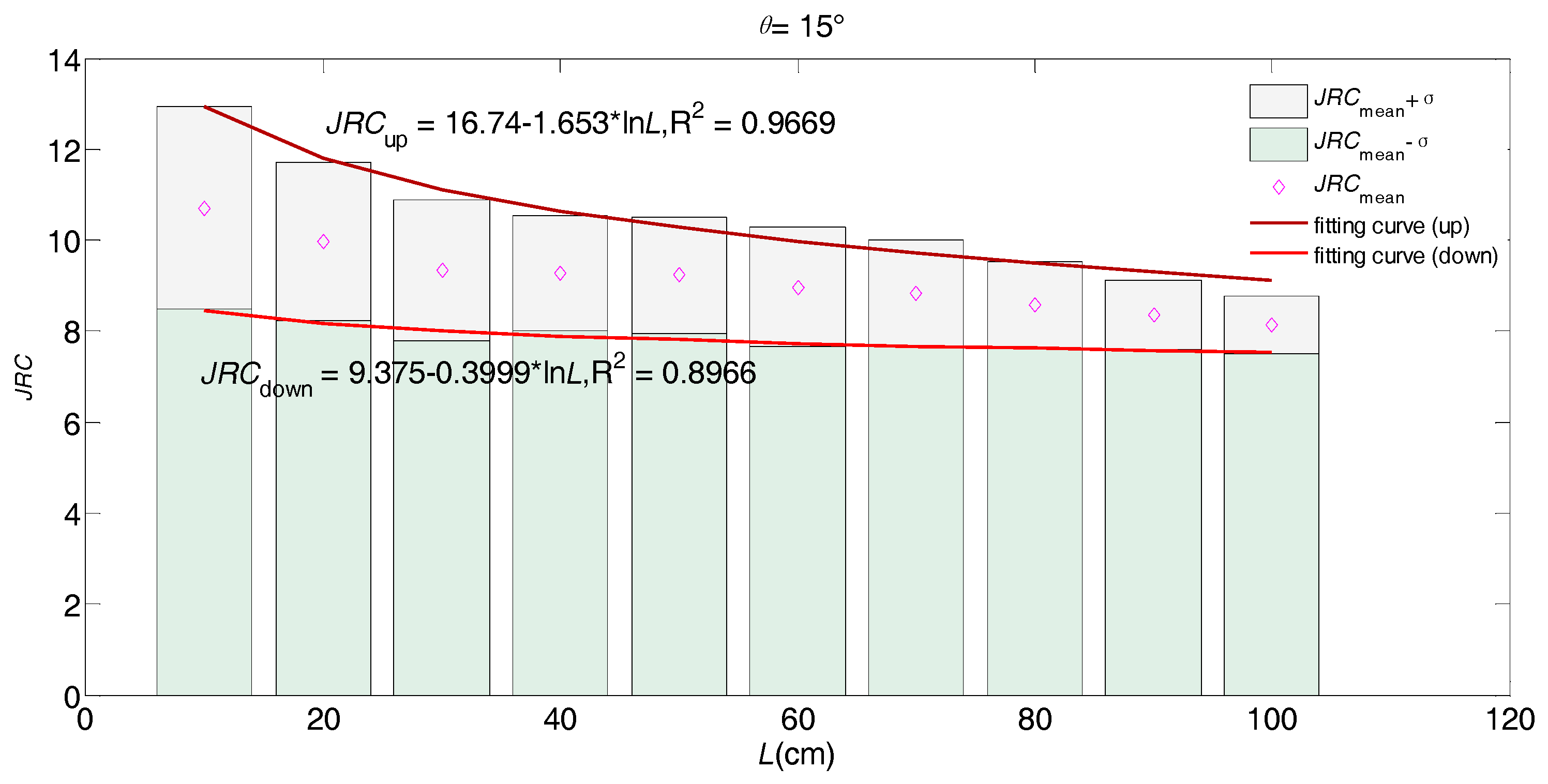
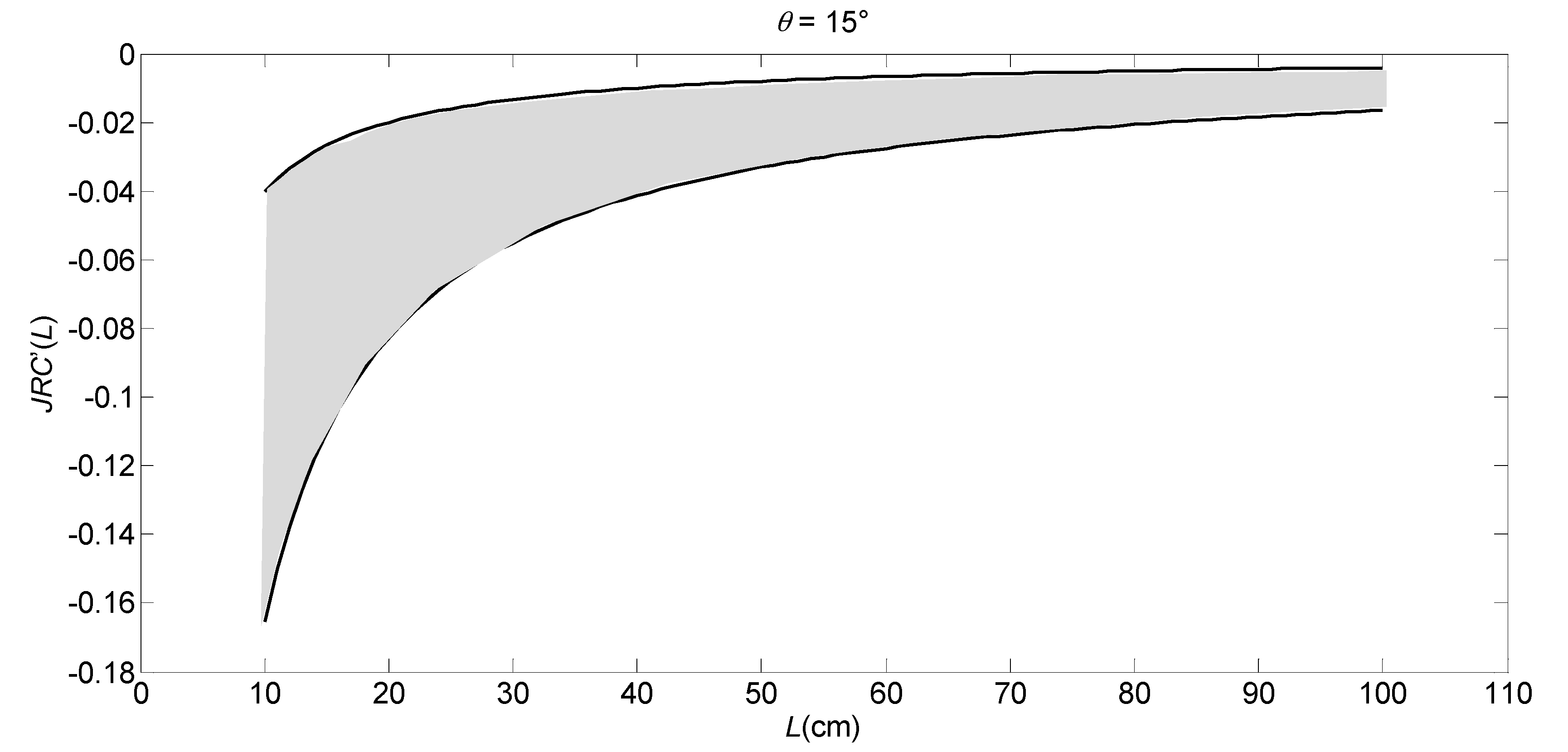
5. NN Functions for Reflecting the Scale Effect of Joint Surface Roughness
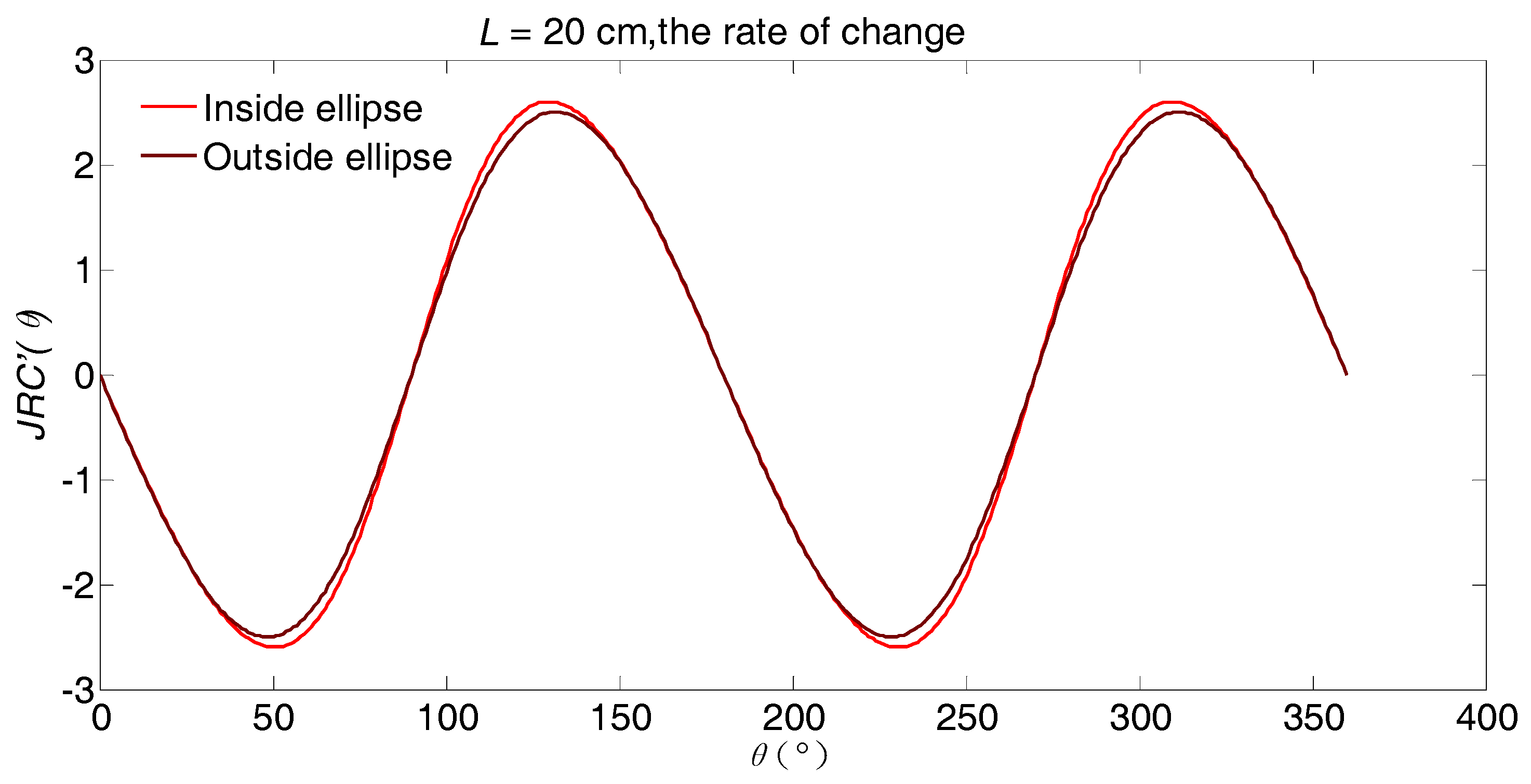
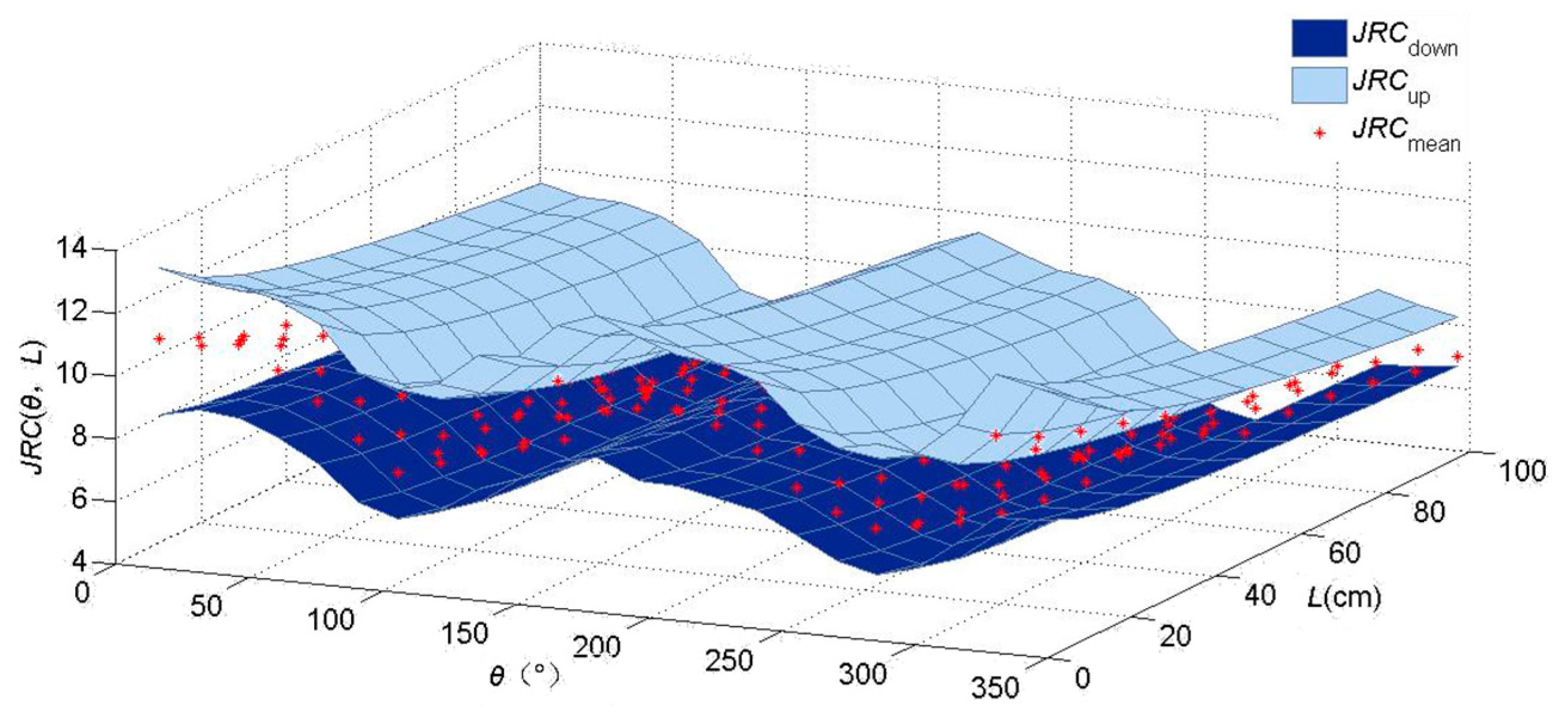
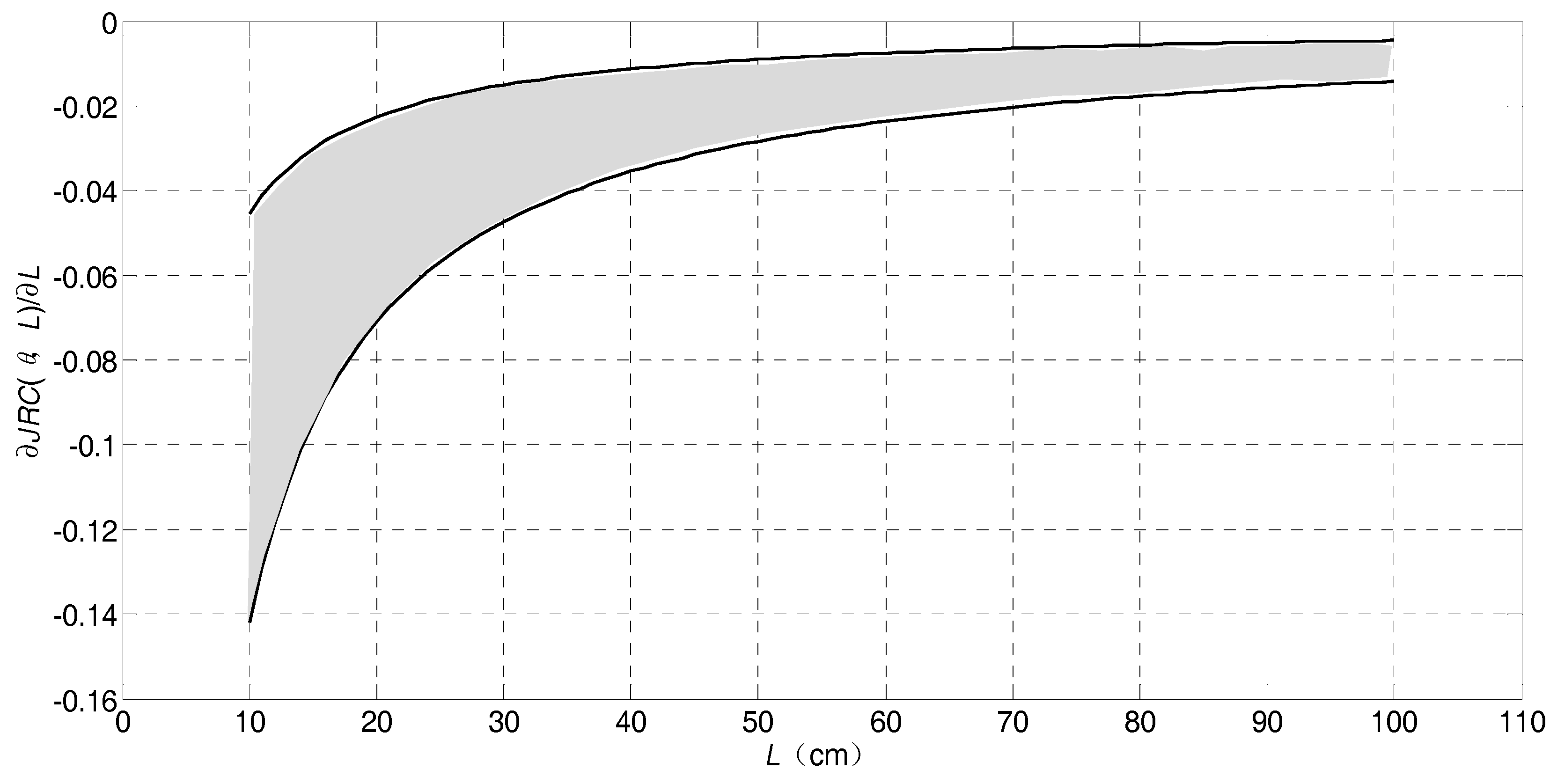
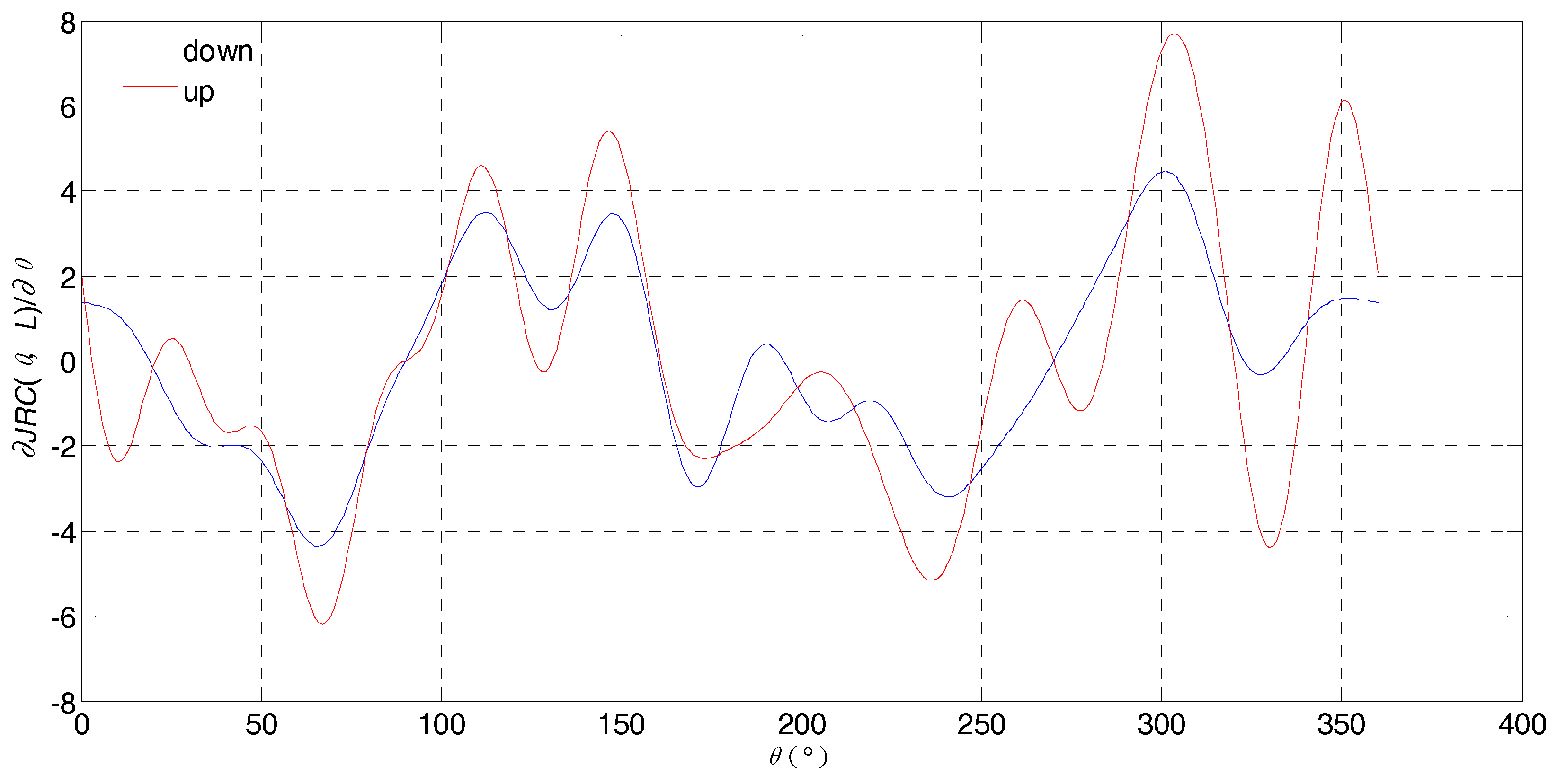
6. NN Function of JRC with the Two Variables θ and L
7. Discussion
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Barton, N.; Choubey, V. The shear strength of rock joints in theory and practice. Rock Mech. 1977, 10, 1–54. [Google Scholar] [CrossRef]
- Chen, S.J.; Zhu, W.C.; Liu, S.X. Anisotropy and size effects of surface roughness of rock joints. J. Eng. Geol. 2015, 34, 57–66. (In Chinese) [Google Scholar]
- Alameda-Hernández, P.; Jiménez-Perálvarez, J.; Palenzuela, J.A.; Hamdouni, R.E.; Irigaray, C.; Cabrerizo, M.A.; Chacón, J. Improvement of the JRC calculation using different parameters obtained through a new survey method applied to rock discontinuities. Rock Mech. Rock Eng. 2014, 47, 2047–2060. [Google Scholar] [CrossRef]
- Jang, H.S.; Kang, S.S.; Jang, B.A. Determination of joint roughness coefficients using roughness parameters. Rock Mech. Rock Eng. 2014, 47, 2061–2073. [Google Scholar] [CrossRef]
- Grasselli, G.; Wirth, J.; Egger, P. Quantitative three-dimensional description of a rough surface and parameter evolution with shearing. Int. J. Rock Mech. Min. Sci. 2002, 39, 789–800. [Google Scholar] [CrossRef]
- Lee, Y.H.; Carr, J.R.; Barr, D.J.; Haas, C.J. The fractal dimension as a measure of the roughness of rock discontinuity profiles. Int. J. Rock Mech. Min. Sci. 1990, 27, 453–464. [Google Scholar] [CrossRef]
- Li, Y.; Huang, R. Relationship between joint roughness coefficient and fractal dimension of rock fracture surfaces. Int. J. Rock Mech. Min. Sci. 2015, 75, 15–22. [Google Scholar] [CrossRef]
- Li, H.; Huang, R. Method of quantitative determination of joint roughness coefficient. J. Eng. Geol. 2014, 33 (Suppl. S2), 2513–2519. (In Chinese) [Google Scholar]
- Sun, F.; She, C.; Wan, L. Research on a new roughness index of rock joint. J. Eng. Geol. 2013, 33, 3489–3497. (In Chinese) [Google Scholar]
- Aydan, O.; Shimizu, Y.; Kawamoto, T. The anisotropy of surface morphology characteristics of rock discontinuities. Rock Mech. Rock Eng. 1996, 29, 47–59. [Google Scholar] [CrossRef]
- Barton, N. Review of a new shear-strength criterion for rock joints. Eng. Geol. 1973, 7, 287–332. [Google Scholar] [CrossRef]
- Barton, N.; Bandies, S. Review of predictive capabilities of JRC-JCS model in engineering practice. Proc. Int. Symp. Rock Jt. 1991, 181, 603–610. (In Chinese) [Google Scholar]
- Du, S.G.; Hang, M.; Luo, Z.Y.; Jia, R.D.; Wang, Y.M. Scale effect of undulation amplitude of rock joints. J. Eng. Geol. 2010, 18, 47–52. (In Chinese) [Google Scholar]
- Chen, S.J.; Zhu, W.C.; Yu, Q.L.; Liu, X.G. Characterization of anisotropy of joint surface roughness and aperture by variogram approach based on digital image processing technique. Rock Mech. Rock Eng. 2016, 49, 855–876. [Google Scholar] [CrossRef]
- Ye, J.; Yong, R.; Liang, Q.F.; Huang, M.; Du, S.G. Neutrosophic functions of the joint roughness coefficient and the shear strength: A case study from the pyroclastic rock mass in Shaoxing City, China. Math. Probl. Eng. 2016, 2016, 4825709. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophy: Neutrosophic Probability, Set, and Logic; American Research Press: Rehoboth, DE, USA, 1998. [Google Scholar]
- Smarandache, F. Introduction to Neutrosophic Measure, Neutrosophic Integral, and Neutrosophic Probability; Sitech & Education Publisher: Craiova, Romania, 2013. [Google Scholar]
- Smarandache, F. Introduction to Neutrosophic Statistics; Sitech & Education Publisher: Craiova, Romania, 2014. [Google Scholar]
- Ye, J. Multiple-attribute group decision-making method under a neutrosophic number environment. J. Intell. Syst. 2016, 25, 377–386. [Google Scholar] [CrossRef]
- Ye, J. Bidirectional projection method for multiple attribute group decision making with neutrosophic numbers. Neural Comput. Appl. 2017, 28, 1021–1029. [Google Scholar] [CrossRef]
- Kong, L.W.; Wu, Y.F.; Ye, J. Misfire fault diagnosis method of gasoline engines using the cosine similarity measure of neutrosophic numbers. Neutrosophic Sets Syst. 2015, 8, 43–46. [Google Scholar]
- Ye, J. Fault diagnoses of steam turbine using the exponential similarity measure of neutrosophic numbers. J. Intell. Syst. 2016, 30, 1927–1934. [Google Scholar] [CrossRef]
- Chen, J.Q.; Ye, J. A projection model of neutrosophic numbers for multiple attribute decision making of clay-brick selection. Neutrosophic Sets Syst. 2016, 12, 139–142. [Google Scholar]
- Liu, P.; Liu, X. The neutrosophic number generalized weighted power averaging operator and its application in multiple attribute group decision making. Int. J. Mach. Learn. Cybern. 2016, 1–12. [Google Scholar] [CrossRef]
- Ye, J. Neutrosophic number linear programming method and its application under neutrosophic number environments. Soft Comput. 2017. [Google Scholar] [CrossRef]
- Du, S.G. A simple longitudinal profiler and its application in the study of roughness coefficient of rock mass structural plane. Geol. Sci. Technol. Inf. 1992, 11, 91–94. [Google Scholar]
- Zhang, G.C.; Karakus, M.; Tang, H.M.; Ge, Y.F.; Zhang, L. A new method estimating the 2D loint roughness coefficient for discontinuity surfaces in rock masses. Int. J. Rock Mech. Min. Sci. 2014, 72, 191–198. [Google Scholar]
- Tatone, B.S. Quantitative Characterization of Natural Rock Discontinuity Roughness In-Situ and in the Laboratory. Master’s Thesis, University of Toronto, Toronto, ON, Canada, 2009. [Google Scholar]

| Scale (cm) | a1 | b1 | a2 | b2 | JRC(θ) |
|---|---|---|---|---|---|
| 10 | 8.6 | 7.8 | 5.8 | 8.4 | |
| 20 | 8.3 | 6.4 | 5.7 | 6.6 | |
| 30 | 8 | 5.6 | 5.5 | 6 | |
| 40 | 7.7 | 5.6 | 5.3 | 5.4 | |
| 50 | 7.4 | 5.8 | 5.2 | 4.6 | |
| 60 | 7.3 | 5.8 | 5.3 | 5.0 | |
| 70 | 7.2 | 5.8 | 5.3 | 4.6 | |
| 80 | 7.0 | 5.6 | 5.2 | 4.4 | |
| 90 | 7.0 | 5.0 | 5.1 | 3.8 | |
| 100 | 7.0 | 4.4 | 5.1 | 3.4 |
| Scale (cm) | JRC’(θ) |
|---|---|
| 10 | |
| 20 | |
| 30 | |
| 40 | |
| 50 | |
| 60 | |
| 70 | |
| 80 | |
| 90 | |
| 100 |
| Orientation (°) | a1 | b1 | a2 | b2 | JRC(L) |
|---|---|---|---|---|---|
| 0 | 9.487 | 11.246 | −0.5415 | −1.253 | |
| 15 | 9.375 | 14.73 | −0.3999 | −1.653 | |
| 30 | 9.22 | 15.34 | −0.4101 | −2.5498 | |
| 45 | 8.83 | 12.78 | −0.4538 | −1.8364 | |
| 60 | 7.432 | 14.736 | −0.3859 | −2.1142 | |
| 75 | 6.454 | 13.952 | −0.2913 | −2.3814 | |
| 90 | 4.447 | 15.086 | 0.1112 | −2.5844 | |
| 105 | 6.18 | 13.62 | −0.2751 | −2.1678 | |
| 120 | 7.748 | 15.544 | −0.359 | −2.712 | |
| 135 | 9.009 | 10.482 | −0.6697 | −1.4586 | |
| 150 | 9.454 | 15.032 | −0.5928 | −2.4184 | |
| 165 | 10.49 | 12.58 | −0.823 | −1.746 | |
| 180 | 8.705 | 12.55 | −0.4852 | −1.6456 | |
| 195 | 8.905 | 14.79 | −0.5113 | −2.3994 | |
| 210 | 9.395 | 11.33 | −0.7162 | −1.5076 | |
| 225 | 8.614 | 9.932 | −0.6189 | −1.1822 | |
| 240 | 7.112 | 10.756 | −0.4301 | −1.6358 | |
| 255 | 5.94 | 11.88 | −0.2837 | −1.8705 | |
| 270 | 4.659 | 12.042 | −0.0052 | −1.7540 | |
| 285 | 6.779 | 6.502 | −0.5106 | −0.5216 | |
| 300 | 7.978 | 10.324 | −0.5043 | −1.5754 | |
| 315 | 9.2 | 14.78 | −0.6081 | −2.2038 | |
| 330 | 8.792 | 13.676 | −0.5216 | −2.1808 | |
| 345 | 9.491 | 12.583 | −0.6661 | −2.0618 |
| Orientation (°) | JRC’(L) |
|---|---|
| 0 | |
| 15 | |
| 30 | |
| 45 | |
| 60 | |
| 75 | |
| 90 | |
| 105 | |
| 120 | |
| 135 | |
| 150 | |
| 165 | |
| 180 | |
| 195 | |
| 210 | |
| 225 | |
| 240 | |
| 255 | |
| 270 | |
| 285 | |
| 300 | |
| 315 | |
| 330 | |
| 345 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, J.; Chen, J.; Yong, R.; Du, S. Expression and Analysis of Joint Roughness Coefficient Using Neutrosophic Number Functions. Information 2017, 8, 69. https://doi.org/10.3390/info8020069
Ye J, Chen J, Yong R, Du S. Expression and Analysis of Joint Roughness Coefficient Using Neutrosophic Number Functions. Information. 2017; 8(2):69. https://doi.org/10.3390/info8020069
Chicago/Turabian StyleYe, Jun, Jiqian Chen, Rui Yong, and Shigui Du. 2017. "Expression and Analysis of Joint Roughness Coefficient Using Neutrosophic Number Functions" Information 8, no. 2: 69. https://doi.org/10.3390/info8020069
APA StyleYe, J., Chen, J., Yong, R., & Du, S. (2017). Expression and Analysis of Joint Roughness Coefficient Using Neutrosophic Number Functions. Information, 8(2), 69. https://doi.org/10.3390/info8020069





