Computer-Generated Abstract Paintings Oriented by the Color Composition of Images
Abstract
:1. Introduction
2. Related Works
3. Our Work
4. Creating Abstract Paintings Using Algorithms
| Algorithm 1 Creating Abstract Paintings method |
| Input: Original color images (I) Output: Abstract paintings Step 1: Segmenting the Colors of Original Pictures Step 2: The Statistics of Color Ratio Information Step 3: Drawing Abstract Paintings |
4.1. Selecting the Original Images and Segmenting the Colors
| Algorithm 2 Segmentation Method |
| Input: Image information () and the number of color clusters k Output: Label Step 1: Convert into a three-channel column vector V, where and Step 2: Use the k-means-based method for segmenting V and obtain the class center C Step 3: For each data point in the dataset V, i.e, , calculate its category by Equation (4) Step 4: For each class, recalculate the class centroid by Equation (5) Step 5: Repeat Step 3 to Step 4 until convergence |
- The image information is contained in a matrix , and we convert I into a three-channel column vector V. When clustering data sets, each element of the vector consists of three color elements in the Lab space, i.e., a three-dimensional column vector,where .
- We determine the number of color clusters k, i.e., the number of color classes (in this paper, ).
- We use the K-means method and initially select k pieces of from dataset V as the starting cluster centers. The basic idea of K-means is that the mutual distances between the initial cluster centers should be as large as possible [32]:
- (a)
- We randomly select a point from dataset V as the center .
- (b)
- For each point i in dataset V, we calculate the distance between it and the nearest cluster center (pre-selected),and then obtain the summation of , i.e.,
- (c)
- Then, we take a random value between 0 and to calculate the next ’center’ using a weighting factor. This algorithm is implemented as follows: take random values Random and random . If , then the point becomes the next “center“; otherwise, select again.
- (d)
- Then, we repeat steps (b) and (c) until k cluster centers are selected, which ensures that the point (at a farther distance) can be selected as the cluster center.
- For each data point i in dataset V, we calculate its category, which belongs towhere , . represents point i and the nearest center within the k clusters, and the value of is between 1 and k.
- For each class, we recalculate the class centroid,where , i.e., the number of elements in the data set.
- Repeat steps 4 to 5 until convergence. We define the distortion function to ensure convergence as follows:
4.2. The Statistics of Color Ratio Information
4.3. Drawing Abstract Paintings
- Initialize ; there is a value visit equal to 0, and the dimension of visit is . indicates that the pixel has been visited. If , the pixel has not been visited. We re-count the number and size of separate patches in the original image and sort them in z and .
- Set a threshold p; and if , we record into the variable ; if , we record into the variable . Thus, we can filter out notably small patches. p is an integer value based on the effect of the generated abstract image; hence, different pictures can have different values.
- The largest color patch obtained using the K-means algorithm is set as the background color.
- The circles are drawn based on the size of the independent color patches and finally sorted in descending order. The radius of a circle is , and the center of a circle is :where is the width of the original picture, i.e., M; is the width of the original picture, N; and is a random number. Using a random number indicates that different abstract images can be generated based on the same original image. The fill color in the round circle is the color after clustering (except for the background color). Figure 5a is an abstract painting generated by our method.
4.4. Adding Visual Elements and Enriching Picture Composition
- Following Section 4.3, based on Figure 6b, we drew lines using the color information recorded by the object, whose lengths and positions were random. Then, a new image was generated, as shown in Figure 6c.
4.5. Experimental Data and Application
5. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Widewalls—Manfred Mohr. Available online: http://www.widewalls.ch/?se=Manfred+Mohr&t=0 (accessed on 13 June 2017).
- Widewalls—Ronald Davis. Available online: http://www.widewalls.ch/?se=Ronald+Davis%2C&t=0 (accessed on 13 June 2017).
- Fisher, Y.; McGuire, M.; Voss, R.F.; Barnsley, M.F.; Devaney, R.L.; Mandelbrot, B.B. The Science of Fractal Images; Springer: New York, NY, USA, 2012. [Google Scholar]
- Wolfram, S.; Gad-el Hak, M. A New Kind of Science; Wolfram Media: Champaign, IL, USA, 2003. [Google Scholar]
- Mandelbrot, B.B.; Pignoni, R. The Fractal Geometry of Nature; W. H. Freeman and Company: New York, NY, USA, 1983. [Google Scholar]
- Barnsley, M.F. Fractals Everywhere; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Taylor, R.P.; Micolich, A.P.; Jonas, D. Fractal analysis of Pollock’s drip paintings. Nature 1999, 399, 422. [Google Scholar] [CrossRef]
- Taylor, R.P.; Micolich, A.P.; Jonas, D. The Construction of Jackson Pollock’s Fractal Drip Paintings. Leonardo 2006, 35, 203–207. [Google Scholar] [CrossRef]
- Laposky, B.F. Oscillons: Electronic abstractions. Leonardo 1969, 2, 345–354. [Google Scholar] [CrossRef]
- Molnar, V. Toward aesthetic guidelines for paintings with the aid of a computer. Leonardo 1975, 8, 185–189. [Google Scholar] [CrossRef]
- Dietrich, F. Visual intelligence: The first decade of computer art (1965–1975). Leonardo 1986, 19, 159–169. [Google Scholar] [CrossRef]
- Deep Dream Web interface. Available online: http://psychic-vr-lab.com/deepdream/ (accessed on 5 December 2017).
- Gatys, L.A.; Ecker, A.S.; Bethge, M. A neural algorithm of artistic style. arXiv, 2015; arXiv:1508.06576. [Google Scholar]
- Franke, H.W. Computers and visual art. Leonardo 1971, 4, 331–338. [Google Scholar] [CrossRef]
- Judelman, G. Aesthetics and inspiration for visualization design: Bridging the gap between art and science. In Proceedings of the Eighth International Conference on Information Visualisation, London, UK, 16–16 July 2004; pp. 245–250. [Google Scholar]
- Marcos, A.F. Digital art: When artistic and cultural muse merges with computer technology. IEEE Comput. Graph. Appl. 2007, 27, 98–103. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Mekler, G.; Martínez, R.A.; del Río, M.B.; Mansilla, R.; Miramontes, P.; Cocho, G. Universality of rank-ordering distributions in the arts and sciences. PLoS ONE 2009, 4, e4791. [Google Scholar] [CrossRef] [PubMed]
- Aragón, J.L.; Naumis, G.G.; Bai, M.; Torres, M.; Maini, P.K. Turbulent luminance in impassioned van Gogh paintings. J. Math. Imaging Vis. 2008, 30, 275–283. [Google Scholar] [CrossRef]
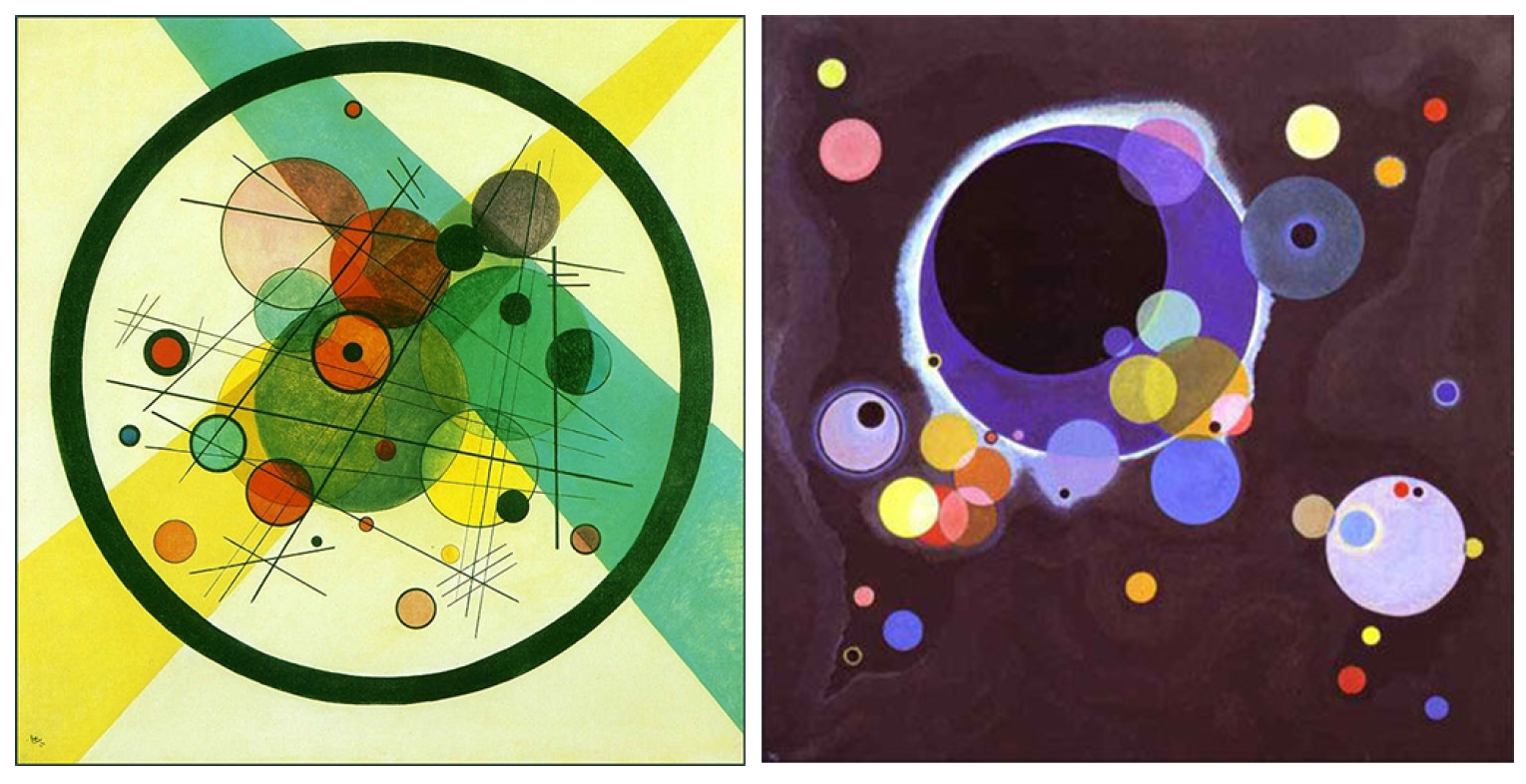
- Kandinsky, W.; Rebay, H. Point and Line to Plane; Courier Corporation: North Chelmsford, MA, USA, 1947. [Google Scholar]
- Nickas, B. Painting Abstraction: New Elements in Abstract Painting; Phaidon Press: London, UK, 2009. [Google Scholar]
- Quan, L. Abstract painting ancestor Kandinsky. Art Panorama 2011, 1, 103. [Google Scholar]
- Tao, W.; Liu, Y.; Zhang, K. Automatically generating abstract paintings in Malevich Style. In Proceedings of the 2014 IEEE/ACIS 13th International Conference on Computer and Information Science (ICIS), Taiyuan, China, 4–6 June 2014; pp. 201–205. [Google Scholar]
- Xiong, L.; Zhang, K. Generation of Miro’s surrealism. In Proceedings of the 9th International Symposium on Visual Information Communication and Interaction, Dallas, TX, USA, 24–26 September 2016; pp. 130–137. [Google Scholar]
- Zhang, K.; Yu, J. Generation of Kandinsky art. Leonardo 2016, 49, 48–54. [Google Scholar] [CrossRef]
- Edward, B. Thinking Like Artists; Northern Literature and Art Publishing House: Harbin, China, 2006. [Google Scholar]
- Holtzschue, L. Understanding Color: An Introduction for Designers; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Ilam, K. Design Geometry-Research on the Proportion and Composition; Intellectual Press: Beijing, China, 2003; p. 104. [Google Scholar]
- Tokumaru, M.; Muranaka, N.; Imanishi, S. Color design support system considering color harmony. In Proceedings of the 2002 IEEE International Conference on Fuzzy Systems, Honolulu, HI, USA, 12–17 May 2002; pp. 378–383. [Google Scholar]
- Cohen-Or, D.; Sorkine, O.; Gal, R.; Leyvand, T.; Xu, Y.Q. Color harmonization. ACM Trans. Graph. 2006, 25, 624–630. [Google Scholar] [CrossRef]
- Kojima, R. Ryohei Kojima’s Design World; Guangxi Fine Arts Publishing House: Nanning, China, 2000; p. 188. [Google Scholar]
- Hammond, D.L. Validation of LAB color mode as a nondestructive method to differentiate black ballpoint pen inks. J. Forensic Sci. 2007, 52, 967–973. [Google Scholar] [CrossRef] [PubMed]
- Arthur, D.; Vassilvitskii, S. K-Means++: The Advantages of Careful Seeding. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–9 January 2007; pp. 1027–1035. [Google Scholar]









© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Lv, J.; Li, X.; Yin, J. Computer-Generated Abstract Paintings Oriented by the Color Composition of Images. Information 2017, 8, 68. https://doi.org/10.3390/info8020068
Li M, Lv J, Li X, Yin J. Computer-Generated Abstract Paintings Oriented by the Color Composition of Images. Information. 2017; 8(2):68. https://doi.org/10.3390/info8020068
Chicago/Turabian StyleLi, Mao, Jiancheng Lv, Xiaojie Li, and Jing Yin. 2017. "Computer-Generated Abstract Paintings Oriented by the Color Composition of Images" Information 8, no. 2: 68. https://doi.org/10.3390/info8020068
APA StyleLi, M., Lv, J., Li, X., & Yin, J. (2017). Computer-Generated Abstract Paintings Oriented by the Color Composition of Images. Information, 8(2), 68. https://doi.org/10.3390/info8020068




