Waves as the Symmetry Principle Underlying Cosmic, Cell, and Human Languages

Abstract

In 1997, the author concluded that living cells use a molecular language (cellese) that is isomorphic with the human language (humanese) based on his finding that the former shared 10 out of the 13 design features of the latter. In 2012, the author postulated that cellese and humanese derived from a third language called the cosmic language (or cosmese) and that what was common among these three kinds of languages was waves—i.e., sound waves for humanese, concentration waves for cellese, and quantum waves for cosmese. These waves were suggested to be the symmetry principle underlying cosmese, cellese, and humanese. We can recognize at least five varieties of waves—(i) electromagnetic; (ii) mechanical; (iii) chemical concentration; (iv) gravitational; and (v) probability waves, the last being non-material, in contrast to the first four, which are all material. The study of waves is called “cymatics” and the invention of CymaScope by J. S. Reid of the United Kingdom in 2002 is expected to accelerate the study of waves in general. CymaScope has been used to visualize not only human sounds (i.e., humanese) but also sounds made by individual cells (cellese) in conjunction with Atomic Force Microscopy (AFM) (unpublished observations of J. Gimzewski of UCLA and J. Reid). It can be predicted that the gravitational waves recently detected by the Interferometer Gravitational-Wave Observatory (LIGO) will be visualized with CymaScope one day, thereby transforming gravitational waves into CymaGlyphs. Since cellese in part depends on RNA concentration waves (or RNA glyphs) and humanese includes hieroglyphs that were decoded by Champollion in 1822, it seems reasonable to use cymaglyphs, RNA glyphs, and hieroglyphs as symbols of cosmese, cellese, and humanese, respectively, all based on the principle of waves as the medium of communication.

1. Introduction

In recent publications [1,2,3], I presented evidence that the wave-particle duality discovered in physics in the early decades of the 20th century may apply not only to quantum physics but also to physicochemical processes in the universe at all scales (see Section 3). In other words, the wave-particle duality that Einstein described as follows may not be confined to physics but apply to situations more generally [4]:

“It seems as though we must use sometimes the one theory and sometimes the other, while at times we may use either. We are faced with a new kind of difficulty. We have two contradictory pictures of reality; separately neither of them fully explains the phenomena of light, but together they do”.

It is well known that the formulation of the concept of complementarity by Niels Bohr was largely motivated by the wave-particle duality [5]. Bohr subsequently suggested that the complementarity concept applied to many phenomena beyond quantum physics is based on the close relation between the complementarity and the Yin–Yang dualism of the Daoist philosophy. However, there was no concrete evidence for this conjecture. Indirect support for the universality of the wave-particle duality was obtained in 2008–2015 as a result of the discovery that the PDE (Planckian Distribution Equation), derived from the Planckian radiation equation (PRE) discovered in 1900, fitted many long-tailed histograms generated in various fields including atomic physics, protein folding, single-molecule enzyme catalysis, RNA metabolism in yeast and human cells, T-cell receptor diversity, fMRI (functional magnetic resonance imaging), decision-making in humans, glottometrics, econometrics, and the Big Bang cosmology [1,2,6] (see Figure 1). The heightened interest in wave phenomena among scientists and the general public in recent years seems to be largely due to the invention of CymaScope by J. S. Reid in 2002 and its commercial availability [7] (see Figure 6 in Section 8). The purpose of this article is to review the evidence for the universality of the wave-particle duality, both mathematical and empirical, and discuss the possible role of what N. Herbert [8] refers to as a wave language in understanding the isomorphism between cell and human languages proposed in [9].

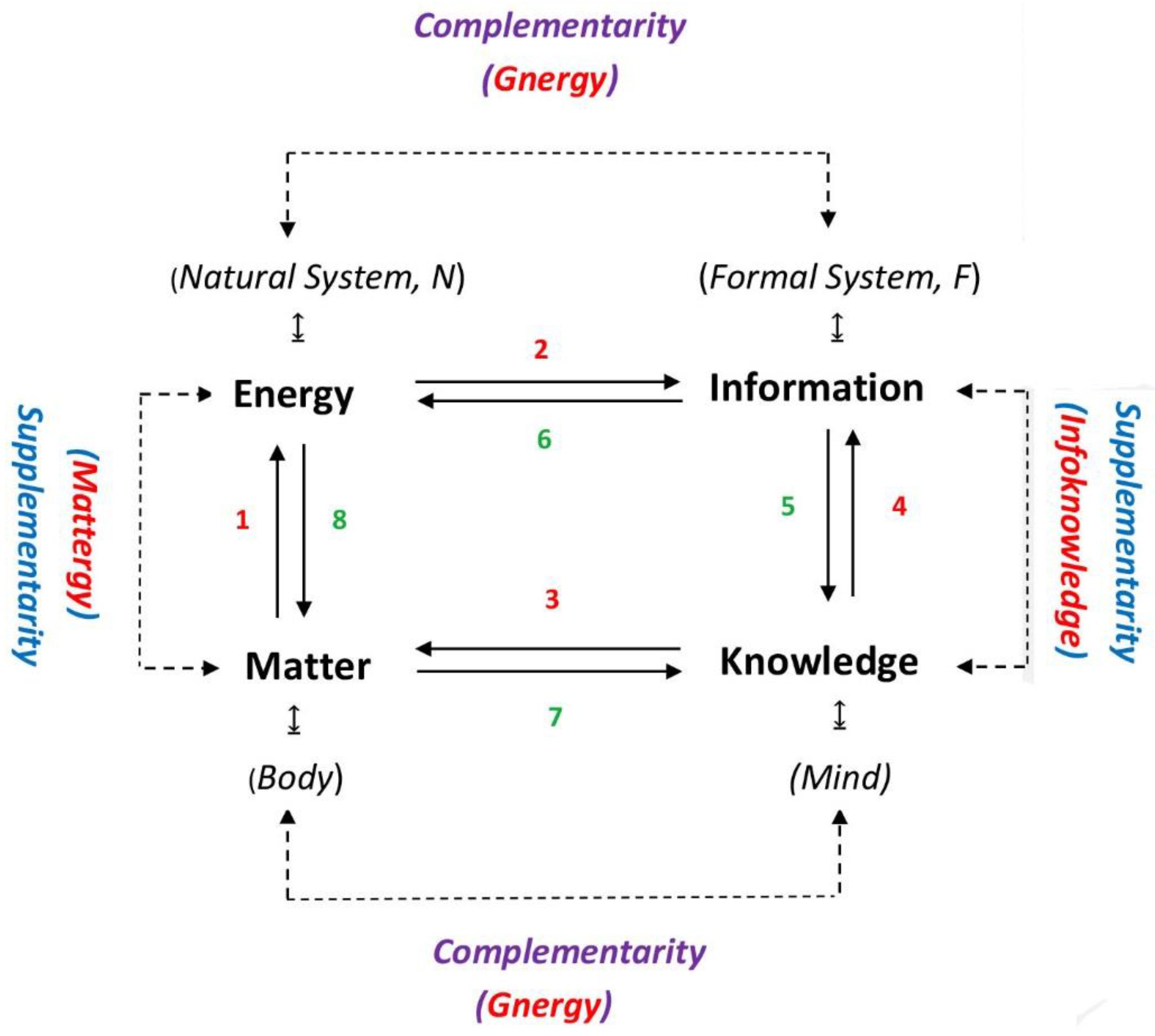
2. Complementarity vs. Supplementarity

The term “complementarity” first appears in William James’s book Principles of Psychology [10], in the context of the idea that human consciousness consists of two parts:

“...in certain persons, at least, the total possible consciousness may be split into parts which coexist but mutually ignore each other, and share the objects of knowledge between them. More remarkable still, they are complementary...”

There is a great similarity between the concept of complementarity that James introduced into psychology in 1890 and that Bohr introduced into physics about four decades later. Whether Bohr’s complementarity was influenced directly or indirectly by James’s notion of complementarity is a challenging question for future philosophers of science to answer.

The concept of complementarity emerged in 1926–1927 from intense discussions that transpired between Bohr and his then-assistant Heisenberg in the wake of the latter’s discovery of the matrix mechanics and uncertainty relations [11]. Bohr discussed his philosophy of complementarity in public for the first time at a meeting held in Como, Italy, in 1927 and published the first paper on complementarity in 1928 [12,13]. In 1958, Bohr summarized the concepts of supplementarity and complementarity as follows:

“...Within the scope of classical physics, all characteristic properties of a given object can in principle be ascertained by a single experimental arrangement, although in practice various arrangements are often convenient for the study of different aspects of the phenomenon. In fact, data obtained in such a way simply supplement each other and can be combined into a consistent picture of the behavior of the object under investigation. In quantum mechanics, however, evidence about atomic objects obtained by different experimental arrangements exhibits a novel kind of complementary relationship. Indeed, it must be recognized that such evidence which appears contradictory when combination into a single picture is attempted, exhausts all conceivable knowledge about the object. Far from restricting our efforts to put questions to nature in the form of experiments, the notion of complementarity simply characterizes the answers we can receive by such inquiry, whenever the interaction between the measuring instruments and the objects forms an integral part of the phenomenon...” (emphasis added)

The supplementary and complementary relations defined above can be conveniently represented as triadic relations among three entities labeled A, B, and C. Supplementarity refers to the relation in which the sum of a pair equals the third:

Supplementarity: C = A + B.

(1)

As an example of supplementarity, Einstein’s equation in special relativity, E = mc², may be cited. Energy (A) and matter (B) may be viewed as extreme manifestations of their source (C), which can be quantitatively combined or added to completely characterize C. As already indicated, there is no common word to represent the C term corresponding to the combination of matter and energy. Therefore, we will adopt in this article the often-used term “mattergy” (meaning matter and energy) to represent C. Through Einstein’s equation, matter and energy can be interconverted quantitatively. The enormity of the numerical value of c², namely, 10²¹, justifies the statement that

“Matter is a highly condensed form of energy.”

(2)

In contrast to supplementarity, complementarity is non-additive: i.e., A and B cannot be combined to obtain C. Rather, C can be said to become A or B depending on measuring instruments employed: i.e., C = A or C = B, depending on measurement. We can represent this complementary relation symbolically as shown in Equation (3):

Complementarity: C = A^B

(3)

where the symbol ^ is introduced here to denote a “complementary relation”. Equation (5) can be read in two equivalent ways:

“A and B are complementary aspects of C.”

(4)

“C is the complementary union of A and B.”

(5)

Statements (4) and (5) should be viewed as short-hand notations of the deep philosophical arguments underlying complementarity, as, for example, discussed recently by Plotnitsky [5] and Camillieri [13]. The principles of complementarity and supplementarity defined above may operate not only in physics but also in biology, as first suggested by Bohr [14,15]. In other words, it may be said that

“Physics and biology are symmetric with respect to the operation of supplementarity and complementarity principles.”

(6)

Statement (6) has been referred to as the Symmetry Principle of Biology and Physics (SPBP) [1]. SPBP appears to be supported by the symmetry evident in

Table 1. The Symmetry Principle of Biology and Physics (SPBP): the principles of supplementarity and complementarity in action in physics and biology. “Wavecles” are complementary unions of waves and particles, and “quons” are quantum mechanical objects exhibiting wave or particle properties depending on the measuring apparatus employed [8]. “Gnergy” is defined as a complementary union of information (gn-) and energy (-ergy) [17]. In other words, energy and information (or more accurately mattergy and liformation) are the complementary aspects of gnergy.

	Physics	Biology
Supplementarity (from Special Relativity Theory)	1. Matter-Energy Equivalence E = mc2	6. Life-Information Equivalence a
	2. Matter-Energy or “Mattergy” b	7. Life-Information or “Liformation” c
	3. “Matter is a highly condensed form of energy.”	8. “Life is a highly condensed form of information.”
Complementarity (from Quantum Mechanics)	4. Wave-Particle d Complementarity; Kinematics-Dynamics Complementarity e	9. “Liformation–Mattergy” Complementarity
	5. “Wavicles” or “Quons” f	10. “Gnergons” g

^a Just as the matter–energy equivalence was unthinkable before Einstein’s special relativity theory published in 1905, so it is postulated here that the life–information equivalence was unthinkable prior to the emergence of molecular theories of life that began with Watson and Crick’s discovery of the DNA double helix in 1953. ^b The term often used to denote the equivalence between (or supplementary union of) matter and energy as indicated by E = mc². ^c A new term coined here to represent the postulated supplementary relation (or the equivalence or continuity) between life and information, in analogy to mattergy, embodying the supplementary relation between matter and energy. ^d The Airy pattern (see Figure 4.2 in [8]) may be interpreted as evidence for a simultaneous measurement of both waves and particles of light, and if such an interpretation proves to be correct, it would deny the validity of the wave–particle complementarity and support the notion of the wave–particle supplementarity. ^e The kinematics–dynamics complementarity is a logically different kind of complementarity that was recognized by Bohr in addition to the wave–particle complementarity ([18] pp. 80–88). ^f Any material entities that exhibit both wave and particle properties, either simultaneously (as claimed by L. de Broglie [19] and D. Bohm [20]) or mutually exclusively (as claimed by Bohr [8]. ^g Gnergons are defined as discrete units of gnergy, the complementary union of information and energy [17]. Gnergy is a type and gnergons are its tokens.

.

In Table 1, two new terms appear, “mattergy” (see Item 2) and “liformation” (Item 7), whose meanings are explained in footnotes. One of the most significant conclusions resulting from Table 1 is the assertion that life and information are intimately related in biology, just as matter and energy are related in physics (see Items 1, 2, 6 and 7), leading to the coining of the new term “liformation” in analogy to “mattergy” (see Items 2 and 7). Another important insight afforded by the symmetry inherent in Table 1 is the “liformation–mattergy complementarity” (see Item 9), which may be related to the view recently expressed by Lloyd ([16] p. 38), if computation can be identified with liformation or information processing:

“...The computational universe is not an alternative to the physical universe. The universe that evolves by processing information and the universe that evolves by the laws of physics are one and the same. The two descriptions, computational and physical, are complementary ways of capturing the same phenomena.”

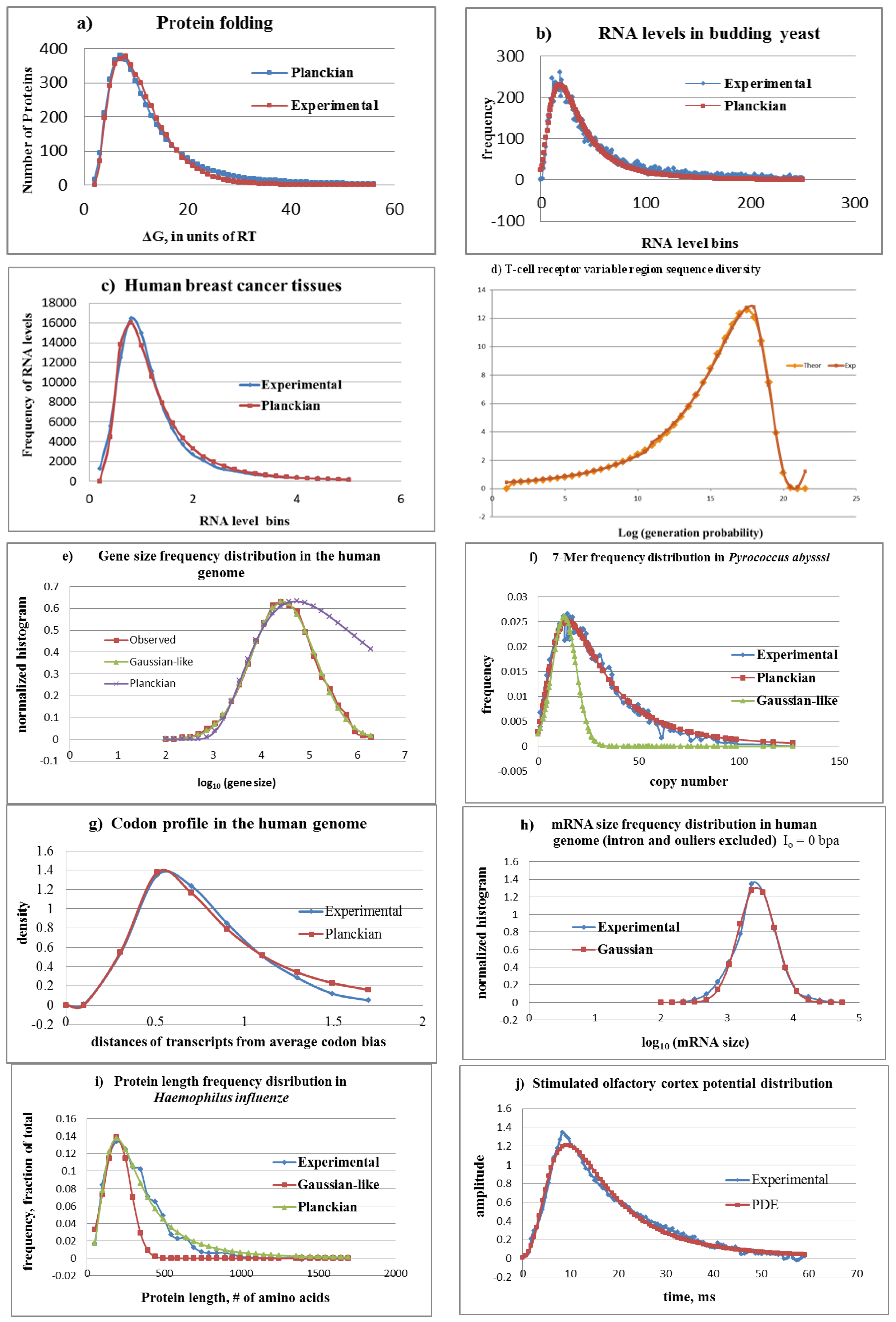
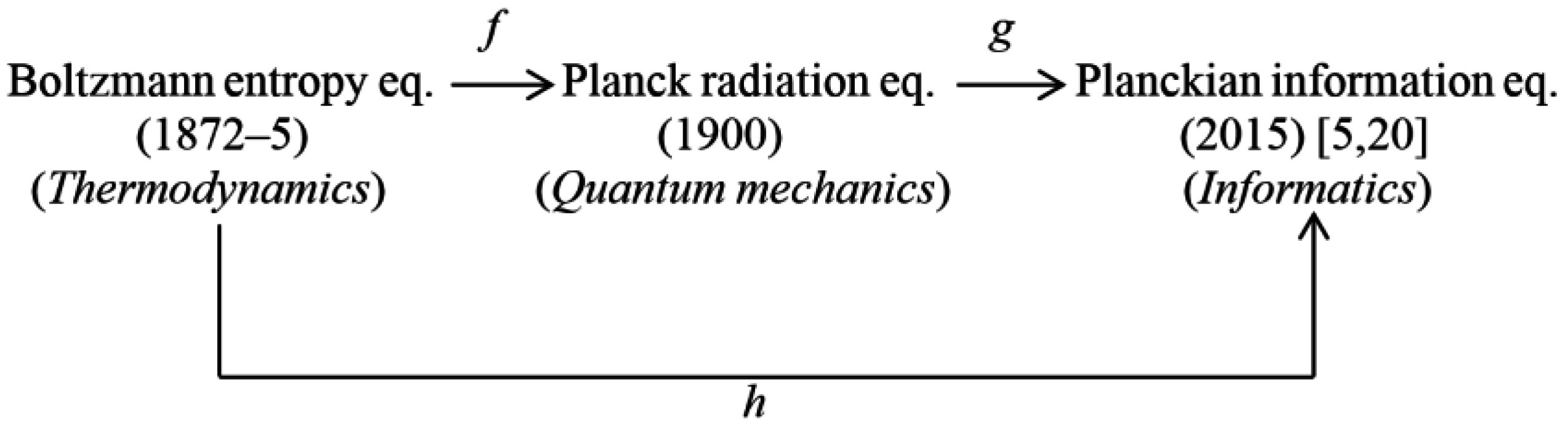
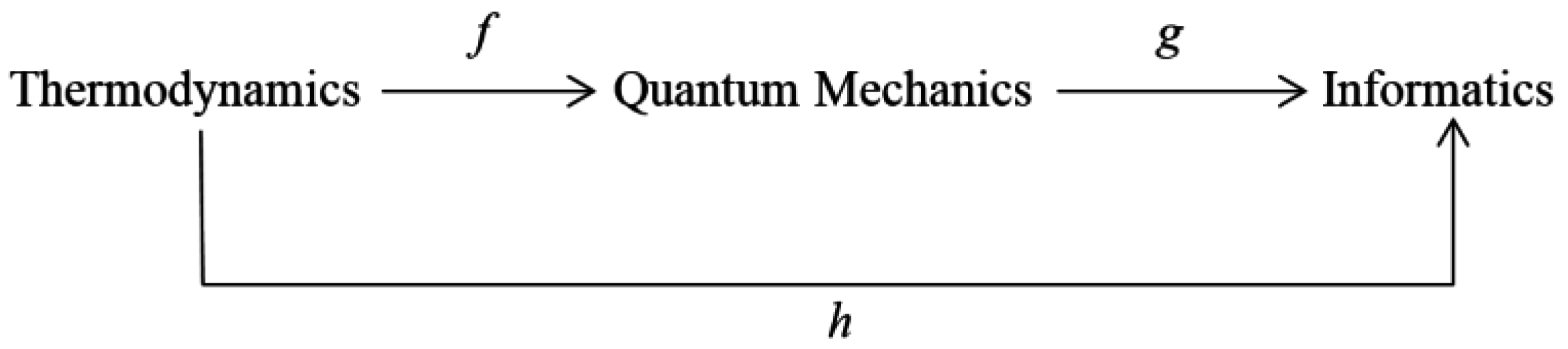
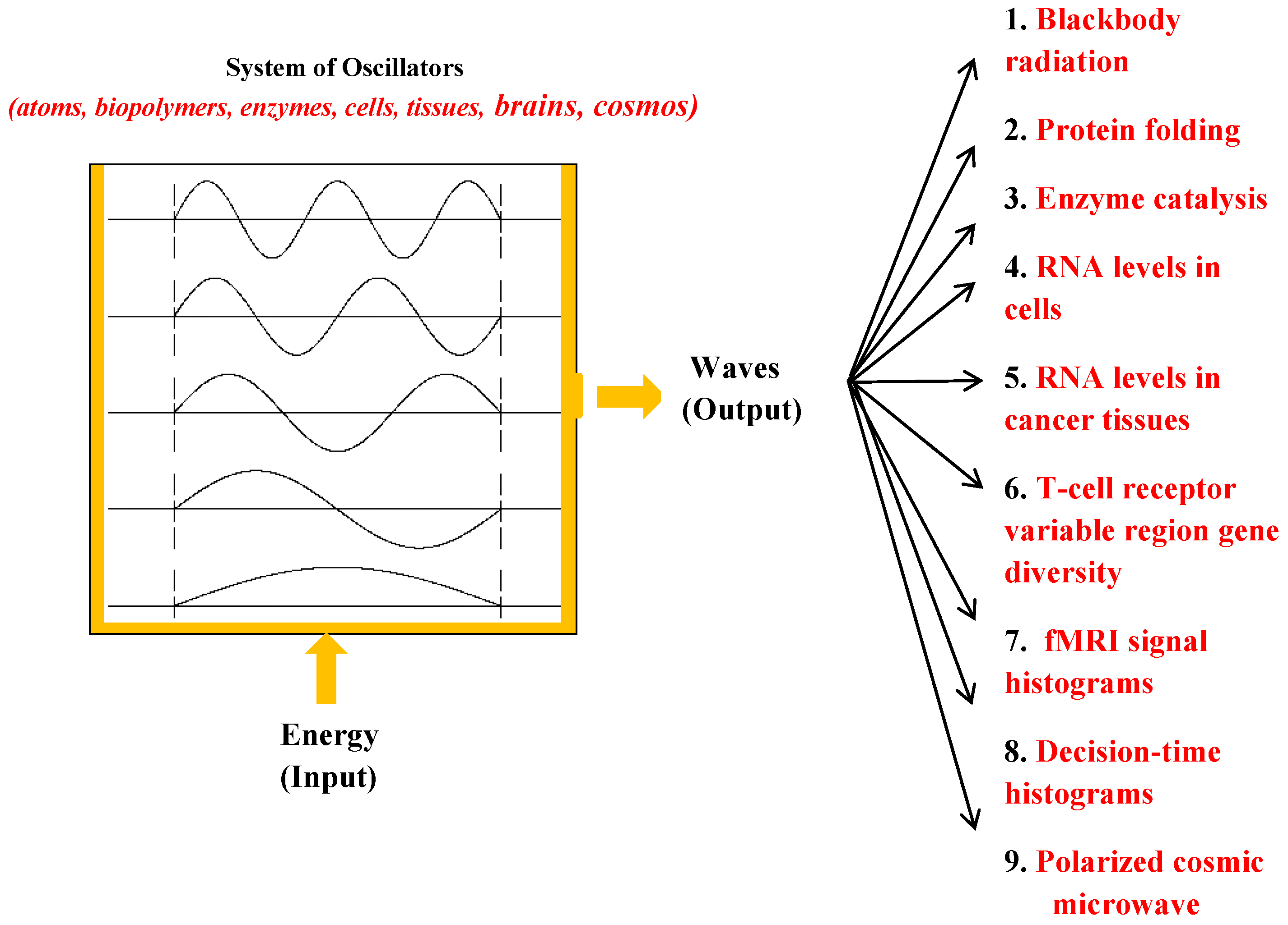
3. Blackbody Radiation and the Planckian Distribution Equation (PDE)

Blackbody radiation refers to the emission of photons by material objects that completely absorb photons impinging on them (hence appearing black). M. Planck (1858–1947) succeeded in deriving the mathematical equation given in Equation (7) that quantitatively accounted for the blackbody radiation spectra. The key to his successful derivation of the so-called Planck radiation equation was his assumption that light is emitted or absorbed by matter in discrete quantities called “quanta of action” which led to the birth of quantum mechanics revolutionizing physics in the early 20th century.

In 2008 ([1] Chapter 11), I noticed that the single-molecule enzyme–turnover–time histogram published by Lu et al. [21] resembled the blackbody radiation spectrum at 4000 °K. This observation led me to generalize the Planck radiation equation, Equation (7), by replacing its universal constants and temperature by free parameters as shown in Equations (8) and (9), the former having four parameters, a, b, A, and B, and the latter three parameters, A, B, and C. Depending on the dataset to be analyzed, either the four- or three-parameter equation is found convenient. The “generalized equation” was originally referred to as the “blackbody radiation-like equation” (BRE), but as the equation was found to apply to more and more datasets, it was thought appropriate to refer to it as either the “generalized Planck equation” (GPE) or, more simply, the “Planckian distribution equation” (PDE), in analogy to the Gaussian distribution equation (GDE). The four-parameter equation can be transformed into a three-parameter equation by utilizing the transforming relations, (10)–(13).

As already alluded to above, PDE has been found to fit long-tailed histograms reported in many fields, ranging from atomic physics to econophysics (see Figure 1a through Figure 1r). These findings may indicate that, underlying all the varied phenomena obeying the Planckian distribution equation, there exist common mechanisms (just as all the phenomena obeying the Gaussian distribution law implicate common mechanisms, namely, random processes). One possible common mechanism underlying the Planckian distribution may be sought in the postulated universality of the wave–particle duality in all organized material systems, from atoms to the universe itself [1,22], and this possibility is in part supported by the fact that the first term of the Planck radiation equation, Equation (7), and hence the Planckian distribution equation, (8) and (9), is related to the number of standing waves in a physical system and the second term to the average energy per mode of the standing waves [23].

$$\mathrm{E}(\lambda ,\mathrm{T})=\frac{2\pi h{c}^2}{{\lambda }^5(e^{\frac{hc}{\lambda k\mathrm{T}}}-1)},$$

(7)

where

• E = Energy
• λ = Wavelength
• c = Speed of light
• k = Boltzmann constant
• h = Planck’s constant
• e = 2.71828182
• [T] = Kelvin (temperature)
• [λ] = Meters
• h = 6.626 × 10³⁴ J·s
• c = 2.998 × 10⁸ m/s
• k = 1.381 × 10⁻²³ J/K.

$$\mathrm{y}=\frac{\mathrm{a}}{{(\mathrm{A}\mathrm{x}+\mathrm{B})}^5}·\frac{1}{e^{\mathrm{b}/(\mathrm{A}\mathrm{x}+\mathrm{B})}-1}$$

(8)

$$\mathrm{y}=\frac{\mathrm{A}}{{(\mathrm{x}+\mathrm{B})}^5}·\frac{1}{e^{\mathrm{C}/(\mathrm{x}+\mathrm{B})}-1}$$

(9)

$$\mathrm{A}=\mathrm{a}/{\mathrm{A}}^5$$

(10)

$$\mathrm{B}=\mathrm{B}/\mathrm{A}$$

(11)

$$\mathrm{C}=\mathrm{b}/\mathrm{A}$$

(12)

3.1. Gibbs Free Energy of Protein Folding

Under normal biological conditions of constant temperature (T) and pressure (P), all spontaneous changes, including protein folding from unfolded to folded states, are driven by a decrease in Gibbs free energy, i.e., by a negative Gibbs free energy change, ΔG < 0. Conversely, when a protein unfolds, the accompanying free energy change is positive, i.e., ΔG = G_unfolded − G_folded > 0, which is referred to as the free energy of protein folding or protein stability [24]. Gibbs free energy G is defined as G = H + PV − TS, where H is enthalpy or heat content, V is the volume, P is the pressure, and S is the entropy of the thermodynamic system under consideration. Under the conditions of constant T and P, this equation leads to ΔG = ΔH + PΔV − TΔS, where ∆ indicates the change calculated by subtracting the initial from the final values. Based on experimentally determined enthalpy, entropy, heat capacity, and the length distributions of 43,000 proteins from E. coli, Dill and co-workers [24] derived a theoretical equation for predicting the protein stability which generated the experimental curve labeled Experimental in Figure 1a. As shown, this theoretical curve is almost perfectly simulated by the Planckian distribution equation.

3.2. RNA Levels in Budding Yeast

When glucose is switched to galactose within a few minutes, budding yeast cells undergo massive changes in the copy numbers (from 0 to several hundred) of its mRNA molecules encoded by 6300 genes over the observational period of hours [25,26]. Garcia-Martinez et al. measured the levels of over 5000 mRNA molecules at six time points (0, 5, 120, 360, 450, and 85 min) after a glucose–galactose shift, using microarrays, generating over 30,000 mRNA level data points. Of these data, 2159 mRNA levels were chosen arbitrarily and grouped into 250 bins to generate a histogram shown in Figure 1b (see Experimental). As can be seen in this figure, the histogram fits the Planckian distribution almost exactly.

3.3. RNA Levels in Human Breast Tissue

Perou et al. [27] measured, using microarrays, the mRNA levels of 8102 genes in normal breast cells and breast cancer tissue before and after treatment with the anticancer drug doxorubicin in 20 breast cancer patients. Of the 8102 genes, we analyzed 4740 genes and their transcripts from 20 patients. A total of 4740 × 20 = 94,800 mRNA levels were divided into 60 bins to generate a histogram, as shown in Figure 1c (see Experimental). Again the experimental curve fitted the Planckian distribution equation with great fidelity. It is significant that PDE fits the mRNA data measured from unicellular (yeast) and multicellular systems (human breast tissues), indicating that PDE captures the basic molecular (e.g., enzyme catalysis) common to both systems.

3.4. Human T-Cell Receptor Gene Sequence Diversity

The T-cell receptor consists of two chains, α and β, and each chain in turn consists of transmembrane, constant, and variable regions. The variable regions of T-cell receptors, called CDR3 (Complement Determining Region 3), recognize pathogens and initiate an immune response. The CDR3 length between conserved residues ranges from 20 to 80 nucleotides. Murugan et al. [28] analyzed the nucleotide sequence data of T-cell beta chain CDR3 regions obtained from nine human subjects, each subject generating on average 232,000 unique CDR3 sequences. The germline DNA encoding the beta chain of human T-cell receptors has 48 V-genes, 2 D-genes, and 13 J-genes. These gene segments are recombined via a series of stochastic recombination mechanisms catalyzed by appropriate enzymes to generate a large repertoire of CDR3 sequences. Each CDR3 sequence can be viewed as the result of a generative event describable by several random variables, including V-, D-, and J-gene choices.

From the set of observed CDR3 sequences, Murugan et al. [28] were able to formulate a mathematical equation called the generative probability function that predicts the probability of generating CDR3 sequence σ, P_gen(σ). P_gen(σ) is the sum of the probabilities of all recombination events involved in producing CDR3 sequence σ. A typical example of the CDR3 sequence histogram predicted by P_gen(σ) for one subject is given in Figure 1d, which fits the Planckian distribution equation excellently (I am grateful to Mr. Vinay Vadali for this fitting).

3.5. Gene Size Frequency Distribution in the Human Genome

Figure 1e shows that the distribution of the gene size in the human genome does not fit PDE but the Gaussian-like equation (GLE), Equation (16), is symmetric, suggesting that the gene size distribution in the human genome is random rather than ordered or organized.

3.6. 7-Mer Frequency Distribution in Pyrococcus Abyssi

In contrast to the gene size distribution in the human genome discussed in Figure 1e, the 7-mer (i.e., DNA words consisting of seven nucleotides [29] frequency distribution in Pyrococcus abyssi fits PDE (Figure 1f), indicating that the nucleotide sequences of the 7-mers are non-random and hence are the results of some selection processes.

3.7. Codon Profile in the Human Genome

There are 64 codons in all organisms, of which 61 code for 20 amino acids. Hence, on average, about three codons encode each amino acid, although the actual numbers vary from one to six in the human genome. In addition, not all the codons encoding an amino acid are utilized with an equal probability—some are utilized more frequently than others, thus giving rise to the phenomenon of the “codon usage bias” (see the left-most two columns in

Table 2. The codon usage and codon profile for the amino acid arginine in the human genome. Adopted from ([30], p. II-23).

Synonymous Codon Usage		Codon Profile
CGT	8%	base	Position in the triplet
CGC	19%		1	2	3
CGA	11%	T	0	0	0.08
CGG	21%	C	0.59	0	0.19
AGA	21%	A	0.41	0	0.32
AGG	20%	G	0	1	0.41
sum	100%	sum	1	1	1

). A codon profile is a record of the preferred use of the four bases at the three positions inside the codon [30] (see the four columns on the right-hand side of Table 2).

As shown in Figure 1g, the codon profile distances of transcripts from average codon bias is distributed non-randomly [30] and fits PDE, indicating that the codon profile is determined by some as-yet-unidentified selection mechanisms in the living cell.

3.8. mRNA Size Frequency Distribution in the Human Genome

It is not surprising that the mRNA size frequency is distributed symmetrically (see Figure 1h), obeying the Gaussian-like equation, Equation (13), just as the gene size frequency is similarly distributed, since the size of mRNA is determined by that of corresponding genes.

3.9. Protein Length Distribution in Haemophilus Influenzae

Unlike the gene and mRNA size frequency distributions, the protein size (or length) frequency distribution is Planckian, as shown in Figure 1i. Similar differential characteristics were observed in word-length frequency distribution in a dictionary (not shown) and word-length frequency distribution in a speech (Figure 1m). These observations led me to the conclusion that glottometrics and genomics may be similar with respect to what Prigogine called “quilibrium structures” and “dissipative structures” ([1] pp. 69–78). In other words, word length and gene size may be viewed as equilibrium structures, while word-length frequency and protein-length frequency distributions may be considered as dissipative structures, since the latter, but not the former, will disappear if free energy dissipation is removed.

3.10. Olfactory Cortex EEG Distribution

Figure 1j shows that the EEG signals from stimulated olfactory cortex are distributed non-randomly, obeying PDE, indicating that these signals resulted from some selection processes imposed on a more or less randomly generated set of the EEG signals intrinsic to the olfactory cortex [31,32].

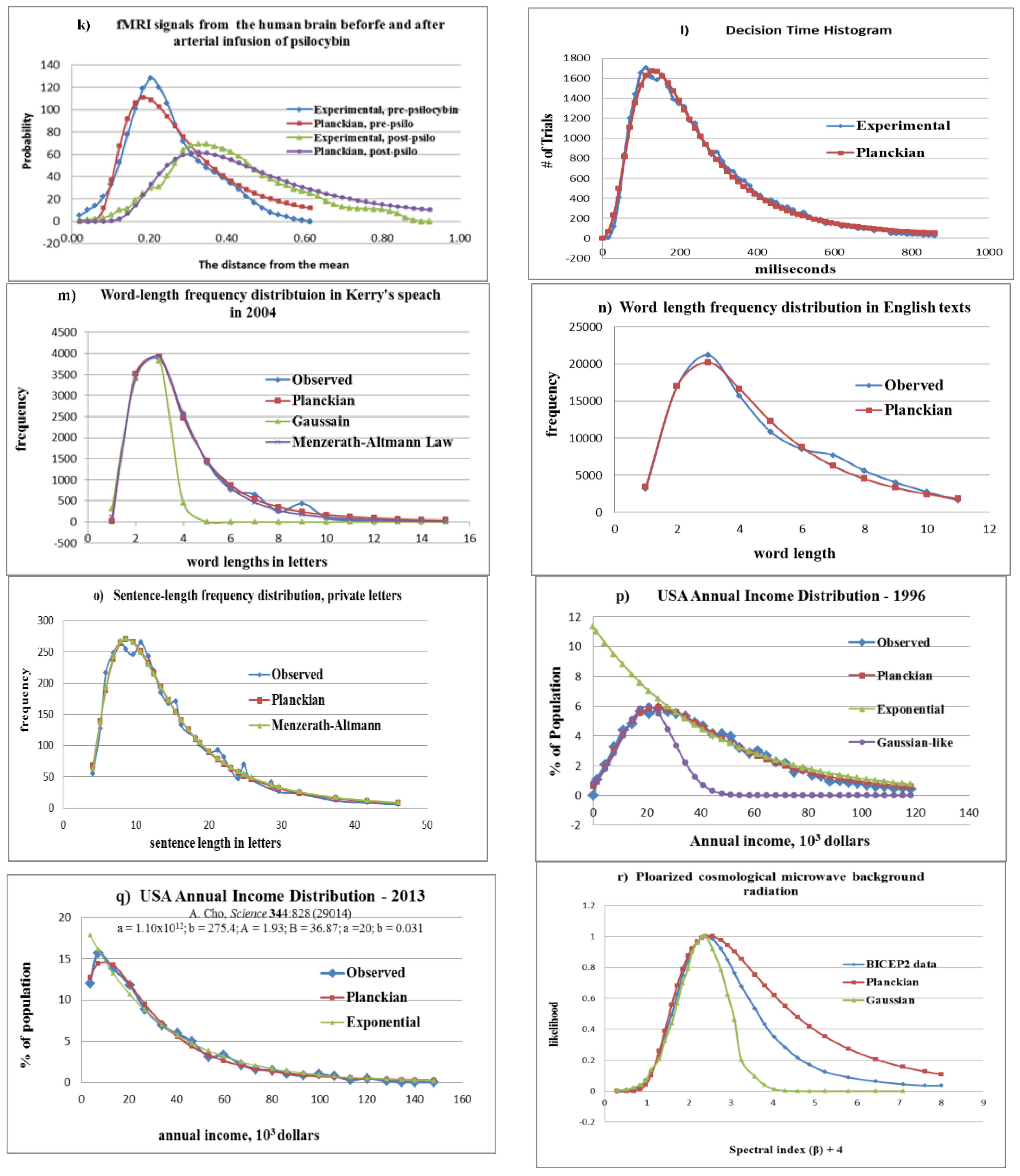
3.11. fMRI Signals from the Human Brain before and after Psilocybin

Carhart-Harris et al. [33] measured the fMRI (functional Magnetic Resonance Imaging) signals from the brains of 15 healthy volunteers before and after the 60-s intravenous infusion of psilocybin. The subject’s consciousness, cerebral blood flow (CBF), and fMRI signals all responded within seconds. Cerebral blood flow (CBF) values decreased in all regions of the brain and the subjects reported that their “thoughts wandered freely”. Out of the nine brain regions examined (2° visual, 1° visual, motor, DAN, auditory, DMN, R-FP, L-FP, salience), four regions exhibited significant changes in their fMRI signals, characterized by increases in the deviations of the local signals from their mean, i.e., an increase in variance. “Local” indicates brain tissue volume elements (voxels) measuring a few mm in linear dimensions. When the distances of the signals of individual voxels from the group-mean fMRI signal were calculated and grouped into bins and their frequencies were counted, the histograms shown in Figure 1k were obtained, which fitted PDE. The numerical values of the Planckian distribution equation fitting these two histograms differed, especially the b/A ratios and the Planckian information, I_p (defined in Section 5), which increased from 0.93 to 1.62 and 1.04 to 1.31, respectively, after the psilocybin infusion (see Row k in

Table 3. The numerical values of the parameters of the Planckian distribution, Equations (8) or (9), that fit the histograms shown in Figure 1 along with the Planckian information (I_P) values (defined in Section 5). The italicized red numbers in Row k are the parameter values measured post-psilocybin. The symbol, “-“ indicates “zero”, “none” or “not applicable”.

Histogram	a	b	A	B	C	b/A, IP (mb) *
(a) Protein folding	1.24 × 1014	368.3	9.45	6.82	-	38.97, 0.877
(b) RNA levels (yeast)	-	-	1.11 × 1012	13.962	159.30	-, 0.989
(c) RNA levels (breast tissue)	8 × 1010	40	8	1.7	-	5.00, 0.855
(d) T-Cell receptor	-	-	7.02 × 106	0.063	25.00	-, -
(f) 7-Mer frequency	-	-	5.05 × 107	12.123	123.78	-, 0.873
(i) Protein chain length	-	-	2.04 × 1013	5.655	1257.4	-, 0.846
	5.0 × 1011	601.7	0.478	30.29	-	1257.7, -
(l) Decision times	8.5 × 1011	101.49	0.1077	6.345	-	942.34, 3.57
(k) fMRI signals	7.6 × 1010 4.4 × 1010	107.67 43.17	115.9 26.7	0 0	- -	0.928, 1.04 1.617, 1.31
(m) Word length in speech	-	-	1.80 × 107	−0.001	12	-, 0.557
(o) Sentence length in letters	-	-	3.11 × 109	0.861	47.57	-, 0.664
(r) Cosmos	3.6 × 102	6.00	1.140	−0.14	-	4.65, -

* millibit, or 0.001 bit.

). This observation suggests to this author that PDE, Equation (9), and its three free parameters, A, B, and C, may be utilized to classify all fMRI signals measured from live individuals under normal and pathological conditions, thereby offering an opportunity for discovering drugs for treating many CNS diseases, including chronic depression and Alzheimer’s disease.

3.12. Decision-Time Histogram

The drift–diffusion model (DDM) of decision-making is a widely employed theoretical model in behavioral neurobiology ([34,35,36,37]. DDM accurately reproduces (i.e., simulates) the decision–time histograms (see Experimental in Figure 1l), which was in turn reproduced by PDE almost exactly. This indicates that PDE may be useful in studying the mechanisms of human decision-making in psychology just as various kinetic equations (including absolute reaction rate equations) are useful in studying the molecular mechanisms of chemical reactions.

3.13. Word-Length Frequency Distribution in Kerry’s Speech

The histogram of the word-length frequency distribution in a speech delivered by John Kerry fits PDE almost perfectly (see Figure 1m). What is most remarkable about Figure 1m is the fact that the histogram also fits the Menzerath–Altmann equation discovered by glottometricians [38,39] equally well. This may indicate that, in general, a given histogram can be fit into more than one mathematical equation, what I referred to as the “Unreasonable Arbitrariness of Mathematics” (UAM) [40], which may be contrasted with Wigner’s thesis that mathematics is unreasonably effective [41].

One possible explanation for the asymmetric distribution of the word-length frequency in Kerry’s speech is to assume (i) that a set of words from Kerry’s memory entered his consciousness more or less randomly; and (ii) that Kerry selected the right word from this set that happened to describe his thought at the moment, thus increasing the probability of rare words leading to a long-tailed histogram, as observed. If Kerry were unable to perform (ii), the word-length frequency distribution in his speech might have been random and hence symmetric, following a Gaussian-like function (Figure 1m).

3.14. Word-Length Frequency Distribution in English Letters

The word-length frequency distribution in private letters shown in Figure 1n can be almost exactly reproduced by PDE, indicating that the writers of the letters selected their words non-randomly, since random selection of words would have led to a Gaussian-like distribution.

3.15. Sentence-Length Frequency Distribution in Private Letters

The sentence-length frequency distribution in private letters also fits PDE, as shown in Figure 1o, indicating that the sentence lengths were selected by letter writers non-randomly.

3.16. Annual U.S. Income Distribution

Some physicists [42,43] have suggested that the distribution of income in a society can be modeled using the Boltzmann–Gibbs equation based on the analogy that money can be treated as energy. This statistical mechanical approach seems to work well for high income levels but fails badly at low income levels in the 1996 U.S. income distribution (see Figure 1p). However, PDE fits the high and low income levels in both the 1996 and 2013 U.S. annual income distributions (see Figure 1p,q). Thus PDE provides a better quantitative method for analyzing annual income distributions in human societies than the Boltzmann–Gibbs equation, which is based on an energy–money analogy, perhaps because PDE has both an energy-related term and a wave-related one (see Equation (8)).

This discrepancy between the Boltzmann–Gibbs and PDE approaches is reminiscent of the ultraviolet catastrophe that occurred in physics about a century ago.

The Rayleigh–Jeans law predicts that the power of radiation emitted by a heated body increases with the frequency raised to a fourth power. This exponential law works fine at long wavelengths but fails dramatically at short wavelengths, leading to the so-called “ultraviolet catastrophe”. If we assume that the exponential distribution shown in Figure 1p,q is analogous to the Rayleigh–Jeans law and the Planckian distributions to the Planck radiation law, Equation (7), we can arguably suggest that the deviation of the exponential distributions from the observed income distributions is analogous to the ‘ultraviolet catastrophe’ in physics.

The resolution of the ultraviolet catastrophe in physics in the early decades of the 20th century was achieved with the discovery of Planck’s radiation law, which introduced a new concept into physics, i.e., quantum of action, as the unit of organizing matter and energy in abiotic systems. Similarly, the resolution of the “econophysics” ultraviolet catastrophe with the Planckian distribution equation demonstrated in Figure 1p,q may introduce another novel concept into natural and human sciences—the quantization of organization in terms of what has been referred to as the Planckian information, I_P, defined in Equation (15) in Section 5.

3.17. Polarized Cosmological Microwave Background Radiation

Although PDE has been found to fit most fat-tailed histograms generated in various disciplines that we have examined so far (over 50, as of late 2015), the polarized CMB (Cosmic Microwave Background) data [44] shown in Figure 1r (see BICEP2 data) are an exception in the sense that they could not be fit into PDE using the Solver software in Excel.

In general, if PDE fits the rising phase of a long-tailed histogram, it also fits the falling phase of the histogram, but this is not the case with the polarized CMB data, as evident in Figure 1r. The areas under the curve (AUC) of the Gaussian-like distribution, CMB distribution, and PDE were found to be, respectively, 10.30, 13.97, and 16.98, indicating that the CMB data are less organized as measured by Planckian information, I_P. Using Equation (18) in Section 5, we can calculate two I_P values, one associated with CMB and the other with PDE—the former was 0.44 bits and the latter 0.72 bits, almost twice the value of the former, indicating that the CMB data are less organized than is predicted by PDE. One possible interpretation of this difference may be that the polarized CMB radiation “lost” some of its information about the Big Bang due to the randomizing effects of galactic dust [3]). If this interpretation proves to be valid, the BICEP2 data may provide an alternative support for the eixistence of the gravitational waves recently demonstrated by the LIGO experiments [45].

A partial list of the numerical values of the parameters of the Planckian distribution equation fitting the diverse sets of data shown in Figure 1 are summarized in Table 3.

4. Planckian Distribution Equation May Be to Dissipative Structures What the Periodic Table Is to Equilibrium Structures

Planckian processes are defined as those physicochemical processes that generate numbers fitting the Planckian distribution equation (PDE) [2,3]. Thus it would follow that all long- or fat-tailed histograms fitting PDE can be inferred to be generated by Planckian processes. Since PDE possesses three free parameters, A, B, and C (see Equation (9)), it would also follow that all Planckian processes (which are ‘dissipative structures’ of Prigogine [1,17], e.g., the intracellular gradients of calcium ions [46]) can be mapped onto and classified in the abstract three-dimensional space formed by three orthogonal axes, A, B, and C (to be called the PDE space).Just as the chemical periodic table classifies all elements into about 100 classes, so perhaps PDE can classify all Planckian processes into 3 × N classes, where N is the number of rows and three is the number of columns in a 3 × N table.

5. The Planckian Information: A New Measure of Order

As illustrated in Figure 1f,i,m,p,r, the Planckian distribution equation (PDE) contains a symmetrical equation that overlaps with PDE in the rising phase of the curves. This symmetrical function is referred to as the Gaussian-like equation (GLE), Equation (13), because it is identical with the Gaussian distribution equation, Equation (14), except that the pre-exponential factor is a free parameter, A, independent of σ:

y = Ae^{−(x − μ)^2/2σ^2}

(13)

y = ((2πσ²)^−0.5) e^{−(x − μ)^2/2σ^2}.

(14)

Using the areas under the curves (AUC) of PDE, Equations (8) or (9), and GLE, Equation (13), a new function was defined called the Planckian information, I_P [2,3]:

I_P = log₂ (AUC(PDE)/AUC(GLE)).

(15)

Our current interpretation of the Planckian information defined in Equation (15) is that it represents the degree of organization (and hence the order) of a physical system resulting from symmetry-breaking selection processes applied to some randomly available (and hence symmetrically distributed) processes, whether the system involved is atoms, enzymes, cells, brains, languages, human societies, or the universe [3]. Therefore, to better understand the meaning of I_P, it may be helpful to compare it with the Boltzmann—Gibbs and Shannon entropies which are, by contrast, measures of disorder. As is well known, the meanings of the terms “entropy” (and its derivative “negentropy”) and “information” are controversial, perhaps because of their lack of precise, mathematical definitions. However, this is, fortunately, not the case for the phrase “quantum of action” or “quanta of action”. Hence, if “entropy” and “information” can be shown to be related to “quanta” mathematically, such a triadic relation may contribute to clarifying the true meanings of “entropy” and “information”.

The concepts of entropy, quanta, and information all share the common property of being characterizable in three distinct ways—(i) experimentally; (ii) statistically and mechanically; and (iii) mathematically, as shown in

Table 4. A possible relationship between entropy, quanta, and information.

1. Concept	Entropy (1)	Quanta (2)	Information (3)
2. Field of study	Thermodynamics	Quantum mechanics	Informatics
3. Experiment/Measurement	S = ΔQ/T	Blackbody radiation spectra	Selecting m out of n possibilities or choices
4. Statistical, mechanical formulations	S = −k Σ pi log pi Boltzmann–Gibbs entropy (1866) *	U(λ,T) = (2πhc2/λ5)/(ehc/λkT − 1), Planck radiation equation (PRE) (1900)	IP = log2(AUC(P)/AUC(G)), where IP = Planckian information, AUC = area under curve; P = PDE, and G = Gaussian-like equation, i.e., y = Ae−(x − µ)^2/(2σ^2)
5. Mathematical formulation	H = −K Σ pi log pi Shannon entropy (1948)	y = (a/(Ax + b)5)/(eb/(Ax + B) − 1), Planckian distribution equation (PDE) (2008)	I = A log2 (n/m) A unified theory of the amount of information (2015a, c)
6. Emerging Concept	A measure of DISORDER	Quantization of action Essential for ORGANIZATION	A measure of the ORDER of an organized system

* Which reduces to S = k ln W when all p_i values are equal and W stands for the number of the microstate consistent with the macrostate of the system.

.

There may be an irreducibly triadic relation among THERMODYNAMICS, QUANTUM MECHANICS, and INFORMATICS, thus forming a mathematical category (the TQI triad or category?). This idea is represented diagrammatically in Figure 2.

The derivation of PRE (see row 4, column 2) by Planck in 1900 utilized the concept of thermodynamic entropy (see row 3, column 1) [47,48], which establishes a paradigmatic (to borrow the concept from linguistics) [49] relation between Entropy and Quanta. Therefore, Quanta seem paradigmatically related to both Entropy and Information, which indicates that Quantum mechanics mediates the interaction between Thermodynamics and Informatics (e.g., energy dissipation under-writes all communication of information), thus suggesting the possible irreducible triad or a category as depicted in Figure 3:

As already indicated, Boltzmann’s entropy equation played a major role in deriving the blackbody radiation equation by Planck in 1900, which in turn led to the derivation of the “Planckian information equation” (PIE) in 2015 [2,3]. PIE is shown in row 4 and column 3 in Table 4 and the related equation, the Planckian distribution equation (PDE), is shown in row 5 and column 2.

Thermodynamics, quantum mechanics, and informatics constitute an irreducible triad of communication (also called semiosis by Peircean scholars [50,51]. That is, it is impossible to communicate, at all scales from microscopic to macroscopic to cosmological without energy dissipation (thermodynamics), discrete objects to choose from (quantum mechanics), and selection of one or more objects from the message source (informatics). The idea of “communication as an irreducible triad of thermodynamics, quantum mechanics and informatics” may be algebraically (?) represented as follows:

COMMUNICATION = (Thermodynamics)^(Quantum mechanics)^(Informatics),

(16)

where C = A^B reads “A and B are the complementary aspects of C”.

6. The Petoukhov Hypothesis

Through an entirely different approach from what is described here, the Russian biophysicist Sergey Petoukhov [52,53] reached the conclusion that the properties of living systems can be modeled using resonance waves, in agreement with the conclusions summarized in Figure 4. To provide a glimpse of his thoughts, I reproduce some of his statements below (from [53]):

“Any living organism is a great chorus of coordinated oscillatory (also called vibrational; my addition) processes (mechanical, electrical, piezoelectric, biochemical, etc.), which are connected with their genetic inheritance along chains of generations.”

“From a formal point of view, a living organism is an oscillatory system with a large number of degrees of freedom, Resonances in such a system can serve as mechanisms for harmonization and ordering of its set of oscillatory processes.”

“A new slogan can be proposed: any living body is a musical instrument (a synthesizer with an abundance of rearrangements of resonant modes).”

These statements are consistent with my own writing published four decades earlier [54]:

“An ordinary enzyme possesses 10³ to 10⁴ vibrational degrees of freedom. It is therefore reasonable to assume that the vibrational motions of individual bonds in the enzyme will be far more important in enzyme catalysis than the translational or rotational motions of the enzyme as a whole. Given all the vibrational frequencies of the individual bonds in an enzyme, as well as their three –dimensional arrangements, we can in principle deduce the thermodynamic and catalytic properties of the enzyme under any conditions.”

All of the above statements support the conclusion drawn in [2] that

“The universal applicability of PDE (Planckian Distribution Equation) to many long-tailed histograms is attributable to

(i)

its role in generating functions and organizations through goal-directed selection of subsets of Gaussian processes (see Figure 4), and

(ii)

the wav–particle duality operating in living systems.”

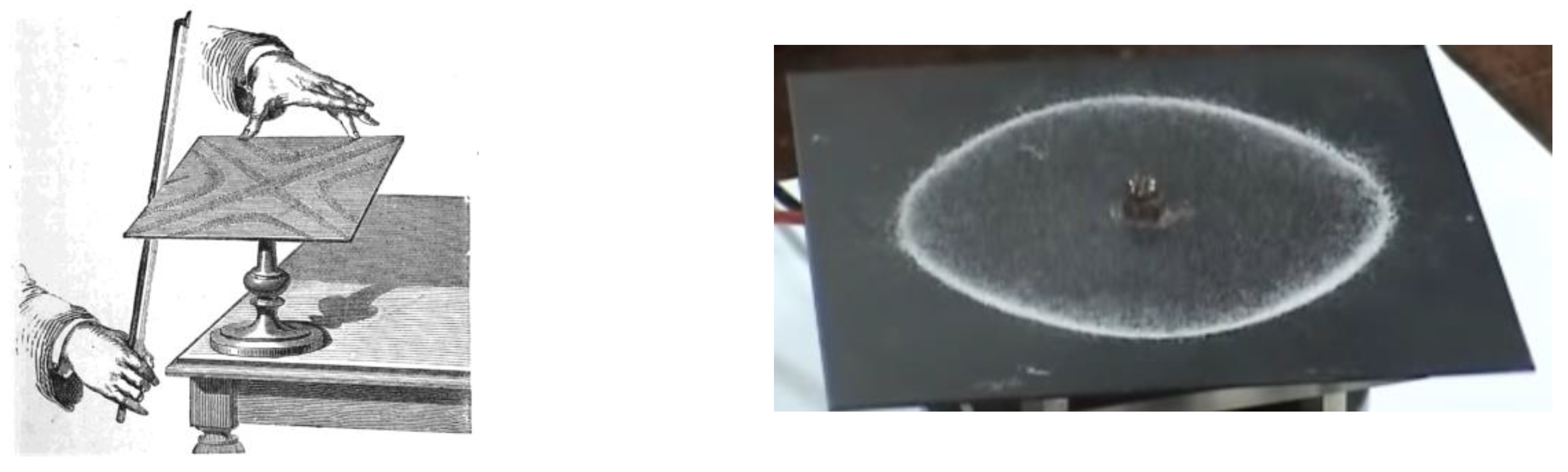
7. Cymatics and Chladni Patterns

The term cymatics, defined as the study of waves (“cyma” means wave in Greek), was probably not widely known until the invention of CymaScope in 2002 [7], which could visualize sound waves using water as the sensitive sound sensor. CymaScope is described in the top panel of Figure 6. Prior to the invention of CymaScope [7], a less sensitive wave-generating device known as Chladni plates [7,55] were used to visualize vibrations (Figure 5). The various vibrational patterns seen in Figure 5 were generated by drawing a bow over a piece of metal plate whose surface was sprinkled with sand particles that rearrange themselves as the metal plate vibrates in sections separated by “nodal lines” where the surface is temporarily motionless, thus attracting sand particles and forming so-called Chladni patterns. It is known that the higher the frequency and the larger the amplitude of the input vibrations, the more complex the Chladni patterns [55,56].

8. Water as the Molecular Sensor of Sound Waves: “Sonoaquascopy”

In [7], John Stuart Reid describes his sound-visualizing device, CymaScope, as follows:

“The CymaScope is a new type of scientific instrument that makes sound visible … The surface tension of water has high flexibility and fast response to imposed vibrations, even with transients as short-lived as a few milliseconds. Therefore, water is able to translate many of the sinusoidal periodicities—in a given sound sample—into physical sinusoidal structures on the water’s surface. Current limits to imprinting sound on water occur in the higher harmonics and are due mainly to there being insufficient energy available in this area of the audio spectrum to cause excursions of the surface tension membrane.”

Any instrument that can visualize sounds using water as a sound-sensor may be referred to as a “sonoaquascope”, i.e, a sound-induced water-wave visualizer. The study of water waves using a sonoaquascope can then be referred to as “sonoaquascopy”, in analogy, say, to Raman spectroscopy. The CymaScope invented in 2002 by J. S. Reid may be the first example of the “sonoaquascope”. The method employed by Kröplin in producing images in “dried” water droplets [58] may be viewed as an example of “sonoaquascope” although the dynamic water waves thought to precede the so-called Kröplin images no longer remain [59]. The method of Emoto [60] of producing water crystals whose structure reflects the characteristics of the environment, including sounds, to which they were exposed before freezing may also be viewed as an example of “sonoaquascope”. With the financial support provided by GreenMedInfo (Douglas Sayer Ji, founder, Bonita Springs, FL, USA), John S. Reid and I have successfully developed, between December 2016 and February, 2017, a digital version of CymaScope, i.e., the “digital” CymaScope (dCS). This new machine may also be referred to as the “digital sonoaquascope” (dSAS), since it is “digital” and “sound” sensing via “viewing water” wave patterns. dSAS can transform CymaGlyphs (i.e., the images produced by CymaScope) into histograms which have been found to fit PDE [61].

Water may be one of the most sensitive detectors of sound waves in nature as demonstrated by CymaScope [7,62]. For example, the different wave structures or patterns (called CymaGlyphs by Reid [63] between, say, musical notes, A0 and A0#, in Figure 6 are produced by the frequency difference of a mere 1.6 Hertz, and between those of B0 and C1 by 1.9 Hz, out of about 30 Hz vibrations for each note. For another example, take a look at the human brain waves visualized as water wave patterns in the last panel of Figure 6.

The frequency difference between the alpha wave and the beta wave is about 10 Hz and that between the beta wave and the delta wave (deep sleep state) is about 18 Hz. Yet their visual images (and the corresponding functional states) are strikingly different, indicating the surprising sensitivity of water as a sound-wave detector. (Please note that EEG signals were first transduced to sound waves before being visualized with CymaScope.) At least a part of water’s extreme sensitivity to waves (including electromagnetic waves) may be due to water molecules’ ability to form ensembles involving millions of molecules that Del Guidice and his colleagues [64] in Italy call “coherence domains”, which, in theory, can amplify very weak electromagnetic signals to macroscopic levels.

9. The Fourier Language as the Cosmic Language (Cosmese)

In his book Quantum Reality ([8] p. 79), Herbert states that Fourier discovered a new language (i.e., the wave language), referring to the Fourier theorem. I did not understand the true meaning of this statement until October–November, 2016, when I actually saw the intricate internal structures of water waves as visualized by CymaScope (Figure 6). Many interesting demonstrations of standing waves generated by vibrating surfaces are available on the Internet. When the solid surfaces employed in generating the so-called Chladni figures (Figure 5) are replaced by water, amazingly detailed wave forms can be visualized (see Figure 6 and Figure 7); this was made possible by the invention of CymaScope [7]. I agree with Reid that the invention of CymaScope may be akin to the inventions of the telescope (essential for astronomy) and the microscope (essential for biomedical sciences), and the area of investigations opened up by CymaScope, I suggest, may be the “cosmic linguistics”, or the study of cosmic language or cosmese. This term was coined in [1] and it was postulated then that the medium of cosmese is “cosmic waves”, in which I now include (i) the strong; (ii) electroweak; (iii) sound; (iv) chemical concentration; and (v) gravitational waves. In other words, I am assuming that, in agreement with Herbert [8], waves are a new language and as such can be both the medium and the message, if the McLuhan equation (asserting that the Medium = the Message) [65] (can be applied here. Examples of “wave messages” are provided by the last panel in Figure 6, where the “meaning” of the first “wave message” is the “relaxed waking state” of the human brain, and that of the second “wave message” is the actively functioning human brain, etc.

CymaGlyphs, some examples of which are shown in Figure 6 and Figure 7, may be viewed as words or sentences of the cosmological language (which I would be happy to refer to as the “Fourier language”, in agreement with Herbert [8], who claims that Fourier (1768–1830) discovered a new language, a wave language. Hence, I would predict that there would be almost infinite number of CymaGlyphs, all obeying the Fourier theorem but reflecting individual situations—just like in the human language, where we can generate an almost infinite number of sentences obeying a small number of grammatical rules and reflecting individual ideas in the human brain. This is of course the well-known principle in linguistics called “rule-governed creativity” [49]. In other words, I maintain that:

(i)

CymaGlyphs are the words and sentences of a cosmological language based on waves discovered by Fourier in 1807.

(ii)

The grammar of the cosmological language is the Fourier theorem.

(iii)

The linguistic principle of rule-governed creativity applies to CymaGlyphs.

If the above conjectures turn out to be validated by further inquiries, future historians may regard the invention of CymaScope as the beginning of cosmic linguistics, just as Galileo’s and others’ invention of the telescope is viewed as the beginning of astronomy.

Thus I am inclined to conclude that waves are the language mediating communication throughout the Universe, i.e., cosmese, and hence, based on the McLuhan equation, the following relations can be inferred:

waves = the medium of cosmic communication, and

CymaGlyphs = the cosmic messages whose meaning may be identified with “BEAUTY” among others, in agreement with Masaru Emoto [66].

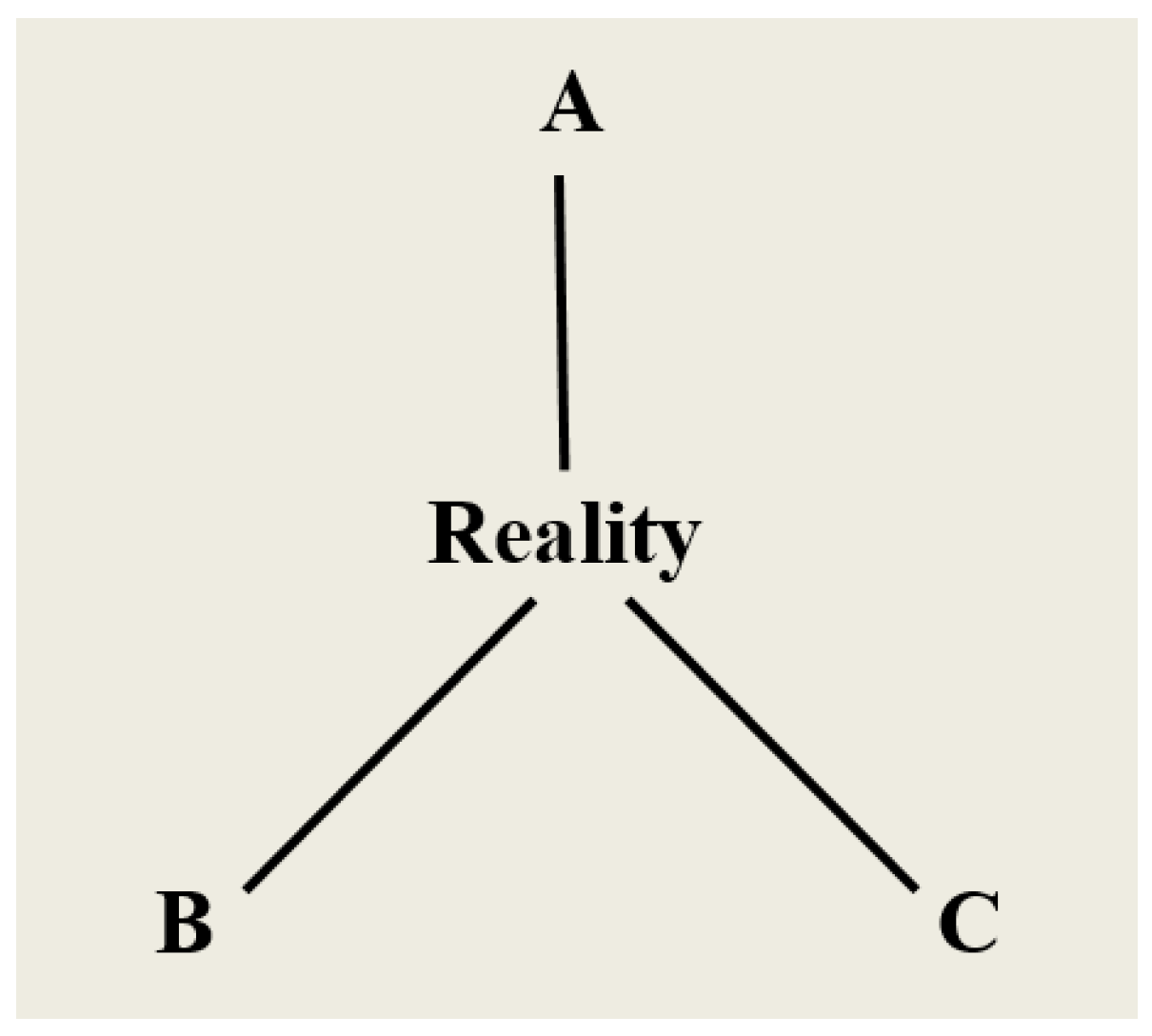
10. Triadic Monism: The Universality of the Irreducible Triadic Relation (ITR)

Burgin’s suggestion that the relationship between information and knowledge (or structure more generally) is akin to that between energy and matter [67] motivated the construction of the scheme shown in Figure 7, the center of which prominently displays his idea (see Arrows 1 and 4 in this figure and Tables 2–21 in [1]). Since energy and matter are quantitatively related through E = mc², which can be viewed as a supplementary relation and, since the combination of energy and matter is conserved according to the First Law of thermodynamics, it would be logical and natural to combine these two terms into one word, matter–energy or mattergy, as is widely done. Similarly, it may be convenient to coin a new word to represent the combination of information and knowledge, namely, “information–knowledge” or “infoknowledge”, more briefly (see Arrows 4/5 relative to Arrows 1/8 in Figure 7).

Figure 7 can be viewed as a network consisting of eight nodes/vertices and 16 arrows/edges. If one focuses on the system of arrows, ignoring the names of the nodes, Figure 7 clearly exhibits a reflection symmetry. “An object has reflectional symmetry (line or mirror symmetry) if there is a line going through it which divides it into two pieces which are mirror images of each other” [68]. The reflection symmetry is in turn composed of two complementary pairs (Nature–Form and Body–Mind pairs) and two supplementary pairs Energy–Matter and Information–Knowledge pairs). Thus, the network in Figure 7 can be said to embody both symmetry when viewed in terms of the organized system of arrows and “broken symmetry” or “antisymmetry” as defined in [69] when viewed in terms of the names of the nodes. Figure 7 is asymmetric as a whole, with symmetric and antisymmetric aspects [69]. Figure 7 is also a diagrammatic representation of the theory of everything (TOE) proposed in ([1], pp. 633–642), which seems consistent with the theories of everything proposed by Popper [70], Rosen [71], Penrose [72], and Burgin [67]. The TOE depicted in Figure 7 is an attempt to correlate and integrate the following three hybrid concepts, i.e., mattergy, gnergy, and infoknowledge, using category theory [73,74]. The first two terms appeared in [1,17] and the last term, infoknowledge, was coined more recently motivated by Burgin’s suggestion [67] that:

“Information is related to structures as energy is related to matter”,

(17)

where the structure includes knowledge and data.

To facilitate possible future discussions, I suggest that Statement (17) be referred to as the Burgin thesis. Since the combination of energy and matter is often referred to as mattergy, the Burgin thesis suggests an analogous hybrid term combining information and knowledge, which is referred to as infoknowledge.

It is instructive to compare Figure 7 with the gnergy tetrahedron (Figure 8). The body-centered tetrahedron (BCT) was found to provide a useful topological template to organize various sets of related ideas and principles discussed in many fields of inquiries (Table 10-5 in [1]), including physics, biology, and philosophy.

Both Figure 7 and the Gnergy Tetrahedron, Figure 8, contain 4 nodes, three of which are common (Energy, Metter, and Information) and one is unique to each diagram, i.e., Knowledge for Figure 7 and Life for the Gnergy Tetrahedron, Figure 8. Thus there is a lack of congruency between these two diagrams, which is somewhat surprising, since both diagrams are rooted in the same symmetry principles, i.e., complementarity and supplementarity. Again, supplementarity is an additive relation, i.e., A + B = C, and complementarity is non-additive, i.e., A^B = C, where the symbol ^ indicates that A and B are complementary aspects of a third entity C or that A appears as B or C depending on the mode of observations employed.

The lack of congruence between Figure 7 and the Gnergy Tetrahedron (Figure 8) may have at least two possible explanations:

(i)

There may be one or more logical errors embedded in the reasoning behind the formulation of one or both of Figure 7 and the Gnergy Tetrahedron, Figure 8, and

(ii)

Knowledge in Figure 7 and Life in the Gnergy Tetrahedron, Figure 8, may be more or less synonymous or refer to the same object.

If Possibility (i) can be ruled out upon further scrutiny, we will be left with Possibility (ii), which in effect asserts that”

“Matter and life are complementary aspects of the ultimate reality.”

(18)

If Statement (18) is accepted, the Gnergy Tetrahedron, Figure 8 and Figure 7 become logically consistent with each other, although different diagrammatically, which may be considered to be an example of antisymmetry discussed by Darvas [69] (see below).

Symmetry is generally defined as “invariance under any kind of transformation” [68,75] or as “the existence of different viewpoints from which the system appears the same” [76]. Darvas [69] provides a more detailed definition:

(19)

The symmetries embedded in Figure 7 may reflect the symmetric properties of the reality itself. The concepts of symmetry and symmetry breaking are fundamental to physics and philosophy [69,76,77]. According to complementarism [78], ultimate reality is irreducibly triadic [3,22], embodying A, which is the complementary union of irreconcilable opposites B and C. That is, complementarism asserts that the ultimate reality is three in one and hence its philosophical framework is here referred to as triadic monism which can be diagrammatically represented as shown in Figure 8. According to Darvas [69], the world is asymmetric, embodying symmetry and antisymmetry:

Asymmetry = Symmetry + Antisymmetry.

(20)

Asymmetry is the absence of symmetry, i.e., those transformations that fail to preserve any structures or regularities (e.g., the human body is asymmetric under a 2-fold rotation). Symmetry is defined in Statement (19). Antisymmetry is exemplified by the yin–yang symbol of the Daoist philosophy: When the symbol is rotated 180°, the shape of the symbol remains invariant but the black and white colors are exchanged.

According to triadic monism, the Ultimate Reality is irreducibly triadic. This notion is depicted diagrammatically as shown in Figure 9. The Ultimate Reality encompasses Complementarity. In complementarity ([1], pp. 24050), A appears as B or C, depending on how A is observed. The transition from A to B or to C may be considered as “symmetry breaking”, as discussed in physics [69,76], which is the universal mechanism of diversification and the structure formation (or structuration) in our universe. In the same vein, the reverse transition, i.e., from B and C to A, may be referred to as “symmetry making”. Symmetry breaking underlies the evolution of the physical universe as it gradually cooled after the Big Bang. In contrast, symmetry-making proceeds in the mental universe as the human mind abstracts invariances from observed diversities in the physical and mental universes. Symmetry breaking and symmetry making may be considered as an example of the yin–yang pair that embodies complementarity or supplementarity [79], depending on context [59].

11. Conclusions

The ancient idea that the universe embodies music (or resonance of waves in the modern idiom) [80] seems to be supported, albeit indirectly, by the discovery in 2008–2012 of the universality of the PDE (Planckian Distribution Equation) [1] and the exquisite sensitivity of water to sound waves, visualized for the first time in 2002 using CymaScope [7]. These recent findings seem to support Herbert’s [8] conjecture that Fourier discovered a new language that he calls “a wave language”. This agrees with the conclusion I reached in 2012 that the two distinct languages used by humans and living cells, i.e., humanese and cellese, derive from a third language called cosmic language or cosmese [1,9]. All these developments seem to indicate to this author that there exists a novel language, here called cosmese or Fourier language and identified with Herbert’s wave language, that is the source of all the languages operating in our universe, including humanese and cellese (see Table 2.13 in [1]).