The Matrix Method of Representation, Analysis and Classification of Long Genetic Sequences
Abstract
:1. Introduction
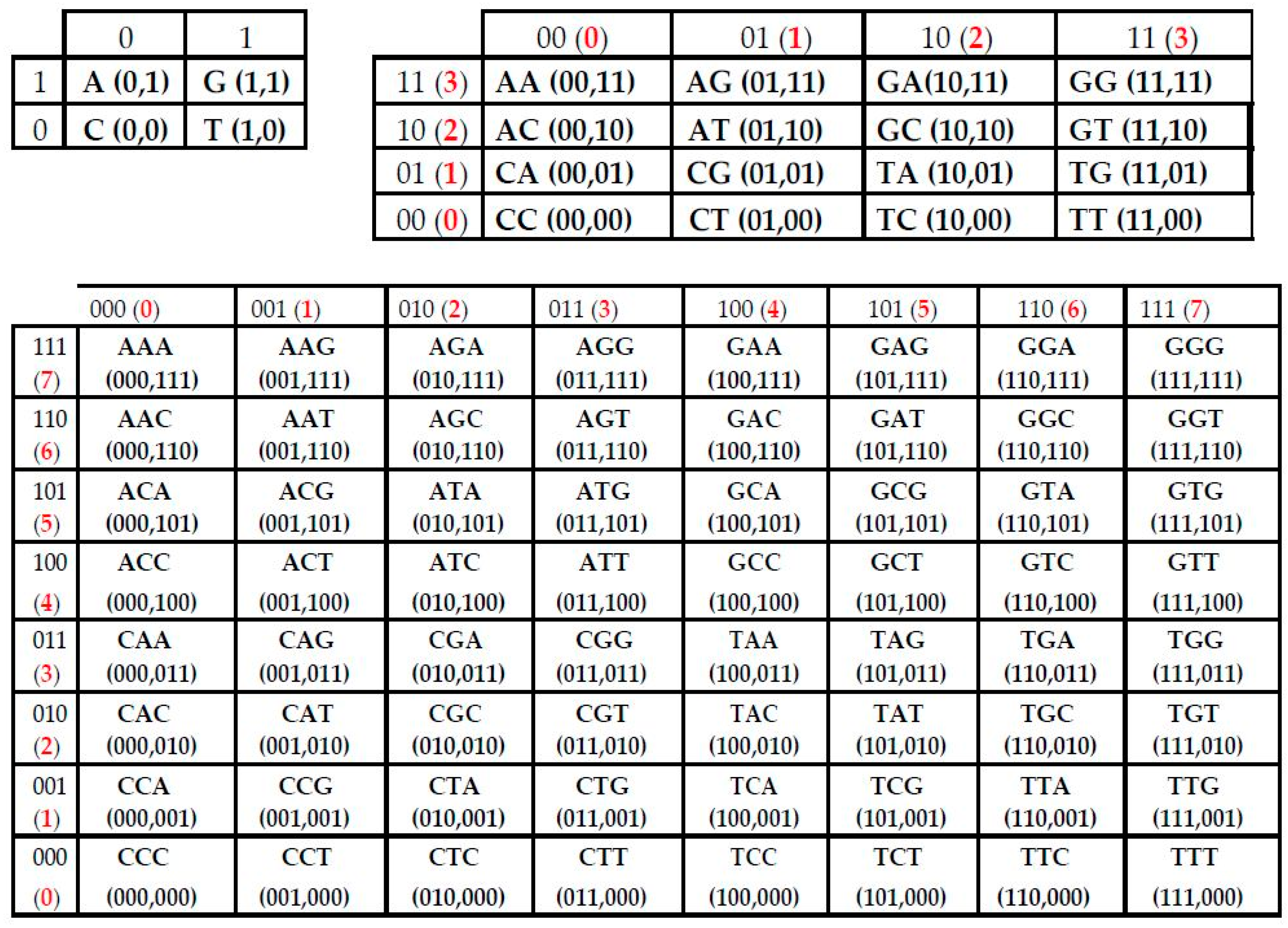
2. Matrix Representations of Whole Sets of N-Plets (or N-Mers)
- the set of 41 monoplets (in DNA: A, C, G, T) (in RNA, uracil U replaces thymine T);
- the set of 42 = 16 duplets (AA, AC, AG, AT, ….);
- the set of 43 = 64 triplets (AAA, AAC, ACA, ACG, ACT, ….);
- etc.
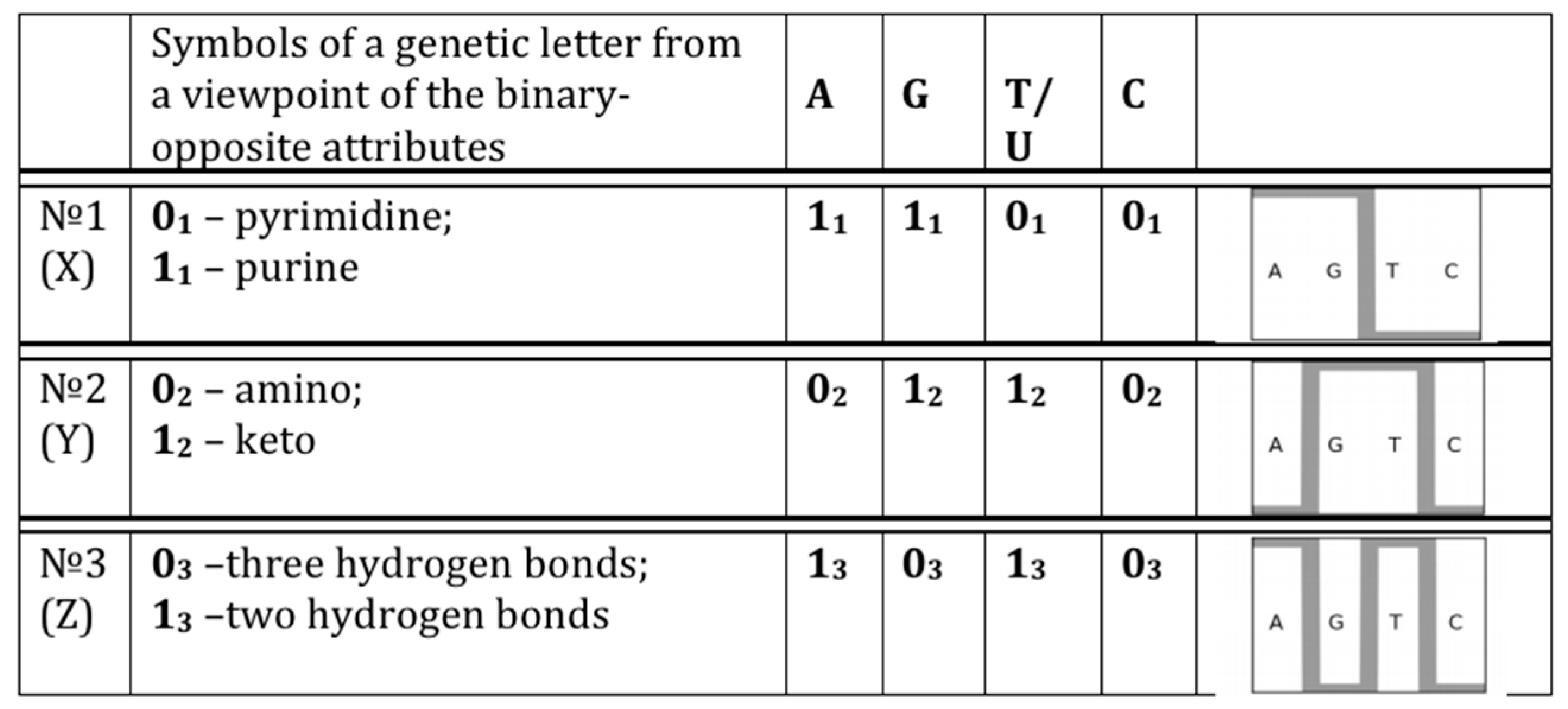
- 10110... (in accordance with the first sub-alphabet; its decimal equivalent can be located on the “X” axis of a Cartesian system of coordinates);
- 01110... (in accordance with the second sub-alphabet; its decimal equivalent can be located on the “Y” axis of a Cartesian system of coordinates);
- 11000... (in accordance with the third sub-alphabet; its decimal equivalent can be located on the “Z” axis of a Cartesian system of coordinates).
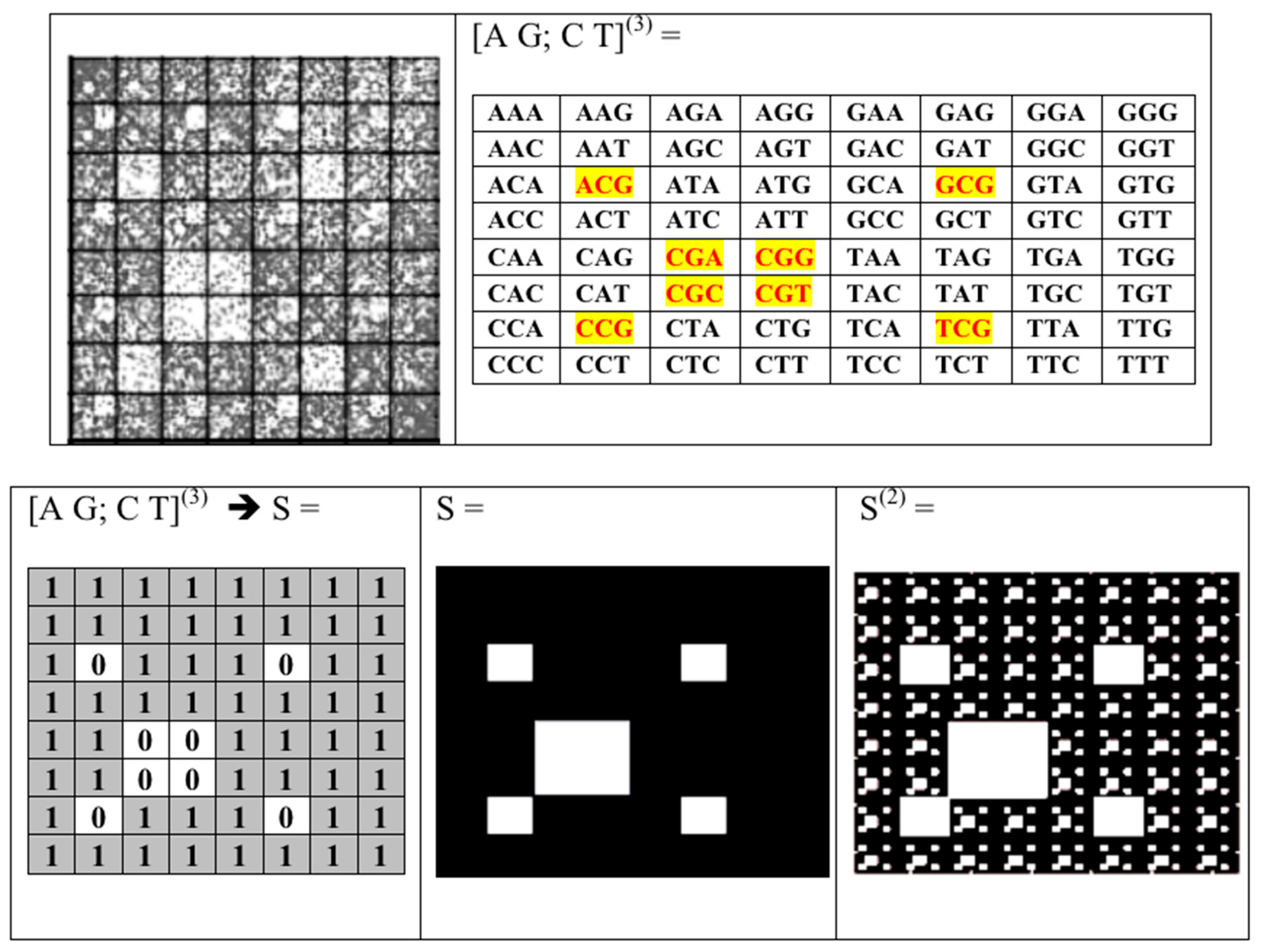
- the plane (x, y) corresponds to matrices [A G; C T](N), whose rows and columns are binary numerated from the point of view of the first sub-alphabet and the second sub-alphabet respectively;
- the plane (x, z) corresponds to matrices [G A; C T](N), whose rows and columns are binary numerated from the point of view of the first sub-alphabet and the third sub-alphabet respectively;
- the plane (y, z) corresponds to matrices [G T; C A](N), whose rows and columns are binary numerated from the point of view of the second sub-alphabet and the third sub-alphabet respectively.
3. The Description of the Matrix Method for Long Nucleotide Sequences
- Any long nucleotide sequence, which contains K nucleotides, is divided into equal fragments of length “N” (N-plets or N-mers), where “N” takes different values: n = 1, 2, 3, …, K; in the result, an appropriate set of different symbolic representations of this sequence as a chain of N-plets appears;
- Each N-plet in every of these representations of the sequence is transformed into three kinds of n-bit binary numbers by means of its reading from the point of view of the three sub-alphabets (Figure 2). Each of these binary numbers is transformed into its decimal equivalent. In the result, an appropriate set of different decimal representations of the initial symbolic sequence appears in a form of three kinds of sequences of decimal numbers respectively for positive integer coordinates on Cartesian axes X, Y, Z (or for numeration of rows and columns of appropriate genetic matrices).
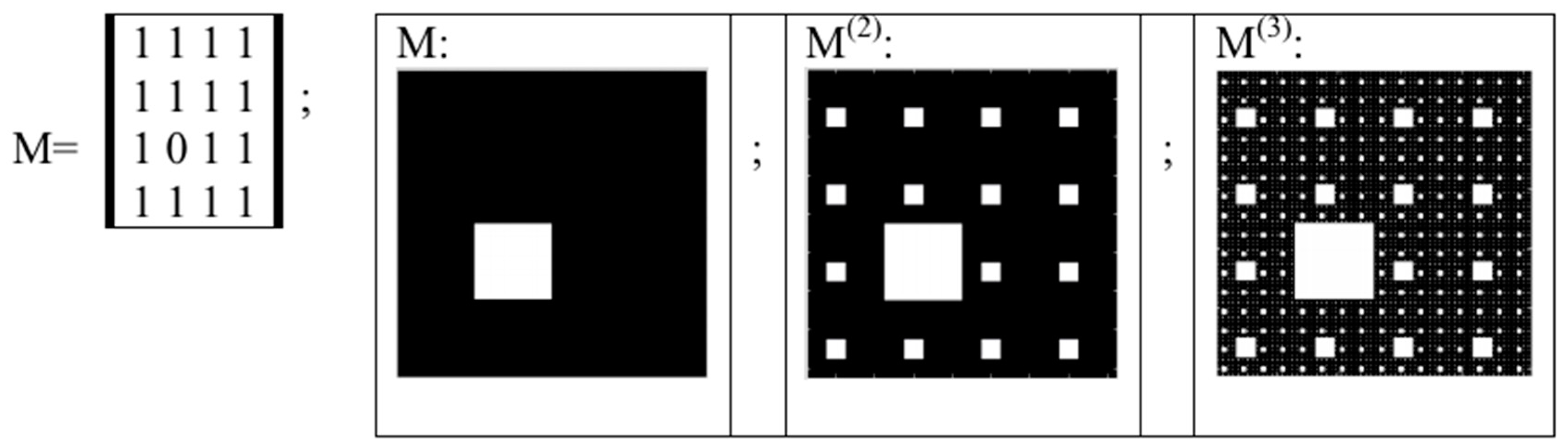
- Any two of the received numeric sequences define an appropriate sequence of pairs of positive integer coordinates of points on the 2-dimensional Cartesian plane (or coordinates of cells inside an appropriate genetic matrix of a Kronecker family). On the base of these pairs of coordinates, a set of corresponding points is built on the 2-dimensional Cartesian plane (or a set of corresponding cells in black inside a respective genetic matrix of a Kronecker family in contrast to other cells, which remain in white).
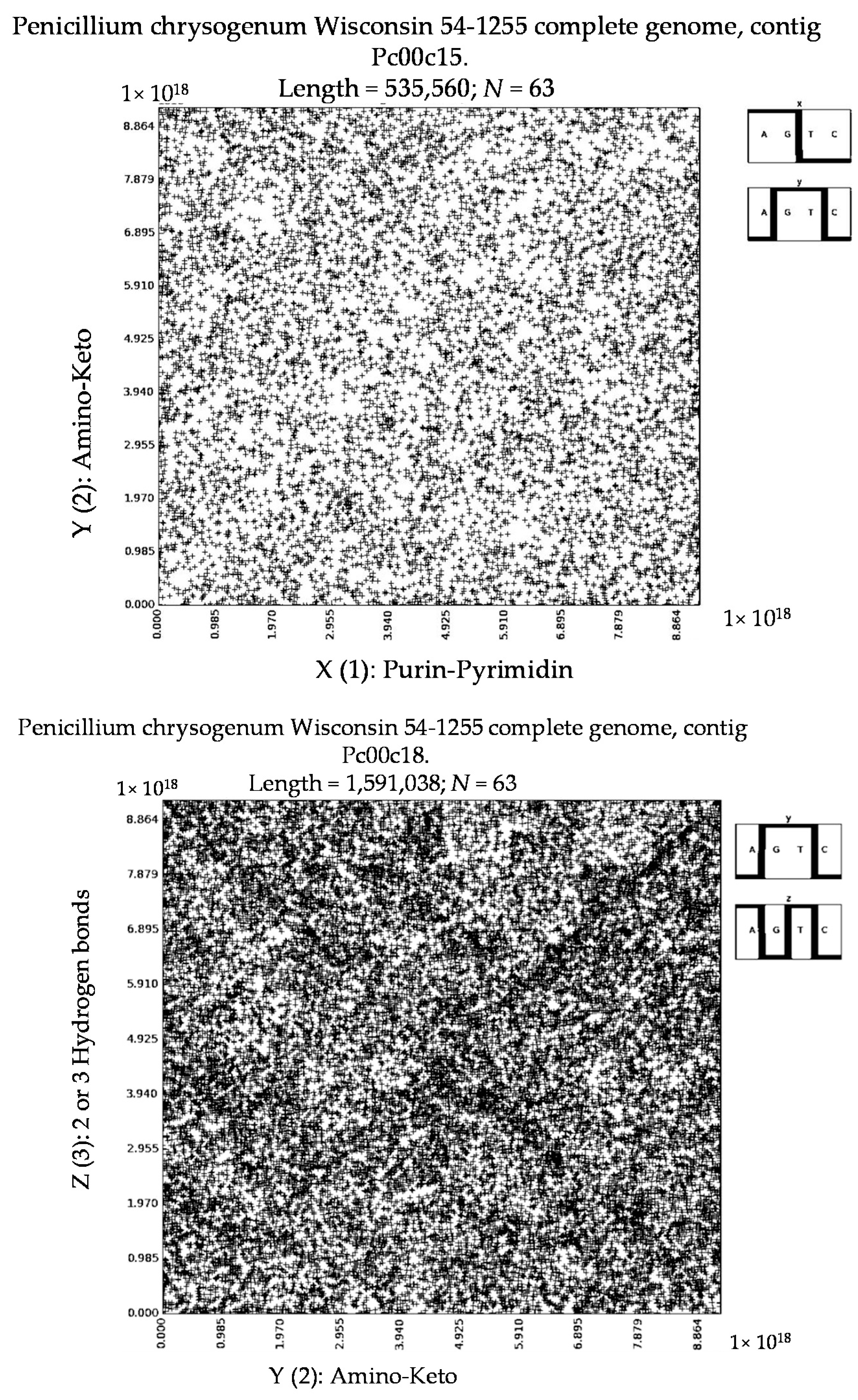
- Homo sapiens contactin associated protein-like 2 (CNTNAP2), RefSeqGene on chromosome 7 (N = 63).
- Homo sapiens contactin associated protein-like 2 (CNTNAP2), RefSeqGene on chromosome 7 (N = 63).
- Sorangium cellulosum So0157-2, complete genome (N = 63).
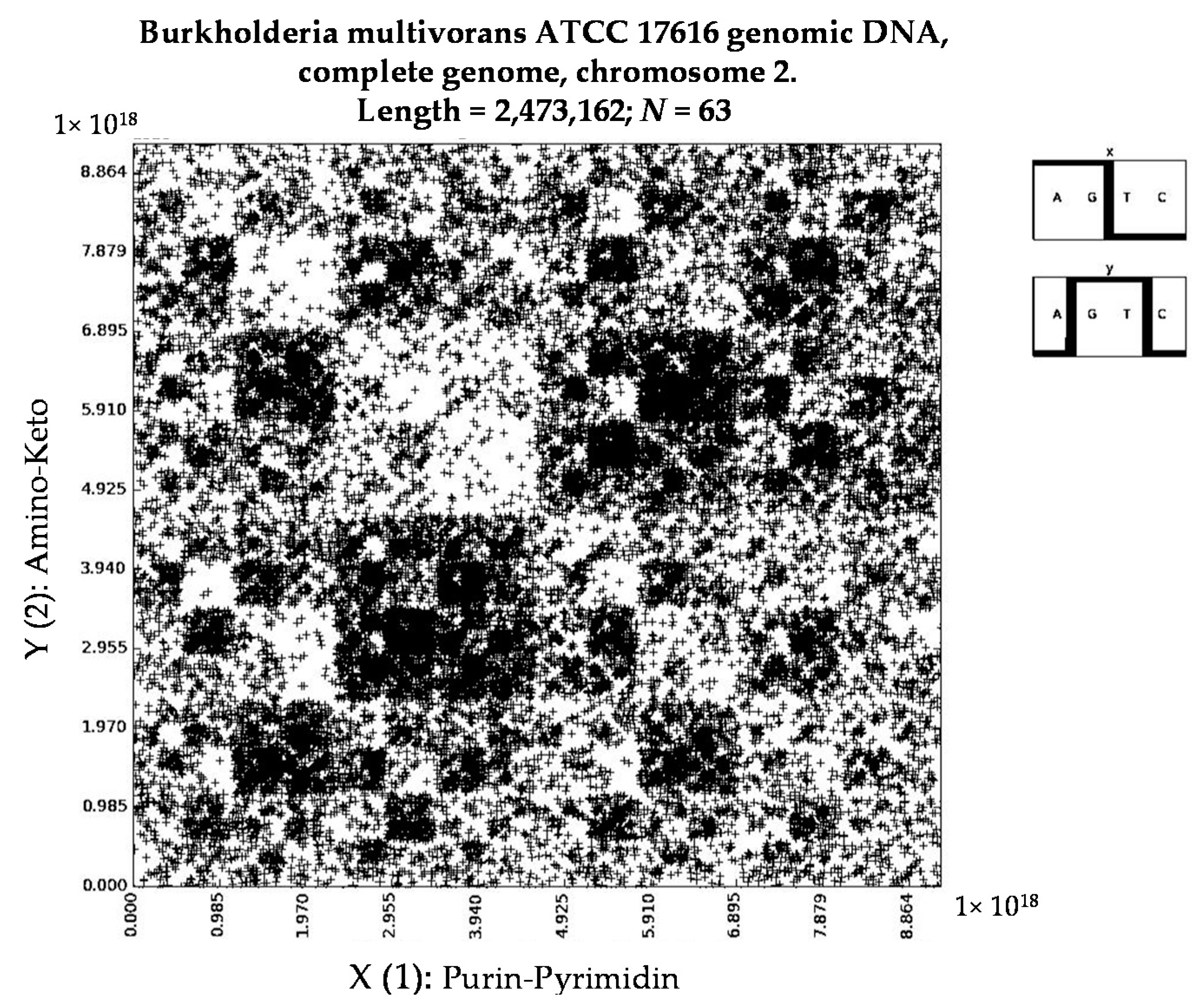
- Burkholderia multivorans ATCC 17616 genomic DNA, complete genome, chromosome 2 (N = 63).
- Thermofilum sp. 1910b, complete genome (N = 63).
- Thermofilum sp. 1910b, complete genome (N = 63).
- Dinoroseobacter shibae DFL 12, complete genome (N = 8).
- Escherichia coli LY180, complete genome (N = 24).
- Francisella tularensis subsp. tularensis SCHU S4 complete genome (N = 24).
- Halomonas elongata DSM 2581, complete genome (N = 24).
- Helicobacter mustelae 12198 complete genome (N = 24).
- Helicobacter mustelae 12198 complete genome (N = 12).
- Invertebrate iridovirus 22 complete genome (N = 8).
- Methanosalsum zhilinae DSM 4017, complete genome (N = 12).
- Methanosalsum zhilinae DSM 4017, complete genome (N = 12).
- Mycobacterium abscessus subsp. bolletii INCQS 00594 INCQS00594_scaffold1, whole genome shotgun sequence (N = 12).
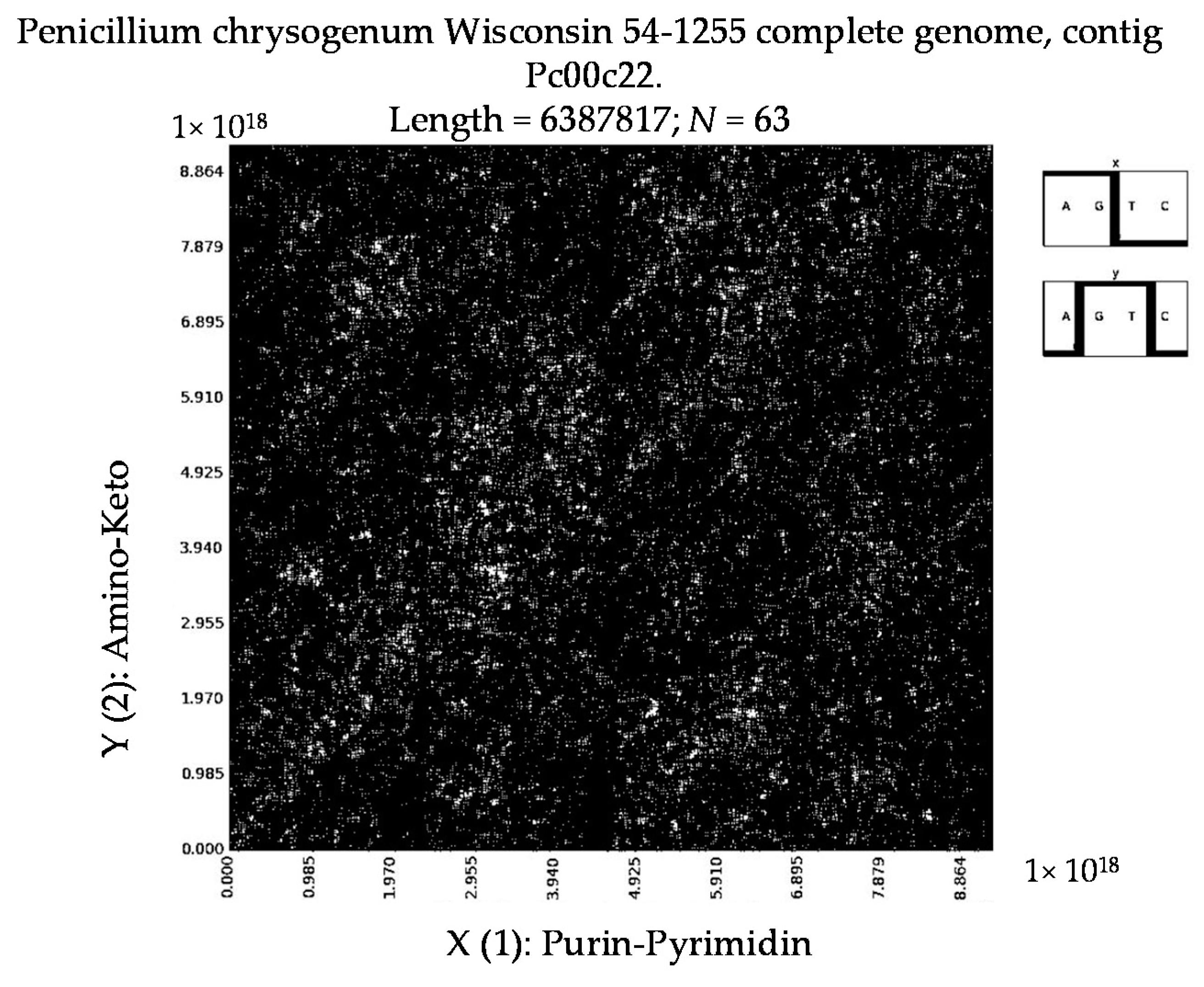
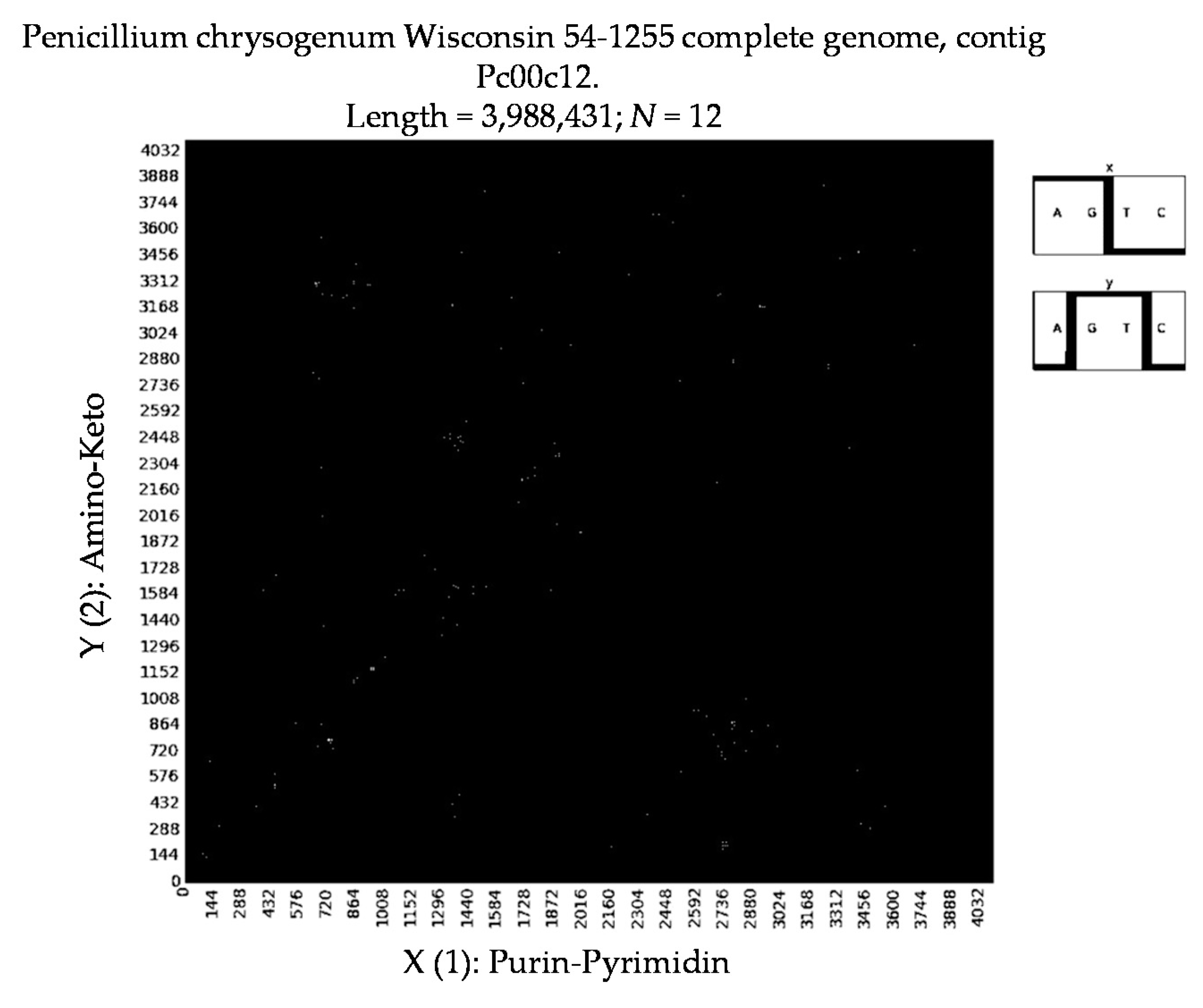
- Penicillium chrysogenum Wisconsin 54-1255 complete genome, contig Pc00c12 (N = 32).
- Riemerella anatipestifer DSM 15868, complete genome (N = 12).
- Riemerella anatipestifer DSM 15868, complete genome (N = 12).
- Burkholderia multivorans ATCC 17616 genomic DNA, complete genome, chromosome 2 (N = 8).
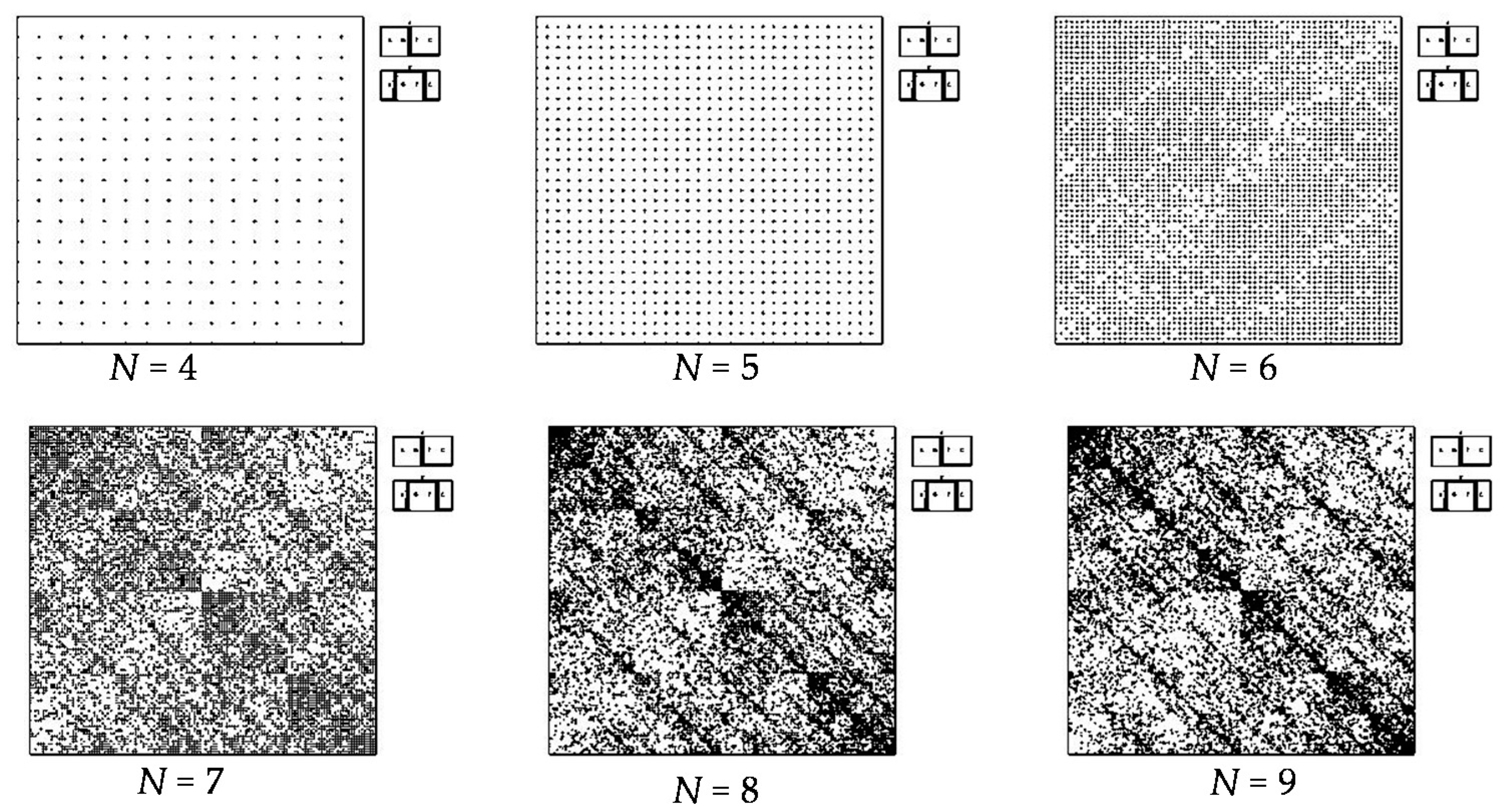
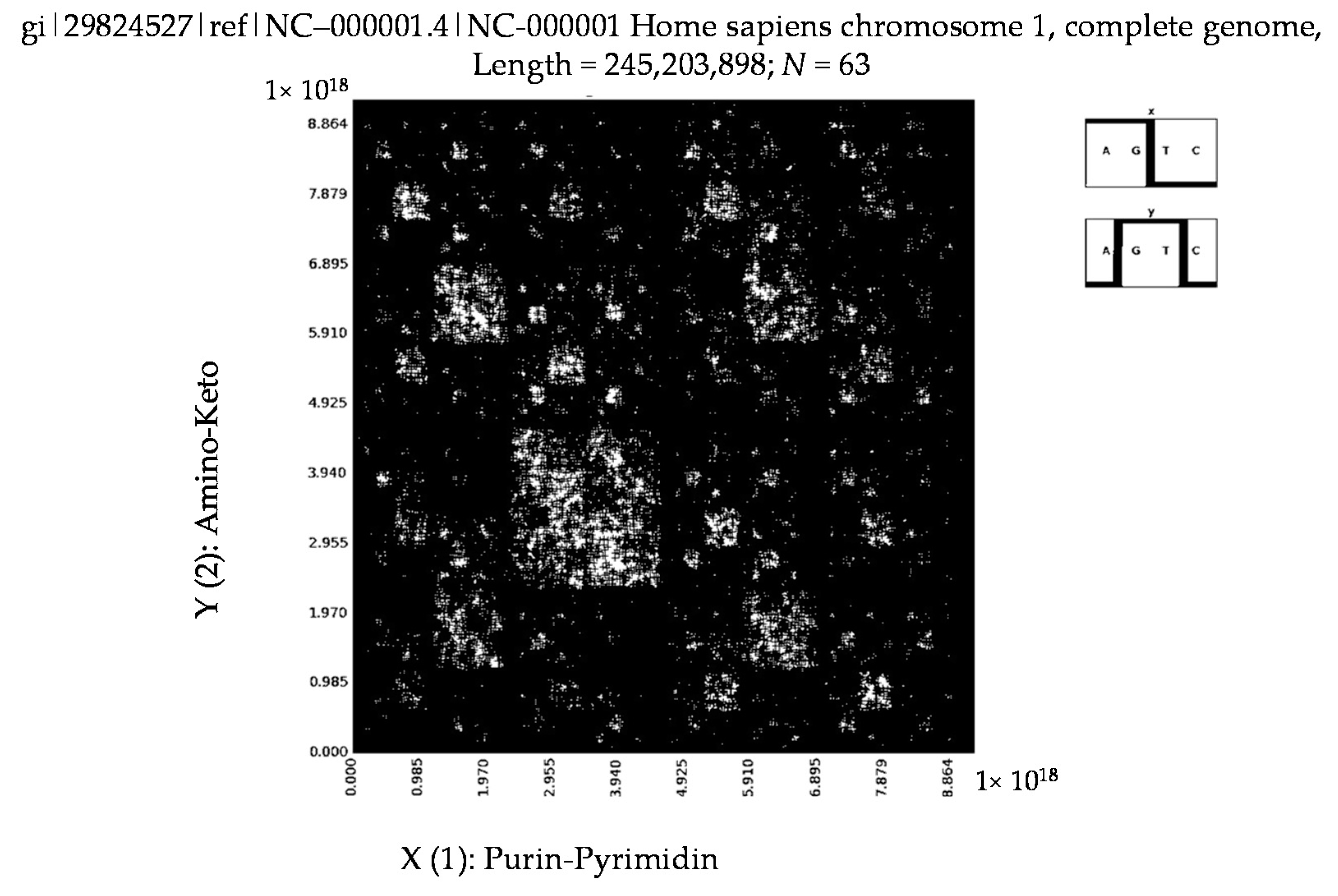
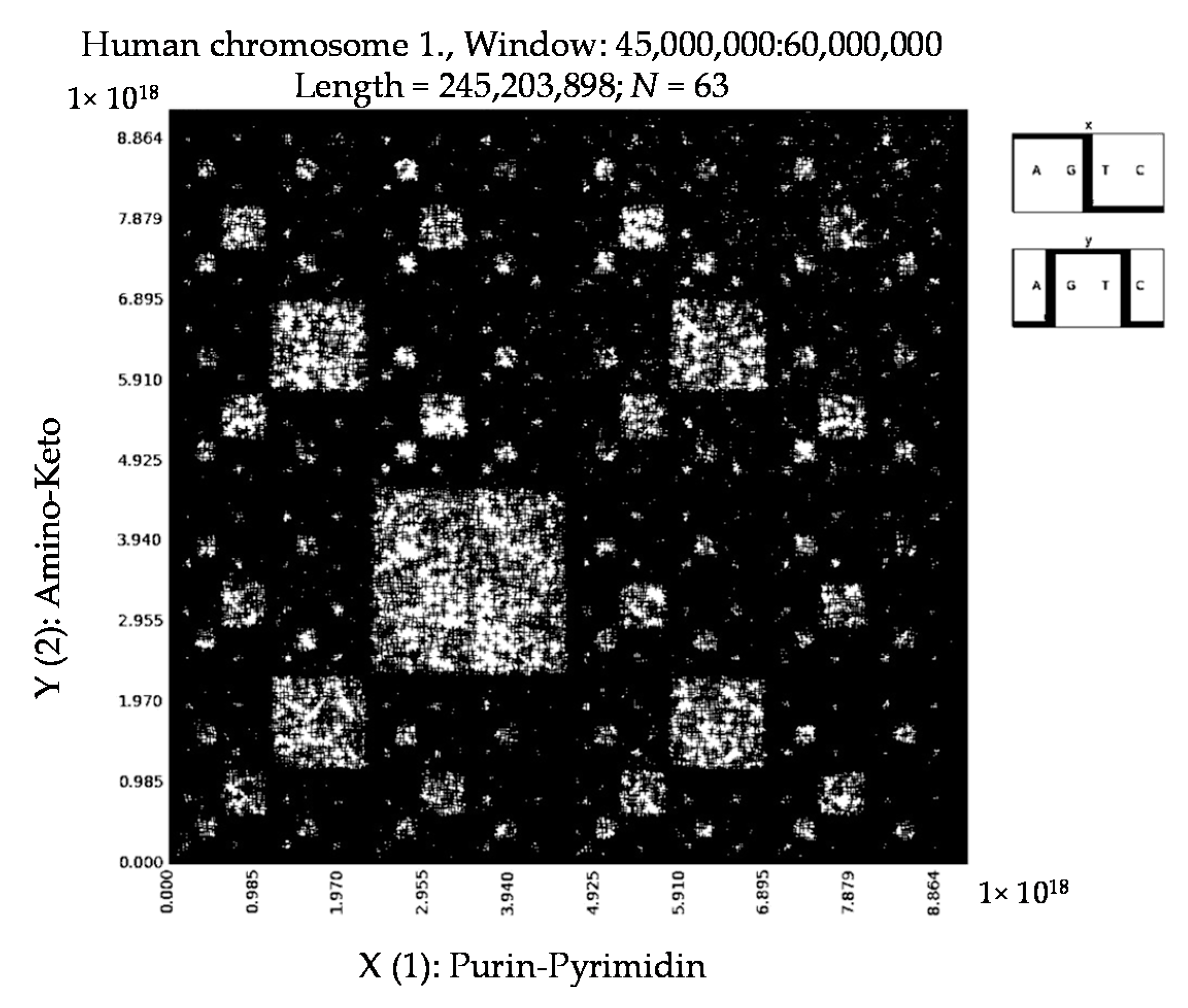
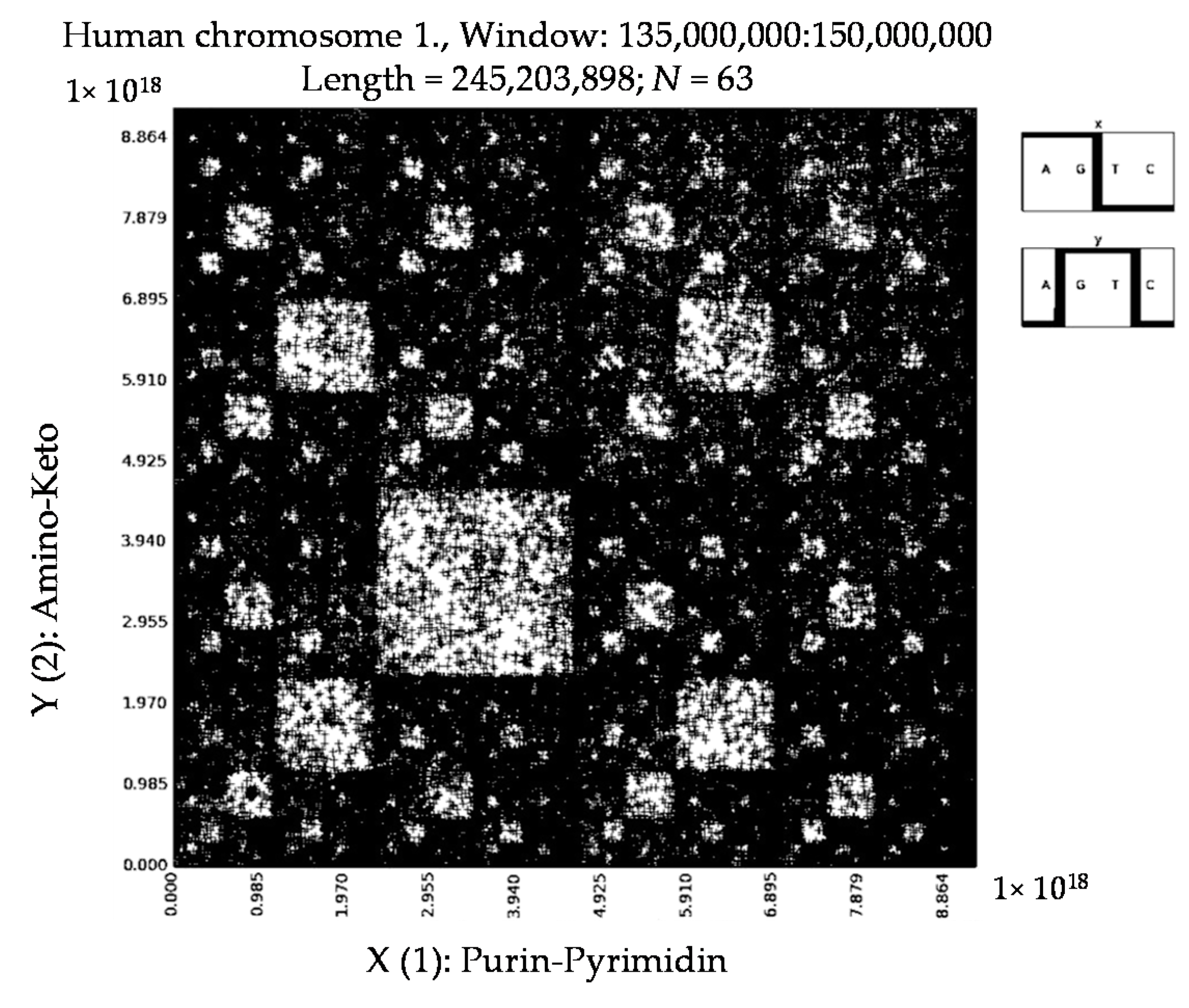
- a long nucleotide sequence, which is divided into relative short N-mers (N = 1, 2, 3, 4), usually contains all possible kinds of such short N-mers; correspondingly, its visual pattern is trivial because it contains all possible points with positive integer coordinates (x, y) inside an appropriate numeric range;
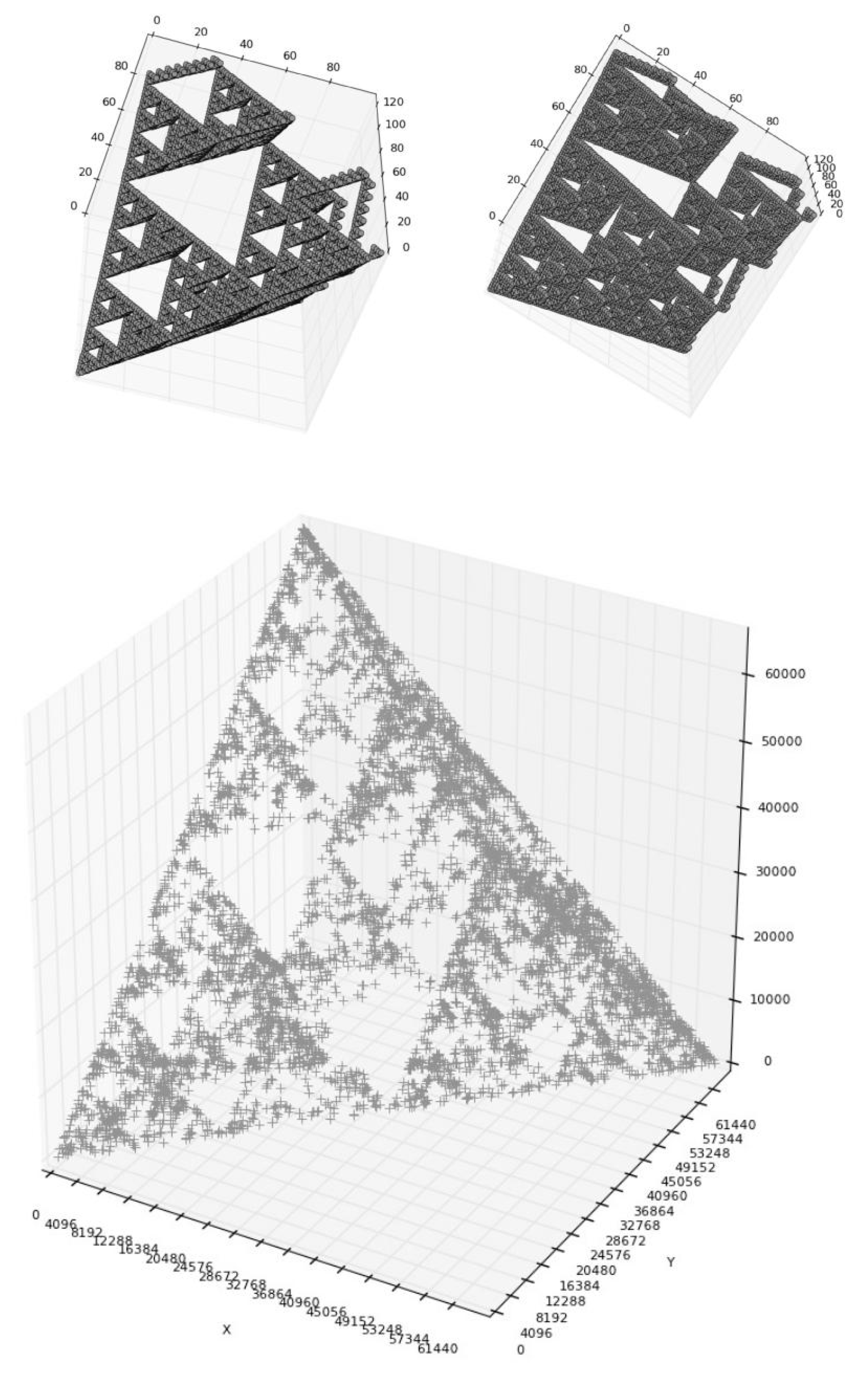
- a long nucleotide sequence, which is divided into relative long N-mers (N = 8, 9, 10, …), usually generates a regular non-trivial mosaic of a fractal-like or other character. This was detected using a special computer program in the course of initial investigations of different long nucleotide sequences by means of the described method.
4. Long Random Sequences
5. Kronecker Multiplication, Fractal Lattices and the Problem of Coding an Organism on Different Stages of Its Ontogenesis
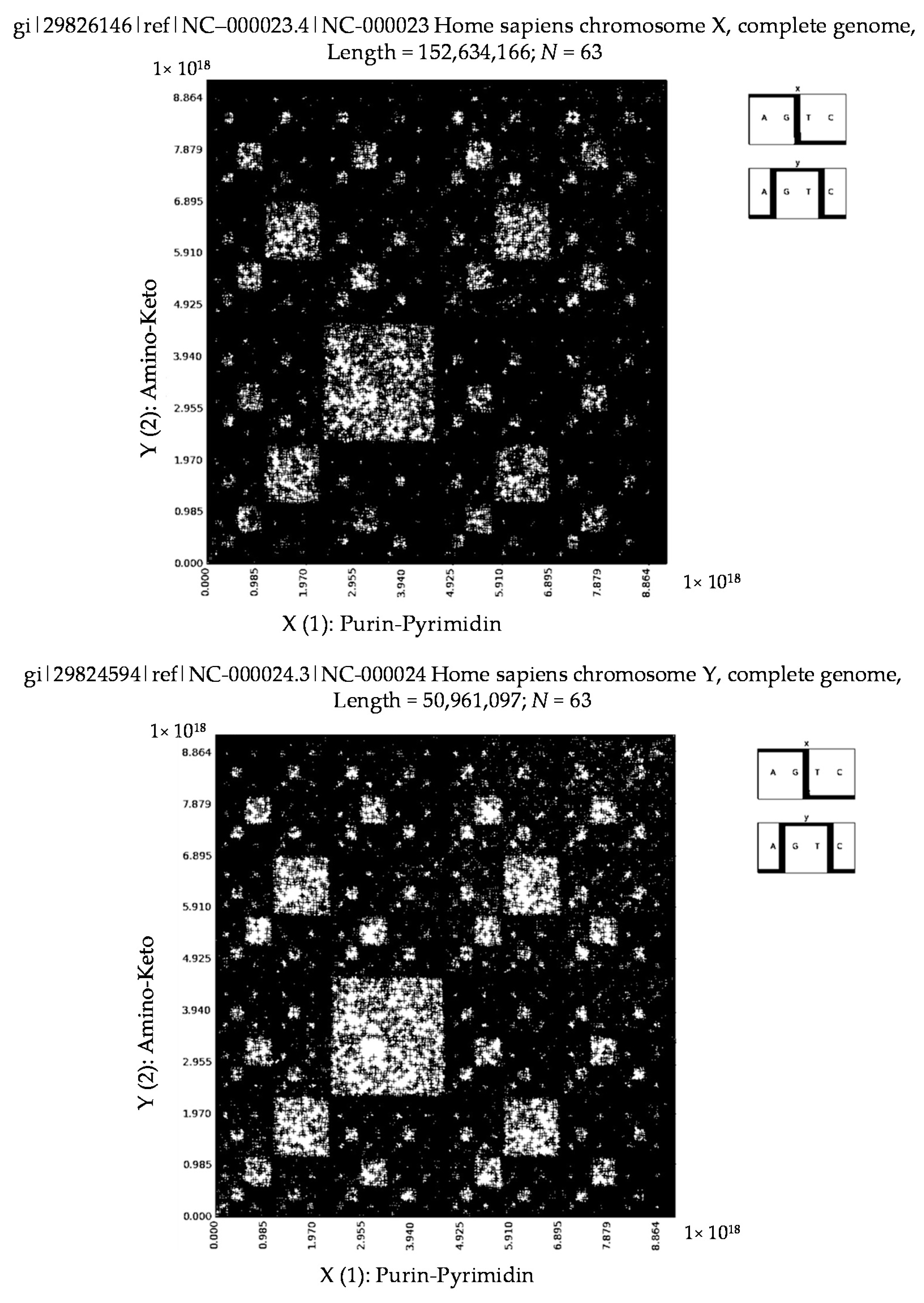
6. Patterns of Human Chromosomes
7. Patterns of Penicillin
8. About 3D-Representations
9. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bell, S.J.; Forsdyke, D.R. Deviations from Chargaff’s second parity rule correlate with direction of transcription. J. Theor. Biol. 1999, 197, 63–76. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Zhao, H. Negative correlation between compositional symmetries and local recombination rates. Bioinformatics 2005, 21, 3951–3958. [Google Scholar] [CrossRef] [PubMed]
- Dong, Q.; Cuticchia, A.J. Compositional symmetries in complete genomes. Bioinformatics 2001, 17, 557–559. [Google Scholar]
- Forsdyke, D.R. A stem-loop “kissing” model for the initiation of recombination and the origin of introns. Mol. Biol. Evol. 1995, 12, 949–958. [Google Scholar] [PubMed]
- Forsdyke, D.R. Symmetry observations in long nucleotide sequences: A commentary on the discovery of Qi and Cuticchia. Bioinform. Lett. 2002, 18, 215–217. [Google Scholar] [CrossRef]
- Forsdyke, D.R.; Bell, S.J. A discussion of the application of elementary principles to early chemical observations. Appl. Bioinform. 2004, 3, 3–8. [Google Scholar] [CrossRef]
- Mitchell, D.; Bride, R. A test of Chargaff’s second rule. BBRC 2006, 340, 90–94. [Google Scholar] [CrossRef] [PubMed]
- Perez, J.-C. Codon populations in single-stranded whole human genome DNA are fractal and fine-tuned by the golden ratio 1.618. Interdiscip. Sci. Comput. Life Sci. 2010, 2, 1–13. [Google Scholar]
- Prabhu, V.V. Symmetry observation in long nucleotide sequences. Nucleic Acids Res. 1993, 21, 2797–2800. [Google Scholar] [CrossRef] [PubMed]
- Grebnev, Y.V.; Sadovsky, M.G. Second Chargaff's rules and symmetry genomes. Fundam. Res. 2014, 12, 965–968. (In Russian) [Google Scholar]
- Yamagishi, M.; Herai, R. Chargaff’s “Grammar of Biology”: New Fractal-like Rules. Available online: https://arxiv.org/pdf/1112.1528.pdf (accessed on 7 December 2011).
- Jeffrey, H.J. Chaos game representation of gene structure. Nucleic Acids Res. 1990, 18, 2163–2170. [Google Scholar] [CrossRef] [PubMed]
- Goldman, N. Nucleotide, dinucleotide and trinucleotide frequencies explain patterns observed in chaos game representations of DNA sequences. Nucleic Acid Res. 1993, 21, 2487–2491. [Google Scholar] [CrossRef] [PubMed]
- Gutierrez, J.M.; Rodriguez, M.A.; Abramson, G. Multifractal analysis of DNA sequences using novel chaos-game representation. Physica A 2001, 300, 271–284. [Google Scholar] [CrossRef]
- Joseph, J.; Sasikumar, R. Chaos game representation for comparison of whole genomes. BMC Bioinform. 2006, 7, 243–246. [Google Scholar] [CrossRef] [PubMed]
- Oliver, J.L.; Bernaola-Galvan, P.; Guerrero-Garcia, J.; Roman-Roldan, R. Entropic profiles of DNA sequences through chaos-game-derived images. J. Theor. Biol. 1993, 160, 457–470. [Google Scholar] [CrossRef] [PubMed]
- Tavassoly, I.; Tavassoly, O.; Rad, M.; Dastjerdi, N. Multifractal analysis of Chaos Game Representation images of mitochondrial DNA. In Proceedings of the IEEE Conference: Frontiers in the Convergence of Bioscience and Information Technologies, Jeju City, Korea, 11–13 October 2007; Howard, D., Ed.; IEEE Press: Jeju City, Korea, 2007; pp. 224–229. [Google Scholar]
- Tavassoly, I.; Tavassoly, O.; Rad, M.; Dastjerdi, N. Three dimensional Chaos Game Representation of genomic sequences. In Proceedings of the IEEE Conference: Frontiers in the Convergence of Bioscience and Information Technologies, Jeju City, Korea, 11–13 October 2007; Howard, D., Ed.; IEEE Press: Jeju City, Korea, 2007; pp. 219–223. [Google Scholar]
- Wang, Y.; Hill, K.; Singh, S.; Kari, L. The spectrum of genomic signatures: From dinucleotides to chaos game representation. Gene 2005, 346, 173–185. [Google Scholar] [CrossRef] [PubMed]
- Petoukhov, S.V. The genetic code, 8-dimensional hypercomplex numbers and dyadic shifts. Available online: https://arxiv.org/pdf/1102.3596v11.pdf (accessed on 15 July 2016).
- Petoukhov, S.V. Symmetries of the genetic code, Walsh functions and the theory of genetic logical holography. Symmetry Cult. Sci. 2016, 27, 95–98. [Google Scholar]
- Petoukhov, S.V.; Petukhova, E.S. Symmetries in genetics, Walsh functions and the geno-logical code. In Periodic Collection of Articles: “Symmetry: Theoretical and Methodological Aspects”, Issue 21; Ammosova, N.V., Ed.; Publishing House LLC “Triad”: Astrakhan, Russia, 2016; pp. 79–87. (In Russian) [Google Scholar]
- Petoukhov, S.V.; Petukhova, E.S. Resonances, Walsh functions and logical holography in genetics and musicology. Symmetry Cult. Sci. 2017, 28, 21–40. [Google Scholar]
- Horimoto, K.; Nakatsui, M.; Popov, N. (Eds.) Algebraic and Numeric Biology, 2012 ed.; In Proceedings of the 4th International Conference, ANB 2010, Hagenberg, Austria, 31 July–2 August 2010; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 6479.
- Hornos, J.E.M.; Hornos, Y.M.M. Algebraic model for the evolution of the genetic code. Phys. Rev. Lett. 1993, 71, 4401–4404. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, D.L. The mathematical structure of the genetic code. In The Codes of Life: The Rules of Macroevolution, Biosemiotics; Barbieri, M., Hoffmeyer, J., Eds.; Springer: Dordrecht, The Netherlands, 2008; Volume 1, Chapter 8; pp. 111–152. [Google Scholar]
- Gonzalez, D.L.; Giannerini, S.; Rosa, R. On the origin of the mitochondrial genetic code: Towards a unified mathematical framework for the management of genetic information. Nat. Proc. 2012. [Google Scholar] [CrossRef]
- Dragovich, B. p-Adic structure of the genetic code. NeuroQuantology 2011, 9, 716–727. [Google Scholar] [CrossRef]
- Fimmel, E.; Giannerini, S.; Gonzalez, D.; Strüngmann, L. Dinucleotide circular codes and bijective transformations. J. Theor. Biol. 2015, 386, 159–165. [Google Scholar] [CrossRef] [PubMed]
- Fimmel, E.; Giannerini, S.; Gonzalez, D.; Strüngmann, L. Circular codes, symmetries and transformations. J. Math. Biol. 2014, 70, 1623–1644. [Google Scholar] [CrossRef] [PubMed]
- Petoukhov, S.V. Biperiodic Table of the Genetic Code and Number of Protons; MKC: Moscow, Russia, 2001; p. 258. (In Russian) [Google Scholar]
- Petoukhov, S.V. Matrix Genetics, Algebras of the Genetic Code, Noise-Immunity; Regular and Chaotic Dynamics: Moscow, Russia, 2008; p. 316. (In Russian) [Google Scholar]
- Petoukhov, S.V. Matrix genetics and algebraic properties of the multi-level system of genetic alphabets. Neuroquantology 2011, 9, 60–81. [Google Scholar] [CrossRef]
- Petoukhov, S.V. Symmetries of the genetic code, hypercomplex numbers and genetic matrices with internal complementarities. Symmetry Cult. Sci. 2012, 23, 275–301. [Google Scholar]
- Petoukhov, S.V. Dyadic Groups, Dyadic Trees and Symmetries in Long Nucleotide Sequences. Available online: http://arxiv.org/abs/1204.6247v2 (accessed on 17 January 2013).
- Petoukhov, S.V. The Genetic Code, Algebra of Projection Operators and Problems of Inherited Biological Ensembles. Available online: http://arxiv.org/abs/1307.7882 (accessed on 31 December 2014).
- Petoukhov, S.V.; He, M. Symmetrical Analysis Techniques for Genetic Systems and Bioinformatics: Advanced Patterns and Applications; IGI Global: Hershey, PA, USA, 2010; p. 271. [Google Scholar]
- Karlin, S.; Ost, F.; Blaisdell, B.E. Patterns in DNA and Amino Acid Sequences and Their Statistical Significance; Waterman, M.S., Ed.; Mathematical Methods for DNA Sequences; CRC Press: Raton, FL, USA, 1989. [Google Scholar]
- Gazalé, M.J. Gnomon: From Pharaons to Fractals; Princeton University Press: Princeton, NJ, USA, 1999; p. 280. [Google Scholar]
- Homo Sapiens Chromosome 22 Genomic Scaffold, Alternate Assembly CHM1_1.0, Whole Genome Shotgun Sequence. NCBI Reference Sequence: NW_004078110.1. Available online: http://www.ncbi.nlm.nih.gov/nuccore/NW_004078110.1?report=genbank (accessed on 31 October 2013).
- Stepanyan, I.V.; Petoukhov, S.V. The Matrix Method of Representation, Analysis and Classification of Long Genetic Sequences. Available online: https://arxiv.org/abs/1310.8469v1 (accessed on 31 October 2013).
- Human Chromosomes. Available online: ftp://ftp.ncbi.nih.gov//genomes/H_sapiens/April_14_2003/ (accessed on 14 April 2003).
- Kappraff, J.; Petoukhov, S.V. Symmetries, generalized numbers and harmonic laws in matrix genetics. Symmetry Cult. Sci. 2009, 20, 23–50. [Google Scholar]
- Petoukhov, S.V.; Svirin, V.I. Fractal genetic nets and symmetry principles in long nucleotide sequences. Symmetry Cult. Sci. 2012, 23, 303–322. [Google Scholar]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stepanyan, I.V.; Petoukhov, S.V. The Matrix Method of Representation, Analysis and Classification of Long Genetic Sequences. Information 2017, 8, 12. https://doi.org/10.3390/info8010012
Stepanyan IV, Petoukhov SV. The Matrix Method of Representation, Analysis and Classification of Long Genetic Sequences. Information. 2017; 8(1):12. https://doi.org/10.3390/info8010012
Chicago/Turabian StyleStepanyan, Ivan V., and Sergey V. Petoukhov. 2017. "The Matrix Method of Representation, Analysis and Classification of Long Genetic Sequences" Information 8, no. 1: 12. https://doi.org/10.3390/info8010012
APA StyleStepanyan, I. V., & Petoukhov, S. V. (2017). The Matrix Method of Representation, Analysis and Classification of Long Genetic Sequences. Information, 8(1), 12. https://doi.org/10.3390/info8010012




