Ultra-Reliable Link Adaptation for Downlink MISO Transmission in 5G Cellular Networks

Abstract

This paper discusses robust link adaptation for a downlink precoded multiple input single output system, for guaranteeing ultra-reliable (99.999%) transmissions to mobile users (e.g., slowly moving machines in a factory) served by a small cell network. The proposed technique compensates the effect of inaccurate channel state information (CSI) caused by user mobility, as well as the variation of precoders in the interfering cells. Both of these impairments translate into instability of the received signal-to-noise plus interference ratios (SINRs), and may lead to CSI mispredictions and potentially erroneous transmissions. We show that, by knowing the statistics of the propagation channels and the precoders variations, it is possible to compute a backoff that guarantees robust link adaptation. The backoff value is based on the statistics of realized SINR, and is consequently used to adapt the transmissions according to current channel state. Theoretical analysis accompanied by simulation results show that the proposed approach is suitable for attaining 5G ultra-reliability targets in realistic settings.

1. Introduction

The evolution of mobile communication systems has culminated in the dawn of a 5G vision, which envisages providing services, both human and machine centric, with diverse quality of service (QoS) requirements and applications [1]. In order to address these challenges, a number of targets have been identified for 5G, to be achieved in 2020 time-frame. The foremost is enhancing existing mobile data volume by a factor of 1000×, which is to be achieved by addition of new spectrum, enhancing spectral efficiency of existing systems, greater number of antennas, and smaller cells. In contrast, new and significantly more challenging targets stem from the application of various wireless technologies to machine-centric domains such as machine type communications (MTC) or machine to machine communications. It comprises of two main paradigms—massive MTC and mission-critical MTC. In massive MTC, the idea is to connect a large number of machines such as sensors, actuators, and other devices to a common platform, paving the way for Internet of Things. Most of these machines will likely be low-cost, requiring low-data volumes and energy consumption, but long deployment periods. On the other hand, mission critical MTC scenarios are usually characterized by very low latency, high reliability, and high availability. This has led to an emergence of new use cases, which often consist of very stringent requirements in terms of latency, reliability, and availability, collectively referred to as ultra-reliable communications (URC) in 5G systems. URC is primarily envisioned to be applied at short time-scales, where it has a multitude of applications such as vehicle-to-vehicle communication and smart grid control.

A target envisioned for URC in 5G is 99.999% reliability with 2 ms latency [2]. This presents novel challenges at multiple levels, and requires complete rethinking of system design approaches. URC networks differ from conventional mobile broadband systems, in that the focus is not on the peak and median performance, but on the situation of lower 0.00001 percentile of users. URC network design is essentially based on the analysis of worst case scenarios, and the preventive measures one can take to avert them.

The concept of reliability pertaining to 5G systems can be defined in many ways, depending on the use case at hand. In order to develop a systematic framework inclusive of all use cases, ultra-reliability can essentially be understood as a network property that constitutes three dimensions [3,4]: availability, reliability, and latency. The network is unavailable when it is undergoing an unscheduled downtime. The main factors that impact availability include hardware/software faults, human errors, natural disasters, depletion of network resources due to overloading, etc. On the other hand, latency is an end-to-end network design issue, and its enhancement may require changes in architecture and procedures at different layers. It can be improved by reducing delays emanating from propagation, processing, large packet sizes, and queuing. Finally, reliability can be considered as the probability of successful transmission across a wireless link, given that the system is available, and is able to meet the minimum latency requirements.

A multitude of factors contribute to reliability at a network level. In particular, mobility related changes in the channels of users and existence of multiple nodes in the network competing for the same resources, may lead to a significant increase in problem complexity. Accordingly, impairments such as interference, inaccuracy in channel state information (CSI), and link adaptation errors cause loss in reliability. These issues can be addressed via an efficient management of network radio resources across multiple degrees of freedom (e.g., time, space, frequency). For instance, in [5], resource allocation is considered to mitigate interference, and guarantee a network-wide target data rate to the users. It is worth noting that high availability and reliability, as well as low latency are needed to ensure URC, but the relative significance of these may vary across use cases.

In this work, we address link adaptation from an URC perspective. In adaptive modulation and coding (AMC) protocols, the transmission rate is selected based on a channel quality indicator (CQI), which is a part of the CSI measured by the intended receiver, and fed back to the transmitter. However, if the channel undergoes fading, the measured CSI becomes outdated due to the unavoidable feedback and processing delays. The channels at the time instant of transmission, can thus differ substantially from the measured channels. With outdated CSI, the outage performance is severely degraded, and the channel capacity is affected [6,7]. In addition to mobility induced variations in the channels, the use of radio resources in interfering cells may also change between the measurement and the transmission instants. For example, changes in precoding may change the interference [8]. In order to ensure that a transmission is received within the tight latency window required by URC, robust link adaptation is needed. Consequently, transmissions can be received with very high reliability.

1.1. Related Work

General aspects of reliability and availability for communication networks have been studied in a number of works. The problem formulation, proposed methods and algorithms are often network specific. In particular, reliable routing and data delivery protocols have been studied quite extensively for mobile ad hoc networks [9], and wireless sensor networks [10].

In the context of 5G networking, the concept of ultra-reliability is, however, different in terms of scope, motivation, and requirements. From a 5G perspective, the area is in its infancy, and existing works mostly discuss ideas at a conceptual level, and propose different use cases which may benefit from ultra-reliability [1]. A detailed exposition is given in [2], which proposes a reliable service composition framework for guaranteeing a high level of reliability—the probability that a certain amount of data is transmitted in the given time frame. Identified sources of unreliability include resource depletion and interference. In [11], an availability indicator parameter is introduced as a key enabler for ultra-reliability in 5G, where availability is defined in terms of absence or presence of link reliability at the time of transmission.

In cellular packet data systems, hybrid automatic repeat requests (HARQ) are utilized in conjunction with AMC to enable robustness [12,13]. A certain probability of retransmissions is desirable, when maximizing the system throughput with a given reliability target, see e.g., [14,15]. In order to achieve near-optimal performance, open-loop link adaptation is a viable option [16], where the AMC thresholds are tuned to keep a desirable retransmission probability. However, when targeting high reliability with strict latency required by URC, one cannot solely rely on HARQ. To make clever link adaptation decisions, it is beneficial to know the statistics of the channel, or the signal-to-interference-plus-noise ratio (SINR), of the realized transmission conditioned on the measured SINR. Next, by selecting a suitable backoff, a suitable modulation and coding scheme can be chosen, which support a target outage probability. An example of such SINR-statistics aware link adaptation related to interferer precoding variation can be found in [17].

1.2. Contributions

In this paper, the idea is to enable robust link adaptation, so that user data rates can be supported with the desired reliability. In order to decode transmissions successfully within delay constraints, a transmission rate has to be selected such that a codeword can be decoded with high reliability. Without loss of generality, we focus on achieving a reliability target of 99.999%, and leave out the availability considerations.

We investigate SINR variations caused by the mobility related changes in the wanted and interfering channels, as well as interferer precoders. It is assumed that the channels are Rayleigh fading with Jakes’ Doppler spectrum [18], and single stream precoding from $N_T$ transmit antennas is used. Link adaptation is based on perfect knowledge of the instantaneous channel state at the time of measurement, channel statistics, and the correlation between measured and realized channels. Using this information we devise robust link adaptation, which can support URC targets. A transmission rate is selected so that the channel capacity at the time of transmission supports the selected rate with high probability. We find that fading of the link between transmitter and receiver, even with moderate mobility, dominates over fading of interference, and interference variability. Moreover, knowledge of channel and interference statistics, as well as the instantaneous channel and interference realization, is invaluable for robust link adaptation for URC.

1.3. Notation and Organization

Vectors are represented using boldface lower-case letters. The conjugate transpose is represented by ${(.)}^H$, and $|.|$ denotes the absolute value. A probability density function (PDF) for random variable (RV)x is represented by $f_X\left(x\right)$ and the corresponding cumulative distribution (CDF) is $F_X\left(x\right)$. Probability of a given event θ is denoted by $\mathrm{P}\left(\theta \right)$. The non-central chi square distribution with non-central parameter δ and degree of freedom (DoF) n is denoted by ${\chi }^2(x;n;\delta )$. The subscripts 0 and τ denote the variables at measurement phase and at a given transmission realization after $t=\tau$ ms from measurement, respectively.

The rest of the paper is organized as follows: Section 2 discusses the system model. Section 3 introduces the sources of SINR variability and the related statistical distributions. User mobility and changes in other-cell precoding are discussed. Backoff selection for robust link adaptation is considered. Finally, conclusions are drawn in Section 4.

2. System Model

A downlink multi-cell system is considered, where a number of base stations are deployed to serve mobile terminals (users). The association of users to base stations is fixed and a priori known, so that each user is served by a unique base station. The total bandwidth is shared by all cells in a universal frequency reuse manner, and the intra-cell resource allocation is orthogonal. Each base station has $N_T$ transmit antennas, and users have a single receive antenna. The multiple transmit antennas at base stations are used for single-stream beamforming towards their respective users.

2.1. SINR Estimation

Link adaptation is based on the measurement performed by the intended receiver at a time $t=0$. Known pilot symbols $z_k$ are transmitted with at least $N_T$ orthogonal precoding vectors ${\mathbf{w}}_k\in {\mathbb{C}}^{N_T\times 1}$, for $k=1,\dots ,N_T$. We assume that all of these transmissions happen essentially simultaneously. With J transmissions from known interferers, the signal received at the user of interest at $t=0$ for pilot transmission k

$$y_{0,k}={\mathbf{h}}_0{\mathbf{w}}_{0,k}{z}_k+{\displaystyle \sum _{j=1}^J}{\mathbf{h}}_{0,j}{\mathbf{v}}_{0,j}{x}_j+n$$

(1)

where ${\mathbf{h}}_0\in {\mathbb{C}}^{1\times N_T}$ is the channel gain vector for the desired transmission, ${\mathbf{h}}_{0,j}$ are the interfering channel vectors from transmitter j to the user of interest, and ${\mathbf{v}}_{0,j}\in {\mathbb{C}}^{N_T\times 1}$ are the precoders applied by the interfering transmitters, all at the time of measurement $t=0$, on the time-frequency resource used for pilot transmission k. Here, $x_j$ are the transmit symbols on jth transmission. All transmitted symbols are assumed to be of unit average energy, and all precoding vectors are assumed unit norm. Moreover, all elements in the channel vectors ${\mathbf{h}}_0$ and ${\mathbf{h}}_{0,j}$ are assumed to be drawn from independent complex Gaussian processes with zero mean and variance $S_{\mathrm{ave}}$ and $I_{\mathrm{ave},\mathrm{j}}$, respectively. These variances carry information of the path losses of the signals. The channel realizations developed under fading processes after the measurement are drawn from the same distribution as the channels at a given measurement instance, and are conditioned on the measurement results. The contribution of interference from other than the J known sources, as well as additive white Gaussian noise (AWGN) is n, with spectral density $N_0$.

We assume multiple orthogonal pilot transmissions of the form Equation (1) extending over multiple transmissions within a coherence time and bandwidth of the channels. This enables the receiver to reliably estimate the channel ${\mathbf{h}}_0$. Canceling the transmissions of the known pilot signals over the estimated channels from signals of Equation (1), interference plus noise powers can be estimated, and accordingly SINRs. Finally, we assume that the receiver knows the pilot signals of the J known interferers as well. In a communication frame at measurement time $t=0$, there would thus be received signals of the type Equation (1) for the pilots of the J known interferers, making it possible to separate the contributions of the interferers to interference plus noise power at the time of measurement. Collecting statistics over longer periods, it is possible to estimate characteristics of the statistical distributions of the channels. Here, we assume these statistics are perfectly known. Collecting such statistics would be possible in environments where the channels remain wide sense stationary for extended periods of time, e.g., in factory environments [19].

For a forthcoming transmission to the user of interest, a precoder ${\mathbf{v}}_0$ is selected, either based on the measurements at time $t=0$, or by some other means. If the transmitter selects the precoder, it is informed to the user. As a result, we have an estimated SINR

$${\gamma }_0=\frac{|{\mathbf{h}}_0{\mathbf{v}}_0{|}^2}{{\sum }_{j=1}^J{\left|{\mathbf{h}}_{0,j}{\mathbf{v}}_{0,j}\right|}^2+N_0}$$

(2)

for a forthcoming transmission. If the precoder is selected based on the user channel only, a typical choice would be to take ${\mathbf{v}}_0$ to be a normalized version of ${\mathbf{h}}_0^H$ , or a quantized version thereof. If the precoder is known to the user, it may be e.g., a common precoder which is used to serve all users in the cell in order to stabilize inter-cell interference. The J interfering transmissions are assumed to be independent. This channel model extends readily to a situation where the interferer is a higher rank transmission. As rank-1 interference is the worst [17], we concentrate on it in the following discussion.

2.2. SINR Realized at Time of Transmission

The measured SINR ${\gamma }_0$ is used in link adaptation to choose an applicable transmission rate. For this, the measurement result is fed back by the receiver to the transmitter. There are delays in feedback, and in processing at the measuring end, and the transmitter. Accordingly, when the channel is used for a data transmission, both the propagation channel carrying the wanted signal component, and the channels of the interferers have changed. In addition, the precoders used in the interfering base stations may be changed according to their scheduling decisions. Accordingly, the SINR experienced by the realized transmission differs from ${\gamma }_0$.

The received signal for a data transmission at a transmission instance which is delayed τ seconds from the measurement is

$$y_{\tau }={\mathbf{h}}_{\tau }{\mathbf{v}}_{\tau }x+{\displaystyle \sum _{j=1}^J}{\mathbf{h}}_{\tau ,j}{\mathbf{v}}_{\tau ,j}{x}_j+n$$

(3)

where ${\mathbf{h}}_{\tau }$ and ${\mathbf{h}}_{\tau ,j}$ are the realized channel coefficients for the desired transmission and the interferers between the intended transmitters and the receiver, respectively, at time τ. The corresponding transmitted symbols are denoted by x and $x_j$. The precoders ${\mathbf{v}}_{\tau ,j}$ applied on the interferers may be the same as the ones during the measurement, or they may be changed according to scheduling decisions. Therefore, the precoder ${\mathbf{v}}_{\tau }$ may either be ${\mathbf{v}}_0$, or a precoder selected on the basis of scheduling decisions. We assume that the precoder of the wanted signal transmission remains the same as the precoder used at SINR estimation.

We assume that ${\mathbf{h}}_{\tau }$ is a random variable drawn from the same distribution as ${\mathbf{h}}_0$. These two channels are correlated for short delays τ. The effect of channel dispersion due to Doppler shift can be modeled by [20]

$${\mathbf{h}}_{\tau }=\rho {\mathbf{h}}_0+\sqrt{1-{\rho }^2}\tilde{\mathbf{h}}$$

(4)

where ${\mathbf{h}}_{\tau }$ is the channel realized under transmission, and ${\mathbf{h}}_0$ is the corresponding measured value. The estimation error $\tilde{\mathbf{h}}$ is an independent sample from the same complex channel distribution as of ${\mathbf{h}}_0$ and ${\mathbf{h}}_{\tau }$. Assuming Jakes’ model, the normalized auto-correlation coefficient of a Rayleigh faded channel with motion at a constant velocity is $\rho =J_0\left(2\pi f_{D,max}\tau \right)$ [18]. The maximum Doppler shift is $f_{D,max}=2\frac{v}{c}f$, and v, c and f are the velocity of the user, velocity of light, and the carrier frequency, respectively. Here, $J_0(·)$ is a zeroth-order Bessel function of the first kind, and delay τ is measured in seconds. We remark that effects of imperfect channel estimation lead to correlation model of the same form as Equation (4), see [21]. In that case, the correlation ρ would depend, not on τ, but on SINR, and the channel estimation algorithm. Accordingly, our model extends to imperfect channel estimation as well, with an appropriate interpretation of ρ for each measured channel.

2.3. Robust Link Adaptation

We assume a family of AMC schemes, consisting of a virtually continuous set of possible rates r for packet transmissions. When transmitted in a block fading channel with SINR γ, a packet error probability (PEP) function ${\mathrm{P}}_{\mathrm{e}}(r,\gamma )$ characterizes this family. This function is monotonously growing in r, and monotonously decreasing in γ. When blocks are sufficiently short such an AMC scheme may be coupled with a retransmission protocol which is able to operate within the target URC latency, see [22].

Based on the measured ${\gamma }_0$, and knowledge of channel statistics, we construct a probability density $f\left({\gamma }_{\tau }\right|{\gamma }_0)$. When rate r is used, the expected probability of packet error is ${\overline{\mathrm{P}}}_{\mathrm{e}}\left(r\right)=\int {\mathrm{P}}_{\mathrm{e}}(r,\gamma )f\left(\gamma \right|{\gamma }_0)d\gamma$. If we could use infinitely long codewords, ${\mathrm{P}}_{\mathrm{e}}(r,\gamma )$ would be a step function at a threshold value ${\gamma }_t\left(r\right)$.

When targeting an outage probability ${\mathrm{P}}_{\mathrm{out}}$, maximizing r with infinitely long codewords would lead to the outage capacity. URC frame lengths are foreseen to be shorter than in LTE. We are interested in indoors factory settings, however, where coherence bandwidths of tens of MHzs are reported [19]. Accordingly, codewords may be of sizeable length in scenarios of interest. When extending to short packets, outage capacity may be an inaccurate performance metric [23]. Knowing the accurate ${\mathrm{P}}_{\mathrm{e}}(r,\gamma )$ and $f\left(\gamma \right|{\gamma }_0)$ would allow finding the maximum r with the given outage probability.

Here, for simplicity, we assume step function ${\mathrm{P}}_{\mathrm{e}}(r,\gamma )$, so that maximizing the rate given ${\mathrm{P}}_{\mathrm{out}}$, can be achieved by first finding a threshold SINR ${\gamma }_t$ so that ${\int }_0^{{\gamma }_t}f\left(\gamma \right|{\gamma }_0)d\gamma ={\mathrm{P}}_{\mathrm{out}}$, and then finding the r which guarantees error free transmission at this ${\gamma }_t$. Accordingly one makes a backoff of $b={\gamma }_0/{\gamma }_t$ related to the link adaptation based on ${\gamma }_0$. Then one can guarantee that irrespectively of the SINR variability, the transmission can be reliably received with a very high probability. We consider URC outage probability ${\mathrm{P}}_{\mathrm{out}}={10}^{-5}$, throughout, i.e., a reliability 99.999%.

3. Sources of SINR Variability

There are a number of sources of SINR/interference variability that can jeopardize reliability in a wireless/cellular network. These include the following:

• Variations in wanted signal channel between time of measurement and time of transmission
• Interference variability caused by changes in the channels of interferers
• Interference variability caused by radio resource management (RRM) in interfering cells (Changing multi-antenna transmissions, channel activity, power control, uplink user scheduling)

We consider all of these separately and jointly. SINR/interference variations caused by RRM may be stabilized by applying persistent RRM strategies. For example, downlink precoded multi-antenna transmissions, where the precoders that are not user specific but frequency resource specific and optimized for a population of users, may be considered. As a result, the SINR misprediction due to 3 partially vanishes. Not much can be done to remove the variability due to 1 and 2, however, if the user and/or the channel is mobile.

To address the impairments caused by 1-3 for URC, we consider robust link adaptation where the SINR statistics of the realized transmission conditioned on the measured SINR are known.

3.1. Changes in Wanted Signal Power

The time selectivity of the desired channel induces SINR variability at the receiver, and is discussed next. Let us assume that the interference experienced by the user of interest remains same until the transmission is realized. The distribution of the signal power $S=|{\mathbf{h}}_{\tau }{\mathbf{v}}_0{|}^2$ is of our interest. From Equation (4) it can be rewritten as

$$S={\left|\rho {\mathbf{h}}_0{\mathbf{v}}_0+\sqrt{1-{\rho }^2}\tilde{\mathbf{h}}{\mathbf{v}}_0\right|}^2.$$

(5)

Then, for a given channel measurement ${\mathbf{h}}_0$ and the precoder used ${\mathbf{v}}_0$, RV, S can be modeled as a magnitude of a sum of two squared independent Gaussian RVs with equal variance $\alpha =(1-{\rho }^2)\frac{S_{\mathrm{ave}}}{2}$, and means ${\mu }_{\Re }=\rho \Re \left\{{\mathbf{h}}_0{\mathbf{v}}_0\right\}$ and ${\mu }_{\Im }=\rho \Im \left\{{\mathbf{h}}_0{\mathbf{v}}_0\right\}$. Note that the probability distribution of the inner product of a channel vector $\mathbf{h}$ with independent and identically distributed (i.i.d) Gaussian elements and an arbitrary unitary vector $\mathbf{v}$ equals the distribution of an element of the channel vector $\mathbf{h}$. Therefore, the PDF of the signal power $f_S\left(s\right)$ can be characterized by a non-central chi-square distribution with two DoF, and the non-centrality $\delta =({\mu }_{\Re }^2+{\mu }_{\Im }^2)/\alpha =\frac{2{\rho }^2}{(1-{\rho }^2)}\frac{S_0}{S_{\mathrm{ave}}}$. Here, $S_0={\left|{\mathbf{h}}_0{\mathbf{v}}_0\right|}^2$ is the measured signal power and $S_{\mathrm{ave}}$ is the average signal power at measurement. Note that this assumes that we indeed know both $S_0$ and $S_{\mathrm{ave}}$, i.e., the measured signal power and the average signal power, together with the signal statistics. That is, we know precisely the current fading state of the signal. The PDF of the signal power is now

$$f_S(s\mid {\mathbf{h}}_0,{\mathbf{v}}_0,S_{\mathrm{ave}})=\frac{1}{2\alpha }\mathrm{Exp}\left\{-\frac{s/\alpha +\delta }{2}\right\}{I}_0\left(\sqrt{\frac{\delta s}{\alpha }}\right)$$

(6)

where $I_0(·)$ is the modified Bessel function of the first kind. The corresponding CDF is given by $F_S(s\mid {\mathbf{h}}_0,{\mathbf{v}}_0,S_{\mathrm{ave}})=1-Q_1(\sqrt{\delta },\sqrt{s/\alpha })$. The SINR variability caused by changing desired transmission signal power can be visualized from CDF, and the realized SINR is ${\gamma }_{\tau }=\frac{S}{I_0+N_0}$ where $I_0={\sum }_{j=1}^J{\left|{\mathbf{h}}_{0,j}{\mathbf{v}}_{0,j}\right|}^2$ is the measured interference power which is considered fixed for the given transmission realization. Now, the outage probability becomes $\mathrm{P}\left({\gamma }_{\tau }<{\gamma }_t\right)$. The URC outage probability target is achieved at a SINR threshold ${\gamma }_t$, and the required backoff to enable robust link adaptation is $b=\frac{{\gamma }_0}{{\gamma }_t}$.

The outage probability can be further simplified to

$$\begin{array}{cc}\hfill \mathrm{P}\left(\frac{S}{I_0+N_0}<{\gamma }_t\right)& =F_X\left({\gamma }_t(I_0+N_0)\right)\hfill \\ & \hfill =1-Q_1\left(\sqrt{\frac{2{\rho }^2}{(1-{\rho }^2)}\frac{S_0}{S_{\mathrm{ave}}}},\sqrt{\frac{2}{(1-{\rho }^2)b}\frac{S_0}{S_{\mathrm{ave}}}}\right)\end{array}$$

(7)

where $Q_M(a,b)$ is the Marcum-Q function, here with $M=1$ [24].

We consider a delay between measurement and transmission of $\tau =1$ ms, in accordance with the URC latency targets. For a carrier frequency $f=3.6$ GHz, user velocities $v\approx 8$, 7 and 5 km/h would lead to auto-correlation coefficients $\rho \approx 0.97$, $0.98$ and $0.99$, respectively.

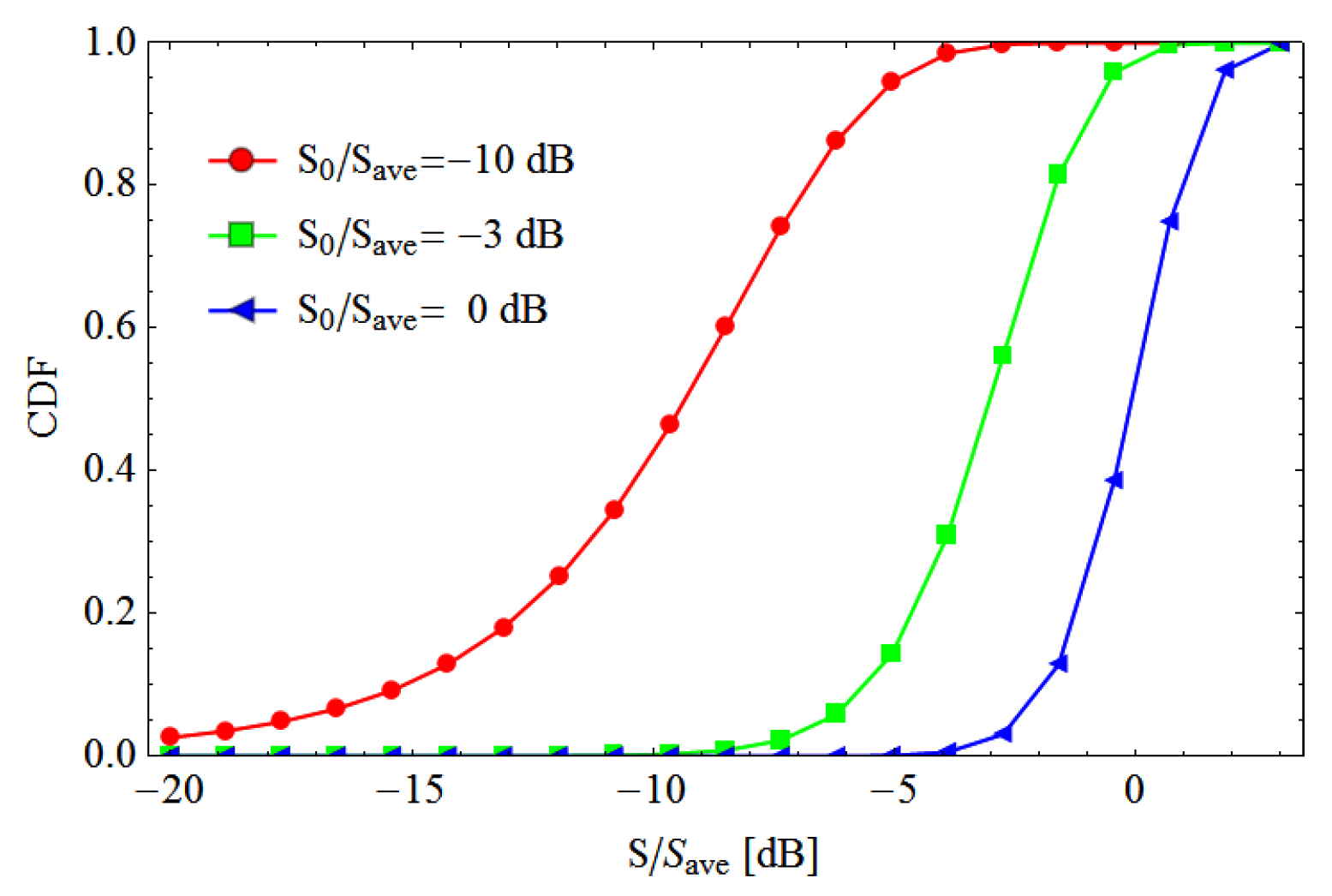
Figure 1 demonstrates how the time selectivity of a channel affects the realized transmission. We consider three situations. In one, the channel of the desired transmission during the measurement is faded ($S_0/S_{\mathrm{ave}}=-10$ dB), in the second it is slightly faded ($S_0/S_{\mathrm{ave}}=-3$ dB), whereas in the third it is not faded ($S_0/S_{\mathrm{ave}}=0$ dB). In the faded state, when the measured signal power of the desired transmission is 10 times smaller than the average, the distribution of the realized signal power is wide, and the probability of dropping into deeper fade increases for the transmission instant at time $t=\tau$. Hence, the required backoff is significantly larger when the channel at the time of measurement is faded as compared to the situation where the channel at the measurement is on an average level, and $S_0/S_{\mathrm{ave}}=0$ dB.

Note that the auto-correlation coefficient statistically characterizes the level of correlation between the measured and realized channels. When the channel (at a given channel instant) is in faded state, and $\rho \approx 1$, the probability of getting to a deeper fade is significant.

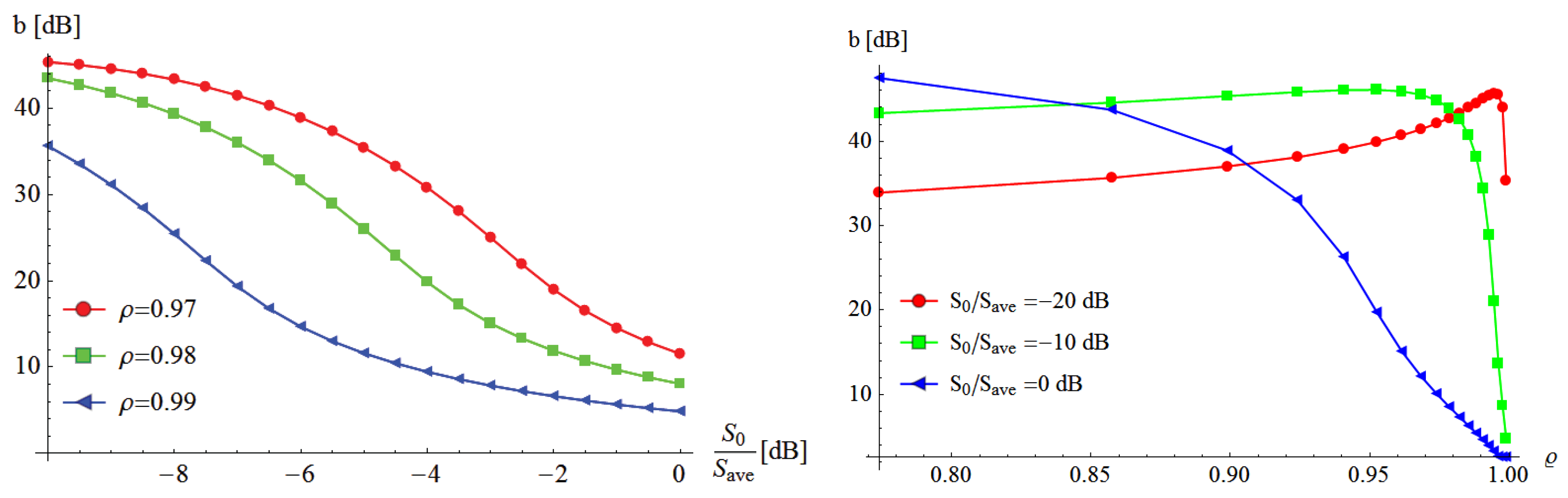
Figure 2 left half shows how the required backoff b (in dB) varies with relative measured signal power $\frac{S_0}{S_{\mathrm{ave}}}$ for three different channel auto-correlation coefficients $\rho =\{0.97,0.98,0.99\}$. If the measured transmission power is in the same order of the average transmission power, i.e., when the measured channel is in a typical fading state, the required backoff is relatively small. However, when the measured signal is in a fade, extreme backoffs are required to provide ultra-reliability. This is a consequence of the Rayleigh fading statistics used here, where arbitrarily deep fades have finite probability.

The right half Figure 2 shows the backoff as a function of ρ. With zero correlation, the wanted signal power at outage is $S_{\mathrm{out}}/S_{\mathrm{ave}}=-50$ dB, and the backoff thus is directly $S_0/S_{\mathrm{out}}$. Here, $S_{\mathrm{out}}$ represents the instantaneous signal power S at URC outage. When the measured channel was in a typical fading state, with $S_0/S_{\mathrm{ave}}=0$ dB, the backoff is $b=50$ dB at $\rho =0$, shrinking monotonously to $b=0$ dB at $\rho =1$. For smaller $S_0/S_{\mathrm{ave}}$, i.e., when the measured channel was faded, the backoff first grows with increasing ρ. This is a consequence of increasing correlation making it more probable that the signal remains in a faded state, and goes into deeper fading. However, after a threshold, the backoff starts shrinking, going to $b=0$ at $\rho =1$. For example, for $S_0/S_{\mathrm{ave}}=-20$ dB, the backoff at $\rho =0$ would be $b=30$ dB, from where it grows to a value of $b\approx 46$ dB at $\rho =0.995$, before shrinking to zero.

3.2. Changes in Interfering Channels

In addition to changes in the wanted signal, mobility also causes changes in the interfering signals. To obtain the statistics of the SINR, the distribution of total interference power is essential. We consider the interference experienced at the receiver of interest, produced by J independent interference sources. Here, we assume that there is no change in the interference precoder from the time of measurement to the time of transmission. The realized interference power then is

$$I_{\tau }={\displaystyle \sum _{j=1}^J}{\left|{\mathbf{h}}_{\tau ,j}{\mathbf{v}}_{0,j}\right|}^2$$

(8)

where the realized channel ${\mathbf{h}}_{\tau ,j}$ follows the autocorrelation model Equation (4). Note that the transmission power level is assumed to be absorbed in the channels. Then the total interference power can be represented as a linear combination of magnitude squared of J mutually independent complex Gaussian RVs with non-zero mean and unit variance, $I_{\tau }={\sum }_{j=1}^J{\alpha }_j{\left|X_j\right|}^2$ where ${\alpha }_j=(1-{\rho }^2)\frac{I_{\mathrm{ave},\mathrm{j}}}{2}$. The RV $X_j$ is again characterized by complex Gaussian distribution with mean $\frac{\rho }{\sqrt{1-{\rho }^2}}\sqrt{\frac{2I_{0,j}}{I_{\mathrm{ave},\mathrm{j}}}}$ where $I_{0,j}={\left|{\mathbf{h}}_{0,j}{\mathbf{v}}_{0,j}\right|}^2$. The real and imaginary components of RV $X_j$ are Gaussianly distributed with unit variance and mean ${\mu }_{\Re }=\frac{\rho }{\sqrt{1-{\rho }^2}}\frac{\Re \left\{{\mathbf{h}}_{0,j}{\mathbf{v}}_{0,j}\right\}}{\sqrt{I_{\mathrm{ave},\mathrm{j}}/2}}$ and ${\mu }_{\Im }=\frac{\rho }{\sqrt{1-{\rho }^2}}\frac{\Im \left\{{\mathbf{h}}_{j,0}{\mathbf{v}}_{j,0}\right\}}{\sqrt{I_{\mathrm{ave},\mathrm{j}}/2}}$, respectively. Hence, $|X_j{|}^2$ can be modeled as a non-central chi square distribution with two degrees of freedom, and non-centrality ${\delta }_j={\mu }_{\Re }^2+{\mu }_{\Im }^2$. In the subsequent analysis, we treat this as the sum of two real RVs. Without loss of generality, we can consider these two to have mean $\sqrt{{\delta }_j/2}$, not ${\mu }_{\Re }$ and ${\mu }_{\Im }$, i.e., we distribute the mean evenly across the real and imaginary components of $X_j$. This is done for ease of notation and analysis, and is precise due to the underlying circular symmetry.

To characterize the distribution of total interference, we use an expansion discussed in [25]. The probability density function of ${\sum }_{i=1}^n{\alpha }_i{\left(Z_i+{\delta }_i\right)}^2$ where $Z_1,Z_2,...,Z_n$ are mutually independent standard normal random variables, is given by

$$f_n(\mathbf{ff},\mathbf{ffi},y)={\displaystyle \sum _{k=0}^{\infty }}{a}_k{\beta }^{-1}{\chi }^2\left(\frac{y}{\beta };n+2k;\Delta \right)$$

(9)

where ${\chi }^2(y/\beta ;n+2k;\Delta )$ is a non-central chi-square distribution, with $n+2k$ DoF and non-centrality parameter $\Delta ={\sum }_{i=1}^n{\delta }_i^2$. The parameter $\beta >0$ can be chosen at will. Applying Equation (9) to the distribution of the total interference, the PDF can be expressed as

$$f_I\left(i_{\tau }\right)={\displaystyle \sum _{n=0}^{\infty }}{a}_n{\beta }^{-1}{\chi }^2\left(\frac{i_{\tau }}{\beta };2(J+n),\Delta \right)$$

(10)

Here, the non-centrality is $\Delta ={\sum }_{j=1}^J\frac{2{\rho }^2}{(1-{\rho }^2)}\frac{I_{0,j}}{I_{\mathrm{ave},j}}$, where $I_{0,j}={\left|{\mathbf{h}}_{0,j}{\mathbf{v}}_{0,j}\right|}^2$ is the measured interference power of the jth interferer, and the average interference power of interferer j is $I_{\mathrm{ave},j}$. The multiplicative coefficients $a_n$ can be derived from a recurrence formula in [26], and $\beta >0$ can be appropriately selected for fast convergence. In Appendix A, it is argued that a choice guaranteeing convergence is

$$\beta =\frac{2{\alpha }_{\max }{\alpha }_{\min }}{{\alpha }_{\max }+{\alpha }_{\min }}$$

(11)

where ${\alpha }_{min}$ and ${\alpha }_{max}$ are the minimum and maximum values of ${\left\{{\alpha }_i\right\}}_1^J$.

In practice, some of the interference signals may be relatively small when compared to some others ($I_{0,j}/\max \left\{I_{0,j}\right\}<0.1$). This may lead to extremely slow convergence of the series Equation (10), even with an optimal selection of β, for details see Appendix A. A Gaussian approximation of the interference power distribution is not optimal. For URC operation, we are especially interested in the tail of the total interference distribution, which a Gaussian approximation would not capture. Instead, the large fluctuations of the distribution Equation (10) can be treated with a moment matching non-central chi-square approximation. The interference powers of the weak interferers is added to the strongest interferer, and moment matching is applied to obtain an equivalent distribution model [27].

For the total realized interference in Equation (8), the kth cumulant is

$${\kappa }_k=2^{k-1}(k-1)!\left[{\displaystyle \sum _{j=1}^J}{\alpha }_j^k+k{\displaystyle \sum _{j=1}^J}{\alpha }_j^k{\delta }_j\right]$$

(12)

A non-central chi-square approximation is derived such that the first two cumulants, the mean ${\kappa }_1$ and the variance ${\kappa }_2$ equal the corresponding statistics of the total realized interference power. The non-centrality parameter and the DoF of the chi-square approximation ${\chi }^2(x;\tilde{J};\tilde{\Delta })$ can be directly obtained from $\tilde{J}=2{\kappa }_1-{\kappa }_2/2$ and $\tilde{\Delta }={\kappa }_2/2-{\kappa }_1$. To achieve more accuracy at the tail of the distribution, the first four cumulants are considered. The parameters $\tilde{\Delta }$ and $\tilde{J}$ are determined so that the skewnesses (${\kappa }_3$) of the actual distribution and the approximation are equal and the difference between the kurtoses (${\kappa }_4$) of two distributions is minimized [27]. If $s_1^2>s_2$, the approximation is characterized by $\tilde{\Delta }=s_1{a}^3-a^2$ and $\tilde{J}=a^2-2\tilde{\Delta }$, with $a=1/(s_1-\sqrt{s_1^2-s_2})$. Else, if $s_1^2\le s_2$, $\tilde{\Delta }=0$ and $\tilde{J}=a^2$ with $a=1/s_1$. Here, $s_1={\kappa }_3/{\kappa }_2^{3/2}$ and $s_2={\kappa }_4/3{\kappa }_2^2$. The proposed method in [27], shows much smaller approximation errors for the model used in Equation (10), compared to Pearson’s method [28].

Figure 3 shows the probability distributions of the total interference power, and its moment matching chi-square approximation. The figure on the left side depicts theoretical probability density Equation (10) for $J=3$ independent interference sources together with a simulated Monte Carlo realization of the distribution, whereas the figure on the right illustrates moment matching approximation together with a Monte Carlo simulation for both approximations. The approximation with first four cumulants is especially good for the tail of the distribution. It is tight to the very high, and improbable interferences, that are of interest when addressing URC.

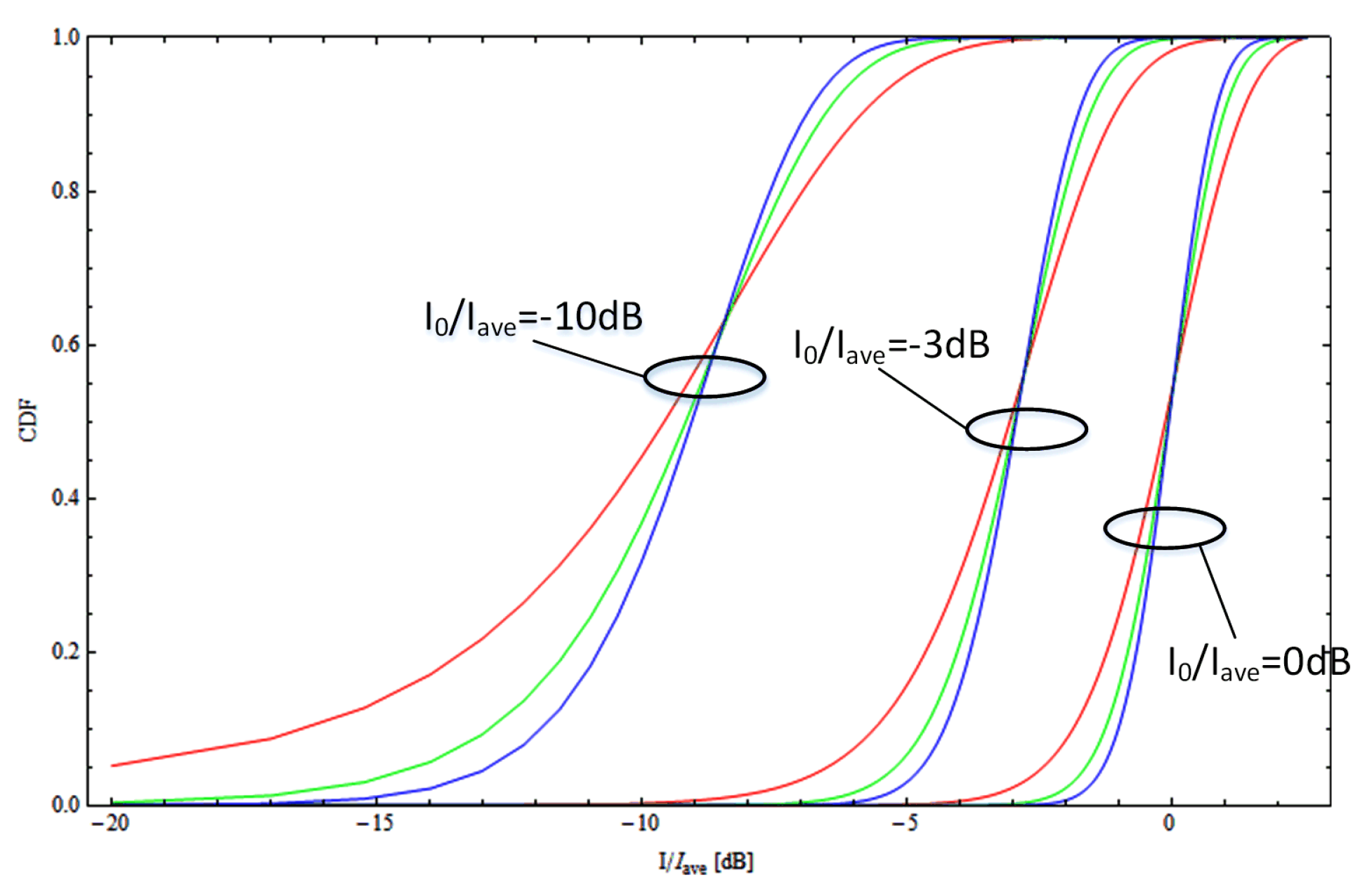
Figure 4 shows CDFs of realized total interference powers when there are $J=1$, 2, 3 independent interferers. The measured total interference $I_0={\sum }_j{I}_{0,j}$ is set to $0,-3,-10$ dB, as compared to the average total interference $I_{\mathrm{ave}}={\sum }_j{I}_{\mathrm{ave},j}$. We assume that the average interference power is the same for all the individual interferers. When there are $J=2$ interferers, the measured interference power ratio between the two is assumed to be $2/3$, $1/3$, whereas for $J=3$ interferers, the ratios of measured interference powers is $1/2$, $1/3$, $1/6$. Note that here, just as in the case of the wanted signal, we assume that we know both the measured power and the average power, independently for all the J interferers. The number of interferers has a great impact on backoff selection. The distribution becomes wider with a decreasing number of interferers.

We proceed by considering the SINR variability caused by interference channel variability only. It is assumed that the measured signal power of the desired transmission, and the precoders on both the desired channel and interferers remain same from the time of measurement to the time τ of transmission. Then, the outage probability with backoff $b={\gamma }_0/{\gamma }_t$ becomes

$$\mathrm{P}\left({\gamma }_{\tau }<{\gamma }_t\right)=1-F_I\left(b(I_0+N_0)-N_0\right)$$

(13)

where $I_0={\sum }_{j=1}^J{I}_{0,j}$ is the total measured interference power, and the CDF of the total interference power is obtained from Equation (10) as

$$F_I\left(i\right)={\displaystyle \sum _{n=1}^{\infty }}{a}_n\left(1-Q_{J+n}\left(\sqrt{\Delta },\sqrt{\frac{i}{\beta }}\right)\right).$$

(14)

For URC, the required backoff can be evaluated at $F_I\left(i\right)=0.99999$ point.

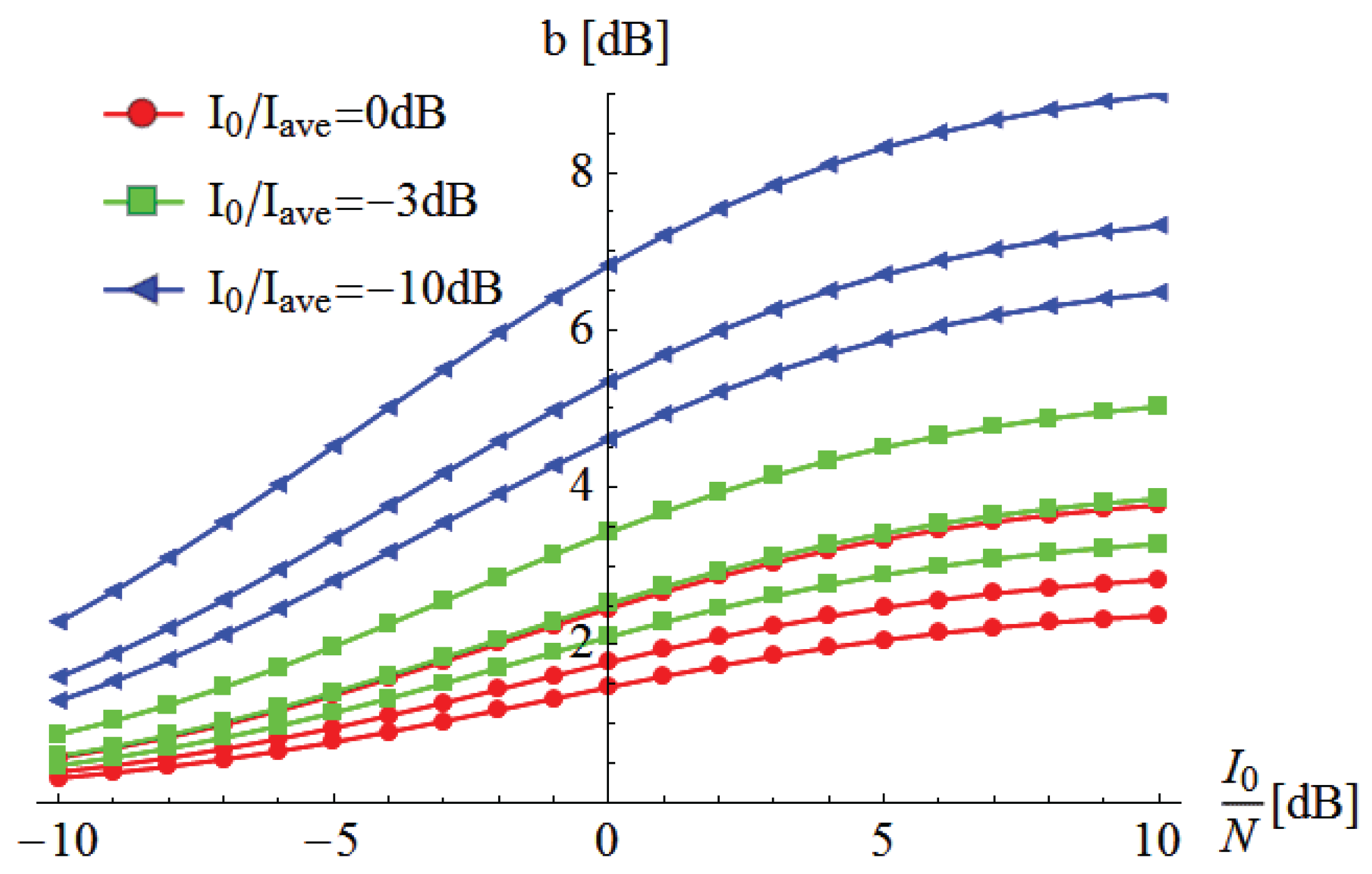
The required URC backoff for three values of the total measured-to-average-interference ratio $I_0/I_{\mathrm{ave}}$ is reported in Figure 5, for different values of $I_0/N_0$. For each value of $I_0/I_{\mathrm{ave}}$, there are three curves, corresponding to $J=1$, 2 , 3. The relative power for $J=2$, 3 are shown in Figure 4. When there are more interferers, the backoff is systematically smaller for the same total average interference $I_0$. The figure emphasizes that the backoff required due to interference variability is large when the interferers at the time of measurement are in a fade, i.e., when $I_0/I_{\mathrm{ave}}$ is small. In these cases, it is likely that the interference will be larger at the time τ of the realized transmission. It should be noted that here, the wanted signal does not vary at all.

3.3. Changes in Precoders of Interferers

The precoders used in interfering base stations may not be the same as the ones used when the channel is measured. This may cause changes in the measured interference power, causing CSI mispredictions and SINR variability [8]. This effect is particularly strong in multiple input single output (MISO) channels. We assume that the precoder on the desired transmission is selected based on the wanted channel ${\mathbf{h}}_i$, and the precoders on J interfering base stations are selected according to the wanted channels of the intended receivers of the interfering transmissions. The precoders ${\mathbf{v}}_{j,\tau }$ used at the interfering base stations depend on the scheduled receivers in the interfering cells. We assume that these are uniformly selected from the space of all MISO precoders. If there is no mobility, the received SINR for the desired transmission is

$${\gamma }_{\tau }=\frac{{\lambda }_0}{{\sum }_{j=1}^J{\lambda }_j{\left|{\mathbf{v}}_j^H{\mathbf{v}}_{\tau ,j}\right|}^2+N_0}$$

(15)

Here, ${\lambda }_0=\left|\right|{\mathbf{h}}_0{\left|\right|}^2$ is the wanted signal power. The powers of interfering channels are ${\lambda }_j$ correspond to the interfering channels ${\mathbf{h}}_{\tau ,j}={\mathbf{h}}_{0,j}$ in Equation (3), and ${\mathbf{v}}_j=h_j/\sqrt{{\lambda }_j}$ are the normalized interfering channels. We assume that the receiver is able to measure the average interference. The measured SINR is thus ${\gamma }_0=\frac{{\lambda }_0}{I_0+N_0}$, where $I_0={\mathrm{E}}_{{\mathbf{v}}_{\tau ,j}}\left\{{\sum }_{j=1}^J{\lambda }_j{\left|{\mathbf{v}}_j^H{\mathbf{v}}_{\tau ,j}\right|}^2\right\}$.

For a given channel vector distributed on a complex sphere with radius ${\lambda }_j=\left|\right|{\mathbf{h}}_{0,j}{\left|\right|}^2$, the cumulative distribution of an inner product of the channel vector and a unitary precoder ${\mathbf{v}}_{\tau ,j}$, $Z_j={\lambda }_j{\left|{\mathbf{v}}_j^H{\mathbf{v}}_{\tau ,j}\right|}^2$ can be obtained from [29]

$$F_Z\left(z_j\right)=1-{\left(1-\frac{z_j}{{\lambda }_j}\right)}^{N_T-1}$$

(16)

The corresponding PDF is then $f_Z\left(z_j\right)=\left(\frac{N_T-1}{{\lambda }_j}\right){\left(1-\frac{z_j}{{\lambda }_j}\right)}^{N_T-2}$. Hence, the PDF of the total interference power $Y={\sum }_{j=1}^J{Z}_j$ induced from J independent interferes can be written as

$$f_Y\left(y\right)=\left(\frac{N_T-1}{{\lambda }_1}\right){\left(1-\frac{z}{{\lambda }_1}\right)}^{N_T-2}*\dots *\left(\frac{N_T-1}{{\lambda }_J}\right){\left(1-\frac{z}{{\lambda }_J}\right)}^{N_T-2}$$

(17)

where * is the convolution operation. Hence, the total interference power is distributed over domain $\left[0{\sum }_j{\lambda }_j\right]$. For J interferers, the CDF is generically divided into $2^J$ regions [30], depending on the relative size of the interferers.

As an example of interference variation due to changes of precoders in neighboring cells, we consider a system with $J=3,2$, or 1 interferers. The eigenvalues of the interferers are ${\lambda }_1={\lambda }_2={\lambda }_3=1$ for $J=3$, ${\lambda }_1=2$ and ${\lambda }_2=1$ for $J=2$, and ${\lambda }_1=3$ for $J=1$. We consider three different numbers of transmit antennas at the interferers, $N_T\in \{2,5,10,100\}$.

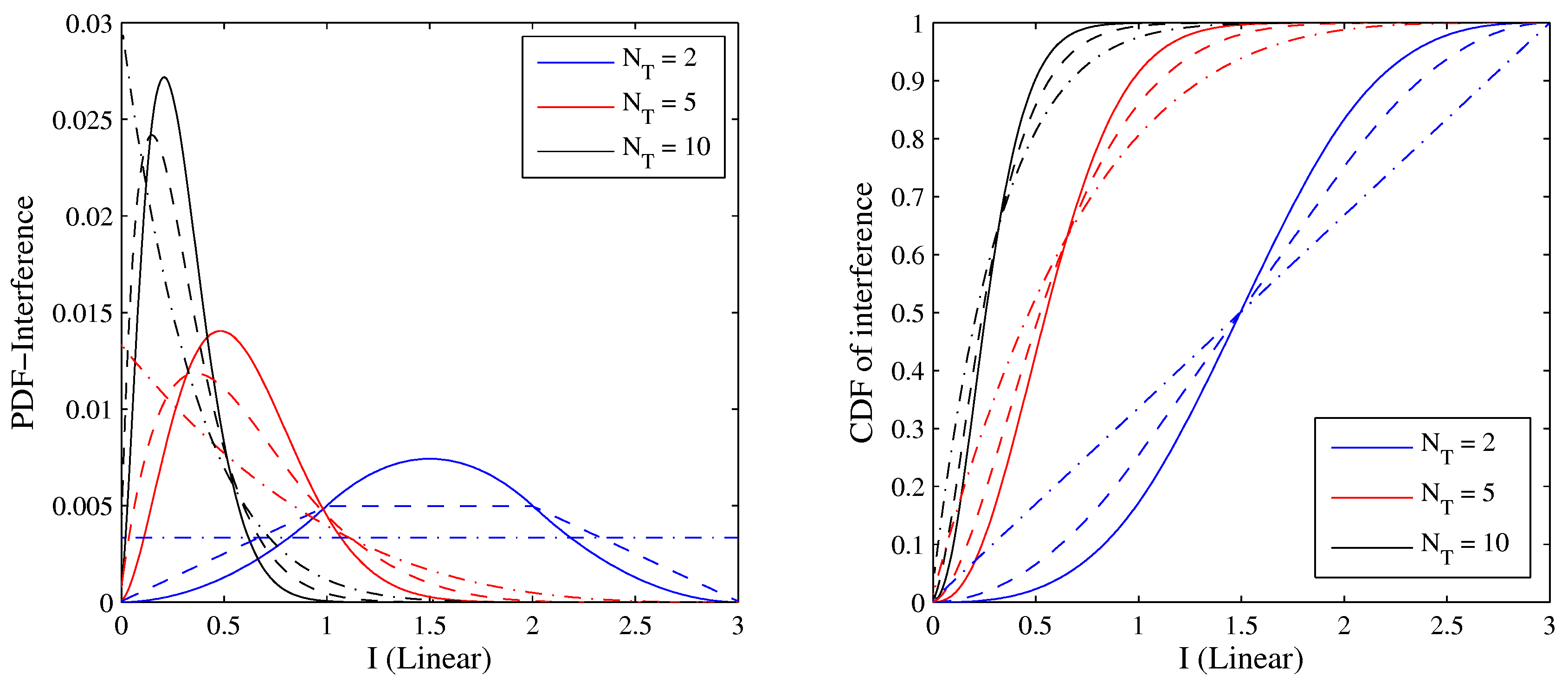
Figure 6 shows the PDF and CDF of the interference at the time of transmission, when the interferers select precoders randomly (for the clarity of the figures, $N_T=100$ is omitted). For $N_T=2$, the ${10}^{-5}$ point of the complementary CDF of interference is virtually indistinguishable from the worst case interference. With increasing $N_T$, worst case precoders become increasingly unlikely — typical interfering signals are almost orthogonal to the wanted signal channel.

The effect observed in Figure 6 that the distribution of the interference I becomes narrower with increasing $N_T$ does not mean that it has become easier to predict URC channel quality. Here, we assume that the channel quality estimated at the time of measurement is given by the average interference power. It turns out that the average is reduced more than the interference at outage, when $N_T$ grows. 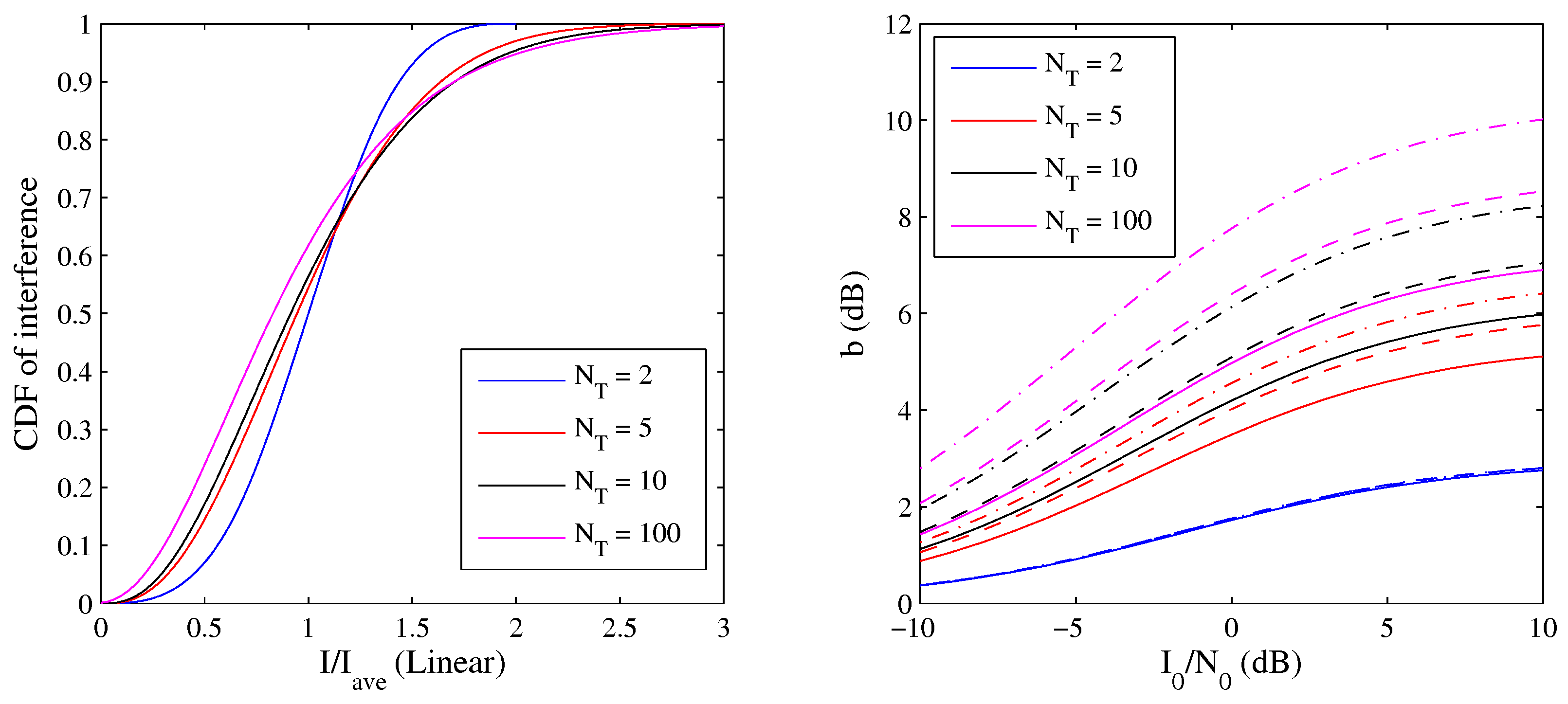To see this, the CDF of the realized interference is plotted in units of $I_{\mathrm{ave}}$ in Figure 7 (left).

For clarity, the distributions are plotted only for the $J=3$ case. For $N_T=2$, the distribution extends to $I/I_{\mathrm{ave}}=2$. The average interference is half of the realized. This distribution becomes broader with increasing $N_T$. The required backoff is plotted in the right part of the figure. The required backoff is $b=\frac{I_t/N_0+1}{I_0/N_0+1}$, where $I_t$ the interference at the URC target. The required backoff grows with $N_T$. For $N_T=2$, the backoff is virtually the same irrespectively of J. As the 0.99999 point of the CDF is close to the maximum interference, $I_t\approx 2I_{\mathrm{ave}}$ in this case, and the backoff in an interference limited network when $I_0/N_0\to \infty$ would be $b\approx 3$ dB.

3.4. Combined Effect

To understand the effect of wanted signal and interference variability, one has to combine these into one. The realized SINR Equation (2) can be modeled by ${\gamma }_{\tau }=\frac{S}{I+N_0}$ where S and I are RVs representing the power of the wanted signal and the interference, respectively. Then, the outage probability $\mathrm{P}\left({\gamma }_{\tau }\le {\gamma }_t\right)$ for SINR with combined wanted signal and interference variability is

$$\mathrm{P}\left({\gamma }_{\tau }<{\gamma }_t\right)={\int }_0^{\infty }{F}_S\left({\gamma }_t(y+N_0)\right)f_I\left(i\right)di$$

(18)

The closed form expression for the outage probability can be derived after some mathematical manipulations. It is given by

$$\mathrm{P}({\gamma }_{\tau }<{\gamma }_t)=1-\frac{e^{-\left(\frac{\Delta }{2}+\frac{{\gamma }_t{N}_0}{2\alpha }\right)}}{2^{p+2q+m+J+n}}{\displaystyle \sum _{n=0}^{\infty }}{\displaystyle \sum _{p=0}^{\infty }}{\displaystyle \sum _{q=0}^{\infty }}\frac{a_n{\Delta }^q}{{\alpha }^p{\beta }^{q+J+n}}\frac{N_0^{p+q+J+n}}{{(p!)}^{2}q!}\left(p!-p\Gamma \left(p,\frac{\delta }{2}\right)\right)U(a,b,\overline{z})$$

(19)

where $U(a,b,\overline{z})$ is a confluent hypergeometric function (A confluent hypergeometric function is defined as $U(a,b,z)=\frac{1}{\Gamma \left(a\right)}{\int }_0^{\infty }{e}^{-zt}{t}^{a-1}{(1+t)}^{b-a-1},\Re \left\{a\right\}>0$). with $a=q+J+n$, $b=p+a+1$, and $\overline{z}=\left(\frac{{\gamma }_t}{2\alpha }+\frac{1}{2\beta }\right)N_0$. Here, $\Gamma (a,b)$ is the incomplete Gamma function. Based on this, a suitable backoff can be numerically evaluated. For the detailed derivation, refer Appendix B.

The required backoffs due to mobility for $J=3$ and $\rho =0.98$ in four different scenarios are reported in

Table 1. Required backoff values for mobility induced SINR variability.

${\mathit{S}}_{\mathbf{0}}\mathbf{/}{\mathit{S}}_{\mathbf{ave}}$	${\mathit{I}}_{\mathbf{0}}\mathbf{/}{\mathit{I}}_{\mathbf{ave}}$	Sig. Power	Intf. Power	Combined Effect
0	0	8.01	2.5	8.53
0	$-10$	8.01	6.76	11.30
$-10$	0	44.17	2.5	44.82
$-10$	$-10$	44.17	6.76	46.96

. The backoffs if only the wanted signal is fading and if only interference is fading are compared to backoff for the combined effect of wanted signal and interference fading. It is assumed that noise is negligible, we have $I_0/N_0=20$ dB. The average signal-to-interference ratio is $S_0/I_0=10$. We see that the larger of the two fading effects dominates the combined effect. By far the most dramatic effects are seen when the measured wanted signal is fading.

SINR variability caused by changes in precoders may be considered together with mobility-induced variability. The precoders used on interfering base stations may vary while transmission is ongoing. The effective interference is $I={\sum }_{j=1}^J|\rho {\mathbf{h}}_{\tau ,j}{\mathbf{v}}_{\tau ,j}+\sqrt{1-{\rho }^2}{\tilde{\mathbf{h}}}_j{\mathbf{v}}_{\tau ,j}|$. For a given precoder ${\mathbf{v}}_{\tau ,j}$, an individual interference can be modeled as a non-central chi-square distributed variable with PDF $f_I(i_j\mid {\mathbf{v}}_{\tau ,j})={\chi }^2(i_j/{\alpha }_j;2;{\delta }_j)$ where ${\alpha }_j=(1-{\rho }^2)I_{\mathrm{ave},\mathrm{j}}/2$, and the non-centrality is ${\delta }_j=\frac{2{\lambda }_j{\rho }^2}{(1-{\rho }^2)}\frac{|{\mathbf{v}}_j^H{\mathbf{v}}_{\tau ,j}{|}^2}{I_{\mathrm{ave},\mathrm{j}}}$. The unconditional PDF can be obtained by integrating over the distribution of the inner product $|{\mathbf{v}}_j^H{\mathbf{v}}_{\tau ,j}{|}^2$. If we have $N_T=2$ transmit antennas, this is a uniform distribution, and the integration can be performed in closed form, resulting in $f_I\left(i_j\right)=1-Q_1\left(\sqrt{i_j},\sqrt{\frac{2{\lambda }_j{\rho }^2}{(1-{\rho }^{s}2)I_{\mathrm{ave},\mathrm{j}}}}\right)$.

When there is one interferer, the outage probability for the joint effect of precoder, wanted signal, and interfering channel variability can thus be obtained in closed form as

$$\mathrm{P}\left({\gamma }_{\tau }\le {\gamma }_t\right)=1-{\int }_0^{\infty }{Q}_1\left(\sqrt{{\delta }_i},\sqrt{{\gamma }_t(i+N_0)}\right)\left[1-Q_1\left(\sqrt{i},\sqrt{{\delta }_j}\right)\right]di$$

(20)

where ${\delta }_i=\frac{{\rho }^2{\left|{\mathbf{h}}_0{\mathbf{v}}_{}\right|}^2}{{\alpha }_i}$ and ${\delta }_j=\frac{{\rho }^2{\lambda }_j}{{\alpha }_j}$ are the non-centrality parameters of the probability distributions of the power of the wanted signal and the interference with $\alpha =(1-{\rho }^2)I_{\mathrm{ave}}/2$. The required backoff value can be numerically evaluated. It is clear that for Rayleigh fading, the required backoff is dominated by the variability of the wanted signal power.

4. Conclusions

We investigated link adaptation for a mobile user, when the wanted signal and the interfering signals undergo fading, and when there may be changes in the transmissions of the interferers. Here, we consider MISO transmissions, and the possible changes in interfering transmission are related to changing the precoders in a cell. Mobility induced signal and interference power changes and precoder variability in a cause SINR variation. Robust link adaptation is considered to meet an URC target of outage probability ${10}^{-5}$ with delay $\tau =1$ ms. For this, we assume that at the time of SINR measurement, the instantaneous values of the wanted signal power, and the individual interferer powers are known, in addition to the average values, and the distribution of these quantities. A suitable back-off is then chosen based on the statistical characteristics of the realized SINR to avoid outage due to CQI misprediction.

Concentrating on Rayleigh fading we develop closed form expressions for the signal and interference power distributions, as well as the SINR distribution. Users experiencing a deep fade in either the interference or wanted signal power during the time of measurement require large backoffs to achieve ultra-reliable transmission with low outage. When the channel during the measurement is close to an average situation, small backoffs are required. This demonstrates how accurate information of the current fading situations, as well as the fading statistics, are crucial for robust link adaptation. In comparison to the mobility-induced backoffs, backoffs related to variability of interference precoders are small, when the number of transmit antennas $N_T<10$.