A Backward Unlinkable Secret Handshake Scheme with Revocation Support in the Standard Model

Abstract

Secret handshake schemes have been proposed to achieve private mutual authentications, which allow the members of a certain organization to anonymously authenticate each other without exposing their affiliations. In this paper, a backward unlinkable secret handshake scheme with revocation support (BU-RSH) is constructed. For a full-fledged secret handshake scheme, it is indispensable to furnish it with practical functionality, such as unlinkability, revocation and traceability. The revocation is achieved in the BU-RSH scheme, as well as the unlinkability and the traceability. Moreover, the anonymity of revoked members is improved, so that the past transcripts of revoked members remain private, i.e., backward unlinkability. In particular, the BU-RSH scheme is provably secure in the standard model by assuming the intractability of the ℓ-hidden strong Diffie-Hellman problem and the subgroup decision problem.

1. Introduction

Since online applications via public networks are widely popularized, privacy is more and more important for the development of web services. Privacy-preserving authentication plays a pivotal role among the whole privacy concerns. A well-known method for realizing privacy-preserving authentication is anonymous credentials [1]. However, anonymous authentication usually needs to exchange the information about the trusted certificate authority (CA; i.e., affiliation). A promising cryptographic protocol named secret handshake was first introduced by Balfanz et al. [2] for mutually-anonymous authentication. During an interactive secret handshake protocol, one user will only reveal his/her affiliation to the other user if they belong to the same organization. Thus, participants only distinguish that they are members of the same organization, without leaking their true identities in this organization. Therefore, secret handshakes can not only protect the identity information of participants, but also provide a privacy-preserving property for their affiliations.

Besides the pioneering publication of Balfanz et al. [2], many two-party secret handshake schemes have been proposed from different cryptographic primitives. For instances, CA-oblivious encryption [3], ElGamal signature [4] and RSA [5]. All of those works use one-time pseudonyms to ensure the unlinkability of secret handshakes, which are executed by the same members. In addition, it is very easy for the group authority (GA) to trace and revoke its members, because the GA knows all one-time pseudonyms of the members. However, those schemes based on one-time pseudonyms require more storage and computation cost in practice. Moreover, since it knows all secret information of the group members, the GA is able to impersonate and frame its members to execute malicious behaviors. Therefore, the anonymity against GA can be hardly achieved by using one-time pseudonyms.

Based on reusable credentials, Xu and Yung [6] first offered a secret handshake scheme that has a “weaker” unlinkability than the schemes from one-time pseudonyms. By using identity-based encryption [7], Ateniese et al. [8] presented the first efficient unlinkable secret handshake scheme with reusable credentials, which can achieve the dynamic matching model. However, Ateniese et al.’s scheme only realizes limited dynamic matching. Since the different sister groups are created and distinguished by group name in Ateniese et al.’s scheme, the different groups still share the same group public/private keys, which are actually managed by an upper operator. Hence, the limited dynamic matching model still relies on a single GA for different groups. Afterwards, Jarecki and Liu [9] proposed a revocable secret handshake scheme with unlinkability via broadcast encryption. However, the scheme [9] is based on the assumption that all groups have the same numbers of revoked members synchronously. Furthermore, the amount of group public keys is increased linearly with the number of group members. Thus, Jarecki and Liu’s scheme [9] becomes inappropriate in practice. Based on Ateniese et al.’s scheme [8], Sorniotti and Molva [10,11] proposed revocable secret handshake schemes. Their proposals provide the revocation checking of the participants who have initiatively left their groups during handshakes. Nevertheless, they are still unable to trace and revoke malicious group members for complete unlinkability and untraceability. Moreover, their proposals still have the same weakness of Ateniese et al.’s scheme [8].

Particularly, a practical secret handshake scheme should realize similar security properties as a group signature scheme. Namely, secret handshakes with reusable credentials are required to be traceable, revocable and unlinkable. The illustration of the practical secret handshake scheme is described in Figure 1. Kawai et al. [12] proposed the definition of strong anonymity for secret handshakes at ISPEC 2009, which takes a malicious GA into consideration. They constructed an unlinkable secret handshake scheme with reusable credentials, which supports strong detector resistance and co-traceability by using a group signature with message recovery. However, the revocation mechanism is not explicitly considered in their scheme. In CRYPTO 2009, Jarecki and Liu [13] proposed a practical unlinkable secret handshake scheme, which supports both revocation and traceability with reusable credentials. However, the anonymity of revoked members cannot be guaranteed in Jarecki and Liu’s scheme [13]. Namely, once a member is revoked, all past transcripts of the member can be recognized and traced by the adversary after running revocation checking. As shown in [14], the property is also considered as backward unlinkability. It has been left by Jarecki and Liu [13] as an open question if there exists a secret handshake scheme with backward unlinkability. Derived from the idea of Kawai et al.’ scheme [12] and Jarecki and Liu’s scheme [13], Wen and Zhang [15] constructed a new revocable secret handshake scheme with backward unlinkability, which is provably secure with random oracles. Yang et al. [16] also proposed a generic approach for providing revocation support in secret handshakes, which did not consider backward unlinkability for revoked members and was still provably secure with random oracles.

Figure 1. An illustration of practical secret handshake scheme.

Figure 1. An illustration of practical secret handshake scheme.

In this paper, we provide a new backward unlinkable secret handshake scheme with revocation supports (BU-RSH). Our new proposal, BU-RSH, aims to presents a more complete secret handshake scheme, which can also be proven secure in the standard model. Compared to the previous schemes, the contributions of our new scheme are three-fold. Firstly, the revocation mechanism is appended to the secret handshake schemes, which is not achieved by Kawai et al.’s scheme [12]. In addition, the anonymity of our schemes is enhanced in view of revoked members, which enables the past transcripts of revoked members to still remain anonymous, i.e., backward unlinkability. More importantly, BU-USH is provably secure without random oracles by assuming the intractability of the ℓ-hidden strong Diffie-Hellman problem and the subgroup decision problem.

The remainder of this paper is organized as follows. In Section 2, we recall some preliminaries related to our work, including the definition and security properties of secret handshakes. In Section 3, BU-RSH is presented in detail. We focus on discussing the security analyses of BU-RSH, along with the performance of the related schemes in Section 4. The conclusion is given in Section 5.

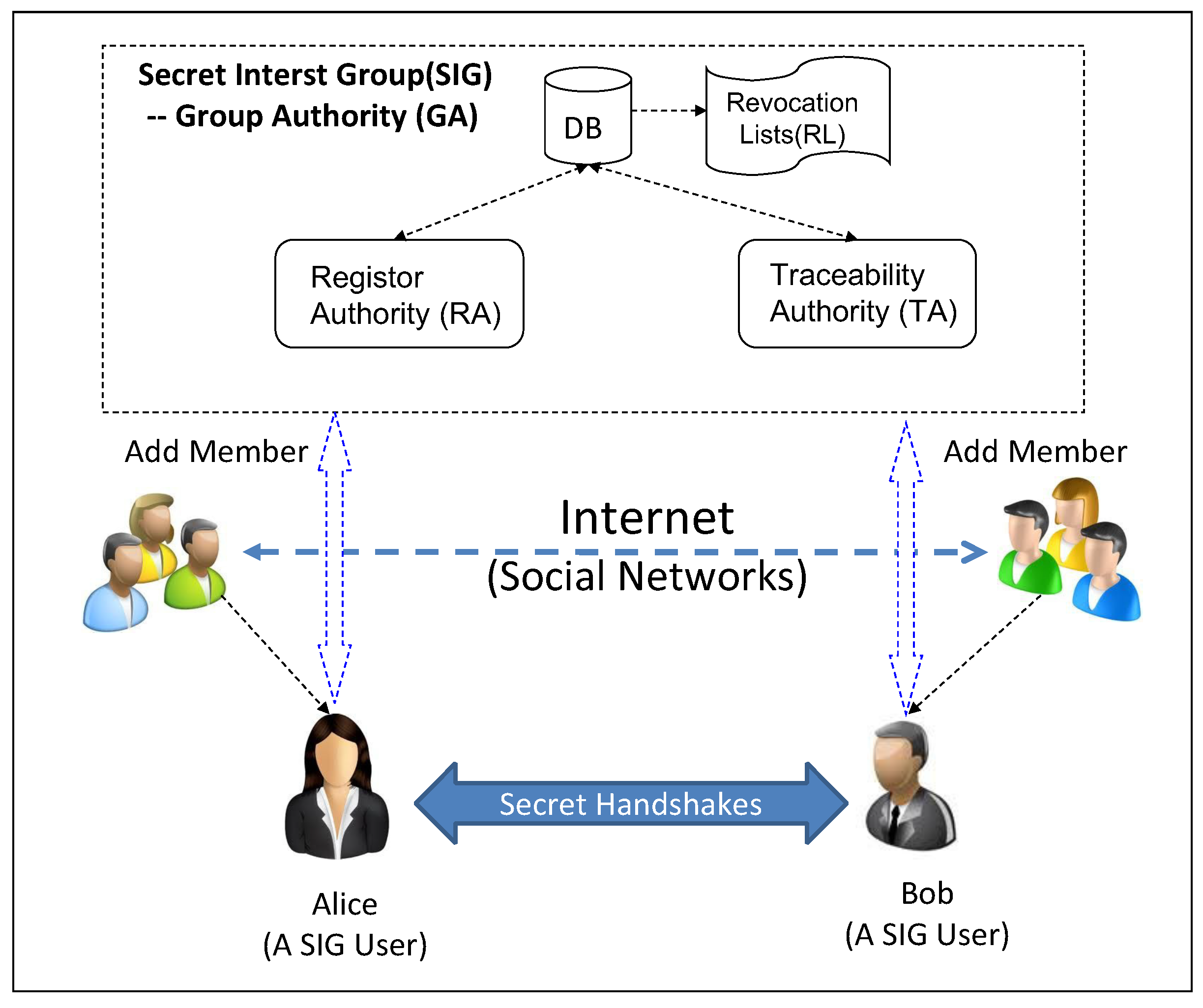
2. Preliminaries

In this section, we recall the notions and definitions of bilinear pairings of composite order [17] and complexity assumptions, which will be used in later sections. Additionally, the definition and security properties of secret handshakes are reviewed.

2.1. Bilinear Pairings of Composite Order

Composite order bilinear pairings were first introduced in [17], which will be used in our proposal. We first review some general notions about bilinear groups and pairings. Most of the cryptosystems based on pairings are based on bilinear groups with prime order for simplicity. In our case, we define $\mathbb{G}$ as a (multiplicative) cyclic group of composite order N, where $N=pq$ is the product of two different primes p and q. Let g be a generator of $\mathbb{G}$. A one-way map $e:\mathbb{G}\times \mathbb{G}\to {\mathbb{G}}_T$ is a bilinear pairing if the following conditions hold.

• Bilinear: For all $g\in \mathbb{G}$, s.t., g is a generator of $\mathbb{G}$ and $a,b\in {\mathbb{Z}}_N$, $e(g^a,g^b)=e{(g,g)}^{ab}$.
• Non-degeneracy: $e(g,g)\ne 1$, i.e., if g generates $\mathbb{G}$, then $e(g,g)$ generates ${\mathbb{G}}_T$ with order N.
• Computability: There exists an efficient algorithm for computing $e(.,.)$.

2.2. Complexity Assumptions

Definition 1. 

(ℓ-hidden strong Diffie-Hellman (ℓ-HSDH) problem [18]): Let $(\mathbb{G},{\mathbb{G}}_T)$ be two cyclic groups of prime order p. For an integer ℓ and $\omega {\in }_R{\mathbb{Z}}_p,g,u\in \mathbb{G}$, given:

$$\{g,\Omega =g^{\omega },u,(g^{s_1},u^{s_1},g^{\frac{1}{\omega +s_1}}),\cdots ,(g^{s_{\ell }},u^{s_{\ell }},g^{\frac{1}{\omega +s_{\ell }}})with{s}_1,\cdots ,s_{\ell }\in {\mathbb{Z}}_p\}$$

compute ($g^s,u^s,g^{\frac{1}{\omega +s}}$) for one $s\notin \{s_1,\cdots ,s_{\ell }\}$.

ℓ-HSDH assumption: We say that the ($\ell ,t,ϵ$)-SR assumption holds if there exists no algorithm that can solve the ℓ-HSDH problem with a non-negligible advantage ϵ in a polynomial time bound t. Since the ℓ-HSDH problem does not rely on the composite order N, the ℓ-HSDH assumption can be applied to the generic group as described in the literature [18].

Definition 2. 

(Subgroup decision (SD) problem [18,19]): Given a tuple $(p,q,\mathbb{G},{\mathbb{G}}_T,e)$, in which p and q are independent secure primes, $\mathbb{G}$ and ${\mathbb{G}}_T$ are two cyclic groups of order $N=pq$ with efficiently-computable group operations and $e:\mathbb{G}\times \mathbb{G}\to {\mathbb{G}}_T$ is a bilinear map. Let ${\mathbb{G}}_q\subset \mathbb{G}$ be the q-order subgroup of $\mathbb{G}$. Given an element x, which is selected randomly either from $\mathbb{G}$ or from ${\mathbb{G}}_q$, the subgroup decision problem is to distinguish whether x is in ${\mathbb{G}}_q$ or not.

The subgroup decision assumption: Let the success probability of solving the subgroup decision problem be defined as $Ad{v}_{sd}=\frac{1}{2}+\epsilon$; we say that the subgroup decision assumption holds if ε is negligible.

2.3. Secret Handshakes: Definition and Security Properties

The secret handshake scheme (SHS) operates in an environment that consists of a set of groups managed by a set of group authorities and a set of users $U_1,\cdots ,U_n$ registered into some groups. Based on the definitions in [2,13,15], a secret handshake scheme consists of the following probabilistic polynomial-time algorithms:

• Setup: The Setup algorithm selects a security parameter κ to generate the public parameters params common to all subsequently generated groups.
• CreateGroup: CreateGroup is a key generation algorithm executed by the GA to establish a group G. It takes params as input and outputs group public key and private key $(gp{k}_G,gs{k}_G)$.
• AddUser: AddUser is a two-party protocol run by the user and the GA. The GA plays the role of the CA for the group, which issues the credentials for a legitimate user of the group. After verifying the users’ real identity, the GA will issue credential $cre{d}_i$ for $i\in [1,n]$ to each user after the protocol.
• Handshake: Handshake is a two-party authenticate protocol executed by a pair of anonymous users (A, B), where (A, B) are possible users who may belong to different groups. This protocol takes as input the anonymous user’ secrets ($cre{d}_i,gp{k}_i,tp{k}_i$) and other public information, where $tp{k}_i$ is a group public key of the target group for the participator’s authentication policy. The output of the protocol for either party is either “1” or “0”. If the output is “1”, this means that the secret handshake protocol is successful, and a session key K will be produced that can be used for subsequent secure communication between the two users. Otherwise, the handshake protocol is a failure, and the two users cannot distinguish the other’s group information.
• TraceUser: TraceUser is a polynomial time algorithm that is executed by the GA. The protocol outputs the identity of user U, whilst a transcript of the secret handshake involved with user U is submitted.
• RemoveUser: RemoveUser is a polynomial time algorithm that is authorized by the GA. It takes its current revocation list (RL) and U’s revocation tokens as the inputs, whilst outputting an up-to-date RL that includes new revocation records.

For the untraceable secret handshake scheme, the TraceUser and RemoveUser algorithms will be not included. Now, we review some basic security definitions of SHS in brief. The formal definitions can be referred to the literature [2,12,13]. In general, a secret handshake scheme must obey the following security properties:

(1)

Completeness: It requires that the SH protocol always outputs “1” when any interactive participators $U_i$ and $U_j$ honestly execute the Handshake protocol and satisfy the authentication policy of the counter-party, respectively.

(2)

Impersonator resistance: An adversary who attempts to impersonate a legitimate user of one group cannot succeed with a non-negligible probability. In other words, any adversary not satisfying the authentication policies cannot accomplish a successful secret handshake.

Formally, the property is defined in the following game ${\mathtt{Game}}^{IR}$ between an adversary $\mathcal{A}$ and a challenger $\mathcal{B}$:

• Init: The adversary $\mathcal{A}$ first sets $Chosen=\{G^{*},i^{*}\}$. Then, $\mathcal{B}$ simulates Setup, CreateGroup and AddMember and sends the group public keys and up-to-date RL to $\mathcal{A}$.
• Queries: $\mathcal{A}$ can make the following queries, such that the responses will be simulated by $\mathcal{B}$.

  –

  Corruption queries: The corruption list $Cor$ is initialized as ∅. The adversary $\mathcal{A}$ can query CreateGroup and AddMember for the secret information of some groups and members, except for $Chosen$. $\mathcal{B}$ will respond to the simulated information and update the corruption list $Cor$.

  –

  Handshake queries: The adversary $\mathcal{A}$ can make queries on the Handshake protocol with the group members. The transcripts of the queried members can be generated by $\mathcal{B}$. During a handshake, $\mathcal{A}$ can query the hash functions used in the Handshake protocol. In particular, $\mathcal{A}$ can request a non-interactive proof of knowledge of a random message for any member at the current interval.

• Challenge: The challenger $\mathcal{B}$ acts as the group member $i^{*}$ of $G^{*}$ and executes the handshake protocol with the adversary $\mathcal{A}$. $\mathcal{A}$ attempts to convince $\mathcal{B}$ that $\mathcal{A}$ is a legitimate member of the group $G^{*}$.
• Output: If the adversary $\mathcal{A}$ on half of a member i in the group $G^{*}$ succeeds in executing Handshake with $\mathcal{B}$, the output of the game is “1”. Otherwise, the output is “0”. Note that it is required that $\mathcal{A}$ never queried any secret information with respect to the member i of the group $G^{*}$, i.e., $i\cap Cor=\text{∅}$.

Let ${\mathtt{Adv}}_{\mathcal{A}}^{IR}=\mathtt{Pr}[{\mathtt{Game}}^{IR}=1]$; we say that SHS satisfies the impersonator resistance if the function ${\mathtt{Adv}}_{\mathcal{A}}^{IR}$ is negligible for any polynomially-bounded adversary.

(3)

Detector resistance: An adversary will not succeed with non-negligible probability when he activates Handshake with one honest member in order to determine whether he satisfies the authentication policies or not.

Formally, the property is defined in the following game ${\mathtt{Game}}^{DR}$ between an adversary $\mathcal{A}$ and a challenger $\mathcal{B}$:

• Init: The adversary $\mathcal{A}$ first sets $Chosen=\{i_0,G_0,i_1,G_1\}$. Then, $\mathcal{B}$ simulates Setup, CreateGroup and AddMember and sends group public keys together with revocation lists of all groups to $\mathcal{A}$.
• Queries: $\mathcal{A}$ can make the following queries, such that the responses will be simulated by $\mathcal{B}$.

  –

  Corruption queries: The corruption list $Cor$ is initialized as ∅. The adversary $\mathcal{A}$ can query CreateGroup and AddMember for the secret information of some groups and members, except for $Chosen$. Thus, $\mathcal{B}$ will respond to the simulated information and update the corruption list $Cor$.

  –

  Handshake queries: The adversary $\mathcal{A}$ can make queries on the $Handshake$ protocol with the group members. The transcripts of the queried members can be generated by $\mathcal{B}$. During a handshake, $\mathcal{A}$ can query the hash functions used in the $Handshake$ protocol. In particular, $\mathcal{A}$ can request the non-interactive proof of knowledge of a random message for any member at the current interval.

• Challenge: The challenger $\mathcal{B}$ selects a random bit $\varphi \leftarrow \{0,1\}$. Then, $\mathcal{B}$ acts as the member $i_{\varphi }$ in the group $G_{\varphi }$ and executes the handshake protocol with the adversary $\mathcal{A}$. $\mathcal{A}$ attempts to distinguish to which group $\mathcal{B}$ belongs.
• Output: The adversary $\mathcal{A}$ outputs ${\varphi }^{\prime }$ as its guess of ϕ.

Let ${\mathtt{Adv}}_{\mathcal{A}}^{DR}=|\mathtt{Pr}[{\mathtt{Game}}^{DR}\left(0\right)=1]-\mathtt{Pr}[{\mathtt{Game}}^{DR}\left(1\right)=1]|$; we say that SHS satisfies the detector resistance if the function ${\mathtt{Adv}}_{\mathcal{A}}^{DR}$ is negligible for any polynomially-bounded adversary.

(4)

Unlinkability: This requirement implies that any adversary cannot find any relation between two instances of the Handshake algorithm, which is involved with the same honest members. Anyone except the GA could not distinguish whether two instances of the SH protocol are executed by the same honest member. In addition, the GA will never link two executions run by the same member, unless it carries out the TraceMember algorithm. Thus, the TraceMember algorithm can be authorized by a separate trace authority of the GA in order to improve the unlinkability. In the security definition of SHS [13], the privacy property explicitly implies both the unlinkability and the detector resistance. The formal definition of unlinkability is easily derived from ${\mathtt{Game}}^{DR}$ of the detector resistance when the “Challenge” phase is executed twice. Let ${\varphi }_0$ and ${\varphi }_1$ be the random bits of the two challenges, respectively. If ${\varphi }_0={\varphi }_1$, let $\varphi =1$, else let $\varphi =0$. Therefore, the adversary outputs ${\varphi }^{\prime }$ as its guess of ϕ to distinguish the two different challenges. We say that SHS satisfies the unlinkability if the probability of outputting the correct ${\varphi }^{\prime }$ is negligible for any polynomially-bounded adversary.

Remark on backward unlinkability: If a group member is removed from his group, i.e., his revocation token is added to the RL, the anonymity of the revoked member before the revocation is desirable to be sustained (i.e., backward unlinkability). This means that even after a member is revoked, all past handshake behaviors produced from the revoked member remain private and unlinkable. The formal definition of the property is easily obtained by revising the $Chosen$ and “Challenge” phase of ${\mathtt{Game}}^{DR}$, which is similar to backward unlinkability in [14].

3. A Backward Unlinkable Secret Handshake Scheme with Revocation Support in the Standard Model

Developed from the idea of group signatures with verifier local revocation and backward unlinkability [19] and private mutual authentications [13], a new backward unlinkable secret handshake scheme (BU-RSH) that supports revocation in the standard model is designed as follows.

• Setup: Given a security parameter κ, the algorithm runs $Setup\left(1^{\kappa }\right)\to \mathtt{params}$. The public parameters $\mathtt{params}=(N,\mathbb{G},{\mathbb{G}}_T,e:\mathbb{G}\times \mathbb{G}\to {\mathbb{G}}_T,g,u,h,H_1,H_2,v_0,\cdots ,v_n,T,{\tau }_1,\cdots ,{\tau }_T,F)$, which are shared by all participators in the scheme. Here, g is a generator of a subgroup $\mathbb{G}$ of composite order $N=pq$, where p and q are random primes. Let ${\mathbb{G}}_p$ and ${\mathbb{G}}_q$ be the cyclic subgroups of $\mathbb{G}$ with respective order p and q. The algorithm picks a generator h of ${\mathbb{G}}_q$. $u,v_0,\cdots ,v_n$ are selected randomly from $\mathbb{G}$. In addition, $H_1:{\{0,1\}}^{*}\to \mathbb{G}$ and $H_2:{\{0,1\}}^{*}\to {\mathbb{Z}}_N^{*}$ are two cryptographic hash functions. T is the number of time intervals in the secret handshake system, and ${\tau }_j{\leftarrow }_R{\{0,1\}}^{*}$ represents the j-th time interval for each $j\in [1,T]$. Finally, F is a function that represents the attribute. Suppose one attribute P is denoted by n-bits string $({\mu }_1,{\mu }_2,\cdots ,{\mu }_n)$, $F\left(P\right)=v_0{\prod }_{i=0}^{i=n}{v}_i^{{\mu }_i}$.
• CreateGroup: The GA chooses $\alpha ,\omega {\leftarrow }_R{\mathbb{Z}}_N^{*}$ and generates $\varphi =e{(g,g)}^{\alpha },\Omega =g^{\omega }$. The GA outputs its group secret key $gsk=(\alpha ,\omega )$ and group public key $gpk=(\varphi ,\Omega )$.
• AddUser(n, T): Assuming that GA can add n users to the group in T time intervals, the GA issues attribute credential for each user. After verifying the identity of a user $U_i$, the GA randomly selects secret key $s_i,{\beta }_i{\leftarrow }_R{\mathbb{Z}}_N^{*}$, and computes attribute credential $cre{d}_{U_i,P}=({\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4)=({\left(g^{\alpha }\right)}^{\frac{1}{\omega +s_i}},g^{s_i},u^{s_i}·F{\left(P\right)}^{{\beta }_i},g^{-{\beta }_i})$. The user verifies that the credential is valid by testing $e({\theta }_1,\Omega ·{\theta }_2)\stackrel{?}{=}\varphi$ and $e({\theta }_2,u)\stackrel{?}{=}e({\theta }_3,g)·e({\theta }_4,F\left(P\right))$. In addition, the GA will calculate this user’s revocation token $urt\left[i\right]\left[j\right]=B_{ij}=h_j^{s_i}$ where $h_j=H_1\left({\tau }_j\right)$ for each time interval ${\tau }_j$, such that $j\in [1,T]$. Then, $U_i$ becomes the valid member of the group, and the GA stores the user’s credential and revocation tokens in the member database.
• Handshake: Suppose A and B are two parties who want to execute a secret handshake protocol to authenticate each other without leaking their privacy at time interval ${\tau }_j$. Participator A runs the protocol with $cre{d}_A$ and $gp{k}_A$, which are created by group $G_A$, and participator B runs it with $cre{d}_B$ and $gp{k}_B$, which are created by group $G_B$. Let $(tp{k}_A,P_{AT})$ and $(tp{k}_B,P_{BT})$ denote the target group public keys and target property (i.e., authentication policy) of the participators A and B, respectively. The protocol proceeds as follows:

  (1)

  $\mathtt{A}\to \mathtt{B}:\left\{\mathtt{PROOF}\left(cre{d}_A\right)\left[r_A\right]\right\}$

  (a)

  A chooses ${\lambda }_A,r_A,\delta ,t_1,t_2,t_3,t_4,t_5{\leftarrow }_R{\mathbb{Z}}_N^{*}$.

  (b)

  A computes ${\sigma }_1={\theta }_1^{{\lambda }_A}·h^{t_1}$, ${\sigma }_2={\theta }_2·h^{t_2}$, ${\sigma }_3={\theta }_3·h^{t_3}·u^{r_A}$, ${\sigma }_4={\theta }_4·h^{t_4}$, ${\pi }_1=h^{t_1·t_2}·{\left({\theta }_1^{{\lambda }_A}\right)}^{t_2}·{({\theta }_2·\Omega )}^{t_1}$, ${\pi }_2=u^{t_2}·g^{-t_3}·F{\left(P_A\right)}^{-t_4}$.

  (c)

  A calculates $T_1=g^{\delta }$, $T_2=e{(h_j,{\theta }_2)}^{\delta }$, ${\theta }_5=h_j^{\delta }$, ${\sigma }_5={\theta }_5·h^{t_5}$, ${\pi }_3={\theta }_5^{t_2}·{\theta }_2^{t_5}·h^{t_2·t_5}$, ${\pi }_4=g^{t_5}$.

  Finally, A sends $\mathtt{PROOF}\left(cre{d}_A\right)\left[r_A\right]=({\sigma }_1,{\sigma }_2,{\sigma }_3,{\sigma }_4,{\sigma }_5,{\pi }_1,{\pi }_2,{\pi }_3,{\pi }_4,T_1,T_2)$ to B.

  (2)

  $\mathtt{B}\to \mathtt{A}:\{\mathtt{PROOF}\left(cre{d}_B\right)\left[r_B\right],V_B\}$

  (a)

  By verifying $T_2\ne e(B_{ij},T_1)$ for all $B_{ij}\in R{L}_j$ of the target group of B, B executes the revocation check to ensure that the A is not revoked at the time interval ${\tau }_j$.

  (b)

  B will verify the correctness of $T_1$ and $T_2$ by testing $e({\sigma }_5,g)\stackrel{?}{=}e(h_j,T_1)·e(h,{\pi }_4)$, $\frac{e({\sigma }_5,{\sigma }_2)}{e(h,{\pi }_3)}\stackrel{?}{=}{T}_2$.

  (c)

  Similarly, B also generates proof knowledge of $k_B$ : $\mathtt{PROOF}\left(cre{d}_B\right)\left[r_B\right]$.

  (d)

  If A does not pass the revocation check, B will generate a random value $V_B{\leftarrow }_R{\mathbb{Z}}_N^{*}$ as the verification response. Otherwise, B will recover $n_A^{\prime }$ and $k_A^{\prime }$ from $\mathtt{PROOF}\left(cre{d}_A\right)\left[r_A\right]$ by using his target group public key $tp{k}_B$ and computes a verification value $V_B$ as follows.

  –

  B retrieves ${\sigma }_1,{\sigma }_2,{\pi }_1$ from $\mathtt{PROOF}\left(cre{d}_A\right)\left[r_A\right]$ and uses his target group public key ${\Omega }_{BT}$ to compute: $n_A^{\prime }=\frac{e({\sigma }_1,{\sigma }_2·{\Omega }_{BT})}{e(h,{\pi }_1)}$.

  –

  B calculates $k_A^{\prime }$ by using ${\sigma }_2,{\sigma }_3,{\sigma }_4,P_{BT},{\pi }_2$ as follows,

  $$k_A^{\prime }=\frac{e({\sigma }_3,g)·e({\sigma }_4,F\left(P_{BT}\right))·e(h,{\pi }_2)}{e({\sigma }_2,u)}$$

  –

  B will compute the following verification value $V_B$, such that:

  $$V_B=H_2({\left(k_A^{\prime }\right)}^{r_B}\left|\right|n_A^{\prime }\left|\right|{\varphi }_B^{{\lambda }_B}\left|\right|0).$$

  Finally, B sends both $\mathtt{PROOF}\left(cre{d}_B\right)\left[r_B\right]$ and $V_B$ to A.

  (3)

  $\mathtt{A}\to \mathtt{B}:V_A$

  (a)

  By checking $T_2\ne e(B_{ij},T_1)$ for all $B_{ij}\in R{L}_j$ after getting $T_1,T_2$ from B, A executes the similar revocation check to ensure that B is also not revoked at the time interval ${\tau }_j$.

  (b)

  If B is revoked at time interval ${\tau }_j$, A responds with a random value $V_A{\leftarrow }_R{\mathbb{Z}}_N^{*}$, as well. Otherwise, A retrieves $n_B^{\prime }$ and $k_B^{\prime }$ from $\mathtt{PROOF}\left(cre{d}_B\right)\left[r_B\right]$ by using its own target group public key $tp{k}_A$.

  (c)

  A verifies the $V_B$ with the equation $V_B\stackrel{?}{=}{H}_2({\left(k_B^{\prime }\right)}^{r_A}\left|\right|{\varphi }_A^{{\lambda }_A}\left|\right|n_B^{\prime }\left|\right|0)$. If the above equation holds, A will output “1” and send $V_A=H_2({\left(k_B^{\prime }\right)}^{r_A}\left|\right|n_B^{\prime }\left|\right|{\varphi }_A^{{\lambda }_A}\left|\right|1)$ to B. Else A outputs “0” and also responds with a random value $V_A{\leftarrow }_R{\mathbb{Z}}_N^{*}$ to B.

  (d)

  B verifies $V_A$ with the following equation $V_A\stackrel{?}{=}{H}_2({\left(k_A^{\prime }\right)}^{r_B}\left|\right|{\varphi }_B^{{\lambda }_B}\left|\right|n_A^{\prime }\left|\right|1)$. B outputs “1” only if the above equation holds, else B outputs “0”.

• TraceUser: When a dispute happens, the GA first retrieves the proof information $T_1$ and $T_2$ from a transcript of a secret handshake instance at time interval ${\tau }_j$. Then, GA checks $T_2\stackrel{?}{=}e(B_{ij},T_1)$ for all $B_{ij}$ in the user lists to identify who has executed the malicious secret handshakes.
• RemoveUser: The GA is responsible for the update of the RL for each time interval after tracing some malicious group users or receiving some users’ revocation requests. In order to remove a user $U_i$ from one group at time interval ${\tau }_{j^{\prime }}$, the GA firstly looks up the user $U_i$’s information from its user lists. Then, the GA removes the user’s revocation tokens $urt\left[i\right]\left[j\right]=B_{ij}$ for all $j\ge j^{\prime }$ from the RL of its group. Consequently, other unrevoked group users can execute the revocation check under the updated RL to identify whether the counter-party is revoked. Particularly, the revocation tokens before the time interval ${\tau }_{j^{\prime }}$ are not added in the updated RL and will not satisfy the revocation check equation. Moreover, it is infeasible to deduce the previous revocation tokens $B_{ij}$ for all $j<j^{\prime }$ from the revocation tokens $B_{ij}$ for all $j\ge j^{\prime }$ that have been added in the updated RL at the time interval ${\tau }_{j^{\prime }}$. Therefore, the past transcripts of revoked users still remain unrecognized and private, which achieves backward unlinkability.

4. Security and Performance Analysis

The security results on the new construction BU-RSH with respect to the impersonator resistance, detector resistance and unlinkability will be provided firstly. Then, the performance of our proposal is also analyzed.

4.1. Security

Theorem 1. 

The BU-RSH scheme satisfies the impersonator resistance (IR) assuming the ℓ-HSDH problem is hard.

Proof. 

Suppose $\mathcal{B}$ is given a ℓ-HSDH challenge, such that for an integer ℓ and $\omega {\in }_R{\mathbb{Z}}_N^{*},g,u\in \mathbb{G}$ and $s_1,\cdots ,s_{\ell }\in {\mathbb{Z}}_N^{*}$, given:

$$\{g,\Omega =g^{\omega },u,(A_1=g^{s_1},B_1=u^{s_1},C_1=g^{\frac{1}{\omega +s_1}}),\cdots ,(A_{\ell }=g^{s_{\ell }},B_{\ell }=u^{s_{\ell }},C_{\ell }=g^{\frac{1}{\omega +s_{\ell }}})\}$$

compute ($g^s,u^s,g^{\frac{1}{\omega +s}}$) for some $s\notin \{s_1,\cdots ,s_{\ell }\}$.

Now, we describe how the algorithm $\mathcal{B}$ can successfully solve the ℓ-HSDH problem by executing a security game with an adversary $\mathcal{A}$. Note that the attribute credentials of users in the BU-RSH scheme are constructed from the initial signature based on the two-level hybrid signature scheme [18]. Actually, the security of IR can depend on the existential unforgeability of the attribute credential derived from the signature. Since the new scheme is converted from the constant-size group signature [19], the detailed proof can be referred to Theorem 2 in [19] with respect to full traceability. Hence, we deduce that the BU-RSH satisfies the impersonator resistance under the ℓ-HSDH assumption.

• Init: To achieve the simulation, B first initiates the interaction settings where $\mathcal{B}$ can simulate Setup, CreateGroup and AddUser(n, T) for every group in BU-RSH. In the Setup phase, B selects $\alpha ,{\rho }_0,\cdots ,{\rho }_n{\leftarrow }_R{\mathbb{Z}}_N^{*}$, as well as $\gamma {\leftarrow }_R\{0,\cdots ,n\}$ and $z_0,\cdots ,z_n{\leftarrow }_R\{0,\cdots ,2q_A-1\}$, where $q_A$ means the number of queries of AddUser, and then prepares the public parameters $\mathtt{params}$ for the adversary $\mathcal{A}$, $\mathtt{params}=(p,\mathbb{G},{\mathbb{G}}_T,e:\mathbb{G}\times \mathbb{G}\to {\mathbb{G}}_T,g,u,h,H_1,H_2,v_0=u^{z_0-2\gamma q_A}·g^{{\rho }_0},v_1=u^{z_1}·g^{{\rho }_1},\cdots ,v_n=u^{z_n}·g^{{\rho }_n},T,{\tau }_1,\cdots ,{\tau }_T,F)$. In the CreateGroup phase, $\mathcal{B}$ first sets $Chosen=\{G^{*},i^{*}\}$. For the group $G^{*}$, $\mathcal{B}$ sets the group public key to be $gp{k}_{G^{*}}=(\varphi =e{(g,g)}^{{\alpha }^{*}},{\Omega }_i^{*}=g^{{\omega }^{*}})$ for group $G^{*}$, where ${\alpha }^{*},{\omega }^{*}{\leftarrow }_R{\mathbb{Z}}_N$. Additionally, $\mathcal{B}$ prepares n pairs $(cre{d}_{U_i,P}=({\theta }_1=A_i,{\theta }_2=B_i,{\theta }_3=C_i·F{\left(P\right)}^{{\beta }_i},{\theta }_4=g^{-{\beta }_i}))$ for each user $i\in [1,n]$, where ${\beta }_i{\leftarrow }_R{\mathbb{Z}}_N^{*}$. $i\in [1,\ell ]$ from the ℓ-HSDH challenge are distributed randomly in the user sets. For each $i\in [1,n]$, we mark either ${\varpi }_i=1$ if $\left(cre{d}_{U_i,P}\right)$ is known or ${\varpi }_i=0$ if $\left(cre{d}_{U_i,P}\right)$ is not from the ℓ-HSDH challenge and selected randomly from ${\mathbb{Z}}_N^{*}$. Finally, B calculates $h_j=g^{{\zeta }_j},{\zeta }_j$ for all ${\tau }_j$ and $B_{ij}=urt\left[i\right]\left[j\right]=h_j^{s_i}=A_i^{{\zeta }_j}$ for all $i\in [1,n]$ and $j\in [1,T]$. For other groups and their users, $\mathcal{B}$ randomly generates $gs{k}_G$ and $s_i$ for every group and user and then executes CreateGroup and AddUser(n, T) just as the underlying algorithms in BU-RSH.
• Queries: $\mathcal{A}$ can make the following queries, each of which is serviced by $\mathcal{B}$ sequentially.

  –

  Corruption queries: The corruption list $Cor$ is initialized as ∅. The adversary $\mathcal{A}$ can query CreateGroup and AddUser for the secret information of some groups and users. If $Cor\cap Chosen=\text{∅}$, $\mathcal{B}$ will respond and update the corruption list $Cor$. If ${\varpi }_i=1$, $\mathcal{B}$ simulates the GA correctly, and $\mathcal{A}$ obtains the credential $cre{d}_{U_i,P}$. Otherwise, $\mathcal{B}$ reports failure and aborts. Since the verification equations $e({\theta }_1,\Omega ·{\theta }_2)=\varphi$ and $e({\theta }_2,u)=e({\theta }_3,g)·e({\theta }_4,F\left(P\right))$ are satisfied, this is not distinguishable from receiving the real credential. However, if $Cor\cap Chosen\ne \text{∅}$, $\mathcal{B}$ aborts, as well.

  –

  Hash queries: The adversary $\mathcal{A}$ can query the hash functions used in the Handshake protocol.

  –

  PROOF Queries: The adversary $\mathcal{A}$ can query a proof of knowledge of message $r_{\mathcal{A}}$ as user i at time interval ${\tau }_j$. If ${\omega }_i=1$, $\mathcal{B}$ responds to the proof $\mathtt{PROOF}\left(cre{d}_i\right)\left[r_{\mathcal{A}}\right]$ using the secret key $\{cre{d}_i,s_i\}$. If $i=i^{*}$, B selects $t^{*}{\leftarrow }_R{\mathbb{Z}}_p^{*}$ and implicitly defines $({\theta }_1^{*}=g^{1/t^{*}},{\theta }_2^{*}=g^{t^{*}}·{\Omega }^{-1},{\theta }_3^{*}=u^{t^{*}}·F{({\mu }_1·{\mu }_n)}^{\beta }·{\Omega }^{\frac{K}{J}},{\theta }_4^{*}=g^{\beta }·{\Omega }^{\frac{1}{J}})$. The function $F({\mu }_1·{\mu }_n)=v_0·{\prod }_{i=0}^{i=n}{v}_i^{{\mu }_i}$ is written as $F({\mu }_1·{\mu }_n)=u^J·g^K$ where $J=z_0-2\gamma q_A+{\sum }_{j=1}^n{z}_j{\mu }_j$, $K={\rho }_0+{\sum }_{j=1}^n$. Based on the above implicit definition $({\theta }_1^{*},{\theta }_2^{*},{\theta }_3^{*},{\theta }_4^{*})$, B can respond with the corresponding proof to the adversary.

  –

  Handshake queries: The adversary $\mathcal{A}$ can make queries on the Handshake protocol with the group users. The transcripts of the queried users can be generated by $\mathcal{B}$ using the corresponding attribute certificates, which are in accordance with the Handshake algorithm.

• Output: The output of the security game is “1”, only if the adversary $\mathcal{A}$ on half of one user $i^{*}$ in the group $G^{*}$ succeeds in executing Handshake with $\mathcal{B}$. After at most $n-1$ total queries, $\mathcal{A}$ will be dedicated to forge the PROOF on one random message $r_{\mathcal{A}}$ on behalf of one group user $i^{*}$ from $G^{*}$ and execute the handshake protocol with $\mathcal{B}$.

According to the description of the above security game, the probability that $\mathcal{B}$ does not abort is $\frac{\ell }{n}$. Hence, for all AddUser queries, $\mathcal{B}$ simulates successfully with the probability $\theta \ge {\prod }_{\lambda =0}^{q_A-1}\frac{\ell -\lambda }{n-\lambda }$, where $q_A(<n)$ is the number of queries for AddUser.

The perfect proof system implies that the adversary has to forge the corresponding blinded credential proof of user $i^{*}$. For some $\beta {\leftarrow }_R{\mathbb{Z}}_p^{*}$, ${\theta }_3^{*}=u^{t^{*}-\omega }F{\left(P^{*}\right)}^{\beta }$, ${\theta }_4^{*}=g^{\beta }$, where $F\left(P^{*}\right)=v_0·{\Pi }_{k=1}^n{v}_k^{{\mu }_k}=u^{J^{*}}·g^{K^{*}}$ and $s^{*}=t^{*}-\omega$. If $J^{*}=0$, $\mathcal{B}$ can generate $u^{*}$ and then retrieves a full tuple $(g^{\frac{1}{s^{*}+\omega }},g^{s^{*}},u^{s^{*}})$ where $s^{*}=t^{*}-\omega$ differs from $s_1,\cdots ,s_{n-1}$ with probability at least $1-(n-1)/N$.

Thus, if $\mathcal{A}$’s successful advantage ϵ is non-negligible, we can deduce the successful probability of $\mathcal{B}$. By using the extractor of the PROOF shown in [18,19], $\mathcal{B}$ can solve the ℓ-HSDH problem with the probability ${ϵ}^{\prime }$. The detailed analysis of ${ϵ}^{\prime }$ can be referred to [18]. ☐

Theorem 2. 

The BU-RSH scheme satisfies the detector resistance (DR), and unlinkability assuming the subgroup decision (SD) problem is hard.

Proof. 

For the DR property, the adversary $\mathcal{A}$ has to distinguish a handshake instance with a true group member from an instance with a simulator $SIM$. During the handshake in our proposed scheme, we notice that the group member (e.g., A) sends only the blinded credential proof $\mathtt{PROOF}\left(cre{d}_A\right)\left[r_A\right]=({\sigma }_1,{\sigma }_2,{\sigma }_3,{\sigma }_4,{\sigma }_5,{\pi }_1,{\pi }_2,{\pi }_3,{\pi }_4,T_1,T_2)$ for authentication, which can provide the anonymity of his identity. Since the transcript of a participant during the handshake seems to be random, $\mathcal{A}$ cannot determine whether it was generated by a true group member or a simulator.

Therefore, the proof of detector resistance relies on proving the anonymity of identities. The blinded credential proof is constructed from the technique of Boyen and Waters’s group signature [18], which is based on the subgroup decision problem. Hence, the proof method is similar to Theorem 5.1 in the group signature scheme of Waters [18], which we adapt to the simpler case and the interactive handshake environment. Therefore, the detailed description is not provided here.

Similarly, two kinds of simulations in the DR attack game (${\Phi }_0$ and ${\Phi }_1$) can be constructed, such that ${\Phi }_0$ is simulated according to the original handshake scheme and ${\Phi }_1$ is the same as in the original scheme, except that h is chosen randomly from $\mathbb{G}$ instead of ${\mathbb{G}}_q$. We denote the adversary’s advantage in the ${\Phi }_0$ by $Ad{v}_{\mathcal{A}}$ and in the modified simulation by $Ad{v}_{\mathcal{A},{\Phi }_1}$. According to the results of Lemma 5.2 in [18], the two simulations are essentially indistinguishable, unless the decision subgroup assumption is easy. Moreover, if h is chosen from $\mathbb{G}$, then the identity of each participant is perfectly hidden based on Lemma 5.3 in [18]. Therefore, the detector resistance is achieved assuming the subgroup decision problem is hard.

For the unlinkability, this property is achieved by using a similar method that is mentioned in [8], in which case each user obtains a reusable attribute credential. Since the reusable credentials are blinded completely by applying different parameters each time, even the GA cannot identify the users’s identities by eavesdropping on the transcripts of handshakes. Therefore, no one, including the GA, can identify and link a user who participates in a secret handshake.

Assuming $\mathcal{A}$ breaks the unlinkability property with a non-negligible probability $\frac{1}{2}+ϵ$, $\mathcal{A}$ has to distinguish whether two handshake instances are related to the same participant or not. The attack game ${\mathtt{Game}}^{Unlink}$ is similar to the parallel executions of the two attack games ${\mathtt{Game}}^{DR}$ for DR. Thus, the proof of unlinkability can be described in a similar way as in the proof of DR. Hence, the detailed proof is not provided here for brevity. ☐

4.2. Performance Analysis

Here, we analyze the performance of our proposed scheme by considering of its computation costs. In the literature, most secret handshake schemes are provably secure under random oracles. Only a few secret handshake schemes are implemented without random oracles, which are basically derived from the first efficient scheme proposed by Ateniese et al. [8]. For clarity, we describe the performance comparison among some representative schemes selected from the existing literature. Each participant’s computational costs are considered with respect to the different phases of the secret handshake schemes, which are described in Table 1.

According to the related experiments’ findings, one pairing operation and modular exponentiation are the most time-consuming computations in the cryptography schemes. Hence, we focus on giving the computation costs about the pairing and modular exponentiation operations. By using Barreto’s ECC (Elliptic Curves Cryptography) Pairing Library [20], we calculate the computational costs of the pairing and the modular exponential operations with respect to the schemes in our comparison. $T_p$ denotes the time for one bilinear pairing operation in the elliptic curve groups, which costs about 12.23 ms. $T_E$ denotes the time for one modular exponential operation, which costs about 2.42 ms. $T_{ME}$ denotes the time for one multi-exponentiation operation, which costs about 3.24 ms. The experiments are based on Intel Pentium-4 2.8 GHz with 512 MB RAM.

Table 1. A comparison of related secret handshake schemes. BU-RSH, backward unlinkable secret handshake scheme with revocation support.

	Ateniese et al. [8]	Kawai et al. [12]	Wen and Zhang [15]	BU-RSH
Setup	$(2n+3)T_E$	0	0	0
CreateGroup	$T_E$	$T_E$	$T_E$	$T_E$
AddUser	$2T_E$	$T_E$	$T_E$	$4T_E$
Handshake	$3T_p+3T_E$	$7T_p+10T_E+15T_{ME}$	$5T_p+8T_E+9T_{ME}$	11$T_p+6T_E+8T_{ME}$
Traceability	No	Yes	Yes	Yes
Revocation	No	No	Yes	Yes
Backward Unlinkability	No	No	Yes	Yes
Random Oracles	without	with	with	without

Table 1. A comparison of related secret handshake schemes. BU-RSH, backward unlinkable secret handshake scheme with revocation support.

	Ateniese et al. [8]	Kawai et al. [12]	Wen and Zhang [15]	BU-RSH
Setup	$(2n+3)T_E$	0	0	0
CreateGroup	$T_E$	$T_E$	$T_E$	$T_E$
AddUser	$2T_E$	$T_E$	$T_E$	$4T_E$
Handshake	$3T_p+3T_E$	$7T_p+10T_E+15T_{ME}$	$5T_p+8T_E+9T_{ME}$	11$T_p+6T_E+8T_{ME}$
Traceability	No	Yes	Yes	Yes
Revocation	No	No	Yes	Yes
Backward Unlinkability	No	No	Yes	Yes
Random Oracles	without	with	with	without

From Table 1, we can see that Kawai et al.’s scheme [12] and Wen and Zhang’s scheme [15] achieve traceability and unlinkability using the group signature method. However, those schemes are proven secure in the random oracle model. Compared to Kawai et al.’s scheme [12], Wen and Zhang’s scheme [15] is more computationally efficient and achieves revocation support. For Ateniese et al’s scheme [8], since it distinguishes different groups through group identities, which are all assumed to be n-bits strings, $2n+3$ modular exponentiations need to be computed in the Setup phase, and every group must know and maintain $n+2$ modular exponentiations as the private values to issue group credentials in the CreateGroup phase. Towards the proposed scheme, BU-RSH, different groups are separate, which have respective group public and private keys without needing the group identities for distinction. Then, the computation costs of BU-RSH are reduced in both of the Setup and CreateGroup phases. More importantly, the revocation support, backward unlinkability and security in the standard model are all accomplished in our proposal, BU-RSH.

Moreover, for the sake of revocation checking, each member needs $|R{L}_j|$ bilinear pairing computations in the Wen and Zhang [15] and BU-RSH scheme. In order to achieve provable security in the standard model, each participant in the interactive handshakes needs a little more computation costs in our BU-RSH scheme. However, it is necessary to authenticate the revocation status of the counter-party in practical secret handshakes. It is also a better expectation if a scheme can be provably secure without random oracles. Hence, the trade-off is reasonable and acceptable in order to adapt our secret handshake scheme to more practical applications.

5. Conclusions

In this paper, we have proposed a backward unlinkable secret handshake scheme with revocation support in the standard model. Specifically, our proposal fulfills some practical functionalities, such as backward unlinkability, revocation, traceability and security, without random oracles. By using the idea of the verifier local revocation group signature in the standard model, our new scheme also achieves the advantages of a standard group signature scheme: the credential of each user could be short and reusable; mutual authentication could take constant rounds; revocation information could be at most linear in the number of revoked participators; and, finally, the scheme is proven in the standard model. In future work, a practical approach is to design an unlinkable secret handshake scheme that satisfies the computations of revocation checking to be sub-linear to the number of revoked users. How to provide a better design derived from multilinear maps or lattices is still a promising challenge.