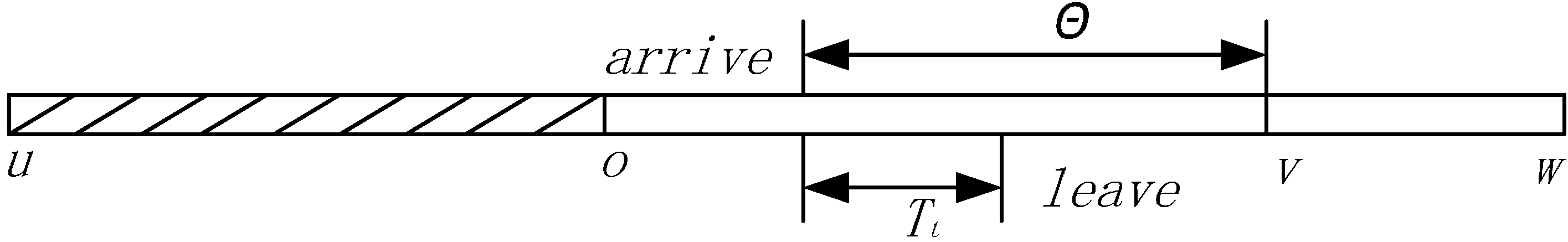An Approach to an Intersection Traffic Delay Study Based on Shift-Share Analysis

Abstract

Intersection traffic delay research has traditionally placed greater emphasis on the study of through and left-turning vehicles than right-turning ones, which often renders existing methods or models inapplicable to intersections with heavy pedestrian and non-motorized traffic. In the meantime, there is also a need for understanding the relations between different types of delay and how they each contribute to the total delay of the entire intersection. In order to address these issues, this paper first examines models that focus on through and left-turn traffic delays, taking into account the presence of heavy mixed traffic flows that are prevalent in developing countries, then establishes a model for calculating right-turn traffic delay and, last, proposes an approach to analyzing how much each of the three types of traffic delay contributes to the total delay of the intersection, based on the application of shift-share analysis (SSA), which has been applied extensively in the field of economics.

1. Introduction

Intersection delay studies play an important role in traffic planning, signal control design and determining the level of service (LOS) at signalized intersections. The study of intersection delay has traditionally focused more on through and left-turn traffic, which may have its merit when the intersection of concern has very little pedestrian traffic. However, in cases like China or any other developing country with a dense urban population, where there are constant flows of pedestrian and non-motorized traffic conflicting with right-turning vehicles, existing methods or models are frequently inadequate in assisting delay analysis of urban intersections.

One major reason for the lack of research on right-turn delay is due to the fact that most signalized intersections do not warrant control on right-turning traffic, which, again, presents a special problem for developing countries, like China and India, where there are a large number of “first-generation” new drivers who lack either the awareness of or the compliance to basic rules of the road, often both. On the other hand, there are also constant violations of traffic rules from the pedestrian side. These two combined often lead to increased total delay at urban intersections and, as a consequence, lowering of the level of service (LOS), as well.

Another area of traffic delay study is the investigation into the relations between different types of delay at an intersection and how they each contribute to the total delay of the intersection. To propose an approach to addressing the problem, this papers introduces shift-share analysis (SSA), which is used in regional science, political economy and urban studies, to determine what portions of regional economic growth or decline can be attributed to national, economic industry and regional factors. SSA is used here to analyze how much each of the three types of delay (i.e., left-turn, through and right-turn delay) contributes to the total delay of the intersection. The introduction of SSA into the study of traffic delay helps broaden the options for determining the causes and understanding the patterns of intersection delay and also provides a new tool for intersection traffic analysis and design.

2. Literature Review

Traffic delay is one of the major criteria in determining the level of service or the effectiveness of traffic operations at signalized intersections [1,2]. The overall level of congestion, driver comfort, vehicle gas consumption and the average loss of travel time, among others, can all be attributed to traffic delay. Traffic delay is also an area of concern in traffic planning, signal design and traffic control management [3,4]. Since the 1950s, intersection delay analysis has been one of the focuses of study for transportation professionals [5,6,7]. Many delay models and evaluation methods were introduced [8,9], a significant number of which were addressing the modeling of through and left-turning vehicular traffic at signalized intersections. The results have been mostly positive in reflecting real-world traffic operations [10].

To better investigate and understand delays involving right-turning vehicles, some researchers took the traditional approach of establishing right-turn delay models [11,12]. Zhang et al. suggested that right-turn delay was caused mostly by pedestrian interference, but did not present situations in which pedestrians are compliant with traffic controls [13]. Qureshi et al. introduced a method of calculating the average delay for right-turning vehicles on red through the use of queuing accumulation polygons (QAP), which was developed from queuing theory [14]; however, situations in which vehicles come under interference from pedestrians were not discussed. Guo et al. put forward a model for calculating delay caused by pedestrians passing through right-turning traffic and made an improvement to delay analysis by bringing vehicle types into consideration [15]. Zhou et al. introduced a choice model based on individual pedestrian crossing behavior [16]. Tao et al. studied vehicle headway and established a mixed distribution model [17]. Zhao et al. conducted a regression-based pedestrian adjustment factor analysis that involves right-turn traffic [18].

Most of the above-mentioned models analyze each type of delay separately from the influences from the others and lack efforts in examining the relations among different types of delay. Moreover, total delay alone does not reflect the delay changes in different ways (legs) and lanes of the intersection. Therefore, it is hard for such analyses to draw deeper conclusions on the true causes and patterns of intersection delay.

A shift-share analysis attempts to identify the sources of regional economic changes [19,20], which helps identify industries in which a regional economy has competitive advantages over the larger economy [21,22]. SSA can be used to provide a set of quantified methods to determine the relations among the three types of intersection delay and how they each contribute to the total delay.

3. Intersection Delay Models

3.1. Unsaturated Straight and Left-Turn Delay Models

All analyses in this paper are based on the right-driving system unless otherwise stated.

Under unsaturated conditions, intersection delays are primarily caused by traffic control [23,24]. This paper first examines the delays from one approach of a typical crossing (four-legged, two-way) intersection, which has exclusive left-turn phases, and left-turning and through approaching traffic do not interfere with each other. Delays for both types of approaching traffic can be calculated [25].

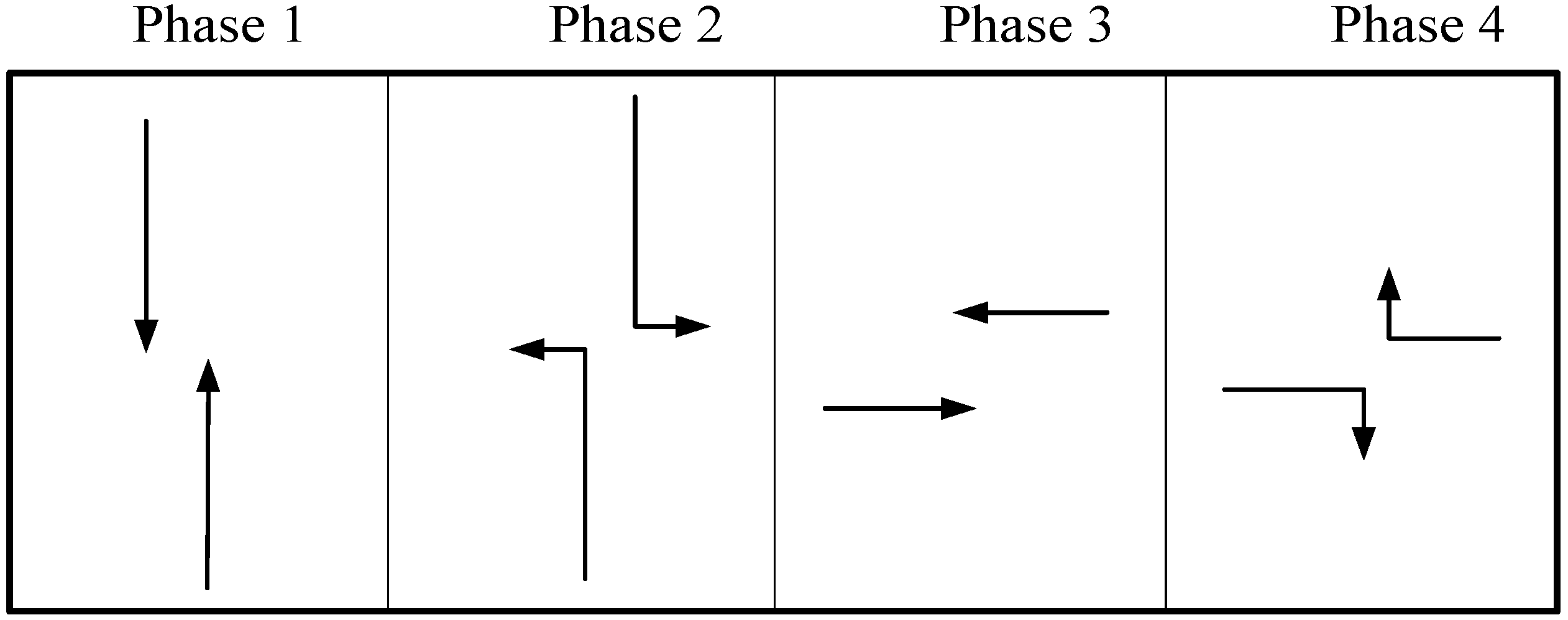
Figure 1. Phase diagram of a typical four-phase signal control.

Figure 1. Phase diagram of a typical four-phase signal control.

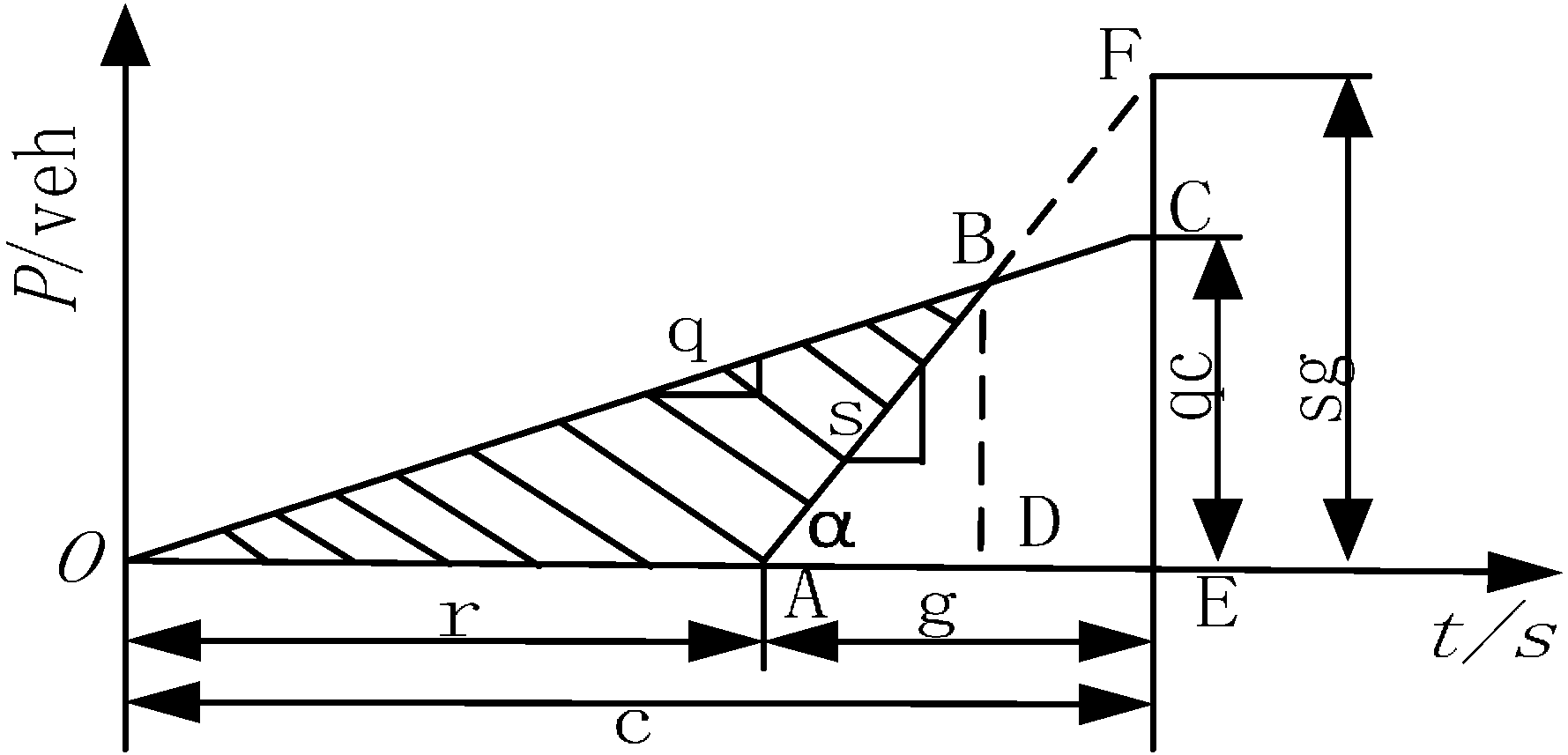
The signal phases of a typical four-legged, two-way intersection with exclusive left-turn phases are illustrated in Figure 1. When the vehicle arrival rate and the capacity of an approach are fixed in any given signal cycle, there is a linear relationship between delay and arrival rate. In Figure 2, the x-axis shows the time t (s); the y-axis represents the total number of vehicles (veh); q is the vehicle arrival rate (veh/s); s is the saturated flow rate of the approach (veh/s); and c, r and g are cycle length, red and green intervals, respectively. The projection of $∆\text{OAB}$ on the x-axis is the delay of every vehicle arriving at the stop line (more precisely, the tail of the vehicle queue); and the projection on the y-axis is the number of vehicles queuing behind the stop line at different moments. Therefore, in any given signal cycle, the phasing delay D (veh/s) of all vehicles coming into the approach equals the area of $∆\text{OAB}$, which is:

$$D=S_{\Delta OAB}=\frac{1}{2}OA\cdot BD$$

(1)

where,

$$OA=r,BD=AD\cdot \tan \alpha =AD\cdot s,$$

also because,

$$AD=\frac{qr}{s-q}, [AD\cdot s=(r+AD)\cdot q],$$

(2)

therefore,

$$D=\frac{1}{2}OA\cdot BD=\frac{qs{r}^2}{2(s-q)}.$$

(3)

Figure 2. Unsaturated vehicle delay.

Figure 2. Unsaturated vehicle delay.

3.2. Right-Turn Delay Models

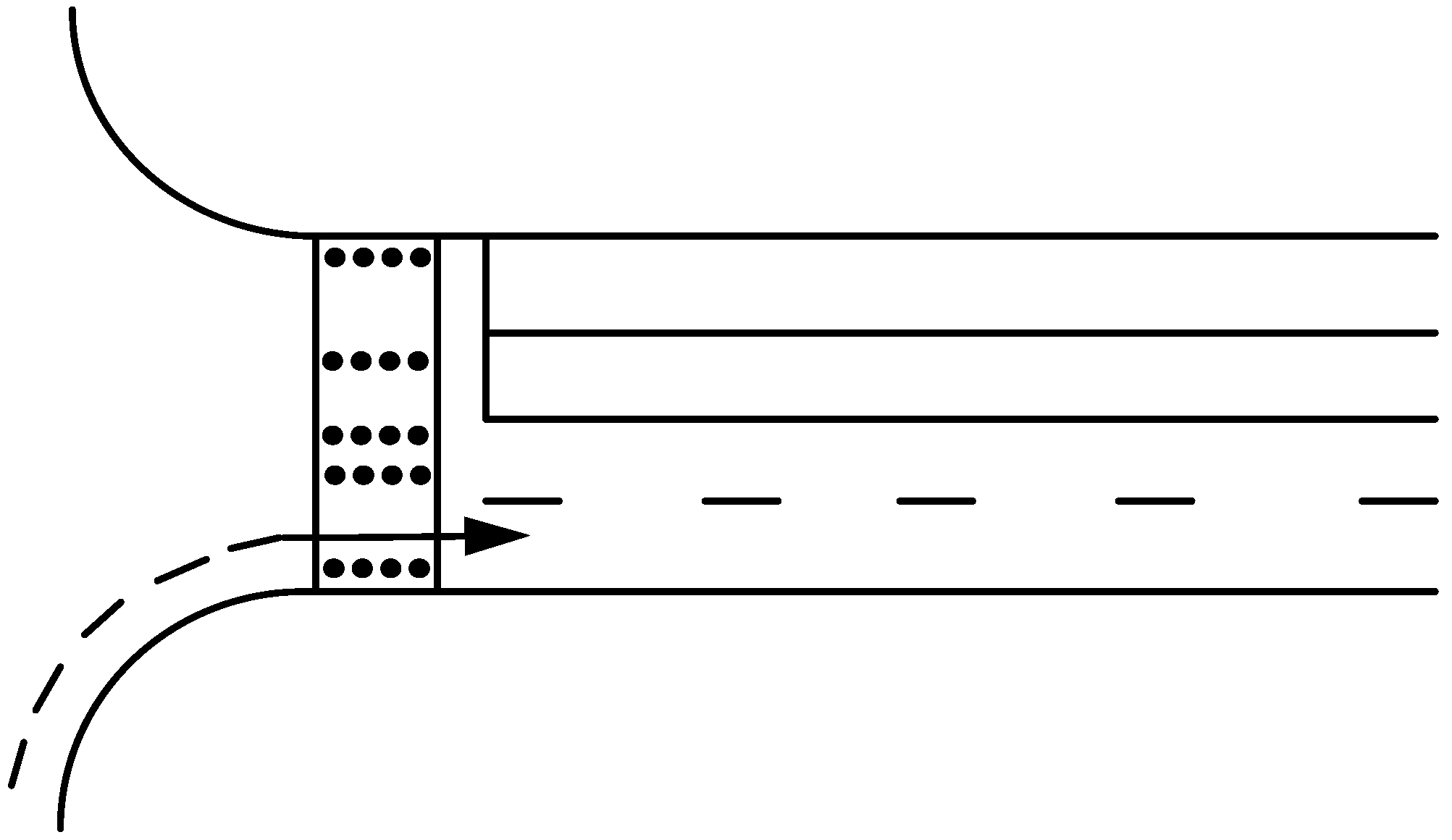
The delay of right-turning vehicles passing through crossing pedestrians can be modeled as the following process: in Figure 3, at S₀, the vehicle arrives at the pedestrian stream and decides whether there is a passable gap, i.e., whether there is a long enough time interval for it to pass through the pedestrian stream. S is the time when there is a passable gap for the vehicle to drive through the conflict area. Therefore, the delay can be calculated with T = S − S₀, with which we could, in turn, conclude that right-turn delay is primarily determined by three factors, namely:

(1)

the randomness of arrival of the right-turning vehicle;

(2)

the randomness of pedestrian arrival;

(3)

the minimum passing interval.

Figure 3. Right-turn delay.

Figure 3. Right-turn delay.

Pedestrian crossing behavior can be modeled in a multi-row format as illustrated in Figure 4. Pedestrian crossing follows the Poisson distribution, and the interval between two adjacent rows obeys the exponential distribution. Minimal passing interval and pedestrian flow both follow the same approximate Poisson distribution.

Figure 4. Illustration of the pedestrian crossing model.

Figure 4. Illustration of the pedestrian crossing model.

Pedestrian crossing happens during the green interval. The process can be described in the following three steps (Figure 5): First, at the onset of the green signal, multiple rows of pedestrians with minimum intervals in between each row initiate the crossing process, which creates no passable gap for the vehicle. Next, pedestrian crossing starts to follow a Poisson distribution, and there are passable gaps for the vehicle to cross the conflict area. Finally, near the end of the green interval, vehicles can pass the crosswalk at will. u, v and w denote the time intervals of each step, respectively.

Figure 5. Illustration of pedestrian crossing process model.

Figure 5. Illustration of pedestrian crossing process model.

Two types of right-turn delay models can be established following this pedestrian crossing process.

3.2.1. Type 1 Delay Model

The Type 1 delay model deals with delay caused by the random pedestrian stream, as illustrated in Figure 6. Variables are defined as follows: random variable $\theta$ is the time at which the vehicle arrives at the conflict area. Its value is the interval between the end of pedestrian crossing and the vehicle arrival time. The probability density of $\theta$ is $\text{g}\left(\theta \right)$, and the corresponding probability distribution is $\text{G}\left(\theta \right)$. The uniform distribution is chosen to describe the arrival time. Random variable $T_t$ is the vehicle delay. In situations of Type 1 delay, $0\ll T_t\ll \text{v}$. The probability density of $T_t$ is ${\text{f}}_{\text{t}}\left(T_t\right)$, and the corresponding probability distribution is ${\text{F}}_{\text{t}}\left(T_t\right)$.

Figure 6. Illustration of the Type 1 delay model.

Figure 6. Illustration of the Type 1 delay model.

The vehicle arrives at $\theta$ moment, waiting for a passable gap. When the first passable gap appears, the vehicle drives through the conflict area, resulting in a delay of $T_t$. According to the remaining life theorem of Poisson streams and the assumption that passable intervals follow a Poisson distribution, we can calculate the remaining life of the passable interval, and the delay obeys the exponential distribution, i.e.:

$$F_t(T_t)=P\left\{T_t\le t\right\}=1-e^{-\lambda t}$$

(4)

where $\lambda$ is the interval parameter and t is the time, $t\gg 0$.

The probability density of $T_t$ is $f_t(T_t)={F_t}^{\prime }(T_t)$, therefore:

$$f_t(T_t)=\lambda e^{-\lambda t}.$$

(5)

When the vehicle arrives at $\theta$ moment, its delay distribution function is ${\text{F}}_{\text{t}}\left(T_t,\theta \right)$, and the corresponding probability density is ${\text{f}}_{\text{t}}\left(T_t,\theta \right)$. When $0\ll T_t<\theta$, right-turning vehicles can pass through immediately upon discovering a passable gap, and the distribution function becomes ${\text{F}}_{\text{t}}\left(T_t,\theta \right)={\text{F}}_{\text{t}}\left(T_t\right)$. When $T_t\gg \theta$, vehicles can only pass through the conflict area after the crossing pedestrians, in which case $T_t=\theta$, and the distribution function becomes $F_t\left(T_t,\theta \right)=1-F\left(\theta \right)$, where $F\left(\theta \right)$ is the distribution function of $\theta$. Therefore, the distribution function of $T_t$ is:

$$F_t\left(T_t,\theta \right)=\{\begin{array}{c}1-e^{-\lambda t}, 0\le t\le \theta \\ e^{-\lambda \theta }, t\ge \theta \end{array}$$

(6)

The time interval for random crossing pedestrians is [0,$\nu$]. During [0,$\nu$], the average delay $D_1$ when the vehicle arrives at $\theta$ moment is:

$$D_1={\displaystyle \iint }t{f}_t\left(T_t,\theta \right)g\left(\theta \right)dtd\theta .$$

(7)

With (5) and (6), we have,

$$D_1=\frac{\lambda \nu +e^{-\lambda \nu }-1}{{\lambda }^2\nu }$$

(8)

$$\text{λ}=\text{q}\raisebox{1ex}{${\text{e}}^{\raisebox{1ex}{$-\text{qα}$}\!\left/ \!\raisebox{-1ex}{$3600$}\right.}$}\!\left/ \!\raisebox{-1ex}{$3600$}\right..$$

(9)

Where $q$ is the pedestrian flow (p/h) and α is the time interval between pedestrian rows (s).

3.2.2. Type 2 Delay Model

The Type 2 delay is comprised of two phases. [0,u] is given as the time interval for multiple rows of pedestrians with no passable gaps in between them to leave the conflict area. As shown in Figure 7, the Type 2 delay can be represented by $T^{\prime }=t_1+t_2$, where $t_1$ is a random variable ($0\ll t_1\ll u$), whose distribution function is $F_1\left(t_1\right)$ and the corresponding probability density $f_1\left(t_1\right)$. $\theta$ is the difference between the time pedestrians leave the conflict area and the arrival time of the right-turning vehicle.

Figure 7. Illustration of the Type 2 delay.

Figure 7. Illustration of the Type 2 delay.

When $t_1$ and $\theta$ are both treated as uniformly distributed, the probability density of $t_1$ is:

$$f_1\left(t_1\right)=\frac{1}{u}.$$

(10)

$t_2$ is a random variable ($0\ll t_2\ll v$), whose distribution function is similar to Equation (3), in which case, the vehicle arrival time is no longer a random variable within [0, v], but is a constant, i.e., the value of v. Therefore, the distribution function of $t_2$ is:

$${\text{F}}_2\left({\text{t}}_2,\text{v}\right)={\text{F}}_{\text{t}}\left({\text{t}}_2,\text{v}\right).$$

(11)

The average Type 2 delay $D_2$ can be calculated with the following equations:

$$D_2=E\left(T^{\prime }\right)=E\left(t_1\right)+E\left(t_2\right)$$

(12)

$$\text{E}\left({\text{t}}_1\right)={{\displaystyle \int }}_0^{\text{u}}{\text{t}}_1{\text{f}}_1\left({\text{t}}_1\right){\text{dt}}_1$$

(13)

$$\text{E}\left({\text{t}}_2\right)={{\displaystyle \int }}_0^{\text{v}}{\text{t}}_2{\text{f}}_2\left({\text{t}}_2\right){\text{dt}}_2+\text{v}\left[1-\text{F}\left(\text{v}\right)\right]$$

(14)

where $f_2\left(t_2\right)$ is the probability density of $t_2$.

By bringing (10), (12) and (13) into (14), we can have:

$$D_2=\frac{u}{2}+\frac{1-e^{-\lambda \nu }-\lambda \nu e^{-\lambda \nu }}{{\lambda }^2\nu }+\nu e^{-\lambda \nu }.$$

(15)

When the arrival time is uniformly distributed, the average delay of right-turning vehicles is:

$$D=\frac{\left(u+\nu \right)D_2+\nu D_1}{u+2\nu }.$$

(16)

To test the validity of the model, $u$, $\nu$ and $\text{α}$ are given the values of 10 s, 15 s and 5 s respectively. Right-turn average delays are calculated under conditions of five sets of pedestrian volume ($\text{q}$), i.e., 700 p/h, 800 p/h, 900 p/h, 1000 p/h and 1100 p/h. All of the values are then fed into Vissim, which is a computer-aided traffic simulation software. The results of the calculations and simulations are then compared.

In Table 1, average delays calculated with the model are either the same as or very close to the results of computer simulation, which suggests that when pedestrian volume is between 700 and 1100 p/h, the model can be used for estimating average right-turn traffic delay to a high degree of accuracy.

Table 1. Comparison of average delays.

Pedestrian Volume (p/h)	700	800	900	1000	1100
Simulation results (s)	10.1	10.1	10.2	10.4	10.8
Calculation results (s)	10.1	10.1	10.2	10.3	10.6

Table 1. Comparison of average delays.

Pedestrian Volume (p/h)	700	800	900	1000	1100
Simulation results (s)	10.1	10.1	10.2	10.4	10.8
Calculation results (s)	10.1	10.1	10.2	10.3	10.6

4. Structured Delay Analysis Based on Shift-Share Analysis

Shift-share analysis has been widely applied in fields of regional science, political economy and urban studies to determine what portions of regional economic growth or decline can be attributed to national, industry and regional factors. A shift-share analysis attempts to identify the sources of regional economic changes, which helps identify industries in which a regional economy has competitive advantages over the larger economy. It is one of the major tools for regional economic and industrial structure analysis. This papers attempts to broaden its application to intersection delay analysis.

4.1. The Premise

With shift-share analysis, a change in regional traffic delay is seen as a dynamic process. Regional traffic or intersection delay is treated as the whole, whose change within a certain period of time is then subdivided into three components, which are the share effect, structural deviation effect and competitiveness effect.

SSA is used here to evaluate the structure of delay at an intersection through the analysis of the competitiveness of each component, with the purpose of determining the structure of future delay growth and, based on the result of which, to provide a more valid and scientific basis for future delay counter-measures.

4.2. The Modeling

The way SSA is applied to intersection delay analysis is by breaking apart the delay growth of the entire intersection into its components, i.e., first into the approaches of the intersection and, after that, further into the flows of each approach, namely through, left-turn and right-turn traffics.

The growth (G) in traffic delay at an intersection can be divided into three parts: (1) share effect (RS); (2) structural deviation effect (PS); and (3) competitiveness effect (DS). Delay growth is the sum of share effect, structural deviation effect and competitiveness effect, i.e., G = RS + PS + DS. What follows is how to calculate each effect.

(1) Share effect (RS):

$$RS={\displaystyle \sum }{Y}_i^{0}R$$

(17)

where i denotes left-turning, through or right-turning traffic flow; RS represents the delay growth of an approach that is proportionate to the total growth of the entire intersection; $Y_i^0$ is the baseline delay of the flow of traffic that is represented by I; and R is the growth rate of the entire intersection delay. If RS is greater than real delay values, then the deviation is positive, otherwise negative.

(2) Structural deviation effect (PS):

$$PS={\displaystyle \sum }{Y}_i^0{R}_i-{\displaystyle \sum }{Y}_i^{0}R={\displaystyle \sum }{Y}_i^0\left(R_i-R\right)$$

(18)

where PS is the difference of the delay growth between that calculated with the growth rate of a traffic flow and that calculated with the growth rate of the total delay. It reflects the relation between the growth rate of one traffic flow and the entire intersection. Additionally, $R_i$ is the delay growth rate of the traffic flow, which is denoted by i.

(3) Competitive effect (DS):

$$DS={\displaystyle \sum }{Y}_i^0{r}_i-{\displaystyle \sum }{Y}_i^0{R}_i={\displaystyle \sum }{Y}_i^0\left(r_i-R_i\right)$$

(19)

where DS is the difference of the delay growth between the actual growth from the traffic flow that is denoted by i and its calculated growth based on the total growth rate of the entire intersection. It reflects the traffic flow’s “competitiveness” in contributing to the total delay growth of the intersection. $r_i$ is the actual delay growth from the traffic flow that is denoted by i.

Putting everything together, we have:

$$G=RS+PS+DS={{\displaystyle \sum }}^{\text{}}{Y}_i^{0}R+{\displaystyle \sum }{Y}_i^0\left(R_i-R\right)+{\displaystyle \sum }{Y}_i^0\left(r_i-R_i\right)$$

(20)

5. Case Study

The intersection between Yong-Chang road and East Bao-xiu road in the Chinese city of Kunming was picked as the site of application after careful examination of its traffic volumes and signal phasing design to ensure that it was indeed a typical four-phase intersection. Two seasons of delay data at the intersection were collected and gathered in Table 2:

Table 2. Delay statistics at the application intersection.

Approaches	Flow	1st Season	4th Season	Increase	Growth (%)
West-east	Total	18	30	12	67
	Through	8	15	7	88
	Left-turn	6	9	3	50
	Right-turn	4	6	2	50
North-south	Total	23	41	18	78
	Through	13	22	9	69
	Left-turn	7	13	6	86
	Right-turn	3	6	3	100

Table 2. Delay statistics at the application intersection.

Approaches	Flow	1st Season	4th Season	Increase	Growth (%)
West-east	Total	18	30	12	67
	Through	8	15	7	88
	Left-turn	6	9	3	50
	Right-turn	4	6	2	50
North-south	Total	23	41	18	78
	Through	13	22	9	69
	Left-turn	7	13	6	86
	Right-turn	3	6	3	100

Here, we take the north approach as the subject of study, whose average left-turn, through and right-turn delays were calculated with the previously introduced formulas and gathered in Table 3.

Table 3. North approach delay data.

Traffic Flow	RS			PS		DS
	Growth	Growth rate (%)	Difference	Growth	Growth rate (%)	Growth	Growth rate (%)
Through	8.67	67	1.67	2.71	21	−2.38	−18
Left-turn	4.67	67	1.67	−1.17	−17	2.5	36
Right-turn	2	67	0	−0.5	−17	1.5	50

Table 3. North approach delay data.

Traffic Flow	RS			PS		DS
	Growth	Growth rate (%)	Difference	Growth	Growth rate (%)	Growth	Growth rate (%)
Through	8.67	67	1.67	2.71	21	−2.38	−18
Left-turn	4.67	67	1.67	−1.17	−17	2.5	36
Right-turn	2	67	0	−0.5	−17	1.5	50

From the above two tables, we could know:

(1) All three traffic flows of the north approach, i.e., left-turn, through and right-turn, have higher delay growth rates than the delay growth of the entire intersection, which suggests that the north-south approaches have larger shares of causing the traffic delay at the intersection than the other direction. There is a newly finished business complex project to the northeast of the intersection, which could be the source of delay growth in the north-south direction.

(2) Through traffic contributes much greater delay to the total delay than left-turn and right-turn traffics, which indicates that the largest share of delay for the intersection comes from through traffic. The increase of through volume and inefficient signal phasing design could be two of the main reasons.

(3) Left-turn and right-turn delays from this approach appear to have higher growth rates than those of the other approaches. However, the through traffic contributes far less to the total delay growth than those of the other approaches. All of this indicates that the cause for the growth could be the traffic attraction from the newly finished business complex, and there is an emerging problem with the signal phasing design that needs to be adjusted to the changes of traffic volume.

6. Conclusions

Two areas of traffic delay study that demand more emphasis are right-turn delay and investigations into the effects of different types of delay on the intersection’s total delay. This paper made an effort to address both of these issues. First, the process or mechanism of right-turn conflict was analyzed and discussed, followed by the establishment right-turn delay models. Second, shift-share analysis was introduced to help provide a structured method of analyzing how each type of traffic delay affects or contributes to the total delay of the intersection. This new approach provides a quantified method of examining the delay changes of different traffic flows within an intersection, their relations and how they contribute to the total delay change of the intersection. The models and methods in this paper can help broaden the options in intersection delay study and provide more scientific bases for intersection planning, lane management, channelization and signal phasing design, etc.

Conflicts between left-turning vehicles and pedestrians in the real-world can be rather random and hard to describe accurately with models; therefore, the right-turn delay models in this paper can only be used as an attempt at calling for more emphasis on related studies and as a reference point to other researchers. The use of shift-share analysis in this paper is still rudimentary and lacks more tests with real-world data, but its potential in studying the relations between different delays and the total intersection delay is well worth further looking into.

What is worth noticing is that the method and model are only applicable when there is a dedicated right-turn lane. When the queue at the right-turning lane overflows or there is a mixed through and right-turning lane existing, the proposed model and the method would be very different from what has been discussed in the paper. Furthermore, all of the analyses were based on right-hand driving situations. Whether the model could be used for the study of left-turn delay in left-hand driving situations could be a topic for future studies