Abstract
Information must have physical support and this physical universe comprises physical interactions. Hence actual information processes should have a description by interactions alone, i.e., an extensional description. In this paper, such a model of the process of information articulation from the universe is developed by generalizing the extensive measurement theory in metrology. Moreover, a model of the attribute creation process is presented to exemplify a step of the informational articulation process. These models demonstrate the valuableness of the extensional view and are expected to enhance the understanding of the extensional aspects of fundamentals of information.
1. Introduction
Imagine an infant or a brand-new tabula rasa autonomous robot just thrown out into the physical universe. When such a system tries to gather and utilize information about its surrounding universe, how can it obtain the information? Suppose that there is a green apple. We, as experienced humans, can recognize that this fragment of the universe (the apple) is green. We have information that the apple is green. But how about the infant or the robot? They do not know what the green is, or, how green something is.
Many researches point out that essential relativeness of information (for instance, see the Locality Principle and other ontological principles in [1]). It is natural, especially in the physical view adopted in this study, because a system (part of the universe) inevitably interacts with surrounding systems (other parts of the universe) in its own way. But then, at the fundamental level, how can a system articulate a specific uniformity (e.g., the color of green) in a part of the universe? The meaning of the word articulate here is “to divide into fragments meaningfully arranged”. In principle, nothing other than the system itself can provide information on how to articulate the universe.
One may wonder if it is determined by the sensory system embedded in the system under consideration—our eyes, the retinae, the visual cortex, and other organs enable us to see the green. Yet this is not completely true. Yes, the visual system actually captures some optical stimuli from the surrounding universe. In general, the stimuli captured by the system that is gathering and utilizing information are actually restricted by the capability of its sensory subsystems. However, the way in which the information system articulates the stimuli is another matter. Although the stimuli may seem to be articulated selfishly, completely arbitrarily, by the information system, this is not the case. In the case of the color system for example, it is known that the color system differs from race to race, from language to language. Some may distinguish green from blue and others may not. However, they also have cognitive commonalities not only within a color system but also among different color systems [2]. So the answer for the question “what is green?” is unclear in the first place.
We consider such an issue in this paper. How does a system articulate and categorize its surrounding environment, and how does it assign an identifier for the properties of the part, i.e., a collection of attributes, to the articulated part of the environment? How can such information be obtained, or generated by a physical system? After all, this universe is a bunch of physical interactions. A system that is going to utilize information from the universe must extract the information through these physical interactions. In other words, if we borrow terminology from logic, we might be able to say that the system must extract the information fully extensionally.
To our knowledge, few studies have been conducted to investigate the fundamentals of information in such a view.
One might consider that, in physics, information is tightly connected to physical phenomena that are obviously extensional. The distinction between the physical phenomena and the informational phenomena is subtle. Even in the study of physics, the materiality or thinginess of nature has been pushed away in recent decades. Many authors have already declared that reality basically is an informational phenomenon (for example, [3,4,5,6,7,8,9]).
However, it may be also true that there is a certain spectrum of informational nature of physical interactions. A falling heavy body makes a dent on the surface of the floor. We, humans, tend to regard this as merely a physical consequence. The falling body or the falling may not be regarded as information for the floor. In contrast to this, let us consider a typical information phenomenon: in many countries, a change of a traffic signal to the red will make cars stopped. This situation may be intuitively informational. The change of the traffic signal may be regarded as information for the cars or the car-driver composite systems. An information theory may or may not distinguish these two situations. Anyway, a fundamental study of information should explain the differences among such information related phenomena in the view of information, even if the phenomena are not apparently causally related, that is, not well-suited to be studied in physics.
Thus, in the view of this paper, such an extensional approach to the fundamentals of information should cover broader scope than the information studies in physics.
In information theories, the approach developed by Alexander Chechkin (see [1]) might be regarded as one of such studies that have the nearest viewpoint.
His approach is based on two main notions: an object and information about object. In his theory, properties of objects are represented (and denoted) by subsets of those objects that has this property, i.e., each property is a subset of all objects and each subset is a property of objects. It is the classical set-theoretical approach to the concept of property [1].
To represent properties of objects extensionally, it seems natural to use the sets of objects, as Chechkin. Needless to say, in many studies in various disciplines, a property of objects, or equivalently in this paper, an attribute of objects, is treated as a set of objects. The attribute green is (represented by) all the green-ish objects. When someone asks “what is green?”, one may answer by indicating something greenish and saying “this is green”. Something green is one of the greenish objects one has ever met, and the attribute “green” can be defined by all the greenish objects one has ever met. Borrowing a term in linguistics, synchronically, this may be sufficient. That is, at a fixed point of time, all the greenish objects that one has ever sensed can represent the attribute green for him/her.
However, if one defines the attribute green by a certain (fixed) set of green-ish objects, there will be no room for a green thing newly accepted. Something newly accepted cannot reside in the set of green-ish objects, which is already fixed as “the definition of the attribute green”. Diachronically, an attribute is not merely that which is equivalent to a set of objects. There is a case in which modeling an attribute as a set of object is not appropriate.
This study addresses such a case. We will pursue the understanding of information as a universal structure that is fully extensionally obtained from finite physical interactions.
Note that, such an understanding may also demystify a kind of the bootstrapping process of information extraction from the universe. From the extensional viewpoint of this study, as already mentioned, information is naturally considered to be essentially relative to the (information receiving) system, the same as physical interactions are essentially relative. Information relative to the system implies the existence of the context, that is, another referred information within the system. But, then, how can a system articulate the universe without any contextual information (i.e., so to speak, criteria), at the most fundamental level of, or, at the very beginning of, information process? In other words, how can a system have information of its own without any presupposed another information? Though this study might be very focused and not general enough, it may be considered as an attempt to understand information from such an absolutely relative viewpoint.
Extracting/creating information from the universe via physical interventions has been discussed in the measurement theory in metrology (see [10], etc.). The theory is called the extensive measurement theory, which will be described in detail in Section 3. The purpose of the present study is to develop a general model of extensional information articulation process as a generalization of the extensive measurement theory.
In this paper, the authors
- present a model of the process of extensional information articulation as a generalized extensive measurement;
- provide a detailed example of a step of the extensional informational articulation process—a model of attribute creation.
The structure of this paper is as follows. Section 2 introduces some terms used in this article. In Section 3, the extensive measurement in metrology is explained in detail. Referencing the steps in the extensive measurement, a model for information articulation process as a generalized measurement is developed in Section 4. Section 5 exemplifies the concepts of the developed process by a model for attribute creation. Section 6 concludes this paper.
2. Information and IGUS
In this section, some terms in this paper are introduced, each of which having a specific meaning.
Information must have a physical support [11]. More modestly, a class of information must have a physical support. Though there seems no definitive agreement on what information is, one may agree that information is induced by a physical phenomenon. That is, at a certain level of investigations, information may be considered to be physical phenomena related to a class of physical interactions between a certain part of the physical universe and another part of the universe. The latter part of the universe, i.e., the receiver of information, is often called an Information Gathering and Using/Utilizing System, abbreviated to IGUS [12,13]. In this article, we will use this abbreviation to specify such a subsystem of the universe. We will call above-mentioned information as a physical phenomenon as information phenomenon. Note that those that regard a physical phenomenon as information for a certain IGUS are another IGUSes—human beings as IGUSes in many cases. This special kind of IGUS will be called a human-IGUS in this paper. In general, such IGUSes are not restricted to humans.
An IGUS is also merely a physical phenomenon in the universe. Ultimately, this physical world is just a bunch of physical interactions. In this article, the word “universe” is used to emphasize this uniformity—the status prior to being articulated. On the side of the universe, there is no criterion for sorting out these interactions as information for the IGUS. A tabula rasa IGUS must build its own information articulation system by itself through its physical interactions with the universe.
In contrast to the word “universe”, in most of the case, the word “world” used in this paper implicates the existence of IGUS(es) capturing it.
In the case of us, human-IGUSes, extracting/creating information from the universe via physical interventions has been well studied in the measurement theory in metrology. In the next section, such a process of measurement—the extensive measurement is reviewed.
3. Extensive Measurement
A good prototype for describing how a system extracts information from the physical universe exists in the metrological measurement theory.
Suppose that we try to measure an attribute of a physical thing, for example, the weight. First, we prepare an apparatus for measuring the attribute (a measuring instrument): an equal arm beam balance. We place a thing a on the left pan and another thing b on the right pan, and we observe which pan drops (we observe if it is balanced). Thus we can introduce an order relation between the attributes of two things a and b. When balanced, two things are virtually the “same” in the aspect of the attribute, the weight. By these equivalences, we can use copies to represent each specific weight, instead of using particular instances (e.g., using sands instead of apples). We can also define the concatenated or composed attributes of two or more things by placing them in the same pan. To evaluate the attribute, we select a thing as the unit, and if another thing is found to be equivalent with n-copies of the unit thing, the attribute value of the latter thing can be determined as n (given in the unit).
Such measurement processes have been generalized and abstracted in the extensive measurement theory.
The extensive measurement (see [10], etc.) was formulated by Herman von Helmholtz [14], Otto Ludwig Hölder [15], and others. The extensive measurement relates the physical measurement situations/operations to a mathematical model. The mathematical model has three primitives [10]: a nonempty set A, a binary relation ≿ on A, and a binary operation ◦ : A × A → A. The interpretations of these primitives are: A is a set of objects or entities that exhibit the attributes in question; a ≿ b holds if and only if a exhibits, in some prescribed qualitative fashion, at least as much of the attribute as b; and a ◦ b is an object in A that is obtained by concatenating (or composing) a and b in some prescribed, ordered fashion.
In this article, our main concern is the way in which the extensive measurement theory builds such a mathematical model from the operations in the real physical world.
The general steps in the extensive measurement are summarized as follows [16]:
- Suppose that there is a collection I of things or events in the real world (in which all things/events are identifiable by the measurer), and let the elements (i.e., things or events) in the collection I be countable. (Countability and identifiability enable to make n-copy of an element, later.)
- A comparator m is introduced as a measuring instrument. It can compare an element in I with another one. That is, the comparator m shows that whether the compared elements are indistinguishable or distinguishable from the comparator’s viewpoint (that is, in the aspect of the attribute under consideration). Introduce an equivalence relation ∼
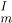 . Elements a and b in I have a relation a ∼
. Elements a and b in I have a relation a ∼ 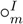 b if and only if the comparator m shows that they are indistinguishable, and under this equivalence relation ∼
b if and only if the comparator m shows that they are indistinguishable, and under this equivalence relation ∼ 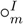 , all the elements in I can be partitioned into equivalence classes X = {α, β, γ, . . .}. Note that the equivalence class consists of real physical tokens (e.g., apples). There can be a collection of comparators M for a measurer and the relation ∼
, all the elements in I can be partitioned into equivalence classes X = {α, β, γ, . . .}. Note that the equivalence class consists of real physical tokens (e.g., apples). There can be a collection of comparators M for a measurer and the relation ∼ 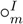 is relative to each comparator m ∈ M.
is relative to each comparator m ∈ M. - Assume that one can define a physical relation ≿
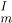 that has a total order, and a physical operation for concatenation (or composition)
that has a total order, and a physical operation for concatenation (or composition) 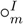 that is associative and strictly increasing. “Physical” here means that the relation and the operation are presented as physical phenomena in the real world. From any pair of the equivalence classes α and β, choose any elements a and b, respectively. Equivalence classes α and β have a relation α ≿
that is associative and strictly increasing. “Physical” here means that the relation and the operation are presented as physical phenomena in the real world. From any pair of the equivalence classes α and β, choose any elements a and b, respectively. Equivalence classes α and β have a relation α ≿ 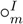 β if and only if the comparator shows a distinctive state: “when a is on the right pan and b is on the left pan, the right pan sinks (or they are balanced)”, for example. Choosing the elements a, b and c respectively from the any equivalence classes α, β, and γ, the concatenation is defined as: the concatenation of equivalent classes α and β, α
β if and only if the comparator shows a distinctive state: “when a is on the right pan and b is on the left pan, the right pan sinks (or they are balanced)”, for example. Choosing the elements a, b and c respectively from the any equivalence classes α, β, and γ, the concatenation is defined as: the concatenation of equivalent classes α and β, α 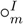 β, is a physical state in which a and b are on the same pan; and α
β, is a physical state in which a and b are on the same pan; and α 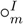 β = γ if and only if c is on the other pan and they are balanced. By an abuse of notation, we also write α ∼
β = γ if and only if c is on the other pan and they are balanced. By an abuse of notation, we also write α ∼ 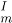 β if and only if α≿
β if and only if α≿ 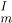 β and α ≾
β and α ≾ 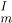 β holds.
β holds. - Choose an equivalence class α from X. For any positive integer n, define nα inductively as follows: 1α = α, (n + 1)α =(nα)
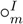 α. This nα is called n-copy of α. A copy of α can be found operationally. As for the weight, for instance, put x1 ∈ α on a pan and find x2 ∈ α which is balanced with x1. Now what is being considered is “the attribute, weight”, hence x2 can be anything, say, a pile of sand, for example. In this way, infinitely many copies of the weight of x1, x3,x4,..., can be made in theory. Then one can define 2α as a unity of x1 and x2, 3α as a unity of x1, x2, and x3, and so on.
α. This nα is called n-copy of α. A copy of α can be found operationally. As for the weight, for instance, put x1 ∈ α on a pan and find x2 ∈ α which is balanced with x1. Now what is being considered is “the attribute, weight”, hence x2 can be anything, say, a pile of sand, for example. In this way, infinitely many copies of the weight of x1, x3,x4,..., can be made in theory. Then one can define 2α as a unity of x1 and x2, 3α as a unity of x1, x2, and x3, and so on. - The Archimedes’ condition is required between the elements in X. The Archimedes’ condition is: for any pair of equivalent classes α and β, there exists a positive number n such that nα≻
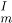 β. Here α ≻
β. Here α ≻ 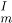 β means α≿
β means α≿ 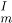 β and not α ∼
β and not α ∼ 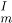 β. Though this condition has issues logically (because it cannot be described in first order predicate logics) and practically (because it implies infinite operations), it has great values to construct the theory.
β. Though this condition has issues logically (because it cannot be described in first order predicate logics) and practically (because it implies infinite operations), it has great values to construct the theory. - Corresponding to the above physical situations, a mathematical model, i.e., a formal system is set up. On the mathematical set A, introduce a totally ordered algebraic relation ≿m that is derived from the corresponding relation in I, and a connective and strictly increasing operation ◦m that is also derived from the corresponding operation in I. (Thus, they have operational meaning in the real physical world.)
- Introduce a measure, φ: A → ℝ as follows: (I) Select an element u from X as a unit, that is, φ(u)=1. (II) Construct φ satisfying following two conditions: (II-i) φ(nx)= nφ(x), (II-ii) If and only if x ≿
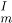 y, φ(x) ≥φ(y) holds. The precision of φ can be arbitrarily increased by the countability and the Archimedes’ condition on the elements of I. Suppose that x is not equivalent to the unit u. If x ≻ u, then the Archimedes’ condition assures there exists a positive integer k such that (k +1)u ≿ x ≿ ku. By this and (II-i),(II-ii) above, φ((k +1)u)= k +1 >φ(x) ≥ k = φ(ku) holds. Thus, φ(x) is obtained within the error 1. Here an error is defined as the upper bound of the difference between the true value and the measured value. Then, taking 2-copy of the each side of the equation above, (2k + 2)u ≿2x ≿2ku. With the Archimedes’ condition, this means (2k + 2)u ≿2x ≿(2k + 1)u or (2k + 1)u ≻2x ≿2ku holds. Applying the function φ and simplifying the equations with the conditions (II-i),(II-ii) yields k +1 ≥φ(x) ≥ kx +
y, φ(x) ≥φ(y) holds. The precision of φ can be arbitrarily increased by the countability and the Archimedes’ condition on the elements of I. Suppose that x is not equivalent to the unit u. If x ≻ u, then the Archimedes’ condition assures there exists a positive integer k such that (k +1)u ≿ x ≿ ku. By this and (II-i),(II-ii) above, φ((k +1)u)= k +1 >φ(x) ≥ k = φ(ku) holds. Thus, φ(x) is obtained within the error 1. Here an error is defined as the upper bound of the difference between the true value and the measured value. Then, taking 2-copy of the each side of the equation above, (2k + 2)u ≿2x ≿2ku. With the Archimedes’ condition, this means (2k + 2)u ≿2x ≿(2k + 1)u or (2k + 1)u ≻2x ≿2ku holds. Applying the function φ and simplifying the equations with the conditions (II-i),(II-ii) yields k +1 ≥φ(x) ≥ kx + 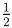 or k +
or k + 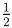 >φ(x) ≥ k. Thus φ(x) is obtained within the error
>φ(x) ≥ k. Thus φ(x) is obtained within the error 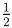 . Thus, by considering the virtual n-copy on the mathematical model A, the function φ can be obtained with arbitrary precision.
. Thus, by considering the virtual n-copy on the mathematical model A, the function φ can be obtained with arbitrary precision.
Thus, we can obtain a measure of attribute associated with the measuring instrument, and the measure can have arbitrary precision, even if it is for a measurement in the potential future.
4. Extensional Information Articulation as Generalized Measurement
In the view of this study, the extensive measurement in metrology is considered a sort of the information articulation of the physical universe.
In this section, we reconfirm the points of the extensive measurement (4.1), clarify the implicit assumptions in the extensive measurement from the viewpoint of information articulation (4.2), consider the requirements imposed on the IGUSes (4.3), and finally, develop a model of the process of extensional information articulation (4.4).
4.1. Review of the extensive measurement
The points of the extensive measurement described in Section 3 are summarized as follows:
- Introduction of a physical apparatus, i.e., a measuring instrument (e.g., equal arm beam for the weight), representing the physical intervention(s): The measuring instrument is introduced by the third person (the measurer) and observed by her/him. This naturally means that the measurer can identify and manipulate the instrument.
- Identification of target objects by a third person (the measurer): In a measurement, the target objects are identified by the measurer beforehand.
- Identification of required physical operations and their structures: Relations such as equivalence relation and operations such as concatenation are introduced physically, in other words, they are introduced with an operational semantics.
- Introduction of n-copy: Beyond actual physical tokens, multiple copies/alternatives for (potential) repetitive operations are modeled to be obtained physically.
- Establishment of maps between physical operations and mathematical operations and relations.
- Establishment of the measure, that is, the map from the mathematical structure representing the physical situation to the real number.
- The Archimedes’ condition: Universality of the measurement even for the potential measurements in the future is theoretically secured by the Archimedes’ condition (and the concatenation operation). The Archimedes’ condition theoretically assures the arbitrary precision of the measurement. Moreover, with the concatenate operation, it theoretically secures the universality of the measurement, in the sense that it enables to measure beyond a particular physical situations specified (by the actual physical tokens) as a measurement.
These points need to be re-interpreted and reconsidered for the extensional information articulation. This will be done in the next section.
4.2. Implicit Assumptions in Extensive Measurement
As Baird [17] pointed out, a measuring instrument plays two roles in information phenomena. (1) To begin with, a measuring instrument has to do something physically. It has to incorporate physical interactions related to the quantity to be measured. An equal arm beam balance, for example, is under the influence of gravity. In addition, the measuring instrument moves in a particular way reliably in the physical interactions. That is, it moves in an approximately same manner in the approximately same situations. The action of the instrument has been separated from human agency and built into the reliable behavior of an artifact. This is simply a physical matter. (2) A measuring instrument also has to provide representations. The results of measuring something must be located in an ordered space of possible measurement outcomes. A representation of this ordered space has to be built into a measurement instrument. This can be as simple as the scale to show the balance on an equal arm beam balance.
The latter role presupposes human agency, e.g., the existence of a measurer. The representations are for the measurer. If one considers the extensive measurement process as simply an information phenomenon, there are several implicit assumptions originated in this presupposition.
Reflecting on the points listed in Section 4.1, major implicit assumptions related to the subject of the present study are:
- Identities of objects in I are secured by the measurer. That is, the measurer is assumed to be able to identify the objects to be measured. In addition, the identities of objects are almost stable. That is, in most cases, the identity of each object under consideration is kept during the measurement (at least).
- The comparator m (a part of the universe) is identified by the measurer. That is, an attribute corresponding to a comparator can be identified by the measurer. Moreover, the comparator can be manipulated by the measurer. Manipulation here means, (1) putting the object(s) into the situation to be measured by the comparator, (2) capturing the information on the object(s) the comparator displays. That is, the physical interactions between the comparator and the measurer are distinguished (and utilized) by the measurer.
- The measurer has abilities to construct the suitable representations (sets for collection of objects, equivalence relations, real numbers for measured values, and so on).
To generalize the extensive measurement process to the information articulation process, these assumptions are reconsidered and turned into the requirements for the IGUS in the next subsection.
4.3. Requirements for the IGUS
The implicit assumptions of the extensive measurement in Section 4.2 do not hold in general information articulation processes.
In an information articulation process, an IGUS plays the role of the measuring instrument and the measurer simultaneously. There is no outsider who can observe and manipulate. There are merely physical interactions. Hence we need to reconsider the assumptions to generalize the extensive measurement.
First of all, before articulating the physical universe by information, there is no identity for everything in principle. We should not assume any privileged physical interactions. It is impossible, at least initially, for an IGUS to identify a fragment of the universe (FoU for short, from now on), because the IGUS has no clue, i.e., information to distinguish a part of the universe from the others. Note that identification here means that to conceive several physical interactions as united even if there is a spacio-temporal separation of these interactions. An IGUS is assumed to extract information to identify an FoU all by itself.
In addition to this, what an IGUS can rely on as a basis of differentiation is the IGUS itself only. There is no specific physical apparatus such as measuring instruments to be used by an IGUS to articulate the universe. If there is such an apparatus, the apparatus should be regarded as a part of the IGUS. The physical construction of the IGUS itself may be used to articulate the universe. We should assume that an IGUS compares FoUs by its own capabilities, and these capabilities might not be distinguished by the IGUS itself (even for this distinction, information might be required). The IGUS might correlate one of the capabilities with one of its own actions, and the capability may be identified indirectly through the action.
Finally, an IGUS is assumed to play the role of the measurer. An IGUS is assumed to have abilities to construct the suitable representations of physical entities that are operated during the information phenomenon.
These revised presuppositions impose physical requirements on IGUSes. Though the outcome might not novel—after all, the IGUS in this paper has similar construction with information agents already proposed—the reasoning may attract some interest.
- An IGUS is assumed to be able to directly indicate an FoU by a certain physical interaction i. Only during interaction, the IGUS can indicate a specific FoU just as it is. When the interaction is lost, the IGUS cannot identify the same FoU (if there is no further information). Using a term in linguistics, diachronically indistinguishable interactions are assumed to work for indicating FoUs. Such kind of interactions will be called as the indicative interactions in this article. The most distinguishable character of the indicative interactions may be their durability. Durability is essentially relative. This durability is related to the similarity detections by the IGUS (see the next item). The “source” of the indicative interaction should be the IGUS. In this sense, metaphorically, the indicative interaction can be regarded as an “active” interaction of an IGUS, and the physical implementation of such an interaction is often called as an actuator of the IGUS. An IGUS may have representations of each FoU paired with the indicative interaction i. Note that this representation is rather loose. If the IGUS activate the same interaction i, the exactness of the indication is governed by chance. That is, the IGUS cannot “specify” the FoU by using the indicative interaction alone.
- Another particular physical interaction p is assumed. An FoU a picked out by an indicative interaction i is compared with another FoU b picked out in the same way (during i is kept). The interaction p tells the IGUS that, from the viewpoint of the IGUS, the compared FoUs are whether indistinguishable or not. Thus this interaction p detects a similarity between a and b. Using a term in linguistics, synchronically indistinguishable interactions are assumed to work for detecting the similarities among FoUs. Such kind of interactions will be called as the comparing interactions in this article. Most of the case, this interaction can be regarded as, metaphorically speaking, a “passive” interaction of an IGUS, and the physical implementation of such an interaction is often called as a sensor of the IGUS.
- And memory is required to store the effects of interactions (physical difference made by another part of the universe), keep them, and utilize them later if necessary.
Thus, an IGUS in this paper is a kind of so-called sensorimotor system (e.g., [18]). But note that we should not use a personification to avoid confusions. An IGUS in general is, ultimately, a mere bunch of physical interactions. (In this sense, memory also should have been more elaborated in the language of physical interaction. But the authors omit unnecessary details for the present study.)
4.4. A Model of Extensional Information Articulation Process
The formulation of the extensive measurement tells us the importance of the distinction between the physical world and the mathematical model, and the importance of the linkage of them.
In general information articulation processes, information is related to a universal structure constructed from FoUs. FoUs are tentative entities, but if the IGUS can extract something universal, that is, existent or operative almost everywhere or under almost all conditions, this universality may be utilized (as information). In the case of the extensive measurement, the universality is simply condensed in a homomorphism φ : A → ℝ, assuming the Archimedes’ condition. But in general information articulations, the differences induced within an IGUS may form various structures, and the IGUS may utilize these various structures. Any models of information articulation process should incorporate such an extraction of universality from rather vague FoUs, at some generic level.
Following the formulation of the extensive measurement, a model of the process of extensional information articulation by an IGUS satisfying the requirements mentioned in Section 4.3 is developed. The model is presented, with one-to-one correspondence to the steps in the Section 3, as follows:
- As already mentioned, there is no a priori thing or object. An IGUS may indicate an FoU by an indicative interaction. An FoU is, as it were, proto-information. A collection of FoUs, I, may be made physically or within the IGUS (as representation of a collection of physical FoUs).
- Comparator (i.e., Sensor) for indifferences m ∈ M is introduced. It is a pair of the indicative interaction and the comparing interaction. The comparator can compare an FoU with another one. That is, the comparator m shows that the compared FoUs are whether indistinguishable or distinguishable from the comparator’s viewpoint. This distinction induces an equivalence relation ∼
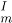 . In addition, the FoUs are partitioned into equivalence classes, tentatively. (Recall that an FoU is not identified by the IGUS at this stage. It is only indicated during the indicative interaction, and at best, has a representation loosely related to the actual physical FoU.) There may be a collection of comparators M for an IGUS and the relation ∼
. In addition, the FoUs are partitioned into equivalence classes, tentatively. (Recall that an FoU is not identified by the IGUS at this stage. It is only indicated during the indicative interaction, and at best, has a representation loosely related to the actual physical FoU.) There may be a collection of comparators M for an IGUS and the relation ∼ 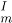 is relative to each comparator m 2 M.
is relative to each comparator m 2 M. - Assume that one can define a physical relation R
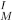 between the (tentative) equivalence classesof FoUs. Suffix for the comparator isreplaced/generalized by the set of comparators because acombination of the comparators is commonly used for articulating one piece of information.
between the (tentative) equivalence classesof FoUs. Suffix for the comparator isreplaced/generalized by the set of comparators because acombination of the comparators is commonly used for articulating one piece of information. - Characterize the physical relation R
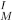 by the physical operations/interactions on the equivalenceclasses of FoUs, if possible.
by the physical operations/interactions on the equivalenceclasses of FoUs, if possible. - Try to deduce a universal structure constructed physically from the equivalence class of FoUs and R
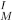 . If this step is not successful, the universal structure is inquired in the formal side, i.e., in the mathematical model (step 7).
. If this step is not successful, the universal structure is inquired in the formal side, i.e., in the mathematical model (step 7). - Corresponding the above physical situations, relate the equivalence classes of the FoU to a set X in the mathematical model. The set X must have the structure reflecting the physical relation R
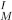 (Thus, they have operational meaning in the real physical world. )
(Thus, they have operational meaning in the real physical world. ) - Introduce the homomorphisms between X and another (known) mathematical structure K, which represents the articulated information. Deduce a universal structure from the K. The universal structure may be a model of the information that is captured (and to be utilized) by the IGUS.
This is a model for describing the process itself, and, simultaneously, this is a model for analyzing information phenomena as information articulation processes. In the latter case, note that the subject of these statements is also an IGUS (typically, human-IGUS) that is investigating the information phenomena.
5. Attributes as Limit
In this section, as a significant instance of the extensional information articulation, the attributes extraction from the universe is considered.
We focus on the step 7 in the extensional information articulation process, because this step for extracting the universality is especially worthy to investigate in information science. Other steps in the information articulation process might be investigated in different disciplines. For example, the steps for detecting similarity of FoUs, the step 1 and 2, can be abstracted using the Curie’s principle in physics. As Joe Rosen [19] explicates, symmetry looms in the foundation of science. Major ingredients of that foundation, reproducibility, predictability and reduction are all symmetry. Hence, physical interactions can be represented at a generic level by the words of symmetry. Thus, we can abstract away the source of equivalence classes of FoUs by assuming certain symmetries.
To focus on the step 7, in this section, following conditions for the IGUS are supposed:
- The IGUS has collections of FoUs each of which forms an equivalence class. Each of the equivalence relations is induced by certain symmetry of the physical interaction (comparing interaction) of the IGUS;
- The inclusion relation between the collections of FoUs is considered as the relation R
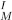 in the step 3;
in the step 3; - The IGUS has enough physical capabilities to meet the requirements for implementing the model described in the following.
By supposing the first condition, the steps 1 and 2 in the extensional information articulation process are skipped; the step 3 is took by the second condition; the steps 4 and 5 are abandoned; the set X in the step 6 is equipped with an order relation induced by the inclusion relation supposed as the second condition; and the last condition ensures taking the step 7.
Let us return to the situation described in the Section 1: Suppose that there is a green apple. The question is: how can a tabula rasa IGUS articulate this part of the universe as the green apple? Let us assume that the IGUS can capture some similarities of parts of the universe through certain symmetries of the interactions. But this does not mean that a particular attribute, e.g., green, can be carved out of the universe by the IGUS. The IGUS must distinguish each attribute by the differences induced within itself.
We, human-IGUSes, often use the Aristotelian concept to specify a certain object out of this uniform universe. In Aristotelian classical category, features of the category members are binary, primitive, universal, abstract and innate, all members of the category have equal status and the categories have clear boundaries (see for example, [20,21]). A concept is defined via a set of necessary and sufficient properties. That is, a concept has two sides: its extension, i.e., a collection of objects, and its intension, i.e., a collection of attributes (which represents the equal status of objects), and these two sides reciprocally define the concept (for a formal model of such “concept”, see [22]).
But as already mentioned, for a tabula rasa IGUS, there is no attributes and objects beforehand. An IGUS must extract them all by itself. A model is required to describe and analyze such a bootstrapping attributes extraction process.
The model presented in this section is developed in three steps.
First, the projective limit is used as a mathematical model to attain universality from finite physical interactions between the universe and the IGUS. In some field in physics such as physical cosmology, researchers have similar problems to explain the situation in which universal information is extracted from finite observations, and our model is along with the line of Sorkin [23].
Second, structural reduction of information is introduced. All of the universal elements obtained in the projective limit are not necessarily used as attributes to specify a part of the universe. Elements for minimal construction of attributes are modeled as irreducible elements of the lattice in the limit.
Third, in the same way as in Formal Concept Analysis [22], Galois correspondence between the inclusion structure of equivalence classes of FoUs and the inclusion structure of attributes obtained in the limit establishes the objects and attributes for the IGUS.
Though the following description includes minimum mathematical information for interested readers, the use of mathematics in this section is to exemplify more concretely the possibility of the extensional information articulation, and is not intended to present a mathematically rigorous formulation.
5.1. Universality
An IGUS, which was initially a tabla rasa, incrementally obtains collections of FoUs each of which forming an equivalence class. The collections of equivalence classes of FoUs at the stage t is denoted as St. Between the equivalence classes A, B in St, there exists a natural inclusion relation ⊆: A ⊆ B if and only if for any a ∈ A, a ∈ B. Here, a is a representation of FoU in the IGUS. It is natural to simply think that a certain uniformity of FoUs, that is, an attribute is represented by each equivalence class (as Chechkin). However, it has some drawbacks as mentioned in the Section 1.
To obtain a required universality of attributes and reflect the proper relationship between them, we should move to down-sets of St, which is denoted as Dt, and the sequence of them. Dt is the down-set of St if, whenever X ∈ Dt and Y ∈ St and Y ⊆ X, we have Y ∈ Dt. Recall that X, Y here are equivalence classes of FoUs.
Because there is a mathematical fact that the family of down-sets ordered by set inclusion forms a lattice isomorphic to the original lattice [24], Dt can be considered to be virtually the same as Et, in the context of this paper.
Thus an IGUS is assumed to have a sequence D0 = ∅,D1,D2,..., which incrementally increases according as the IGUS has more experiences, that is, more interactions with the universe. The universality is extracted from this virtually infinite sequence.
From T -indexed family of sets, {Dt}t∈T and appropriately defined functions ftu : Du → Dt, one can construct a mathematical structure called a projective system (Dt, (ftu)t≤u). ftu can be defined as:
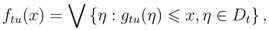 where gtu : Dt '→ Du is the inclusion map preserving the top and the bottom in Dt, and the symbol ⋁denotes the least upper bound.
where gtu : Dt '→ Du is the inclusion map preserving the top and the bottom in Dt, and the symbol ⋁denotes the least upper bound.
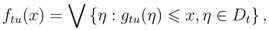
For a projective system, a universal concept, that is, the projective limit is defined:
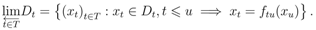
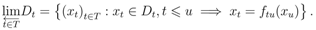
What characterizes the projective limit is its universality. For a projective system (Dt,ftu) t,u∈T, a set D and a family of maps (pt : D → Dt)t∈T are given, and for any t, u ∈ T satisfying t ≤u, if pt = ftu ◦ pu, then there exists a unique map ρD : D → 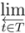 Dt that satisfies pt = πt ◦ ρD for any t ∈ T where πt is the projection map for t-th component of
Dt that satisfies pt = πt ◦ ρD for any t ∈ T where πt is the projection map for t-th component of 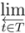 Dt. This is a realization of universality in a mathematical model.
Dt. This is a realization of universality in a mathematical model.
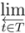 Dt that satisfies pt = πt ◦ ρD for any t ∈ T where πt is the projection map for t-th component of
Dt that satisfies pt = πt ◦ ρD for any t ∈ T where πt is the projection map for t-th component of 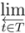 Dt. This is a realization of universality in a mathematical model.
Dt. This is a realization of universality in a mathematical model.The projective limit gradually changes as the IGUS is affected by new interactions. But as far as the interactions do not induce a significant structural change in Dt, the limit remains the same. In this sense, the attributes modeled as this structural limit can be said to be universal, and this corresponds to the mathematical universality mentioned above.
Finite sequence up to Dt, i.e., (Ds)s ≤t∈T can be considered to be a finite approximation of the projective limit 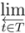 Dt. By construction from the family of down-sets, the finite sequence up to Dt can be easily retrieved from Dt, hence Dt can be identified with (Ds) s ≤t∈T as a finite approximation of
Dt. By construction from the family of down-sets, the finite sequence up to Dt can be easily retrieved from Dt, hence Dt can be identified with (Ds) s ≤t∈T as a finite approximation of 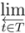 Dt.
Dt.
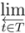 Dt. By construction from the family of down-sets, the finite sequence up to Dt can be easily retrieved from Dt, hence Dt can be identified with (Ds) s ≤t∈T as a finite approximation of
Dt. By construction from the family of down-sets, the finite sequence up to Dt can be easily retrieved from Dt, hence Dt can be identified with (Ds) s ≤t∈T as a finite approximation of 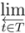 Dt.
Dt.Metaphorically speaking, suppose that each Dt is an approximate value of the ratio of the circumference of a circle to its diameter, π, that is, D0 =3, D1 =3.1, D2 =3.14, D3 =3.141,.... Then the projective limit is the value π. The universal value π is represented extensionally as
However, note that the projective limit above in general is for the structures, not simply for values. In the present study, the projective limit is the limit of inclusion structures of (down-sets of) the equivalence classes of FoUs.
π = {3, 3.1, 3.14, 3.141,...}
5.2. Specifiability
However, not all of them are required to specify a part of the universe as an attribute. There seems, so to speak, an economic principle.
The projective limit obtained in Section 5.1 can be assumed to have the structure mathematically called lattice. There is a fact that in a lattice, any element of the lattice can be obtained as a certain combination of its specific part of elements [25]. These special elements, which form the basis of the lattice, are mathematically called the meet irreducible elements of the lattice.
Therefore, these meet irreducible elements of the projective limit (of the family of down-sets of the collections of equivalence classes of FoUs) may be regarded as attributes derived from the structural differences induced within the IGUS by the physical interactions. We will call them as s-attributes (“s” for structural) if it is required to emphasize on the distinction from other ordinary uses of the word “attributes”.
When one of the meet irreducible elements of the projective limit is labeled as attribute a, roughly speaking, all of the FoUs belonging to the element of the projective limit have this attribute a. More precisely, we might be able to say that an FoU hereditarily succeeds to the labeling as attribute a, because an element of the projective limit is a set of the down-sets Dt each of which consists of a set of equivalence classes of FoUs.
In this way, an IGUS can equip enough s-attributes to (virtually) specify the equivalence classes of FoUs, i.e., particular parts of universe. Besides, the IGUS is now able to handle attributes extensionally, because the s-attributes are virtually represented extensionally. “Virtually” here is placed for worrying that this model of the attributes seems rather conceptual because the s-attributes are defined “in the limit”. However, even if it is merely conceptual, by understanding in this way, we can define a clear concept of the approximation of an attribute in Dt, that is, the projection of an s-attribute in 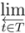 Dt. These approximations can clearly be handled extensionally. Moreover, there might be a physical implementation of the limit, which provides extensionality of the attributes directly.
Dt. These approximations can clearly be handled extensionally. Moreover, there might be a physical implementation of the limit, which provides extensionality of the attributes directly.
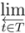 Dt. These approximations can clearly be handled extensionally. Moreover, there might be a physical implementation of the limit, which provides extensionality of the attributes directly.
Dt. These approximations can clearly be handled extensionally. Moreover, there might be a physical implementation of the limit, which provides extensionality of the attributes directly.5.3. Galois Connection
As described in the above subsections, an IGUS can obtain a set of s-attributes that are somewhat universal, and the IGUS can handle the s-attributes extensionally.
But recall that actual physical FoUs are merely loosely related to the representation within the IGUS. At this stage, there is no specific object with which these s-attributes are associated.
The connection between the s-attributes obtained and the specific part of the universe may be established by the Galois connection on the model. Physically, it may be established by the indicative interactions that are correlated with the representation of FoUs within the IGUS. Through this correlation, the indicative interactions are also correlated with the s-attributes. Therefore, the IGUS can activate the indicative interaction correlated with one of the s-attributes and indicate some part of the universe. The part of the universe may or may not strictly agree with the FoUs initially indicated. But, anyway, this indication is stable for the IGUS in comparison with the initial indication to the FoUs, because it has its ground within the IGUS itself. And if the indication correlated with the s-attributes specify a part of the universe, the part of the universe is/becomes the object corresponding to the s-attributes.
This situation is mathematically modeled as the Galois connection between the lattice of equivalence classes of FoUs and the lattice of the s-attributes. See [22] for general formulation in detail.
Thus, in this model, a universal structure, i.e., the projective limit, is built from the structures of the inclusion relation of the FoUs, and using extensionality of the universal structure, via the Galois connection, another universal structure— (the inclusion relation of) the pairs of objects and attributes. The IGUS has now got the extensionally specifiable attributes and objects, In this way, the information phenomena may be understood as the transformation of extensional structures, that is, the transformation of extensional differences.
6. Discussion and Conclusions
It has not been well investigated to understand the fundamentals of information as fully extensional physical phenomena. Studies of information in physics, or a few studies in information theory, e.g., Chechkin (see [1]) indeed treated information extensionally. However, their treatments have seemed to be not thorough enough. They did not provide any general enough model that could be used in a fundamental level of information phenomena, such as the articulation of information from the universe.
In this paper, we have developed a model of the process of extensional information articulation, generalizing the theory of the extensive measurement in metrology. In addition to this, a model of the attribute creation process has been presented as a detailed example of a step of the extensional informational articulation process.
The former model provides an abstract model to represent a concrete information articulation process extensionally. By establishing the relation between the components in the model and those in an actual, concrete situation, an information phenomenon may be sorted out and analyzed as an extensional information articulation. Thus, this model may play the similar role as that of the extensive measurement theory in metrology.
The latter model has exemplified the concepts of the former model. It has demonstrated a concrete formulation along the line of the former model, i.e., the model of the process of extensional information articulation, and presented the possibility of a new understanding of the attributes in which attributes are extracted fully extensionally from the universe.
This study has exploratory nature. Some points that are not within the scope of this paper remain to be addressed in the future studies.
Though it might not be in the field of information studies, the (possibility of) physical implementation of the model is one of the issues. Most disputable point might be the physical implementation of the projective limit—in general, the mechanism to obtain universality from finite interactions. Physical phenomena such as nonlinear dynamics might be candidates. Future work is required to clarify whether if it is possible to implement the limit directly within an IGUS.
In the same vein, the system identification of an IGUS as simply a collection of physical interactions is another issue. How can a part of the universe recognize another part of the universe as an IGUS? In this paper, the authors sometimes rely on the intuitive understanding of the human-IGUSes. After all, the language of physics is (basically) for human-IGUSes. However, the information theory, which is based on the physical interactions, i.e., extensional entities, should be more fully developed without assuming human-IGUSes.
In this extensional view, the distinction between information and the physical phenomena is further obscured. The distinctive characteristics of physical phenomena from the extensional information viewpoint might be worth pursuing. Superficially, the information phenomena might be associated with the existence of retarded physical interactions and a choice of reactions of the IGUS. Future work should explore the distinction, or the difference of the intensity of informationality, from this extensional information viewpoint.
There are many other approaches for investigating the problem of interrelation of physical and informational reality. The most contrasting approach to this study is the approach that tries to explain the reality with information only. As already mentioned in the Section 1, many researches adopt such an approach from various motives. It is true, even in the view of this study, that the physical reality for us may be considered to be constructed by information for us humans. But it seems also true that there exists something (i.e., the universe) in which we do not have our own way in everything, something that is the never-exhausting source of information. Though it is not the case that the authors had fully evaluated every study adopting a purely informational approach, the physical approach (such as this study) and the informational approach seem to, so to speak, complement or adjoin each other. Future studies should address such matters to clarify the relationship between these two approaches.
These models developed in this study may have its applications in the field of exploratory data analysis by their extensional nature. Immanent universal property, e.g., the s-attribute, of collected data can be represented structurally, i.e., extensionally by the collected data themselves. This information extracted from the data can be manipulable through its extensionality.
We expect the models of this study to be applied in theory and in practice, and to enhance the understanding of the extensional aspects of fundamentals of information.
References
- Burgin, M. Theory of Information—Fundamentality, Diversity and Unification; World Scientific: Singapore, 2010. [Google Scholar]
- Berlin, B.; Kay, P. Basic Color Terms: Their Universality and Evolution; CSLI Publications: Stanford, CA, USA, 1999. [Google Scholar]
- von Weizsäcker, C.F. Aufbau der Physik; Hanser: Munich, Germany, 1985; (Japanese translation: Butsurigaku no Kouchiku; Housei University Press: Tokyo, Japan, 2008). [Google Scholar]
- Wheeler, J.A. Information, Physics, Quantum: The Search for Links. In Complexity, Entropy and the Physics of Information; Zurek, W., Ed.; Addison-Wesley: Redwood City, CA, USA, 1990; Volume VIII, pp. 3–28. [Google Scholar]
- Frieden, R.B. Physics from Fisher Information; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Khrennikov, A. Classical and quantum mechanics on information spaces with applications to cognitive, psychological, social, and anomalous phenomena. Found. Phys. 1999, 29, 1065–1098. [Google Scholar] [CrossRef]
- Lloyd, S. Programming the Universe: A Quantum Computer Scientist Takes on the Cosmos; Random House: New York, NY, USA, 2006. [Google Scholar]
- Floridi, L. A defence of informational structural realism. Synthese 2008, 161, 219–253. [Google Scholar] [CrossRef]
- Floridi, L. Against digital ontology. Synthese 2009, 168, 151–178. [Google Scholar] [CrossRef]
- Krantz, D.H.; Luce, R.D.; Tversky, A.; Suppes, P. Foundations of Measurement Volume I: Additive and Polynomial Representations; Dover: Mineola, NY, USA, 2007. [Google Scholar]
- Marinescu, D.C. Classical and Quantum Information; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Zurek, W. Algorithmic Information Content, Church Turing Thesis, Physical Entropy and Maxwell’s Demon. In Complexity, Entropy and the Physics of Information; Zurek, W., Ed.; Addison-Wesley: Redwood City, CA, USA, 1990; Volume VIII, pp. 73–89. [Google Scholar]
- Gell-Mann, M.; Hartle, J.B. Quantum Mechanics in the Light of Quantum Cosmology. In Complexity, Entropy and the Physics of Information; Zurek, W., Ed.; Addison-Wesley: Redwood City, CA, USA, 1990; Volume VIII, pp. 425–458. [Google Scholar]
- von Helmholtz, H. Zählen und Messen, erkenntnistheoretisch betrachtet. In Philosophische Aufsätze, Eduard Zeller zu seinem fünfzigjäthrigen Doctorjubilätum gewidmet; Fues’ Verlag: Leipzig, Germany, 1887; pp. 17–52. [Google Scholar]
- Hőlder, O.L. Die Axiome der Quintitätt und die Lehre vom Mass. Mathematisch-Physikalische Klasse 1901, 53, 1–64. [Google Scholar]
- Yoshino, R.; Chino, N.; Yamagishi, K. Suurishinrigaku (Mathematical Psychology) [in Japanese]; Baifukan Co., Ltd.: Tokyo, Japan, 2007. [Google Scholar]
- Baird, D. Thing Knowledge: A Philosophy of Scientific Instruments; University of California Press: Berkeley, CA, USA, 2003. [Google Scholar]
- Harnad, S. To Cognize is to Categorize: Cognition is Categorization. In Handbook of Categorization in Cognitive Science; Cohen, H., Lefebvre, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 19–43. [Google Scholar]
- Rosen, J. Symmetry in Science: An Introduction to the General Theory; Springer-Verlag New York, Inc.: New York, NY, USA, 1995. [Google Scholar]
- Langacker, R.W. Foundations of Cognitive Grammar, Volume I: Theoretical Prerequisites; Stanford University Press: Palo Alto, CA, USA, 1987. [Google Scholar]
- Taylor, J.R. Linguistic Categorization: Prototypes in Linguistic Theory, 2nd ed; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Ganter, B.; Wille, R. Formal Concept Analysis: Mathematical Foundations; Springer-Verlag Berlin Heidelberg: Berlin, Germany, 1999. [Google Scholar]
- Sorkin, R.D. Finitary Substitute for Continuous Topology. Int. J. Theor. Phys. 1991, 30, 923–947. [Google Scholar] [CrossRef]
- Birkhoff, G. Lattice Theory, 3rd ed; AMS Colloquium Publications, American Mathematical Society: Providence, RI, USA, 1967; Volume 25. [Google Scholar]
- Davey, B.; Priestley, H. Introduction to Lattices and Order; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).