Abstract
We survey a few aspects of the thermodynamics of computation, connecting information, thermodynamics, computability and physics. We suggest some lines of research into how information theory and computational thermodynamics can help us arrive at a better understanding of biological processes. We argue that while a similar connection between information theory and evolutionary biology seems to be growing stronger and stronger, biologists tend to use information simply as a metaphor. While biologists have for the most part been influenced and inspired by information theory as developed by Claude Shannon, we think the introduction of algorithmic complexity into biology will turn out to be a much deeper and more fruitful cross-pollination.
1. Unifying Information and Energy through Computation
When Alan Turing defined the concept of universal computation, he showed that any given Turing machine could be encoded as the input of another (universal) Turing machine. As Cooper would have it, this amounted to the disembodiment of computation [1], because Turing made clear that even though computation seemed to require a physical carrier, the physical carrier itself could be transformed into information. There was therefore no clear-cut distinction between hardware and software. In some sense, Turing’s unification is comparable to certain unifications in physics.
Computational thermodynamics, as developed by Szilárd [2], Landauer [3], Bennett [4,5], Fredkin and Toffoli [6], among others, made a similar breakthrough. These individuals showed that there was a fundamental connection between information and energy—that one could extract work from information—and moreover that this connection could serve as one of the strongest arguments for the necessity of unifying information and physical properties. Their work provided a framework within which to consider questions such as Maxwell’s paradox—and its possible solution.
Suggested by Maxwell himself [7], the basic idea conveyed by the paradox is that if a “being” or a “demon” were placed between two halves of a chamber, one could use knowledge about the micro-state of the chamber/system to make one side of it hotter, rather than having it reach thermal equilibrium. A solution emerged from information theory and computation [4,5]. It turns out that the demon would only be able to do what he was believed capable of by actually delivering more heat to the gate that he was supposed to be cooling down.
Leó Szilárd established a connection between energy and information [2] when he replaced the “demon” with a simple machine. The connection is that information can be exchanged for energy because it can help to extract energy. Gaining information lowers the entropy (uncertainty) of a system. The use of a fundamental unit of information such as the bit to produce energy, as suggested by Shannon, is well explained in [8] and [9]. Szilárd showed that if one had one bit of information about a system, one could use that information to extract an amount of energy given by E = (log2)kT (where k is Boltzmann’s constant, and T the temperature of the system).
Landauer studied this thermodynamical argument [3] and proposed a principle: if a physical system performs a logically irreversible classical computation, then it must increase the entropy of the environment with an absolute minimum of heat release amounting to E per lost bit. Landauer further noticed that any irreversible computation could be transformed into a reversible one by embedding it within a larger computation where no information was lost.
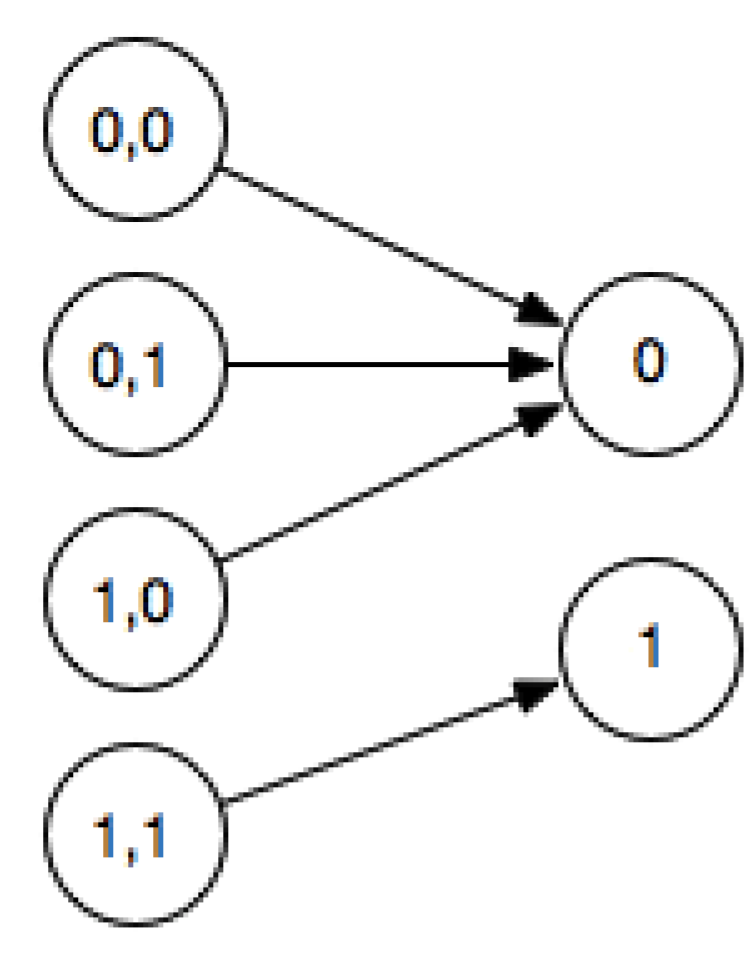
Figure 1.
The logical gate and is not reversible as can be seen in this truth table diagram, because given 0 as output one cannot tell which of the 3 inputs generated it.
A nand irreversible gate, for example, can be embedded in a bijection known as a Toffoli gate [10]. The Fredkin gate [6] is another example of a reversible logical gate, capable of implementing universal computation as well as computing with no energy (in principle). When several input states are mapped onto the same output state, then the function is irreversible (e.g., Figure 1), since it is impossible to identify the initial state if one knew only the final state.
Using these ideas, Feynman invented a simple physical model [8] of a one-bit register to set up a “piston Turing machine” with which to illustrate the processes that require and those that do not require thermodynamic work, and Bennett [11] used it to illustrate how to produce thermodynamic work (other good accounts can be found in [9] and [12]). The machine consists of a cylinder divided into two compartments by a central partition (a piston). The cylinder contains a molecule that can either be in the left compartment (representing a 0) or in the right compartment (representing a 1). From Landauer [3] we know that the cost of resetting such a machine is M(log2)kT every time M bits are erased. We have a good sense of how to connect these concepts using algorithmic information theory. If a string is algorithmically random, for example, there is no way the machine can be set up to make it produce usable work, because the more predictable the string (the lower its algorithmic—Kolmogorov—complexity [13,14]) the more the quantity of work that can be extracted from it. This is consistent with the second law of thermodynamics—computational thermodynamics basically says that one cannot extract work from an (algorithmically) random string. The machine would either not be able to fully predict the incoming input or it would require more energy to actually predict its bits and prepare itself to take advantage of the incoming input and produce work. In the words of Feynman ([8]), a random tape has zero fuel value.
So how exactly would one design a useful piston machine? The best approach is to use the concept of universal gambling, based on algorithmic probability [15,16]. The machine would try to evaluate the complexity of the incoming string by, for example, using a compression algorithm or an a priori distribution indicating the probability of the frequency of the next bit being 1 or 0 (interpreted as being on one side or the other of the piston box), and quickly slip the piston into position accordingly (see Figure 2).
But imagine a random stream of bits serving as input to the machine with a piston. The piston needs to be set in such a way that if a bit comes in then it moves to the correct side and returns to wait for the next push. If the string is known to be a sequence of 1’s, for example, one can just set the piston in such a way that it will always expand in the same direction and will produce work (e.g., movement or heat). But if the string is random there is no way to set the piston correctly because it will get as many pushes in one direction as in the other—so if the piston is used for motion the machine will move back and forth. If the string is uniformly random, it will describe a one-dimensional random walk and end up not far from its original point of departure. In this case, adding more pistons will not work either, because if each piston moves according to adjacent contents of the tape and the tape is random, the machine will produce as much energy as it loses.
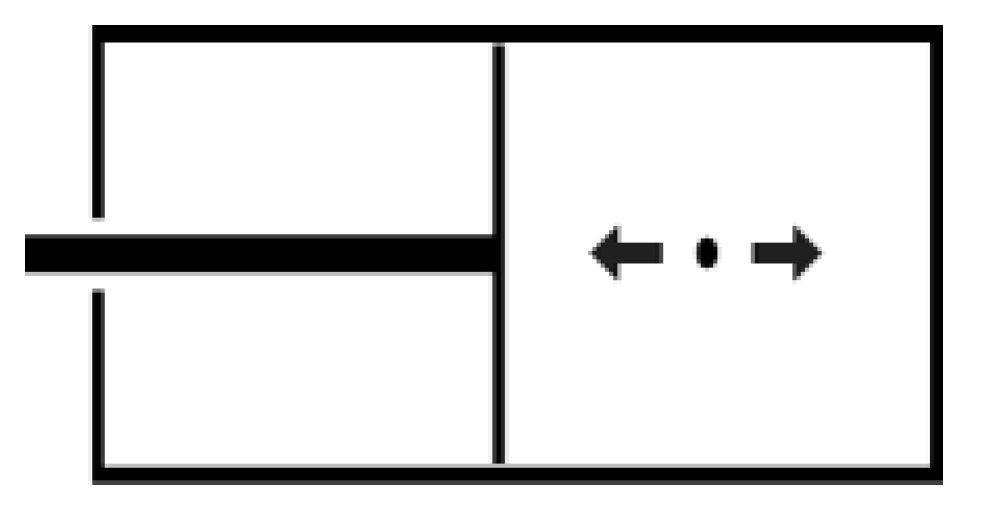
Figure 2.
A bit for work regarded as a particle pushing the piston if it is known whether the bit will be 1 or 0 (interpreted as coming from one direction or the other). Every bit in the sequence determines whether the piston will expand one way or the other, but in order to do so the piston has to be in the right position.
1.1. Thermodynamics, Computation and Computability
Algorithmic probability (just like algorithmic—Kolmogorov—complexity [13,14]) is non-computable [14,16], which means that one cannot predict an incoming string with complete accuracy, and therefore that there is no way, not even in principle, to extract work from a piston Turing machine if the incoming input is random. It also means that the more one wishes to extract, the more one needs to invest either in producing the a priori distribution or in trying to compress the incoming sequences in order to evaluate the complexity of the string and to predict what the forthcoming bit is likely to be, which is time and energy consuming because the resources available are finite and the machine will likely need to reset the memory at least once in a while if not every time. Given that by a simple combinatorial argument (there are far fewer binary programs strictly shorter in length than binary strings), there can only be more algorithmically random strings than non-random ones. This strongly suggests that one would in general need to invest more energy than it would be possible to extract from a Turing machine fed with a random input. Beyond the dissipation of an actual physical piston Turing machine, which would release heat (e.g., because of the friction of the pistons against the cylinders and the movement of the head over the tape), there is an even more fundamental reason to avoid building a perpetual motion piston Turing machine: the eventual need to erase or reset the machine because its resources are finite, resulting in the release of heat, as found by Landauer and Bennett [3,4]. The other reason—from computability theory—is that algorithmic randomness is uncomputable, that is, there is no Turing machine that, when given a string, can decode it into its minimal description by finding the regularities in it. In other words, no algorithm can predict the next bit of an algorithmically random sequence.
2. The Role of Information in Physics
Black holes are objects theoretically predicted by general relativity (and discovered experimentally). Surprisingly, they play a central role in the application of information theory to physics, for several reasons. Black holes are, as it were, the meeting places of physical theories describing the largest and the smallest objects in the universe, i.e., general relativity theory and quantum mechanics. This is because black holes are so massive that they produce what the core of Einstein’s relativity theory predicts as being a consequence of gravity (the deformation of space-time due to a massive object), a singularity point with no length, which therefore subsists on a subatomic scale. The quest to unify the theories has therefore focused its attention on black holes. A second interesting property of black holes is that they recapitulate what is believed to have been the condition of the universe at its inception. If we assume the expansion of the universe and move backwards in time we arrive at a situation exactly like the one that obtains with black holes, where a great amount of mass is concentrated in a very small (ultimately null) space, since according to the Big Bang theory everything started out of nothing—or out of what we have no idea of, to put the matter more accurately, since both theories, general relativity and quantum mechanics, fail to offer a persuasive account of what is obtained at the singularity moment (or for matter before that moment). But there is a third reason why black holes play a pivotal role, the reason that matters most to us here, and that is their relation to matter and energy, and indeed to information itself.
What falls into a black hole was once thought to be lost, because by definition not even light can make it out of a black hole’s event horizon. The first law of thermodynamics, however, asserts that no mass or energy is ever lost. In terms of information, the world is reversible in theory [11], but if things fall into black holes information would be lost forever with no way to recover it, not even in principle. It was found, however, that black holes “leak” information to the outside due to a quantum phenomenon occurring at the event horizon [17,18].
That black holes “evaporate” in this way is important because there is a connection to the first and second laws of thermodynamics. The first law of thermodynamics is concerned with an important symmetry property of the world. The first law is the law of energy conservation, which says that though processes involve transformations of energy, the total amount of energy is always conserved, implying time-translation symmetry. In other words, there is no distinction between past and future, as time can be reversed and the laws of physics would still hold; they remain invariant under time transformations. Unlike the first law, however, the second law introduces an apparent asymmetry, but it is an asymmetry of a statistical nature. There are many statements of the second law, all of them equivalent. The best-known formulation is that of Clausius [19]: “The entropy of the universe tends to a maximum”. This is of course a simplified version of a more complex mathematical description that has the following form for an isolated system: ∂S/∂t ≥ 0, where S is the entropy and t is time.
More recently, an even deeper connection between physics and information has been suggested in the context of theories of quantum gravity, which involves the relation between the mass of what falls into a black hole and the size of the black hole (the surface area of its event horizon). The so-called Holographic Principle [20,21,22] states that the description of a volume of space can be thought of as encoded on a boundary of the region. In fact, ’t Hooft uses a cellular automaton to speculate on the constraints faced in constructing models of quantum gravity [23]. In ’t Hooft’s own words:
It is tempting to take the limit where the surface area goes to infinity, and the surface is locally approximately at. Our variables on the surface then apparently determine all physical events at one side (the black hole side) of the surface. But since the entropy of a black hole also refers to all physical fields outside the horizon the same degrees of freedom determine what happens at this side. Apparently one must conclude that a two-dimensional surface drawn in a three-space can contain all information concerning the entire three-[dimensional] space. ... This suggests that physical degrees of freedom in three-space are not independent but, if considered at Planckian scale, they must be infinitely correlated.
According to some theories of quantum gravity, this suggests that black holes are acting as data compressors for information.
Wheeler identified the shortest possible scales at the quantum size (∼ 10−33 cm and ∼ 10−43 s) at which general relativity breaks down and should be replaced by laws of “quantum gravity” (Wheeler is also credited with having coined the terms Planck time and Planck length). Wheeler [24] thought that quantum mechanics would eventually be rooted in the “language of bits”. According to [25], Wheeler’s last blackboard contained the following, among several other ideas: “We will first understand how simple the universe is when we recognize how strange it is.” Wheeler himself provides examples of the trend from physics to information in his “it from bit” programme, suggesting that all of reality derives its existence from information. He asserted that any formula with units involving the Planck length ħ would be indisputable evidence of the discrete nature of the world. It was perhaps not by chance that the same person who coined the term “black hole” for the strange solutions that general relativity produced, leading to singularities, proposed the “it from bit” dictum, suggesting that everything could be written in, and ultimately consisted of, bits of information.
In fact, Wheeler thought that it was possible to translate all physical theories into the language of bits, and no account of information in relation to energy could be considered complete if it does not take into account the possible interpretations of quantum mechanics. Physical information and its connections to reversible computation are of particular importance in the theory of quantum computation, as it has been proven that if something can be reversibly computed it can also be computed on a quantum computer [11].
According to classical mechanics, randomness is apparent in the macroscopic world, but under the standard interpretation of quantum mechanics things may be fundamentally different. The position that the history of the world is computationally reversible [5] is compatible with the determinism imposed by classical mechanics, despite the arrow of time derived from the second law of thermodynamics, which makes it impossible in practice to reverse any conceivable process in the world. At the quantum scale, however, it would seem as though entangling a particle would cause it to irretrievably lose track of its previous state, leaving no avenue for obtaining information about it. Quantum logic gates, however, are all reversible because events occur by unitary transformations [11,26], which are bijective and therefore invertible (but the measurement problem is not so). According to Bennett, there is no current evidence or known phenomenon that would imply a real loss of information [4,11], so physical laws are fully reversible.
As surprising as it may seem, this is the position of some who are considered digital ontologists in the tradition of Wheeler, Feynman and Wolfram (Wheeler was a professor of Feynman and Feynman of Wolfram). Wolfram’s position, contrary to common belief, is also mostly epistemic in character, as is shown by his approach to natural science [27].
3. Information and Biology
If Wheeler’s aphorism applies anywhere in physics, it certainly applies to biological systems. Over the past decades the concept of information has also gained a prominent place in many areas in biology. A central element in living systems turns out to be digital: DNA sequences (a digitised linear polymer), refined by evolution, encode the components and the processes that guide the development of living organisms. It is therefore natural to turn to computer science, which possesses concepts designed to characterise digital information, but also to computational physics in order to understand the processes of life. Terminology such as reading and writing is routinely used in discussing genetic information, while genes are described as being transcribed, translated and edited, in a purely informational/computational narrative over and above simple analogy.
Computer simulations performed as part of research in artificial life have reproduced various known features of life processes and biological evolution. Evolution seems to manifest some fundamental properties of computation, and not only does it seem to resemble an algorithmic process [27,28], it often seems to produce the kind of persistent structures and output distributions that a computation could be expected to produce [29], including links to optimisation programs [30,31].
The order we see in nature is clearly at least partly a result of self-assembly processes (e.g., molecules and crystals, multicellular organisms and even galaxy clusters, to mention just a few examples). Among the most recent discoveries in molecular biology is the finding that genes form the building blocks out of which living systems are constructed [32,33], a finding that sheds light on the common principles underlying the development of organs as functional components rather than mere biochemical ingredients.
Recently there has been an interest in the “shape” of a self-assembled system as output of a computational process [34,35,36,37,38]. These kinds of processes have been modelled using computation before [39], and the concept of self-assembly has been extensively studied by computer scientists since von Neumann (and Ulam) [40], who studied features of computational systems capable of displaying persistent self-replicating structures as an essential aspect of life, notably using cellular automata. Eventually these studies produced systems manifesting many features of life processes [27,41,42], all of which have turned out to be profoundly connected to the concept of (Turing) universal computation (Conway’s game of Life (Figure 3), Langton’s ant, Wolfram’s Rule 110). Some artificial self-assembly models [35], for example, demonstrate all the features necessary for Turing-universal computation and are capable of yielding arbitrary shapes [43] such as a Turing-universal biomolecular system.
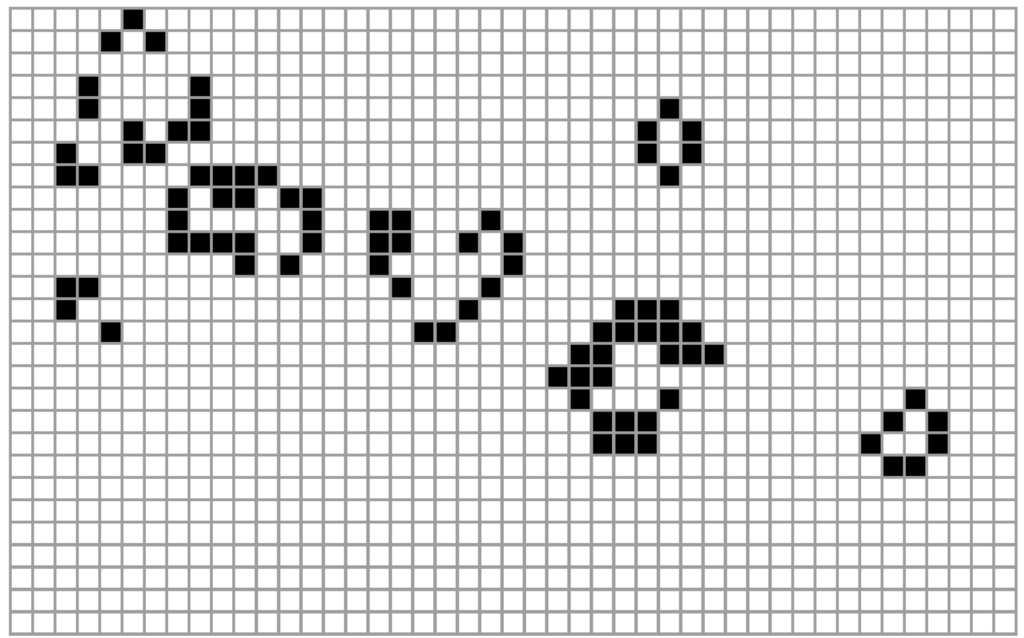
Figure 3.
A step configuration of Conway’s Game of Life [41] (each cell looks to its neighbours to stay alive or die—stay black or white). Surprisingly, simple processes like this rule system, today called a cellular automaton, can capture fundamental aspects of life such as self-assembly, robustness and self-replication, and are capable of the most important feature of computation: Turing universality. von Neumann [40] sought to model one of the most basic life processes—reproduction—by designing these kinds of lattice-based rules where space is updated altogether in discrete steps for studying self-replication.
Natural selection works well for systems that have evolved a heritable system of replication, but natural selection comes into play only after life has emerged. In his computer experiments, A.N. Barricelli concluded that “mutation and selection alone... [prove] insufficient to explain evolutionary phenomena” [44,45]. According to Dyson, the engineers at Princeton (where Barricelli worked) in charge of running Barricelli’s experiments were actually incredulous, and believed that there was something in his code that they had not been apprised of. George Dyson [46] reads this as a reflection of the engineers’ surprise that a set of simple instructions could generate such apparent complexity. As Wolfram has shown [27], systems such as Conway’s game of Life do not have any special features; they do not stand out from a set of similar rule systems capable of the same complexity. In fact, today we know that the elements necessary for (Turing) computational universality are minimal, as shown by Wolfram’s Rule 110 and tag systems that have led to the construction of the smallest Turing machines capable of universal computation [27,47,48].
Dyson suggests [46] that biology was ported to computers just as they were born, that computers imported the concept of natural selection into machines from the inception. Barricelli’s main contribution consists in viewing the world, particularly life processes and life itself, as software. It was a later development than—though it is not connected with—what is today a collection of nature-inspired techniques of heuristic search problem solving, such as evolutionary computation [49,50], and even more radical forms of unconventional computation (e.g., [51]).
Many fundamental challenges in biology require an understanding of how environmental change impacts the dynamics of interacting populations. If biological systems can be regarded as computational systems, one may inquire into biological systems as one would into computational systems. This is not a strange position, and indeed an informational/computational perspective on biological processes has begun to be adopted in the literature (as an example see [52]).
In [53], Chaitin also suggests that biological evolution can be studied with tools from software engineering and information theory. An organism can then be seen as a computer program and mutations as changes to the program rather than to (or on top of) DNA loci, leading to subroutines that produce more coherent and reusable changes, which natural evolution can then test in the field more efficiently than would be possible with incremental punctual mutation.
But if algorithmic concepts can be successfully adapted to the biological context, key concepts developed in computation theory may not only be relevant to biology but also help explain other aspects of biological phenomena. For example, it has recently been shown that information is a fitness-enhancing resource, as acquiring information will eventually pay off against the alternative of remaining ignorant [54]. We are also suggesting how algorithmic probability may explain simplicity bias in biological distributions (e.g., the distribution of biological shapes) [55] and interactions with computational thermodynamics, leading to what we believe is a fundamental trade-off between energy and information in biological systems, as related to fitness. We have made some connections between computational thermodynamics and predictability in the relation between organisms and their stochastic environments [56], connections such as we have made before between the power of artificial neural networks and the mind [57].
To understand the role of information in biological systems, one can think of a computer as an idealised information-processing system. Converting energy into information is fairly easy to understand today from a practical point of view [3,4,8]. Computers may be thought of as engines transforming energy into information. Instead of having to use “fuel binary tapes” one need only connect one’s computer to the electrical grid in order to have it perform a task and produce new information at the cost of an electricity bill.
Even if the trade-off is not yet precisely understood in detail, it is clear how animals convert information into energy—for example, by using information to locate food [58], or in learning how to hunt [59]. Similarly, it is clear that energy can be used to extract even greater quantities of energy from the environment—through investment in the construction and operation of a brain. From this it follows that the extent to which an organism is adapted to or able to produce offspring in a particular environment depends on a positive exchange ratio between information and energy.
3.1. Computational Thermodynamics and Biology
The discrepancies between energy and information are not entirely incompatible. Imagine an animal sharing information about the location of food. The amount of food is finite and will have to be split between two organisms having knowledge of it; sharing the information will not produce more food. However, if the food supply were large enough to feed both organisms, both would benefit from sharing the information. So in fact here the exchange makes sense despite the fact that information and energy (in the form of food) have radically different properties.
In exchanging information for energy and energy for information, some energy inevitably escapes into the environment (see Section 1 and [3]). Hence this is also a subject relevant to ecology, and ultimately to climate change. Dissipation is a general phenomenon in the real world and it tells us that something is lost in the exchange process, something which itself interacts with the environment, affecting other organisms. In accordance with the second law of thermodynamics, one can see this as information about the system’s irreversibility. In biology, this kind of exchange happens all the time. Neurons, for example, dissipate about 1011kT per discharge [4]. Computers (mainly because of their volatile memory devices—the RAM memory) also dissipate energy by at least 1kT per bit [3,4], which is also the reason computers heat up and require an internal fan.
4. Concluding Remarks
As pointed out in [60], natural selection can be seen as extracting information from the environment and coding it into a DNA sequence. But current efforts in the direction of quantifying information content typically do not venture beyond Shannon’s communication theory [61]. Nevertheless, as we are suggesting, analogies with computation and algorithmic complexity may help us understand how selection accumulates and exchanges information and energy from the environment in the replacement of populations, as they have already helped connect computation and physics in thermodynamics.
In this short review, we have seen how information and computation play an increasingly important role in modern physics. Information will continue to play a role in unifying the seemingly disconnected fields of knowledge. It will also turn out to be a serviceable tool for biology, constituting a powerful unifying apparatus as well as a resource for modelling living systems phenomena and thereby advancing the life and environmental sciences.
References and Notes
- Cooper, S.B. “The Mathematician’s Bias”, and the Return to Embodied Computation. In A Computable Universe: Understanding Computation & Exploring Nature as Computation; Zenil, H., Ed.; World Scientific Publishing Company: Singapore, 2012. [Google Scholar]
- Szilárd, L. Über die Entropieverminderung in einem thermodynamischen System bei Eingriffenin telligenter Wesen (On the reduction of entropy in a thermodynamic system by the interference of intelligent beings). Z. Physik 1929, 53, 840–856. [Google Scholar] [CrossRef]
- Landauer, R. Irreversibility and heat generation in the computing process. IBM J. Res. Dev 1961, 5, 183–191. [Google Scholar] [CrossRef]
- Bennett, C.H. The thermodynamics of computation—A review. Int. J. Theor. Phys. 1982, 21, 905–940. [Google Scholar] [CrossRef]
- Bennett, C.H. Demons, Engines and the Second Law. Sci. Am. 1987, 257, 108–116. [Google Scholar] [CrossRef]
- Fredkin, E.; Toffoli, T. Conservative logic. Int. J. Theor. Phys. 1982, 21, 219–253. [Google Scholar] [CrossRef]
- Maxwell, J.C. Theory of Heat, 9th; Pesic, P., Ed.; Dover: Mineola, NY, USA, 2001. [Google Scholar]
- Feynman, R.P. Feynman Lectures on Computation; Hey, J.G., Allen, W., Eds.; Addison-Wesley: Boston, MA, USA, 1996; p. 147. [Google Scholar]
- Sethna, J. Statistical Mechanics: Entropy, Order Parameters and Complexity; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Toffoli, T. Reversible Computing; Technical memo MIT/LCS/TM-151; MIT Lab for Computer Science: Cambridge, MA, USA, 1980. [Google Scholar]
- Bennett, C.H. Logical reversibility of computation. IBM J. Res. Dev. 1973, 17, 525. [Google Scholar] [CrossRef]
- Cerny, V. Energy, Entropy, Information, and Intelligence. Available online: http://arxiv.org/pdf/1210.7065.pdf (accessed on 19 November 2012).
- Kolmogorov, A.N. Three approaches to the quantitative definition of information. Probl. Inform. Transm. 1965, 1, 1–7. [Google Scholar]
- Chaitin, G.J. A Theory of Program Size Formally Identical to Information Theory. J. Assoc. Comput. Mach. 1975, 22, 329–340. [Google Scholar] [CrossRef]
- Solomonoff, R.J. A formal theory of inductive inference: Parts 1 and 2. Inform. Control 1964, 7, 1–22, 224–254. [Google Scholar]
- Levin, L. Laws of information conservation (non-growth) and aspects of the foundation of probability theory. Probl. Inform. Transm. 1974, 10, 206–210. [Google Scholar]
- Preskill, J. Do Black Holes Destroy Information? Available online: http://arxiv.org/abs/hep-th/9209058 (accessed on 19 November 2012).
- Giddings, S.B. Comments on information loss and remnants. Phys. Rev. D. 1994, 49, 4078–4088. [Google Scholar] [CrossRef]
- Read in a presentation at the Philosophical Society of Zurich on April 24, 1865.
- Bekenstein, J.D. Information in the Holographic Universe. Sci. Am. 2003, 289, 61. [Google Scholar]
- Susskind, L. The World as a Hologram. J. Math. Phys. 1995, 36, 6377–6396. [Google Scholar] [CrossRef]
- Bousso, R. The holographic principle. Rev. Mod. Phys. 2002, 74, 825–874. [Google Scholar] [CrossRef]
- t Hooft, G. Dimensional Reduction in Quantum Gravity. Available online: http://arxiv.org/abs/gr-qc/9310026 (accessed on 19 November 2012).
- Wheeler, J.A. Information, physics, quantum: The search for links. In Complexity, Entropy, and the Physics of Information; Zurek, E., Ed.; Addison-Wesley: Boston, MA, USA, 1990. [Google Scholar]
- Misner, C.W.; Thorne, K.S.; Zurek, W.H. John Wheeler, relativity, and quantum information. Phys. Today 2009, 62, 40. [Google Scholar]
- Deutsch, D. Quantum Theory, the Church-Turing Principle, and the Universal Quantum Computer. Proc. R. Soc. Lond. 1985, A400, 97–117. [Google Scholar]
- Wolfram, S. A New Kind of Science; Wolfram Media: Champaign, IL, USA, 2002. [Google Scholar]
- Dennett, D.C. Darwin’s Dangerous Idea: Evolution and the Meanings of Life; Simon & Schuster: New York, NY, USA, 1996. [Google Scholar]
- Zenil, H.; Delahaye, J.P. On the Algorithmic Nature of the World. In Information and Computation; Dodig-Crnkovic, G., Burgin, M., Eds.; World Scientific: Singapore, 2010. [Google Scholar]
- Grafen, A. The simplest formal argument for fitness optimization. J. Genet. 2008, 87, 1243–1254. [Google Scholar]
- Grafen, A. The formal Darwinism project: A mid-term report. J. Evolution. Biol. 2007, 20, 1243–1254. [Google Scholar]
- Hunt, P. The Function of Hox Genes. In Developmental Biology; Bittar, E.E., Ed.; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Shetty, R.P; Endy, D.; Knight, T.F., Jr. Engineering BioBrick vectors from BioBrick parts. J. Biol. Eng. 2008, 2. [Google Scholar] [CrossRef]
- Adleman, L.M. Toward a Mathematical Theory of Self-Assembly; USC Technical Report: Los Angeles, CA, USA, 2000. [Google Scholar]
- Rothemund, P.W.K.; Papadakis, N.; Winfree, E. Algorithmic Self-Assembly of DNA Sierpinski Triangles. PLoS Biol. 2004, 2. [Google Scholar] [CrossRef]
- Adleman, L.M.; Cheng, Q.; Goel, A.; Huang, M.-D.A. Running time and program size for self-assembled squares. In ACM Symposium on Theory of Computing, Crete, Greece; 2001; pp. 740–748. [Google Scholar]
- Rothemund, P.W.K.;Winfree, E. The program-size complexity of self-assembled squares (extended abstract). In ACM Symposium on Theory of Computing, Portland, OR, USA; 2000; pp. 459–468. [Google Scholar]
- Aggarwal, G.; Goldwasser, M.; Kao, M.; Schweller, R.T. Complexities for generalized models of self-assembly. In Symposium on Discrete Algorithms, New Orleans, LA, USA; 2004. [Google Scholar]
- Winfree, E. Algorithmic Self-Assembly of DNA Thesis. Ph.D Thesis, 1998. [Google Scholar]
- von Neumann, J. The Theory of Self-reproducing Automata; Burks, A., Ed.; University of Illinois Press: Urbana, IL, USA, 1966. [Google Scholar]
- Gardner, M. Mathematical Games—The fantastic combinations of John Conway’s new solitaire game “life”. Sci. Am. 1970, 223, 120–123. [Google Scholar] [CrossRef]
- Langton, C.G. Studying artificial life with cellular automata. Physica D 1986, 22, 120–149. [Google Scholar] [CrossRef]
- Winfree, E. Simulations of Computing by Self-Assembly; Technical Report CS-TR:1998.22; Caltech: Pasadena, CA, USA, 1998. [Google Scholar]
- Barricelli, N.A. Numerical testing of evolution theories Part I Theoretical introduction and basic tests. Acta Biotheor. 1961, 16, 69–98. [Google Scholar] [CrossRef]
- Reed, J.; Toombs, R.; Barricelli, N.A. Simulation of biological evolution and machine learning. I. Selection of self-reproducing numeric patterns by data processing machines, effects of hereditary control, mutation type and crossing. J. Theor. Biol. 1967, 17, 319–342. [Google Scholar]
- Dyson, G. Darwin Among the Machines; Penguin Books Ltd.: London, UK, 1999. [Google Scholar]
- Cook, M. Universality in Elementary Cellular Automata. Complex Syst. 2004, 15, 1–40. [Google Scholar]
- Neary, T.; Woods, D. Small weakly universal Turing machines. In 17th International Symposium on Fundamentals of Computation Theory (FCT 2009); Springer: Warsaw, Poland, 2009; Volume 5699 of LNCS, pp. 262–273. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Martínez, G.J.; Adamatzky, A.; Stephens, C.R. Cellular automaton supercolliders. Int. J. Mod. Phys. C 2011, 22, 419–439. [Google Scholar] [CrossRef]
- Livnat, A.; Pippenger, N. An optimal brain can be composed of conflicting agents. PNAS 2006, 103, 9. [Google Scholar]
- Chaitin, G.J. Metaphysics, Metamathematics and Metabiology. In Randomness Through Computation; Zenil, H., Ed.; World Scientific: Singapore, 2011; pp. 93–103. [Google Scholar]
- McNamara, J.M.; Dall, S.R.X. Information is a fitness enhancing resource. Oikos 2010, 119, 231–236. [Google Scholar] [CrossRef]
- Zenil, H.; Marshall, J.A.R. Some Computational Aspects of Essential Properties of Evolution and Life. ACM Ubiquity 2012, 12, 11. [Google Scholar]
- Zenil, H.; Gershenson, C.; Marshall, J.A.R.; Rosenblueth, D. Life as Thermodynamic Evidence of Algorithmic Structure in Natural Environments. Entropy 2012, 14, 2173–2191. [Google Scholar] [CrossRef]
- Zenil, H.; Hernandez-Quiroz, F. On the Possible Computational Power of the Human Mind. In Worldviews, Science and Us: Philosophy and Complexity; Gershenson, C., Aerts, D., Edmonds, B., Eds.; World Scientfic: Singapore, 2007. [Google Scholar]
- Paz Flanagan, T.; Letendre, K.; Burnside, W.; Fricke, G.M.; Moses, M. How ants turn information into food. IEEE Artificial Life (ALIFE) 2011. Paris, France. [Google Scholar]
- Catalania, K.C. Born knowing: Tentacled snakes innately predict future prey behaviour. PLoS ONE 2010, 5, 6. [Google Scholar]
- de Vladar, H.P.; Barton, N.H. The contribution of statistical physics to evolutionary biology. Trends Ecol. Evol. 2011, 26, 424–432. [Google Scholar] [CrossRef]
- Shannon, C. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 279–423, 623–656. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).