Beyond Bayes: On the Need for a Unified and Jaynesian Definition of Probability and Information within Neuroscience

Abstract

It has been proposed that the general function of the brain is inference, which corresponds quantitatively to the minimization of uncertainty (or the maximization of information). However, there has been a lack of clarity about exactly what this means. Efforts to quantify information have been in agreement that it depends on probabilities (through Shannon entropy), but there has long been a dispute about the definition of probabilities themselves. The “frequentist” view is that probabilities are (or can be) essentially equivalent to frequencies, and that they are therefore properties of a physical system, independent of any observer of the system. E.T. Jaynes developed the alternate “Bayesian” definition, in which probabilities are always conditional on a state of knowledge through the rules of logic, as expressed in the maximum entropy principle. In doing so, Jaynes and others provided the objective means for deriving probabilities, as well as a unified account of information and logic (knowledge and reason). However, neuroscience literature virtually never specifies any definition of probability, nor does it acknowledge any dispute concerning the definition. Although there has recently been tremendous interest in Bayesian approaches to the brain, even in the Bayesian literature it is common to find probabilities that are purported to come directly and unconditionally from frequencies. As a result, scientists have mistakenly attributed their own information to the neural systems they study. Here I argue that the adoption of a strictly Jaynesian approach will prevent such errors and will provide us with the philosophical and mathematical framework that is needed to understand the general function of the brain. Accordingly, our challenge becomes the identification of the biophysical basis of Jaynesian information and logic. I begin to address this issue by suggesting how we might identify a probability distribution over states of one physical system (an “object”) conditional only on the biophysical state of another physical system (an “observer”). The primary purpose in doing so is not to characterize information and inference in exquisite, quantitative detail, but to be as clear and precise as possible about what it means to perform inference and how the biophysics of the brain could achieve this goal.

1. Introduction

It is almost universally agreed that the nervous system is specialized for processing information. But for most people, that statement would seem too vague to be meaningful. While everyone has some intuitive notion of the meaning of “information” for most people, including neuroscientists, the concept is too poorly defined to provide any deep insight into the function of the nervous system. I myself had both a bachelor’s degree and a Ph.D. in neuroscience before I discovered, to my surprise, that there exists a precise quantitative definition of information. Although Claude Shannon gave this definition in 1948 [1], his work is still not widely known and understood in biology and medicine. By contrast, his “information theory” is nearly universally known and accepted by engineers, physicists and mathematicians.

There are several remarkable facts that suggest serious shortcomings in our basic approach to understanding the brain and information. First, despite its considerable contributions with respect to engineering, information theory still has not found its way into biology and medical textbooks after 60 years. Even standard neuroscience textbooks, including the authoritative text of Kandel and colleagues [2] with 1414 pages, make no reference to information theory or Claude Shannon. Thus one might reasonably conclude that, thus far, information theory has been of limited use in understanding brain function. Second, despite the explosion of knowledge about the mechanics of the nervous system that has taken place over the last 60 years, there has been relatively little progress towards understanding the information processing function of the nervous system. For example, there has not been a corresponding explosion in the development of artificial intelligence. This is in spite of the fact that virtually all scientists believe that information processing is inextricably linked to biophysical mechanisms, and thus one might expect our understanding of information processing to grow in parallel with our understanding of mechanics. Third, we lack consensus even on the gross general function of the brain. The authoritative text of Dayan and Abbott, entitled Theoretical Neuroscience, does not even speculate about whether or not the bran has a general computational goal [3]. All three of the factors above suggest that modern neuroscience may be missing something of fundamental importance.

I propose here that these difficulties can be attributed in large part to confusion about the nature of information. Scientists have often mistaken their own knowledge about physical systems for inherent properties of the systems themselves. One consequence of this confusion has been that the concept of information has been divorced from the biophysical substrates that constitute the nervous system. Here I suggest that, properly understood, the concept of information can be grounded in biophysics and it can offer insight into neural function.

2. The Computational Goal of the Nervous System

The concepts of probability and information are of fundamental importance to the computational goal of the nervous system. Since at least as far back as von Helmholz (1896) [4], it has been recognized that inferring the state of the world is critical to brain function (or equivalently, “estimating” or “predicting”). This intuitive idea has now been expressed within a formal mathematical framework that is typically summarized by the term “Bayesian”. There has been a rapidly growing view that Bayesian principles of reason and inference may provide us with a general computational description of brain function (e.g., [5,6]). In recent years, great progress has been made in understanding the information and inference that underlies a wide variety of perceptual, cognitive and motor phenomena in humans (e.g., [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]). There have also been efforts to relate Bayesian principles to neuronal mechanisms, although these have generally been quite speculative (e.g., [5,27,28,29,30,31,32]).

According to Bayesian accounts, the function of the brain is to infer or predict the state of the world for the purpose of selecting motor outputs (“decision-making” in a broad sense of the term). I have proposed that the only fundamental problem in making decisions is uncertainty (lack of information) about the world [5]. Introspection tells each of us that if we knew everything about the world, and thus we had no uncertainty, then we would always know exactly what to do and we could choose the best possible motor outputs. The less uncertainty we have, the better our decisions will be. Thus the general function of the nervous system can be described in quantitative terms as the minimization of uncertainty (or more specifically, the minimization of uncertainty about biologically relevant aspects of the world), which is essentially the same as maximization of information.

As scientists who view the goal of the brain as inference, our goal is to try to use our knowledge to infer the information and inference of a brain. Thus we try to “take the brain’s point of view”, a challenge that has been approached through a variety of different methods [5,21,24,33]. In this endeavor, we are presented with three entities, the scientist, the neural system under investigation, and the environment external to the neural system (Figure 1). A major problem addressed here is that scientists have often misattributed their own knowledge to the systems that they study. This problem can be substantially avoided by adherence to the principles developed by E.T. Jaynes [34,35]. Although Jaynes expressed these principles in the rigorous mathematical form of probability theory, they apply to all knowledge and reason, and thus they are relevant far beyond the formal application of probabilities. Since my experience suggests that there is minimal awareness of Jaynes within neuroscience, the present work is also intended to introduce his ideas to this field.

Figure 1. Are the information and probabilities used in neuroscience properties of the environment (an observed object), the neural system under investigation, or the scientist? The frequentist view is that probabilities are a property of a physical system (or object) that generates frequency distributions, and they exist independent of any observer of that system. The physical system could correspond to a neural system or anything else. Here I argue in favor of the view of Jaynes (and Laplace, shown at left) that probabilities are always conditional on the information of an observer about an object. I presume that the observer’s information must be in a physical form inside the observer. There could be many observers, but in neuroscience, the observer of interest would usually correspond either to the scientist (who observes a neural entity as well as its environment from a “third-person” perspective), or to the neural entity under investigation (for example, a brain, neuron or ion channel, which observes its environment from its “first-person” perspective). The arrows indicate the typical direction of information flow. The distinction between “observer” and “object” is merely one of perspective, and does not imply any fundamental distinction between the qualities of the two.

Figure 1. Are the information and probabilities used in neuroscience properties of the environment (an observed object), the neural system under investigation, or the scientist? The frequentist view is that probabilities are a property of a physical system (or object) that generates frequency distributions, and they exist independent of any observer of that system. The physical system could correspond to a neural system or anything else. Here I argue in favor of the view of Jaynes (and Laplace, shown at left) that probabilities are always conditional on the information of an observer about an object. I presume that the observer’s information must be in a physical form inside the observer. There could be many observers, but in neuroscience, the observer of interest would usually correspond either to the scientist (who observes a neural entity as well as its environment from a “third-person” perspective), or to the neural entity under investigation (for example, a brain, neuron or ion channel, which observes its environment from its “first-person” perspective). The arrows indicate the typical direction of information flow. The distinction between “observer” and “object” is merely one of perspective, and does not imply any fundamental distinction between the qualities of the two.

3. Information and Probability

3.1. Two Definitions of Probability

Two fundamentally distinct definitions of probability have been proposed, “Jaynesian” (better known as “Bayesian”) and “frequentist” (summarized in Table 1). The key difference is that the Jaynesian definition asserts that probabilities are a property of the information possessed by an observer about an object, whereas the frequentist definition asserts that the probabilities are a property of the object itself, independent of any observer (Figure 1). The two definitions can be illustrated by the differing answers that might be given to a simple question: “An event has four possible outcomes which are mutually exclusive, A, B, C, and D. What is the probability of each outcome?” The Jaynesian answer is that, in the absence of any additional information, logic requires that all outcomes be considered equally likely, and thus the probability of each is 1/4 or 0.25. The frequentist response is that the question is inappropriate. In order to apply the concept of probability, one must first observe the frequency with which each outcome occurs. As one makes repeated observations of the outcome, one can begin to “estimate” the probabilities. To be certain of the probabilities, one would have to make an infinite number of observations. According to a strict frequentist definition, probabilities are equivalent to frequencies; they are a physical property of a system, and they are independent of an observer’s knowledge of the system.

Table 1. Two definitions of probability. These can be illustrated by the following scenario: There are four mutually exclusive possibilities, A, B, C, and D. What is the probability of each?

Definition	Frequentist	Jaynesian
Answer	Probabilities are unknown and undefined because there are no frequencies	1/4 = 0.25
Meaning	Probabilities come from measuring frequencies	Probabilities describe information (from any source)
Derivation	A collection of ad hoc rules allow us to estimate probabilities	Logic (common sense) precisely specifies probabilities through the principle of maximum entropy
Attribution	Probabilities are a property of a physical system	Probabilities are a property of an observer of a physical system

Table 1. Two definitions of probability. These can be illustrated by the following scenario: There are four mutually exclusive possibilities, A, B, C, and D. What is the probability of each?

Definition	Frequentist	Jaynesian
Answer	Probabilities are unknown and undefined because there are no frequencies	1/4 = 0.25
Meaning	Probabilities come from measuring frequencies	Probabilities describe information (from any source)
Derivation	A collection of ad hoc rules allow us to estimate probabilities	Logic (common sense) precisely specifies probabilities through the principle of maximum entropy
Attribution	Probabilities are a property of a physical system	Probabilities are a property of an observer of a physical system

3.2. A Very Brief History of Probability Theory

Thomas Bayes was the first to explicitly and formally introduce the concept that probabilities can be conditional on information in what is now known as Bayes’s Theorem (BT) (he died in 1761, and his theorem was published posthumously). Like others before him, he simply used his own intuition to derive probabilities from information. Simon Pierre Laplace (shown in Figure 1) was arguably the most important person in the early development and application of probability theory. In the early 19th century, he referred to probability theory as “nothing but common sense reduced to calculation” [36]. To derive probabilities from knowledge, he suggested mathematical expressions of common sense, such as the “principle of indifference”. However, the principle of indifference was of only limited applicability, and it appeared to some scientists to be arbitrary. In an effort to give probabilities an “objective” status, others proposed that the formal use of probabilities should be restricted to cases in which there was a clear relationship to measured frequencies of events. R.A. Fisher promoted this view in the early 20th century, and it formed the basis of William Feller’s classic text from 1950 on probability theory [37]. But even with the use of probabilities restricted to cases involving measured frequencies, steps were required to transform a frequency into a probability. Without any general and unified principle to guide this transformation, statisticians developed an ad hoc collection of rules that were applicable in special cases. In 1948, Shannon demonstrated that entropy could be used to quantify information [1]. Shannon’s entropy is a more general expression of Laplace’s “indifference,” and common sense tells us that in making inferences, we should not assume any information that we do not actually have. In 1957, E.T. Jaynes demonstrated that the maximization of entropy provided an objective basis for deriving probabilities from information [34]. He and others went on to develop a unified account of logic and information generally referred to as “Bayesian probability theory” [35,38]. For reasons disclosed below (Section 3.9), I will use the term “Jaynesian” rather than “Bayesian” in referring to probability theory according to Jaynes.

3.3. The Jaynesian Definition of Probability: The Maximum Entropy Principle

Jaynesian theory ultimately seeks to provide a unified account of information (knowledge) and logic (reason), and thus its relevance extends far beyond formal applications of probability theory. The Jaynesian definition of probability has been advanced by many authors over the years (e.g., [38]), but the account given here is based upon the posthumous textbook of Jaynes from 2003 [35]. According to Jaynes, probability theory is a natural extension of earlier work on logic. Conventional logic is restricted to cases in which knowledge is sufficient to categorize propositions as either true (1) or false (0), and thus it is not applicable to the conditions of uncertainty that characterize reality. Jaynesian probability theory incorporates uncertainty by describing confidence (or strength of belief) in a proposition on a continuous scale of 0 to 1. Conventional logic and deductive reasoning can therefore be understood as a special case of Jaynesian rationality. Jaynesian probability theory is a formal expression of logic (or reason).

At the risk of oversimplification, the approach of Jaynes can be summarized by the statement:

Logic is Objective, Information is Subjective

Logic is universal and indisputable, whereas information is localized in space and time to an observer, and it typically differs over time between observers.

The probability of a particular proposition (or state) is always entirely conditional on a particular set of knowledge or information. This conditionality is the defining feature of Jaynesian probabilities. The rules relating knowledge to probability are essentially just “common sense” or logic, as embodied within the principle of maximum entropy. The maximum entropy principle requires that we fully acknowledge our ignorance by considering all possibilities equally probable unless we have evidence to the contrary. For example, if the only information available is that “there are four possible outcomes”, then the probability distribution that describes that information is “flat” since entropy is maximized when the probabilities are all equal. Since by definition the sum of the probabilities must equal one (which is merely a trivial but useful convention), the probability of each outcome is 0.25. In contrast to this contrived example, we often have information that does not constrain the number of possible states, but does constrain the location and scale. If a state of knowledge consists only of the location and scale (such as mean and variance), with no bounds on the state space, that knowledge is described by a Gaussian probability distribution, which has the maximum entropy given this knowledge. In some cases our knowledge derives almost entirely from observing the past frequency of an event, in which case the probability distribution that best describes our knowledge may closely resemble the observed frequency distribution. Thus knowledge derived from measurement of frequency distributions is treated just like any other knowledge.

The bridge between information and a probability distribution is the principle of maximum entropy. The probability distribution that correctly describes a state of knowledge is the one with maximum entropy, and thus mathematical methods to find a probability distribution should seek to maximize the entropy (H).

(1)

The entropy (H(x|XY) of a probability distribution is defined as the negative sum over all possible values of the probability (p_i) of a specific value of x (x_i) multiplied by its logarithm (this is the “Shannon entropy”) [1]. The entropy is conditional on information XY (see below for distinction between X and Y). (Here and in all present notation, uppercase letters denote precise information that is possessed by the observer, and lowercase letters denote unknown variables that are the object of inference.) The maximum entropy distribution (MED) is the one that most fully acknowledges ignorance, making no assumptions beyond those required by the available evidence. According to Jaynes, all probability distributions are (or should be) MEDs. Since the founding of probability theory, when people have correctly formulated probabilities based on their intuition or any ad hoc method, they have done so through a process equivalent to maximizing entropy, whether they realized it or not.

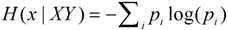
3.4. Quantifying the Amount of Information

A probability distribution is conditional on information, and it fully and quantitatively characterizes the information upon which it is conditional (with respect to a particular state space). Having derived a probability distribution, we can also measure the amount of information. In many applications of probability theory, including efforts to understand the neural basis of inference, it is not necessary to quantify the amount of information as a practical matter. However, it was Shannon’s effort to quantify information that led him to entropy [1], which in turn inspired Jayne’s maximum entropy principle. Shannon’s measure of information also directly inspired the “efficient coding hypothesis” of Barlow (1961), which has probably been the most successful of any computational theory in explaining the properties of neurons (e.g., [33,39,40,41,42,43,44]).

Information and entropy (uncertainty) have a fairly simple and intuitive relationship: The more information, the narrower the probability distribution, and the less the entropy. The information determines the probabilities, and the entropy, through the maximum entropy principle. If one were to quantify information, it would simply be the difference between the entropy (H) that would correspond to the absence of the information, and the entropy that corresponds to the presence of the information.

(2)

In Equation 2, “Y” corresponds to the information that we wish to quantify, and “X”; corresponds to “background” or “prior” information that is also available to the observer. This equation states that the quantity of information I(Y|X) depends on information X and its interaction with Y (the interaction is implicit in information XY). This is essentially just Shannon’s expression for information, in which I(Y|X) is the “information gain” and XY is the total information of the observer. However, it is important to emphasize that because probabilities are always entirely conditional on information, entropies and information “gain” are also conditional on information. They are all relative to the information X of the observer, and thus for two observers to agree on their values, the two observers must work from the same frame of reference X. Shannon did not state this explicitly, at least in his original work [1].

The relativistic nature of Shannon information (Equation 2) can cause confusion and limit its general utility as a measure of information. Intuitively, we would like to quantify the amount of information in such a way that entropy corresponds directly to an absence of information, similar to the way in which a vacuum corresponds to an absence of matter. We would like to use a single and universal scale, allowing us to measure it in an absolute sense, in isolation and without consideration of any other information. This would allow us to quantify all of an observer’s information (XY in the present case). It could also help us to overcome the potentially confusing fact that “information gain” can actually be a negative number corresponding to information loss. For example, common language agrees without intuition that an observation Y corresponds to information and should have a positive value. But it is always possible that an observation will actually increase our overall uncertainty (H(x|XY) > H(x|X)) (overthrowing a hypothesis that had been strongly favored, for example). Thus Shannon information can actually increase uncertainty, which at the least is confusing.

We could quantify information on an absolute scale using Equation 2 if we can identify a probability distribution corresponding to a state X of complete ignorance (so that no distribution could have a higher entropy). A truly complete state of ignorance may not exist in reality, and in any case, it is not possible to derive a corresponding probability distribution (since complete ignorance should correspond to a flat distribution over an infinite state space, but no such distribution can sum to one as required of a probability distribution). The next best thing would be to identify a primitive state of minimal information that is universal (shared by all observers). If all observers quantify the amount of information (in states A, B, C, etc.) relative to the same “universal prior” information X, then they will all measure information on a common scale and they will agree on the amount of information. Furthermore, if X corresponds to information that is minimal (very high entropy), then any additional information (XA, XB, etc.) will reduce entropy and thus have a positive value. Whether or not there could be a “truly universal” prior, once we conceive of a prior representing an appropriately high level of ignorance, then the “maximum entropy principle” of Jaynes could be restated as the “minimum information principle” (maximizing H(x|XY) in Equation 2 would be the same as minimizing I(Y|X)). This fits with common intuition and helps to elucidate the rationale for Jaynes’s maximum entropy principle: any distribution that has less than the maximum entropy assumes information that is not actually available (and any distribution that has higher entropy ignores the available information).

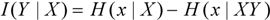
3.5. Bayes’s Theorem

The maximum entropy principle of Jaynes is a formal expression of logic, and it is the most fundamental principle within probability theory, since it defines probabilities and enables their derivation. All probabilities should be maximum entropy distributions (MEDs). In principle, all probabilities could be derived through entropy maximization, and thus it is sufficient to encapsulate all of probability theory. However, except for the simplest states of information, deriving MEDs directly is challenging if not impossible as a practical matter. Fortunately there is a rule known as Bayes’s Theorem (BT) that allows us to manipulate probabilities without the trouble of directly maximizing entropy (in a formal, mathematical sense). BT takes two or more MEDs, each based on distinct information, and finds a single MED for all the information. Like all of probability theory, BT is simply an expression of logic acting on information. It is an equality derived from the decomposition of a joint probability into a product of its components.

(3)

Verbally, it is typically described as stating that the posterior probability distribution equals the product of the prior distribution (p(x|X)) and the likelihood function (p(Y|X, x = x’) divided by an appropriate normalization factor (p(Y|X)). Information X, x = x’; is knowledge of the likelihood of evidence Y if we imagine that x were to have the value x’; (it is not standard notation to distinguish x and x’;, but it is done here to clarify that in the likelihood function, the observer does not possess information x, which after all is the “object” of inference in the prior and posterior. However, the observer does know the general nature of the relationship between x and Y, and thus imagines that x has the specific value x’; so as to find its consequences for the probability of the evidence Y. All of the probabilities in BT are conditional on “prior” information X. However, within neuroscience, BT is routinely shown without explicitly acknowledging the existence of any prior information (e.g., [3,33]), leaving readers to guess as to whether the authors believe the prior probability to be unconditional and equivalent to a frequency, or whether the omission of X from the equation is merely a convenience.

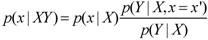
3.6. The General Method of Jaynes

The general method of Jaynesian probability theory can be summarized as a sequence of steps that apply to the formal derivation and manipulation of probabilities (Figure 2). Here it is described in four steps, only the first two of which are universal and essential to any application.

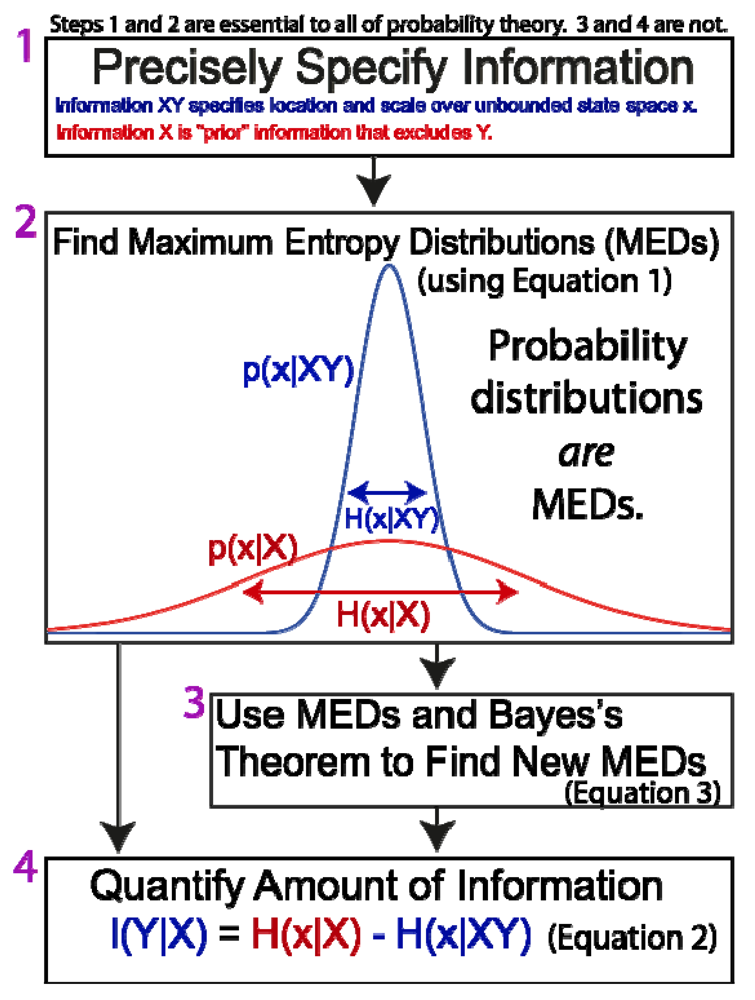
• Precisely and explicitly state the information upon which the probabilities should be conditional. In the view of Jaynes, this is the most important step. Ambiguity or failure to explicitly acknowledge information at the outset has led to severe confusion and misunderstanding about the meaning of probabilities and their derivation (in addition to countless examples provided by Jaynes [35], there has been decades of debate about the “Monty Hall problem”, one of many trivial applications of probability theory that are made needlessly controversial by ambiguity about the relevant information). Agreement and understanding requires that all observers are utilizing the same information (a fact which is universally apparent to anyone above a certain mental age, and which is not at all unique to probability theory). It should be noted that this first and most critical step in the method of Jaynes does not involve mathematics.

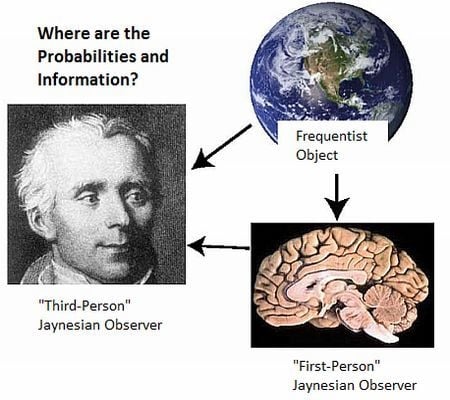
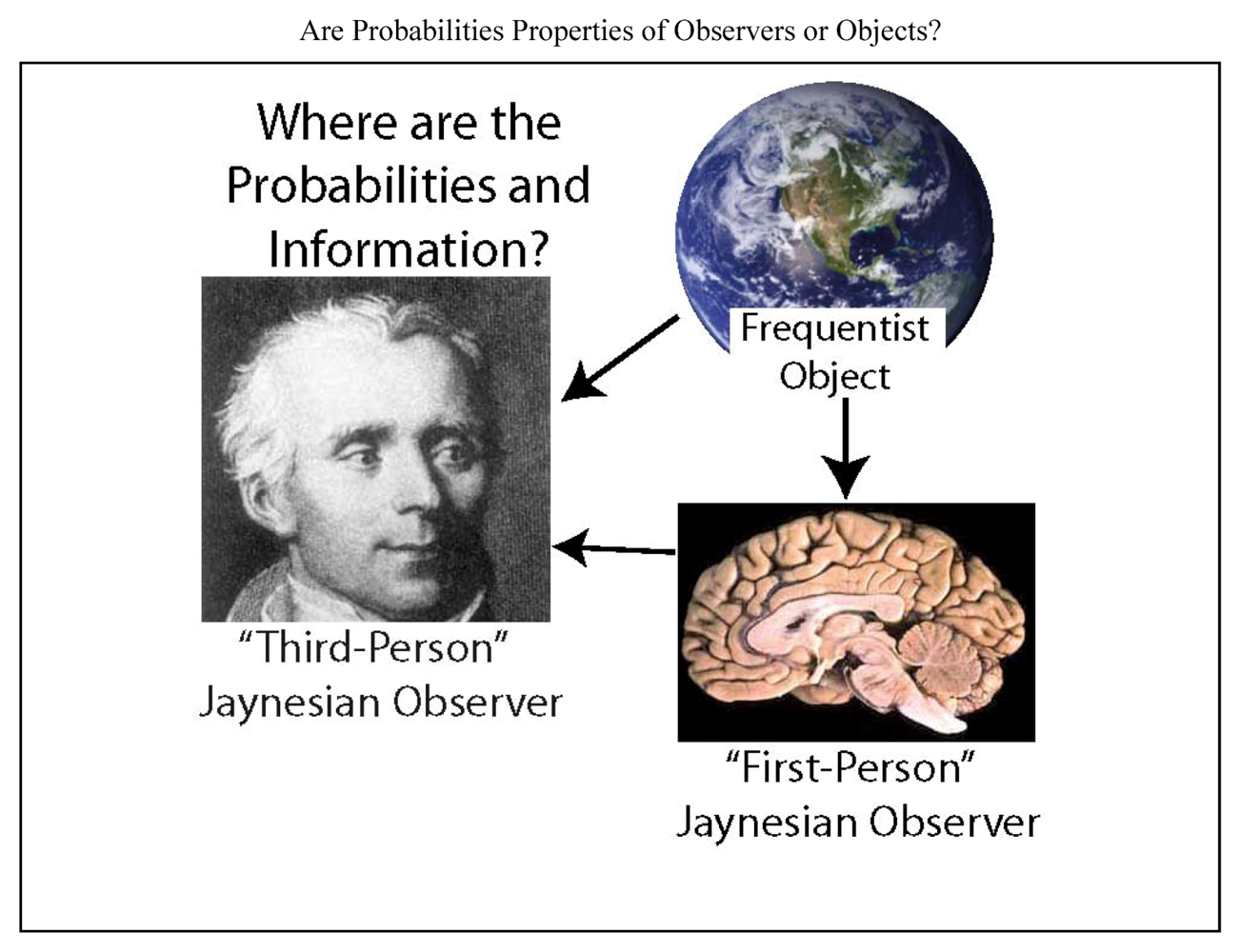
  • There is a further stipulation that is particularly critical for understanding the brain and the physical basis of information and inference. In addition to precisely stating the information, we must also specify where we believe that information to be, and if possible, its putative physical basis. “Where” must at least specify whether it is possessed by a scientist, a neural system under investigation, or whether it is in the environment external to the neural system (Figure 1). Failure to do so has resulted in the misattribution of the information possessed by scientists to the physical systems they study (such as brains; documented in Sections 4 and Sections 5.2 ).

  Figure 2. The General Methodological Sequence of Jaynes.

  Figure 2. The General Methodological Sequence of Jaynes.
• Maximize entropy. The function that correctly describes the information is the one that maximizes the entropy of Equation 1 (and sums to one, as all probability distributions must). This is conceptually simple, although the mathematical difficulty can range from trivial to intractable, depending on whether the information state is simple or complex (for example, estimating the value of a company based on one sample of trading value on a stock market, versus a diverse set of financial and economic data). All “correct” probability distributions are MEDs.
• Use MEDs and Bayes’s Theorem to derive new MEDs. Since the general goal of probability theory is to derive probabilities distributions (MEDs), and since in principle this can be done directly through entropy maximization, BT is not essential, in principle. As a practical matter, it is extremely useful because it allows us to generate new MEDs from existing MEDs in a manner that is much easier mathematically than directly maximizing entropy. Faced with a complex set of information, it can be useful to break the information into simpler “pieces”, maximize entropy to find a MED for each piece, and then use BT to derive a single distribution for the whole set of information.
• Quantify the amount of information. For inference and most applications, this is not necessary.

3.7. Response to Criticisms of Jaynesian Probabilities

Several criticisms have been made of Jaynesian probabilities. Extensive counterarguments have been given elsewhere (e.g., [35,38]), but I will briefly summarize several general points and relate these to models of brain function.

• Jaynesian probabilities have been criticized as being “subjective”, and thus ambiguous and not appropriate for science. The simple characterization of Jaynesian probabilities as “subjective” can be misleading. As expressions of logic, Jaynesian probabilities are objective properties of information without any ambiguity. Two observers with the same information will apply the same probabilities, and two observers with different information will apply different probabilities. The information is subjective in the sense that it tends to differ across observers, in accord with reality. It is the ability of Jaynesian probabilities to objectively describe subjective information that makes them so useful in understanding brain function.
• A second criticism of Jaynesian probabilities is that it is not always clear how they should be calculated. Although this is undoubtedly true, it is not a valid criticism of Jaynesian methods. To derive Jaynesian probability distributions, one must first be able to specify precisely what information is relevant, and then perform the mathematics. In the case of brain research, each of these might be difficult or even impossible as a practical matter, but there is no reason to think that it cannot be done as a matter of principle. Furthermore, there is reason to think this may not be so challenging with respect to the neural basis of inference (see Section 5.3).
• A third criticism stems from confusion of the subjective aspect of Jaynesian probabilities with our conscious attempts at quantifying the strength of our beliefs. Jaynesian probabilities are not simply a number that a person verbally reports based upon introspection. A person typically struggles to state the probability that one of their beliefs is true. This may be in part for the same reason that scientists and experts on probability theory struggle to rationally calculate probabilities in cases in which a great diversity of information is relevant. Of perhaps greater importance is the fact that, although human behavior is routinely based upon perceptions of what is probable and what is not, to be asked to verbally state (or consciously perceive) a probability is highly unusual and seldom important. To solve any particular problem, the brain must have information about some relevant aspect of the world (with a corresponding state space). If the brain is then asked to verbally specify a probability, the relevant aspect of the world (and its state space) now corresponds to the abstract notion of “probabilities” themselves, and the problem facing the brain has radically changed. The brain may have substantial information about some aspect of the world, but may have little information about the probabilities. In other words, information about “X” is not the same as information about the probability of “X”.The former concerns the probability of “X”, whereas the latter concerns the probability of a probability of “X”.
• A fourth criticism is not aimed at Jaynesian probabilities themselves, but rather questions their utility in understanding brain function on the grounds that behavior is not rational (optimal in its use of information). Although a full discussion of this issue is beyond the scope of the present work, several important points should be noted.

  • Humans are capable of reason, and there are numerous instances in which brain function is at least semi-rational.
  • To assess whether a brain is rational, we first must know what relevant information is in the brain. We should not confuse ignorance with lack of reason.
  • We know for a fact that the brain does not rationally integrate all of its information at all times. However, logical integration of smaller amounts of information, perhaps at the level of single neurons, is certainly conceivable.
  • Although the application of Jaynesian principles to the brain is often viewed as prescriptive, specifying how the brain ought to function, my view is that Jaynesian principles are better viewed as descriptive (see Section 5.3). In this view, a pathological brain could be just as Jaynesian as a healthy brain (though likely possessing less information) [45].

3.8. Faults with the Frequentist Definition of Probability

Like any other intellectual endeavor, the frequentist approach to probabilities relies on the application of reason to information. It may be understood as a poorly formulated and incomplete implementation of Jaynesian principles. The most general point to be made here is that those maintaining a frequentist view are in reality basing their probabilities on their own information. Frequentist probabilities are not actually properties of an observed system, as frequentists claim.

Some specific faults with the frequentist definition of probability are summarized below. Criticisms 1–5 have all been made previously by Jaynes and others (e.g., [35,38]).

• The frequentist definition contradicts intuition, and is of limited use, because it completely fails to account for information that is obviously relevant to probabilities. The simple example given above is the statement that “there are ‘N’ mutually exclusive states” (Table 1). It is obvious that this statement is informative, but a frequentist definition cannot even attempt to specify any probability distribution as a matter of principle. The problem is not merely that frequency distributions may not be available as a practical matter, but rather that in many cases no relevant frequency distribution could ever exist. A more glaring illustration of this fault, with respect to neuroscience, is that a frequentist view has no means to address the plain fact that different brains have different information and therefore place different probabilities on the same event. Thus, frequentist methods are frequently inapplicable.
• In those cases in which frequency distributions are available, it is unclear over what finite range or period they ought to be measured in order to derive probabilities. It is common to assume that the world is “stationary” and then to extrapolate an observed frequency to its limit as one imagines an infinite set of observations. But the real world is seldom if ever known to be stationary, and the actual data is always finite. To imagine otherwise is wishful thinking. Without any real, unique, and well-defined frequency distribution, the concept of a “true” probability, which we try to estimate, is just fantasy.
• Because measurement of a frequency distribution over a finite period is never sufficient to fully specify a probability distribution, derivation of a probability distribution requires incorporation of additional information that is not present in the observed frequency distribution. This is done in the form of “assumptions”, which in many cases are not stated explicitly and thus remain hidden. Statisticians assume “stationarity”, or a “Gaussian process”, or “statistical independence”. These assumptions actually constitute relevant information (or lack thereof) that the statistician possesses and uses. But conventional (frequentist) statistics does not have overarching principles for how to use this information, only a collection of ad hoc rules. Regardless of how this “hidden” information is used, its use contradicts the pretense that probabilities are derived directly from measurable frequencies and are thus “objective”.
• Empirical evidence has shown that given the same information, there are many cases in which frequentist methods make less accurate predictions than Jaynesian methods [35]. Thus frequentist methods do not consistently make optimal (logical) use of information.
• A common perception is that while some probabilities come directly from frequencies, others are conditional on information, and therefore the frequentist definition is applicable in some situations and the Jaynesian definition in others. But Jaynesian methods have no problem incorporating information derived from frequency distributions. In those cases in which frequentist methods succeed, they give the same probabilities that could be derived from Jaynesian methods. At their best, frequentist methods are a special case of the more general Jaynesian methods. Thus there is no virtue or advantage to the frequentist definition of probability.
• The most glaring faults of frequentist probabilities are not evident in conventional applications of probability theory in which scientists are always the observer, but arise solely when an observer (such as a scientist) wishes to understand how another observer (such as a brain) can perform inference.

  • Frequentist methods are narrow in their objective and do not address inference in general.
  • Frequentist methods do not incorporate logic in a formal sense, and thus cannot help in understanding its neural basis.
  • The most severe fault is the misattribution of knowledge. When frequentist approaches have been used to study the neural basis of inference [27,28,29,30,31,32,33], the result has been that scientists have mistakenly attributed their own information (and ignorance) to the brain. Thus probabilities attributed to a brain under investigation have in fact been entirely a property of the scientist’s brain, an error of gross proportions.

Despite these serious flaws with frequentism, I have found one small and not so serious piece of evidence in its favor. Before discussing any of the relevant issues in my lectures to graduate and undergraduate students, I simply present the same questions and answers presented above and in

Table 1 to illustrate the two definitions (“There are 4 possibilities....”). I then require them to vote on whether they favor the frequentist or Jaynesian definition. Across multiple classes of students, I consistently find that at least two of three students favor the frequentist definition. If Jaynes is to follow his own logic, he would be forced to conclude that given only these empirical results, there is at least a two thirds chance that his views on probability are wrong. A serious point to this amusing example is that according to Jaynes, the students who reject Jaynes’s definition may be making a perfectly rational inference given their limited knowledge.

3.9. Jaynesian and Not Merely Bayesian

Although Jaynes referred to his own work as “Bayesian”, as opposed to “frequentist”, there are reasons to favor the term “Jaynesian” for many aspects of contemporary probability theory. The maximum entropy principle of Jaynes is the most primitive and fundamental principle within probability theory. It alone defines probability and provides an objective function to derive probabilities from information. By contrast, BT (Equation 3) is irrelevant to the definition, as it does not specify precisely what probabilities are or how they are related to information. It can only be used to derive probabilities from other probabilities. There are remarkably successful applications of probability theory that do not even use BT [34]. It is not even known whether Bayes himself subscribed exclusively to the “Bayesian definition” of probability. I therefore propose that the term “Bayesian” be replaced with “Jaynesian” in making general reference to probability theory and inference, and in particular in referring to the definition of probabilities based on maximum entropy. The term “Bayesian” is appropriate when simply referring to the use of BT, which may or may not be strictly Jaynesian.

Within the field of “Bayesian brain theory”, “Bayesian” has indeed been used to denote any use of BT. In fact, BT has often been used with frequentist rather than Jaynesian probabilities (see Section 4). BT is not essential to probability theory, and the emphasis on it has been excessive in my view (see Section 5.3). The term “Jaynesian” may draw attention to the more fundamental importance of the definition of probabilities as exclusively conditional. The most critical problem which has been created by frequentist notions, and which still persists in work purported to be “Bayesian”, is the misattribution of knowledge, as documented below. The method of Jaynes avoids this by insisting on very careful specification of the information upon which probabilities are conditional (Figure 2).

4. Conventional Approaches to Probability and Information in Neuroscience

4.1. The Frequentist View in Neuroscience

The frequentist view of probability may be very slowly falling out of favor, but it still exerts a dominant influence within neuroscience. In 2004, a prominent neuroscientist wrote in a letter to the author: “How can probabilities of external events be conditional on the internal information an animal has, unless we assume telekinesis”? Another vivid example of the frequentist perspective comes from a 2010 “Review” in Nature Reviews Neuroscience [6]. Friston attributes entropy to a fish, stating “a fish that frequently forsook water would have high entropy”. He goes on to define a mathematical measure of “surprise” (as well as entropy) as a function of probabilities, yet he does not specify that these probabilities are conditional on any information. He then writes “a system cannot know whether its sensations are surprising...” These statements suggest that a frequentist view, in which probability and entropy are properties of objects rather than observers, is still pervasive. Personal dialogue with these neuroscientists and others, and published discourse with Friston [46,47], indicated that they were not intentionally advocating the frequentist view over the Jaynesian view, but rather that they had been substantially unaware of the distinct definitions. Indeed, Friston is among the most prominent advocates of a Bayesian approach to understanding brain function. He does derive Jaynesian probabilities that are conditional on models of brain function, but he also evokes frequentist probabilities in trying to characterize the entropy of an entire system (brain plus environment) (where he uses the term “entropy” in its conventional thermodynamic sense and it is therefore not conditional on the knowledge of the brain under consideration) [6]. That he utilizes both Jaynesian and frequentist definitions, side by side and without acknowledgement, is not at all exceptional within the field of Bayesian brain theory (see below).

The prevalence of the frequentist view in neuroscience is not immediately obvious because it is routinely used without any acknowledgment that more than one definition of probability exists. Even books that make extensive use of probabilities and quantify information do not clearly state a definition of probability or mention that there is more than one definition [3,33,48,49]. However, one can often infer a frequentist view. For example, it is routine to find language related to “estimating” or “measuring” or “approximating” a “true” probability distribution. Similarly, it is often said that sensory “samples” are “randomly drawn” from an “ensemble” (e.g., [33]), much as balls are said to be drawn from an urn in frequentist textbooks on statistics (e.g., [37]). This implies that probabilities are an inherent property of an object (such as an “urn”), and they exist independent of the knowledge of any observer.

A natural consequence of frequentist probabilities is the need to imagine “probabilities of probabilities”, with the former probabilities being conditional on an observer and the latter being unconditional properties of an object (observed system). Similarly, distinctions have been made between the neural representation of “known and unknown probabilities” (e.g., [50]), and between “expected and unexpected uncertainty” [51]. As in the quotations described above, this language makes sense only if some probabilities are essentially the same as frequencies. To a frequentist, the probabilities themselves are uncertain and must be estimated, and it follows that there should be specialized neural circuits that are devoted to processing information about probabilities (frequencies). In contrast, according to a Jaynesian definition, probabilities are fully and precisely specified by a state of knowledge. With respect to the brain, we could either say that the brain unconsciously “knows” the probabilities precisely, or that the brain knows nothing about probabilities, but that probabilities provide a means by which we can quantitively describe the information in a brain. (Note that it can be useful within Jaynesian probability theory to consider “probabilities of probabilities” as an intermediate mathematical step in trying to calculate a probability of something believed to be “real”. But all probabilities are conditional and descriptive and are never presumed to exist in an ontological, physical sense.)

Additional evidence of a partially frequentist perspective comes from the use of Bayes’s Theorem (BT). Within books [3,33,48,49] as well as many papers, BT is written and described as if the prior distribution is not (or at least, may not be) conditional on any information. In many cases, it is implied that the prior distribution comes directly from a frequency distribution, without even any speculation of how the observer might have knowledge of that distribution. This is evident in the work of Rieke and colleagues [33], which represents perhaps the most comprehensive effort to date to relate information theory to neural function in a quantitative sense. In using BT to characterize the information in a neuron’s spike output, purportedly from “the neuron’s point of view,” they assume that the prior distribution is equivalent to the frequency distribution of the neuron’s input. Careful reading of a footnote (page 23 [33]) could be interpreted to imply that the authors believe that by controlling the frequency distribution of inputs (stimulus intensities), they have avoided the controversy over the definition of probability. In addition, their choice of words throughout the text implies a frequentist definition (see above). However, they also make extensive use of conditional probabilities, as well as the maximum entropy principle advocated by Jaynes (for example, see footnote on page 118 [33]). Thus they seem to imply that both definitions of probability are valid, and that the frequentist definition offers advantages over the Jaynesian definition in some instances. In fact, they and others go a step further by proposing that both types of probabilities can be combined in BT, in which the prior is implied to be frequentist and unconditional, whereas the likelihood function and the posterior distribution must then be hybrids, derived using a combination of the two distinct definitions. Even someone who sees merit in both definitions could question the validity of such a hybrid.

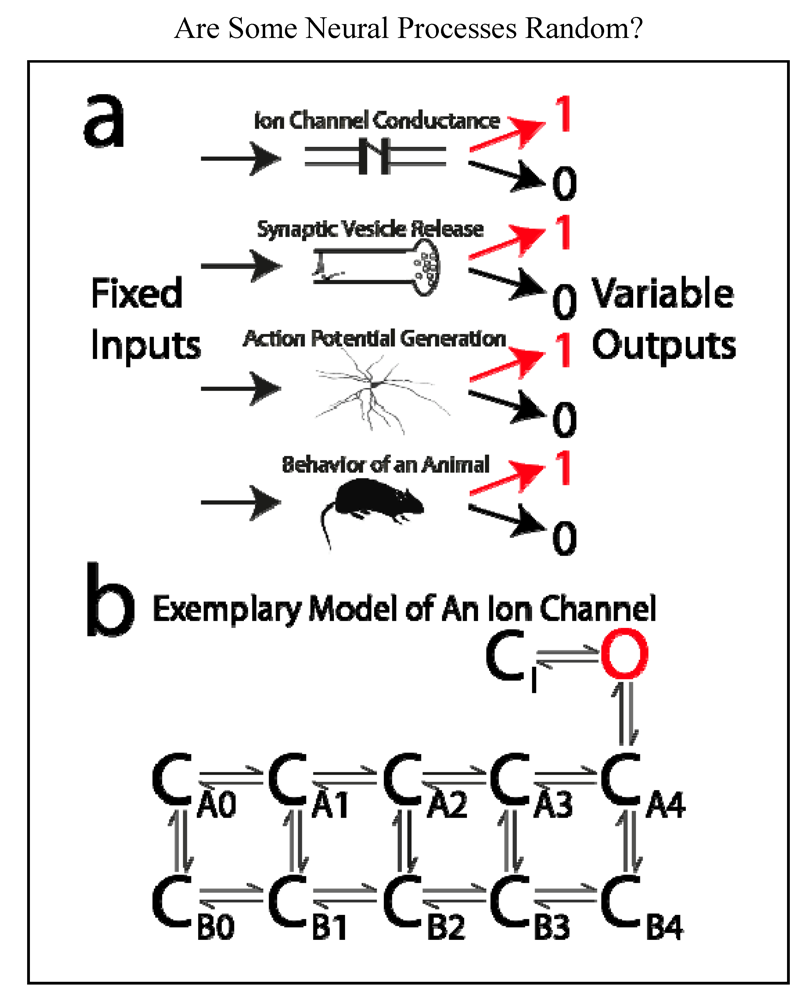
4.2. What is a “Random Process”?

The frequentist perspective and its terminology have a powerful influence on how we view natural processes, including those in the brain. It is routine to refer to neural processes as “random” or “stochastic” or “probabilistic”. These are all adjectives that are properly used to describe an observed system, not the observer (“noisy” is sometimes used in this manner as well). Thus the strong implication of this language is that these are intrinsic properties of these physical systems, rather than merely a description of our own ignorance and consequent inability to make accurate predictions. The notion of randomness is another example of the misattribution of information and probabilities. The apparent randomness of neural activity has provided the uncertainty in purportedly “Bayesian” models of how neurons can perform inference (see Section 4.3).

Consider the output of each of four systems in the case of a known and invariant input (Figure 3a). At a brief moment in time:

• An ion channel is either open or closed.
• A vesicle containing neurotransmitter is either released or not released from a presynaptic terminal.
• A neuron either generates an action potential or it does not.
• In a “tail-flick assay”, a rat either removes its tail from a hotplate or it does not.

In each of these cases, the input can be invariant (over time or “trials”), and yet the output is variable. Thus the input does not fully determine the output. Cases 1 and 2, on a more microscopic scale, are routinely referred to as “stochastic” or “random” processes, case 3 at the “cellular level” is sometimes referred to in this manner. Case 4 concerning behavior is usually not said to be “random”, and most neuroscientists would probably agree that no behavior is a “truly random process”. Are these cases fundamentally distinct from one another? What is a “random process”, and how would one recognize it?

Figure 3. Illustration of neural systems that are sometimes said to be “random, stochastic, noisy, or probabilistic.” (a) Fixed and known inputs to these systems result in variable outputs. From top to bottom: In response to a certain concentration of neurotransmitter, or a specific membrane voltage, an ion channel can be open or closed; in response to arrival of an action potential, a presynaptic terminal may or may not release a vesicle of neurotransmitter; in response to a given amount of excitatory postsynaptic current, a neuron may or may not generate an action potential; in response to a given temperature, a rat may or may not remove its tail from a hotplate. According to contemporary physics, none of these systems are “random”, “stochastic”, etc. These terms purport to describe a physical system, but they only indicate our ignorance of the system; (b) an example of a typical model of an ion channel. The channel can exist in any one of multiple states. With a patch electrode, we can only discriminate open (“O”) from closed (“C”) states. The various closed states are “hidden” from our observation, but we can infer their existence through careful analysis. The other three cases illustrated in “a” are analogous, but because they are less microscopic in scale, their “hidden” states can be more readily observed.

Figure 3. Illustration of neural systems that are sometimes said to be “random, stochastic, noisy, or probabilistic.” (a) Fixed and known inputs to these systems result in variable outputs. From top to bottom: In response to a certain concentration of neurotransmitter, or a specific membrane voltage, an ion channel can be open or closed; in response to arrival of an action potential, a presynaptic terminal may or may not release a vesicle of neurotransmitter; in response to a given amount of excitatory postsynaptic current, a neuron may or may not generate an action potential; in response to a given temperature, a rat may or may not remove its tail from a hotplate. According to contemporary physics, none of these systems are “random”, “stochastic”, etc. These terms purport to describe a physical system, but they only indicate our ignorance of the system; (b) an example of a typical model of an ion channel. The channel can exist in any one of multiple states. With a patch electrode, we can only discriminate open (“O”) from closed (“C”) states. The various closed states are “hidden” from our observation, but we can infer their existence through careful analysis. The other three cases illustrated in “a” are analogous, but because they are less microscopic in scale, their “hidden” states can be more readily observed.

If input does not fully determine the output of a physical system, is the system partially “random”? The answer, with respect to each of the four cases above, is “no” according to the view of contemporary physics. In each case, the system is believed to exist in a state that is “hidden” from the observation of the scientist at the time of the input. These hidden states act “behind the scenes” to determine the observed output of the system for any given input. The apparent randomness of the system is merely the product of the ignorance of the scientist. According to present scientific dogma, it is only at the very small scale of quantum physics that physical systems are “truly random”. One could question, as Jaynes did, how physicists could ever be confidant that their inability to predict the behavior of any system, including systems on a very small scale, is not merely due to their own ignorance [52]. Regardless of the interpretations of quantum physics, there should not be any controversy within neuroscience, where according to modern physics, no system of interest is “truly random”. The inability of neuroscientists to predict the state of a neural system should be entirely attributed to the ignorance of neuroscientists.

It may be useful to consider these neural systems in more detail. Ion channels are the most microscopic of the four systems listed above. Until the invention of the patch-clamp method of electrophysiological recording, it was not possible for us to observe the electrical behavior of single channels. Now we know that many single channels have just two conductance states, open or closed, and we cannot predict with high accuracy the conductance state of a single channel at any moment. However, our best models of ion channels consist of numerous open and closed states (mostly closed states), which are indistinguishable in patch-clamp recordings (Figure 3b) [53]. As new experimental data have been collected, new models have been made with more “hidden states” in order to better account for the experimental data. Unfortunately we do not currently have a technique that can “see” the states that are hidden from patch electrodes, but it is conceivable that one day these states may no longer be hidden from us. In principle, we might also be able to “see” the microscopic effects of heat (such as collisions of an ion channel with other molecules), which would then need to be considered as additional inputs. What had once appeared to some to be “random” could then be reclassified as “deterministic”, but of course all that would have changed is the knowledge of scientists.

The case of action potential generation is better understood and is generally thought to be more directly relevant to neural inference. Action potentials can be recorded with electrodes that are intracellular and measure voltage across the neuron’s membrane, or with extracellular electrodes that are sensitive to the time of the action potential but not to the membrane voltage. If extracellular electrodes are used, then it is observed that the neuron’s spike output varies even when its input (“stimulus”) is the same. The neuron’s output (firing rate) has thus been modeled as a Poisson “random” process. However, the neuron’s output does not appear nearly so “random” when one uses an intracellular electrode, in which case action potentials are always preceded by a depolarization towards a threshold. According to well known models of neuronal membrane biophysics (such as Hodgkin-Huxley models), there is nothing random about the generation of action potentials [53]. When synaptic excitation occurs, whether or not the neuron emits a spike will be determined by a large variety of “hidden” variables that cannot usually be observed even by intracellular electrodes, such as the conductance of potassium channels. If one knew the state of all of the ion channels, as well as other biophysical properties of the neuron, then one could accurately predict a neuron’s output for any known input.

It is obvious that the same system cannot be “random” when observed with one technique and “deterministic” when observed with another technique. It is also clear that neuroscience would have suffered a tremendous setback if early pioneers of extracellular recording had concluded that action potential generation was substantially random, and that we should therefore be satisfied merely to characterize Poisson spike statistics without seeking greater knowledge of underlying mechanisms. With such a view, Hodgkin and Huxley might not have attempted to construct a biophysical and deterministic model of action potential generation. The entire scientific enterprise is based on our belief that Nature is full of information that we can acquire through careful observation. Were we to abandon this belief in favor of the view that a particular system is “random”, then the implication is that the system has no further information to yield and thus we should not invest our time in searching for a deeper understanding of it.

How then are we to use the words “random, stochastic, and probabilistic”? The use of these words to describe physical systems is at best misleading, and at worst, pathological and harmful to science. However, it is perfectly clear and appropriate to state that a model of a physical system has a “random” or “stochastic” component. This does not imply that the scientist necessarily believes any physical system to be “truly random”. The random component typically corresponds to a component of the model that is not sufficiently understood, or not sufficiently important, for the scientist to specify in detail. The scientist has complete knowledge of the model, which he or she created. The model naturally corresponds to a hypothesis about a physical system, based upon the scientist’s knowledge, and the random components of the model correspond to our ignorance about the physical system. As emphasized repeatedly here, we should not confuse our knowledge of a physical system with the physical system itself (which we believe to have an independent existence).

4.3. “Random” Neural Activity in Models of Bayesian Inference

In much of neuroscience it is of limited practical consequence whether an event, such as the release of a vesicle, is inherently random or merely unpredictable for the scientist. However, biological models of Bayesian inference have relied on this apparent randomness to derive probability distributions that are purported to be conditional on neural activity but are derived simply from measuring frequency distributions of firing rate across time (repeated “trials”) (e.g., [27,28,29,30,31,32,33]). In many of these “Bayesian” models (e.g., [29,30,31,33]), the variability (“randomness”) in the firing rate of a neuron given some stimulus provides the basis for the uncertainty in the neuron’s estimate of the stimulus. Similarly, this variability has been declared to be “noise” which could only increase a brain’s subjective uncertainty about the “signal” (e.g., [54,55]). In most of the cases cited above, the authors do not know the source of the variability, they do not speculate about the source, they do not state whether the source of the variability even matters, and they do not state whether they believe that the variability is inherently random. But if this variability is not inherently random, and is instead determined by the information of ion channels (as described by Hodgkin-Huxley models) about the external stimulus, then it is far from clear why it should have any correspondence to subjective uncertainty. If one accepts the Jaynesian definition of probabilities, and concludes as Jaynes did that there is nothing inherently random about neural activity or any other physical system, then it becomes clear that the uncertainty that has been attributed to neurons in these Bayesian models is actually the uncertainty of the scientists themselves about the neuron’s activity (which is itself shaped by highly arbitrary choices of neuronal models and measurement techniques) (see Section 5.2). Jaynesian methods prevent this sort of misattribution of information, as described above.

5. Jaynesian Approaches in Neuroscience

The value of Jaynesian probability theory is in providing the foundational framework for understanding information and logic. Jaynes did not address the physical or neurobiological basis of information and logic. In another article in this same issue of Information, Phillips also explores the work of Jaynes in relation to brain function and he comes to conclusions that are similar in several respects to my own [56]. In addition, he suggests how Jaynesian inference may relate to the function of networks of cortical neurons through a process known as “Coherent Infomax” [56,57].

5.1. Why Is a Strict Jaynesian View Critical to Neuroscience?

The advantages of Jaynesian probability theory have been well documented (Section 3). But in many applications, these advantages may be seen as rather philosophical and technical matters that have only modest influence on the actual probabilities. The main rationale for arguing forcefully for a Jaynesian definition is that it allows us to describe and quantify sets of information other than our own, or that of Science. This is a tremendous virtue, since different brains have different information.

5.2. Two Jaynesian Approaches: First-person (Neurocentric) versus Third-person (Xenocentric)

In studying a physical system, a scientist is an observer, and the physical system is the object of inference. Although we necessarily observe brains (and people) as objects, we also believe that they themselves are observers (Figure 1). The distinction made here between an object and an observer is only one of perspective, or frame of reference, with no connotation of any particular physical distinction (other than displacement of the two in space). We can distinguish two observers, or perspectives, that are critical within neuroscience. As an observer of the brain, a scientist is analogous to the role of a “third-person” narrator in literature, whereas the observed system (brain, neuron, or ion channel) is analogous to the “first-person”. The third-person perspective of the scientist could be denoted as “xenocentric”, since the scientist is “foreign” and external with respect to the brain and its world, whereas the first-person perspective of the brain could be denoted as “neurocentric”. Although the conventional perspective of Science is xenocentric (with respect to the physical systems being observed), the value of a neurocentric approach is implicit throughout the literature on “Bayesian” inference, even where there have been disagreements (e.g., [43,44]). To take a neurocentric approach, we must try to imagine seeing the world from the brain’s perspective, and a variety of formal approaches have been used for this purpose [5,21,24].

Scientists ideally try to work from a common, shared body of knowledge, and to thereby describe nature from the common perspective of a unified Science. To the extent that two rational scientists share the same information, they will naturally agree on the probabilities. Indeed, the sharing of information is why the Jaynesian versus frequentist debate sometimes appears to be of only slight consequence with respect to the actual probabilities. Frequentist probabilities tend to be very similar (numerically) to third-person Jaynesian probabilities. However, we can expect that the information of a brain or neuron is likely to be very different from that of a scientist about that same aspect of the world, in which case the probabilities will be very different.

The distinction between neurocentric and xenocentric is not at all restricted to probabilities. Whether in science or our personal lives, we must always observe from a particular perspective. In psychology and cognitive neuroscience, this same issue was once actively debated. B.F. Skinner was the most prominent advocate of a xenocentric approach to behavior (“behaviorism”), in which the input-output relationship of an animal or human is studied as an object like any other physical system. Although this approach can be useful, the input-output relationships are hopelessly complex. Indeed, we cannot even adequately understand the function of a single ion channel without consideration of its many hidden internal states (Figure 3b). Since the rejection of Skinner’s xenocentric approach some decades ago, psychologists have adopted a neurocentric approach (“cognitivism”), treating a person or even an animal as an observer.

Within neuroscience today, the perspective taken depends almost entirely on whether the system being studied is viewed by the scientist as “high” or “low”. In studying “high-level”, “cognitive” systems that are presumed closer in function to the conscious experience of humans (e.g., prefrontal cortex), a neurocentric perspective is adopted. But in considering parts of the nervous system that are viewed as sensory or motor, or in considering any brain region in a “lower” animal, biologists have seldom taken a neurocentric approach. In studies at the cellular or molecular level, xenocentric input-output analyses in the spirit of Skinner are the absolute rule. Even when the goal of “taking the neuron’s point of view” has been explicitly stated by the authors, the actual probability distributions have been conditional on the information of the scientists about a neuron’s inputs and outputs. This is true of the work of Rieke and colleagues [33] (see Section 4.1 and Section 4.3), as well as that of many others (e.g., [3,27,28,29,30,31,32,33,39,40,41,42,43,44,58,59,60,44,58]). In Jaynesian terms, “likelihood functions” have typically been shaped entirely by the experimenter’s knowledge of variability in a neuron’s output (“noise”) without any account of the neuron’s “hidden” states. In those cases in which (non-flat) priors have been used, they have been determined by the experimenter’s knowledge of a frequency distribution and they have had no known biophysical basis. The failure of the authors to adopt a neurocentric perspective might be attributed to lingering frequentist notions (see Section 4.1).

5.3. Beyond Bayes’s Theorem

I believe that one virtue of Jaynesian theory in contemporary neuroscience is to counter what I see as an excessive emphasis on BT (Equation 3). Whereas the mainstream view seems to be that to “be Bayesian” is synonymous with the “performance” of BT, BT is not an absolutely essential aspect of probability theory (Section 3). An underlying assumption of the mainstream view is that it is not sufficient for the brain to merely integrate biologically relevant information in a physical sense, but that it must go further by using that information for computing probabilities and performing the associated mathematics [3,6,27,28,29,30,31,49]. For example, at the heart of Friston’s “free energy” formulation of brain function is the proposal that in order to perform BT, neurons must overcome the difficulties of integration (in calculus), and that they may do so by implementing approximation techniques known to statisticians, such as “expectation-maximization” or “variational Bayes” [6]. Thus the mathematical techniques that we have developed may prescribe how a brain should be rational, and the brain may have evolved to be rational through the evolutionary pressure to perform such mathematics. There are at least three important criticisms of this view.

• First, these models presume that the brain needs to “know the probabilities” and that a probability is the answer to an inference problem and should thus correspond to a neuronal output. This implies that a brain could have information and yet be incapable of inference because of its inability to do the math. But although the brain needs to know about aspects of the real world, it is not at all clear that it needs to “know about the probabilities” of aspects of the real world. Information about “X”is not the same as information about the probability of “X”,the latter relating to the probability of the probability of “X”(Section 3.6). As Jaynes emphasized, probabilities describe knowledge about the real world, but they are not “real” in themselves anymore than any number is real. Their status is epistemic and not ontological.
• Second, if the brain does in fact need to calculate probabilities, then the first calculations must identify maximum entropy distributions that are conditional on the brain’s information. BT is useless until probabilities are available. Thus it is at best premature to focus on the math of BT rather than the more fundamental precursor of entropy maximization. And if maximization of entropy can somehow be achieved readily, even for complex sets of information, then BT is unnecessary.
• Third, it has been proposed that neurons perform BT, taking a prior and one or more likelihood functions as inputs, and generating an output that represents the posterior [6,27,28,29,30,31]. It is important to keep in mind that BT is merely an equality in which the same information is represented on both sides of the equation; the posterior simply describes the information with one distribution rather than two or more. Thus the inputs and output of a neuron that performs BT would have the same information content. This contradicts the common and well supported notion that by transforming inputs to output, a neuron transforms information about one object (“stimulus” or “cause”, as determined by its receptive field) into information about another object. For example, the output of a neuron in primary visual cortex can signify information about orientation, whereas none of its individual presynaptic input neurons does so. BT does not specify any transformation of information, it only expresses the same information in alternate forms. In this regard, BT is fully analogous to a statement of the form 12 = 3 × 4 = 24/2, etc. To suggest that BT captures the essential feature of higher brain function, and that the brain should “compute BT” because the posterior (“12”) is in some way better than the product of the prior and likelihood (“3 × 4”), is to suggest that a calculator is an apt analogy for the essential computational function of t

The alternate view favored here is that to function well the nervous system needs to have the right information in the right place at the right time, but that it has no need to perform any of the mathematics of probability theory [5,61]. I suggest that when information is integrated in both space and time, it can be described by Jaynesian probabilities in the same way that calculus describes the motion of objects. There is no meaningful sense in which a moving object “performs” the methods of calculus. The methods of calculus simply help us to accurately describe the motion. Likewise, the use of probabilities is purely descriptive with respect to a neuron’s information and uncertainty. Though not strictly Jaynesian (see Section 4.3 and Section 5.2), studies that have applied information theory to “the neural code” have also used probabilities, and BT, in a purely descriptive manner without any implication that the neurons should or do “perform the math” [33,39,40,41,42,43,44]. The argument for seeing probabilities as descriptive of a physical system, with no need for the system to perform the math, is based in part on the fact that entropy maximization is universal, and it can be viewed at once as a principle of both physics and inference. Thus I propose that Jaynesian theory should not been seen to prescribe how neurons should function, or place any constraints on them, beyond the simple but critical point that, other things being equal, more information is better.

If Jaynesian logic is viewed as prescriptive, then this would naturally call for experimental tests to verify how well, if at all, the brain follows Jaynesian principles. The results may be expected to vary on a case by case basis, with the brain being rational in some respects but not in others. By contrast, if Jaynesian probabilities are viewed as purely descriptive, then the issue of empirical verification does not arise. The probabilities merely describe the information in the brain, whether the brain functions well or is pathological [45]. It is critical to note in this regard that although Jaynesian logic may be “perfect”, it does not necessarily imply intelligence. It merely describes information, which could be substantial or minimal. However, the proposal that the computational goal of the brain is to reduce Jaynesian uncertainty [5,61] would predict that a brain or neuron with greater information would tend to generate outputs that are of greater utility with respect to the biological goals of the animal. In principle, this could be tested experimentally.

5.4. Characterizing the Information that One Physical System Has about Another

In virtually all applications of probability theory, the probabilities and information have no known physical basis. Jaynesian probabilities are conditional on information, and we can presume that the information must be within some physical substrate, but we cannot say precisely what the substrate is or how the probabilities are conditional on that physical reality. What we would like is to be able to identify a probability distribution over states of one physical system (“the object”) conditional exclusively on the information inherent within the state of another physical system (“the observer”). To the best of my knowledge, this “physical inference” has never been described in a precise quantitative manner for any physical system, either in physics or neuroscience.

Although Jaynes was a physicist, he did little to directly address the physical basis of information or logic. Like Laplace before him, he developed probability theory to allow us to characterize the information of scientists about the world, and he primarily applied probabilities towards problems in physics. Among his greatest achievements in this regard was his simultaneous introduction in 1957 of the maximum entropy principle and its application to the field of statistical mechanics (SM) [34]. The central challenge in SM is to estimate the properties of microscopic molecules (their positions and velocities, for example) given knowledge of macroscopic factors that we can readily measure, such as pressure and temperature. The foundations of SM had been laid decades earlier by people such as Maxwell, Boltzmann, and Gibbs. They had developed SM through statistical inferences, but because of frequentist notions, SM had not been recognized as purely a matter of inference. Given the lack of any objective basis for inference, the derivation of probability distributions was conceptually complex and full of assumptions (such as “ergodicity”) that seemed presumptuous and rather arbitrary. Jaynes reconceptualized SM as entirely a matter of inference, and he used his maximum entropy principle to derive all the essential results of SM for systems at equilibrium [34]. In addition to introducing maximum entropy inference, Jaynes provided an amazingly short and simple derivation of SM, and he demonstrated that the probability distributions of SM are based on an extremely simple state of information. Specifically, he demonstrated that given only knowledge of the temperature (average or expected energy) of a physical system, the maximum entropy probability distribution over energies within the observed system is exponential (in the case of just one degree of freedom). This is the “Boltzmann distribution” and it allows for the derivation of many other distributions, such as the Maxwell-Boltzmann distribution of velocities for particles in a gas. (It is noteworthy that Jaynes accomplished all of this without any use of BT [34].)

Jaynes demonstrated that a small and simple state of information is sufficient to derive probability distributions, and in some cases it can be extremely powerful in making accurate predictions about the world. This suggests that the physical basis of inference may be an approachable problem, at least in cases in which the observer possesses only a small amount of information. Mathematically, the derivation of probabilities is simpler for simpler sets of information. Furthermore, when we consider physical inference, it may be that we typically need to consider only small and relatively simple states of information.

When we think of a brain, or a computer, we imagine a large and complex set of information of the sort that in practice would overwhelm a team of the best probability theorists. This information is akin to a vast library (e.g., Google’s servers), but a library does not consist of integrated information. To perform logic and inference, the information must be physically integrated in both space and time. In computers, this physical integration occurs in transistors, and in a nervous system, it occurs most notably in proteins (such as ion channels) and within the membrane voltage of neurons (which integrate information from many ion channels). Here I consider that an “observer” corresponds to an entity that physically integrates information in both space and time. With respect to the nervous system, a single observer could correspond to a protein or a neuron’s membrane voltage, but not to a network of neurons or an entire brain (which would be rather analogous to a library, with most information not being integrated). The necessity of physical integration tremendously simplifies the problem, because a physical observer does not possess a great diversity of information at any one time (though of course a nervous system consists of many such observers).

We can presume that the knowledge of an observer about the external world corresponds to “knowledge of self”. An observer knows with certainty its own state, including its configuration, temperature, mass, etc., and its estimate of the external world must be entirely conditional on this information. Jaynes derived the probability distributions of SM, most notably the Boltzmann distribution, conditional only on a single “observation” (or “sample”) of temperature. If scientists can infer the state of molecules given such information, why should molecules themselves not be able to infer the state of other molecules given the same information (assuming that probabilities are purely descriptive and an observer does not need to “perform the math”)? This idea formed the basis for my previous proposal that the Boltzmann distribution can describe the information held within an ion channel (and less directly, the information held within membrane voltage, which is determined by ion channels) [5,61]. This information includes the channel’s temperature, its present configuration, and its inherent sensitivity to an external factor (such as neurotransmitter concentration or membrane voltage, which may in turn carry information about something external to the brain, such as light intensity). Scientists routinely use the Boltzmann distribution to describe the probability that a voltage-sensitive channel will be in a particular conformation (and therefore have a particular conductance across the membrane) conditional on knowledge of the membrane voltage [53]. Thus my proposal is that we can take the neurocentric perspective of an ion channel by using the Boltzmann distribution in the opposite of its conventional direction. However, it should be noted that this use of the Boltzmann distribution has not yet been rigorously justified. A single sensor was proposed to specify a sigmoidal probability distribution [5,61], but a probability distribution over an inherently infinite state space (such as voltage) cannot have a sigmoid shape (since the probabilities must sum to one). Thus further work is needed to precisely specify probabilities that are entirely conditional on the information held within a simple sensor.

To understand how a single molecule could “perform inference”, it is not essential to understand proteins or biophysics or even Boltzmann’s distribution. The simple point is that at each moment in time, a molecular sensor “observes” a single “sample” of some external quantity (external to the neuron), such as neurotransmitter concentration. As Jaynes demonstrated, in SM and numerous other cases, that is all the information that is necessary to derive a probability distribution and “perform” inference. By observing that sample, the probability distribution conditional on the information of the molecular sensor (and thus the neuron) is narrower than it would be were the sensor not there to observe the sample (see Figure 1 in [61]). Thus uncertainty (entropy) is reduced from the perspective of the molecule and the neuron. Accordingly, when we say that the brain “performs inference” or “minimizes uncertainty”, we can have a very clear understanding of what this means, even if as a practical matter we cannot actually quantify it using probabilities.

If a single molecule is capable of performing inference and reducing uncertainty, then one could reasonably argue that this is trivial. Every cell in the body is full of such molecular sensors, and this certainly does not in itself provide clear insight into the structure of the nervous system. However, some sensors, and some synaptic inputs, provide more information than others depending on the statistical structure of the neuron’s environment, and this forms an objective basis for understanding which inputs a neuron should select and what sorts of learning rules it should implement [5,61]. In addition, the goal is not to minimize uncertainty in general, but specifically to minimize uncertainty about biologically relevant aspects of the world. The synaptic connectivity of the nervous system is such that, if one considers successive neurons spanning the spectrum from sensory to motor, each successive neuron has less information about sensory aspects of the world and more information about biological goals, thereby achieving the general computational goal and producing a behavioral output that corresponds to the system’s best guess as to the action most relevant to biological goals [5]. Thus it is not difficult to relate inference at the molecular level to the computational goal of neurons and nervous systems.

6. Conclusions

Whereas it is commonly implied that our lack of understanding of brain function should be attributed primarily to its complexity, and to its many mechanistic properties that we have not yet characterized, the alternative view presented here is that confusion about the nature of information has been a more fundamental problem. A major source of that confusion has been the longstanding frequentist notion that the probabilities and information that scientists have characterized are properties of the physical systems that scientists observe, when in fact these probabilities describe the information of the scientists themselves about those systems. Jaynes referred to this as the “mind projection fallacy” [35]. There is reason to expect that once this practice has been recognized as a fallacy, progress towards understanding the brain will be greatly accelerated.