Abstract
Student success is a multifaceted outcome influenced by academic, behavioral, contextual, and socio-environmental factors. With the growing availability of educational data, machine learning (ML) offers promising tools to model complex, nonlinear relationships that go beyond traditional statistical methods. However, the lack of interpretability in many ML models remains a major obstacle for practical adoption in educational contexts. In this study, we apply explainable artificial intelligence (XAI) techniques—specifically SHAP (SHapley Additive exPlanations)—to analyze a synthetic dataset simulating diverse student profiles. Using LightGBM, we identify variables such as hours studied, attendance, and parental involvement as influential in predicting exam performance. While the results are not generalizable due to the artificial nature of the data, this study reframes its purpose as a methodological exploration rather than a claim of real-world actionable insights. Our findings demonstrate how interpretable ML can be used to build transparent analytic pipelines in education, setting the stage for future research using empirical datasets and real student data.
1. Introduction
Student success is a central concern in educational research and policy. It is widely acknowledged that academic achievement is shaped by a complex interplay of cognitive, behavioral, institutional, and socio-economic factors [1,2]. Traditional approaches, such as linear regression and factor analysis, have historically been used to identify predictors of performance, but they often fall short in capturing nonlinear interactions and contextual variability.
The increasing availability of large-scale educational datasets has enabled new analytical possibilities. Machine learning (ML) methods, in particular, have demonstrated their capacity to model complex and high-dimensional data, showing promise in tasks such as predicting academic performance, identifying at-risk students, and optimizing resource allocation. However, the opacity of many ML models—particularly ensemble and deep learning methods—has raised significant concerns about their interpretability, transparency, and ethical implications in educational decision-making [3].
Explainable Artificial Intelligence (XAI) has emerged as a response to this challenge. XAI provides tools and techniques to make ML outputs understandable to human stakeholders. Among these tools, SHAP (SHapley Additive exPlanations) has gained attention for its consistency and theoretical grounding, especially in models based on decision trees [4]. Despite this, XAI methods have been underutilized in education, where interpretability is particularly vital.
This study aims to contribute to this emerging field by applying interpretable ML techniques to a synthetic dataset simulating educational outcomes. The use of synthetic data allows us to explore methodological possibilities without the privacy and access constraints of real-world data. However, we acknowledge that such data has limitations in external validity, and we frame our results accordingly; this work is a methodological exploration, not an empirical generalization.
By analyzing feature importance using SHAP in the context of a high-performing LightGBM model, we aim to demonstrate how ML and XAI can be combined into a transparent, replicable analytic workflow. While our findings are not transferable to real educational settings, they provide a framework for future empirical research using actual student data.
2. State of the Art
In recent years, the application of ML techniques in educational research has gained significant momentum, fueled by the digital transformation of academic environments and the increasing availability of rich student data [5,6]. While traditional statistical methods, such as linear regression and factor analysis, have long been employed to identify predictors of academic achievement, ML algorithms offer several advantages in handling high-dimensional, nonlinear, and often noisy data [7].
Within educational contexts, ML models have been extensively used to predict a variety of outcomes, including student dropout rates, academic performance, course recommendations, and even patterns of engagement within Learning Management Systems (LMS) [8]. Notably, ensemble methods—such as Random Forests, XGBoost, and LightGBM—have consistently shown superior performance due to their robustness and ability to capture complex interactions [8].
However, a persistent challenge in applying ML to education lies in the interpretability of the models. Non-technical stakeholders, such as teachers, administrators, and policymakers, often require transparent models that not only predict outcomes but also explain the reasoning behind these predictions [9]. This necessity has sparked considerable interest in XAI, a field dedicated to demystifying ML models and elucidating the contributions of individual features to predictions [10].
Among the most prominent XAI techniques, SHAP and LIME have been increasingly applied in educational data mining. SHAP employs concepts from cooperative game theory to fairly distribute the contribution of each feature to the model’s output, offering insights that are both consistent and theoretically grounded [11]. LIME, meanwhile, generates local surrogate models to explain individual predictions, providing a complementary perspective on feature importance [12]. Both methods have been successfully employed to identify critical factors in student success, including prior academic performance, engagement levels, socioeconomic status, and access to educational resources [13].
This paper seeks to integrate the advancements of ML and XAI into a comprehensive framework to identify the most influential factors in student success. By doing so, it aims not only to predict academic outcomes accurately but also to offer actionable insights for educators and policymakers striving to improve student performance. This dual focus on predictive power and interpretability is essential for data-driven decision-making in education, enabling interventions that are both evidence-based and tailored to the diverse needs of students.
Recent work has further highlighted the importance of SHAP as a powerful interpretability method in educational machine learning contexts. Studies such as [1,2] showcase its utility for uncovering meaningful patterns in synthetic and institutional data alike, while [3] stress the need for trust and transparency in educational AI systems. Together, these insights underscore the relevance of explainable ML for improving both model accountability and stakeholder confidence.
3. Materials and Methods
The dataset used in this study is synthetic and does not reflect any real-world individuals, institutions, or educational systems. As such, it lacks detailed demographic information such as age, academic level, nationality, or geographic region. These omissions limit the contextualization of the findings and preclude any claims of external validity. Our analysis should therefore be understood as exploratory and methodological, intended to demonstrate the interpretability of ML pipelines rather than derive empirically generalizable insights.
This section describes the dataset used in the study, the transformations applied to ensure its validity, and the machine learning algorithms implemented during the analysis.
3.1. Proposed Framework
The following image (Figure 1) shows the step-by-step methodology carried out for this investigation.
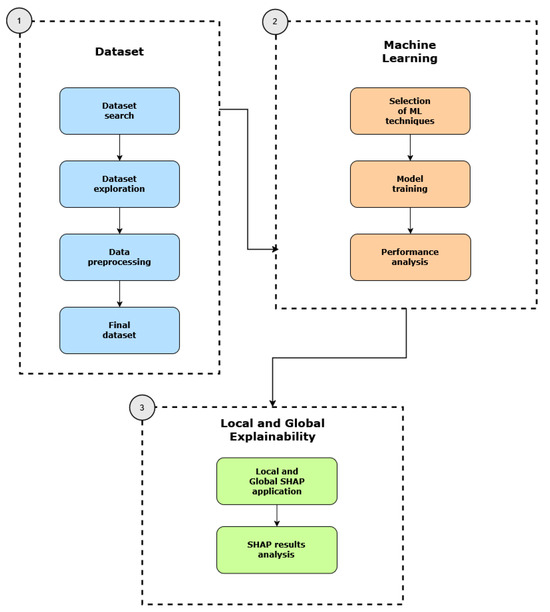
Figure 1.
Methodology proposed.
The dataset should be searched, analyzed, and pre-processed until a suitable group of data is obtained. Subsequently, ML models are selected, trained, and their results analyzed. Finally, the best performing model is chosen, and SHAP is applied to interpret the outcomes.
All experiments were conducted using Python 3.11, along with commonly used data science libraries. Pandas (2.2.2) and NumPy (2.0.2) were used for data manipulation and analysis, while Matplotlib (3.10.0) and Seaborn (0.13.2) supported data visualization. The machine learning models—Random Forest, XGBoost, and LightGBM—were implemented using Scikit-learn (1.6.1) and their respective native libraries. Model interpretability was carried out with the SHAP library (0.48.0).
3.2. Dataset
The dataset is synthetic and released under a CC0 (Creative Commons Zero) license, ensuring that it can be freely used for research and educational purposes. The dataset, entitled “Student Performance Factors”, was originally published by Lai Nguyen on Kaggle and is publicly available at https://www.kaggle.com/datasets/lainguyn123/student-performance-factors (accessed on 27 April 2025). It was not created by the authors but selected for its suitability in demonstrating the proposed methodological framework.
This dataset contains information on 6607 students and includes a variety of variables related to academic performance, lifestyle, family background, resource access, and psychosocial factors. For clarity, these variables have been grouped thematically in Table 1. Notably, the Exam Score variable serves as the target outcome in our analysis.

Table 1.
Classification of dataset variables by thematic group, feature type, and description.
Although the dataset includes variables that simulate demographic and psychosocial traits (e.g., gender, family income, and parental education), it is important to note that these values do not correspond to real individuals. As such, there is no actual demographic distribution underlying the data. This limitation prevents us from describing concrete characteristics of the sample or making any empirical claims about specific populations. The analysis and results should therefore be interpreted solely in the context of model behavior and interpretability within a synthetic environment.
The decision to work with synthetic data stems from the lack of complete, anonymized, public datasets that meet the specific requirements of our project. Moreover, this synthetic collection can serve as a preliminary reference for designing and gathering our own dataset in future studies.
This study was conceived as an initial exploration to test how machine learning and, in particular, explainable AI techniques such as SHAP can be applied in the educational domain. While we considered collecting real data through surveys, strict privacy and ethical restrictions, as well as the need for institutional approval, limited the feasibility within this study. Therefore, a synthetic dataset was adopted as a viable alternative for methodological exploration, enabling us to focus on evaluating the potential and limitations of interpretable ML workflows in this context.
3.3. Data Analysis
Before training the machine learning models, an initial exploratory data analysis (EDA) was conducted to understand the structure and distribution of the dataset variables. This analysis serves to identify potential patterns, outliers, or imbalances that may influence the learning process. Table 2 summarizes the main descriptive statistics for the numerical variables, including central tendency and dispersion measures. These figures provide a preliminary indication of student behaviors and performance levels across the sample. In parallel, Figure 2 displays the distribution of categorical features using bar plots, offering insights into the relative prevalence of various psychosocial, demographic, and contextual attributes. Together, these descriptive analyses establish a foundational understanding of the data and support informed decisions in subsequent preprocessing and modeling stages.

Table 2.
Descriptive statistics for the numerical variables in the dataset.
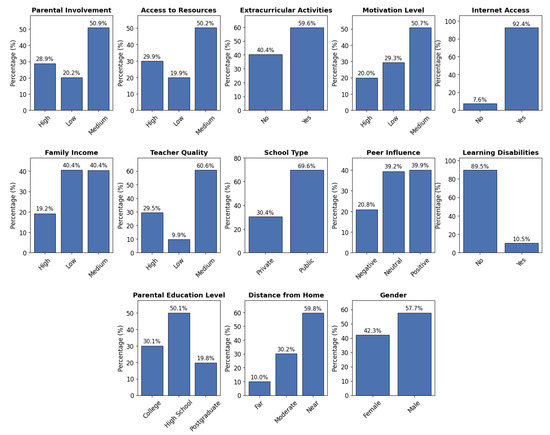
Figure 2.
Distribution of categorical variables in the dataset. The plots show the relative frequency (in percentage) of each category for all categorical features.
3.4. Data Preprocessing
3.4.1. Null Values Treatment
During the preprocessing phase, missing values were identified in three columns of the dataset, each affecting less than 2% of the total records (Table 3). To address this issue, imputation techniques were applied—a commonly used strategy to preserve the integrity of the dataset without discarding valuable information.

Table 3.
Descriptive statistics for missing values.
Imputation involves replacing missing values with reasonable estimates, such as the mean, median, or mode, depending on the variable type and its distribution. In this case, missing values were present exclusively in categorical columns; therefore, the mode—i.e., the most frequent category—was used as the imputation method. This approach helped maintain the internal consistency of the dataset without introducing significant bias, while also avoiding the loss of potentially useful records in subsequent stages of the analysis.
3.4.2. Categorical Variables Encoding
After handling the missing data, it was necessary to convert the categorical variables into a numerical format compatible with the machine learning algorithms used. Models such as Random Forest, XGBoost, and LightGBM (which will be described in the following section) cannot inherently process categorical features and therefore require appropriate encoding to ensure effective training and interpretation.
To this end, a two-step encoding strategy was implemented based on the nature of the categorical variables. For ordinal variables—those with an inherent order among their categories (e.g., Low, Medium, and High)—the OrdinalEncoder technique was applied. This method encodes each category as an integer, preserving the ordinal relationship of the variable, which may improve the model’s ability to learn relevant patterns from the data.
In contrast, nominal binary variables—those without a meaningful order (e.g., Gender and Internet Access)—were encoded using the LabelEncoder, which assigns a unique integer to each class. Given the binary nature of these variables, this simple encoding approach is sufficient.
This encoding process ensured the seamless integration of categorical features into the modeling pipeline without introducing ambiguity in the interpretation of results (see Appendix A for detailed mappings).
3.5. Machine Learning Models
Three widely used and proven machine learning algorithms were chosen for this research: Random Forest, XGBoost, and LightGBM. All three models are based on decision trees and stand out for their ability to capture non-linear relationships between variables, as well as for their robustness to noisy data. Random Forest is characterized by the construction of multiple trees in parallel and the subsequent averaging of their results, which reduces the risk of overfitting. XGBoost and LightGBM use boosting techniques, where trees are built sequentially to correct for the errors of previous trees, which generally improves predictive accuracy.
To compare the performance of these models, three complementary metrics were used: root mean squared error (RMSE), mean absolute error (MAE), and the coefficient of determination (R2). The RMSE penalizes large errors more heavily and provides an idea of how much the predictions differ from the true value. The MAE, on the other hand, measures the average error without considering its relative magnitude, being less sensitive to outliers. Finally, the R2 indicates what proportion of the variability of the dependent variable is explained by the model: a value close to 1 suggests a good fit.
This combination of models and metrics allows both accuracy and consistency of predictions to be assessed, facilitating a rigorous comparison for the selection of the most appropriate model for the subsequent explainability analysis using SHAP. The source code can be found at this address: https://github.com/davidogm/PaperEducation (accessed on 24 June 2025).
3.6. Explainability Methods
XAI plays a pivotal role in bridging the gap between predictive accuracy and human interpretability. In this study, we adopt SHAP as our primary explainability method due to its strong theoretical foundations and wide applicability to tree-based models like LightGBM. SHAP computes feature contributions by considering all possible combinations of features and calculating the average marginal contribution of each one to the prediction. This approach, based on cooperative game theory’s Shapley values, ensures that the attribution of importance is fair, consistent, and additive. In practice, SHAP values indicate how much each feature increases or decreases the prediction relative to the model’s baseline expectation, both at the global and individual instance level.
XAI techniques can be broadly classified into global and local explainability approaches. Global explainability aims to provide an overall view of the model’s behavior across the entire dataset. It answers questions such as the following: Which features are generally most important? In which direction do they tend to affect predictions? In our work, this is operationalized through the SHAP summary plot, which aggregates SHAP values across all instances, highlighting the average magnitude and direction of each feature’s impact. This type of analysis is particularly useful for identifying consistent trends and informing high-level educational policy decisions [14].
In contrast, local explainability focuses on individual predictions. It allows us to inspect why the model made a specific prediction for a given student, identifying the precise contribution of each feature to that outcome. We employ SHAP waterfall plots to illustrate this process. These visualizations begin with the model’s expected output and sequentially apply each feature’s SHAP value, showing how they cumulatively shape the final prediction. Local explanations are essential in educational contexts for supporting personalized interventions and tailoring recommendations to individual students’ profiles [15].
By combining both global and local explanations, we ensure a comprehensive interpretability strategy that supports both institutional decision-making and individual-level guidance. This dual perspective reinforces trust in the model and enables actionable insights for educators and stakeholders.
Table 4 summarizes the main differences between global and local explainability in the context of educational machine learning models.

Table 4.
Comparison between global and local explainability.
4. Results
This section presents the results obtained after training and evaluating the selected machine learning models. Additionally, model interpretability is examined using SHAP in order to identify the features with the greatest influence on the predictions.
4.1. Model Performance
During the model evaluation phase, the algorithms presented in Section 3.1 were trained and compared. To assess the performance of each model, three complementary metrics were used: root mean squared error (RMSE), mean absolute error (MAE), and the coefficient of determination (R2).
To evaluate model performance, the dataset was split into training (80%), validation (10%), and test (10%) subsets. All hyperparameter tuning was performed on the validation set, and final performance metrics were computed using the test set. This split helps mitigate overfitting and provides a more reliable assessment of the model’s generalization capacity.
The performance results of the trained models are presented in the following Table 5.

Table 5.
Performance results of the trained models.
Clear differences emerged when comparing the performance of the model. The model that achieved the best overall results was LightGBM, with an RMSE of 1.957, an MAE of 0.804, and an R2 of 0.729. These metrics indicate a strong predictive accuracy and a notable ability to explain the variability in the target variable. Random Forest followed closely, demonstrating solid performance with an RMSE of 2.175, an MAE of 1.084, and an R2 of 0.665, although slightly behind LightGBM. Lastly, XGBoost obtained more modest results (RMSE of 2.226, MAE of 0.986, and R2 of 0.649), suggesting lower predictive effectiveness in this particular scenario.
During the analysis of the model’s performance, an interesting pattern was observed in the exam score predictions. Although some values in the original dataset exceeded 80 points, the model tended to predict scores within a narrower range, approximately between 55 and 75. This limitation can likely be attributed to the distribution of the training data, which was heavily concentrated within that interval. Figure 3 shows a scatter plot comparing the actual exam scores (x-axis) to the predicted ones (y-axis), where each point represents a single student. It becomes evident that the model systematically underestimates the highest scores, particularly when the actual exam score surpasses 80 points. This effect is caused by the limited representation of high scores in the training data, which reduces the model’s ability to learn accurate mappings in that range. As a result, the model regresses toward the mean and struggles to generalize at the upper extreme.
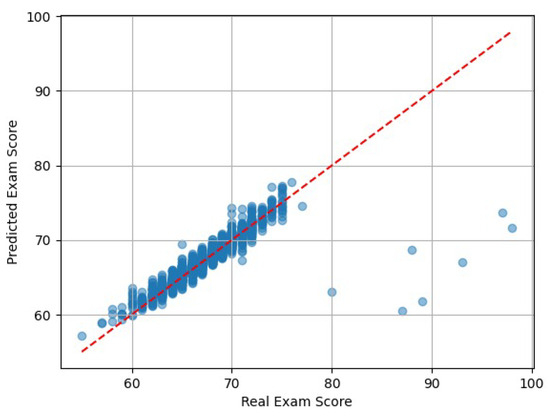
Figure 3.
Scatter plot of actual vs. predicted exam scores using the LightGBM model. The model tends to underpredict high scores due to training data imbalance.
4.2. Model Explainability
Tree-based ensemble methods such as LightGBM are known for their strong predictive performance, but they are not inherently interpretable. While a single decision tree offers clear and transparent rules that make it easy to trace how input features lead to a given prediction, ensemble methods combine hundreds or even thousands of such trees. This complexity results in a black-box model, where the contribution of individual features and the reasoning behind predictions are not directly observable.
Since LightGBM outperformed all other models across the three evaluation metrics, it was selected as the base model for the explainability analysis. By focusing our interpretation efforts on the most accurate model, we ensure that the insights obtained are grounded in reliable and representative predictions. It is important to note that all results presented in this section are derived from a synthetic dataset. Therefore, they should be interpreted as hypothetical illustrations of the model’s internal behavior, not as validated empirical insights. To better understand the internal decision-making process of the LightGBM algorithm, we first use SHAP to analyze its global behavior. This approach allows us to assess the overall importance of each feature and the direction in which it affects the model’s output.
To visualize these global insights in a comprehensive and interpretable way, we rely on the SHAP summary plot, which provides a compact representation of the impact and value distribution of all features across the dataset, as illustrated in Figure 4. In this plot, each dot represents a single prediction (i.e., a student), with its position along the x-axis indicating the SHAP value, which reflects how much that specific feature contributed to increasing or decreasing the predicted academic performance (Exam Score). The y-axis lists the input features, sorted by their overall importance, placing the most influential features at the top. Color represents the actual value of the feature for each instance: red corresponds to high feature values and blue to low values. This color encoding helps us understand not only which features are important, but also how their high or low values tend to influence the model’s predictions.
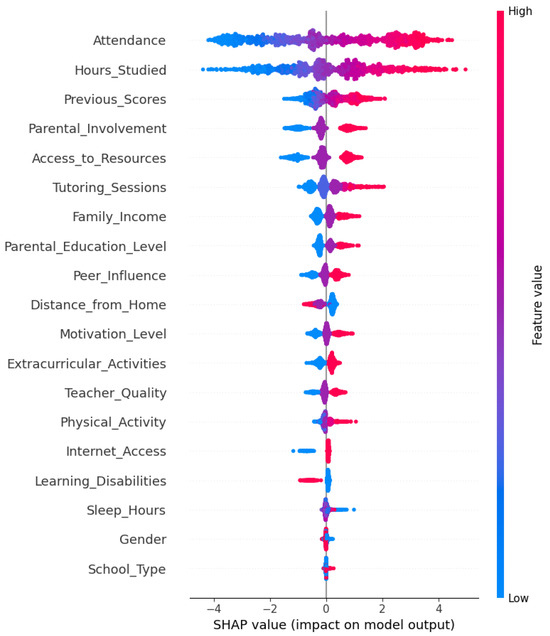
Figure 4.
SHAP summary plot for LightGBM predictions.
Attendance and Hours_Studied stand out as the two most influential features affecting predicted exam scores. High values of these features (shown in red) are consistently associated with positive SHAP values, indicating that students with higher attendance rates and more study hours are predicted to perform better academically. These findings are consistent with long-established constructs in educational research, where behavioral engagement and prior preparation are widely recognized as key drivers of academic performance.
Previous scores also play a key role, reaffirming the predictive power of historical academic performance, as students who have performed well in the past are likely to maintain strong results. Other features that contribute positively to the model’s output include Parental_Involvement and Access_to_Resources, which are ordinally encoded, with higher values corresponding to greater levels of involvement or access. Their positive SHAP values suggest that increased parental support and better access to educational resources are associated with improved student outcomes. On the other hand, Tutoring_Sessions also shows a positive effect, indicating that additional academic support contributes to higher predicted performance.
In contrast, variables such as Distance_from_Home and Learning_Disabilities are associated with negative SHAP values, particularly when their values are high. This implies that students who live farther from school or who face learning challenges are generally predicted to potentially have lower exam scores, reflecting some structural disadvantages or barriers to effective learning. Furthermore, an asymmetric pattern is observed in the case of Internet_Access and Learning_Disabilities: while having internet access or not having a learning disability contributes little to the prediction (i.e., their SHAP values are close to zero), the opposite conditions, lacking internet access or having a learning disability, are associated with a clear negative impact on predicted performance. This suggests that these features primarily influence the model when they reflect a disadvantage or a lack of support.
While some demographic and contextual features, such as Gender and School_Type, are included in the model, their SHAP values cluster closely around zero, indicating a minor contribution to the overall predictions. This suggests that the model primarily bases its decisions on academic, behavioral, and socioeconomic variables rather than demographic characteristics.
The second way we apply SHAP is by focusing on local explainability, which aims to interpret individual predictions. This allows us to understand how each feature influences the outcome for a specific student, offering insights into the model’s decision process at the individual level.
To illustrate this, we use SHAP waterfall plots, which decompose an individual prediction into additive contributions from each input feature. These visualizations begin with the model’s baseline value () and sequentially apply the SHAP values for each feature to arrive at the final predicted outcome. Positive contributions are represented in red and move the prediction upward, while negative contributions are shown in blue and shift the prediction downward.
Figure 5a shows a student with a high predicted exam score (approximately 76.95). In this case, the model attributes this strong outcome primarily to behavioural factors, particularly consistent attendance and a high number of study hours per week, which emerge as the most influential drivers of academic success. The student’s prior academic achievements also contribute positively, indicating that historical academic performance plays a role in reinforcing a strong prediction. While certain contextual variables—such as limited access to educational resources, lower family income, and a longer commuting distance—exert a modest negative influence, their impact is outweighed by the strength of the student’s engagement and academic habits.
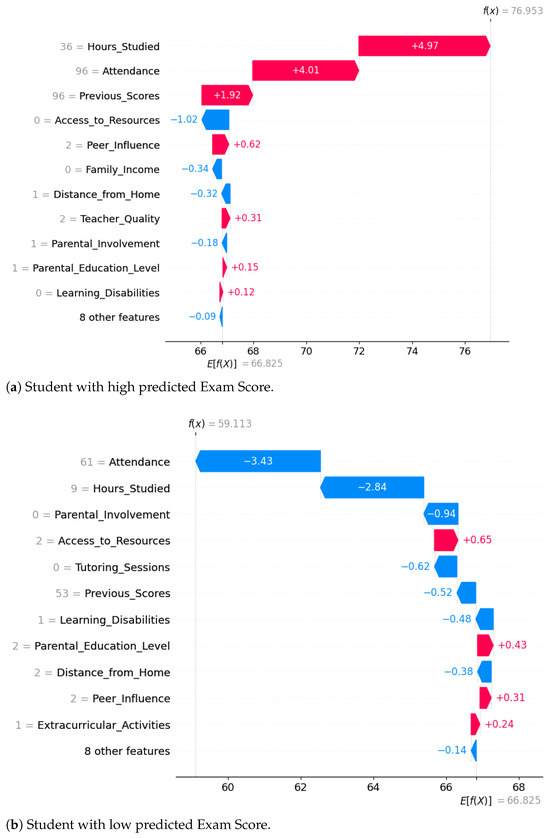
Figure 5.
SHAP waterfall plots for two different students. Red bars indicate features that increase the predicted Exam Score, while blue bars indicate features that decrease it.
This example illustrates how, within this synthetic dataset, behavioral engagement can play a decisive role in academic performance. Even in the presence of structural disadvantage, the student’s strong commitment to studying and consistent school attendance appear to counterbalance the contextual challenges. This finding highlights the potential of individual effort-related variables to mitigate the negative effects of contextual constraints, underscoring the importance of supporting self-regulated learning and attendance-driven policies in educational planning.
In contrast, the second example presented in Figure 5b shows a student with a low predicted exam score (approximately 59.11), largely driven by low attendance and limited study hours—both strong negative contributors in the model. Although the student benefits from moderate levels of family income and access to resources, these favourable contextual conditions are not enough to compensate for the lack of academic engagement. Moreover, the student has a learning disability and receives limited parental support, which likely restricts access to additional tutoring sessions. Together, these factors intensify the difficulties encountered by the student, which is reflected in the model’s lower prediction. This case emphasizes the critical importance of sustained behavioral engagement and targeted support, along with active parental involvement, particularly for students with additional learning needs. It also reinforces the need for early interventions aimed at fostering consistent study habits and school attendance.
These localized interpretations are meant to showcase the explanatory power of SHAP, rather than serve as evidence for causal relationships or generalized trends.
5. Discussion
The findings of this study demonstrate the potential of ensemble-based machine learning models—particularly LightGBM—in accurately predicting student performance using multifactorial data. The LightGBM model outperformed both Random Forest and XGBoost across all evaluation metrics, achieving an RMSE of 1.957, an MAE of 0.804, and an R2 value of 0.729. These results indicate a strong fit and suggest that the model can explain approximately 73% of the variance in student exam scores, a notable achievement given the heterogeneity of the input variables.
The application of SHAP provided interpretable insights into the model’s predictions, allowing for a transparent identification of key predictors. Notably, features related to prior academic performance—such as previous scores, hours studied, and attendance—emerged as the most influential. These findings reinforce long-standing assumptions in the educational literature about the centrality of academic engagement and preparation [16,17]. However, the analysis also highlighted the relevance of factors often considered secondary in predictive modeling, including parental involvement, access to resources, and teacher quality, which showed moderate but consistent contributions to the model’s outputs.
One of the key contributions of this work lies in its demonstration that interpretable machine learning can surface both expected and nuanced relationships within educational data. For example, although motivation level and peer influence were not among the top-ranked features, their influence varied substantially across individual predictions, as shown through local explanations. This underscores the importance of combining global and instance-level analyses when deploying predictive models in sensitive domains such as education.
This study demonstrates the potential of interpretable machine learning as a tool for educational hypothesis generation. Using synthetic data, we applied LightGBM and SHAP to explore plausible relationships among behavioural, contextual, and academic features. Our results align with long-standing educational theories: variables such as attendance, study time, and prior achievement emerged as important, followed by parental involvement and access to resources. However, we caution that these findings are not generalizable. The dataset does not reflect real institutional practices, student demographics, or learning environments. Rather than offering practical recommendations, our contribution is methodological. We provide a transparent and replicable analytic framework that can be reused with real datasets when they become available. The framework also facilitates transparency and interpretability, making it suitable for eventual application in educational decision-making tools.
Despite these strengths, several limitations should be acknowledged. First, the use of a synthetic dataset—while valuable for reproducibility and ethical transparency—inevitably introduces constraints in terms of external validity. The data may not fully reflect the diversity of real-world student experiences, institutional structures, or socioeconomic contexts. Moreover, synthetic datasets often lack the natural variance, noise, and longitudinal dependencies present in actual academic records. Future research should apply this framework to real-world datasets from diverse institutions to validate the generalizability of the results. This is further evidenced by the moderate predictive performance of our models, which underscores the limitations of using synthetic data. Achieving stronger results will likely require richer data with greater realism, variability, and contextual depth.
Second, the scope of the variables was limited to those available in the dataset, omitting potentially relevant dimensions such as emotional well-being, self-efficacy, digital literacy, or institutional policies, which are known to impact academic trajectories. Additionally, the model assumes static relationships among variables and does not account for temporal dynamics or feedback loops that might emerge over time.
We also acknowledge that machine learning is not a universal solution to all educational challenges. Education involves highly individualized, context-dependent, and motivational factors; therefore, statistical models can only capture certain aspects of its complexity. Our framework should therefore be seen as a complementary tool rather than a substitute for pedagogical expertise. From a methodological perspective, although SHAP offers robust tools for model interpretability, they rely on assumptions that may not always hold in complex datasets, such as feature independence or linear approximations. Careful interpretation and triangulation with domain expertise are essential when drawing conclusions from such techniques.
Overall, this study illustrates how integrating interpretable ML models with educational data can support data-informed decision-making. Educational stakeholders—such as school leaders, policy designers, and academic advisors—can leverage these insights to design targeted interventions, early-warning systems, and personalized learning pathways.
Future work should validate these insights using empirical data from diverse educational settings. Moreover, it should explore fairness-related aspects of predictive models (e.g., subgroup disparities) and extend the approach to longitudinal data, which can better capture temporal dynamics and causality. These directions are essential to ensure not only the robustness of predictive models but also their ethical alignment and trustworthiness when applied in real educational contexts.
6. Conclusions
This study demonstrates the value of combining advanced machine learning models with explainability techniques to enhance our understanding of student success in educational settings. Using a synthetic dataset with multifactorial information, we showed that ensemble models—particularly LightGBM—can predict academic performance with high accuracy, while SHAP provides transparent and interpretable explanations of the underlying predictive mechanisms.
Our findings reaffirm the central role of academic engagement indicators, such as attendance, hours studied, and previous scores, in shaping student outcomes. At the same time, they highlight the importance of secondary contextual factors—like parental involvement and access to educational resources—which, although less prominent, contribute meaningfully to prediction accuracy and fairness. Although the results are not actionable for real-world decision-making, the framework proposed here can inform future research and system design using real educational data.
The proposed approach illustrates a viable pathway for integrating interpretable artificial intelligence into educational analytics pipelines. By identifying both general trends and individualized insights, this framework supports the development of early intervention strategies and personalized learning plans, once validated with empirical data.
Future work should focus on validating these results using real-world datasets from diverse educational institutions and exploring longitudinal or causal models to better capture temporal dynamics. From a practical standpoint, the results of this study can inform the design of data-driven tools for educational professionals. These tools could assist in identifying at-risk students early, allocating resources more effectively, and tailoring pedagogical strategies to individual learning needs. Moreover, the use of interpretable models fosters trust among educators and stakeholders, paving the way for the responsible adoption of AI in schools and universities.
Author Contributions
Conceptualization, B.S.-P. and D.G.; Methodology, C.G.-B., M.G.A. and D.G.; Software, C.G.-B. and M.G.A.; Validation, C.G.-B.; Formal analysis, C.G.-B. and M.G.A.; Investigation, B.S.-P., C.G.-B., M.G.A. and D.G.; Resources, C.G.-B., M.G.A. and D.G.; Writing—original draft, B.S.-P., C.G.-B., M.G.A. and D.G.; Writing—review & editing, C.G.-B. and D.G.; Visualization, C.G.-B. and M.G.A.; Supervision, C.G.-B. and D.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The dataset analyzed in this study is publicly available on Kaggle under the title “Student Performance Factors” and is released under a Creative Commons Zero (CC0) license. It can be accessed at https://www.kaggle.com/datasets/lainguyn123/student-performance-factors (accessed on 27 April 2025). The source code used for data preprocessing, model training, and explainability analysis is publicly available at the following GitHub repository: https://github.com/davidogm/PaperEducation (accessed on 24 June 2025) The repository includes all scripts necessary to reproduce the experiments and visualizations presented in this study. No additional data were generated during this study.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Categorical Variable Encodings

Table A1.
Encoding schemes used for categorical variables.
Table A1.
Encoding schemes used for categorical variables.
| Variable | Encoding Mapping |
|---|---|
| Parental_Involvement | Low = 0, Medium = 1, High = 2 |
| Access_to_Resources | Low = 0, Medium = 1, High = 2 |
| Motivation_Level | Low = 0, Medium = 1, High = 2 |
| Family_Income | Low = 0, Medium = 1, High = 2 |
| Teacher_Quality | Low = 0, Medium = 1, High = 2 |
| Parental_Education_Level | High School = 0, College = 1, Postgraduate = 2 |
| Distance_from_Home | Near = 0, Moderate = 1, Far = 2 |
| Peer_Influence | Negative = 0, Neutral = 1, Positive = 2 |
| School_Type | Private = 0, Public = 1 |
| Extracurricular_Activities | No = 0, Yes = 1 |
| Internet_Access | No = 0, Yes = 1 |
| Learning_Disabilities | No = 0, Yes = 1 |
| Gender | Female = 0, Male = 1 |
References
- Xu, Y.; Ma, L.; Wang, Z.; Sun, S. Explainable Machine Learning for Early Warning in Education: A SHAP-based Analysis. In Proceedings of the 15th International Conference on Educational Data Mining (EDM), Durham, UK, 23 July 2022; pp. 456–461. [Google Scholar]
- Harron, K.; Dibben, C.; Boyd, J.; Hjern, A.; Azimaee, M.; Barreto, M.L.; Goldstein, H. Challenges in administrative data linkage for research. Big Data Soc. 2017, 4, 2053951717745678. [Google Scholar] [CrossRef]
- Holstein, K.; Wortman Vaughan, J.; Daumé III, H.; Dudik, M.; Wallach, H. Improving fairness in machine learning systems: What do industry practitioners need? In Proceedings of the CHI ’19: CHI Conference on Human Factors in Computing Systems, Glasgow, UK, 4–9 May 2019; pp. 1–16. [Google Scholar]
- Lundberg, S.M.; Erion, G.; Lee, S.I. Consistent individualized feature attribution for tree ensembles. Nat. Mach. Intell. 2020, 2, 252–259. [Google Scholar]
- Baker, R.S.; Siemens, G. Educational data mining and learning analytics. In Cambridge Handbook of the Learning Sciences; Cambridge University Press: Cambridge, UK, 2019; pp. 253–274. [Google Scholar]
- Romero, C.; Ventura, S. Data mining in education. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2013, 3, 12–27. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Salal, Y.K.; Abdullaev, S.M. Deep learning based ensemble approach to predict student academic performance: Case study. In Proceedings of the 2020 3rd International Conference on Intelligent Sustainable Systems (ICISS), Thoothukudi, India, 3–5 December 2020; IEEE: Palladam, India, 2020; pp. 191–198. [Google Scholar]
- Lipton, Z.C. The mythos of model interpretability. Queue 2018, 16, 31–57. [Google Scholar] [CrossRef]
- Doshi-Velez, F.; Kim, B. Towards a rigorous science of interpretable machine learning. arXiv 2017, arXiv:1702.08608. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You?”: Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 1135–1144. [Google Scholar]
- Bodily, R.; Dellinger, J.D.; Wiley, D. Toward content-agnostic learning analytics: Using patterns in students’ usage data to inform course design and facilitate personalized learning. Internet High. Educ. 2020, 45, 100728. [Google Scholar]
- Carvalho, D.V.; Pereira, E.M.; Cardoso, J.S. Machine learning interpretability: A survey on methods and metrics. Electronics 2019, 8, 832. [Google Scholar] [CrossRef]
- Viberg, O.; Hatakka, M.; Bälter, O.; Mavroudi, A. The current landscape of learning analytics in higher education: A systematic review. Comput. Hum. Behav. 2018, 89, 98–109. [Google Scholar] [CrossRef]
- Kuh, G.D.; Kinzie, J.L.; Buckley, J.A.; Bridges, B.K.; Hayek, J.C. What Matters to Student Success: A Review of the Literature; National Postsecondary Education Cooperative: Washington, DC, USA, 2006; Volume 8. [Google Scholar]
- Tinto, V. Leaving College: Rethinking the Causes and Cures of Student Attrition; University of Chicago Press: Chicago, IL, USA, 2012. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).