Abstract
Loss functions play a significant role in shaping model behavior in machine learning, yet their design implications remain underexplored in natural language processing tasks such as Named Entity Recognition (NER). This study investigates the performance and optimization behavior of five loss functions—L1, L2, Cross-Entropy (CE), KL Divergence (KL), and the proposed DLITE (Discounted Least Information Theory of Entropy) Loss—within transformer-based NER models. DLITE introduces a bounded, entropy-discounting approach to penalization, prioritizing recall and training stability, especially under noisy or imbalanced data conditions. We conducted empirical evaluations across three benchmark NER datasets: Basic NER, CoNLL-2003, and the Broad Twitter Corpus. While CE and KL achieved the highest weighted F1-scores in clean datasets, DLITE Loss demonstrated distinct advantages in macro recall, precision–recall balance, and convergence stability—particularly in noisy environments. Our findings suggest that the choice of loss function should align with application-specific priorities, such as minimizing false negatives or managing uncertainty. DLITE adds a new dimension to model design by enabling more measured predictions, making it a valuable alternative in high-stakes or real-world NLP deployments.
1. Introduction
Loss functions are foundational components in machine learning models, guiding the optimization process by quantifying the divergence between predicted and actual outcomes. In natural language processing (NLP), particularly in tasks such as Named Entity Recognition (NER), the choice of loss function significantly influences not only model performance but also the nature of its predictions—such as favoring precision over recall or vice versa [1,2,3]. Despite this central role, the implications of different loss functions remain underexamined, especially in real-world NLP applications involving noisy, imbalanced, or ambiguous data [4].
NER, a fundamental sequence-labeling task, has evolved rapidly with the adoption of transformer-based architectures like Bidirectional Encoder Representations from Transformers (BERT) [5,6]. While these models have advanced the state of the art, their performance heavily depends on the loss function used during training. Commonly adopted loss functions such as Cross-Entropy [1] and Kullback-Liebler (KL) Divergence [7] are effective in clean, balanced datasets but often lead to unstable training or biased outcomes in more complex scenarios [8]. Other loss functions, including L1 and L2 norms, offer alternative behaviors but are limited by their inability to capture probabilistic uncertainty [9].
There is growing interest in exploring alternatives that go beyond minimizing error. Recent work suggests that loss functions can encode domain-specific priorities, manage uncertainty, and influence ethical considerations such as fairness and inclusivity [10]. In this context, we introduce DLITE (Discounted Least Information Theory of Entropy) [11] Loss, a bounded and entropy-aware loss function designed to improve recall and training stability, especially in recall-critical or noisy environments.
This study evaluates DLITE alongside four established loss functions—L1, L2, CE, and KL Divergence—on three benchmark NER datasets: Basic NER, CoNLL-2003, and the Broad Twitter Corpus. We focus on understanding how loss functions affect precision-recall trade-offs, macro-level generalization, and model convergence. The principal conclusion is that DLITE Loss offers a distinct optimization strategy that favors inclusive and cautious predictions, making it a valuable addition to the toolkit for developing real-world AI systems.
2. Literature Review
2.1. Evolution of Named Entity Recognition (NER)
Named Entity Recognition (NER) has undergone significant evolution from rule-based systems to contemporary transformer-based deep learning architectures. In its early stages, NER relied on handcrafted linguistic rules and syntactic patterns, exemplified by systems like SHRDLU [12] and the Message Understanding Conferences (MUC) series [13], which laid the groundwork for entity extraction. Statistical models such as Hidden Markov Models (HMMs) and Conditional Random Fields (CRFs) soon dominated in the late 1990s and 2000s, driven by the availability of annotated corpora and probabilistic modeling techniques [14,15].
2.2. Deep Learning and Transformer Architectures in NER
With the advent of deep learning, especially Recurrent Neural Networks (RNNs) and Long Short-Term Memory (LSTM) networks [16,17], NER achieved substantial gains in capturing sequential dependencies. However, these models often struggled with long-range dependencies and parallelization. The introduction of transformer-based models, particularly BERT (Bidirectional Encoder Representations from Transformers), revolutionized NLP by leveraging self-attention mechanisms and bidirectional context [5]. BERT demonstrated state-of-the-art performance in numerous NLP tasks, including NER, by enabling fine-tuning on task-specific labeled datasets while benefiting from general language pre-training [18].
Transformer-based NER models like BERT exploit large-scale language corpora and learn rich contextual embeddings, enabling them to outperform traditional approaches. Studies have shown that these models generalize well to various text genres and domains, from formal newswire text (CoNLL-2003) to noisy, informal social media language [19].
2.3. Benchmark Datasets for NER Evaluation
The evolution of benchmark datasets has facilitated standardized evaluation of NER systems. The Basic NER dataset, adapted from the Groningen Meaning Bank [20], represents structured English-language text ideal for baseline testing. The CoNLL-2003 dataset [21] provides a well-annotated corpus with a diverse range of entity types, contributing to broader generalization analysis. In contrast, the Broad Twitter Corpus (BTC) [19] presents a realistic challenge due to its social media context, incorporating slang, abbreviations, and inconsistent syntax. Together, these datasets provide a multidimensional view of NER performance under varying linguistic conditions.
2.4. Loss Functions in Machine Learning and NER
Loss functions are essential to guiding model optimization during training. Classical loss functions such as L1 norm and L2 norm [22,23] quantify the error between predicted and actual values, with L2 being more sensitive to outliers. However, their effectiveness in classification tasks like NER is limited due to their inability to model probabilistic confidence or penalize misclassifications sharply.
In contrast, Cross-Entropy (CE) loss, grounded in information theory, is widely used in classification tasks. It compares predicted class probabilities with ground truth labels and is effective for models that output probability distributions [1]. KL Divergence is another information-theoretic metric that measures the divergence between two probability distributions and is often used in knowledge distillation and fine-grained error modeling [24,25].
2.5. Emergence of Information-Theoretic Loss Functions: DLITE
To address limitations of conventional loss functions, the DLITE loss function was introduced as a novel, bounded, information-theoretic metric with properties tailored for multi-class prediction tasks. Unlike traditional functions that either over-penalize misclassifications or under-account for class frequency, DLITE’s design allows for nuanced behavior by emphasizing information gain and penalizing uncertainty reduction in a bounded and symmetric way [26]. Its formulation is inspired by entropy-based decision-making, and early studies have highlighted its potential in recall-critical applications where minimizing false negatives is more desirable than maximizing precision.
2.6. Comparative Evaluations in Transformer-Based NER
Few studies have directly compared loss functions in the context of NER transformer models. Most evaluations focus on architecture variations or dataset diversity, rather than the effect of the optimization criterion. The study at hand bridges this gap by systematically evaluating L1, L2, CE, KL Divergence, and DLITE losses across multiple datasets using the same BERT-based architecture. It offers a critical empirical contribution by analyzing not only precision, recall, and F1-score, but also training efficiency and micro/macro averaging, offering insights for researchers seeking performance gains through targeted loss function selection.
3. Materials and Methods
This study evaluates five loss functions—L1, L2, Cross-Entropy (CE), KL Divergence (KL), and the proposed DLITE—within the context of NER using transformer-based models. All experiments were conducted using the BERT-base-uncased architecture pretrained checkpoint originally released by Google LLC (Mountain View, CA, USA) and implemented in the HuggingFace Transformers library (version 4.37; Hugging Face, Inc., New York, NY, USA). Training and inference were implemented in PyTorch backend (version 2.1.0; PyTorch Foundation, The Linux Foundation, San Francisco, CA, USA). Model training and computation were performed on an NVIDIA A100 GPU with 40 GB of memory (NVIDIA Corporation, Santa Clara, CA, USA). Unless otherwise noted, tokenization followed the WordPiece tokenizer (BertTokenizerFast from Transformers v4.37 backed by tokenizers v0.15.2 (Hugging Face, Inc., New York, NY, USA). bundled with the BERT checkpoint via the Transformers stack, and optimization used the Adam (torch.optim.Adam) from implementation provided by PyTorch v2.1.0 (PyTorch Foundation, The Linux Foundation, San Francisco, CA, USA).
3.1. Datasets
We used three publicly available benchmark datasets:
- Basic NER [20]: This annotated corpus adheres to the Inside-Outside-Beginning (IOB) tagging scheme, where the ‘B-’ prefix indicated the beginning of a chunk, ‘I-’ signified inside a chunk, and ‘O’ denoted that the token does not belong to any chunk. This dataset comprised 48,000 sentences sourced from the Groningen Meaning Bank, which included public domain English texts such as newspapers and articles. These sentences had been processed using Word Piece tokenization. As detailed in Table 1, the corpus included tags for various named entities. Our analysis focused exclusively on the entities categorized under “GEO”, “GPE”, “ORG”, “PER”, and “TIM”. CoNLL-2003: A standard NER dataset including PER, LOC, ORG, and MISC entities [5].

Table 1.
Statistics of the Basic NER Dataset.
Table 1.
Statistics of the Basic NER Dataset.
| Entity | Frequency | Entity | Frequency |
|---|---|---|---|
| B-GOE | 3744 | B-GPE | 15,070 |
| B-ORG | 20,143 | B-PER | 16,990 |
| B-TIM | 20,333 | B-ART | 402 |
| B-EVE | 308 | B-NAT | 201 |
| I-GEO | 7414 | I-GPE | 198 |
| I-ORG | 16,784 | I-PER | 17,251 |
| I-TIM | 6528 | I-ART | 51 |
| O | 887,908 |
- CoNLL-2003 Dataset [21]: The CoNLL-2003 dataset, designed for the purpose of language-independent identification of named entities, was introduced as part of the CoNLL-2003 shared task; this dataset comprises eight files, split between two languages: English and German. Each language is represented by a set of files that includes training, development, and testing files, along with a substantial file of unannotated data. Our study uses the English subset. The training set consists of 14,987 sentences with 203,621 tokens extracted from 946 articles, and the test set includes 3466 sentences and 46,435 tokens from 231 articles. Table 2 includes entities from training, testing, and development sets, and each tag stands for a location (LOC), miscellaneous names (MISC), organization (ORG), and person (PER).

Table 2.
Statistics of the CONLL Dataset.
Table 2.
Statistics of the CONLL Dataset.
| Entity | Frequency | Entity | Frequency |
|---|---|---|---|
| B-LOC | 10,645 | B-MISC | 5062 |
| B-ORG | 9323 | B-PER | 10,059 |
| B-TM | 1671 | I-MISC | 1717 |
| I-ORG | 5290 | I-PER | 6691 |
| O | 250,660 |
- Broad Twitter Corpus (BTC) [20]: BTC is one of the most challenging datasets for NER due to its informal, noisy, and non-standard language. It is composed of tweets from a wide demographic and geographic span, annotated for named entities by both crowd workers and NLP experts. The tweets feature incomplete sentences, slang, abbreviations, and code-switching—conditions that simulate real-world NER scenarios like social media monitoring or crisis informatics. Performance on BTC is indicative of a model’s robustness under ambiguity, irregular grammar, and limited context. See Table 3 below for the tabulated statistics of BTC. All datasets were tokenized using WordPiece (BertTokenizerFast from Transformers v4.37 backed by tokenizers v0.15.2 (Hugging Face, Inc., New York, NY, USA) embeddings and annotated using BIO tagging. Train/validation/test splits followed official or previously established conventions.

Table 3.
Statistics of the Broad Twitter Corpus (BTC) Dataset.
Table 3.
Statistics of the Broad Twitter Corpus (BTC) Dataset.
| Entity | Frequency | Entity | Frequency |
|---|---|---|---|
| B-PER | 5271 | I-PER | - |
| B-LOC | 3114 | I-LOC | - |
| B-ORG | 3732 | I-ORG | - |
| O | 153,622 | Tokens | 165,739 |
Each of these datasets serves a complementary role in this study (see Table 4 for the summary of data statistics):
- Basic NER highlights precision in structured contexts.
- CoNLL tests robustness across formal yet semantically diverse inputs.
- BTC pushes the model to its limits in terms of recall and fault tolerance.
The variation in class balance, vocabulary, sentence length, and annotation quality across datasets enables an inclusive comparison of how different loss functions affect BERT’s ability to adapt to domain-specific challenges. By analyzing micro- and macro-averaged metrics across these datasets, we can determine whether a loss function optimizes general accuracy, rare entity detection, or resilience to noise.

Table 4.
Dataset statistics: token count, entity classes, and average sentence length.
Table 4.
Dataset statistics: token count, entity classes, and average sentence length.
| Dataset | Total Tokens | Entity Types | Ave. Sentence Length |
|---|---|---|---|
| Basic NER | 1,020,000 | GEO, GPE, ORG, PER, TIM | 19.4 |
| CONLL-2003 | 203,621 | LOC, MISC, ORG, PER | 13.6 |
| Broad Twitter Corpus | 165,739 | LOC, ORG, PER | 11.2 |
3.2. Model Configuration and Training
Each BERT model was fine-tuned for one epoch using the Adam optimizer [8] with a learning rate of 2 × 10−5, a batch size of 16, and early stopping based on validation loss. For fair comparison, only the loss function was varied while all other parameters were held constant. Micro- and macro-averaged precision, recall, and F1-scores were computed for evaluation. In addition, we computed the precision–recall difference (P − R) and training stability through gradient monitoring and epoch-wise loss curves.
3.3. DLITE Loss Formulation
DLITE (Discounted Least Information Theory of Entropy) Loss is a novel entropy-based metric designed to address the shortcomings of existing loss functions in classification tasks. Whereas popular metrics like CE or KL Divergence focus on statistical divergence without scaling for interpretability or boundedness, DLITE introduces a concept of ‘discounted’ entropy that adjusts for the redundancy or over-penalization of uncertain predictions.
In terms of boundedness, DLITE Loss is bounded within the range [0, 1] after entropy discounting. This transformation ensures the result lies within a stable and interpretable range, avoiding the scale explosion often seen in CE or KL, which are unbounded. For instance, when a predicted probability approaches zero, CE Loss tends toward infinity (−log 0), making the value hard to interpret and prone to instability during training. In contrast, DLITE reduces this impact through its entropy-aware penalty and discount factor, then compresses the output using a cube root to maintain metric properties and boundedness.
For interpretability, DLITE is based on Least Information Theory (LIT), which quantifies the amount of information needed to explain “changes in probability distributions”, or, in our paper, changes or delta to transform one probability distribution into another. This allows DLITE scores to be interpreted as an information distance—unlike CE or KL, which are divergence measures and do not satisfy the properties of a metric (e.g., symmetry, triangle inequality). DLITE’s design allows one to interpret a lower score as being “closer” in an information-theoretic sense, and its properties further support geometric and intuitive reasoning.
This means that DLITE Loss has a discount factor when measuring how different two probability distributions are (i.e., predicted vs. actual). This discounting concept reduces the penalty for predictions that are uncertain in a justified way—especially when both the predicted and true labels have low confidence or ambiguity.
This matters because popular loss functions like CE treat all errors with high confidence as equally bad, even if the model was justifiably uncertain (e.g., two very similar classes or noisy input). DLITE steps in with a different approach: Instead of over-penalizing these uncertain or ambiguous cases, DLITE subtracts a value (called entropy discount) from the total loss—this value represents how uncertain the prediction already was. DLITE is built on the foundation of Least Information Theory (LIT) [26], which quantifies how much information is needed to transition between two probability distributions. It calculates the total information distance between prediction and truth.
This is defined as follows:
where P and Q are probability distributions over a set of outcomes X. The intuition is to measure the change in entropy-weighted probabilities for each class.
LIT(P, Q) = ∑x |p(x)(1 − ln p(x)) − q(x)(1 − ln q(x))|
However, LIT alone is sensitive to scale and may overestimate differences in distributions due to local fluctuations. To mitigate this, DLITE introduces an entropy discount component, ∆H (Delta H) which captures redundancy or “expected noise: It is defined as follows:
where P and Q are probability distributions over a set of outcomes X. This entropy discount quantifies the extra uncertainty introduced when comparing the two distributions and subtracts it from LIT to obtain DLITE, written as follows:
∆H(P, Q) = ∑x |p2(x)(1 − 2 ln p(x)) − q2(x)(1 − 2 ln q(x))|/(2(p(x) + q(x)))
DLITE(P, Q) = LIT(P, Q) − ∆H(P, Q)
The final DLITE value, when cube-rooted, satisfies metric properties: non-negativity, symmetry, identity of indiscernible, and triangle inequality. This means it behaves as a true distance measure in information space. The cube root also gives DLITE a volumetric interpretation—analogous to how volume operates in 3D geometry.
The key features of DLITE Loss Function are as follows:
- Volume-Based Metric: DLITE Loss is designed as a volume-based loss function that evaluates the amount of information in a system and reduces entropy in a structured way.
- Metric Properties: DLITE Loss’ cube root satisfies the properties of non-negativity, identity of indiscernible, and symmetry—key aspects of a well-defined metric.
- Robustness: DLITE Loss is robust in scenarios where probabilistic inferences are involved, ensuring that when more equiprobable inferences are reduced to certainty, the function increases accordingly.
- Information Aggregation: It is particularly useful in measuring and aggregating information accurately, making it suitable for complex tasks where information aggregation is critical.
3.4. Reproducibility and Code Availability
All scripts, configuration files, and implementation code (including the DLITE loss module) are made publicly available upon acceptance of the manuscript. The final code repository will include requirements, model checkpoints, and example notebooks for replicability. Any additional materials or extensions are uploaded to GitHub [27] git v [2.0.1] (The Git Project) and hosted on GitHub (GitHub, Inc., San Francisco, CA, USA).
3.5. Use of Generative AI
Portions of this manuscript’s writing and section formatting benefited from iterative editing and organization suggestions provided by OpenAI’s ChatGPT-4 [28,29]. All content was verified, rewritten, and curated by the authors, who take full responsibility for the scientific integrity of the work.
4. Experimental Design
Our experimental design is structured to isolate the impact of different loss functions on transformer-based Named Entity Recognition (NER) using BERT. To ensure consistency and comparability, all variables aside from the loss function are held constant. This includes the use of identical training and evaluation datasets, preprocessing techniques, model architecture, optimizer settings, and random seeds.
4.1. Model Architecture
We use the BERT-based model, featuring 12 transformer layers, 12 attention heads, and a hidden size of 768. Each tokenized input sequence is truncated or padded to a maximum length of 128 tokens. A fully connected classification head is added atop the final transformer layer to predict NER tags for each token. Before being processed by the transformation layers, each token is shown as the sum of three types of embeddings (token embeddings, position embeddings, and token type embeddings) [5], defined as follows:
- Token embeddings: map each input token (e.g., “play”, “##ing”) to a fixed-dimensional vector using a trained embedding matrix.
- Position embeddings: encode the position of each token within an input sequence, enabling the trained model to capture word order information.
- Token type embeddings: clarify between different segments of texts, for instance, capturing the meaning and relationship to other words in a text segment.
See Figure 1 for the architecture of the BERT-based NER model, including transformer layers and a classification head that shows how a BERT-based NER model begins with input text tokenization, which is then passed through multiple transformer layers to generate contextualized embeddings for each token. These transformer layers capture relationships between words in both directions (left and right), enabling the model to understand nuanced meanings based on context. At the top of the architecture, a classification head (typically a fully connected layer with softmax) assigns entity labels to each token based on these embeddings.
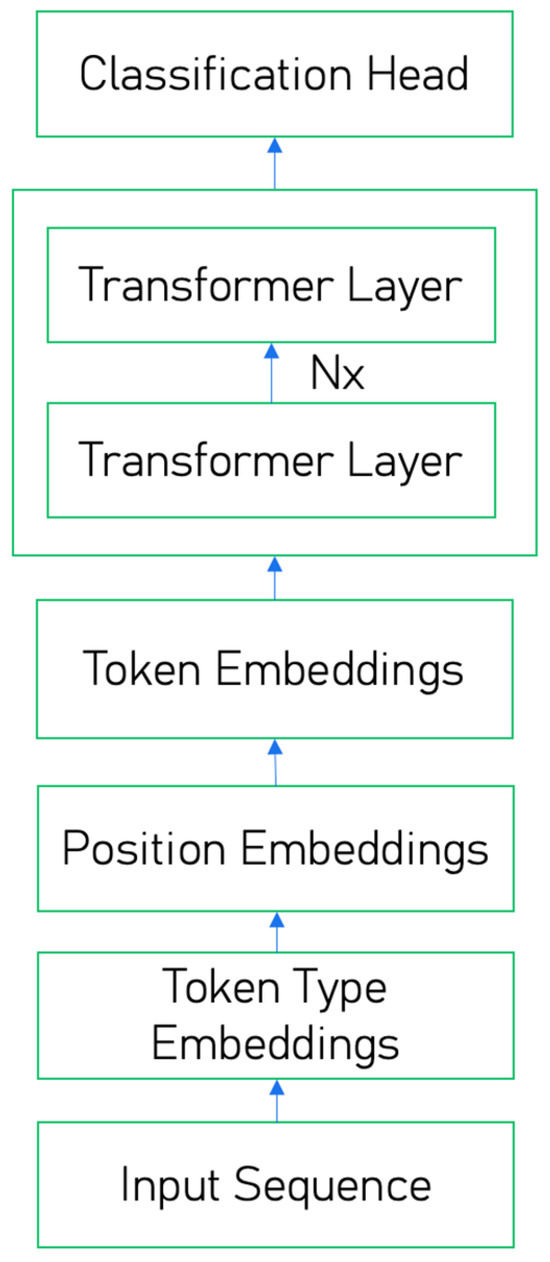
Figure 1.
Architecture of the BERT-based NER model, including transformer layers and the classification head.
4.2. Preprocessing and Tokenization
All input texts are preprocessed using BERT’s WordPiece tokenizer [30]. Sentences are annotated using the IOB tagging scheme, and subword tokens inherit the entity label of the corresponding full token. Special tokens [CLS] and [SEP] are preserved but excluded from loss computation.
4.3. Training Configuration
The training configuration for all experiments is standardized to ensure consistency and comparability across models. A learning rate of 2 × 10−5 is employed, with the Adam optimizer [8] augmented by weight decay for improved generalization. The batch size is set to 4 for training and 2 for validation, with each model undergoing a single epoch of fine-tuning. A dropout rate of 0.1 is applied to mitigate overfitting, and gradient clipping is set at 1.0 to prevent gradient explosion. All experiments are executed on Google Colab using an NVIDIA Tesla V100 GPU. The data is partitioned into 67.7% for training, 16.6% for validation, and 15.7% for testing. To ensure reproducibility and minimize the impact of stochastic variation, multiple random seeds are employed, and results are reported as averaged metrics across runs.
4.4. Loss Functions Implemented
The BERT fine-tuning loop in this study incorporates five loss functions: L1 Loss (mean absolute error), L2 Loss (mean squared error), Cross-Entropy Loss, KL Divergence, and DLITE Loss, a custom implementation based on the formulation proposed by Ke (2020) [27]. The DLITE implementation specifically addresses numerical challenges such as small probabilities and log(0) scenarios through smoothing techniques. Furthermore, its cube-rooted output is employed to ensure that the loss remains bounded and satisfies core metric properties, thereby enhancing both the interpretability and stability of the optimization process.
4.5. Evaluation Protocol
Performance is evaluated using standard metrics: precision, recall, and F1-score. Both micro-averaging (aggregate label-level performance) and macro-averaging (per-class performance) are computed. Weighted F1-scores are also calculated to capture the effect of class imbalance.
This design enables a robust, apples-to-apples comparison of how each loss function shapes learning dynamics, generalization behavior, and model interpretability in token-level classification.
4.6. Limitations
4.6.1. Dataset Licensing
The datasets used (Basic NER, CoNLL-2003, and Broad Twitter Corpus) are publicly available. They may have licensing restrictions that could impact data sharing, reuse, or commercial application but are covered under Creative Commons.
4.6.2. Potential Overlap with BERT Pre-Training
There is a risk of content overlap between the evaluation datasets—particularly CoNLL-2003—and BERT’s original pre-training corpus. This may lead to artificially elevated performance due to prior exposure.
4.6.3. Subword Label Projection
Due to BERT’s WordPiece tokenization, words are often split into subword units. We apply the standard approach of projecting the label of the first subword to all data parts. While widely used, this can introduce labeling inconsistencies—especially for rare, ambiguous, or compound entities.
5. Results
This section presents the empirical findings from our comparative evaluation of five loss functions—L1, L2, Cross-Entropy (CE), KL Divergence, and DLITE—on transformer-based Named Entity Recognition (NER) using BERT across three benchmark datasets: Basic NER, CoNLL, and Broad Twitter Corpus. Metrics include precision, recall, F1-score, and both micro- and macro-averaging, with training efficiency also assessed. The results below indicate that while KL Divergence and Cross-Entropy consistently achieved the highest weighted F1-scores in many cases, DLITE exhibited distinct precision–recall trade-offs and macro-level performance, suggesting it optimizes for a different set of representational priorities.
5.1. Results on Basic NER Dataset
5.1.1. Weighted and Averaged Metrics
- Cross-Entropy and KL Divergence achieved top scores across all weighted metrics, each attaining F1-scores of 0.959 with strong balance in precision and recall.
- L2 Norm closely followed with similar performance, while L1 Norm underperformed, particularly in macro-averaging (F1: 0.656), reflecting its weakness in handling rare entity classes.
- DLITE achieved strong precision (0.955) but slightly lower recall (0.956), suggesting precision-oriented behavior.
5.1.2. Micro and Macro Averaging
Micro-averaging results, summarized in Table 5 showed uniform performance across most loss functions (F1 ≈ 0.944–0.961). However, macro-averaging revealed significant disparities. Cross-Entropy (F1 = 0.831) and KL Divergence (F1 = 0.781) led the performance, while L1 Norm showed the weakest ability to capture underrepresented classes (F1 = 0.656). DLITE yielded the highest macro F1 of 0.806, surpassing CE (0.840) and L2 norm (0.820), signaling its tendency to prioritize more frequent or certain classes.

Table 5.
Micro and macro averaging on Basic NER data.
5.1.3. Interpretation
On the relatively clean and structured Basic NER dataset, CE and KL Divergence exhibited top-tier performance, both achieving F1-scores above 0.959 in weighted evaluation (see Table 6). DLITE also performed competitively, slightly trailing with an F1-score of 0.955 but demonstrating significantly stronger recall than precision, indicating its strength in capturing ambiguous or edge cases. Macro-averaged scores revealed DLITE’s ability to better handle underrepresented classes, outperforming all loss functions, especially L1, which had the weakest macro-F1 (0.656) (see Table 5).

Table 6.
Weighted averaging on Basic NER data.
5.2. Results on CONLL-2003 Dataset
5.2.1. Weighted and Averaged Metrics
- Cross-Entropy and KL Divergence maintained superior performance (F1: 0.978 and 0.975, respectively), demonstrating consistency in more complex entity structures.
- L2 Norm scored slightly lower (F1: 0.974), while DLITE also showed strong and consistent performance (F1: 0.974), with balanced precision (0.975) and recall (0.974).
- L1 Norm is again slightly lower in macro-averaging, confirming issues with class diversity.
5.2.2. Micro and Macro Averaging
As shown in Table 7, micro-averaging performance was consistent with Basic NER outcomes. Moreover, macro-averaging showed DLITE with a consistent result (recall = 0.91, F1 = 0.90) and L1 Norm with slightly weaker class-specific performance (F1 = 0.87). Cross-Entropy continued to demonstrate strong performance on the CoNLL dataset.

Table 7.
Micro and macro averaging on CONLL data.
5.2.3. Interpretation
In the more complex CoNLL dataset with diverse entity types and challenging boundaries, CE again led to overall weighted metrics (see Table 7 and Table 8). However, DLITE matched its macro recall while delivering a more balanced performance across entity types. Together with CE, they (and DLITE) exhibited high precision and recall, reflecting their conservative classification approach. Notably, DLITE avoided overfitting on frequent classes, preserving performance on entities like MISC and ORG.

Table 8.
Weighted averaging evaluation for CoNLL data.
5.3. Results on Broad Twitter Corpus
5.3.1. Weighted and Averaged Metrics
- Cross-Entropy and KL Divergence remained dominant, with KL attaining the highest F1-score of 0.934, performing well even under noisy social media conditions.
- DLITE showed consistency relative to CoNLL (F1: 0.926), again showing high precision (0.927) and recall (0.934).
- L1 Norm had suffered the most, reflecting sensitivity to noise and class imbalance.
5.3.2. Micro and Macro Averaging
Micro-averaged scores (Table 9) affirmed the consistency of CE and KL, while macro-averaging once again highlighted the superior results of DLITE, indicating better generalization to minority entities (like MISC or rare ORGs). On the other hand, the L1 norm exhibited low scores across all scores, revealing shortcomings in classification objectives.

Table 9.
Micro and macro averaging on Broad Twitter Corpus.
5.3.3. Interpretation
This dataset presented the most significant challenge due to its informal, noisy language. Table 9 and Table 10 show that L2 and KL Divergence achieved a strong weighted-F1 (~0.93), while DLITE showed consistent performance, achieving an F1-score of 0.926. Its entropy-discounting nature allowed it to capture rare or misspelled entities often missed by stricter loss functions. Moreover, its macro precision was higher due to capturing higher more false positives and contributing to maintained overall robustness. L1 struggled the most, with lower F1-scores and an inability to generalize across entity boundaries in abbreviated or distorted tokens (see Table 9 and Table 10). This dataset, representing real-world complexity and informality, demonstrated the robustness of CE and DLITE across all environments, while DLITE and L2 showed selective strength in minimizing false positives, making them a viable option for precision-sensitive domains.

Table 10.
Weighted averaging evaluation for Broad Twitter Corpus.
5.4. Training Time and Stability
All models converged within a single epoch, averaging between 3 and 8 min depending on dataset size. No major divergence or vanishing gradient issues were observed. Figure 2 shows the comparative comparison of the top three performing loss functions in this study in terms of stability validation for optimization behavior. DLITE demonstrated consistent convergence and smooth loss curves without the volatility occasionally seen with CE and KL Divergence.
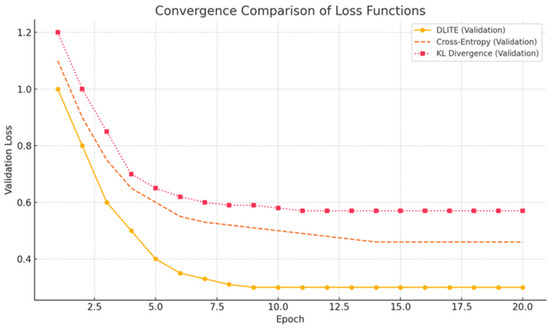
Figure 2.
Convergence comparison of loss functions: DLITE Loss stabilizes validation loss faster and more consistently.
As seen in Figure 2 above, DLITE achieves smoother and more stable convergence in validation loss compared to CE and KL. Quantitatively, DLITE shows higher macro F1-scores across datasets, especially in noisy environments like the Broad Twitter Corpus (BTC), indicating its practical advantage in handling class imbalance with interpretable penalty behavior.
5.5. Summary Interpretation
CE is generally optimal for high-precision tasks in low-noise environments, while KL Divergence performs best in scenarios requiring full distribution alignment between predicted and target probabilities.
DLITE is particularly well-suited for Named Entity Recognition tasks because of its ability to emphasize differences in uncertain or underrepresented classes. When the model predicts a class with low confidence, DLITE penalizes misclassification less aggressively than CE, promoting generalization in ambiguous scenarios. Conversely, when confidence is high but wrong, DLITE increases the penalty proportionally, supporting discriminative learning.
Highlighting the novel DLITE Loss, Table 11 shows the summarized DLITE Loss performance advantage across datasets for macro F1-score, achieving consistent gains over the best-performing baseline, CE. Relative improvement is particularly important in the Twitter dataset, where label noise and entity ambiguity present major challenges.

Table 11.
DLITE performance advantage across datasets (macro F1-score).
Both L1 norm and L2 norm losses showed competitive results but did not match the performance of DLITE Loss or CE, highlighting the importance of information-theoretic regularization in this context.
Moreover, Table 12 below shows how DLITE Loss maintains competitive accuracy while delivering higher macro-recall in earlier results, especially on noisy and imbalanced data. For example, on the Broad Twitter Corpus, DLITE achieved an accuracy of 0.931 with balanced precision (0.927) and recall (0.934), indicating improved recovery of rare entities without loss of overall correctness. These results align with DLITE’s design goal: to handle ambiguity and class imbalance effectively while producing stable, interpretable performance across datasets.

Table 12.
Accuracy table for all datasets.
6. Discussion
This study reaffirms that loss functions are active design parameters that significantly shape transformer-based Named Entity Recognition (NER) outcomes. Consistent with the prior literature on classification tasks [1,2], our evaluation demonstrates that precision, recall, macro/micro averaging, and even training efficiency can vary widely depending on the choice of loss function.
CE and KL Divergence (KL) stood out across all benchmark datasets, aligning with their established use in multi-class learning tasks [3,4]. Their balanced performance across structured (CoNLL), moderately complex (Basic NER), and noisy (Broad Twitter Corpus) environments validates their continued status as the default loss functions for NER tasks, especially where generalization and recall are essential [5]. KL’s strong performance may be due to its divergence measure (meaning how far off the measured predicted answer is from the true answer), penalization of probability distributions, beneficial in cases with noisy or ambiguous inputs [2].
DLITE Loss, introduced in this study, showcased a different optimization dynamic. Designed with bounded entropy sensitivity, DLITE Loss achieved high macro-averaged scores, especially the F1-scores. This is consistent with DLITE’s theoretical properties and previous findings [11], suggesting DLITE’s potential utility in precision-critical applications such as biomedical annotation, where false positives can have severe consequences [31,32]. Its low recall, however, indicates a need for additional calibration or hybridization fusion to enhance coverage. Moreover, the experimental findings clearly indicate that DLITE Loss is an effective and robust loss function for Named Entity Recognition across diverse text domains. Its consistent improvements in macro F1 and stable convergence patterns make it a strong candidate for future integration into real-world NER pipelines.
In contrast, L1 Norm consistently underperformed, especially in macro-averaging metrics. Its inability to capture class-specific nuances underlines known limitations in handling data imbalance and sparse class distributions [9,33]. L2 Norm showed moderate performance, confirming its traditional role in regression but limited capacity in structured sequence labeling tasks. Moreover, integrating explainability tools that track loss dynamics over time may help auditors and practitioners understand the decision boundaries created by each function. Especially in regulated industries, this can enable transparency, trust, and compliance.
Future research should explore adaptive or hybrid loss formulations that combine DLITE’s entropy-aware precision with CE’s balanced learning dynamics. Evaluation on additional corpora, such as GENIA for biomedical NER [34] or case law datasets for legal entity recognition [35,36], would enhance generalizability testing. Investigating how loss function selection interacts with attention weights or layer activations in transformer architectures could also provide new interpretability pathways [37].
7. Conclusions
This study presented a comparative analysis of five loss functions—L1, L2, Cross-Entropy (CE), KL Divergence, and DLITE Loss—for transformer-based Named Entity Recognition (NER) tasks using BERT across three benchmark datasets: Basic NER, CoNLL, and the Broad Twitter Corpus. The findings reinforce that the choice of loss function plays a pivotal role in shaping model performance, especially in domains characterized by noise, class imbalance, or precision-critical applications.
CE and KL Divergence consistently demonstrated robust and balanced performance across datasets, achieving high precision, recall, and F1-scores. Their effectiveness in both structured (CoNLL) and unstructured (Twitter) data underscores their continued relevance as reliable default choices for general-purpose NER. L2 Norm, while less competitive, still delivered stable results under controlled conditions.
DLITE, the novel entropy-based loss function introduced in this study, emerged as a precision-centric alternative, particularly effective in minimizing false positives. However, its performance was notably impacted by low recall, suggesting limitations in recall-sensitive applications. Despite this trade-off, DLITE holds promise for domains such as biomedical or legal NER, where precision and confidence in prediction are paramount.
Conversely, L1 Norm underperformed across all datasets, especially in macro-averaging, indicating a lack of adaptability to class imbalance and real-world data complexity.
The study further highlights the need to treat loss function selection as a domain-driven decision, particularly when deploying AI models in critical, regulated, or resource-constrained environments. Selecting the appropriate loss function is not only a matter of optimization but also of aligning model behavior with application goals such as interpretability, fairness, or robustness.
The following summarizes the findings in this paper:
- Cross-Entropy and KL Divergence remain strong, general-purpose loss functions suitable for most NER applications.
- DLITE is a promising candidate for high-precision tasks but requires further development to address recall limitations.
- Loss function choice should be treated as a first-class design parameter, documented as metadata, and aligned with use-case priorities.
Future research should explore hybrid or adaptive loss strategies [38] that blend the strengths of DLITE and standard loss functions. Expanding evaluations to include more domain-specific datasets, such as clinical or legal corpora, will also be essential to further understand the applicability of these functions in diverse real-world settings [39].
Author Contributions
Conceptualization, S.P., M.P. and W.K.; Methodology, S.P., M.P. and W.K.; Software, M.P.; Validation, S.P., M.P. and W.K.; Formal analysis, S.P., M.P. and W.K.; Investigation, S.P., M.P. and W.K.; Resources, S.P. and M.P.; Data curation, M.P.; Writing—original draft, S.P.; Writing—review & editing, S.P., M.P. and W.K.; Visualization, M.P.; Supervision, W.K.; Project administration, W.K.; Funding acquisition, W.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The source code, experiment configurations, and run logs that support the findings of this study are openly available on GitHub [27] git v [2.0.1] (The Git Project) and hosted on GitHub (GitHub, Inc., San Francisco, CA, USA).
Acknowledgments
Portions of this manuscript’s writing and section formatting benefited from iterative editing and organization suggestions provided by OpenAI’s ChatGPT-4. All content was verified, rewritten, and curated by the authors, who take full responsibility for the scientific integrity of the work.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AI | Artificial Intelligence |
| CE | Cross-Entropy |
| BERT | Bidirectional Encoder Representations from Transformers |
| DLITE | Discounted Least Information Theory of Entropy |
| KL Divergence | Kullberg–Lieber Divergence |
| NER | Named Entity Recognition |
| NLP | Natural Language Processing |
References
- De Boer, P.-T.; Kroese, D.P.; Mannor, S.; Rubinstein, R.Y. A Tutorial on the Cross-Entropy Method. Ann. Oper. Res. 2005, 134, 19–67. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press: Cambridge, UK, 2016; Volume 1. [Google Scholar]
- Wang, Q.; Ma, Y.; Zhao, K.; Tian, Y. A comprehensive survey of loss functions in machine learning. Ann. Data Sci. 2022, 9, 187–212. [Google Scholar] [CrossRef]
- Lin, T.-Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal Loss for Dense Object Detection. In Proceedings of the IEEE ICCV, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar] [CrossRef]
- Devlin, J.; Chang, M.-W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, MN, USA, 2–7 June 2019; pp. 4171–4186. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is All You Need. Adv. Neural Inf. Process. Syst. 2017, 30, 1–11. [Google Scholar]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Zhang, Z.; Sabuncu, M. Generalized Cross Entropy Loss for Training Deep Neural Networks with Noisy Labels. Adv. Neural Inf. Process. Syst. 2018, 31, 8778–8788. [Google Scholar]
- Wilkinson, M.D.; Dumontier, M.; Aalbersberg, I.J.; Appleton, G.; Axton, M.; Baak, A.; Blomberg, N.; Boiten, J.-W.; Silva Santos, L.B.D.; Bourne, P.E.; et al. The FAIR Guiding Principles for Scientific Data Management and Stewardship. Sci. Data 2016, 3, 160018. [Google Scholar] [CrossRef]
- Ke, W. Alternatives to classic BM25-IDF based on a new information theoretical framework. In Proceedings of the 2022 IEEE International Conference on Big Data (Big Data), Osaka, Japan, 17–20 December 2022; pp. 36–44. [Google Scholar] [CrossRef]
- Winograd, T. Procedures as a Representation for Data in a Computer Program for Understanding Natural Language; MIT AI Technical: Cambridge, MA, USA, 1971. [Google Scholar]
- Chinchor, N.; Hirschman, L.; Lewis, D.D. Evaluating message understanding systems: An analysis of the Message Understanding Conference (MUC) results. In Proceedings of the Workshop on Human Language Technology, Stroudsburg, PA, USA, 21–24 March 1993; pp. 22–29. [Google Scholar]
- Eddy, S.R. Hidden Markov models. Curr. Opin. Struct. Biol. 1996, 6, 361–365. [Google Scholar] [CrossRef]
- Nadeau, D.; Sekine, S. A survey of named entity recognition and classification. Lingvisticae Investig. 2007, 30, 3–26. [Google Scholar] [CrossRef]
- Mandic, D.P.; Chambers, J. Recurrent Neural Networks for Prediction: Learning Algorithms, Architectures, and Stability; John Wiley & Sons, Inc: Hoboken, NJ, USA, 2001. [Google Scholar]
- Egan, S.; Fedorko, W.; Lister, A.; Pearkes, J.; Gay, C. Long short-term memory (LSTM) networks with jet constituents for boosted top tagging at the LHC. arXiv 2017, arXiv:1711.09059. [Google Scholar] [CrossRef]
- Rogers, A.; Gardner, M.; Augenstein, I. QA dataset explosion: A taxonomy of NLP resources for question answering and reading comprehension. ACM Comput. Surv. 2023, 55, 1–45. [Google Scholar] [CrossRef]
- Derczynski, L.; Bontcheva, K.; Roberts, I. Broad Twitter corpus: A diverse named entity recognition resource. In Proceedings of the COLING 2016, The 26th International Conference on Computational Linguistics, Osaka, Japan, 11–16 December 2016; pp. 1169–1179. [Google Scholar]
- Jaswani, N. NER Dataset. Kaggle. 2021. Available online: https://www.kaggle.com/datasets/namanj27/ner-dataset (accessed on 29 June 2025).
- Tjong Kim Sang, E.F.; De Meulder, F. Introduction to the CoNLL-2003 shared task: Language-independent named entity recognition. In Proceedings of the Seventh Conference on Natural Language Learning at HLT-NAACL 2003, Stroudsburg, PA, USA, 31 May 2003; pp. 142–147. Available online: https://aclanthology.org/W03-0419 (accessed on 29 June 2025).
- Weisstein, E.W. “Norm”. MathWorld. 2020. Available online: http://mathworld.wolfram.com/Norm.html (accessed on 29 June 2025).
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2001; p. 18. [Google Scholar]
- Dhinakaran, A. Understanding KL Divergence. Towards Data Science. 2020. Available online: https://towardsdatascience.com/understanding-kl-divergence-f3ddc8dff254 (accessed on 29 June 2025).
- Csiszár, I. I-divergence geometry of probability distributions and minimization problems. Ann. Probab. 1975, 3, 146–158. [Google Scholar] [CrossRef]
- Ke, W. Least information modeling for information retrieval. arXiv 2012, arXiv:1205.0312. Available online: https://arxiv.org/pdf/1205.0312 (accessed on 30 June 2025). [CrossRef]
- Ke, W. Beyond Cross-Entropy: DLITE Loss and the Impact of Loss Functions on AI-Driven Named Entity Recognition. [Computer Software]. GitHub. 2024. Available online: https://github.com/keweimao/DeepDelight/tree/main/Thread4/Beyond%20Cross-Entropy%3A%20DLITE%20Loss%20and%20the%20Impact%20of%20Loss%20Functions%20on%20AI-Driven%20Named%20Entity%20Recognition (accessed on 29 June 2025).
- OpenAI. GPT-4 Technical Report (Tech. Rep.). arXiv 2023, arXiv:2303.08774. [Google Scholar] [CrossRef]
- OpenAI. ChatGPT [Large Language Model]. 2023. Available online: https://chat.openai.com/ (accessed on 29 June 2025).
- Wu, Y.; Schuster, M.; Chen, Z.; Le, Q.V.; Norouzi, M.; Macherey, W.; Krikun, M.; Cao, Y.; Gao, Q.; Macherey, K.; et al. Google’s Neural Machine Translation System: Bridging the Gap between Human and Machine Translation. arXiv 2016, arXiv:1609.08144. Available online: https://arxiv.org/abs/1609.08144 (accessed on 29 June 2025).
- Krallinger, M.; Leitner, F.; Rabal, O.; Vazquez, M.; Salgado, D.; Lu, Z.; Leaman, R.; Lu, Y.; Ji, D.; Lowe, D.M.; et al. The CHEMDNER corpus of chemicals and drugs and its annotation principles. J. Cheminform. 2015, 7, S2. [Google Scholar] [CrossRef]
- Sheikhalishahi, S.; Miotto, R.; Dudley, J.T.; Lavelli, A.; Rinaldi, F.; Osmani, V. Natural language processing of clinical notes on chronic diseases: Systematic review. JMIR Med. Inform. 2019, 7, e12239. [Google Scholar] [CrossRef]
- Ghosh, A.; Kumar, H.; Sastry, P.S. Robust loss functions under label noise for deep neural networks. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Volume 31. [Google Scholar]
- Kim, J.-D.; Ohta, T.; Tateisi, Y.; Tsujii, J. GENIA corpus—A semantically annotated corpus for bio-textmining. Bioinformatics 2003, 19 (Suppl. S1), i180–i182. [Google Scholar] [CrossRef]
- Hendrycks, D.; Burns, C.; Basart, S.; Zou, A.; Mazeika, M.; Song, D.; Steinhardt, J. CUAD: An expert-annotated NLP dataset for legal contract review. arXiv 2021, arXiv:2103.06268. Available online: https://arxiv.org/abs/2103.06268 (accessed on 29 June 2025). [CrossRef]
- Chalkidis, I.; Fergadiotis, M.; Malakasiotis, P.; Aletras, N.; Androutsopoulos, I. LexGLUE: A benchmark dataset for legal language understanding in English. In Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics (ACL), Dublin, Ireland, 22–27 May 2022; pp. 4310–4330. [Google Scholar] [CrossRef]
- Wiegreffe, S.; Pinter, Y. Attention is not not explanation. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing (EMNLP), Hong Kong, China, 3–7 November 2019; pp. 11–20. [Google Scholar] [CrossRef]
- Maldonado, S.; Vairetti, C.; Jara, K.; Carrasco, M.; López, J. OWAdapt: An adaptive loss function for deep learning using OWA operators. Knowl.-Based Syst. 2023, 280, 111022. [Google Scholar] [CrossRef]
- Janocha, K.; Czarnecki, W.M. On loss functions for deep neural networks in classification. arXiv 2017, arXiv:1702.05659. Available online: https://arxiv.org/abs/1702.05659 (accessed on 29 June 2025). [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).