A Novel Approach to the Collatz Conjecture with Petri Nets

Abstract

The Collatz conjecture is a famous unsolved problem in mathematics, known for its deceptively simple rules that generate complex, unpredictable behaviour. It can be efficiently modelled using a Petri net that represents its inverse graph, where each place corresponds to an integer and each transition encodes an inverse rule. The net, constructed up to a bound n, reveals the tree-like structure of predecessors and highlights properties such as recurrence, reachability, and liveness. Token flows simulate possible trajectories towards 1. This formal approach enables the investigation of the problem through discrete event systems theory and opens perspectives for parametric or inductive extensions beyond the bounded domain. The model proposed provides a structured framework for visualising and analysing the inverse dynamics of the conjecture. Some key numerical results highlight the challenges of working within a finite domain: for $n_{max}=1000$, the constructed Petri net comprises 1000 places and 667 transitions, including 417 source nodes (no predecessors), 333 sink nodes (no successors), and 218 isolated orphans, i.e., nodes only reachable via $\mathrm{Div}2$ transitions with no incoming $3n+1$ edge.

1. Introduction

The Collatz conjecture [1] is a well-known mathematical problem, also referred to as the “Syracuse conjecture” [2] or the “3x + 1 problem” [3]. It defines a deceptively simple arithmetic process whose dynamics remain surprisingly complex and unpredictable. It can be described briefly as follows: (1) take a positive integer; (2) if it is even, divide it by 2; if it is odd, multiply it by 3 and add 1; (3) repeat step 2. What makes the conjecture particularly intriguing is the fact that, despite its deterministic nature, it exhibits behaviour resembling pseudo-randomness. Additionally, it is assumed that for any integer, it will eventually reach the value 1. Although extensively verified numerically, a general proof remains elusive and continues to attract considerable research attention [4,5,6,7]. Beyond its mathematical interest, the Collatz process has found practical applications in several domains, including cryptography [8] (increasingly important even in the case of Smart Grid security [9]), image encryption [10] (for cryptography algorithms with low memory consumption [11]), the generation of pseudo-random numbers [12], and medicine, supporting schizophrenia detection [13].

Unlike standard numerical approaches, a Petri net framework enables explicit tracking of state transitions, concurrency, and structure [14], making it well suited for exploring the recursive and branching nature of the Collatz dynamics. Petri nets [15] offer a graphical and mathematically precise way to model, analyse, and verify event-driven systems. They have so far proved to be useful in many application areas, including business process management [16], cyber–physical systems [17], freight logistics and transportation systems [18], space systems [19], healthcare systems [20], manufacturing systems [21], power systems [22], and reliability and safety engineering in general  [23]. Their graphical representation includes only four elements (places, transitions, arcs, and tokens), while allowing for the specification of complex behaviour.

In this paper, a Petri net-based model of the Collatz dynamics is proposed. Transitions naturally encode the recursive rules of the sequence, while places correspond to integer values. This model not only captures the operational semantics of the process but also potentially enables additional features, like parallel simulation of multiple Collatz trajectories. Moreover, Petri net theory provides analytical techniques such as invariants, boundedness, reachability, and liveness, which can be leveraged to study the global behaviour of the system. The net then becomes a platform not only for visualising trajectories but also for generalising or altering the dynamics in a controlled, formalised setting. Importantly, instead of modelling the Collatz conjecture in a standard forward direction, starting from the chosen integer, an inverse approach that explores all possible predecessors of 1 is proposed. This perspective allows the construction of a branching structure of potential paths converging to 1, revealing the underlying structure of the conjecture in a novel, formalised and accessible way.

It should be emphasised that the present work adopts an inverse modelling perspective: rather than iterating the Collatz function forward from a chosen integer to follow its trajectory, the Petri net is constructed starting from the root $P_1$ and expanding all possible predecessors under the inverse rules.

This approach contrasts with “forward” modelling, where the state space is generated by successive forward iterations $n\mapsto n/2$ or $n\mapsto 3n+1$. While the forward viewpoint produces a single deterministic path for each initial value, the inverse construction yields a branching structure that simultaneously encodes all possible trajectories converging to $P_1$. Existing studies have modelled the Collatz process using directed graphs [24,25] or automata [26,27], including both forward and inverse variants. In particular, inverse Collatz trees have been analysed for their binary representation patterns and algebraic properties. However, to the best of our knowledge, Petri nets have not previously been used to model the Collatz conjecture in either direction.

The present work is therefore original in (i) introducing Petri net semantics to the known Collatz problem, (ii) focusing on the inverse formulation, and (iii) leveraging Petri net analysis techniques (reachability, liveness, and invariants) to investigate its structural properties.

As far as we are aware, this is the first approach that applies Petri nets to model the Collatz conjecture, especially from the inverse perspective. The novel contribution of the paper can be summarised as follows:

• A formal Petri net construction is proposed that encodes inverse Collatz dynamics;
• A graphical visualisation of the branching structure converging to 1 is shown;
• An exploratory framework for analysing reachability and structural properties (boundedness and liveness) in the Collatz process is proposed.

The rest of the article is organised as follows. Section 2 presents some related work on and the basic theory of Petri nets. Section 3 presents the modelling idea. Section 4 introduces a novel inverse approach to Collatz conjecture with Petri nets. Section 5 discusses and analyses the results. Finally, Section 6 concludes the paper and outlines directions for future work.

2. Theory Background

2.1. Related Work

Let us first present the related work regarding the Collatz conjecture and its visualisations.

Definition 1

(Collatz Conjecture). Let $T:\mathbb{N}\to \mathbb{N}$ be the function defined by

$$T\left(n\right)=\left\{\begin{array}{cc}{\displaystyle \frac{n}{2}},\hfill & \mathrm{if}n\mathrm{is}\mathrm{even},\hfill \\ 3n+1,\hfill & \mathrm{if}n\mathrm{is}\mathrm{odd}.\hfill \end{array}\right.$$

The Collatz conjecture [28] states that for every $n\in \mathbb{N}$, there exists $k\in \mathbb{N}$ such that

$$T^{\left(k\right)}\left(n\right)=1,$$

where $T^{\left(k\right)}$ denotes the k-fold composition of T.

To better understand the structure of the Collatz conjecture, several researchers have proposed and analysed diverse forms of its visualisation. A common graphical form is a directed graph or a tree showing changing values [29]. Nodes represent integers, and directed edges correspond to transitions dictated by the Collatz rules. In the standard Collatz graph, each node is connected to the next value in the sequence, thus producing a deterministic path from any starting value. In contrast, the inverse Collatz tree begins at the root node 1 and explores all possible predecessor values that could lead to it using inverse operations. This approach highlights the branching structure and reveals how values converge towards 1. Such visualisations help researchers observe patterns, identify potential cycles or regularities, and examine the density or sparsity of trajectories. For example, Stérin [24] developed an inverse Collatz graph rooted at 1 and analysed structural properties through binary representations. Diedrich’s preprint [30] proposes an algebraic notion of inverse trees aimed at characterising the structure of predecessors of 1. Olgac [25] defined a deterministic inverse–Collatz tree on odd integers via two modular edge-generating functions, demonstrating surjectivity and establishing a complete ancestral structure rooted at 1. This work lends algorithmic credibility to inverse-domain modelling, analogous to but distinct from the Petri net framework. More generally, the incremental construction of directed acyclic graphs has been formalised by Olgac in a separate work on graph topology and structure [31]. His approach provides foundational insights into how branching structures evolve while preserving global connectivity—a perspective relevant to the recursive expansion of inverse Collatz trees.

Emmert-Streib [32] investigated the state-space network formed by Collatz iterations, while exploring connectivity, node types, and complexity measures in a graph-theoretic context. Andaloro [33] used directed graph models and their implications, introducing the notion of a weakly connected graph. Laarhoven and de Weger [34] connected Collatz iteration dynamics to binary De Bruijn graph theory, introducing novel structured representations of the orbits. Andrei et al. [3] formulated a notion of “chain subtrees” in the Collatz tree, providing new theoretical insights.

The graph-based approaches are complemented by automata, as proposed by Ren and Xiao in [26], or cellular automata, as shown by Kari in [27]. Automata turned out to be suitable for modelling individual Collatz trajectories, especially considering state-based insights.

A recent contribution by Owada [35] proposed a structural interpretation of the Collatz conjecture using tree representations. While his approach is not based on Petri nets, it shares the objective of unveiling the underlying dynamics and branching behaviours of the inverse Collatz process.

Kosobutskyy and Rebot [36] examined the inverse Collatz dynamics through the lens of Newtonian binomial forms, highlighting the emergence of distinct inverse cycles and lower-bound oscillations. Their formulation—marked by explicit algebraic constraints—reinforces the relevance of inverse-domain analysis, while differing from our Petri net implementation in its algebraic rather than structural modelling approach.

In contrast, Petri nets provide a more expressive framework for modelling and allow the exploration of the system as a whole and the simulation of multiple paths simultaneously, with strong support for formal verification. Petri nets enable a higher-level abstraction that facilitates not only visualisation but also formal verification of complex dynamics. For these reasons, the Petri net formalism is particularly well suited for investigating the inverse and structural properties of the Collatz graph.

2.2. Petri Nets

Several preliminary concepts from the Petri net theory are introduced to enhance clarity and readability (the definitions are mainly based on [37,38]).

Definition 2

(Petri net). A Petri net can be defined as a four-tuple $PN=(P,T,F,M_0)$, where P is a finite set of places (drawn as circles), T is a finite set of transitions (visually, bars), $F\subseteq (P\times T)\cup (T\times P)$ is a finite set of arcs (arrows), and $M_0$ is an initial marking (a token is represented by a dot).

In a Petri net, places may be connected via arcs only with transitions and vice versa. However, it is possible to model various behaviours, like choice or concurrency, by using the appropriate net structure [39].

A markinginvolves all places that contain a token. A transition is said to be enabled if each of its input places contain a token. A transition can be fired if it is enabled. Then, a token is removed from all its input places and added to all its output places. A marking is reachable from any other marking if it can be reached by a sequence of transition firings.

Definition 3

(Liveness). A Petri net is $live$ if, from any reachable marking, it is always possible to fire any transition, whether directly or indirectly, by a sequence of firings of other transitions.

Definition 4

(Safeness). A Petri net is $safe$ if there is no reachable marking such that any place contains more than one token.

It is possible to add some guards to the net structure in order to model choice. They are then assigned to transitions. Furthermore, if referring to the Mealy automaton, some actions can also be assigned to transitions and are then executed when a transition is fired. A sample Petri net with choice is shown in Figure 1. The guards are written in green font, while the actions are written in red font. The structure is based on three places and four transitions. The initial marking involves place $p1$. In the case of detected sun (guard sun = 1), transition $t1$ is fired, the lamp is turned off (action lamp := 0), and place $p2$ becomes active. After some specified timeout, transition $t3$ is fired, and the initial marking is reached again. If there is not enough sun (guard sun = 0), transition $t2$ is fired, the lamp is turned on (action lamp := 1), and place $p3$ becomes active. After the timeout, transition $t4$ is fired, returning to the initial marking. The net is live and safe.

2.3. Suitability of Petri Nets for Modelling the Collatz Conjecture

While Petri nets are widely applied in system analysis, their adequacy for number-theoretic problems such as the Collatz conjecture deserves clarification. The following points highlight structural and conceptual reasons why Petri nets provide a natural framework for this modelling task.

• Natural encoding of rules: Petri nets map integer states to places and iteration rules to transitions, preserving the logical structure of the Collatz process.
• Petri nets offer both graphical insights (branching structure and depth) and algebraic tools (with formal verification methods) that can be exploited for structural reasoning.
• Reachability-based reformulation—the conjecture becomes a reachability property: place $P1$ is reachable from any $Pn$, enabling the use of established Petri net reachability theory.
• Reformulation of the conjecture: T-invariant study.
• Parametric generalisation (an + b) allowing comparative structural analysis.
• Extending the study by reformulating the Collatz problem in Petri net terms creates a bridge between number theory, system modelling, and computer science, thereby broadening its interdisciplinary relevance.
• Petri nets are, by construction, bipartite directed graphs where places and transitions alternate. This structure aligns closely with directed graph representations of the Collatz problem, such as those explored by Olgac [31], while adding formal semantics for token flow, concurrency, and state change. This dual nature allows the Petri net to inherit the visual clarity of graph-based models while enabling algebraic analysis through incidence matrices and invariants.

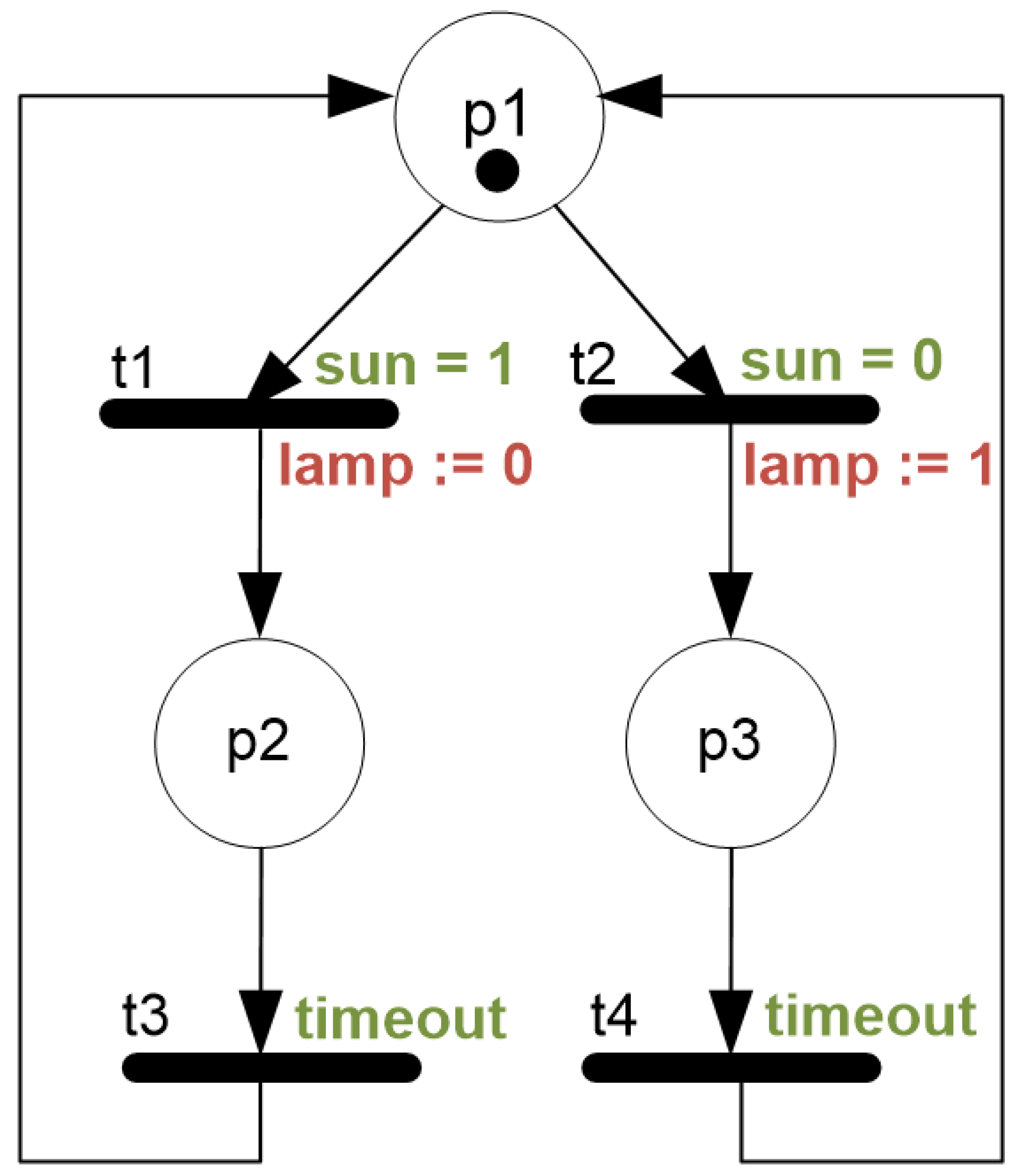
3. Inverse Collatz Modelling in the Petri Net Framework

3.1. Modelling Principle

The main modelling principle can be sketched as follows. Starting from the integer 1, the inverse Collatz structure is constructed by recursively applying the inverse rules of the standard process. For each integer n, all valid predecessors, i.e., integers m such that either $n=m/2$ or $n=(3m+1)/2^k$ for some $k\in \mathbb{N}$, are computed and linked to n through directed edges. This inverted representation yields a branching graph rooted at 1, capturing all possible paths that could lead to it under the Collatz dynamics. A schematic view of this construction is shown in Figure 2.

Within the Petri net formalism, such a structure is naturally interpreted, with transitions representing backwards computational steps and places corresponding to integer states. This approach enables the representation of multiple trajectories in parallel, as well as explicit modelling of branching and convergence. However, when restricted to a finite domain $[1,n]$, the construction exhibits structural limitations: several valid predecessors fall outside the considered interval, resulting in an incomplete or disconnected graph. These limitations are further discussed in Section 5.

To formalise the generation process, the method for building the Petri net is summarised in the pseudo-code Algorithm 1. The procedure is independent of the development tool and directly follows the two inverse rules described above: the even branch ($2n\to n$) and the odd branch (${\displaystyle \frac{n-1}{3}}\to n$ when valid). It ensures that each integer within the bounded domain is represented by a unique place and that each valid inverse step is represented by a dedicated transition. This formalisation provides a clear mapping from the mathematical definition of the inverse Collatz graph to a Petri net structure, facilitating subsequent analysis of reachability, liveness, and invariants.

Algorithm 1 Build Inverse Collatz Petri Net

($n_{max}$) 1: $P\leftarrow \varnothing$, $T\leftarrow \varnothing$, $F\leftarrow \varnothing$ 2: Create places $P_n$ for $n=1\dots n_{max}$ 3: $M_0\leftarrow \left\{(P_{n_{max}},1)\right\}$ {Initial marking after place creation} 4: for $n=1$ to $n_{max}$ do 5:    if $2n\le n_{max}$ then 6:      Create transition $t_n^{\left(2\right)}$: $P_{2n}\to P_n$ 7:      Add arcs $(P_{2n},t_n^{\left(2\right)})$ and $(t_n^{\left(2\right)},P_n)$ 8:    end if 9:    if $(n-1)mod3=0$ then 10:      $p\leftarrow (n-1)/3$ 11:      if $1\le p\le n_{max}$ and p odd then 12:         Create transition $t_n^{\left(3\right)}$: $P_p\to P_n$ 13:         Add arcs $(P_p,t_n^{\left(3\right)})$ and $(t_n^{\left(3\right)},P_n)$ 14:      end if 15:    end if 16: end for 17: return  $\mathcal{N}=(P,T,F,M_0)$

Algorithm 1 starts by initialising empty sets for places P, transitions T, and arcs F (line 1). The procedure then creates one place $P_n$ for each integer n in the bounded domain (line 2) and sets the initial marking $M_0$ (line 3), here with one token at $P_{n_{max}}$ as an example (line 3). The main loop (lines 4–16) iterates over all n to identify valid inverse predecessors. For the even branch, $2n$ is connected to n through a transition $t_n^{\left(2\right)}$ if $2n$ lies within the domain (lines 5–7). For the odd branch, $(n-1)/3$ is connected to n through $t_n^{\left(3\right)}$ only when $(n-1)$ is divisible by 3, the predecessor p is odd, and p is within the domain (lines 9–13). Each valid branch results in the creation of a transition and the corresponding arcs, ensuring a faithful Petri net representation of the inverse Collatz graph. Finally, line 17 returns the Petri net $\mathcal{N}$.

3.2. Computational Complexity and Feasibility

The construction algorithm runs in linear time and space with respect to the upper bound $n_{max}$. It generates exactly $n_{max}$ places and approximately $\frac{2}{3}{n}_{max}$ transitions. The space usage is dominated by the storage of places and transitions.

The initial algorithm in Python (version 3.11.4) has been slightly modified, adding performance assessment: time.perf_counter for timing and tracemalloc for peak memory usage.

Table 1. Benchmark results of the inverse Collatz construction in Python.

${\mathit{n}}_{max}$	Places	Transitions	Time [s]	Peak mem [KB]
1000	1000	667	0.0025	111.2
$10,000$	$10,000$	6667	0.0280	1446.4
$100,000$	$100,000$	$66,667$	0.2978	13,875.5
$500,000$	$500,000$	$333,333$	1.5357	65,972.4

reports the results for increasing bounds $n_{max}$. For example, the case $n_{max}=500,000$ was built in $1.54$ s with a peak memory of 65 MB, confirming the linear growth and showing that large-scale experiments (up to millions of nodes) remain feasible on standard hardware.

Exporting the entire structure in DOT format is practical only for moderate $n_{max}$, as file size and rendering overhead quickly become prohibitive.

4. The Proposed Inverse Approach with Petri Nets

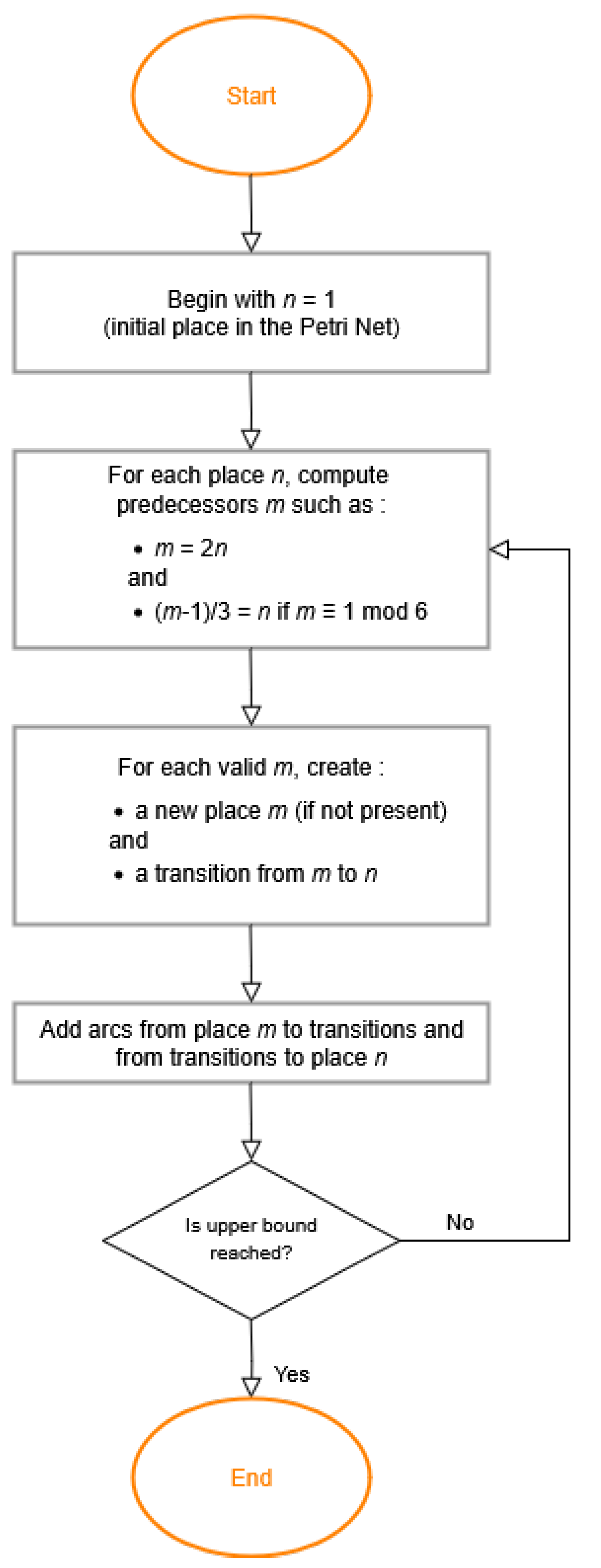
4.1. Construction of the Inverse Collatz Petri Net

The inverse Collatz Petri net can be constructed algorithmically using a recursive rule set applied to each integer in a bounded domain. It is based on a simple rule set applied iteratively for each integer $i\in [1,n]$:

• For each integer i, create a place $P_i$ (unless it already exists).
• If i is even:

  -

  Create the place $P_{i/2}$ if it does not exist.

  -

  Add a transition labeled Div2 from $P_{i/2}$ to $P_i$.

• If $(i-1)mod3=0$ and $(i-1)/3$ is an odd integer:

  -

  Create the place $P_{(i-1)/3}$ if it does not exist.

  -

  Add a transition labeled 3n + 1 from $P_{(i-1)/3}$ to $P_i$.

The implementation of this algorithm in Python is based on the Snakes Petri net library combined with Graphviz for visualisation.

This process results in a Petri net graph rooted at $P_1$, where each node corresponds to an integer.

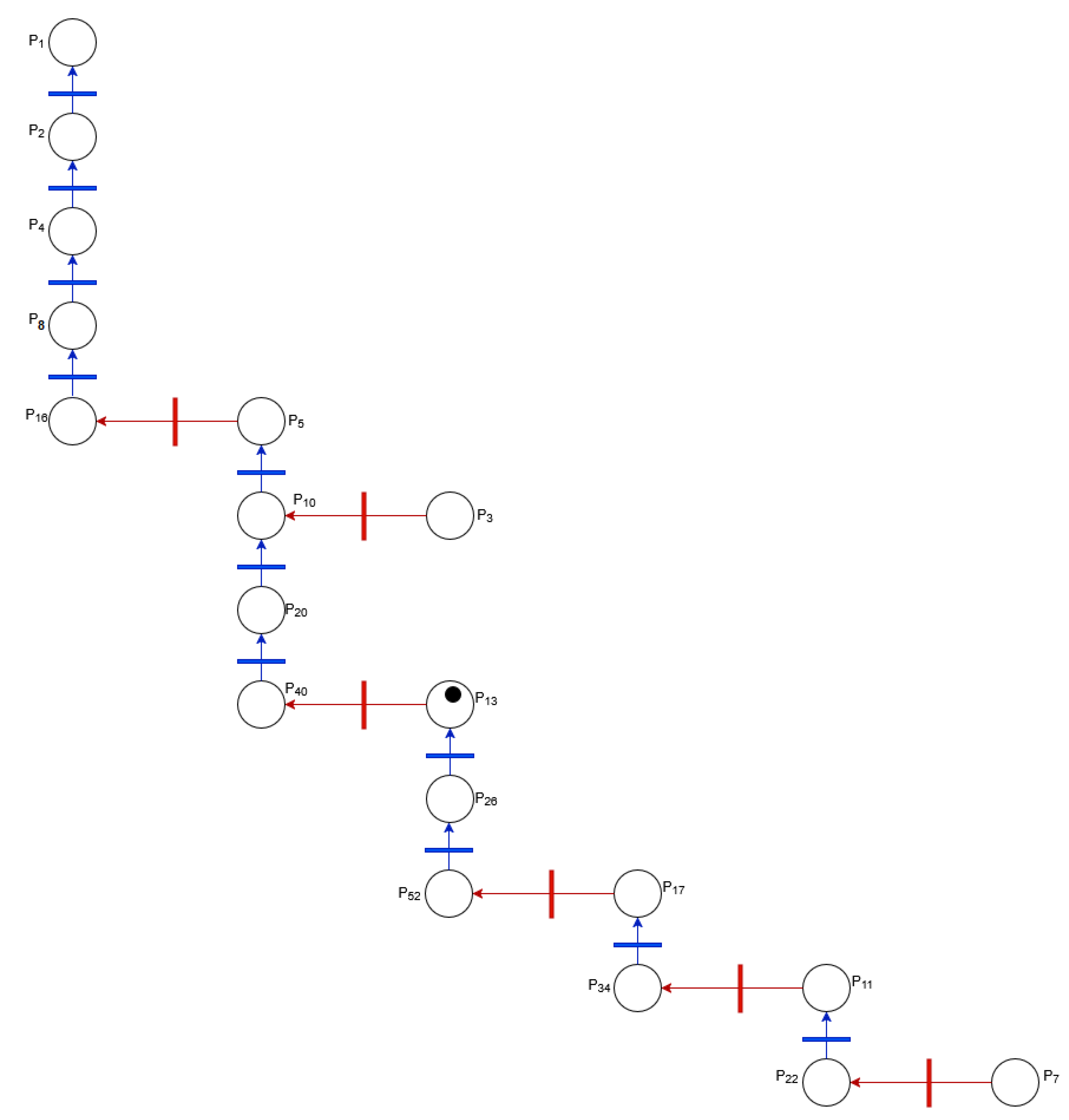
4.2. Visualisation of the Inverse Collatz Petri Net (Up to $n=127$)

The inverse Collatz graph up to $n=127$ is presented in Figure 3. Each node $P_n$ corresponds to an integer n, and edges represent valid inverse transitions under the Collatz function. Two types of transitions are distinguished: Div2 in blue ($n\to 2n$) and 3n + 1 in red ($n\to (n-1)/3$ when applicable and when the result is odd).

A set of nodes (framed at the bottom left) forms the group of isolated orphans, i.e., nodes that are only accessible via Div2 transitions and have no incoming 3n + 1 edge. This subset illustrates a key asymmetry in the inverse Collatz structure: many odd integers do not allow a valid $(n-1)/3$ backwards transition and remain structurally “linear”.

4.3. Reordering the Graph by Transition Types

The inverse Collatz Petri net presented earlier can be reorganised according to the number and type of transitions leading to each node. In particular, this layout emphasises the distinction between nodes reached through binary divisions (Div2, in blue) and those additionally reached through inverse 3n + 1 transitions (in red). An example of such a reordering can be seen in Figure 4 (with the current marking in place $P13$). The obtained Petri net is safe (only one token in any place at any time), and thus it is also bounded. It is live, as it is always possible to fire any transition (either directly or via a firing sequence). Moreover, the net is conservative—tokens are neither created nor destroyed—they only move between places, inevitably leading to place $P1$.

The visual separation induced by the reordering suggests a natural stratification of the integers based on their inverse Collatz reachability properties. Such a layout may facilitate further investigations into path depth, entry multiplicity, or recurrence properties, especially when extended to larger domains.

4.4. Limitations of the Petri Net-Based Inverse Construction

When restricted to a finite interval, the inverse Collatz graph suffers from an inherent incompleteness. Although all successors of integers up to a given bound (e.g., $n\le 1000$) can be listed, their valid predecessors often lie beyond this bound and are therefore excluded from the model. As a consequence, many places in the Petri net appear isolated or without incoming transitions, not due to the structure of the Collatz process itself but as an artefact of the truncation. This limitation affects the coherence of the net and hinders the reliable analysis of reachability or global behaviour within the inverse framework.

Furthermore, demonstrating the conjecture is impossible on a finite domain. Although the inverse Collatz Petri net has been elaborated to be acyclic within the considered bounded domain, a formal proof of acyclicity for the unbounded case is not provided here. Likewise, convergence towards $P_1$ is only supported by empirical inspection of the generated graphs and remains unproven in general. Rigorous arguments, for example through induction over the net’s recursive construction rules or structural invariants in an infinite-state setting, are recommended for future work.

4.5. Description of Used Tools

The modelling and visualisation work was conducted in a local Python 3.x environment using a custom Petri net construction strategy. The network was built programmatically with the Snakes library (v0.9.33), a formal and extensible framework for Petri net modelling in Python [40]. Due to plugin limitations in precompiled versions, the model was exported in DOT format and visualised using Graphviz (dot CLI tool) to produce high-quality PNG and SVG renderings. This fully open-source toolchain ensured complete control over the network generation and guaranteed platform independence and reproducibility of the results.

5. Discussion

5.1. Reformulating the Collatz Conjecture in Petri Nets Terms

The classical Collatz conjecture asserts that every positive integer will eventually reach the value 1 under the repeated application of the function:

$$n\mapsto \left\{\begin{array}{cc}{\displaystyle \frac{n}{2}}\hfill & \mathrm{if}n\equiv 0mod2\hfill \\ 3n+1\hfill & \mathrm{if}n\equiv 1mod2\hfill \end{array}\right.$$

In the Petri net framework, the inverse process is considered: for each number n, the possible predecessors are identified under the Collatz mapping and encoded as transitions leading to $p_n$. The resulting inverse graph is modelled as a Petri net, where tokens represent possible computational paths.

Under this interpretation, the conjecture can be reformulated as a dynamic property of the net:

For any place $P_n$, the place $P_1$ is reachable via a finite sequence of transition firings.

In other words, starting from any initial marking with one token in $P_n$, the token will eventually reach $P_1$. This makes the conjecture equivalent to the global reachability of $P_1$, making Petri net analysis tools a possible formal framework to study its structure and behaviour.

5.2. Structural Properties: Reachability and Liveness

Beyond visualisation, the Petri net representation enables the investigation of structural properties inherent to the Collatz process.

Reachabilityis central to the conjecture: the assertion that every integer eventually reaches 1 translates naturally to the requirement that the place $P_1$ is reachable from any initial marking $P_n$. In this model, verifying that a token placed in $P_n$ can reach $P_1$ corresponds to confirming the conjecture for that value. Reachability analysis thus becomes a formal interpretation of convergence.

Liveness, in the classical Petri net sense, refers to the ability to fire any transition eventually, from any reachable marking. Since the inverse Collatz net is acyclic and bounded to a finite domain, global liveness does not apply: each token inevitably reaches a terminal node or the domain boundary. However, local liveness can still be evaluated, especially to detect structurally inactive transitions caused by truncation or unreachable predecessors. Such analysis may help identify dead zones in the graph and suggest refinements in the generation strategy or bounding heuristics.

5.3. Interpretation of Apparent Ascending Paths

The inverse construction used in the Petri net model involves transitions from predecessors m to successors n, where $f\left(m\right)=n$. As a result, the direction of arcs in the graph goes from larger integers to smaller ones. This can lead to the impression of upward movement when interpreting the graph numerically.

Figure 4 illustrates this apparent paradox: the node $P_{16}$, part of the binary “spine”, receives a 3n + 1 transition from $P_5$, and $P_5$ itself is reached via a Div2 from $P_{10}$. While the numerical values increase (10 → 5 → 16), the token progresses downward through the graph structure towards $P_1$. This confirms that despite the numerical rise, the graph remains acyclic and structurally oriented towards the root. The propagation of tokens consistently follows a descending logical path, which is crucial for ensuring the absence of cycles and deadlocks in the Petri net representation.

5.4. A Structural Reordering of the Integers

It can be observed in Figure 4 that the inverse Collatz Petri net implicitly defines a reordering of the integers. Instead of being arranged by their numerical value, places are connected based on their functional ancestry under the inverse Collatz rules. This leads to a topology in which higher-valued integers may appear “before” smaller ones when considered from the perspective of token propagation towards $P_1$.

Such a structure reorders the integers by their topological distance to the root, measured not in arithmetic terms but in the number of transition firings required to reach $P_1$. As a result, the Petri net encodes a form of structural hierarchy reflecting the computational flow of the conjecture, rather than a simple numerical sequence.

5.5. Structure Induced by Inverse Collatz Dynamics

The inverse construction of the Collatz graph, when modelled as a Petri net, gives rise to a non-trivial structural organisation of the integers. Unlike the natural ordering $1<2<3<4<\dots$, the net creates a hierarchy defined by the directed arcs between places, which correspond to valid inverse transitions.

This results in a functional reordering of the integers, where the relative “priority” of a number is determined by its position within the inverse dependency tree. Tokens propagating through the net follow these arcs, ultimately converging towards $P_1$. The number of transitions required to reach $P_1$ from a given place $P_n$ can be interpreted as a structural depth or distance to the root, reflecting the complexity of the inverse trajectory rather than the magnitude of n.

5.6. Analysis of T-Invariants and P-Invariants

In Petri net theory, a P-invariant (place invariant) is an integer-valued vector over the set of places that satisfies $y^T·C=0$, where C is the incidence matrix of the net. Such a vector identifies a linear combination of places whose total number of tokens is preserved for all possible transition firings. Place invariants are often used for Petri net decomposition, aimed at splitting the control algorithm into sequential subsystems, where each of the decomposed modules can be implemented separately [41]. A T-invariant (transition invariant) is an integer-valued vector over the set of transitions that satisfies $C·x=0$. It corresponds to a multiset of transitions whose firing sequence returns the net to its original marking. T-invariants are often used to analyse crucial properties of the net, such as liveness or boundedness [42].

Let us now consider possible P-invariants for the Collatz conjecture modelled with Petri nets, which indicate linear combinations of places where the total number of tokens is preserved for all possible transitions. The achieved Petri net models are essentially chain-like structures, showing the inverse Collatz steps, with some branching (various starting points as possible initial markings), but neither token creation nor destruction. Therefore, each connected sequence of places and transitions conserves the token count.

Coming to the T-invariants, they usually mean multisets of transitions that return the net to its original marking. As the obtained Petri net models are acyclic, non-trivial T-invariants do not exist there. There is no possibility of returning to the initial marking, as firing any sequence of transitions strictly moves tokens forward with no way to go back. In the unbounded case, the absence of non-trivial T-invariants would be equivalent to the absence of non-trivial cycles in the Collatz dynamics, which in turn would constitute a proof of the conjecture.     

6. Conclusions

The Petri net modelling of the inverse Collatz process offers an interesting reformulation of the conjecture. By translating arithmetic rules into transitions and integer states into places, this framework reveals an uncommon architecture of the problem. Beyond visualisation, the net structure introduces a new topological ordering of the integers, where reachability, transition types, and structural depth replace conventional arithmetic hierarchy. This reformulation opens new perspectives for analysing the conjecture through symbolic, inductive, or recurrence-based methods. This paper shows how the Petri net formalism can be used to model the Collatz conjecture in order to benefit from the advantages of formal specification techniques.

The truncation imposed by the Petri net makes the conjecture impossible to fully demonstrate. This observation motivates further research into dynamic or symbolic approaches capable of transcending strict enumeration. Future works may include, but are not limited to the following:

• Inductive reasoning over the Petri net structure. Instead of reasoning on individual trajectories, it may be possible to attempt structural induction over the net itself. For instance, proving that if all immediate predecessors of a place $P_n$ lead to $P_1$, then $P_n$ does as well. Such a recursive propagation of reachability could, in principle, generalise the conjecture beyond finite bounds.
• Recurrence-based formalisms. The Collatz process lends itself to recursive formulations of stopping times or path lengths. In the inverse Petri net, it may be possible to model the depth $D\left(n\right)$ of a place as a function of the depths of its predecessors, enabling symbolic analysis of convergence or complexity.
• Parametrised generalisations of the transition rules. By extending the transition set beyond the standard $n\mapsto n/2$ and $n\mapsto 3n+1$, it becomes possible to study a wider class of integer mappings. A parametrised Petri net could capture variations such as $an+b$ rules, offering a comparative view and potentially tractable analogues of the original conjecture.
• Ordering the integers based on transition sequences. The topological structure of the Petri net defines a new partial ordering of the integers, no longer based on magnitude but on their functional ancestry within the graph. Future work could explore this ordering formally, for example by defining a “transition-depth” metric that weights red and blue transitions differently (e.g., assigning greater cost to 3n+1 arcs). This would provide a transition-aware hierarchy of integers, potentially revealing new stratifications of complexity or path redundancy across the net.
• Studying transition-induced depth metrics. Building on the above, one could define for each place $P_n$ a vector $(d_b,d_r)$ representing the number of blue and red transitions required to reach $P_1$. This bi-dimensional metric may help detect families of integers with similar structural positions and perhaps inform conjectural bounds on stopping times or convergence rates.

As a case study, let us consider the formulation of the Collatz conjecture in terms of T-invariants. In the Petri net representation, a non-trivial T-invariant corresponds to a sequence of transitions returning the marking to its initial configuration without reducing to the trivial 1→4→2→1→4→2→1 cycle. Detecting the absence of such invariants in the infinite net would be equivalent to proving the conjecture. While exhaustive computation is only feasible for bounded domains, structural analysis of the truncated net reveals no non-trivial invariants, suggesting a possible inductive strategy: if every local sub-net beyond a certain depth remains acyclic, the property could be propagated upwards to cover the entire infinite structure. This highlights the potential of Petri net theory not only as a visualisation tool but as a formal framework for reasoning about one of mathematics’ most famous unsolved problems.

While the full resolution of the Collatz problem remains out of reach, this approach has proved both insightful and methodologically fruitful. It demonstrates how discrete dynamic systems—such as Petri nets—can be used not merely to simulate behaviour but also to restructure and reinterpret longstanding mathematical questions.