A Hybrid Classical-Quantum Neural Network Model for DDoS Attack Detection in Software-Defined Vehicular Networks

Abstract

A typical Software-Defined Vehicular Network (SDVN) is open to various cyberattacks because of its centralized controller-based framework. A cyberattack, such as a Distributed Denial of Service (DDoS) attack, can easily overload the central SDVN controller. Thus, we require a functional DDoS attack recognition system that can differentiate malicious traffic from normal data traffic. The proposed architecture comprises hybrid Classical-Quantum Machine Learning (QML) methods for detecting DDoS threats. In this work, we have considered three different QML methods, such as Classical-Quantum Neural Networks (C-QNN), Classical-Quantum Boltzmann Machines (C-QBM), and Classical-Quantum K-Means Clustering (C-QKM). Emulations were conducted using a custom-built vehicular network with random movements and varying speeds between 0 and 100 kmph. Also, the performance of these QML methods was analyzed for two different datasets. The results obtained show that the hybrid Classical-Quantum Neural Network (C-QNN) method exhibited better performance in comparison with the other two models. The proposed hybrid C-QNN model achieved an accuracy of 99% and 90% for the UNB-CIC-DDoS dataset and Kaggle DDoS dataset, respectively. The hybrid C-QNN model combines PennyLane’s quantum circuits with traditional methods, whereas the Classical-Quantum Boltzmann Machine (C-QBM) leverages quantum probability distributions for identifying anomalies.

1. Introduction

Amid numerous key vehicular communication technologies, the success of integrating Software Defined Networking (SDN) with Vehicular Ad Hoc Networks (VANETs) to form SDVN has helped achieve improved management, reliability, and flexibility in policy implementation. SDVN has now become an integral part of large-scale vehicular networks. Despite their obvious advantages, unlike conventional VANETs, SDVNs’ integrity and security concerns remain unaddressed, especially for their centralized network intelligence. Also, the centralized placement of the main controller required for complete network management contributes to a weak spot of failure, and if the central controller is compromised, then it may lead to chaos in the network [1,2]. SDVNs are open to various cyberattacks, including sniffing, DoS, and impersonation, among others [3,4]. The main issue is that DDoS attacks have the potential to seriously impair communication between vehicles, slowing down the transmission of data, lowering available bandwidth, and limiting effective information sharing amongst vehicles [5,6].

QML is a recent scientific sub-discipline that integrates the features of quantum computing with machine learning theory [7]. To address these critical security challenges, this study explores QML, leveraging quantum computing to tackle intricate issues. A subclass of variational quantum algorithms, QNNs are made up of quantum circuits with parameterized gate operations. A feature map or state preparation procedure is considered to first encode information into a quantum state [8]. In particular, we focus on developing an intrusion detection system with C-QNNs, which are well suited for classification tasks due to their potential to handle data concurrently through quantum mechanics principles.

Our proposed system shows impressive results. The proposed hybrid technique achieved an accuracy of 99% and 90%, demonstrating its potential to accurately identify threats. This research also highlights the benefits of using platforms like PennyLane [9], which allow researchers to train quantum models on local machines or simulators. However, the current limitation of available qubits in these environments is a constraint that must be considered for large-scale deployment [10,11]. Multiple challenges were encountered in the development of the proposed model for the SDVN environment, such as:

• Running complex quantum circuits in simulation can lead to memory overloads or crashes, especially when handling huge datasets [12].
• Quantum simulations, especially with hybrid models, can be significantly slower in notebook environments, causing delays in iterative experimentation and model tuning [13].
• PennyLane’s default simulators are CPU-based [9] and not optimized for speed. Accessing real quantum devices via plugins from notebooks can introduce additional latency or connection issues.
• There is a dearth of SDVN-specific DDoS attack datasets, necessitating the adaptation of general DDoS datasets (like [14,15]) for vehicular network scenarios.

To secure the SDN-based VANET environment, it is crucial to first understand the underlying technology and develop a lightweight security solution that minimizes the execution time of cryptographic operations. This work focuses on leveraging QML for the detection of DDoS attacks in SDVN, aiming to enhance threat detection efficiency while ensuring computational feasibility. Designing efficient quantum-assisted defense mechanisms and acquiring the necessary expertise in quantum-enhanced cybersecurity are essential to addressing the security challenges of vehicular networks. The key contributions of this research are as follows:

• We developed a hybrid C-QNN architecture that combines quantum circuits from PennyLane with classical input and output layers for effective DDoS attack detection in SDVNs.
• We tested three different quantum machine learning approaches, C-QNN, C-QBM, and C-QKM, to determine DDoS attacks in vehicular networks.
• Using a hybrid C-QNN model, a 99% accuracy on the UNB-CIC-DDoS dataset and about 90% on the Kaggle DDoS dataset was achieved, outperforming other existing quantum techniques.

Integrating quantum models like QNNs with classical Layers can enhance their efficiency while minimizing computational load [16].

2. Literature Survey

Numerous researchers have published studies in the field of VANETs and SDN. However, only a few have focused on integrating these technologies, and even less research has been conducted for QML-based DDoS attack detection (Figure 1). The authors Rivas et.al. [17] proposed a novel quantum autoencoder that combines quantum computing methods with classical deep learning techniques to enhance cybersecurity. They proposed the usage of randomized quantum circuits for the analysis of time series data from DDoS attacks, which acts as an alternative to conventional convolutional neural networks. The proposed quantum autoencoder was able to learn DDoS hive plots, leading to improved anomaly detection. But the study also points out the limitations of the model concerning scalability, general dataset, and complex computations due to 16-qubit entanglement. The proposed model was trained faster, i.e., it required 15 fewer epochs than its conventional counterpart. This research was able to prove that quantum-based models can improve network security but require further study in scalability and applicability for different datasets.

The authors Kadi et.al. [18] have conducted a comparative study on quantum-classical encoding methods for Network Intrusion Detection Systems (NIDS), addressing the challenges of high-dimensional data processing in cybersecurity. Traditional Intrusion Detection Systems (IDSs) struggle with complex and ever-changing cyber threats, particularly DDoS attacks and IoT-based intrusions. To address this problem, the study evaluates four quantum-classical encoding methods—Amplitude Embedding, Angle Embedding, Instantaneous Quantum Polynomial (IQP) Encoding, and Quantum Approximate Optimization Algorithm (QAOA) Embedding—by implementing a hybrid quantum-classical model for malicious traffic detection. The results reveal that QAOA and Amplitude Embedding achieved the highest accuracy (~89%), whereas IQP Encoding showed lower performance due to encoding inefficiencies.

Said [19] in his paper focuses on vulnerabilities of Smart Micro-Grids (SMGs) to cyber-attacks, especially DDoS attacks, due to their dependency on conventional technologies. The author identified that the current machine learning-based security methods lack the computational speed and power that quantum computing promises. The author proposes a Quantum Support Vector Machine (QSVM) technique for DDoS attack identification in SMGs. This is implemented using the HHL (Harrow-Hassidim-Lloyd) algorithm. Accuracy, precision, and recall between 99.91% and 99.94%. Ninety-three percent reduction in execution time compared to classical SVM. QSVM outperformed classical SVM in both detection performance and computational efficiency. Quantum systems are prone to errors like bit and phase flipping; quantum error correction and fault tolerance (QECFT) mechanisms are essential but challenging.

In the study by Saritha et al. [20], it is highlighted that SDNs decouple the control and data planes, which renders the centralized controller particularly open to DDoS attacks. The study introduces a Quantum-Inspired Ensemble Model (QIEM) that combines a traditional group of machine learning methods with concepts drawn from quantum mechanics. The proposed framework was able to achieve an accuracy of 98% for various DDoS attack types, performing better than standalone classical models. Its layered structure promotes improved scalability and reduces both false positives and false negatives.

The study by Said et al. [21] tackles the issue of determining DDoS attacks within smart grid systems that can severely impact their real-time functionality. The authors introduce a combined approach that integrates Quantum Entropy with Reinforcement Learning to pinpoint DDoS incidents. The proposed method involves quantum entropy analysis, which evaluates irregularities in network traffic patterns, using entropy shifts as early warning signs of attacks. Their model achieved a detection accuracy of 94.4%, surpassing alternatives like Random Forest, SVM, and standard Neural Networks. However, the computational demands of merging quantum entropy with deep reinforcement learning could hinder its use in resource-limited smart grid devices. Additionally, while quantum entropy analysis is theoretically valuable, it currently depends on classical simulation due to constraints in practical quantum computing technology.

Table 1. Key differences and contributions of our research work.

Aspect	Our Contribution	Difference from Existing Literature
Target Domain	Focused on Software-Defined Vehicular Networks (SDVNs)	Other works mainly address Smart Micro-Grids (SMG), generic SDNs, or NIDS.
Model Type	Hybrid Classical-Quantum Neural Network (C-QNN), QBM, and QKM	Other studies use single models like QSVM, QAOA, or conceptually inspired methods.
Quantum Integration	Implemented real quantum circuits using PennyLane	Many existing works are quantum-inspired only or rely on classical simulations.
Learning Paradigms	Combination of supervised (C-QNN), unsupervised (QKM), and probabilistic (QBM) models	Most papers focus on only one paradigm (e.g., QSVM or Ensemble methods).
Benchmark Datasets	Tested on two real-world DDoS datasets: UNB-CIC-DDoS and Kaggle DDoS	Some existing works use limited or synthetic datasets; not all benchmark multiple datasets.
Performance	Achieves ~99% accuracy on UNB-CIC and ~90% on the Kaggle dataset	Higher or comparable performance, with broader applicability to vehicular networks.
Scalability and Realism	Addresses realistic traffic in SDVN, including multi-model performance	Other methods often lack domain-specific tuning or real deployment scenarios.

provides a summary of the key differences and contributions of our paper compared to the existing literature:

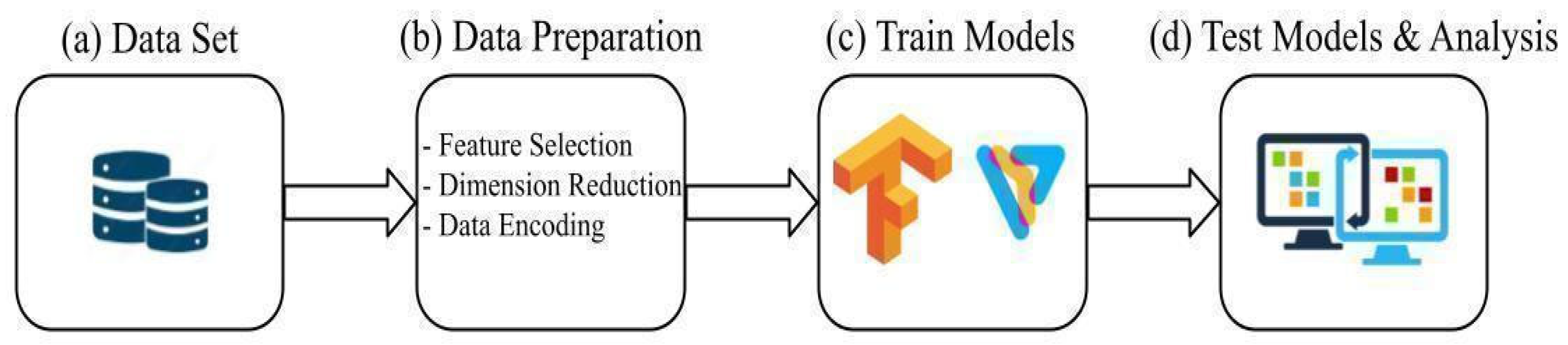
3. Model Formulation, Architecture, and Deployment

The preprocessing phase of any machine learning pipeline plays an important role in ensuring that the data are clean, consistent, and ready for use in model training. In this case, the dataset X ∈ R^n×d represents n samples with d numerical features extracted from traffic flows. Each corresponding label in Y ∈ {0,1}ⁿ denotes whether a given sample is benign (0) or a DDoS attack (1). Before feeding the data into the hybrid quantum-classical model, standardizing the features is crucial, such that each feature has an equal contribution in the analysis. Standardization transforms each feature x_j such that it has a mean of 0 and a standard deviation of 1. This is achieved using the transformation in Equation (1):

$${\mathrm{x}}_{\mathrm{j}}^{\prime }={\displaystyle \frac{{\mathrm{x}}_{\mathrm{j}}-{\mathrm{\mu }}_{\mathrm{j}}}{{\mathsf{\sigma }}_{\mathrm{j}}}}$$

(1)

where μ_j is the mean and σ_j is the standard deviation of feature j.

After standardization, the dataset may still contain redundant or less informative features. To address this and lower the input dimensionality, Principal Component Analysis (PCA) [22,23] is applied. PCA transforms the standardized data X into a fresh feature space X′ ∈ R^n×4 where the top four primary components are retained, because the four components captured the highest variance in the data while minimizing information loss, and the quantum circuit architecture used in our model supports four qubits, which aligns well with the reduced dimensionality. This balance ensures effective learning with computational efficiency under current quantum hardware constraints. This approach ensures that the data fed into the hybrid model is both normalized and reduced in complexity, which can increase the effectiveness of learning and classification accuracy [24,25].

PCA [22,23] is a broadly used technique for dimensionality reduction, which aims to project high-dimensional data into a lower-dimensional subspace while retaining the highest amount of variance in the dataset. In the instance of quantum machine learning, reducing the quantity of input features is especially important because of the current hardware limitations of quantum computers, such as limited qubit counts and gate fidelity. The input dataset X ∈ R^n×d is transformed into a lower-dimensional representation X′ ∈ R^n×4 via matrix multiplication with the PCA weight matrix W ∈ R^d×4 as shown in Equation (2) [24,26]:

$${\mathrm{X}}^{\prime } = \mathrm{X}·\mathrm{W}$$

(2)

where W ∈ R^d×4 is the matrix of the top four eigenvectors of the covariance matrix $\mathsf{\Sigma }={\displaystyle \frac{1}{\mathrm{n}}}{\mathrm{X}}^{\mathrm{T}}\mathrm{X}$.

The reduced classical input vector x ∈ R⁴, obtained after PCA, is passed into a variational quantum circuit (VQC) [27], also called a QNode in the PennyLane framework. The first stage involves encoding this classical data into the quantum state space using Angle Embedding. Each component of x_i of the input is utilized as a rotation angle for the quantum gate RY(x_i), which rotates the i-th qubit around the Y-axis of the Bloch sphere. This encoding process effectively prepares a quantum state that reflects the form of the input in the quantum domain. The full embedding operation can be denoted as represented in Equation (3), where each qubit receives a data-dependent rotation [9,28,29,30].

$${\mathrm{U}}_{\mathrm{e}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{d}}\left(\mathrm{x}\right)=\prod _{\mathrm{i}=0}^3\mathrm{R}\mathrm{Y}\left({\mathrm{x}}_{\mathrm{i}}\right)$$

(3)

Following the embedding step, a series of parameterized quantum gates are applied via a template known as Strongly Entangling Layers. This template includes a fixed number of layers L = 3, and each layer consists of three single-qubit rotations RZ$\left({\mathsf{\theta }}_{\mathrm{l},\mathrm{i},0}\right),\mathrm{R}\mathrm{X}\left({\mathsf{\theta }}_{\mathrm{l},\mathrm{i},1}\right)$ and RZ$\left({\mathsf{\theta }}_{\mathrm{l},\mathrm{i},2}\right)$, where: l ∈ {1, 2, …, L} denotes the layer index, i ∈ {0, 1, 2, 3} denotes the qubit index, and θ_l,i,k are the trainable parameters associated with the quantum rotation gates in each layer, are applied sequentially to each qubit i, followed by entangling gates between adjacent qubits. This combination of rotations and entanglement allows the circuit to capture complex feature interactions and correlations that are difficult for classical models to express. The trainable parameters $\theta$ are updated during training through gradient-based optimization as represented in Equation (4) [9,28,29,30]:

$$\mathrm{U}\left(\mathsf{\theta }\right)={\prod }_{\mathrm{l}=1}^{\mathrm{L}}\left({\prod }_{\mathrm{i}=0}^3\mathrm{R}\mathrm{Z}\left({\mathsf{\theta }}_{\mathrm{l},\mathrm{i},0}\right)\mathrm{R}\mathrm{X}\left({\mathsf{\theta }}_{\mathrm{l},\mathrm{i},1}\right)\mathrm{R}\mathrm{Z}\left({\mathsf{\theta }}_{\mathrm{l},\mathrm{i},2}\right)\right)·\mathsf{\epsilon }$$

(4)

where $\mathrm{“}\mathsf{\epsilon }$” represents the entangling layer applied after each set of single-qubit rotations in a layer, L = 3: number of layers and θ: trainable weights ∈ R^3×4×3.

Once the quantum state has evolved through the entangling layers, measurement is performed in the Pauli-Z basis for each qubit. The yield of the quantum circuit is a vector z ∈ R⁴, where each component ${\mathrm{z}}_{\mathrm{i}}=⦑\mathsf{\Psi }\left|{\mathrm{Z}}_{\mathrm{i}}\right|\mathsf{\Psi }⦒$ corresponds to the expectation value of the Pauli-Z operator on qubit i. These expectation merits are real numbers in the range [−1, 1] and represent the quantum-transformed features, which are then forwarded to subsequent classical layers for final classification. Although PCA reduces the original input features to four principal components, the quantum circuit does not act as a simple pass-through. Instead, it performs additional non-linear transformation of these components through a combination of rotation gates and entanglement operations. This process yields a new, enriched set of features (quantum expectation values) that better capture intricate patterns in the data. These are then passed to the classical layers for classification. Thus, the quantum-classical pipeline acts as a learnable and expressive feature transformation stage, beyond the initial PCA-based reduction. [9,28,29,30].

The quantum output vector z, from the quantum circuit, comprising expectation values measured from the Z basis of each qubit, is passed into classical neural network layers to complete the hybrid quantum-classical learning model. The first classical layer is a fully connected (Dense) layer with learnable weights W₁ and bias vector b₁. The activation function used in this hidden layer is the ReLU [31], due to its simplicity, computational efficiency, and effectiveness in avoiding vanishing gradient problems during training. ReLU is widely adopted in hybrid quantum-classical models, especially when paired with variational quantum circuits, as it tends to provide stable gradients and faster convergence. The ReLU operation is presented in Equation (5)

$$\mathrm{h}=\mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}({\mathrm{W}}_1\mathrm{z}+{\mathrm{b}}_1)$$

(5)

where h ∈ R^m serves as the intermediate representation for the next layer.

The second classical layer is the output layer, a fully connected single-node layer used for binary classification. Here, h ∈ R^m×1 is the output of the previous hidden layer, and W₂ ∈ R^1×m is a weight vector, not a full matrix. The bias term b₂ ∈ R is a scalar. The multiplication W₂h yields a scalar, and the final prediction is computed by applying a sigmoid function [32]. This final prediction $\widehat{y}$ given in Equation (6) is compared to the true label y, using a standard binary classification loss.

$$\widehat{\mathrm{y}}=\mathsf{\sigma }\left({\mathrm{W}}_2\mathrm{h}+{\mathrm{b}}_2\right), \mathsf{\sigma }\left(\mathrm{x}\right)={\displaystyle \frac{1}{1+{\mathrm{e}}^{-\mathrm{x}}}}$$

(6)

The Binary Cross-Entropy loss function [33] is used to lead the training procedure. This loss penalizes wrong projections more severely as they diverge from the true labels, making it greatly suitable for tasks involving binary classification. Given n training samples, the losses are calculated as shown in Equation (7):

$$\mathrm{L}\left(\mathrm{y},\widehat{\mathrm{y}}\right)=-{\displaystyle \frac{1}{\mathrm{n}}}{\sum }_{\mathrm{i}=1}^{\mathrm{n}}\left[{\mathrm{y}}_{\mathrm{i}}\mathrm{l}\mathrm{o}\mathrm{g}{\widehat{\mathrm{y}}}_{\mathrm{i}}+\left(1-{\mathrm{y}}_{\mathrm{i}}\right)\mathrm{l}\mathrm{o}\mathrm{g}\left(1-{\widehat{\mathrm{y}}}_{\mathrm{i}}\right)\right]$$

(7)

This loss is minimized during training through backpropagation, which also updates the quantum circuit’s parameters via differentiable quantum programming supported by frameworks like PennyLane and TensorFlow [34]. The proposed hybrid classical-quantum model, as shown in Figure 2, integrates both quantum and classical computational layers to perform binary classification in the context of SDVN, particularly targeting applications like DDoS attack detection.

The hybrid quantum-classical model is created using PennyLane and TensorFlow, as presented in Figure 3 and Algorithm 1. The relative analysis of the two DDoS datasets, the Kaggle DDoS SDN Dataset [15] and the CIC-DDoS2019 Dataset [14] from the Canadian Institute for Cybersecurity (CIC), is shown in

Table 2. Comparison between the Kaggle and CIC DDoS dataset.

Aspect	Kaggle DDoS SDN Dataset [15]	CIC-DDoS2019 Dataset [14]
Source	Kaggle (Contributed by Aiken Kazin)	Canadian Institute for Cybersecurity (CIC)
Year of Release	2020	2019
Environment	Simulated SDN environment using Mininet emulator with Ryu controller.	Realistic testbed simulating a victim network with multiple operating systems and a firewall.
Features	23 features including switch ID, packet count, byte count, duration, source/destination IPs, ports, tx_bytes, rx_bytes, and timestamp.	Over 80 features, including flow duration, packet counts, byte counts, and various statistical measures.
Data Format	CSV files with labelled flows.	CSV files with labelled flows.
Labeling	Binary labels indicating normal or attack traffic.	Detailed labelling with specific attack types and timestamps.
Use Case	Designed for evaluating DDoS detection mechanisms in SDN environments.	Suitable for developing and evaluating intrusion detection systems, especially for DDoS attack determination and taxonomy studies.

. The Kaggle DDoS SDN dataset is tailored for SDN environments, making it suitable for researchers focusing on SDN-specific DDoS detection mechanisms. Its simplicity and smaller size make it ideal for initial experiments and model prototyping. The CIC-DDoS2019 Dataset, with a comprehensive set of attack types and a large volume of data, is well suited for developing and evaluating robust intrusion detection systems. The detailed documentation and realistic traffic scenarios enhance its applicability in real-world settings.

Algorithm 1: Hybrid C-QNN for Classification

Input: A Dataset with features and labels Output: Trained model and performance measurement.         1. Standardize the dataset to normalize feature scales. Apply dimensionality reduction to project the original high-dimensional data to a lower dimension suitable for quantum embedding.         2. Initialize a quantum circuit with several qubits equal to the decreased feature dimensions.         3. Define quantum operations to encode the data and create entanglement between qubits.         4. Initialize classical neural network layers, including hidden layers with activation functions and a final output layer for binary classification.         5. Repeat for each epoch and each training batch:                 a. Pass the input sample through the quantum circuit to obtain intermediate quantum features.                 b. Feed the quantum output to the classical neural network layers.                 c. Compute the prediction and compare it with the actual label using a suitable loss function.                 d. Update the parameters of both the quantum circuit and classical layers using hybrid optimization techniques.         6. Evaluate the trained model on the test dataset.         7. Measure performance using metrics such as accuracy, precision, recall, and F1-score.         8. Deploy the trained hybrid model within the application plane of the SDVN Ryu controller. Use the model to analyze incoming traffic and classify it as normal or DDoS in real time.

The proposed QML models are trained for a maximum of 30 epochs. The dataset is split into 70% for training and 30% for testing. After training, the framework is evaluated on unseen test data to assess its generalization capability. Once trained, the hybrid model is deployed within the SDVN as a real-time detection engine integrated into the Ryu controller as shown in Figure 4.

During deployment, the controller receives flow statistics from the OpenFlow switches. These statistics are preprocessed and passed through the trained quantum-classical model, which predicts whether the flow is a DDoS attack or not. Based on the model’s output, the Ryu controller [35] enforces appropriate actions such as dropping malicious packets, rerouting legitimate traffic, or updating flow rules dynamically. This intelligent decision-making mechanism significantly enhances the responsiveness and resilience of the SDVN against evolving DDoS threats, all while leveraging the potential computational advantage of QML in feature representation and classification.

Figure 4. Implementing the proposed hybrid Classical-Quantum model in SDVN [36].

Figure 4. Implementing the proposed hybrid Classical-Quantum model in SDVN [36].

4. Simulation Environment Configuration

4.1. Simulation Objective

The main aim of this simulation is to check the effectiveness of different QML models in identifying malicious traffic (DDoS) from normal traffic. It aims to check the feasibility of implementing the QML model in the application layer of the SDVN controller.

4.2. Simulation Tools Used

Mininet-WiFi version 2.3.0 [37] was employed to imitate vehicle movement and wireless interactions among nodes. The Ryu controller version 4.34 [38] is part of the SDN control plane. Python version 3.5.2 is used as the main language for simulation scripts. The hybrid model was built using PennyLane version 0.23.0. The quantum circuits were implemented using PennyLane, and the classical layers, including ReLU and sigmoid activations, were implemented using TensorFlow version 2.3.1 and Keras version 2.10.0 [39]. The simulation relied on two datasets, the Kaggle DDoS SDN Dataset and the CIC-DDoS2019 Dataset, to train and test the model under diverse network attack scenarios.

4.3. Performance Metrics

The machine learning models’ outcome is determined based on the following metrics:

• Accuracy: It is the ratio of correctly predicted observations to the total observations, as presented in Equation (8) [40]. It is the most intuitive performance measure.

  Accuracy = (TN + TP)/(Total no. of samples)

  (8)

  where TP = True Positives, TN = True Negatives.
• Precision: Also called the Positive Predictive Value, is the ratio of correctly predicted positive observations to the total predicted positives as presented in Equation (9) [40].

  Precision = TP/(TP + FP)

  (9)

  where TP = True Positives, FP = False Positives.
• Recall (Sensitivity): It is the ratio of correctly predicted positive observations to all actual positives, as presented in Equation (10) [40].

  Recall = TP/(TP + FN)

  (10)

  where TP = True Positives, FN = False Negatives.
• F1 Score: It is the harmonic mean of precision and recall values. It combines both metrics and is especially useful in imbalanced datasets, as shown in Equation (11) [40].

  F1 Score = 2 ∗ (Precision ∗ Recall)/(Precision + Recall)

  (11)
• Adjusted Rand Index (ARI): It checks the similarity between two clustering by considering all pairs of samples and counting pairs that are assigned in the same or different clusters in the predicted and true labels [41], as represented in Equation (12). It adjusts for the chance grouping of elements.

  ARI = (RI − E[RI])/(max(RI) − E[RI])

  (12)

  where RI is the Rand Index and E[RI] is the expected RI for random labeling.
• Normalized Mutual Information (NMI): It measures the amount of information shared between the predicted cluster assignments and the ground truth labels [42], as shown in Equation (13). It normalizes the Mutual Information score to scale between 0 (no mutual info) and 1 (perfect correlation). Let “U” and “V” be the sets of clusters and true labels, then

  NMI(U,V) = 2 ∗ I(U,V)/(H(U) + H(V))

  (13)

  where: I(U, V) is the mutual information between U and V, and
  H(U), H(V) are the entropies of clustering U and V.
• Silhouette Score (SS): In contrast to other clusters (separation), it evaluates how similar an object is to its cluster (cohesion) [43] as presented in Equation (14). The score ranges from −1 (incorrect clustering) to 1 (well clustered), with values near 0 indicating overlapping clusters.

For each sample i:

a(i) is the average intra-cluster distance (mean distance to other points in the same cluster), and b(i) is the average nearest-cluster distance (mean distance to points in the nearest cluster)

SS(i) = (b(i) − a(i))/max(a(i), b(i))

(14)

4.4. Experimental Setup

The experimental setup for the proposed architecture was planned to evaluate its effectiveness in determining DDoS attacks within an SDVN environment. In this research, a comprehensive evaluation of three QML approaches was conducted: Quantum Neural Networks (QNNs), Quantum Boltzmann Machines (QBMs), and Quantum-Assisted K-Means (QKM) Clustering. Among these, a hybrid Classical-Quantum Neural Network (C-QNN) model was proposed for effectively detecting DDoS attacks in SDVN environments. The C-QNN architecture was implemented by integrating quantum circuits developed using PennyLane with classical deep learning layers constructed in TensorFlow, creating a seamless hybrid model. For anomaly detection, the C-QBM model utilized quantum-generated probability distributions, while the C-QKM method was employed as an unsupervised learning strategy to identify malicious traffic clusters. The experimental setup involved simulating vehicular network topologies using Mininet-WiFi and controlling the data flow through a Ryu SDVN controller. DDoS attack scenarios were emulated within this environment. The datasets were pre-processed and used to train and test the three models. Simulation and training were conducted using the PennyLane quantum simulator for quantum components and classical backends for neural layers. The overall experimental setup effectively replicates an SDVN environment and allows for rigorous testing of the proposed quantum-enhanced intrusion detection model.

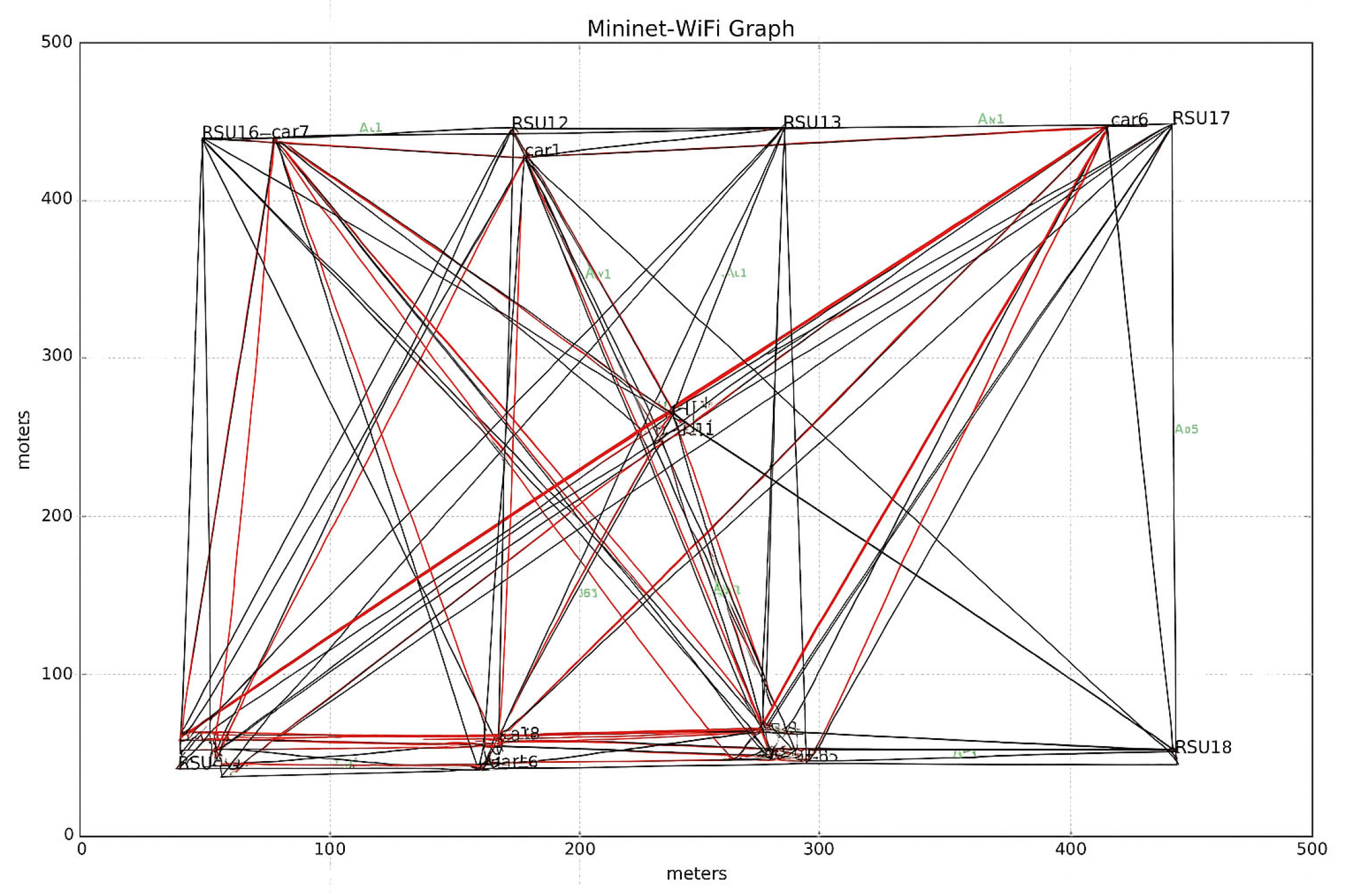
4.5. Testbed Deployment

The proposed Hybrid Quantum-Classical Models were tested in an SDVN environment using a flooding-based DDoS attack simulation as shown in Algorithm 2 and the hyper settings used for all hybrid Classical-Quantum models has been represented in

Table 3. Hyper settings for all hybrid Classical-Quantum models.

Model Type	Dataset	Qubits	Layers	Learning Rate	Epochs	Batch Size	Optimizer	PCA Components
C-QNN	UNB-CIC-DDoS	2	1	0.01	30	5	Adam (PennyLane)	2
C-QNN	Kaggle DDoS	4	3	default (Adam)	30	5	Adam (PennyLane)	2
C-QKM	UNB-CIC-DDoS	4	–	–	30	–	– (iterative update)	2
C-QKM	Kaggle DDoS	2	–	–	30	–	– (iterative update)	2
C-QBM	UNB-CIC-DDoS	2	–	0.005	30	–	Adam (PennyLane)	2
C-QBM	Kaggle DDoS	2	–	0.05	30	–	Adam (PennyLane)	2

.

Algorithm 2: Testing Quantum Models in SDVN Environment via Flooding

Input: Trained quantum and hybrid quantum-classical models (C-QNN, QBM, QKM), SDVN testbed (Mininet-WiFi with Ryu controller) Output: Classification of incoming traffic as benign or an attack. 1. Initialize the SDVN Testbed \\ Launch Mininet-WiFi and start Ryu controller 2. Deploy Monitoring Agents 3. Load the pretrained C-QNN model into the evaluation environment 4. Generate benign vehicular traffic using Iperf application flows. 5. Initiate a UDP flooding attack from vehicular nodes using the tool ‘hping3’ 6. Continue the attack for a predefined interval (e.g., 30–60 s) 7. For the hybrid classical quantum model:       a. Feed preprocessed traffic data       b. Capture predicted labels (benign or attack) 8. Repeat steps 4–7 for robustness analysis

This testing algorithm ensures a realistic SDVN scenario where flooding-based DDoS attacks are executed in a controlled environment, and the effectiveness of quantum-based detection models is evaluated. The custom network is developed using the mininet-wifi graph as presented in Figure 5, and network simulation parameters are provided in

Table 4. Network simulation parameters.

Parameter	Value/Setting
Simulator	Mininet-Wifi (Python-based network simulator)
Controller	Ryu SDVN Controller
Number of Vehicles (Nodes)	10
Number of APs (RSUs)	9
Vehicle Interfaces	WLAN interfaces
Vehicle speed range	min_speed = 0 kmph, max_speed = 100 kmph (randomised input mobility model)
RSU Mode	802.11 n/ac
Propagation Model	Friss (path loss model)
Wireless link type	wmediumd (interference mode: Realistic link quality modelling)

.

5. Result Analysis

The comparative analysis of the three Quantum Machine Learning (QML) methods from the results in

Table 5. Results obtained for different QML models for UNB-CIC-DDoS dataset.

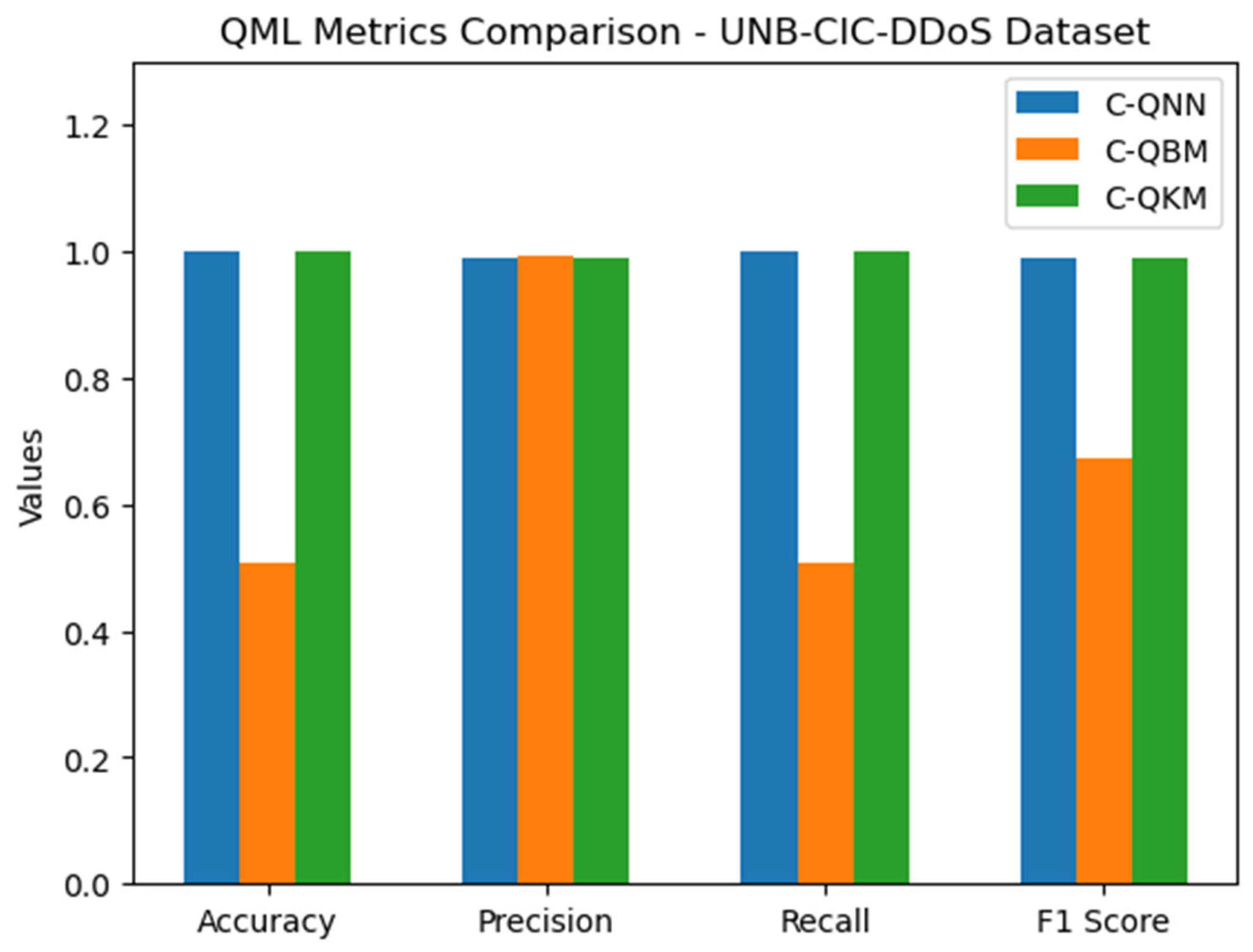
QML Method	Accuracy	Precision	Recall	F1 Score	ARI	NMI	Silhouette Score
C-QNN	0.9989	0.99	0.9994	0.99	-	-	-
C-QBM	0.5062	0.9933	0.5068	0.6712	-	-	-
C-QKM	0.9988	0.99	0.9988	0.99	0.9075	0.8431	0.9772

and Figure 6 shows that both C-QNN and C-QKM deliver exceptionally high classification performance, while C-QBM lags significantly behind in key areas. C-QNN achieves the highest accuracy of 99.89%, just slightly outperforming C-QKM by 0.01%, and vastly outperforming C-QBM, which stands at 50.62%, indicating that C-QNN is nearly twice as accurate. Regarding recall, which measures the model’s capacity to detect true positives, C-QNN leads with 99.94%, slightly above C-QKM’s, and substantially better than C-QBM’s, a difference of approximately 49%. The F1 score, which balances precision and recall, is 0.99 for both C-QNN and C-QKM, showing their robustness in classification tasks, while C-QBM’s F1 score is only 0.6712, making C-QNN roughly 47.4% better in harmonic performance. Although C-QBM shows high precision (99.33%), it does so at the cost of extremely low recall, meaning it predicts very few actual positives correctly. C-QKM also shows strength in clustering metrics, with an Adjusted Rand Index (ARI) of 0.9075, Normalized Mutual Information (NMI) of 0.8431, and a Silhouette Score of 0.9772, all indicating excellent cluster quality and cohesion. However, since C-QNN is a supervised model and does not report clustering metrics, its superiority is evident in all classification-related aspects.

The performance comparison between the three QML methods presented in

Table 6. Results obtained for different QML models for Kaggle DDoS dataset.

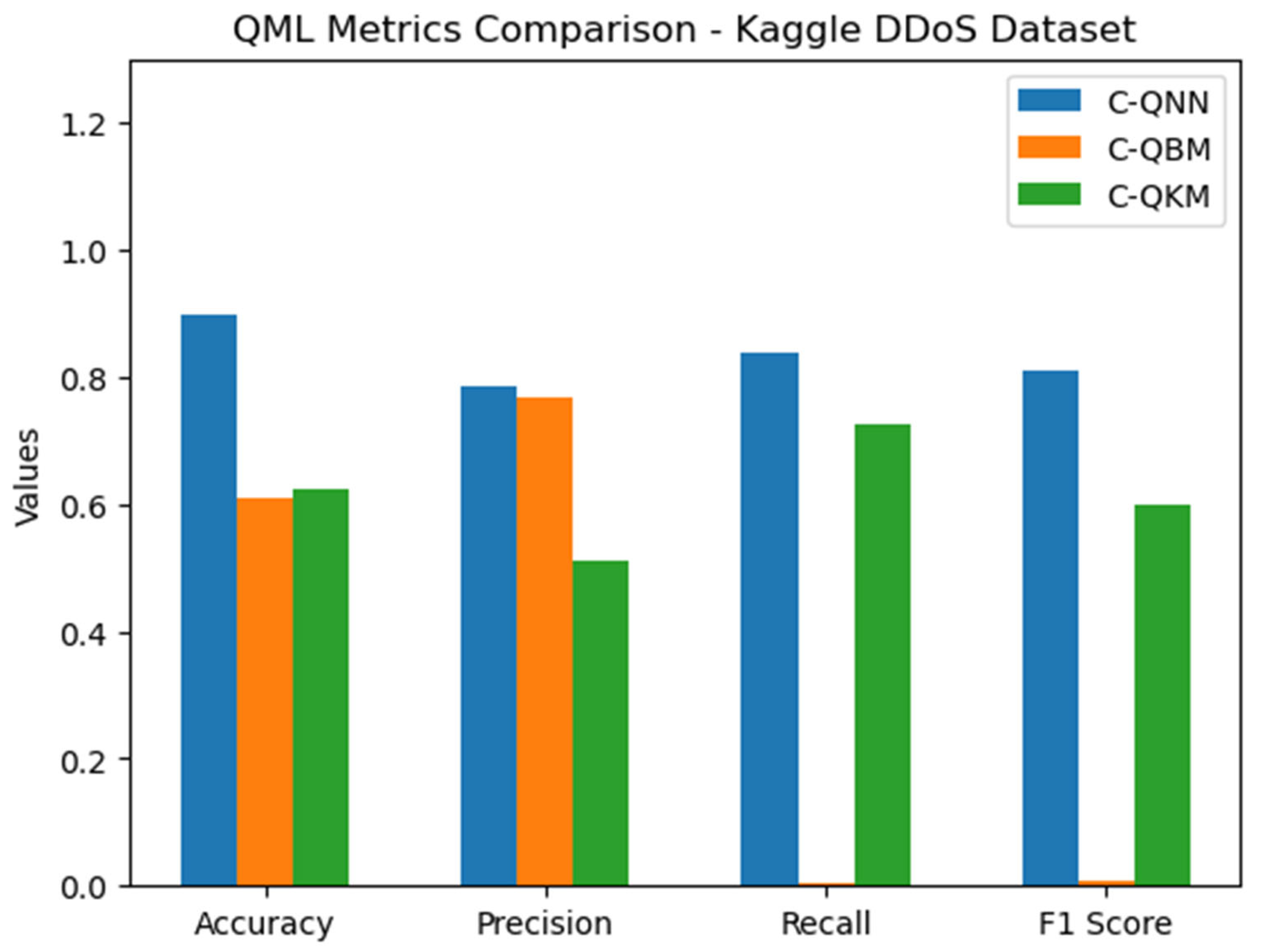
QML Method	Accuracy	Precision	Recall	F1 Score	ARI	NMI	Silhouette Score
C-QNN	0.8996	0.7855	0.8364	0.8109	-	-	-
C-QBM	0.6108	0.7692	0.0039	0.0065	-	-	-
C-QKM	0.6219	0.5107	0.7247	0.5992	0.0588	0.05746	0.1791

and Figure 7 reveals that the C-QNN significantly outperforms the others across all key classification metrics. In terms of accuracy, C-QNN achieves 89.96%, which is significantly higher than C-QBM and C-QKM, indicating its superior ability to correctly classify samples. For precision, C-QNN scores 78.55%, which is 2.1% higher than C-QBM and 27.1% higher than C-QKM, showing it makes fewer false positive predictions. The recall of C-QNN is 83.64%, a dramatic improvement over C-QBM’s near-zero 0.39%, and 15.4% higher than C-QKM, suggesting it captures far more actual positives. Similarly, the F1 score of C-QNN stands at 81.09%, vastly outperforming C-QBM and C-QKM by about 35.3%, reflecting a better balance between precision and recall. Additionally, while clustering metrics like ARI, NMI, and Silhouette Score are reported only for C-QKM due to its unsupervised nature, their relatively low values further affirm that C-QNN is a highly robust and reliable method amongst the three for accurate and meaningful classification in this application context.

6. Results Discussion

The C-QNN outperformed the other QML models across all key evaluation metrics. This superior performance can be credited to the hybrid nature of C-QNN, which combines classical techniques with quantum circuits. Specifically, it employs parameterized quantum circuits using strongly entangling layers and angle embedding schemes. These quantum components allow the model to represent complex, non-linear relationships in data through high-dimensional quantum state spaces, enabling more accurate and nuanced classification than the other methods. The C-QNN model is trained with labeled data, enabling direct optimization of its parameters to improve performance. It employs gradient-based backpropagation with the Adam optimizer (optimization process), which effectively fine-tunes both classical and quantum parameters. In contrast, the C-QBM model operates on energy-based learning principles and usually faces challenges in arriving at an optimal solution, especially with small quantum circuits and limited qubits. The experimental comparison of these QML approaches is significantly relevant for developing intelligent, adaptive systems. The proposed framework has better recall and F1 scores, highlighting its ability to detect both majority and minority classes, indicating its effectiveness in managing imbalanced data, which is common in real-world network environments.

7. Conclusions and Future Work

In this study, we provided a comparison study on three Quantum Machine Learning models, Classical-Quantum Neural Network (C-QNN), Quantum Boltzmann Machine (C-QBM), and Quantum k-Means (C-QKM), on two real-world datasets to evaluate their performance in classification and clustering tasks. The results obtained show that the C-QNN model outperforms the other two techniques across all key classification metrics, like accuracy, precision, recall, and F1 score. The experiment results showed encouraging outcomes, but it also showcased significant drawbacks and practical difficulties in the current state of QML development. The basic constraint is limited access to actual quantum hardware, as quantum computers with adequate qubits are not publicly available. The execution time for even a single model is significantly large, and hence it becomes very challenging to scale the experiment or to explore other techniques with a local simulation setup. Also, these simulations are time-consuming because of computational complexities and limited qubits. This hardware limitation restricts us from using data in its original form and requires PCA for dimensionality reduction. This reduction may have restricted the model’s capability to fully represent the underlying relations, potentially affecting performance. Additionally, few QML algorithms are available in comparison to traditional machine learning algorithms, narrowing the scope for exploring quantum solutions.

Future researchers may use cloud-based quantum computers as they become more easily available, allowing experiments with more qubits and real-time processing. We used ReLU as the activation function in the classical hidden layer due to its efficiency and empirical effectiveness in hybrid learning settings. A comparative analysis with other activation functions can be planned as future work. Expanding the range of QML algorithms, refining encoding techniques, and enhancing hybrid quantum-classical frameworks will be critical for improving the practicality, efficiency, and accuracy of QML models.