Towards Fair Graph Neural Networks via Counterfactual and Balance
Abstract
1. Introduction
- Preliminary Analysis. From the perspective of causality, we propose a counterfactual node generation framework based on adversarial networks, which provides a new causal analysis paradigm for fair graph learning.
- Algorithm Design. We propose a FairCNCB fairness GNNs model, which performs well in dealing with data distribution bias and imbalance during the training process. Compared with the existing fair GNN models, our model achieves better performance.
- Experimental Evaluation. We conducted a large number of experiments on the real datasets, and the results showed that FairCNCB performed well in the evaluation indicators of utility and fairness. At the same time, we deployed the model on several different compilers available in GNNs, and the results performed well.
2. Related Work
2.1. Graph Neural Networks
2.2. Fairness in Graph Neural Networks
3. Preliminaries
3.1. Notations and Problem Definition
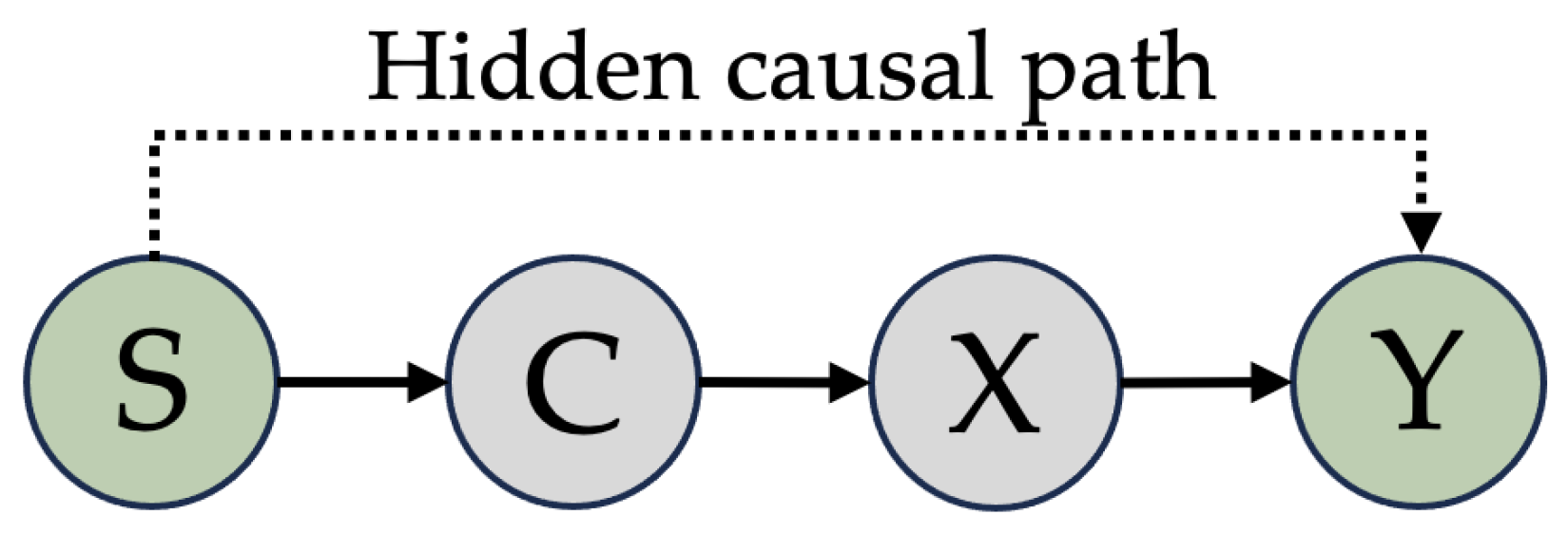
3.2. Necessity for Fair Graph Learning
3.2.1. Sources of Bias
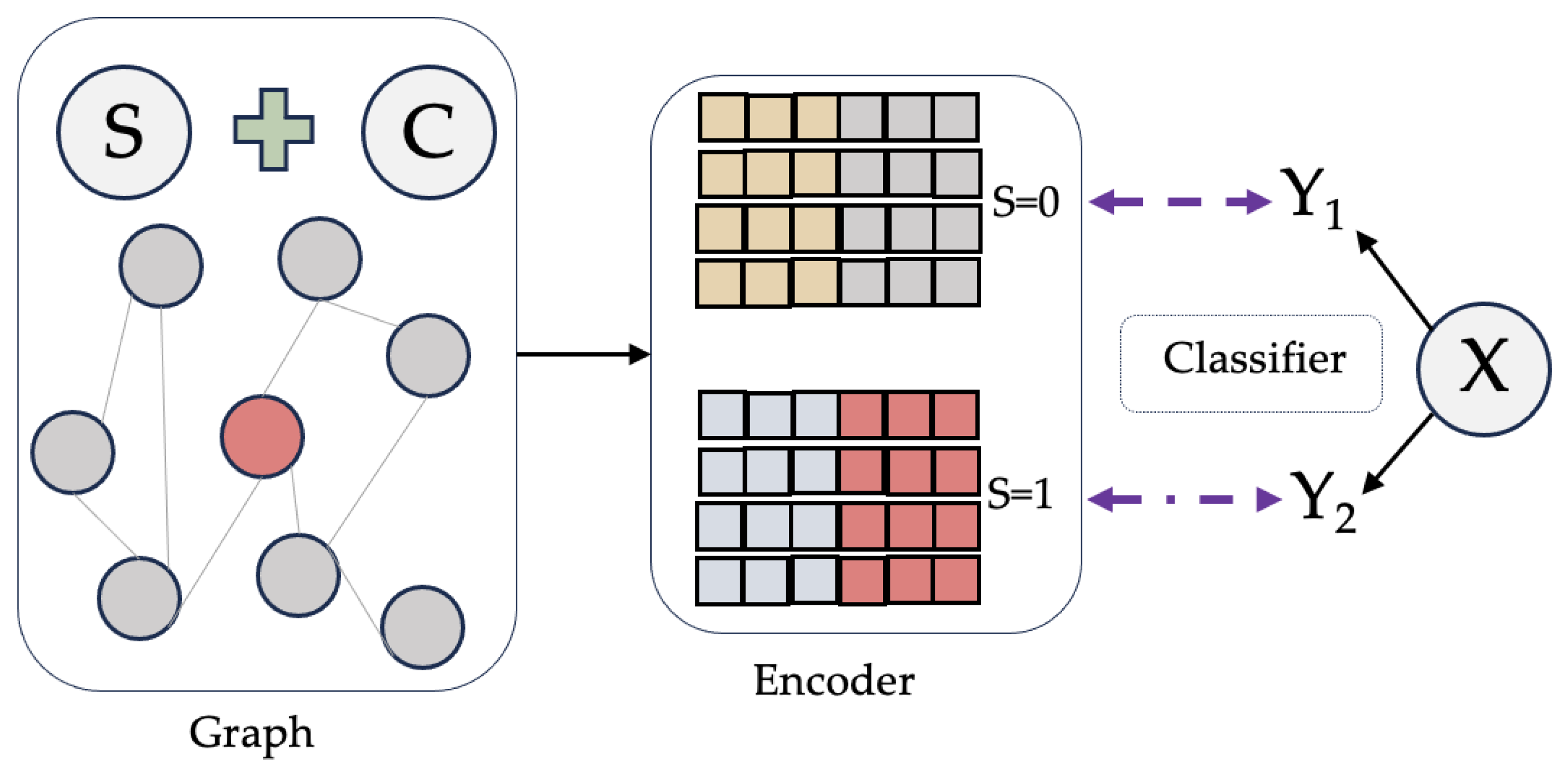
3.2.2. Fair Representation Learning of Debiasing
4. Methodology
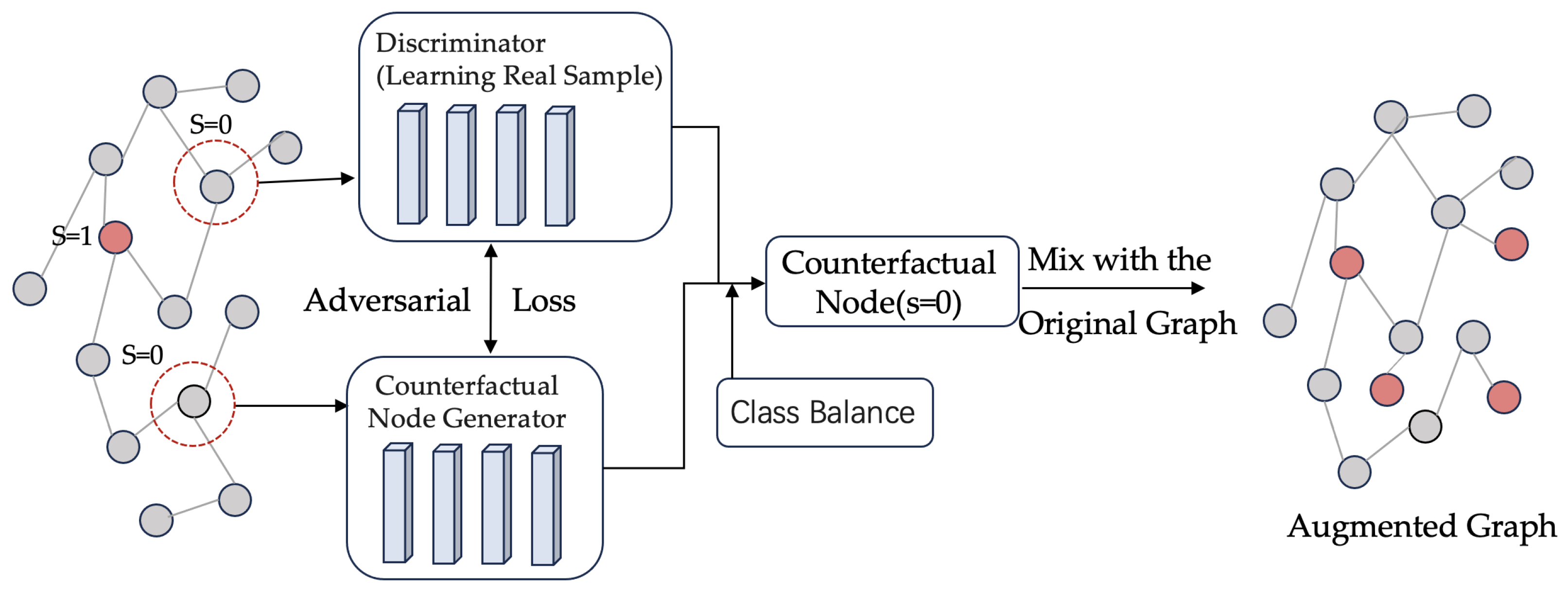
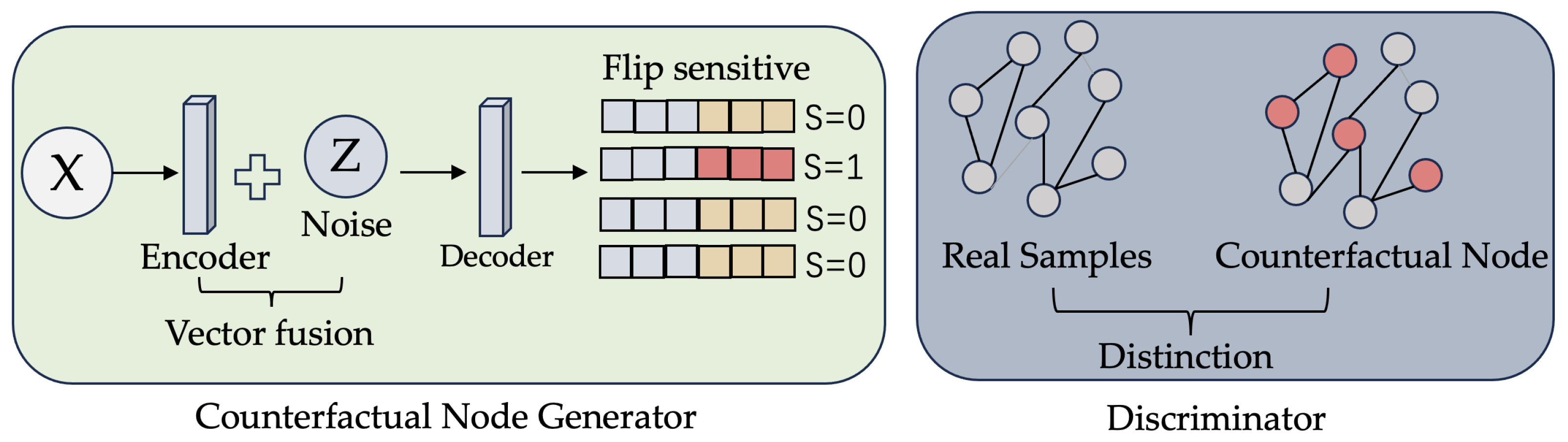
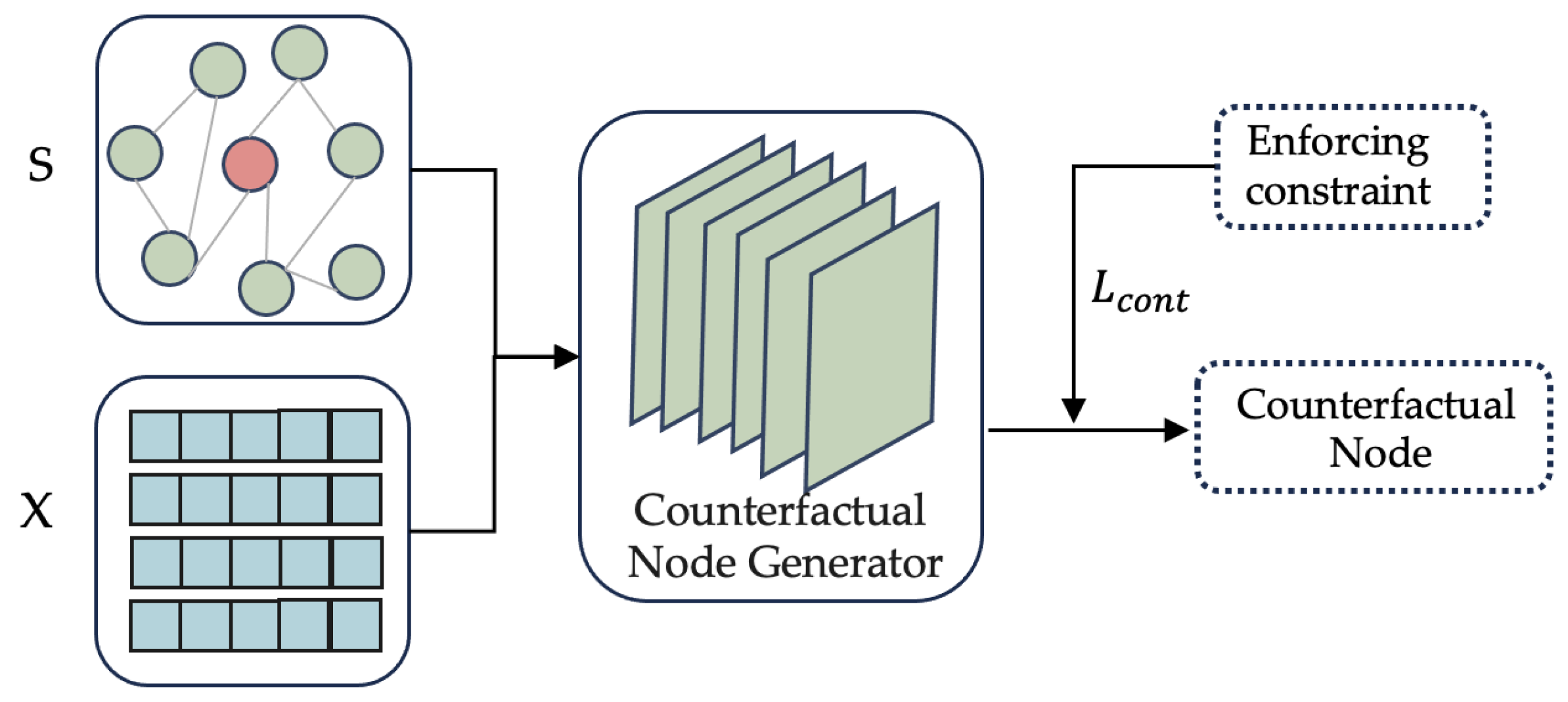
4.1. Counterfactual Node Generation Based on Adversarial Networks
4.1.1. Counterfactual Node Generator and Discriminator
4.1.2. Adversarial Training of Counterfactual Node Generator and Discriminator
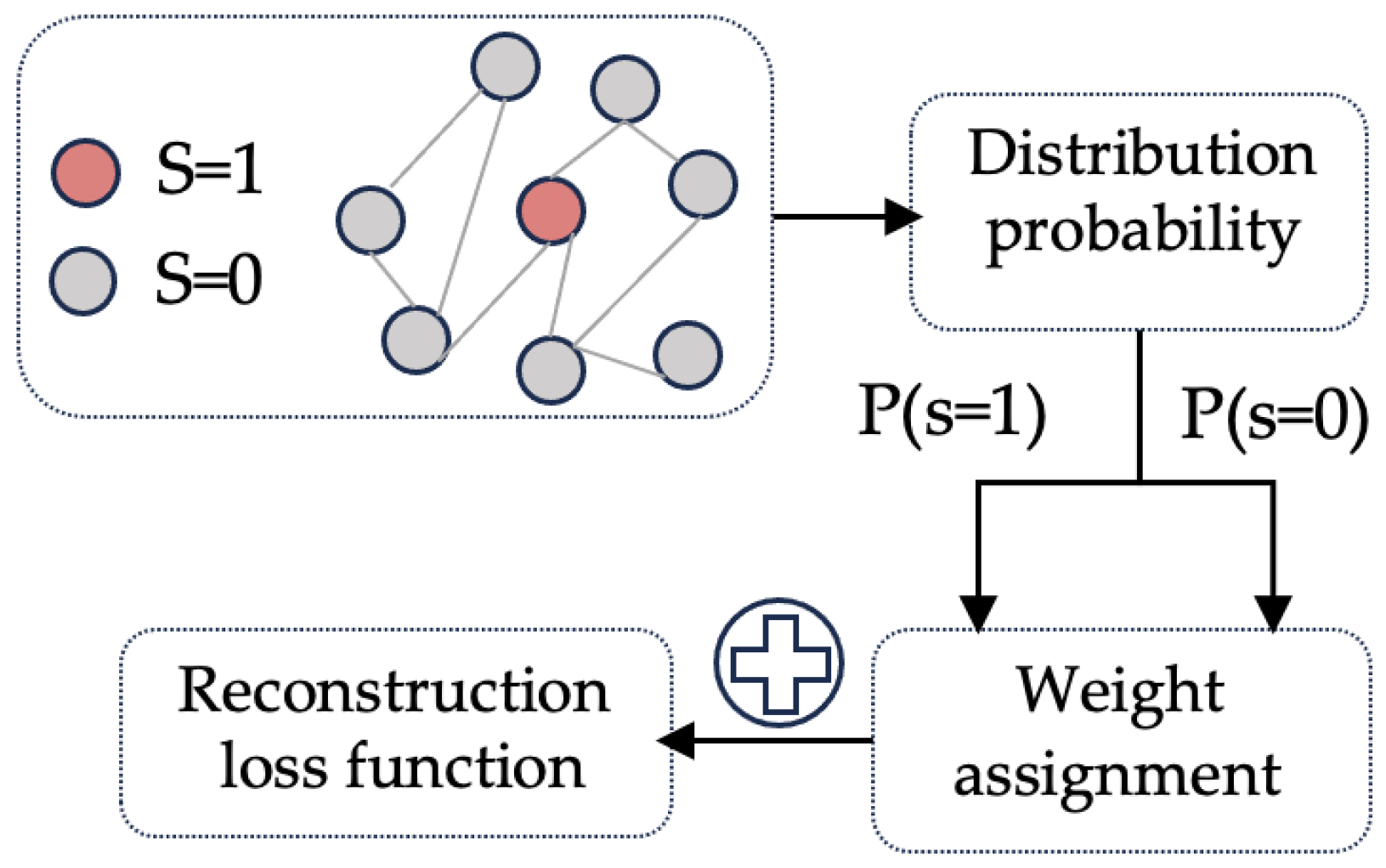
4.2. Class Balancing Mechanic
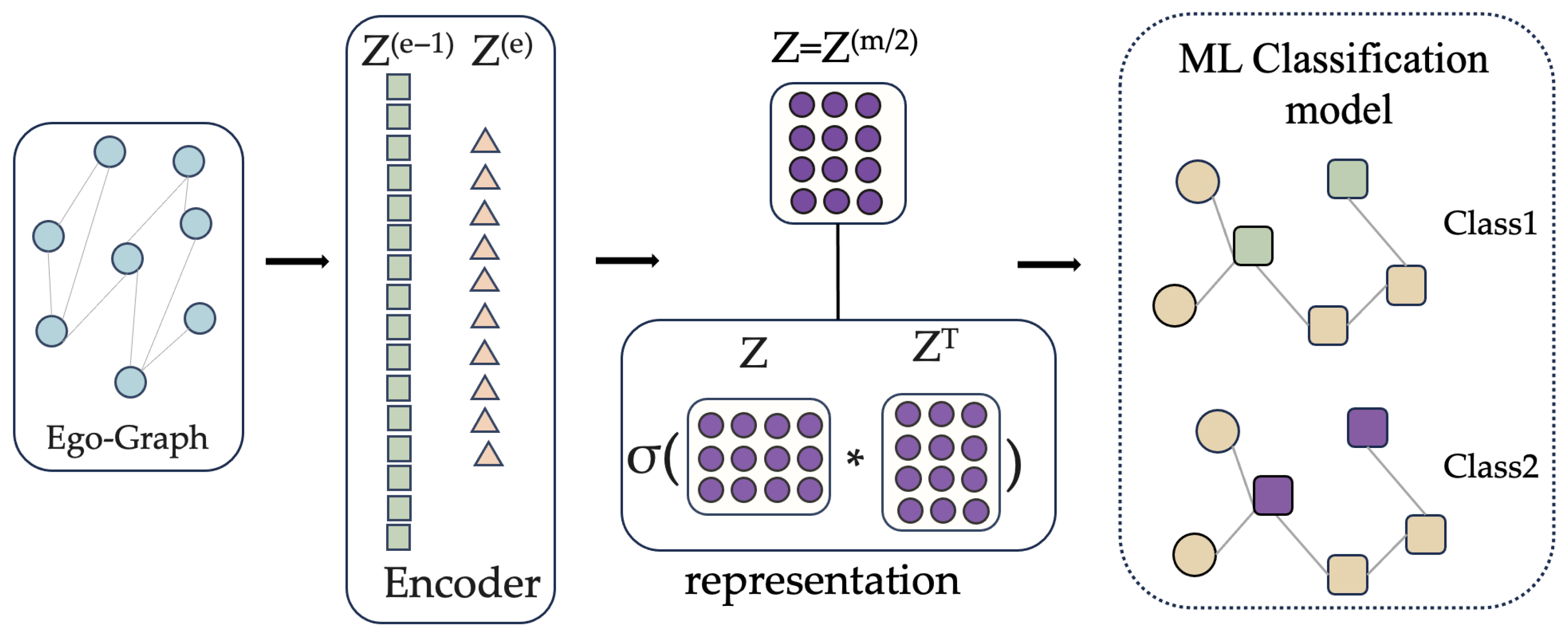
4.3. The Fair Representation Learning
4.4. Final Objective Function of FairCNCB
| Algorithm 1: The training process of FairCNCB |
Input: = (V, A, X, S), η, Counterfactual Node Generator, Discriminator, , T. Output: prediction label . Pre-train based on for T do: Generate counterfactual nodes by Counterfactual Node Generator(Z, X ); Determine the rationality of counterfactual nodes by Discriminator(X); Hybrid nodes prediction label =() ← Recontribution Alignment Loss; Back-propagation; end |
5. Experiments
- (RQ1)
- In these five evaluation indicators can FairCNCB show better performance compared to the GNN model and the fairness model?
- (RQ2)
- How does each module affect the working performance of the model?
- (RQ3)
- What are the effects of different GNN encoders in classification tasks?
- (RQ4)
- How do hyperparameters in the model affect FairCNCB?
5.1. Experimental Settings
5.1.1. Real-World Datasets
- German Credit [49]: The node information in the graph structure datasets is the clients. If the credit accounts of the two nodes are highly similar, they are connected. The task at hand is to classify the credit risk level as either high or low, taking into account the sensitive attribute of “gender”.
- Bail [50]: The node information in the graph structure datasets is that of the defendant on bail. The edges between the two nodes are connected based on past criminal records and demographic similarities. The task is to classify whether a defendant is released on bail with the sensitive attribute “race”.
- Credit Defaulter [51]: The node information in the graph structure datasets is the credit card users. The edges connected by the nodes represent the payment information if the user’s payment information is similar to each other. The task is to classify the default payment method using the sensitive attribute “age”.
5.1.2. Baselines
- GCN [33] proposes a very popular first-order approximate semi-supervised classification method based on spectral convolution on graphs, which can effectively encode graph network nodes.
- GraphSAGE [34] solves the problem of unsupervised node embedding in large graphs using a function to sample and aggregate the node representations from neighbor nodes to generate an embedding.
- GAT [52] used an attention mechanism to calculate the importance weights of neighboring nodes, capturing different types of neighbor relationships.
- GIN [35] designed a single-shot aggregate function to learn the node representations, which can capture different graph structure data for application in graph classification tasks.
- FairGNN [15] is grounded in adversarial learning. This approach serves to mitigate bias when dealing with limited sensitive attribute information.
- EDITS [19] proposes a new metric to reduce bias by directly removing sensitive information.
- GEAR [53] is an interpretable graph representation learning model based on a dual-channel graph attention mechanism, which realizes graph data generation and prediction.
- NIFTY [17] introduces a new objective function to flip the counterfactual nodes to address the stability and fairness of GNNs.
- CAF [25] can directly select the fair nodes to learn the real counterfactual pairs from the training samples, and can learn the fair node representation.
5.1.3. Evaluation Metrics
5.1.4. Implementation Details
5.2. Performance Comparison
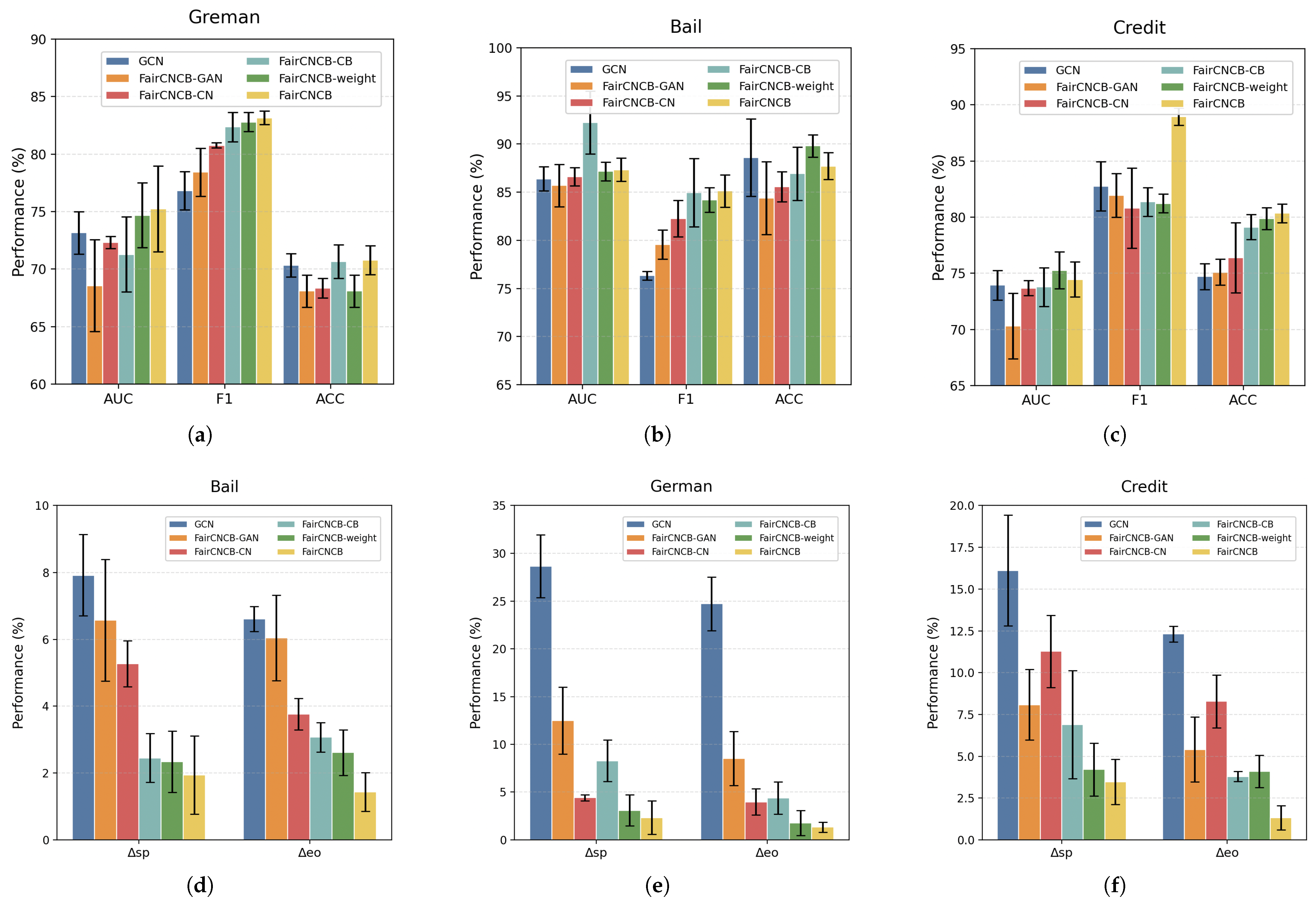
5.3. Ablation Study
5.4. Deploying on Different Encoders
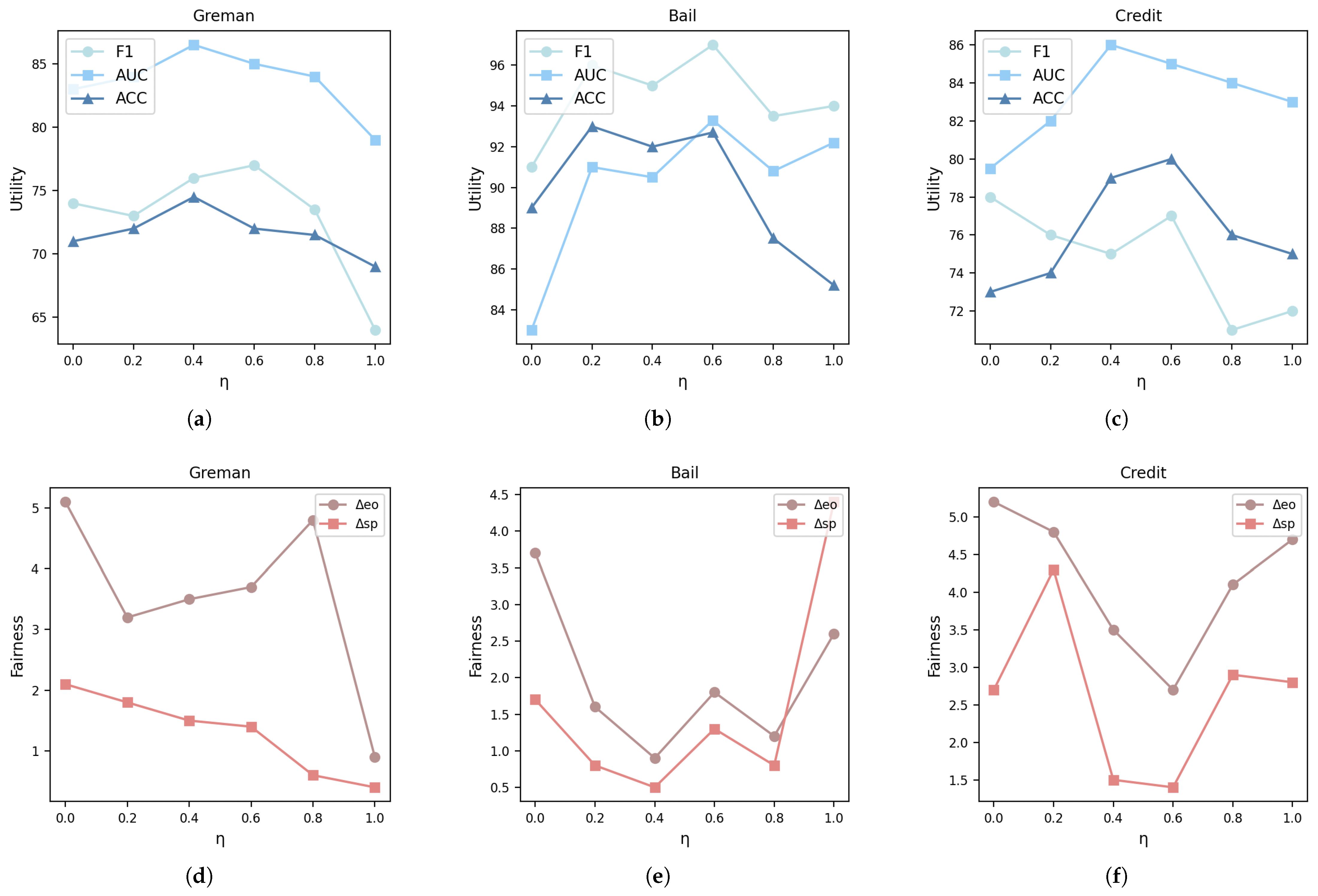
5.5. Parametric Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, S.; Ni, W.W.; Fu, N. Community-Preserving Social Graph Release with Node Differential Privacy. J. Comput. Sci. Technol. 2023, 38, 1369–1386. [Google Scholar] [CrossRef]
- Berk, R. Accuracy and fairness for juvenile justice risk assessments. J. Empir. Leg. Stud. 2019, 16, 175–194. [Google Scholar] [CrossRef]
- Liu, Y.C.; Tian, J.; Glaser, N.; Kira, Z. When2com: Multi-agent perception via communication graph grouping. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 4106–4115. [Google Scholar]
- Martinez-Riano, A.; Wang, S.; Boeing, S.; Minoughan, S.; Casal, A.; Spillane, K.M.; Ludewig, B.; Tolar, P. Long-term retention of antigens in germinal centers is controlled by the spatial organization of the follicular dendritic cell network. Nat. Immunol. 2023, 24, 1281–1294. [Google Scholar] [CrossRef]
- Fofanah, A.J.; Leigh, A.O. EATSA-GNN: Edge-Aware and Two-Stage attention for enhancing graph neural networks based on teacher–student mechanisms for graph node classification. Neurocomputing 2025, 612, 128686. [Google Scholar] [CrossRef]
- Ma, T.; Wang, H.; Zhang, L.; Tian, Y.; Al-Nabhan, N. Graph classification based on structural features of significant nodes and spatial convolutional neural networks. Neurocomputing 2021, 423, 639–650. [Google Scholar] [CrossRef]
- Pang, J.; Gu, Y.; Xu, J.; Yu, G. Semi-supervised multi-graph classification using optimal feature selection and extreme learning machine. Neurocomputing 2018, 277, 89–100. [Google Scholar] [CrossRef]
- Said, A.; Janjua, M.U.; Hassan, S.U.; Muzammal, Z.; Saleem, T.; Thaipisutikul, T.; Tuarob, S.; Nawaz, R. Detailed analysis of Ethereum network on transaction behavior, community structure and link prediction. PeerJ Comput. Sci. 2021, 7, e815. [Google Scholar] [CrossRef]
- Li, X.; Shang, Y.; Cao, Y.; Li, Y.; Tan, J.; Liu, Y. Type-aware anchor link prediction across heterogeneous networks based on graph attention network. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 147–155. [Google Scholar]
- Dai, E.; Cui, L.; Wang, Z.; Tang, X.; Wang, Y.; Cheng, M.; Yin, B.; Wang, S. A unified framework of graph information bottleneck for robustness and membership privacy. In Proceedings of the 29th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Long Beach, CA, USA, 6–10 August 2023; pp. 368–379. [Google Scholar]
- Köse, Ö.D.; Shen, Y. Fairness-aware node representation learning. arXiv 2021, arXiv:2106.05391. [Google Scholar]
- Ma, J.; Deng, J.; Mei, Q. Subgroup generalization and fairness of graph neural networks. Adv. Neural Inf. Process. Syst. 2021, 34, 1048–1061. [Google Scholar]
- Beutel, A.; Chen, J.; Zhao, Z.; Chi, E.H. Data decisions and theoretical implications when adversarially learning fair representations. arXiv 2017, arXiv:1707.00075. [Google Scholar]
- Mehrabi, N.; Morstatter, F.; Saxena, N.; Lerman, K.; Galstyan, A. A survey on bias and fairness in machine learning. ACM Comput. Surv. (CSUR) 2021, 54, 1–35. [Google Scholar] [CrossRef]
- Dai, E.; Wang, S. Say no to the discrimination: Learning fair graph neural networks with limited sensitive attribute information. In Proceedings of the 14th ACM International Conference on Web Search and Data Mining, Virtual Event, 8–12 March 2021; pp. 680–688. [Google Scholar]
- Bao, H.; Dong, L.; Wang, W.; Yang, N.; Piao, S.; Wei, F. Fine-tuning pretrained transformer encoders for sequence-to-sequence learning. Int. J. Mach. Learn. Cybern. 2024, 15, 1711–1728. [Google Scholar] [CrossRef]
- Agarwal, C.; Lakkaraju, H.; Zitnik, M. Towards a unified framework for fair and stable graph representation learning. In Proceedings of the Uncertainty in Artificial Intelligence, PMLR, Online, 27–30 July 2021; pp. 2114–2124. [Google Scholar]
- Dong, Y.; Kang, J.; Tong, H.; Li, J. Individual fairness for graph neural networks: A ranking based approach. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Singapore, 14–18 August 2021; pp. 300–310. [Google Scholar]
- Dong, Y.; Liu, N.; Jalaian, B.; Li, J. Edits: Modeling and mitigating data bias for graph neural networks. In Proceedings of the ACM Web Conference 2022, Lyon, France, 25–29 April 2022; pp. 1259–1269. [Google Scholar]
- Dong, Y.; Ma, J.; Wang, S.; Chen, C.; Li, J. Fairness in graph mining: A survey. IEEE Trans. Knowl. Data Eng. 2023, 35, 10583–10602. [Google Scholar] [CrossRef]
- Dong, Y.; Zhang, B.; Yuan, Y.; Zou, N.; Wang, Q.; Li, J. Reliant: Fair knowledge distillation for graph neural networks. In Proceedings of the 2023 SIAM International Conference on Data Mining (SDM), Minneapolis, MI, USA, 27–29 April 2023; SIAM: Bangkok, Thailand, 2023; pp. 154–162. [Google Scholar]
- Ma, J.; Guo, R.; Wan, M.; Yang, L.; Zhang, A.; Li, J. Learning fair node representations with graph counterfactual fairness. In Proceedings of the Fifteenth ACM International Conference on Web Search and Data Mining, Virtual Event, AZ, USA, 21–25 February 2022; pp. 695–703. [Google Scholar]
- Wang, Y.; Zhao, Y.; Dong, Y.; Chen, H.; Li, J.; Derr, T. Improving fairness in graph neural networks via mitigating sensitive attribute leakage. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 1938–1948. [Google Scholar]
- Dai, E.; Zhao, T.; Zhu, H.; Xu, J.; Guo, Z.; Liu, H.; Tang, J.; Wang, S. A comprehensive survey on trustworthy graph neural networks: Privacy, robustness, fairness, and explainability. Mach. Intell. Res. 2024, 21, 1011–1061. [Google Scholar] [CrossRef]
- Guo, Z.; Li, J.; Xiao, T.; Ma, Y.; Wang, S. Towards fair graph neural networks via graph counterfactual. In Proceedings of the 32nd ACM International Conference on Information and Knowledge Management, Birmingham, UK, 21–25 October 2023; pp. 669–678. [Google Scholar]
- Song, W.; Dong, Y.; Liu, N.; Li, J. Guide: Group equality informed individual fairness in graph neural networks. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 1625–1634. [Google Scholar]
- Rahman, T.; Surma, B.; Backes, M.; Zhang, Y. Fairwalk: Towards fair graph embedding. In Proceedings of the 28th International Joint Conference on Artificial Intelligen, Macao, China, 10–16 August 2019. [Google Scholar]
- Zhao, T.; Zhang, X.; Wang, S. Graphsmote: Imbalanced node classification on graphs with graph neural networks. In Proceedings of the 14th ACM International Conference on Web Search and Data Mining, Virtual Event, Israel, 8–12 March 2021; pp. 833–841. [Google Scholar]
- Mukherjee, D.; Yurochkin, M.; Banerjee, M.; Sun, Y. Two simple ways to learn individual fairness metrics from data. In Proceedings of the International Conference on Machine Learning, PMLR, Online, 13–18 July 2020; pp. 7097–7107. [Google Scholar]
- Fan, S.; Wang, X.; Mo, Y.; Shi, C.; Tang, J. Debiasing graph neural networks via learning disentangled causal substructure. Adv. Neural Inf. Process. Syst. 2022, 35, 24934–24946. [Google Scholar]
- Jiang, W.; Liu, H.; Xiong, H. Survey on trustworthy graph neural networks: From a causal perspective. arXiv 2023, arXiv:2312.12477. [Google Scholar]
- Sui, Y.; Wang, X.; Wu, J.; Lin, M.; He, X.; Chua, T.S. Causal attention for interpretable and generalizable graph classification. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 1696–1705. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How powerful are graph neural networks? arXiv 2018, arXiv:1810.00826. [Google Scholar]
- Xiao, T.; Wang, D. A general offline reinforcement learning framework for interactive recommendation. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 2–9 February 2021; Volume 35, pp. 4512–4520. [Google Scholar]
- Jin, G.; Wang, Q.; Zhu, C.; Feng, Y.; Huang, J.; Zhou, J. Addressing crime situation forecasting task with temporal graph convolutional neural network approach. In Proceedings of the 2020 12th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA), Phuket, Thailand, 28–29 February 2020; IEEE: New York, NY, USA, 2020; pp. 474–478. [Google Scholar]
- Diana, E.; Gill, W.; Kearns, M.; Kenthapadi, K.; Roth, A. Minimax group fairness: Algorithms and experiments. In Proceedings of the 2021 AAAI/ACM Conference on AI, Ethics, and Society, Virtual Event, USA, 19–21 May 2021; pp. 66–76. [Google Scholar]
- Fleisher, W. What’s fair about individual fairness? In Proceedings of the 2021 AAAI/ACM Conference on AI, Ethics, and Society, Virtual Event, USA, 19–21 May 2021; pp. 480–490. [Google Scholar]
- Sharifi-Malvajerdi, S.; Kearns, M.; Roth, A. Average individual fairness: Algorithms, generalization and experiments. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Chiappa, S. Path-specific counterfactual fairness. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 7801–7808. [Google Scholar]
- Kusner, M.J.; Loftus, J.; Russell, C.; Silva, R. Counterfactual fairness. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Makhlouf, K.; Zhioua, S.; Palamidessi, C. Survey on causal-based machine learning fairness notions. arXiv 2020, arXiv:2010.09553. [Google Scholar]
- Zečević, M.; Dhami, D.S.; Veličković, P.; Kersting, K. Relating graph neural networks to structural causal models. arXiv 2021, arXiv:2109.04173. [Google Scholar]
- Lin, W.; Lan, H.; Li, B. Generative causal explanations for graph neural networks. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 6666–6679. [Google Scholar]
- Wang, X.; Wu, Y.; Zhang, A.; Feng, F.; He, X.; Chua, T.S. Reinforced causal explainer for graph neural networks. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 2297–2309. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Adiga, A.; Chen, J.; Sadilek, A.; Venkatramanan, S.; Marathe, M. Causalgnn: Causal-based graph neural networks for spatio-temporal epidemic forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 22 February–1 March 2022; Volume 36, pp. 12191–12199. [Google Scholar]
- Pearl, J. Causality; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Asuncion, A.; Newman, D. UCI Machine Learning Repository; University of California: Irvine, CA, USA, 2007. [Google Scholar]
- Jordan, K.L.; Freiburger, T.L. The effect of race/ethnicity on sentencing: Examining sentence type, jail length, and prison length. J. Ethn. Crim. Justice 2015, 13, 179–196. [Google Scholar] [CrossRef]
- Yeh, I.C.; Lien, C.h. The comparisons of data mining techniques for the predictive accuracy of probability of default of credit card clients. Expert Syst. Appl. 2009, 36, 2473–2480. [Google Scholar] [CrossRef]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Wang, H.; Wang, J.; Wang, J.; Zhao, M.; Zhang, W.; Zhang, F.; Xie, X.; Guo, M. Graphgan: Graph representation learning with generative adversarial nets. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
| Dataset | German Credit | Bail | Credit Defaulter |
|---|---|---|---|
| Nodes | 1000 | 18,876 | 30,000 |
| Edges | 22,242 | 321,308 | 1,436,858 |
| Attributes | 27 | 18 | 13 |
| Sens. | Gender | Race | Age |
| Label | Credit status | Bail decision | Future default |
| Datasets | Metrics (%) | GAT | GIN | SAGE | FairCNCB |
|---|---|---|---|---|---|
| German | AUC (↑) | 70.84 ± 0.71 | 73.59 ± 1.36 | 73.43 ± 1.81 | 75.25 ± 3.74 |
| F1 (↑) | 87.62 ± 1.57 | 82.32 ± 1.82 | 82.38 ± 1.12 | 83.16 ± 0.58 | |
| ACC (↑) | 71.63 ± 0.82 | 72.56 ± 0.87 | 70.83 ± 0.59 | 70.78 ± 1.25 | |
| △sp (↓) | 11.27 ± 1.93 | 17.46 ± 6.31 | 26.35 ± 5.17 | 2.23 ± 1.74 | |
| △eo (↓) | 9.03 ± 0.31 | 10.28 ± 7.36 | 17.39 ± 3.28 | 1.32 ± 0.53 | |
| Bail | AUC (↑) | 76.94 ± 1.16 | 85.27 ± 0.42 | 91.38 ± 0.46 | 87.34 ± 1.20 |
| F1 (↑) | 83.59 ± 2.06 | 77.83 ± 0.49 | 81.17 ± 1.32 | 85.13 ± 1.69 | |
| ACC (↑) | 85.02 ± 1.35 | 82.71 ± 0.82 | 88.72 ± 4.25 | 87.72 ± 1.38 | |
| △sp (↓) | 4.73 ± 0.59 | 8.53 ± 1.27 | 3.52 ± 2.52 | 1.94 ± 1.17 | |
| △eo (↓) | 7.86 ± 0.31 | 8.39 ± 0.65 | 1.92 ± 3.92 | 1.43 ± 0.58 | |
| Credit | AUC (↑) | 70.94 ± 1.08 | 72.53 ± 2.37 | 71.67 ± 1.38 | 74.45 ± 1.56 |
| F1 (↑) | 85.03 ± 1.41 | 83.15 ± 0.14 | 83.92 ± 1.17 | 83.35 ± 0.77 | |
| ACC (↑) | 79.36 ± 1.17 | 77.96 ± 0.18 | 75.27 ± 2.45 | 80.35 ± 0.83 | |
| △sp (↓) | 7.91 ± 2.49 | 5.36 ± 1.12 | 16.39 ± 1.98 | 3.47 ± 1.36 | |
| △eo (↓) | 11.58 ± 3.11 | 3.46 ± 2.73 | 12.17 ± 4.32 | 3.31 ± 0.72 |
| Datasets | Metrics (%) | FairGNN | EDITS | GEAR | NIFTY | CAF | FairCNCB |
|---|---|---|---|---|---|---|---|
| German | AUC (↑) | 69.52 ± 1.07 | 71.01 ± 1.30 | 70.42 ± 0.81 | 70.32 ± 4.42 | 71.87 ± 1.33 | 75.25 ± 3.74 |
| F1 (↑) | 80.71 ± 1.31 | 82.43 ± 0.69 | 80.02 ± 1.13 | 81.98 ± 0.82 | 82.16 ± 0.22 | 83.16 ± 0.58 | |
| ACC (↑) | 68.45 ± 2.83 | 68.73 ± 1.04 | 68.42 ± 0.73 | 65.53 ± 3.94 | 68.39 ± 1.06 | 70.78 ± 1.25 | |
| △sp (↓) | 11.55 ± 1.93 | 8.30 ± 3.10 | 5.48 ± 1.49 | 15.08 ± 8.82 | 6.60 ± 1.66 | 2.23 ± 1.74 | |
| △eo (↓) | 6.18 ± 2.17 | 3.75 ± 3.30 | 6.81 ± 0.16 | 12.56 ± 8.60 | 1.58 ± 1.14 | 1.32 ± 0.53 | |
| Bail | AUC (↑) | 85.69 ± 0.77 | 85.73 ± 3.02 | 89.60 ± 0.16 | 88.51 ± 3.08 | 91.39 ± 0.34 | 87.34 ± 1.2 |
| F1 (↑) | 83.47 ± 1.32 | 79.97 ± 1.29 | 80.00 ± 0.31 | 79.92 ± 4.09 | 83.09 ± 0.98 | 85.13 ± 1.69 | |
| ACC (↑) | 85.81 ± 0.64 | 83.26 ± 0.40 | 85.20 ± 0.26 | 84.61 ± 1.27 | 85.91 ± 1.78 | 87.72 ± 1.38 | |
| △sp (↓) | 2.09 ± 0.48 | 3.93 ± 0.59 | 5.80 ± 0.17 | 3.82 ± 1.09 | 2.29 ± 1.06 | 1.94 ± 1.17 | |
| △eo (↓) | 1.91 ± 0.35 | 2.30 ± 0.77 | 1.90 ± 0.23 | 5.47 ± 1.79 | 1.17 ± 0.52 | 1.43 ± 0.58 | |
| Credit | AUC (↑) | 74.56 ± 1.38 | 70.16 ± 0.60 | 74.00 ± 0.08 | 71.92 ± 0.19 | 73.42 ± 1.89 | 74.45 ± 1.56 |
| F1 (↑) | 81.61 ± 0.84 | 81.44 ± 0.20 | 83.5 ± 0.08 | 81.99 ± 0.63 | 83.63 ± 0.89 | 83.35 ± 0.77 | |
| ACC (↑) | 78.97 ± 1.30 | 72.67 ± 0.91 | 76.55 ± 0.11 | 77.74 ± 3.97 | 78.41 ± 2.90 | 80.35 ± 0.83 | |
| △sp (↓) | 4.79 ± 0.59 | 9.13 ± 1.20 | 1.04 ± 0.13 | 12.40 ± 1.62 | 8.63 ± 2.13 | 3.47 ± 1.36 | |
| △eo (↓) | 7.14 ± 2.86 | 7.88 ± 1.00 | 8.60 ± 0.18 | 10.09 ± 1.55 | 6.85 ± 1.55 | 3.31 ± 0.72 |
| Datasets | Metrics (%) | GCN | FairCNCB-GAN | FairCNCB-CN | FairCNCB-CB | FairCNCB-Weight | FairCNCB |
|---|---|---|---|---|---|---|---|
| German | AUC (↑) | 73.16 ± 1.86 | 68.57 ± 4.00 | 72.32 ± 0.54 | 71.28 ± 3.27 | 74.69 ± 2.81 | 75.25 ± 3.74 |
| F1 (↑) | 76.84 ± 1.65 | 78.43 ± 2.10 | 80.76 ± 0.22 | 82.36 ± 1.27 | 82.79 ± 0.83 | 83.16 ± 0.58 | |
| ACC (↑) | 71.76+1.02 | 68.09 ± 1.40 | 68.36 ± 0.86 | 70.67 ± 1.46 | 71.68 ± 1.39 | 70.78 ± 1.25 | |
| △sp (↓) | 28.65 ± 3.26 | 12.50 ± 3.50 | 4.41 ± 0.32 | 8.28 ± 2.17 | 3.07 ± 1.63 | 2.23 ± 1.74 | |
| △eo (↓) | 24.73 ± 2.82 | 8.50 ± 2.38 | 3.97 ± 1.38 | 4.38 ± 1.69 | 1.75 ± 1.32 | 1.32 ± 0.53 | |
| Bail | AUC (↑) | 86.38 ± 1.26 | 85.71 ± 2.20 | 86.62 ± 0.95 | 92.26 ± 3.73 | 87.17 ± 0.96 | 87.34 ± 1.2 |
| F1 (↑) | 76.33 ± 1.47 | 79.55 ± 1.51 | 82.25 ± 1.89 | 84.96 ± 4.53 | 84.20 ± 1.28 | 85.13 ± 1.69 | |
| ACC (↑) | 88.61 ± 4.03 | 84.39 ± 1.77 | 85.57 ± 1.55 | 86.93 ± 2.76 | 89.81 ± 1.14 | 87.72 ± 1.38 | |
| △sp (↓) | 7.92 ± 1.21 | 6.57 ± 1.82 | 5.27 ± 0.69 | 2.45 ± 0.73 | 2.34 ± 0.92 | 1.94 ± 1.17 | |
| △eo (↓) | 6.61 ± 0.37 | 6.04 ± 1.28 | 3.76 ± 0.47 | 3.07 ± 0.44 | 2.61 ± 0.78 | 1.43 ± 0.58 | |
| Credit | AUC (↑) | 72.94 ± 1.32 | 70.31 ± 2.93 | 73.68 ± 0.67 | 73.78 ± 1.72 | 75.27 ± 1.63 | 74.45 ± 1.56 |
| F1 (↑) | 82.75 ± 2.2 | 81.95 ± 1.23 | 80.82 ± 3.57 | 81.36 ± 1.28 | 81.22 ± 0.83 | 83.35 ± 0.77 | |
| ACC (↑) | 75.82 ± 3.56 | 75.11 ± 1.15 | 76.4 ± 4.52 | 79.12 ± 1.12 | 79.88 ± 0.98 | 80.35 ± 0.83 | |
| △sp (↓) | 16.13 ± 3.31 | 8.09 ± 2.11 | 11.28 ± 2.16 | 6.89 ± 3.23 | 4.21 ± 1.58 | 3.47 ± 1.36 | |
| △eo (↓) | 12.32 ± 0.48 | 5.41 ± 1.95 | 8.29 ± 1.58 | 3.79 ± 2.31 | 4.10 ± 0.96 | 3.31 ± 0.72 |
| Datasets | Metrics (%) | GCN | FairGCN | SAGE | FairSAGE | GAT | FairGAT | GIN | FairGIN |
|---|---|---|---|---|---|---|---|---|---|
| German | AUC (↑) | 73.16 ± 1.86 | 75.42 ± 1.22 | 73.43 ± 1.81 | 74.37 ± 0.71 | 70.84 ± 0.71 | 72.63 ± 1.02 | 73.59 ± 1.36 | 76.25 ± 2.19 |
| F1 (↑) | 76.84 ± 1.65 | 83.79 ± 2.73 | 82.38 ± 1.12 | 84.54 ± 1.02 | 87.62 ± 1.57 | 85.39 ± 2.23 | 82.32 ± 1.82 | 80.58 ± 0.44 | |
| ACC (↑) | 71.76 ± 1.02 | 77.19 ± 0.31 | 70.83 ± 0.59 | 80.12 ± 1.19 | 71.63 ± 0.82 | 76.17 ± 1.03 | 72.56 ± 0.87 | 74.31 ± 1.93 | |
| △sp (↓) | 28.65 ± 3.26 | 2.4 ± 0.77 | 26.35 ± 5.17 | 1.91 ± 0.59 | 11.27 ± 1.93 | 4.58 ± 1.94 | 17.46 ± 6.31 | 2.83 ± 1.19 | |
| △eo (↓) | 24.73 ± 2.82 | 1.91 ± 0.21 | 17.39 ± 3.28 | 2.77 ± 1.03 | 9.03 ± 0.31 | 5.27 ± 1.33 | 10.28 ± 7.36 | 2.84 ± 1.92 | |
| Bail | AUC (↑) | 86.38 ± 1.26 | 86.73 ± 1.17 | 91.38 ± 0.46 | 88.49 ± 3.12 | 76.94 ± 1.16 | 79.11 ± 0.72 | 85.27 ± 0.42 | 81.26 ± 0.75 |
| F1 (↑) | 76.33 ± 1.47 | 77.67 ± 1.18 | 81.17 ± 1.32 | 81.39 ± 0.91 | 83.59 ± 2.06 | 85.51 ± 1.19 | 77.83 ± 0.49 | 79.31 ± 2.16 | |
| ACC (↑) | 88.61 ± 4.03 | 85.92 ± 2.03 | 88.72 ± 4.25 | 89.76 ± 1.81 | 85.02 ± 1.35 | 83.41 ± 1.55 | 82.71 ± 0.82 | 74.69 ± 0.71 | |
| △sp (↓) | 7.92 ± 1.21 | 5.43 ± 2.84 | 3.52 ± 2.52 | 1.89 ± 1.27 | 4.73 ± 0.59 | 4.41 ± 1.03 | 8.53 ± 1.27 | 4.31 ± 2.11 | |
| △eo (↓) | 6.61 ± 0.37 | 1.40 ± 1.26 | 1.92 ± 3.92 | 1.69 ± 0.73 | 7.86 ± 0.31 | 3.77 ± 2.09 | 8.39 ± 0.65 | 5.47 ± 0.93 | |
| Credit | AUC (↑) | 72.94 ± 1.32 | 76.59 ± 0.18 | 71.67 ± 1.38 | 77.42 ± 1.12 | 70.94 ± 1.08 | 72.37 ± 1.48 | 72.53 ± 2.37 | 76.82 ± 0.44 |
| F1 (↑) | 82.75 ± 2.2 | 83.71 ± 1.18 | 83.92 ± 1.17 | 85.33 ± 2.02 | 85.03 ± 1.41 | 86.26 ± 0.81 | 83.15 ± 0.14 | 82.39 ± 0.41 | |
| ACC (↑) | 75.82 ± 3.56 | 80.81 ± 0.15 | 75.27 ± 2.45 | 79.04 ± 2.26 | 79.36 ± 1.17 | 82.69 ± 1.36 | 77.96 ± 0.18 | 80.53 ± 1.87 | |
| △sp (↓) | 16.13 ± 3.31 | 3.79 ± 0.31 | 16.39 ± 1.98 | 3.77 ± 1.03 | 7.91 ± 2.49 | 3.79 ± 1.32 | 5.36 ± 1.12 | 2.23 ± 0.33 | |
| △eo (↓) | 12.32 ± 0.48 | 3.49 ± 0.94 | 12.17 ± 4.32 | 2.67 ± 0.74 | 11.58 ± 3.11 | 3.55 ± 2.19 | 3.46 ± 2.73 | 1.83 ± 0.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Z.; Zhou, Y.; Li, D.; Wang, K. Towards Fair Graph Neural Networks via Counterfactual and Balance. Information 2025, 16, 704. https://doi.org/10.3390/info16080704
Xiao Z, Zhou Y, Li D, Wang K. Towards Fair Graph Neural Networks via Counterfactual and Balance. Information. 2025; 16(8):704. https://doi.org/10.3390/info16080704
Chicago/Turabian StyleXiao, Zhiguo, Yangfan Zhou, Dongni Li, and Ke Wang. 2025. "Towards Fair Graph Neural Networks via Counterfactual and Balance" Information 16, no. 8: 704. https://doi.org/10.3390/info16080704
APA StyleXiao, Z., Zhou, Y., Li, D., & Wang, K. (2025). Towards Fair Graph Neural Networks via Counterfactual and Balance. Information, 16(8), 704. https://doi.org/10.3390/info16080704






