A Spatiotemporal Deep Learning Framework for Joint Load and Renewable Energy Forecasting in Stability-Constrained Power Systems
Abstract
1. Introduction
- 1.
- A CNN-Transformer hybrid model is constructed to enable accurate forecasting of multivariate time series in power systems.
- 2.
- A stability-aware scheduling optimization module is introduced to ensure frequency and voltage stability under high renewable penetration.
- 3.
- The effectiveness and generalization capability of the proposed framework are validated on multiple real-world power system datasets, showing significant improvements over state-of-the-art baseline models.
2. Related Work
2.1. Development of Power Load and New Energy Prediction Methods
2.2. The Application of Deep Learning in Power System Dispatch Optimization
2.3. Load—New Energy Coordinated Scheduling and System Stability
3. Materials and Method
3.1. Data Collection
3.2. Data Preprocessing and Augmentation
3.3. Proposed Method
3.3.1. Spatiotemporal Forecasting Module (CNN-Transformer Hybrid Network)
3.3.2. Stability-Aware Scheduling Module
3.3.3. Uncertainty Modeling and Robust Optimization Module
| Algorithm 1: Uncertainty Modeling and Robust Scheduling Pseudocode |
 |
4. Results and Discussion
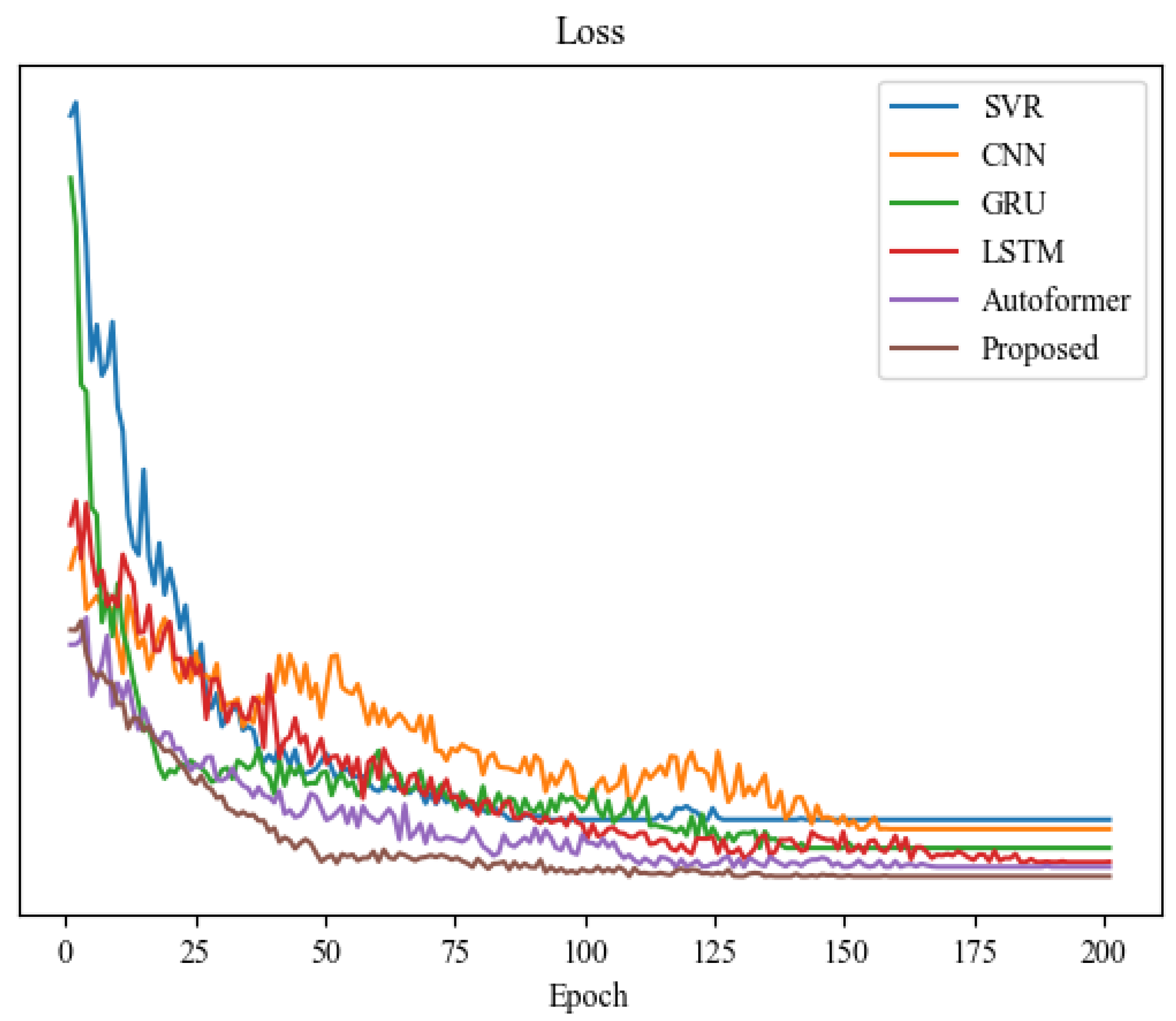
4.1. Experimental Setup
4.1.1. Data Split
4.1.2. Evaluation Metrics
4.1.3. Baseline
4.1.4. Hardware and Software Platform
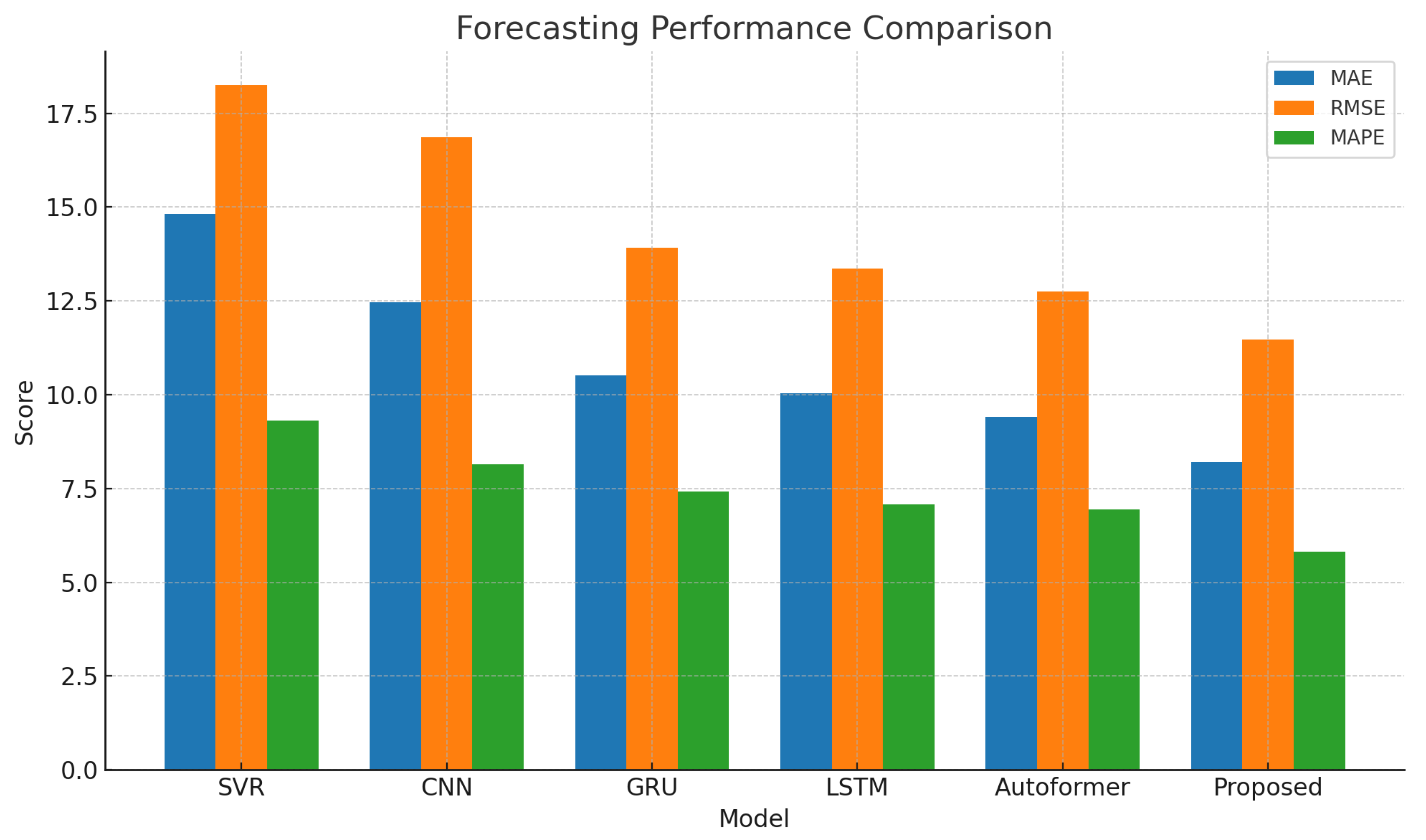
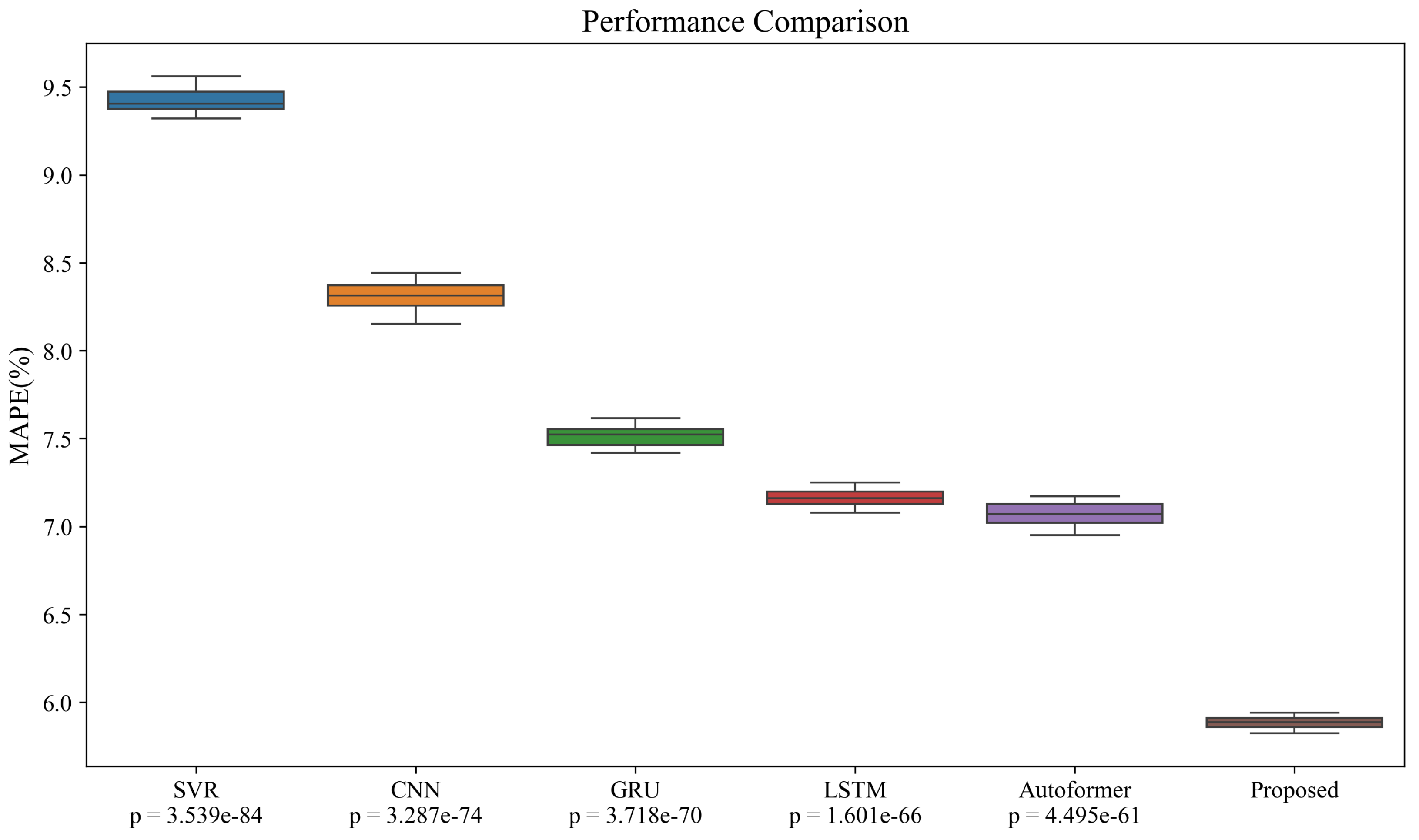
4.2. Forecasting Performance Comparison
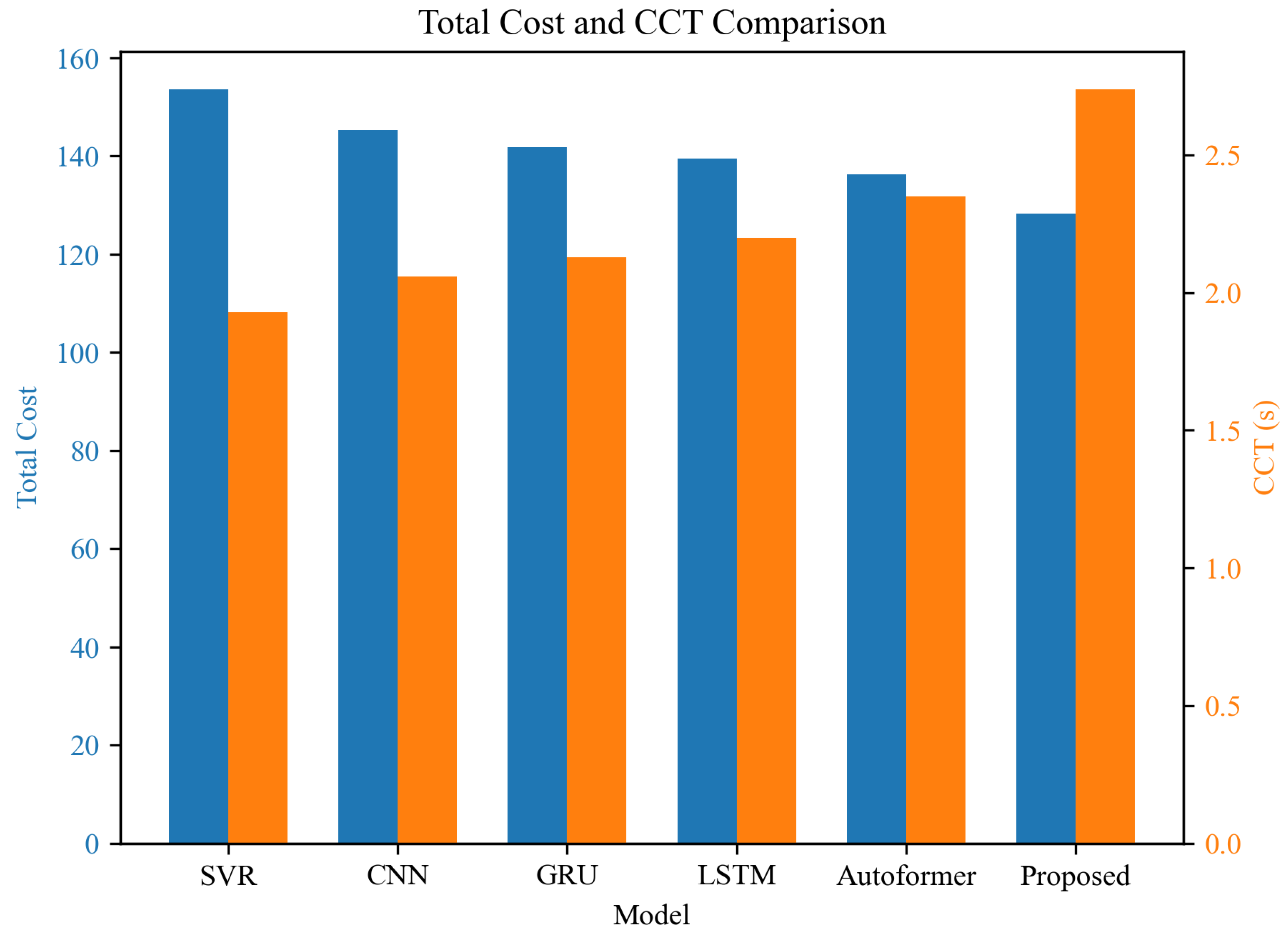
4.3. Economic Cost and Stability Performance Comparison
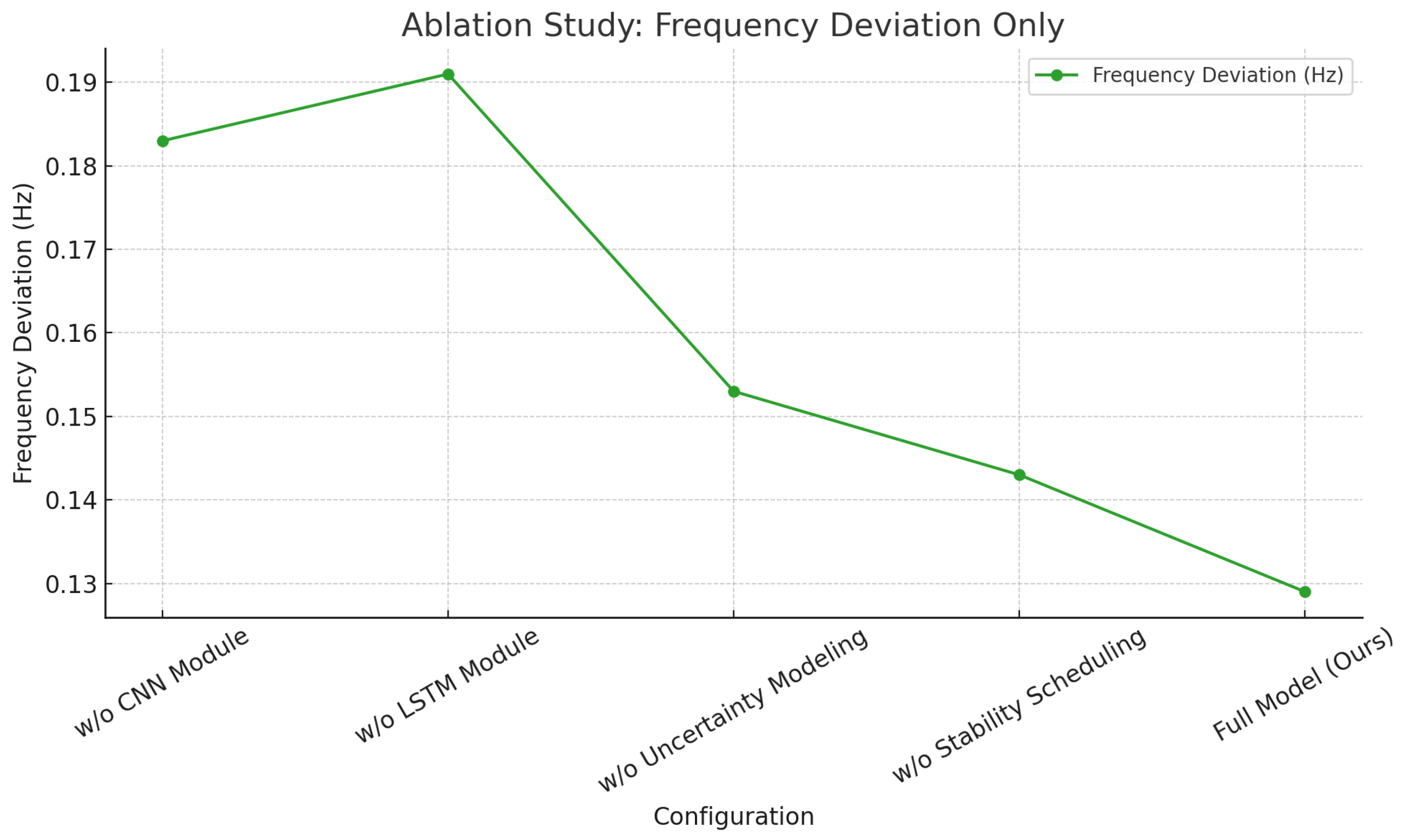
4.4. Ablation Study of Key Modules
4.5. Robustness Evaluation on Public SmartMeter Dataset
4.6. Discussion
4.7. Limitation and Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Chen, S.; Liu, P.; Li, Z. Low carbon transition pathway of power sector with high penetration of renewable energy. Renew. Sustain. Energy Rev. 2020, 130, 109985. [Google Scholar] [CrossRef]
- Li, X.; Wang, L.; Yan, N.; Ma, R. Cooperative dispatch of distributed energy storage in distribution network with PV generation systems. IEEE Trans. Appl. Supercond. 2021, 31, 0604304. [Google Scholar] [CrossRef]
- Luo, J.; Teng, F.; Bu, S. Stability-constrained power system scheduling: A review. IEEE Access 2020, 8, 219331–219343. [Google Scholar] [CrossRef]
- Zhu, J.; Zhou, B.; Qiu, Y.; Zang, T.; Zhou, Y.; Chen, S.; Dai, N.; Luo, H. Survey on modeling of temporally and spatially interdependent uncertainties in renewable power systems. Energies 2023, 16, 5938. [Google Scholar] [CrossRef]
- Wu, Y.; Fang, J.; Ai, X.; Xue, X.; Cui, S.; Chen, X.; Wen, J. Robust co-planning of AC/DC transmission network and energy storage considering uncertainty of renewable energy. Appl. Energy 2023, 339, 120933. [Google Scholar] [CrossRef]
- Dong, Y.; Shan, X.; Yan, Y.; Leng, X.; Wang, Y. Architecture, key technologies and applications of load dispatching in China power grid. J. Mod. Power Syst. Clean Energy 2022, 10, 316–327. [Google Scholar] [CrossRef]
- Cerna, F.V.; Contreras, J. A MILP model to relieve the occurrence of new demand peaks by improving the load factor in smart homes. Sustain. Cities Soc. 2021, 71, 102969. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, C.; Rao, X.; Zhang, X.; Zhou, Y. Spatial-temporal load forecasting of electric vehicle charging stations based on graph neural network. J. Intell. Fuzzy Syst. 2024, 46, 821–836. [Google Scholar] [CrossRef]
- Wang, S.; Wang, S.; Chen, H.; Gu, Q. Multi-energy load forecasting for regional integrated energy systems considering temporal dynamic and coupling characteristics. Energy 2020, 195, 116964. [Google Scholar] [CrossRef]
- Ibrahim, I.A.; Hossain, M. Short-term multivariate time series load data forecasting at low-voltage level using optimised deep-ensemble learning-based models. Energy Convers. Manag. 2023, 296, 117663. [Google Scholar] [CrossRef]
- Ma, Z.; Mei, G. A hybrid attention-based deep learning approach for wind power prediction. Appl. Energy 2022, 323, 119608. [Google Scholar] [CrossRef]
- Tang, X.; Chen, H.; Xiang, W.; Yang, J.; Zou, M. Short-term load forecasting using channel and temporal attention based temporal convolutional network. Electr. Power Syst. Res. 2022, 205, 107761. [Google Scholar] [CrossRef]
- Ibrahim, M.S.; Gharghory, S.M.; Kamal, H.A. A hybrid model of CNN and LSTM autoencoder-based short-term PV power generation forecasting. Electr. Eng. 2024, 106, 4239–4255. [Google Scholar] [CrossRef]
- Liu, W.; Mao, Z. Short-term photovoltaic power forecasting with feature extraction and attention mechanisms. Renew. Energy 2024, 226, 120437. [Google Scholar] [CrossRef]
- Vasudevan, A.K.; Anandhan, A. Effects of Steel Confinement on the Impact Responses of Precast Concrete Segmental Columns. Int. J. Adv. Eng. Emerg. Technol. 2022, 13, 167–181. [Google Scholar]
- Abdulameer, Y.H.; Ibrahim, A.A. Forecasting of Electrical Energy Consumption Using Hybrid Models of GRU, CNN, LSTM, and ML Regressors. J. Wirel. Mob. Netw. 2025, 16, 560–575. [Google Scholar] [CrossRef]
- Fara, L.; Diaconu, A.; Craciunescu, D.; Fara, S. Forecasting of energy production for photovoltaic systems based on ARIMA and ANN advanced models. Int. J. Photoenergy 2021, 2021, 6777488. [Google Scholar] [CrossRef]
- Elsaraiti, M.; Ali, G.; Musbah, H.; Merabet, A.; Little, T. Time series analysis of electricity consumption forecasting using ARIMA model. In Proceedings of the 2021 IEEE Green Technologies Conference (GreenTech), Denver, CO, USA, 7–9 April 2021; pp. 259–262. [Google Scholar]
- Nepal, B.; Yamaha, M.; Yokoe, A.; Yamaji, T. Electricity load forecasting using clustering and ARIMA model for energy management in buildings. Jpn. Archit. Rev. 2020, 3, 62–76. [Google Scholar] [CrossRef]
- Nguyen, R.; Yang, Y.; Tohmeh, A.; Yeh, H.G. Predicting PV power generation using SVM regression. In Proceedings of the 2021 IEEE Green Energy and Smart Systems Conference (IGESSC), Long Beach, CA, USA, 1–2 November 2021; pp. 1–5. [Google Scholar]
- Meng, Z.; Sun, H.; Wang, X. Forecasting energy consumption based on SVR and Markov model: A case study of China. Front. Environ. Sci. 2022, 10, 883711. [Google Scholar] [CrossRef]
- Yan, Y.; Zhang, Z. Cooling, heating and electrical load forecasting method for integrated energy system based on SVR model. In Proceedings of the 2021 6th Asia Conference on Power and Electrical Engineering (ACPEE), Chongqing, China, 8–11 April 2021; pp. 1753–1758. [Google Scholar]
- Rao, C.; Zhang, Y.; Wen, J.; Xiao, X.; Goh, M. Energy demand forecasting in China: A support vector regression-compositional data second exponential smoothing model. Energy 2023, 263, 125955. [Google Scholar] [CrossRef]
- Pierre, A.; Akim, S.; Semenyo, A.; Babiga, B. Peak Electrical Energy Consumption Prediction by ARIMA, LSTM, GRU, ARIMA-LSTM and ARIMA-GRU Approaches. Energies 2023, 16, 4739. [Google Scholar] [CrossRef]
- Ciechulski, T.; Osowski, S. High precision LSTM model for short-time load forecasting in power systems. Energies 2021, 14, 2983. [Google Scholar] [CrossRef]
- Wu, K.; Gu, J.; Meng, L.; Wen, H.; Ma, J. An explainable framework for load forecasting of a regional integrated energy system based on coupled features and multi-task learning. Prot. Control Mod. Power Syst. 2022, 7, 1–14. [Google Scholar] [CrossRef]
- Jailani, N.L.M.; Dhanasegaran, J.K.; Alkawsi, G.; Alkahtani, A.A.; Phing, C.C.; Baashar, Y.; Capretz, L.F.; Al-Shetwi, A.Q.; Tiong, S.K. Investigating the power of LSTM-based models in solar energy forecasting. Processes 2023, 11, 1382. [Google Scholar] [CrossRef]
- Jin, N.; Yang, F.; Mo, Y.; Zeng, Y.; Zhou, X.; Yan, K.; Ma, X. Highly accurate energy consumption forecasting model based on parallel LSTM neural networks. Adv. Eng. Informatics 2022, 51, 101442. [Google Scholar] [CrossRef]
- Wang, J.Q.; Du, Y.; Wang, J. LSTM based long-term energy consumption prediction with periodicity. Energy 2020, 197, 117197. [Google Scholar] [CrossRef]
- Iruela, J.; Ruiz, L.; Criado-Ramón, D.; Pegalajar, M.; Capel, M. A GPU-accelerated adaptation of the PSO algorithm for multi-objective optimization applied to artificial neural networks to predict energy consumption. Appl. Soft Comput. 2024, 160, 111711. [Google Scholar] [CrossRef]
- Iruela, J.; Ruiz, L.; Pegalajar, M.; Capel, M. A parallel solution with GPU technology to predict energy consumption in spatially distributed buildings using evolutionary optimization and artificial neural networks. Energy Convers. Manag. 2020, 207, 112535. [Google Scholar] [CrossRef]
- Iruela, J.; Ruiz, L.B.; Capel, M.; Pegalajar, M. A tensorflow approach to data analysis for time series forecasting in the energy-efficiency realm. Energies 2021, 14, 4038. [Google Scholar] [CrossRef]
- Wang, S.; Shi, J.; Yang, W.; Yin, Q. High and low frequency wind power prediction based on Transformer and BiGRU-Attention. Energy 2024, 288, 129753. [Google Scholar] [CrossRef]
- Wang, L.; He, Y.; Liu, X.; Li, L.; Shao, K. M2TNet: Multi-modal multi-task Transformer network for ultra-short-term wind power multi-step forecasting. Energy Rep. 2022, 8, 7628–7642. [Google Scholar] [CrossRef]
- Galindo Padilha, G.A.; Ko, J.; Jung, J.J.; de Mattos Neto, P.S.G. Transformer-based hybrid forecasting model for multivariate renewable energy. Appl. Sci. 2022, 12, 10985. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Y.; Ding, Z.; Zheng, T.; Hu, J.; Zhang, K. A transformer-based method of multienergy load forecasting in integrated energy system. IEEE Trans. Smart Grid 2022, 13, 2703–2714. [Google Scholar] [CrossRef]
- L’Heureux, A.; Grolinger, K.; Capretz, M.A. Transformer-based model for electrical load forecasting. Energies 2022, 15, 4993. [Google Scholar] [CrossRef]
- Guo, C.; Luo, F.; Cai, Z.; Dong, Z.Y. Integrated energy systems of data centers and smart grids: State-of-the-art and future opportunities. Appl. Energy 2021, 301, 117474. [Google Scholar] [CrossRef]
- Xu, B.; Xiang, Y. Optimal operation of regional integrated energy system based on multi-agent deep deterministic policy gradient algorithm. Energy Rep. 2022, 8, 932–939. [Google Scholar] [CrossRef]
- Yang, T.; Zhao, L.; Li, W.; Zomaya, A.Y. Dynamic energy dispatch strategy for integrated energy system based on improved deep reinforcement learning. Energy 2021, 235, 121377. [Google Scholar] [CrossRef]
- Ebrie, A.S.; Kim, Y.J. Reinforcement learning-based optimization for power scheduling in a renewable energy connected grid. Renew. Energy 2024, 230, 120886. [Google Scholar] [CrossRef]
- Jiang, W.; Liu, Y.; Fang, G.; Ding, Z. Research on short-term optimal scheduling of hydro-wind-solar multi-energy power system based on deep reinforcement learning. J. Clean. Prod. 2023, 385, 135704. [Google Scholar] [CrossRef]
- Liu, S.; Liu, J.; Ye, W.; Yang, N.; Zhang, G.; Zhong, H.; Kang, C.; Jiang, Q.; Song, X.; Di, F.; et al. Real-time scheduling of renewable power systems through planning-based reinforcement learning. arXiv 2023, arXiv:2303.05205. [Google Scholar]
- Zhou, X.; Wang, J.; Wang, X.; Chen, S. Optimal dispatch of integrated energy system based on deep reinforcement learning. Energy Rep. 2023, 9, 373–378. [Google Scholar] [CrossRef]
- Meng, Q.; Tong, X.; Hussain, S.; Luo, F.; Zhou, F.; He, Y.; Liu, L.; Sun, B.; Li, B. Enhancing distribution system stability and efficiency through multi-power supply startup optimization for new energy integration. IET Gener. Transm. Distrib. 2024, 18, 3487–3500. [Google Scholar] [CrossRef]
- Poulose, A.; Kim, S. Transient stability analysis and enhancement techniques of renewable-rich power grids. Energies 2023, 16, 2495. [Google Scholar] [CrossRef]
- Zhou, J.; Li, M.; Du, L.; Xi, Z. Power Grid transient stability prediction method based on improved CNN under big data background. In Proceedings of the 2022 Asian Conference on Frontiers of Power and Energy (ACFPE), Chengdu, China, 21–23 October 2022; pp. 183–187. [Google Scholar]
- Fan, S.; Zhao, Z.; Guo, J.; Ma, S.; Wang, T.; Li, D. Review on data-driven power system transient stability assessment technology. In Proceedings of the CSEE, Shanghai, China, 27–29 February 2024; Volume 44, pp. 3408–3429. [Google Scholar]
- El-Bahay, M.H.; Lotfy, M.E.; El-Hameed, M.A. Computational methods to mitigate the effect of high penetration of renewable energy sources on power system frequency regulation: A comprehensive review. Arch. Comput. Methods Eng. 2023, 30, 703–726. [Google Scholar] [CrossRef]
- Li, J.; Qiao, Y.; Lu, Z.; Ma, W.; Cao, X.; Sun, R. Integrated frequency-constrained scheduling considering coordination of frequency regulation capabilities from multi-source converters. J. Mod. Power Syst. Clean Energy 2023, 12, 261–274. [Google Scholar] [CrossRef]
- Li, L.; Zhu, D.; Zou, X.; Hu, J.; Kang, Y.; Guerrero, J.M. Review of frequency regulation requirements for wind power plants in international grid codes. Renew. Sustain. Energy Rev. 2023, 187, 113731. [Google Scholar] [CrossRef]
- Alonso, A.M.; Nogales, F.J.; Ruiz, C. A single scalable LSTM model for short-term forecasting of massive electricity time series. Energies 2020, 13, 5328. [Google Scholar] [CrossRef]
- Boucetta, L.N.; Amrane, Y.; Arezki, S. Wind power forecasting using a GRU attention model for efficient energy management systems. Electr. Eng. 2024, 107, 2595–2620. [Google Scholar] [CrossRef]
- Ju, Y.-f.; Wu, S.-w. Village electrical load prediction by genetic algorithm and SVR. In Proceedings of the 2010 3rd International Conference on Computer Science and Information Technology, Chengdu, China, 9–11 July 2010; Volume 2, pp. 278–281. [Google Scholar] [CrossRef]
- Shaikh, A.K.; Nazir, A.; Khalique, N.; Shah, A.S.; Adhikari, N. A New Approach to Seasonal Energy Consumption Forecasting Using Temporal Convolutional Networks. Results Eng. 2023, 19, 101296. [Google Scholar] [CrossRef]
- Sun, D.; He, Z. Innovative Approaches to Long-term Power Load Forecasting with Autoformer. In Proceedings of the 2024 13th International Conference of Information and Communication Technology (ICTech), Xiamen, China, 12–14 April 2024; pp. 176–181. [Google Scholar]
- Greater London Authority. SmartMeter Energy Use Data in London Households; Greater London Authority: London, UK, 2017. [Google Scholar]
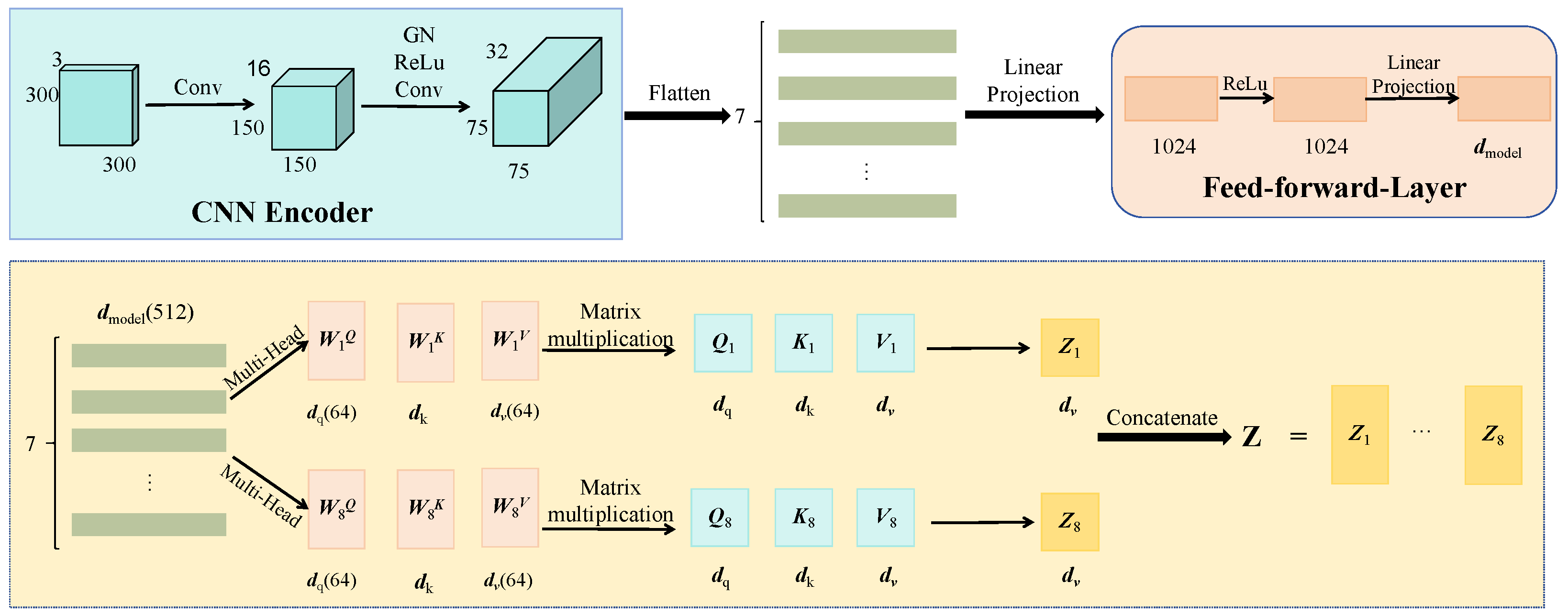
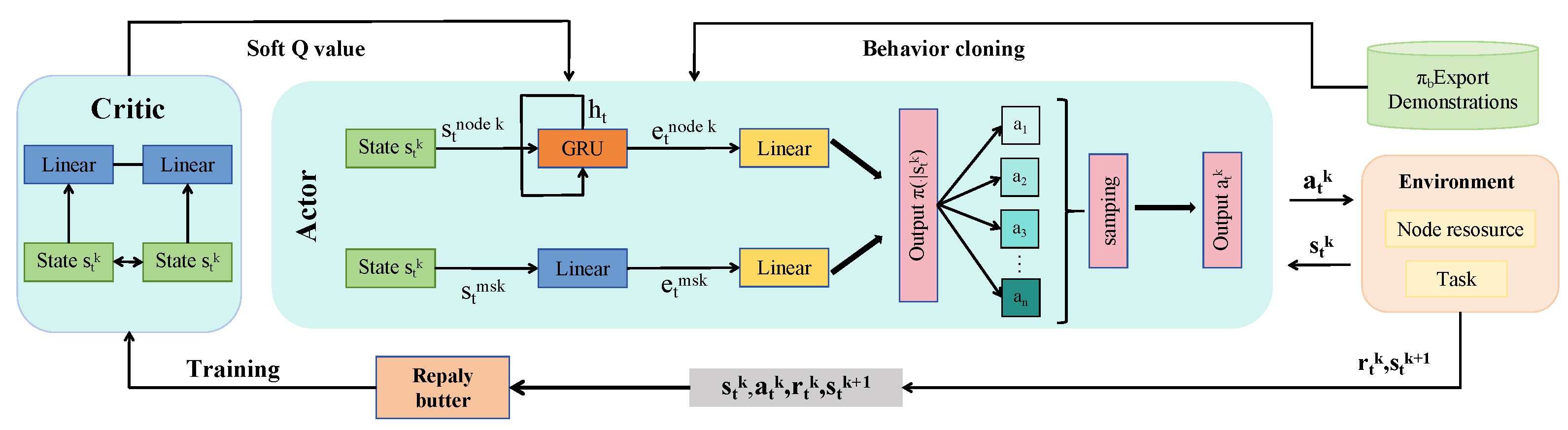
| Data Type | Source | Number of Variables | Number of Samples |
|---|---|---|---|
| Load power | Grid control system | residential/industrial/commercial | 96k |
| Wind generation | NEA/SCADA | wind speed, direction, pitch, output, etc. | 96k |
| Solar generation | SCADA system | irradiance, temperature, power output, etc. | 96k |
| Meteorological | CMA/AWS | temperature, humidity, pressure, wind, etc. | 96k |
| Grid status | RTU (IEC-104 protocol) | frequency, voltage, angle, margin, etc. | 96k |
| Dispatch instruction | Scheduling platform | type, duration, magnitude, etc. | 96k |
| Model | MAE (↓) | RMSE (↓) | MAPE (%) (↓) |
|---|---|---|---|
| SVR | 14.82 | 18.25 | 9.32 |
| CNN | 12.46 | 16.87 | 8.15 |
| GRU | 10.51 | 13.92 | 7.42 |
| LSTM | 10.03 | 13.37 | 7.08 |
| Autoformer | 9.41 | 12.76 | 6.95 |
| Proposed | 8.21 | 11.48 | 5.82 |
| Model | Total Cost (↓) | Frequency Deviation (Hz) (↓) | CCT (s) (↑) |
|---|---|---|---|
| SVR | 153.6 | 0.238 | 1.93 |
| CNN | 145.2 | 0.194 | 2.06 |
| GRU | 141.8 | 0.176 | 2.13 |
| LSTM | 139.4 | 0.169 | 2.20 |
| Autoformer | 136.2 | 0.158 | 2.35 |
| Proposed | 128.3 | 0.129 | 2.74 |
| Configuration | MAE | Total Cost | Frequency Deviation (Hz) |
|---|---|---|---|
| w/o CNN Module | 10.74 | 143.5 | 0.183 |
| w/o LSTM Module | 11.26 | 147.2 | 0.191 |
| w/o Uncertainty Modeling | 9.85 | 137.1 | 0.153 |
| w/o Stability Scheduling | 9.02 | 131.6 | 0.143 |
| Full Model (Ours) | 8.21 | 128.3 | 0.129 |
| Model | MAE (↓) | RMSE (↓) | MAPE (%) (↓) |
|---|---|---|---|
| SVR | 15.04 | 18.57 | 9.48 |
| CNN | 12.87 | 16.64 | 8.32 |
| GRU | 10.78 | 14.23 | 7.58 |
| LSTM | 10.32 | 13.62 | 7.24 |
| Autoformer | 9.74 | 13.05 | 6.91 |
| RO (Two-stage) | 10.12 | 13.34 | 6.78 |
| SO (Two-stage) | 9.87 | 12.96 | 6.52 |
| Transformer | 9.41 | 12.74 | 6.33 |
| Galindo Transformer | 9.02 | 12.23 | 6.01 |
| MultiDeT | 8.88 | 11.95 | 5.93 |
| Proposed (Ours) | 8.45 | 11.73 | 5.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, M.; Yu, J.; Wu, M.; Zhu, Y.; Zhang, Y.; Zhu, Y. A Spatiotemporal Deep Learning Framework for Joint Load and Renewable Energy Forecasting in Stability-Constrained Power Systems. Information 2025, 16, 662. https://doi.org/10.3390/info16080662
Cheng M, Yu J, Wu M, Zhu Y, Zhang Y, Zhu Y. A Spatiotemporal Deep Learning Framework for Joint Load and Renewable Energy Forecasting in Stability-Constrained Power Systems. Information. 2025; 16(8):662. https://doi.org/10.3390/info16080662
Chicago/Turabian StyleCheng, Min, Jiawei Yu, Mingkang Wu, Yihua Zhu, Yayao Zhang, and Yuanfu Zhu. 2025. "A Spatiotemporal Deep Learning Framework for Joint Load and Renewable Energy Forecasting in Stability-Constrained Power Systems" Information 16, no. 8: 662. https://doi.org/10.3390/info16080662
APA StyleCheng, M., Yu, J., Wu, M., Zhu, Y., Zhang, Y., & Zhu, Y. (2025). A Spatiotemporal Deep Learning Framework for Joint Load and Renewable Energy Forecasting in Stability-Constrained Power Systems. Information, 16(8), 662. https://doi.org/10.3390/info16080662





