The cryptographic application of the three options presented is the sharing of a secret over an insecure channel between two entities, A and B. The three options are strategies for sharing a secret, each using a different formula involving several , but each function calculation is the same in each of them.
This secret can then be used, for example, as the key of a symmetric cryptographic system. All options assume that the values , , , and are agreed upon between A and B through this insecure channel and are, therefore, public. We also evaluated that the values and are integers chosen randomly, respectively, by A and B, being taken from the set of keys , thus being a secret variable for A and another for B. Also, is the index up to which B will perform the sum of the list of values A shared.
3.2.4. Limitations and Susceptibility to Attacks
In this section, we analyze each one-variable option and point out its limitations and susceptibility to attacks.
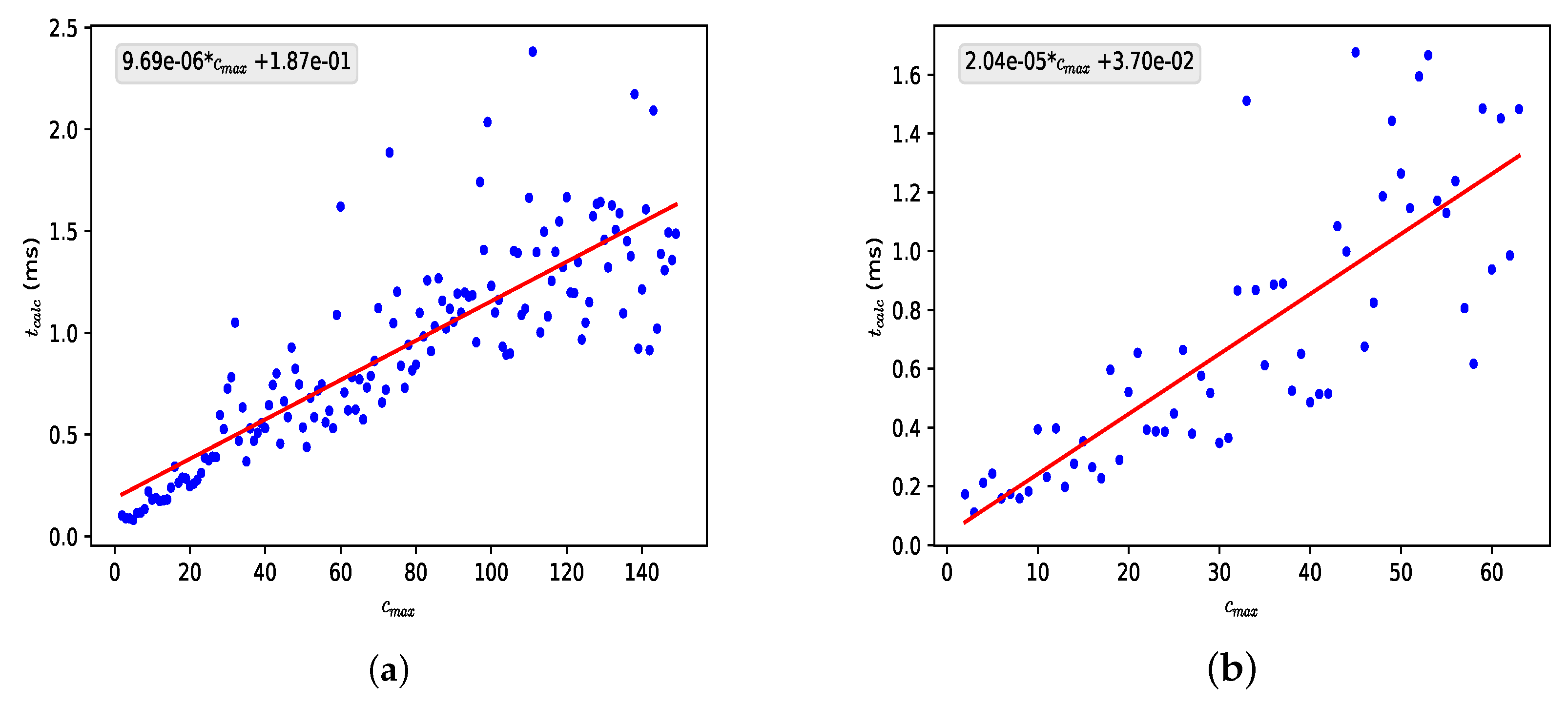
Option 1 uses only two equations for partitioning integers into k parts, one corresponding to and one corresponding to . Therefore, its implementation is simple, and increasing the number does not result in a large increase in computational time since this time continues to be the time required to replace the variable in an equation similar to a polynomial.
However, since the equations are known to everyone and the number is public, by sharing an element of the list sent by A, it is possible to solve the equation corresponding to this element and reveal since this equation has only one variable and it is known that the root sought is an integer. Let us take the following examples.
Let us take
,
,
,
, and
.
A performs the operation:
, for the eight possible values of
, and sends this list of values to
B.
B similarly sends the following list:
A then chooses the third element from the list sent by B and computes the secret with , finding . B chooses the fourth element from the list sent by A and computes the secret, .
However, if an attacker has access to the list that
A sends, they can deduce the value of
by using the equation
, equating it to the first value in the list:
We see that by replacing or with a larger number, or even increasing the value of , the problem would persist since the equations of are similar to polynomials and known by everyone. It is also noted that the number would be revealed to an observer of the channel by the same procedure.
Therefore, option 1 is insufficient to perform the secret exchange since by revealing and , the secret exchanged is revealed to a potential attacker.
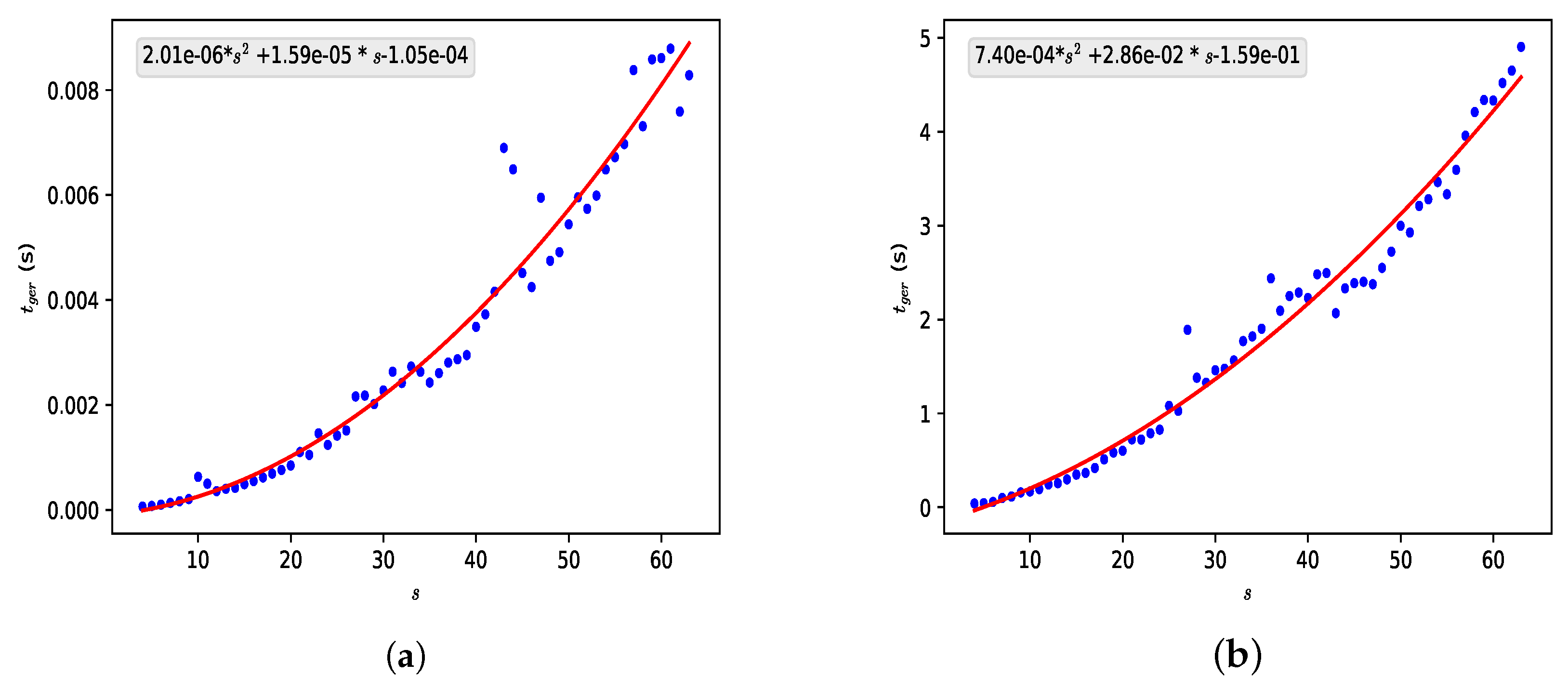
Option 2 uses several different “k”. Therefore, its use is conditioned on such equations being known or on there being another algorithm that can obtain in a reasonable time since the ideal would be to have a large number of possible values of and . The recurrence equation could be used to obtain values of for small n (<), but these values would not be useful for generating cryptographic keys of considerable size.
However, even if this obstacle is overcome, there is an attack that allows an observer of the channel to know and . Since we assume that and are known to everyone, an observer would simply compute a list of values for , varying the value X, and compare it with the lists that are exchanged. Let us take the following example.
Let us take
,
,
,
, and
.
A performs the operation:
, for the eight possible values of
, and sends this list of values to
B.
B similarly sends the following list:
A then chooses the third element of the list sent by B and computes the secret with , finding 376. B chooses the fourth element from the list sent by A and computes the secret .
However, the attacker can generate the following list of possible first values:
Thus, by comparing the values, the attacker determines and .
As in the case of option 1, increasing the values of and will have no effect on the attack. One can increase the value of , causing an attacker to have to calculate and compare more values for , but this would come at an additional computational cost for A and B, proportional to this possible increase in .
Therefore, option 2 is insufficient to perform the secret exchange.
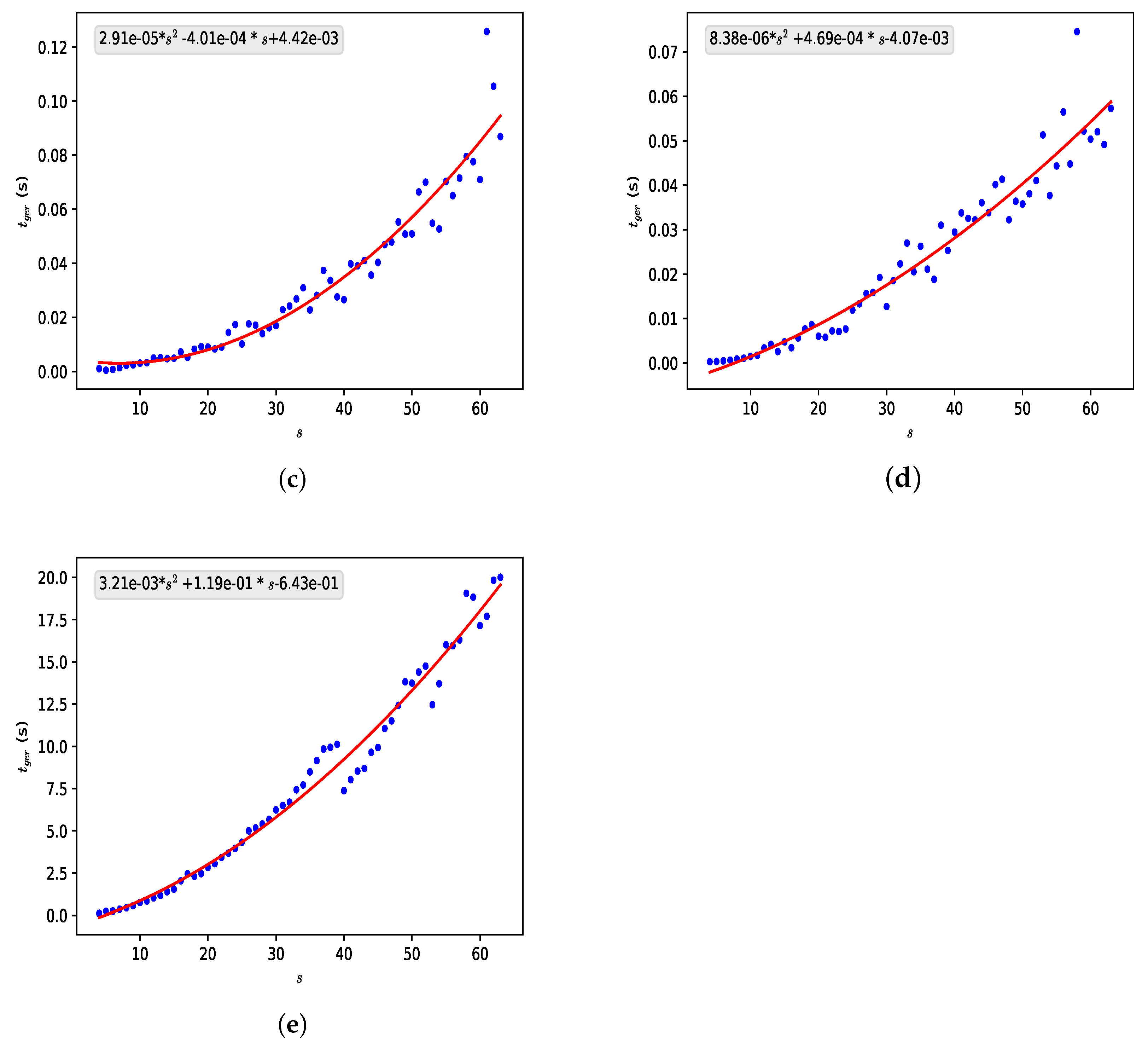
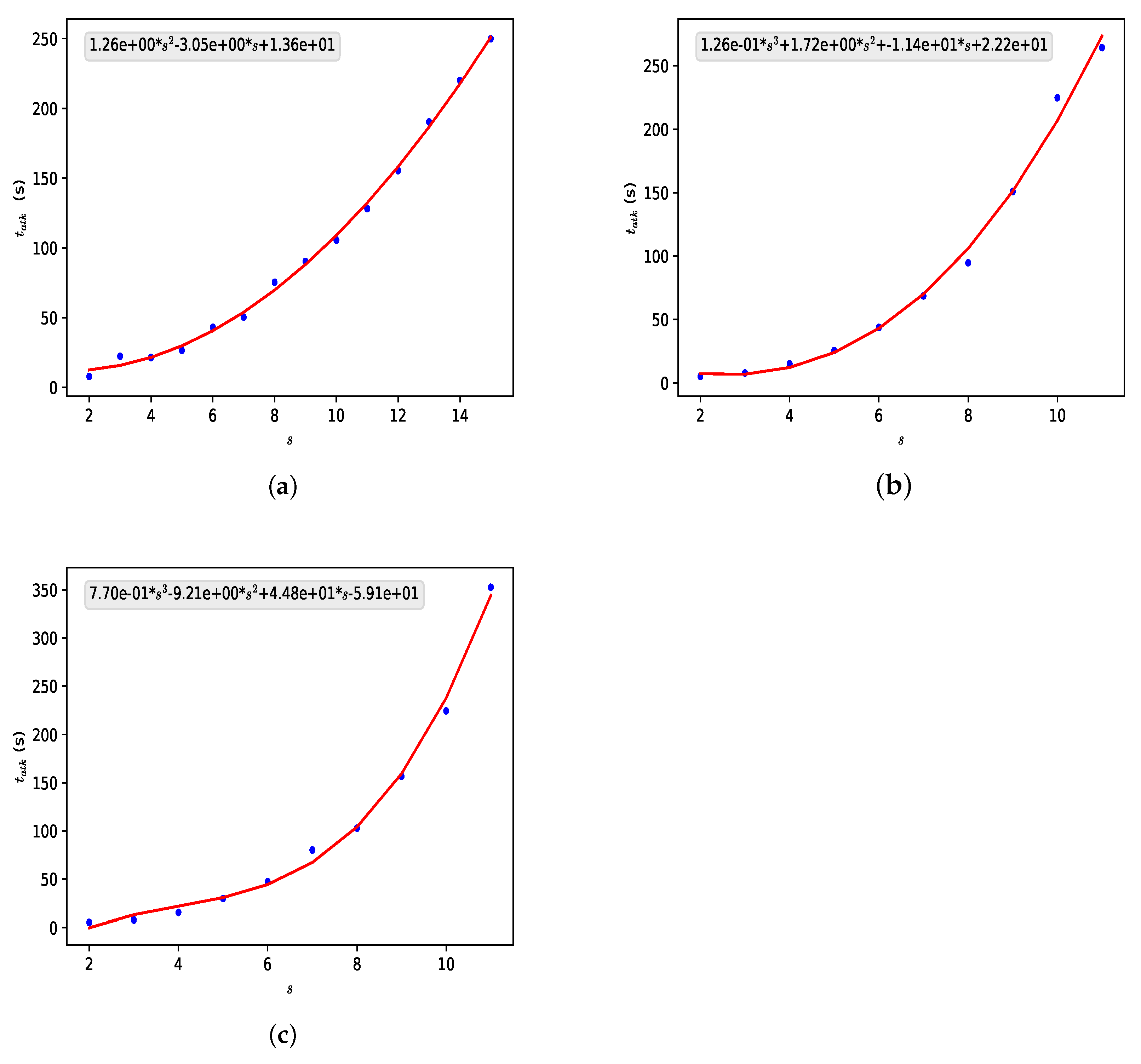
Option 3 combines the advantages of options 1 and 2. Concerning the part coming from option 1, we can use large numbers without greatly increasing the computational time used. By adding the part coming from option 2 in the generation of the exchanged list of values, we also have the change of not using only one equation of , but two, and an attacker would not know a priori which equation is in each position of the list since the equation varies with the values of (or ).
However, the increase in the complexity of the key continues to occur only with the increase in the value of , which in turn causes an increase in the amount of calculations necessary to generate the lists since the size of the lists is , a factor that greatly limits our key space. This leads us to explore other possibilities to increase the complexity of the system.