Abstract
Artificial Intelligence (AI) and computer-aided diagnosis (CAD) have revolutionised various aspects of modern life, particularly in the medical domain. These technologies enable efficient solutions for complex challenges, such as accurately segmenting brain tumour regions, which significantly aid medical professionals in monitoring and treating patients. This research focuses on segmenting glioma brain tumour lesions in MRI images by analysing them at the pixel level. The aim is to develop a deep learning-based approach that enables ensemble learning to achieve precise and consistent segmentation of brain tumours. While many studies have explored ensemble learning techniques in this area, most rely on aggregation functions like the Weighted Arithmetic Mean (WAM) without accounting for the interdependencies between classifier subsets. To address this limitation, the Choquet integral is employed for ensemble learning, along with a novel evaluation framework for fuzzy measures. This framework integrates coalition game theory, information theory, and Lambda fuzzy approximation. Three distinct fuzzy measure sets are computed using different weighting strategies informed by these theories. Based on these measures, three Choquet integrals are calculated for segmenting different components of brain lesions, and their outputs are subsequently combined. The BraTS-2020 online validation dataset is used to validate the proposed approach. Results demonstrate superior performance compared with several recent methods, achieving Dice Similarity Coefficients of 0.896, 0.851, and 0.792 and 95% Hausdorff distances of 5.96 mm, 6.65 mm, and 20.74 mm for the whole tumour, tumour core, and enhancing tumour core, respectively.
1. Introduction
Brain tumours are abnormal cell growths in the brain or surrounding tissues, classified as primary (originating in the brain) or secondary (metastatic, from other parts of the body) tumours. While their causes are not fully understood, genetic factors, radiation exposure, and environmental influences may contribute. Treatment typically involves surgery, radiation therapy, and chemotherapy, depending on tumour type, location, and stage. Medical imaging, particularly MRI, plays a critical role in diagnosing and managing brain tumours due to its superior soft tissue contrast. However, manual diagnosis faces challenges such as subjective interpretation, variability in radiologist expertise, and complex tumour morphology, leading to potential misdiagnoses or delays in treatment [1,2].
Conventional approaches to brain tumour segmentation primarily rely on manual delineation by expert radiologists or traditional image processing techniques, such as thresholding, region growing, edge detection. These methods mainly utilize handcrafted features—such as intensity, texture, and shape descriptors—to distinguish tumour tissue from healthy brain structures. While these techniques have contributed to advancements in medical imaging analysis, they frequently suffer from limitations, including sensitivity to image noise, poor generalizability across diverse patient populations, and an inability to capture the intricate and heterogeneous nature of brain tumours [3]. Furthermore, manual segmentation is time-consuming and subject to intra- and inter-observer variability, which can compromise diagnostic consistency and accuracy.
Artificial Intelligence (AI) offers solutions to these challenges, enhancing diagnostic accuracy and reducing variability. Deep learning methods, especially Convolutional Neural Networks (CNNs), have proven effective for tasks like tumour segmentation, enabling early detection and personalized treatment [1,4]. Ensemble learning further improves model performance by combining predictions from multiple algorithms, though traditional aggregation methods like the Arithmetic Mean or Weighted Arithmetic Mean fail to account for classifier interactions. Advanced methods, such as fuzzy integrals (e.g., the Choquet integral), address these limitations by considering both the importance of individual classifiers and their interactions [5].
Calculating fuzzy measures for such integrals is computationally complex, but the Lambda fuzzy approximation balances complexity and applicability. This study uses the Lambda fuzzy approximation, supported by coalition game theory, to compute fuzzy measures and applies the Choquet integral to aggregate predictions from multiple CNN models [6]. Segmentation of brain tumours remains challenging due to complex tumour morphology and imaging variability. While U-Net-based architectures have shown success [7], improvements are needed in capturing spatial relationships. This study introduces the following two novel feature concatenation techniques to enhance U-Net models:
- 1.
- Channel shuffling: Intermixes encoder and decoder feature maps to improve hierarchical feature processing and spatial detail capture;
- 2.
- Width shuffling: Shuffles feature map widths to enhance spatial resolution, particularly for high-dimensional 3D data.
An ensemble framework aggregates predictions from six U-Net variants using the Choquet integral, which accounts for interactions between subsets of models. Fuzzy measures calculated using the Lambda fuzzy approximation and coalition game theory address the limitations of traditional ensemble methods [8]. Key contributions include the following:
- Novel channel and width shuffling techniques to enhance U-Net-based architectures;
- A method for fuzzy measure calculation using coalition game theory and the Lambda fuzzy approximation;
- Application of the Choquet integral to aggregate predictions, enabling robust tumour segmentation.
The remainder of the paper is structured as follows: Section 2 reviews related work on brain tumour diagnosis and segmentation. Section 3 describes the dataset and details the proposed method. Section 5 outlines the experimental setup and methodology. Section 6 presents experimental results, including error analysis and comparisons with state-of-the-art methods. Section 7 concludes the paper and discusses potential future research directions.
2. Related Work
The field of brain tumour segmentation has seen significant advancements through deep learning techniques, benchmarked on datasets such as BraTS-2020. These developments span network architectures, loss functions, optimisers, and data augmentation strategies. Related work can be organised into three categories: standalone models, ensemble-based approaches, and methods leveraging recent deep architectures.
2.1. Standalone Models for Brain Tumour Segmentation
Standalone models form the foundation of brain tumour segmentation research. Various techniques focus on optimising networks, incorporating attention mechanisms, and leveraging hierarchical or probabilistic designs. Sun et al. [9] introduced HAD-Net, which incorporates hyper-scale shifted aggregating and max-diagonal sampling techniques to optimise multi-scale interactions in U-Net frameworks. Yu [10] proposed DTASUnet, a U-shaped network employing dual transformers to extract local and global features, achieving robust results on BraTS and BTCV datasets. S and Clement [11] developed IC-Net with multi-attention blocks and feature concatenation networks to address challenges like tumour heterogeneity. Soulaiman et al. [12] proposed an efficient LinkNet-34 model with an EfficientNetB7 encoder, achieving a Dice Coefficient of 0.915 and reducing computational costs while maintaining segmentation accuracy. Zhang et al. [13] developed AugTransU-Net, which combines U-Net with Transformer modules and paired attention mechanisms to capture long-range dependencies. Guan et al. [14] introduced 3D AGSE-VNet, incorporating anisotropic convolutional layers, Squeeze and Excite (SE) modules, and Attention Guide Filters (AG) to handle anisotropic voxel sizes and reduce noise. Zhuang et al. [15] developed ACMINet, employing cross-modality feature fusion and dual interaction graph reasoning for improved spatial and channel feature relationships. Ahmad et al. [16] presented MH-UNet, leveraging hierarchical structures and residual-inception blocks to integrate global and local information. Xu et al. [17] proposed CH-UNet, which incorporates corner attention mechanisms (CAM) and high-dimensional perceptual loss (HDPL) to enhance inter-slice information modelling and preserve local consistency. Liu [18] introduced a noise diffusion probability model for multi-class segmentation, enhancing recognition in challenging regions like enhancing tumours (ET) using a two-step approach that combines diffusion-based modelling with ET boundary recognition.
2.2. Ensemble-Based Approaches
Ensemble methods have emerged as a promising strategy to improve segmentation accuracy by combining the strengths of multiple models. Rajput et al. [19] proposed a tri-planar ensemble model for robust segmentation using multi-parametric MRI (mpMRI) data, incorporating attention mechanisms to enhance feature focus. Henry et al. [20] introduced a deeply supervised 3D U-Net ensemble, utilizing Stochastic Weight Averaging (swa) to prevent overfitting. Nguyen et al. [21] employed nested U-Nets and BiFPN ensembles combined with a classification network for improved tumour boundary differentiation. Zaho et al. [22] proposed UMM, integrating predictions from 2D-CNN, 2.5D-CNN, and 3D-CNN models using uncertainty-aware soft labels. Furthermore, a fuzzy ensemble framework based on the Choquet integral was introduced, leveraging fuzzy measures and coalition game theory to account for inter-model interactions. Wen et al. [23] designed a deep ensemble framework using multimodal MRI data, combining asymmetric convolution and dual-domain attention mechanisms for simultaneous segmentation and glioma risk grading. Litijens et al. [3] utilized modality-pairing learning in a 3D U-Net for the BraTS-2020 Challenge, incorporating ensemble strategies and post-processing for refined segmentation.
2.3. Methods Leveraging Recent Deep Architectures
Recent innovations in deep architectures have further improved tumour segmentation through attention mechanisms, feature aggregation, and novel optimisers. Akbar et al. [24] proposed MRAB-UNet, integrating Multipath Residual Attention Blocks (MRABs) and attention gates in skip connections for focused feature extraction. Liu et al. [25] replaced ADHDC-Net standard convolutions with hierarchical decoupled convolutions (HDC), enhancing focus on tumour regions. Ref. [26] introduced MSegNet, a Transformer-based framework with cross-modal attention mechanisms for capturing spatial and depth dimensions in multimodal MRI data. Silva et al. [27] introduced a multi-stage deep layer aggregation framework that uses Gaussian filters and auxiliary losses to reduce aliasing artefacts and improve spatial fusion. Fidon et al. [28] proposed a 3D U-Net with the generalized Wasserstein Dice loss to address the hierarchical structure of tumour regions. They employed robust optimisation techniques and the Ranger optimiser for stability. Rastogi et al. [29] developed a hybrid approach combining 3D Replicator Neural Networks and 2D Volumetric Convolutional Networks for enhanced feature extraction and segmentation.
Table 1 summarizes related work, outlining the proposed methods, the datasets employed for experimentation, and the primary results obtained. Performance is evaluated primarily using the Dice coefficient and Hausdorff distance. The latter is a metric for quantifying the spatial discrepancy between the boundaries of two segmentations, such as a ground truth and a predicted mask. Because the standard Hausdorff distance is highly sensitive to outliers and noise, the 95th percentile Hausdorff distance (HD95) is used, considering the 95th percentile of all boundary-to-boundary distances instead of the maximum. This makes HD95 more stable and clinically relevant, particularly in medical imaging, where it can reveal significant boundary errors that may not be captured by overlap-based metrics like the Dice similarity. Mathematically, HD95 is defined as the 95th percentile of the set of minimum distances from each point on one segmentation boundary to the other, considering both directions. It is expressed by Equation (1).

Table 1.
Summary of related work methods and findings.
- A and B are two sets of points (e.g., boundary points of two segmentations).
- : A point from set A.
- : A point from set B.
- : The Euclidean distance between points a and b.
- : The shortest distance from a point a in A to any point in B.
- : The shortest distance from a point b in B to any point in A.
- ∪: The union operator, combining the distances calculated in both directions.
- : The 95th percentile value of the combined set of minimum distances, making the metric robust to outliers.
3. Methodology
The methodology proposed for brain tumour segmentation follows a structured pipeline, as illustrated in Figure 1. This overall pipeline is composed of three key stages: image preprocessing, data augmentation, and the segmentation stage.
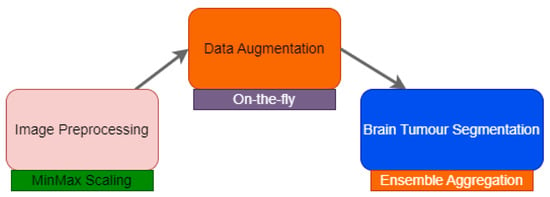
Figure 1.
General pipeline of the proposed methodology.
Initial image preprocessing standardizes the data by correcting for artefacts and variations. Data augmentation expands the dataset to prevent overfitting and improve the model’s generalization. The segmentation stage utilizes the prepared data to accurately delineate tumour regions. It consists of training deep models, aggregating predictions to reconstruct the segmentation, and refining segmentation. The implementation of each stage is tailored to the specific characteristics of the target dataset, as discussed below.
The BraTS-2020 dataset, a publicly available benchmark, includes four MRI modalities from glioma patients: T1, T1ce, T2, and T2-FLAIR [30,31,32,33,34]. These are paired with expert-generated ground truth masks delineating peritumoural oedema (ED), necrotic and non-enhancing tumour core (NCR/NET), and enhancing tumour (ET).
The dataset presents challenges due to heterogeneity in imaging protocols. The model was trained on 295 BraTS-2020 training cases and validated on 74 cases. Inference was performed on the BraTS-2020 online validation set (125 cases). Figure 2 shows a sample MRI scan and annotations.
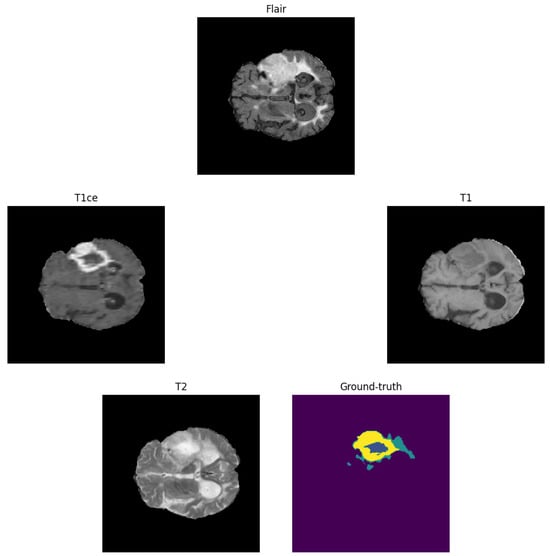
Figure 2.
Example of a brain tumour from the BraTS-2020 training dataset. Yellow: enhancing tumour (ET), blue: non-enhancing tumour/necrotic tumour (NET/NCR), and green: peritumoural oedema (ED).
3.1. Image Pre-Processing
To standardize images, min-max scaling is applied to each MRI sequence after clipping intensity values, as follows:
where is the normalized intensity in [0, 1]. Images were cropped and re-cropped to for training and for validation. This enabled the elimination of the majority of irrelevant background present in the original volume, thereby facilitating the analysis of a nearly complete representation of each brain tumour.
3.2. Data Augmentation
On-the-fly data augmentation is employed to mitigate overfitting. Augmentations include the following:
- 1.
- Input channel rescaling: Voxel values are multiplied by a factor with a probability of 70–80%, as follows:
- 2.
- Input channel intensity shift: A constant is added to each voxel with a probability of 5–10%, as follows:
- 3.
- Additive Gaussian noise: Noise is added to each voxel, as follows:
- 4.
- Input channel dropping: A randomly selected input channel is set to zero with a probability of 12–16%.
- 5.
- Random flipping: Inputs are flipped along spatial axes with a probability of 70–80%.
3.3. Proposed Brain Tumour Segmentation
This work proposes a lambda fuzzy-based ensemble method for brain tumour segmentation. It combines outputs from multiple DCNNs (3D U-Net variants) using the Choquet integral, leveraging fuzzy measures from coalition game theory, information theory, and heuristic weighting. The final segmentation masks are computed for enhancing tumour (ET), tumour core (TC), and whole tumour (WT).
The workflow can be summarized in the following steps:
- Deep Models: Train multiple U-Net variants.
- Ensemble Aggregation: Aggregate predictions using the Choquet integral with fuzzy measures.
- Post-Processing: Refine segmentation masks.
3.3.1. Neural Network Architectures
The backbone of the proposed network is a 3D U-Net architecture (Figure 3) with a classic encoder–decoder structure. The encoder consists of four stages, each comprising two convolutional layers, followed by group normalization and ReLU activation. Spatial dimensions are progressively reduced using 3D MaxPooling or RelatedPooling operations, with the number of filters doubling after each downsampling step, starting from 48. At the deepest layer, dilated convolutions are applied to increase the receptive field.
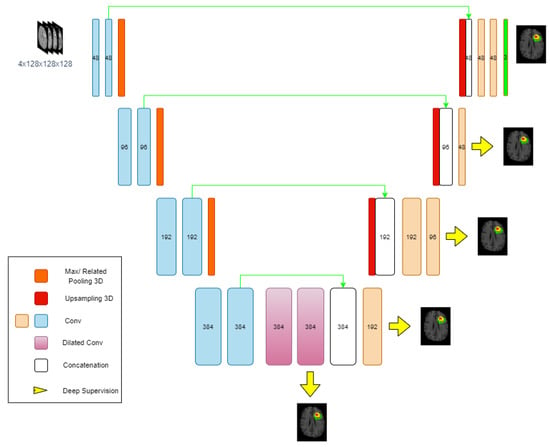
Figure 3.
Overview of the proposed deep neural network architecture.
The decoder mirrors the encoder, using trilinear interpolation for upsampling and reconstructing segmentation masks. To preserve and effectively utilize spatial information, shortcut connections are established between matching encoder and decoder stages. Uniquely, instead of the conventional concatenation along the channel axis as in standard U-Net variants, this architecture employs a channel shuffling strategy (Figure 4) and width shuffling (Figure 5). Specifically, the encoder’s output and the upsampled decoder feature maps are first stacked along the last axis, creating a more intricate structure. They are then reshaped to interleave and mix the corresponding feature channels from both pathways before being fed into the subsequent decoder layer. This channel shuffling approach introduces greater flexibility in information flow, potentially enabling the network to capture more detailed spatial and hierarchical features.
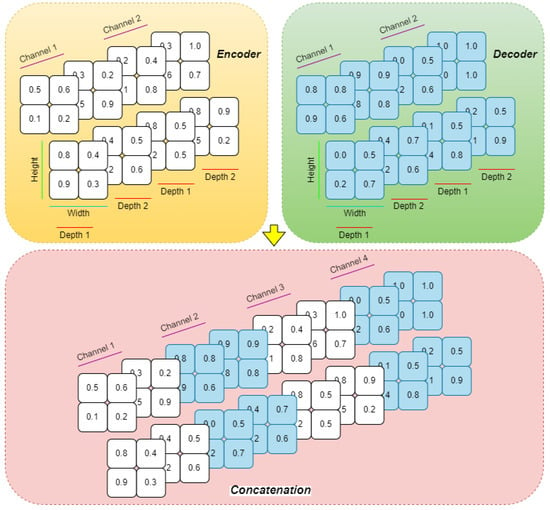
Figure 4.
The proposed channel shuffling technique.
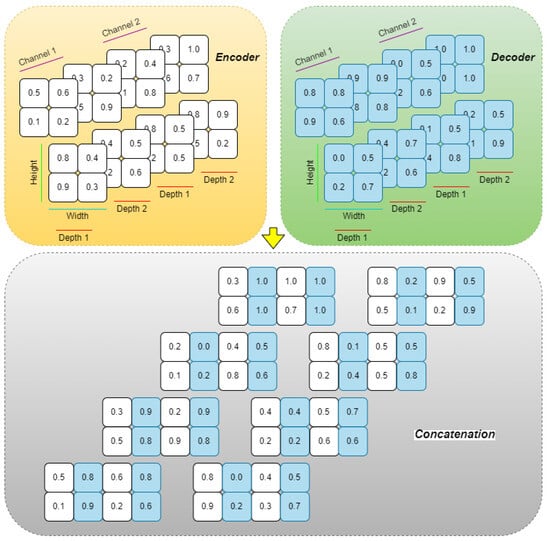
Figure 5.
The proposed width shuffling technique.
In the final decoder layer, three output channels (ET, TC, WT) are produced with sigmoid activation. Additionally, the dilation trick [35] is applied to further enhance receptive field coverage.
3.3.2. Ensemble Method for Brain Tumour Segmentation
The ensemble method uses the Choquet integral to combine predictions (Figure 3). This allows for a sophisticated combination of predictions by considering the interactions between classifiers rather than assuming their independence.
- 1.
- Shapley Values: The Shapley value , represented by Equation (6), represents the average contribution of classifier i to all possible coalitions.where n is the total number of classifiers, S is a subset of classifiers excluding i, is the cardinality of S, is the characteristic function indicating the value of coalition S, and is the value with classifier i included. is the marginal contribution of classifier i on coalition S. It is calculated by Equation (7).where is the conditional mutual information between the predictions of classifier and the ground truth labels, based on the outputs of classifiers in the set L, and is the mutual information between L’s classifiers and the true labels.Based on the values of and , classifiers can be as follows:
- Redundant:
- Independent:
- Interdependent:
- 2.
- Lambda Fuzzy Approximation: Computational tractability is enhanced using a parameter , which facilitates the estimation of fuzzy measures for all subsets X, as follows:Here, N is the number of classifiers, and refers to individual classifiers. is used to compute fuzzy measures for larger subsets by leveraging those of individual classifiers. The fuzzy measure of the union of two classifiers and can be calculated by Equation (12), given that , as follows:A heuristic based on mutual information is utilized (Equation (13)), as follows:L is the current set of selected classifiers with cardinality l, and is the mutual information between and . This heuristic estimates the marginal contribution of a classifier by taking into account its relevance and redundancy.
Weighting Schemes
To further penalize redundancy, the marginal contribution is adjusted through Equation (14), as follows:
Here, the penalty term relates to the mutual information between and the other classifiers in L, weighted according to classifier accuracy. Based on validation accuracies, the following three distinct weighting schemes are considered:
- 1.
- Weighting Scheme 1:and are respectively the validation accuracies of and . This approach assigns lower weights to classifiers with superior validation accuracy.
- 2.
- Weighting Scheme 2:Here, the reciprocal of validation accuracy is used, such that higher accuracy corresponds to lower weight.
- 3.
- Weighting Scheme 3:This scheme utilizes the negative logarithm of validation accuracies, similarly reducing the weight for more accurate classifiers.
The final fuzzy measures are computed by averaging the results obtained from these three schemes.
Choquet Integral
The discrete Choquet integral serves as an advanced aggregation operator for the outputs of multiple models. The Choquet integral incorporates both the individual importance of each model and the interactions among models by means of fuzzy measures defined over all subsets of classifiers. Each model’s prediction is thus weighted according to, in addition to its standalone performance, its contribution with other models. This allows the Choquet integral to effectively aggregate model outputs, which is particularly advantageous in complex scenarios such as brain tumour segmentation, where models may capture complementary information dimensions. The discrete Choquet integral is formally defined as in the following Equation (18) [36]:
where denotes the i-th smallest element of the input vector x, is the fuzzy measure for subset , and n is the number of classifiers. This formulation expresses the Choquet integral as a weighted sum over the ordered inputs.
An equivalent form, as presented in [37], is given by the following Equation (19):
where . This alternative formulation computes the integral as the sum of differences between consecutive ordered input values, each weighted by the fuzzy measure of the corresponding subset.
4. Fuzzy Measures
Fuzzy measures are a generalization of traditional measures (like probability measures) that allow for the representation of uncertainty and imprecision. They are particularly useful in scenarios where the relationships between elements are not strictly additive, which is often the case in real-world applications, such as in ensemble learning. In the context of fuzzy measures, you need to balance these properties, as follows:
Let X be a universe of discourse; then is a fuzzy measure if it satisfies the following:
- 1.
- Boundary Condition: The measure of the empty set is zero, and the measure of the entire universe of discourse X is one, as follows:
- 2.
- Monotonicity: This refers to the requirement that fuzzy measures respect the natural inclusion relationship between subsets. Specifically, for , if , then .
- 3.
- Continuity: If you have a sequence of sets that are either increasing or decreasing, the measure of the limit of these sets should equal the limit of their measures, as follows: or , then .
- 4.
- Super-additivity and Sub-additivity: These concepts refer to how the measure of the union of sets relates to the measures of the individual sets. Super-additivity means that the measure of the union is at least as large as the sum of the measures of the individual sets, while sub-additivity means that it is at most that sum.
5. Experimental Setup
5.1. Configuration Setup
Hardware and software specifications are summarized in Table 2. Cython v3.1.2 was employed to decrease processing time by enhancing execution speed.

Table 2.
Hardware and software setup for the experimental pipeline.
5.2. Evaluation Metrics
The model performance was assessed using metrics like Dice Similarity Coefficient (DSC), sensitivity, specificity, and Hausdorff distance (HD95).
- Dice Similarity Coefficient (DSC): Measures overlap between predicted and ground truth segmentations.
- Sensitivity: Measures the ability to detect positive instances.
- Specificity: Measures the ability to detect negative instances.
- Dice Loss: Used to train the network.
The models were trained using five-fold cross-validation for 400 epochs. Key training strategies included the following:
- 1.
- Learning Rate Schedule: Initial learning rate of 0.0001 reduced using cosine decay after 100 epochs.
- 2.
- Stochastic Weight Averaging: Applied after 250 epochs.
- 3.
- Optimiser: Ranger optimiser for primary training, Adam optimiser during Stochastic Weight Averaging.
- 4.
- Model Selection: The two best-performing models were selected based on validation loss.
During prediction, six trained U-Net models were evaluated on 74 patients. The process involved the following:
- 1.
- Predicted Masks: Each model generated binary masks for ET, TC, and WT.
- 2.
- Pixel-Wise Aggregation: Predictions were combined using the Choquet integral.
- 3.
- Final Labelmap Reconstruction: Tumour sub-regions were combined to construct a 3-channel labelmap.
6. Results and Discussion
Table 3 summarizes the used models, the number of parameters and epochs, and the training time.

Table 3.
Overall models, epochs, and training time.
6.1. Performance Analysis of the Proposed Approach
Figure 6 illustrates validation Dice scores and loss curves, with all models achieving Dice scores exceeding 0.8 for each tumour region and WT achieving the highest Dice scores. The models had 19,167,819 trainable parameters, with training requiring approximately 254 s per epoch and validation requiring 70 s (doubled during swa).
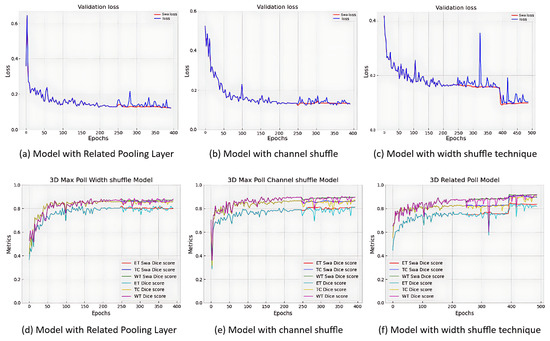
Figure 6.
Validation loss with Dice score metrics of the 3D-UNET models.
For segmentation, three U-Net model variants were ensembled using the Choquet integral. The computation of Shapley values required approximately 8.72 h per tumour region, while the time required for Choquet integral calculations varied depending on the specific GPU utilized. Table 4 presents the performance metrics of both individual models and ensemble methods on the BraTS-2020 validation dataset, which comprises 125 cases. The table includes results for six distinct 3D U-Net classifiers and the proposed ensemble approaches. In this context, the notation W or C within a method name indicates the concatenation mode, specifically referring to width shuffling or channel shuffling, respectively. The label R denotes the implementation of a 3D pooling layer in place of conventional MaxPooling. The term swa signifies the use of a sophisticated weight averaging technique. Additionally, WS-1, WS-2, and WS-3 correspond to different weighting schemes applied during ensemble construction. All evaluations were conducted using the official BraTS platform at https://synapse.org/brats (accessed on 12 February 2025).

Table 4.
Validation results for Dice, sensitivity, specificity, and Hausdorff95 metrics for the 3-class segmentation of MRI images.
- Individual Model Performance: Dice scores for TC ranged from 0.82436 to 0.83919, WT ranged from 0.87065 to 0.88439, and ET ranged from 0.76689 to 0.78964. Specifically, Model 2 achieved a Dice score of 0.82436 for TC, while Model 5 reached 0.83919. For WT, Model 1 scored 0.87065, and Model 6 achieved 0.88439. ET segmentation showed the highest variability, with scores between 0.76689 (Model 6) and 0.78964 (Model 3). Sensitivity values for ET were highest for Model 1 (0.81825) and lowest for Model 6 (0.78967). WT sensitivity showed excellent performance across all models, with values exceeding 0.918, whereas TC sensitivity varied, with Model 3 performing the worst (0.8306) and Model 2 performing the best (0.85453). Specificity was consistently high across all models for all tumour sub-regions, with values close to 0.999. The Hausdorff distance (95%) for ET was lowest for Model 3 (20.71231), reflecting better boundary prediction, while Model 6 had the highest (32.78875), indicating less accurate boundary delineation. For WT and TC, the Hausdorff distances were generally low, with the best values for Models 6 and 5, respectively.
- Weighted Ensembles: Weighted ensemble techniques optimised model performance, especially for WT segmentation. Weight1 achieved strong results for WT segmentation (Dice = 0.89318) and specificity (0.99976 for TC), while Hausdorff distances showed improvements, particularly for WT (6.02998). Weight2 performed comparably with the highest Dice score for ET (0.77724) and slightly better TC segmentation than Weight1 (Dice = 0.82411). WT sensitivity also improved (0.92054), demonstrating that the ensemble effectively integrated complementary strengths of the models. Weight3 had slightly lower performance overall but maintained competitive metrics for specificity (0.99977 for ET and TC) and WT segmentation. A simple average ensemble yielded stronger results for TC and ET but lagged in WT performance. The simple average approach outperformed the weighted techniques for Dice scores in TC (0.84869) and ET (0.79047), but it did not achieve the same level of performance in WT segmentation (Dice = 0.88571). It demonstrated good sensitivity for all sub-regions, particularly TC (0.84953) and WT (0.94181). The Hausdorff distance for TC (6.62945) was notably the best among all approaches, while ET and WT distances remained competitive. The weighted ensembles (Weight1, Weight2, and Weight3) provided consistent performance improvements for WT segmentation compared with individual models, highlighting the ensemble’s ability to leverage diverse model outputs effectively. The Dice scores and Hausdorff distances suggest that the ensembles prioritize overall stability, particularly for WT segmentation, where the weights focus on integrating the strengths of all models. However, for the more challenging ET region, none of the ensembles managed to outperform the simple average, indicating that additional refinement or ET-specific weighting strategies may be required to address the small size and variability of this tumour sub-region.
Table 5 demonstrates the Shapley values for six classifiers across the three weighting schemes, i.e., enhancing tumour (ET), whole tumour (WT), and tumour core (TC). It is clear that, for all the weighting schemes, the Shapley values for ET are much smaller than those for TC and WT. This confirms that the ET region, being small and sometimes nonexistent, is challenging to segment effectively. Weight2 shows relatively higher values for ET compared with Weight1 and Weight3, suggesting that it is more sensitive to the ET region. Shapley values for TC are consistently higher than ET but still smaller than WT. Weight2 consistently gives higher contributions for TC compared with Weight1, suggesting better performance for this region. Weight3 shows negative contributions, which could mean a different scale or prioritization compared with the other weights. WT consistently has the highest Shapley values across all weights, reflecting the larger size and better segmentation performance. Weight2 gives significantly higher values than Weight1, and Weight3 has negative values but maintains the same relative model ranking. ET consistently had the lowest Shapley values. Adjustments to Shapley values (Table 6) prioritised ET and TC. For W1_20 and W2_20, adjustments were based on the original Shapley values from Weight1 and Weight2, prioritizing Model 3 (0.2077) for ET and Model 5 (0.2077) for TC. In the new Weight3, a balanced approach was adopted by combining the WT Shapley values from Weight3 with the adjusted ET and TC values from Weight1.

Table 5.
Shapley values for the six 3D U-Net classifiers calculated using three weighting schemes: WS-1, WS-2, and WS-3.

Table 6.
Adjusted Shapley values for the six 3D U-Net classifiers calculated for four variations of weighting schemes: WS-1-20, WS-2-20, WS-1-17, and WS-2-17.
Table 7 shows results after applying adjusted Shapley values. The Choquet-based ensemble consistently improved upon the simple average ensemble. For the enhancing tumour (ET) region, the Choquet ensemble achieved a Dice score of 0.79227, outperforming the simple average (0.79047). In the tumour core (TC) region, the Choquet ensemble showed a slight improvement (0.85051) compared with the simple average (0.84869). The largest gain was observed for the whole tumour (WT) region, where the Dice score of the Choquet ensemble reached 0.89602, significantly higher than the simple average (0.88571). Sensitivity for ET improved from 0.81294 in the simple average to 0.81833 in the Choquet ensemble. For TC, sensitivity increased to 0.85677 from 0.84953. WT sensitivity decreased slightly in the Choquet ensemble (0.91051) compared with the simple average (0.94181). The Choquet ensemble maintained high specificity across all tumour regions, comparable to the simple average, with values of 0.99965, 0.99909, and 0.99952 for ET, WT, and TC, respectively. For boundary accuracy, the Choquet ensemble outperformed the simple average for ET (20.74244 vs. 23.74679) and WT (5.9681 vs. 6.89449). Metrics include Dice, sensitivity, specificity, and Hausdorff95 values for ET, WT, and TC. WT sensitivity slightly decreased, suggesting a trade-off prioritising small tumour regions. The Choquet ensemble achieved better Hausdorff distances for ET and WT. The results demonstrate that the Choquet ensemble consistently outperforms the simple average approach in terms of Dice scores and Hausdorff distance for most tumour regions. The Choquet integral effectively leverages the strengths of individual models, leading to better segmentation accuracy for the challenging ET and TC regions, as well as improved boundary delineation (lower Hausdorff distances), particularly for ET and WT.

Table 7.
Performance on the BraTS20 Online Validation Data for the Choquet ensemble strategy compared with the simple average ensemble.
6.2. Comparison with State-of-the-Art Methods
Table 8 compares the proposed method with other state-of-the-art approaches for brain tumour segmentation. The included solutions are those that participated in the BraTS competition, which officially closed in 2024. Consequently, related work published after the competition has been excluded from this comparison.

Table 8.
Comparison of the proposed Choquet ensemble strategy with other state-of-the-art methods on BraTS-20 Online Validation Data.
The proposed method achieved competitive Dice scores (ET = 0.792, TC = 0.851, WT = 0.896), outperforming several approaches, including those by [21,28]. The proposed method achieved competitive Dice scores across all tumour regions: 0.792 for enhancing tumour (ET), 0.896 for whole tumour (WT), and 0.851 for tumour core (TC). Sensitivity values were robust across all regions, with significant improvements for ET and TC compared with [24]. The proposed method demonstrated robust sensitivity values for all tumour regions and performed better than Akbar et al. [24] for ET (0.818 vs. 0.786) and WT (0.910 vs. 0.905). Specificity was nearly perfect (0.999 across all regions). For specificity, the proposed method achieved near-perfect results with 0.999 for all tumour regions (ET, WT, and TC), matching the highest values reported by Wang et al. [3] and Akbar et al. [24]. Additionally, the method achieved the lowest Hausdorff distances among all methods for ET (20.74), WT (5.96), and TC (6.65). The proposed method outperformed all compared methods with distances of 20.74 (ET), 5.96 (WT), and 6.65 (TC). Notably, it performed better than Fidon et al. (2021) [28], Nguyen et al. [21], and Zhang et al. [13], particularly for ET (20.74 vs. 26.80, 24.02, and 24.31, respectively).
7. Conclusions
This paper has proposed a deep learning-based approach for the segmentation of brain lesions from MRI images. Specifically, it utilized the Choquet integral for aggregation, which considers the decisions made by subsets of classifiers along with individual classifiers, unlike other aggregation functions. A novel method for the calculation of Fuzzy measures was also introduced, leveraging coalition game theory (Shapley value), information theory, and the Lambda fuzzy approximation. As deep learning strategies, the proposed approach employed three pre-trained 3D U-Net models with minor modifications, combining their outputs to achieve robust segmentation results. This approach assumes that all segmentation models contribute to classification to some extent, though some classifiers may provide more valuable information than others. Experiments conducted on the BraTS-2020 dataset demonstrate the algorithm’s competitive performance, achieving superior segmentation accuracy compared with existing state-of-the-art methods. These results underscore the effectiveness of the proposed method, which combines innovative architectural modifications (channel/width shuffling) and advanced ensemble techniques (Choquet integral) to consistently deliver superior performance across all tumour regions. A limitation of our method lies in the selection of useful classifiers from a set that may vary in informativeness. This issue will be addressed in future work. A conceivable solution would be to use multi-head attention models, where heads could be used to measure the usefulness of classifiers and select the most adequate ones.
Author Contributions
Conceptualization, M.D., M.E.B.Y., M.S.K., M.G., and M.C.G.; methodology, M.D., M.E.B.Y., M.S.K., M.G., and M.C.G.; software, M.D., M.E.B.Y., and M.S.K.; validation, M.D., M.E.B.Y., M.S.K., M.G., and M.C.G.; formal analysis, M.D., M.E.B.Y., M.S.K., M.G., and M.C.G.; investigation, M.D., M.E.B.Y., M.S.K., and M.G.; resources, M.D., M.E.B.Y., M.S.K., M.G., and M.C.G.; data curation, M.D., M.E.B.Y., M.S.K., M.G., and M.C.G.; writing—original draft preparation, M.D., M.E.B.Y., M.S.K., M.G., and M.C.G.; writing—review and editing, M.G. and M.C.G.; visualization, M.D., M.E.B.Y., M.S.K., M.G., and M.C.G.; supervision, M.G. and M.C.G.; project administration, M.D., M.E.B.Y., M.S.K., M.G., and M.C.G.; funding acquisition, M.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yahiaoui, M.E.; Derdour, M.; Abdulghafor, R.; Turaev, S.; Gasmi, M.; Bennour, A.; Aborujilah, A.; Sarem, M.A. Federated Learning with Privacy Preserving for Multi- Institutional Three-Dimensional Brain Tumor Segmentation. Diagnostics 2024, 14, 2891. [Google Scholar] [CrossRef]
- Sulaiman, A.; Anand, V.; Gupta, S.; Al Reshan, M.; Alshahrani, H.; Shaikh, A.; Elmagzoub, M. An intelligent LinkNet-34 model with EfficientNetB7 encoder for semantic segmentation of brain tumor. Sci. Rep. 2024, 14, 1345. [Google Scholar] [CrossRef] [PubMed]
- Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; Van Der Laak, J.A.; Van Ginneken, B.; Sánchez, C.I. A survey on deep learning in medical image analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef] [PubMed]
- Elbachir, Y.M.; Makhlouf, D.; Mohamed, G.; Bouhamed, M.M.; Abdellah, K. Federated Learning for Multi-institutional on 3D Brain Tumor Segmentation. In Proceedings of the 2024 6th International Conference on Pattern Analysis and Intelligent Systems (PAIS), El Oued, Algeria, 24–25 April 2024; pp. 1–8. [Google Scholar] [CrossRef]
- Bhowal, P.; Sen, S.; Yoon, J.; Geem, Z.W.; Sarkar, R. Choquet Integral and Coalition Game-based Ensemble of Deep Learning Models for COVID-19 Screening from Chest X-ray Images. IEEE J. Biomed. Health Inform. 2021, 25, 4328–4339. [Google Scholar] [CrossRef]
- Lee, K.M.; Leekwang, H. Identification of λ-fuzzy measure by genetic algorithms. Fuzzy Sets Syst. 1995, 75, 301–309. [Google Scholar] [CrossRef]
- Qin, J.; Xu, D.; Zhang, H.; Xiong, Z.; Yuan, Y.; He, K. BTSegDiff: Brain tumor segmentation based on multimodal MRI Dynamically guided diffusion probability model. Comput. Biol. Med. 2025, 186, 109694. [Google Scholar] [CrossRef]
- Habchi, Y.; Kheddar, H.; Himeur, Y.; Ghanem, M.C. Machine learning and vision transformers for thyroid carcinoma diagnosis: A review. arXiv 2024, arXiv:2403.13843. [Google Scholar] [CrossRef]
- Sun, J.; Li, Y.; Wu, X.; Tang, C.; Wang, S.; Zhang, Y. HAD-Net: An attention U-based network with hyper-scale shifted aggregating and max-diagonal sampling for medical image segmentation. Comput. Vis. Image Underst. 2024, 249, 104151. [Google Scholar] [CrossRef]
- Ma, B.; Sun, Q.; Ma, Z.; Li, B.; Cao, Q.; Wang, Y.; Yu, G. DTASUnet: A local and global dual transformer with the attention supervision U-network for brain tumor segmentation. Sci. Rep. 2024, 14, 28379. [Google Scholar] [CrossRef]
- S, C.; Clement, J.C. Enhancing brain tumor segmentation in MRI images using the IC-net algorithm framework. Sci. Rep. 2024, 14, 15660. [Google Scholar] [CrossRef]
- Habchi, Y.; Kheddar, H.; Himeur, Y.; Ghanem, M.C.; Boukabou, A.; Al-Ahmad, H. Deep transfer learning for kidney cancer diagnosis. arXiv 2024, arXiv:2408.04318. [Google Scholar]
- Zhang, M.; Liu, D.; Sun, Q.; Han, Y.; Liu, B.; Zhang, J.; Zhang, M. Augmented Transformer network for MRI brain tumor segmentation. J. King Saud Univ. Comput. Inf. Sci. 2024, 36, 101917. [Google Scholar] [CrossRef]
- Guan, X.; Yang, G.; Ye, J.; Yang, W.; Xu, X.; Jiang, W.; Lai, X. 3D AGSE-VNet: An automatic brain tumor MRI data segmentation framework. BMC Med. Imaging 2022, 22, 6. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, Y.; Liu, H.; Song, E.; Hung, C.C. A 3D Cross-Modality Feature Interaction Network With Volumetric Feature Alignment for Brain Tumor and Tissue Segmentation. IEEE J. Biomed. Health Inform. 2023, 27, 75–86. [Google Scholar] [CrossRef]
- Ahmad, P.; Jin, H.; Alroobaea, R.; Qamar, S.; Zheng, R.; Alnajjar, F.; Aboudi, F. MH UNet: A multi-scale hierarchical based architecture for medical image segmentation. IEEE Access 2021, 9, 148384–148408. [Google Scholar] [CrossRef]
- Xu, W.; Yang, H.; Zhang, M.; Cao, Z.; Pan, X.; Liu, W. Brain tumor segmentation with corner attention and high-dimensional perceptual loss. Biomed. Signal Process. Control 2022, 73, 103438. [Google Scholar] [CrossRef]
- Liu, Z. Innovative multi-class segmentation for brain tumor MRI using noise diffusion probability models and enhancing tumor boundary recognition. Sci. Rep. 2024, 14, 29576. [Google Scholar] [CrossRef]
- Rajput, S.; Kapdi, R.; Roy, M.; Raval, M. A triplanar ensemble model for brain tumor segmentation with volumetric multiparametric magnetic resonance images. Healthc. Anal. 2024, 5, 100307. [Google Scholar] [CrossRef]
- Henry, T.; Carré, A.; Lerousseau, M.; Estienne, T.; Robert, C.; Paragios, N.; Deutsch, E. Brain tumor segmentation with self-ensembled, deeply-supervised 3D U-net neural networks: A BraTS 2020 challenge solution. In Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries; Proceedings of the 6th International Workshop, BrainLes 2020, Held in Conjunction with MICCAI 2020, Lima, Peru, 4 October 2020; Revised Selected Papers, Part I 6; Springer: Cham, Switzerland, 2021; pp. 327–339. [Google Scholar]
- Nguyen, H.T.; Le, T.T.; Nguyen, T.V.; Nguyen, N.T. Enhancing MRI brain tumor segmentation with an additional classification network. In Proceedings of the International MICCAI Brainlesion Workshop, Lima, Peru, 4 October 2020; Springer: Cham, Switzerland, 2020; pp. 503–513. [Google Scholar]
- Zhao, J.; Xing, Z.; Chen, Z.; Wan, L.; Han, T.; Fu, H.; Zhu, L. Uncertainty-Aware Multi-Dimensional Mutual Learning for Brain and Brain Tumor Segmentation. IEEE J. Biomed. Health Inform. 2023, 27, 4362–4372. [Google Scholar] [CrossRef]
- Wen, L.; Sun, H.; Liang, G.; Yu, Y. A deep ensemble learning framework for glioma segmentation and grading prediction. Sci. Rep. 2025, 15, 4448. [Google Scholar] [CrossRef]
- Akbar, A.S.; Fatichah, C.; Suciati, N. Single level UNet3D with multipath residual attention block for brain tumor segmentation. J. King Saud Univ. Comput. Inf. Sci. 2022, 34, 3247–3258. [Google Scholar] [CrossRef]
- Liu, H.; Huo, G.; Li, Q.; Guan, X.; Tseng, M.L. Multiscale lightweight 3D segmentation algorithm with attention mechanism: Brain tumor image segmentation. Expert Syst. Appl. 2023, 214, 119166. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, J.; Guan, Y.; Ahmad, F.; Mahmood, T.; Rehman, A. MSegNet: A Multi-View Coupled Cross-Modal Attention Model for Enhanced MRI Brain Tumor Segmentation. Int. J. Comput. Intell. Syst. 2025, 18, 63. [Google Scholar] [CrossRef]
- Silva, C.A.; Pinto, A.; Pereira, S.; Lopes, A. Multi-stage Deep Layer Aggregation for Brain Tumor Segmentation. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Cham, Switzerland, 2021; Volume 12659, pp. 179–188. [Google Scholar] [CrossRef]
- Fidon, L.; Ourselin, S.; Vercauteren, T. Generalized wasserstein dice score, distributionally robust deep learning, and ranger for brain tumor segmentation: BraTS 2020 challenge. In Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries; Proceedings of the 6th International Workshop, BrainLes 2020, Held in Conjunction with MICCAI 2020, Lima, Peru, 4 October 2020; Revised Selected Papers, Part II 6; Springer: Cham, Switzerland, 2021; pp. 200–214. [Google Scholar]
- Rastogi, D.; Johri, P.; Donelli, M.; Kadry, S.; Khan, A.; Espa, G.; Feraco, P.; Kim, J. Deep learning-integrated MRI brain tumor analysis: Feature extraction, segmentation, and Survival Prediction using Replicator and volumetric networks. Sci. Rep. 2025, 15, 1437. [Google Scholar] [CrossRef] [PubMed]
- Çiçek, Ö.; Abdulkadir, A.; Lienkamp, S.S.; Brox, T.; Ronneberger, O. 3D U-net: Learning dense volumetric segmentation from sparse annotation. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Cham, Switzerland, 2016; Volume 9901, pp. 424–432. [Google Scholar] [CrossRef]
- Bakas, S.; Akbari, H.; Sotiras, A.; Bilello, M.; Rozycki, M.; Kirby, J.S.; Freymann, J.B.; Farahani, K.; Davatzikos, C. Advancing The Cancer Genome Atlas glioma MRI collections with expert segmentation labels and radiomic features. Sci. Data 2017, 4, 170117. [Google Scholar] [CrossRef]
- Bakas, S.; Reyes, M.; Jakab, A.; Bauer, S.; Rempfler, M.; Crimi, A.; Shinohara, R.T.; Berger, C.; Ha, S.M.; Rozycki, M.; et al. Identifying the Best Machine Learning Algorithms for Brain Tumor Segmentation, Progression Assessment, and Overall Survival Prediction in the BRATS Challenge. arXiv 2018, arXiv:1811.02629. [Google Scholar] [CrossRef]
- Bakas, S.; Akbari, H.; Sotiras, A.; Bilello, M.; Rozycki, M.; Kirby, J.; Freymann, J.; Farahani, K.; Davatzikos, C. Segmentation labels and radiomic features for the pre-operative scans of the TCGA-LGG collection. Cancer Imaging Arch. 2017, 286. [Google Scholar] [CrossRef]
- Bakas, S.; Akbari, H.; Sotiras, A.; Bilello, M.; Rozycki, M.; Kirby, J.; Freymann, J.; Farahani, K.; Davatzikos, C. Segmentation labels and radiomic features for the pre-operative scans of the TCGA-GBM collection. Cancer Imaging Arch. 2017, 9. [Google Scholar] [CrossRef]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 40, 834–848. [Google Scholar] [CrossRef]
- Murofushi, T.; Sugeno, M. An interpretation of fuzzy measures and the Choquet integral as an integral with respect to a fuzzy measure. Fuzzy Sets Syst. 1989, 29, 201–227. [Google Scholar] [CrossRef]
- Beliakov, G.; James, S.; Wu, J.Z. Discrete Fuzzy Measures: Computational Aspects, 1st ed.; Springer Publishing Company, Incorporated: New York, NY, USA, 2019. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).