A KeyBERT-Enhanced Pipeline for Electronic Information Curriculum Knowledge Graphs: Design, Evaluation, and Ontology Alignment
Abstract
1. Introduction
2. Related Work
2.1. Keyword (Knowledge-Point) Extraction
2.2. Graph Construction and Visualisation
2.3. Relationship Enrichment
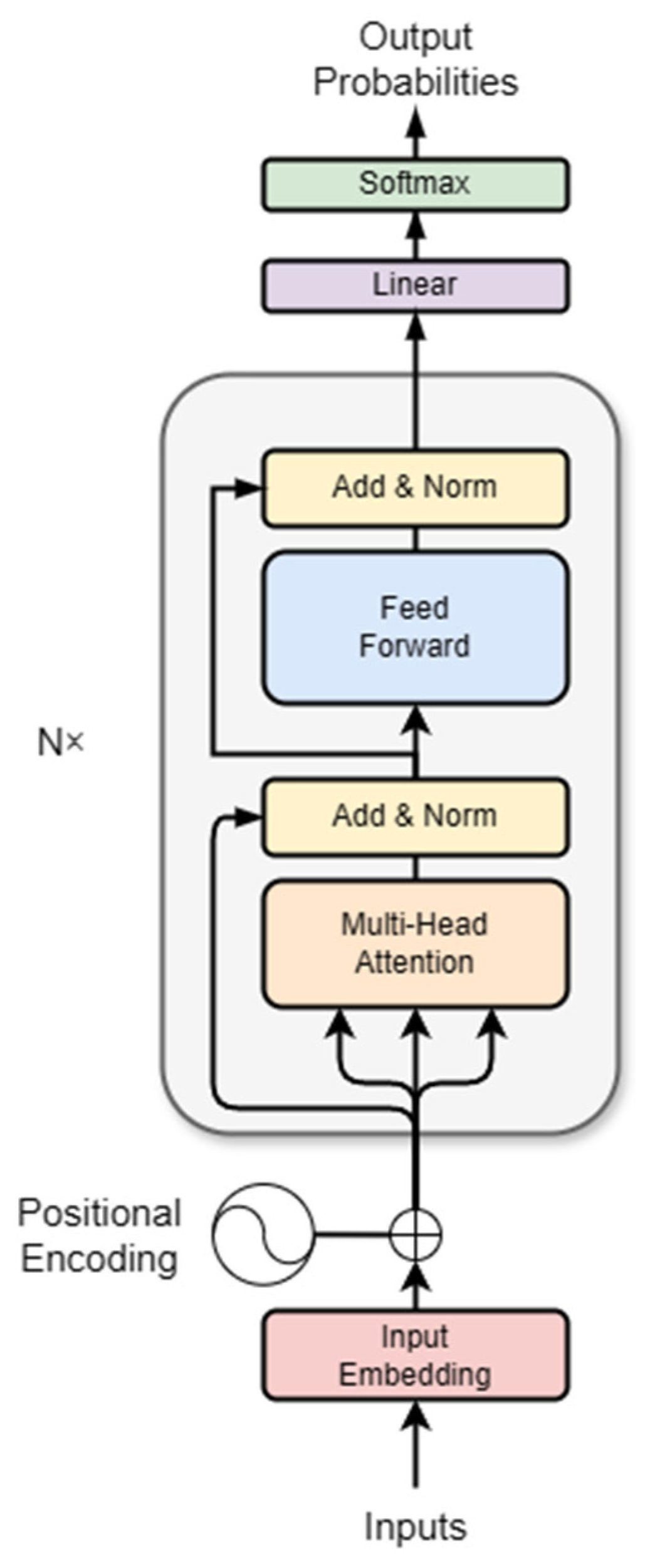
2.4. Transformer and GCN Applications in Educational Knowledge Graphs
2.4.1. Transformer-Driven Concept Extraction
2.4.2. GCN-Driven Graph Enhancement and Downstream Tasks
2.4.3. End-to-End Transformer + GCN Trends
2.5. Position of This Study
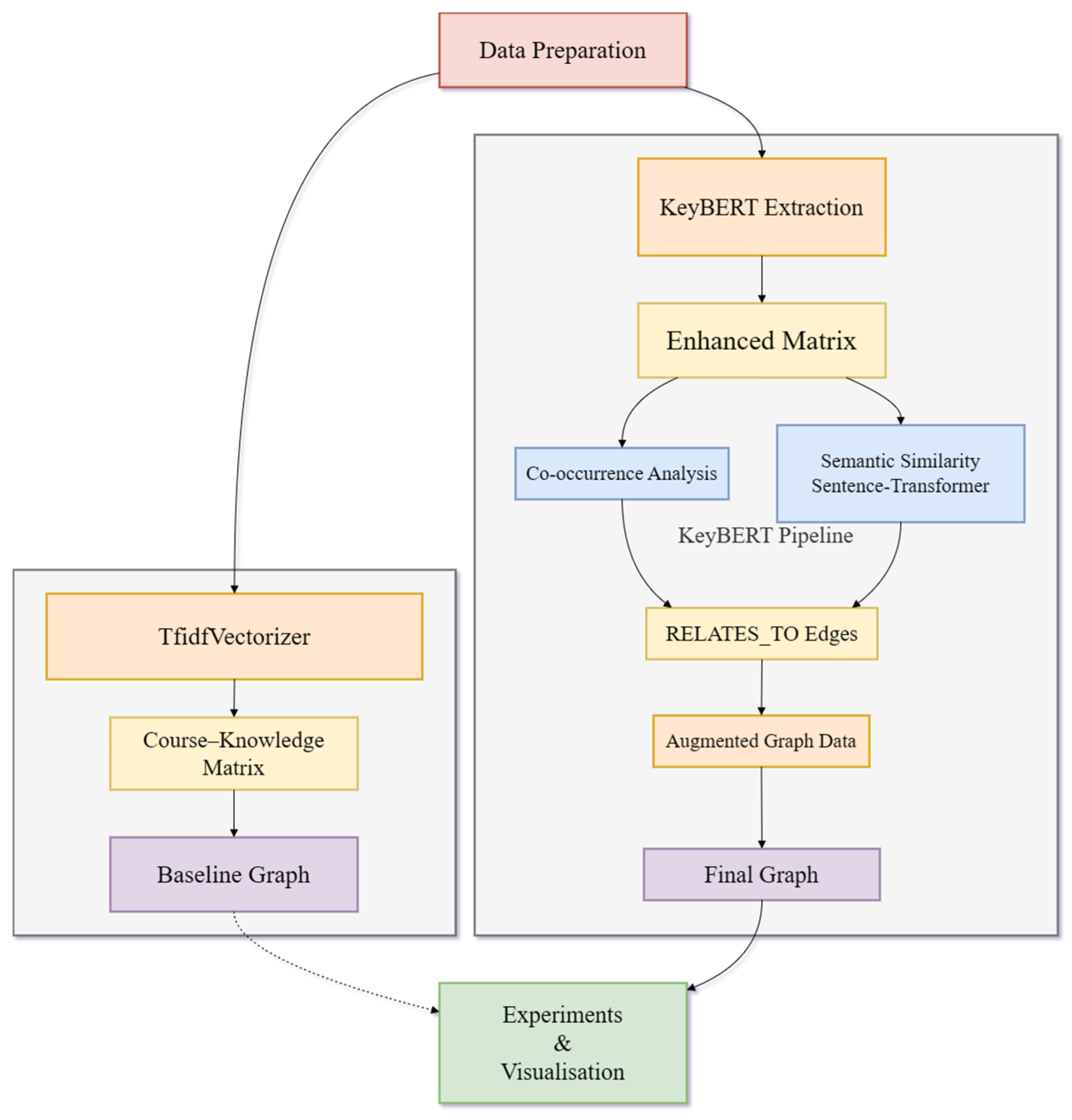
3. Methodology
3.1. Data Preparation
3.2. TF-IDF-Based Construction
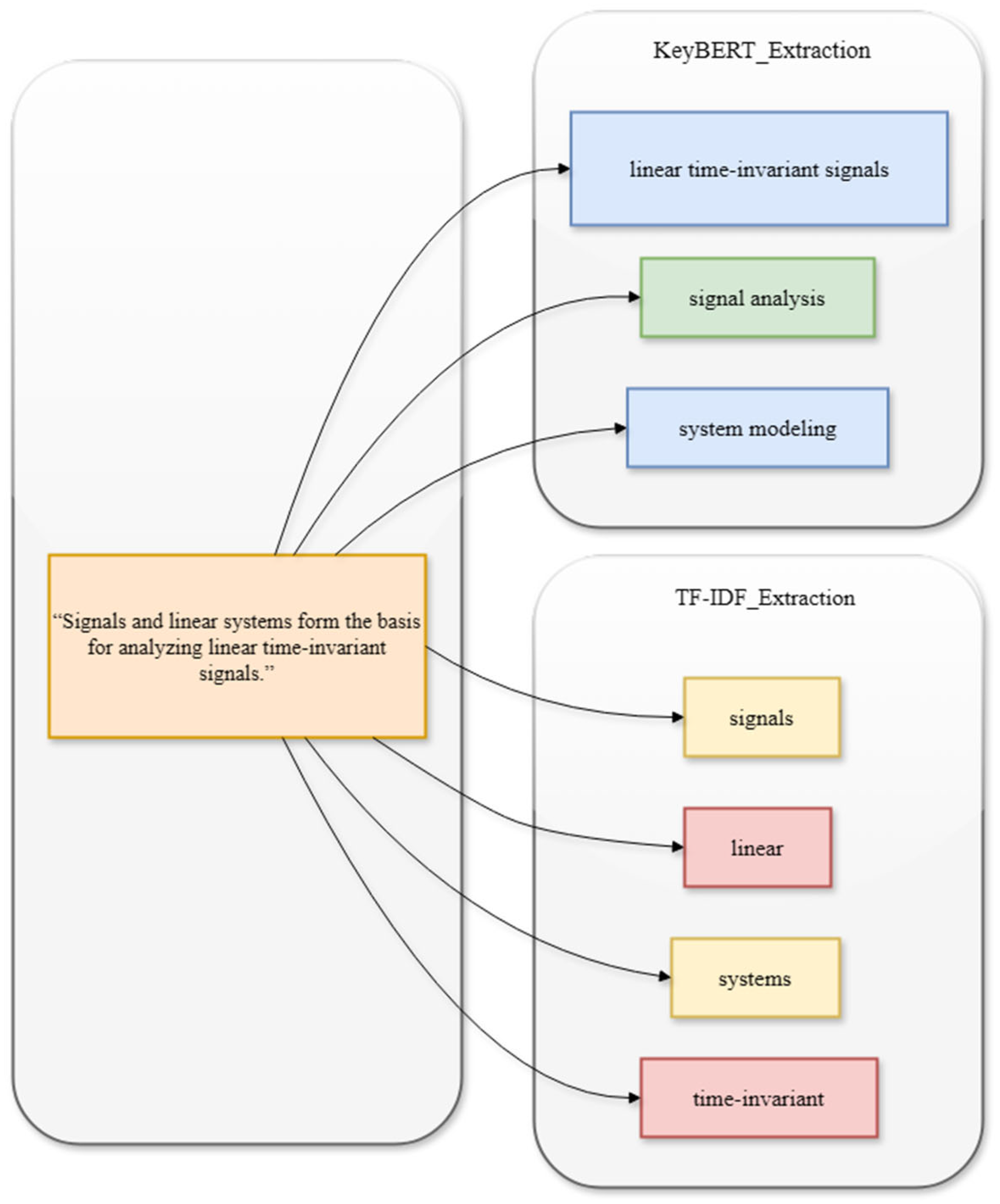
3.3. Enhanced Extraction with KeyBERT
3.4. Enhancement of Knowledge Points Relationships
3.5. Graph Construction and Visualization
4. Experiments
4.1. Experimental Setup
4.2. Experimental Procedure
4.2.1. Preliminary Graph Construction with TF-IDF
4.2.2. Enhanced Knowledge Points Extraction with KeyBERT
4.2.3. Enhancement of Knowledge Points Relationships and Graph Update
4.2.4. Threshold Sensitivity Analysis Procedure
4.2.5. Error Analysis Procedure
- Applied the same prediction rule to label each course–KP pair as positive or negative.
- Computed the confusion matrix components—True Positives (TP), False Positives (FP), False Negatives (FN), and True Negatives (TN).
- Sampled five representative FP cases and five FN cases for manual inspection.
- Classified each sampled error by its likely cause (e.g., high-frequency noise, multi-word clipping, semantic ambiguity).
4.2.6. Ontology Alignment Procedure
- Merged all positive predictions (co_occurrence ≥ 5 and similarity ≥ 0.7) with their original phrase labels.
- Loaded the cleaned IEEE Taxonomy (2025) term list.
- For each predicted phrase, applied a fuzzy-matching step (Levenshtein distance ≤ 2 or cosine similarity ≥ 0.85) to map it to the nearest taxonomy term.
- Replaced mapped phrases with their standard taxonomy IDs; unmatched phrases were marked “Unknown” and discarded.
- Recomputed the prediction flag (‘aligned_pred = 1’ if successfully mapped, else 0) and compare against the 600-sample gold set.
4.2.7. Hyperparameter Ablation Procedure
- Reran KeyBERT extraction on the full course corpus.
- Built the corresponding co_occurrence and similarity scores.
- Applied our default thresholds (co_occurrence ≥ 5, similarity ≥ 0.7) to generate predictions.
- Computed Precision, Recall, and F1 against the gold labels.
4.2.8. GCN Sparsity Impact Procedure
- 1.
- Feature Sparsity Measurement: Compute the non-zero element ratio of each matrix:
- 2.
- Graph Construction: Use the same bipartite course–KP edge set from Section 4.3. Node features are taken from either the TF-IDF matrix or the KeyBERT matrix.
- 3.
- GCN Training: Employ a two-layer GCN to perform link prediction. Train on all positive edges plus an equal number of random negative samples for 20 epochs.
- 4.
- Evaluation: After training, compute Accuracy and F1-score over a fresh set of negative samples of the same size as the positives.
4.3. Results and Analysis
4.3.1. Knowledge Points Extraction
4.3.2. Matrix Density and Sparsity Comparison
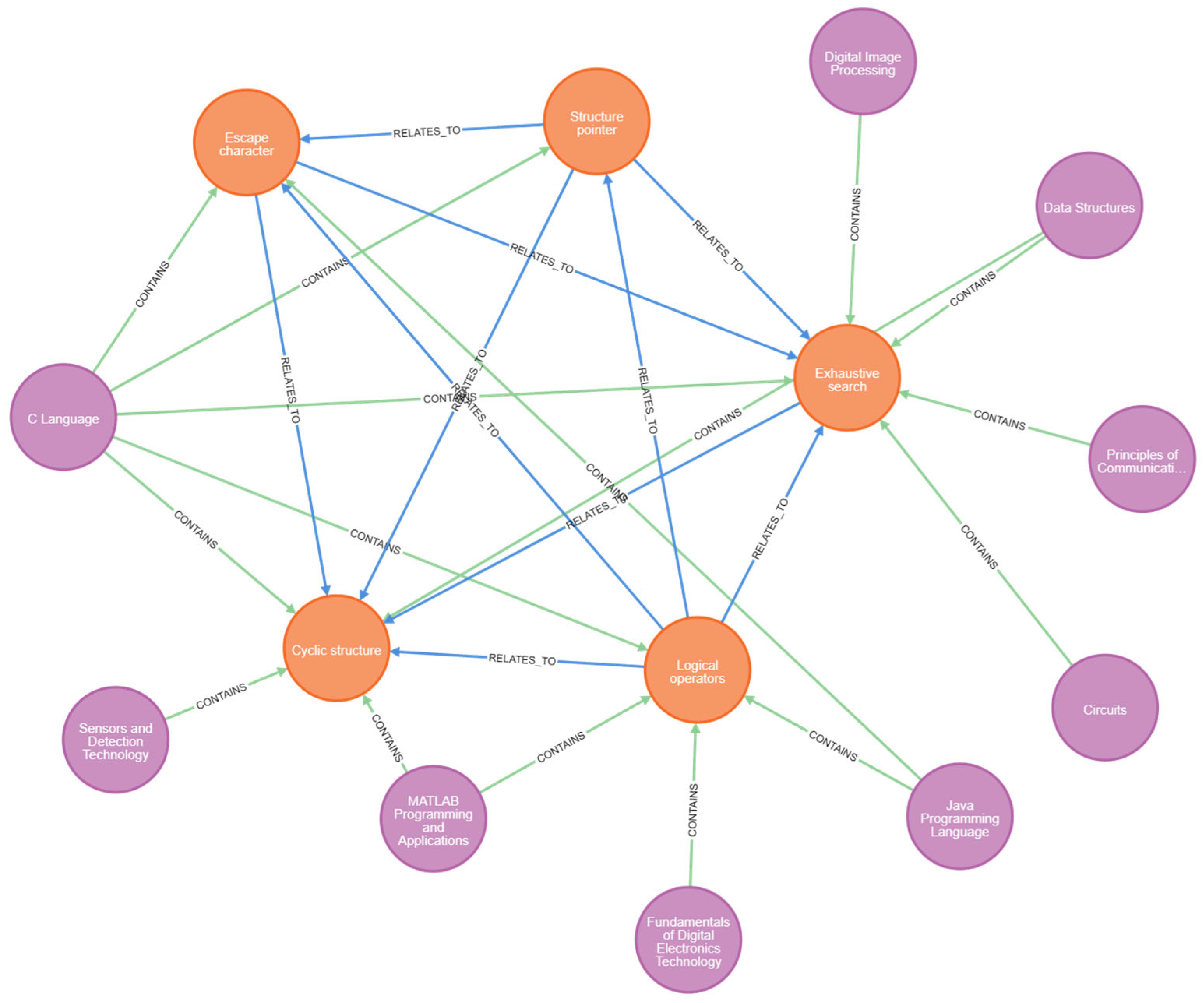
4.3.3. Graph Connectivity
4.3.4. Visualization Results
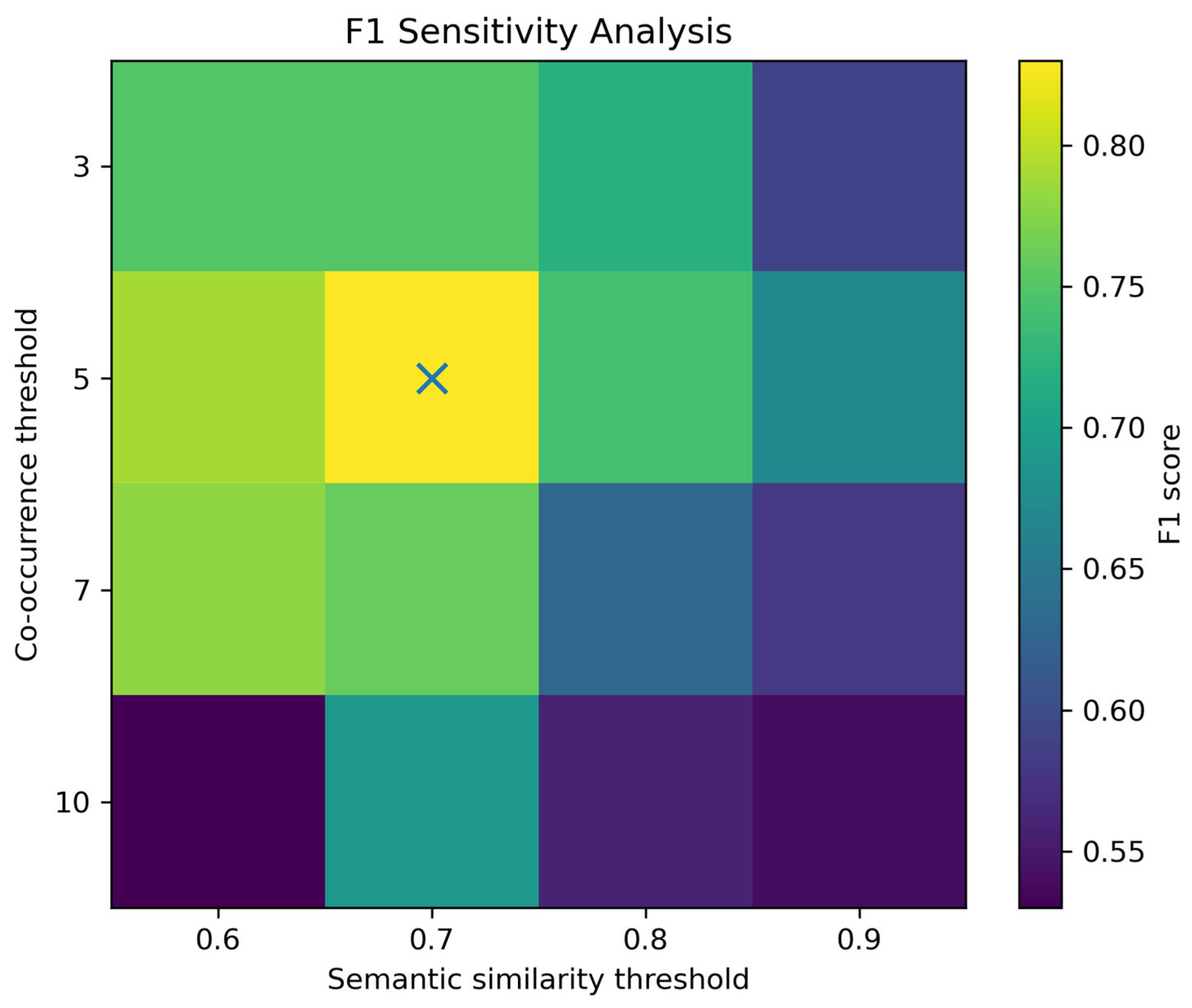
4.3.5. Threshold Sensitivity Results
4.3.6. Error Analysis Results
4.3.7. Ontology Alignment Results
4.3.8. Hyperparameter Ablation Results
4.3.9. GCN Sparsity Impact Results
5. Discussion
5.1. Semantic Depth vs. Computational Cost
5.2. Graph Enrichment and Curriculum Insight
5.3. Threshold Robustness and Error Patterns
5.4. Hyperparameter Validation and Generalizability
5.5. Downstream Graph Learning with Sparse Features
5.6. Limitations
- Compute and Scalability. GPU-dependent embedding limits real-time or large-scale deployment.
- Corpus Scope. Seventeen courses (~500 k words) may omit low-frequency but pedagogically critical terms.
- Edge Semantics. Current relations (co-occurrence, cosine similarity) capture only two link types; richer relation taxonomies remain unexplored.
- Interpretability. GCN link scores do not explain why a connection is predicted; attention-based explanations are a future direction.
5.7. Future Directions
- Interactive, User-in-the-Loop Refinement: Integrate teacher/student feedback to iteratively correct FP/FN and expand or prune taxonomy concepts [32].
- LLM-Assisted Augmentation: Use large language models to suggest new concept relations and fill sparse regions of the KG [33].
- Cross-Disciplinary Generalization: Apply the pipeline to adjacent STEM domains (e.g., control systems, power electronics) to test transferability.
- Multimodal Fusion: Incorporate video transcripts, slide images, and code snippets to enrich the KG with non-textual evidence [36].
- Explainable GCN: Embed interpretability modules (e.g., graph attention) to highlight which concepts and edges drive each prediction.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Definitions and Formulas of TF, IDF, and TF-IDF
Appendix B. Definitions and Formulas of Attention and Cosine_Similarity
References
- Giarelis, N.; Karacapilidis, N. Deep learning and embeddings-based approaches for keyphrase extraction: A literature review. Knowl. Inf. Syst. 2024, 66, 6493–6526. [Google Scholar] [CrossRef]
- Ain, Q.U.; Chatti, M.A.; Bakar, K.G.C.; Joarder, S.; Alatrash, R. Automatic Construction of Educational Knowledge Graphs: A Word Embedding-Based Approach. Information 2023, 14, 526. [Google Scholar] [CrossRef]
- Issa, B.; Jasser, M.B.; Chua, H.N.; Hamzah, M. A comparative study on embedding models for keyword extraction using keybert method. In Proceedings of the 2023 IEEE 13th International Conference on System Engineering and Technology (ICSET), Shah Alam, Malaysia, 2 October 2023; pp. 40–45. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems (NIPS 2017)), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Li, Z.; Cheng, L.-X.; Zhang, C.-X.; Zhu, X.; Zhao, H.-J. Multi-Source Education Knowledge Graph Construction and Fusion for College Curricula. In Proceedings of the 2023 IEEE International Conference on Advanced Learning Technologies (ICALT), Orem, UT, USA, 10–13 July 2023; pp. 359–363. [Google Scholar]
- Oveh, R.O.; Adewunmi, M.; Solomon, A.O.; Christopher, K.Y.; Ezeobi, P.N. Heterogenous analysis of KeyBERT, BERTopic, PyCaret and LDAs methods: P53 in ovarian cancer use case. Microelectron. J. 2024, 10, 100182. [Google Scholar] [CrossRef]
- Reimers, N.; Gurevych, I. Sentence-BERT: Sentence Embeddings using Siamese BERT-Networks. arXiv 2019, arXiv:1908.10084. [Google Scholar] [CrossRef]
- Amur, Z.H.; Hooi, Y.K.; Soomro, G.M.; Bhanbhro, H.; Karyem, S.; Sohu, N. Unlocking the Potential of Keyword Extraction: The Need for Access to High-Quality Datasets. Appl. Sci. 2023, 13, 7228. [Google Scholar] [CrossRef]
- Meisenbacher, S.; Schopf, T.; Yan, W.; Holl, P.; Matthes, F. An Improved Method for Class-specific Keyword Extraction: A Case Study in the German Business Registry. arXiv 2024, arXiv:2407.14085. [Google Scholar] [CrossRef]
- Li, Y.; Liang, Y.; Yang, R.; Qiu, J.; Zhang, C.; Zhang, X. CourseKG: An Educational Knowledge Graph Based on Course Information for Precision Teaching. Appl. Sci. 2024, 14, 2710. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. arXiv 2016, arXiv:1609.02907. [Google Scholar] [CrossRef]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Hou, Y.; Liu, B.; Fan, Q.; Zhou, J. Research on the application mode of knowledge graph in education. In Proceedings of the 2023 6th International Conference on Educational Technology Management, Guangzhou, China, 3–5 November 2024; pp. 215–220. [Google Scholar]
- Su, Z.; Li, Y.; Li, Q.; Yan, Z.; Zhao, L.; Liu, Z.; Sun, J.; Liu, S. Hypergraph Convolutional Networks for course recommendation in MOOCs. IEEE Trans. Knowl. Data Eng. 2025. early access. [Google Scholar] [CrossRef]
- Canal-Esteve, M.; Gutierrez, Y. Educational Material to Knowledge Graph Conversion: A Methodology to Enhance Digital Education. In Proceedings of the 1st Workshop on Knowledge Graphs and Large Language Models (KaLLM 2024), Bangkok, Thailand, 15 August 2024; pp. 85–91. [Google Scholar]
- Niu, S.J.; Luo, J.; Niemi, H.; Li, X.; Lu, Y. Teachers’ and Students’ Views of Using an AI-Aided Educational Platform for Supporting Teaching and Learning at Chinese Schools. Educ. Sci. 2022, 12, 858. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, S.; Wang, H. Personalized Learning Path Recommendation for E-Learning Based on Knowledge Graph and Graph Convolutional Network. Int. J. Softw. Eng. Knowl. Eng. 2023, 33, 109–131. [Google Scholar] [CrossRef]
- Qu, K.; Li, K.C.; Wong, B.T.M.; Wu, M.M.F.; Liu, M. A Survey of Knowledge Graph Approaches and Applications in Education. Electronics 2024, 13, 2537. [Google Scholar] [CrossRef]
- Rezayi, S.; Zhao, H.; Kim, S.; Rossi, R.A.; Li, S. Edge: Enriching Knowledge Graph Embeddings with External Text. arXiv 2021, arXiv:2104.04909. [Google Scholar] [CrossRef]
- Abu-Salih, B.; Alotaibi, S. A systematic literature review of knowledge graph construction and application in education. Heliyon 2024, 10, e25383. [Google Scholar] [CrossRef]
- Katyshev, A.; Anikin, A.; Sychev, O. Using Transformer Models for Knowledge Graph Construction in Computer Science Education. In Proceedings of the 54th ACM Technical Symposium on Computer Science Education V. 2, Toronto, ON, Canada, 15–18 March 2023; p. 1421. [Google Scholar]
- Zhao, B.; Sun, J.; Xu, B.; Lu, X.; Li, Y.; Yu, J.; Liu, M.; Zhang, T.; Chen, Q.; Li, H. EDUKG: A heterogeneous sustainable k-12 educational knowledge graph. arXiv 2022, arXiv:2210.12228. [Google Scholar] [CrossRef]
- Alatrash, R.; Chatti, M.A.; Ain, Q.U.; Fang, Y.; Joarder, S.; Siepmann, C. ConceptGCN: Knowledge concept recommendation in MOOCs based on knowledge graph convolutional networks and SBERT. Comput. Educ. Artif. Intell. 2024, 6, 100193. [Google Scholar] [CrossRef]
- Li, L.; Wang, Z. Knowledge relation rank enhanced heterogeneous learning interaction modeling for neural graph forgetting knowledge tracing. PLoS ONE 2023, 18, e0295808. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Y.; Li, J.; Luo, T. Degree aware based adversarial graph convolutional networks for entity alignment in heterogeneous knowledge graph. Neurocomputing 2022, 487, 99–109. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Z.; Shi, Z.; Cai, J.; Ji, S.; Wu, F. Duality-induced regularizer for semantic matching knowledge graph embeddings. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 1652–1667. [Google Scholar] [CrossRef]
- Schopf, T.; Klimek, S.; Matthes, F. Patternrank: Leveraging pretrained language models and part of speech for unsupervised keyphrase extraction. arXiv 2022, arXiv:2210.05245. [Google Scholar] [CrossRef]
- Wu, D.; Ahmad, W.U.; Chang, K.-W. Pre-trained language models for keyphrase generation: A thorough empirical study. arXiv 2022, arXiv:2212.10233. [Google Scholar] [CrossRef]
- Sanh, V.; Debut, L.; Chaumond, J.; Wolf, T. DistilBERT, a distilled version of BERT: Smaller, faster, cheaper and lighter. arXiv 2019, arXiv:1910.01108. [Google Scholar] [CrossRef]
- Jiao, X.; Yin, Y.; Shang, L.; Jiang, X.; Chen, X.; Li, L.; Wang, F.; Liu, Q. Tinybert: Distilling bert for natural language understanding. arXiv 2019, arXiv:1909.10351. [Google Scholar] [CrossRef]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar] [CrossRef]
- Linxen, A.; Endel, F.; Opel, S.; Beecks, C. Knowledge Graphs for Competency-Based Education. In Proceedings of the 2023 IEEE International Conference on Big Data (BigData), Sorrento, Italy, 15–18 December 2023; pp. 2942–2945. [Google Scholar]
- Abu-Rasheed, H.; Jumbo, C.; Amin, R.A.; Weber, C.; Wiese, V.; Obermaisser, R.; Fathi, M. LLM-Assisted Knowledge Graph Completion for Curriculum and Domain Modelling in Personalized Higher Education Recommendations. arXiv 2025, arXiv:2501.12300. [Google Scholar] [CrossRef]
- Dong, C.; Yuan, Y.; Chen, K.; Cheng, S.; Wen, C. How to Build an Adaptive AI Tutor for Any Course Using Knowledge Graph-Enhanced Retrieval-Augmented Generation (KG-RAG). In Proceedings of the 2025 14th International Conference on Educational and Information Technology (ICEIT), Online, 14–16 March 2025; pp. 152–157. [Google Scholar]
- Jain, M.; Kaur, H.; Gupta, B.; Gera, J.; Kalra, V. Incremental learning algorithm for dynamic evolution of domain specific vocabulary with its stability and plasticity analysis. Sci. Rep. 2025, 15, 272. [Google Scholar] [CrossRef]
- Li, L.; Wang, Z. Knowledge Graph-Enhanced Intelligent Tutoring System Based on Exercise Representativeness and Informativeness. Int. J. Intell. Syst. 2023, 2023, 2578286. [Google Scholar] [CrossRef]
- Hu, S.; Wang, X. FOKE: A Personalized and Explainable Education Framework Integrating Foundation Models, Knowledge Graphs, and Prompt Engineering. In Proceedings of the China National Conference on Big Data and Social Computing, Harbin, China, 8–10 August 2024; Springer Nature: Singapore, 2024. [Google Scholar]

| Element/Parameter | Configuration |
|---|---|
| Python Version | Python 3.8 |
| CPU | Intel Core i7-12700 |
| GPU | NVIDIA GeForce RTX 3060 (12 GB VRAM) |
| KeyBERT | Version 0.7.0 |
| SentenceTransformer | Version 2.2.2 |
| Neo4j Version | 4.4.9 Community Edition |
| KeyBERT Parameters | n-gram_range = (1,3), top_n = 10, use_mmr = True, diversity = 0.5 |
| TF-IDF Parameters | max_features = 500, min_df = 2 |
| Level | Taxonomy Term |
|---|---|
| 1 | Aerospace and electronic systems |
| 2 | Aerospace electronics |
| 2 | Electronic warfare |
| 1 | Antennas and propagation |
| 2 | Antennas |
| 2 | Electromagnetic propagation |
| 1 | Circuits and systems |
| 2 | Analog circuits |
| 2 | Digital circuits |
| 1 | Communications technology |
| 2 | Digital communication |
| 2 | Wireless communication (5 G/6 G) |
| 1 | Signal processing |
| 2 | Digital signal processing |
| 2 | Image processing |
| Matrix Type | Knowledge Points | Non-Zero Entries | Sparsity (%) |
|---|---|---|---|
| TF-IDF Baseline | 500 | 5100 | 40.0 |
| KeyBERT Enhanced | 1000 | 6120 | 64.1 |
| Co_Occurrence_Thresh | Similarity_Thresh | Precision | Recall | F1 |
|---|---|---|---|---|
| 3 | 0.6 | 0.77 | 0.74 | 0.75 |
| 0.7 | 0.82 | 0.69 | 0.75 | |
| 0.8 | 0.71 | 0.74 | 0.72 | |
| 0.9 | 0.67 | 0.52 | 0.59 | |
| 5 | 0.6 | 0.83 | 0.76 | 0.79 |
| 0.7 | 0.86 | 0.81 | 0.83 | |
| 0.8 | 0.72 | 0.76 | 0.74 | |
| 0.9 | 0.69 | 0.66 | 0.67 | |
| 7 | 0.6 | 0.84 | 0.72 | 0.78 |
| 0.7 | 0.79 | 0.74 | 0.76 | |
| 0.8 | 0.71 | 0.56 | 0.63 | |
| 0.9 | 0.68 | 0.51 | 0.58 | |
| 10 | 0.6 | 0.66 | 0.44 | 0.53 |
| 0.7 | 0.71 | 0.67 | 0.69 | |
| 0.8 | 0.62 | 0.51 | 0.56 | |
| 0.9 | 0.59 | 0.49 | 0.54 |
| Category | Count | Rate (%) |
|---|---|---|
| TP | 490 | 6.9 |
| FP | 60 | 0.8 |
| FN | 110 | 1.5 |
| TN | 6480 | 90.8 |
| Course | Extracted Knowledge Points | Total Number of Occurrences | Similarity | Error Type | Possible Cause |
|---|---|---|---|---|---|
| Digital Signal Processing | Filter | 6 | 0.72 | FP | Although “filter” is a high-frequency term, the course focuses on filtering at the signal processing algorithm level, not general filter principles. |
| Analog Circuits | Resistance | 8 | 0.68 | FP | “Resistance” is a basic concept that appears frequently, but the course emphasizes amplifier design and does not have a dedicated chapter on resistor details |
| Communication Principles | Network | 7 | 0.75 | FP | “Network” has high semantic similarity, but the course does not cover network layer protocols, making the concept too broad |
| Microprocessor Principles | Cache | 5 | 0.70 | FP | “cache” appears in examples, but the course does not delve into cache architecture, which is contextually distracting |
| Digital Image Processing | Color Space | 9 | 0.65 | FP | “color space” is mentioned in the textbook but is not a core knowledge point of this study and is prone to being selected by mistake |
| Course | Missed Knowledge Points | Total Number of Occurrences | Similarity | Error Type | Possible Causes |
|---|---|---|---|---|---|
| Digital Signal Processing | Fourier Transform | 4 | 0.83 | FN | Co-occurrence < 5, filtered by threshold; this concept is important but occurs too infrequently in the segments |
| Analog Circuits | Operational Amplifier | 3 | 0.65 | FN | Multi-word expressions are truncated; “operational amplifier” is outside the n-gram window after segmentation |
| Communication Principles | Modulation | 8 | 0.68 | FN | Similarity 0.68 is slightly below the 0.7 threshold; the contextual semantic boundaries of this word are unclear |
| Microprocessor Principles | Discrete Cosine Transform | 10 | 0.60 | FN | Although co-occurrence frequency is high, similarity 0.60 is too low; matching long and short phrases is challenging |
| Digital Image Processing | Interrupt Service Routine | 7 | 0.75 | FN | “Interrupt Service Routine” is a phrase of three or more words; MMR retains only the first two parts of the phrase |
| Setting | Precision | Recall | F1 |
|---|---|---|---|
| Before alignment | 0.86 | 0.81 | 0.83 |
| After alignment | 0.88 | 0.79 | 0.83 |
| Ngram_Range | Top_n | Precision | Recall | F1 |
|---|---|---|---|---|
| (1,1) | 5 | 0.78 | 0.69 | 0.73 |
| 10 | 0.8 | 0.71 | 0.75 | |
| 15 | 0.79 | 0.75 | 0.77 | |
| (1,2) | 5 | 0.81 | 0.72 | 0.76 |
| 10 | 0.84 | 0.76 | 0.80 | |
| 15 | 0.83 | 0.73 | 0.78 | |
| (1,3) | 5 | 0.79 | 0.74 | 0.76 |
| 10 | 0.86 | 0.81 | 0.83 | |
| 15 | 0.81 | 0.78 | 0.79 |
| Feature | Sparsity (%) | GCN Accuracy | GCN F1-Score |
|---|---|---|---|
| TF-IDF | 40 | 0.66 | 0.69 |
| KeyBERT | 64 | 0.78 | 0.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, G.; Lu, X. A KeyBERT-Enhanced Pipeline for Electronic Information Curriculum Knowledge Graphs: Design, Evaluation, and Ontology Alignment. Information 2025, 16, 580. https://doi.org/10.3390/info16070580
Zhuang G, Lu X. A KeyBERT-Enhanced Pipeline for Electronic Information Curriculum Knowledge Graphs: Design, Evaluation, and Ontology Alignment. Information. 2025; 16(7):580. https://doi.org/10.3390/info16070580
Chicago/Turabian StyleZhuang, Guanghe, and Xiang Lu. 2025. "A KeyBERT-Enhanced Pipeline for Electronic Information Curriculum Knowledge Graphs: Design, Evaluation, and Ontology Alignment" Information 16, no. 7: 580. https://doi.org/10.3390/info16070580
APA StyleZhuang, G., & Lu, X. (2025). A KeyBERT-Enhanced Pipeline for Electronic Information Curriculum Knowledge Graphs: Design, Evaluation, and Ontology Alignment. Information, 16(7), 580. https://doi.org/10.3390/info16070580






