Dynamic Mixture of Experts for Adaptive Computation in Character-Level Transformers

Abstract

This paper challenges the prevailing assumption that Mixture of Experts (MoE) consistently improves computational efficiency through a systematic evaluation of MoE variants in Transformer models. We implement and compare three approaches: basic MoE, top-k routing, and capacity-factored routing, each progressively addressing load-balancing challenges. Our experiments reveal critical trade-offs between performance and efficiency: while MoE models maintain validation performance comparable to baselines, they require significantly longer training times (a 50% increase) and demonstrate reduced inference speeds (up to 56% slower). Analysis of routing behavior shows that even with load-balancing techniques, expert utilization remains unevenly distributed. These findings provide empirical evidence that MoE’s computational benefits are highly dependent on model scale and task characteristics, challenging common assumptions about sparse architectures and offering crucial guidance for adaptive neural architecture design across different computational constraints.

1. Introduction

Transformer models [1] have revolutionized natural language processing (NLP), demonstrating remarkable performance across a wide range of tasks. Foundational models like BERT [2] and its variants [3,4] have established powerful pre-training paradigms. The success of these models has led to a trend of increasing model size to achieve better performance, exemplified by models like GPT-3 [5], PaLM [6], and LLaMA [7].

Recent developments in large language models have pushed the boundaries of model capabilities even further, with advanced systems like GPT-4 and subsequent iterations demonstrating remarkable performance across diverse tasks, including human-like conversational abilities and complex reasoning. While these frontier models represent significant achievements in artificial intelligence, they operate at scales requiring substantial computational resources that are often inaccessible for many practical applications and research scenarios.

This scaling approach creates significant computational challenges, particularly for deployment in resource-constrained environments [8]. As a result, there is growing interest in techniques that can maintain or improve model performance while enhancing computational efficiency [4,9]. Our work contributes to this effort by focusing on architectural efficiency at smaller scales, where the fundamental trade-offs between computational cost and model performance may differ significantly from those observed in billion-parameter frontier models. However, systematic analysis of these techniques’ applicability across different scales and task types remains limited.

Mixture of Experts (MoE) has gained attention for its ability to scale model capacity with only a modest increase in computational cost [10,11]. MoE models employ a routing mechanism to dynamically select specialized subnetworks (experts) for different inputs, enabling conditional computation where only a subset of the model’s parameters is activated for each input [12]. This approach has been successfully applied in large-scale Transformer models such as GShard [13], Switch Transformers [11], and, most recently, Mixtral 8x7B [14], often supported by specialized infrastructure [15,16].

The widespread acceptance of MoE as an efficiency-enhancing technique stems primarily from theoretical arguments and empirical observations in very large-scale settings. The efficiency assumption is fundamentally based on the principle that activating only a fraction of model parameters should reduce computational cost proportionally. For instance, if only two out of eight experts are activated per token (as in Mixtral), the theoretical FLOP count suggests a 4× reduction in computation compared to dense models with an equivalent total parameter count. This reasoning has been empirically validated in billion-parameter models, where the routing overhead becomes negligible relative to the massive expert computations.

However, this efficiency narrative relies on several critical assumptions that may not hold universally: (1) the computational overhead of routing mechanisms is negligible compared to expert computation; (2) expert networks are sufficiently large that sparse activation provides meaningful computational savings; (3) hardware and software implementations can effectively exploit the sparsity patterns for actual speedup; and (4) the load-balancing challenges do not require additional computational mechanisms that offset the theoretical gains. These assumptions, while reasonable for very large models, become increasingly questionable as the model scale decreases.

Furthermore, much of the existing literature evaluates MoE efficiency in the context of distributed training across multiple accelerators, where communication costs and parallelization strategies fundamentally differ from single-device scenarios typical in smaller models. The predominant focus on word-level or subword-level language modeling also raises questions about whether the efficiency benefits extend to character-level tasks, where the sequence lengths, pattern granularity, and computational characteristics differ substantially.

These implementations demonstrate that MoE can significantly increase model capacity while maintaining reasonable computational requirements. However, our understanding of MoE effectiveness across different scales and representation levels remains limited, particularly concerning whether the advantages observed in large models consistently extend to all model scales and task types—a crucial consideration for practical architecture decisions.

Despite these advances, the applicability and efficiency trade-offs of MoE across different computational scenarios remain understudied [17,18]. Previous work has predominantly focused on ultra-large-scale models [19,20], leaving a gap in our comprehensive understanding of MoE performance across different computational scales and language representation granularities. This knowledge gap limits our ability to make informed architectural design decisions in practical application environments [21].

Standard Transformer architectures employ fixed-capacity feed-forward networks (FFNs) within each block, processing all inputs with the same computation regardless of their complexity [22]. This uniform allocation of computational resources may be suboptimal for tasks where input importance varies significantly [22]. Implementing MoE in smaller models presents several technical challenges: (1) unlike large models, where MoE spans millions of parameters, smaller models may not benefit from the same efficiency gains [23]; (2) effective routing is critical but can be unstable during training, leading to load imbalance and “expert collapse” [24,25]; and (3) routing mechanisms introduce computational overhead that may significantly impact both training and inference efficiency [26].

In this paper, we address these challenges by conducting a systematic empirical study of MoE-based Transformer models. We modify the standard FFN component in Transformer blocks, replacing it with different MoE configurations while maintaining approximately equal parameter counts. Our approach explores various MoE designs, including a basic configuration with softmax routing, top-k routing, and capacity-factored routing with different thresholds [24]. We evaluate these models on the Shakespeare dataset, analyzing both performance metrics and computational efficiency.

Our experiments reveal a nuanced picture of the trade-offs involved in applying MoE to Transformers. While all MoE variants maintain validation performance comparable to the baseline model (within ±0.2%), they exhibit significantly higher training losses (+18%), suggesting a potential regularization effect or different learning dynamics [27]. Furthermore, MoE models incur substantial computational costs, with training time increasing by approximately 50% and inference speed decreasing by up to 56% [21]. Analysis of router behavior shows emergent specialization patterns, with experts developing preferences for specific patterns or structures [28].

Our findings have broad implications for neural network design, demonstrating that the computational advantages typically observed in ultra-large-scale models may not automatically extend to all scenarios [29]. This insight challenges the prevailing assumptions of “bigger is better” [30] and “sparse equals efficient” [11], pointing toward a more nuanced and context-dependent paradigm for architecture design [31].

The main contributions of this work are summarized as follows:

• We challenge the widely held assumption that MoE improves computational efficiency by providing systematic empirical evidence that MoE’s computational benefits are highly dependent on the model scale and task type [32].
• We provide the first detailed quantitative analysis of the trade-offs between performance and computational cost for MoE across different routing strategies, revealing significant increases in training time and reductions in inference speed.
• We conduct an in-depth analysis of routing behavior and expert utilization patterns, finding that even with load-balancing techniques, specific patterns still lead to uneven expert utilization.
• We provide empirical guidance for the application of conditional computation in neural networks, articulating key considerations for balancing performance and efficiency under different computational constraints [33].

The remainder of this paper is organized as follows. Section 2 reviews related works. Section 3 provides background on Transformers and MoE. Section 4 details our MoE-based MLP modifications. Section 5 describes the experimental setup. Section 6 presents and discusses the results. Finally, Section 7 concludes this paper and discusses future work.

2. Related Works

We organize our review of related works into three main categories: Transformer models and their evolution, Mixture-of-Experts architectures, and character-level language modeling approaches.

2.1. Transformer Models and Efficiency

Since their introduction by [1], Transformer models have become the dominant architecture for NLP tasks. Foundational models like BERT [2] and its variants [3,4] paved the way for large language models. Their success has led to increasingly larger models, such as GPT-3 [5] with 175B parameters, as well as models optimized for specific modalities or tasks, like Transformer-XL [34], and for cross-lingual applications [35]. However, this trend raises concerns about computational efficiency and accessibility.

Several approaches have been proposed to address the computational challenges of Transformer models. These include architectural modifications such as Transformer-XL [34], which improves the handling of long-range dependencies, and optimizations targeting specific components of the architecture. For instance, attention mechanisms have been made more efficient through approximations or sparse implementations [36,37].

The feed-forward network (FFN) or multi-layer perceptron (MLP) component of Transformer blocks has received comparatively less attention, despite accounting for a significant portion of the computational cost. Our work specifically targets this component, exploring how conditional computation through MoE can improve efficiency without sacrificing performance.

2.2. Mixture-of-Experts Approaches

Mixture of Experts (MoE) was initially introduced by [12] as a machine learning technique, in which multiple expert networks specialize in different parts of the input space, with a gating network determining which experts to use for a given input. The application of MoE to deep neural networks was significantly advanced by [10], who demonstrated that sparsely gated MoE layers could dramatically increase model capacity without proportionally increasing computational cost.

In the context of Transformer models, MoE has been applied primarily to very large-scale models. GShard [13] and Switch Transformers [11] demonstrated that replacing dense feed-forward layers with MoE layers could increase model capacity while improving training efficiency [17]. GLAM [38] further refined this approach, incorporating techniques to improve load balancing and routing stability.

Recent work has also explored alternative routing mechanisms and training procedures for MoE. Base Layers [24] utilized specialized training schemes for sparse expert models, while [39] introduced hash layers as an alternative to learned routing. Other research has investigated residual MoE layers [40], mixture of tokens as an alternative [41], MoE for continual learning [42], memory-efficient or private training [43], and structured pruning for MoE efficiency [25]. Studies have provided theoretical insights into how MoE models scale with increasing parameters and computational resources, explored multimodal applications [44], and focused on scaling instruction-tuned MoE models [45]. Systems like DeepSpeed-MoE aim to advance the scalability of MoE inference and training [15,16]. Research continues into understanding and improving MoE training dynamics [18].

Critical Analysis of Scale-Dependent MoE Performance: The predominant focus on large-scale MoE implementations benefits from massive expert networks, where routing overhead becomes negligible relative to expert computation, a condition that does not hold for smaller models, where routing costs can dominate. In addition, the distributed training paradigms common in large-scale studies fundamentally differ from single-device scenarios typical of smaller models, where communication patterns, memory hierarchies, and parallelization strategies differ entirely.

Furthermore, the expert specialization dynamics observed in billion-parameter models may not translate to smaller scales where limited model capacity constrains the degree of specialization that is possible. Large models have sufficient capacity for experts to develop highly specific functions, whereas smaller models may face resource contention that prevents effective specialization. The load-balancing techniques developed for large-scale systems also assume expert networks large enough for capacity constraints to be meaningful, an assumption that becomes questionable as expert size decreases.

Recent Small-Scale MoE Investigations: While the majority of MoE research focuses on large-scale implementations, a limited number of recent studies have begun exploring MoE applications in smaller models, although not specifically in the character-level domain we investigate here. Chen et al. [23] examined MoE efficiency in moderately sized language models and found diminishing returns below certain scale thresholds. Komatsuzaki et al. [32] investigated sparse architectures in smaller Transformers but focused primarily on attention sparsity rather than expert routing. Recent work by Muqeeth et al. [26] provided a theoretical analysis suggesting that MoE efficiency gains require minimum expert sizes to offset routing overhead, supporting our empirical observations.

However, these limited investigations did not systematically address the specific challenges of character-level modeling, where the sequence lengths, pattern granularity, and computational characteristics differ substantially from word-level tasks. Our work addresses this gap by providing the first comprehensive evaluation of MoE trade-offs specifically in the character-level, small-scale setting, where the fundamental assumptions underlying large-scale MoE success may not hold.

Unlike previous works that primarily focused on applying MoE in very large language models (typically with billions of parameters), our work examines MoE in smaller-scale Transformer models specifically for character-level tasks. We provide a systematic comparison of different MoE configurations, focusing on the performance-efficiency trade-offs that are particularly relevant for resource-constrained environments.

2.3. Character-Level Language Modeling

Character-level language modeling involves predicting sequences of characters rather than word or subword tokens. This approach offers certain advantages, including the ability to handle out-of-vocabulary words and to capture sub-word patterns, but also presents unique challenges due to the longer sequence lengths and finer granularity of dependencies.

Early works on character-level language modeling primarily used recurrent neural networks (RNNs) [46]. With the rise of Transformer architectures, character-level models have been adapted to this framework, demonstrating competitive performance despite the increased sequence lengths involved.

Character-level modeling is particularly well-suited for certain domains, such as programming languages or specialized texts like Shakespeare’s works, where the vocabulary is relatively constrained and character-level patterns are informative. However, the computational requirements of character-level models can be challenging due to the longer sequences they must process.

Our work bridges the gap between character-level language modeling and MoE architectures, exploring whether the adaptive computation capabilities of MoE can be beneficial in this specific context. We investigate whether different characters or character sequences might benefit from specialized expert processing and how this affects both model performance and computational efficiency.

2.4. Positioning of Our Work

Table 1. Comparison with related works.

Approach	MoE	Character-Level Modeling	Small-Scale Models	Performance–Efficiency Trade-Off Analysis
GShard [13]	✓			✓
Switch Transformer [11]	✓			✓
Character Transformers		✓	✓
DeepSpeed-MoE	✓			✓
Mixtral [14]	✓			✓
Our Work	✓	✓	✓	✓

Note: ✓ indicates that the approach incorporates the corresponding characteristic.

summarizes the key differences between our work and previous approaches. While prior studies have applied MoE to large-scale Transformer models or explored character-level modeling with standard architectures, our work uniquely focuses on the intersection of these areas. We specifically investigate the following:

• The application of MoE specifically within the MLP component of character-level Transformer models.
• The comparative performance of different MoE configurations (basic, top-k, capacity-factored) in this context.
• A detailed analysis of performance–efficiency trade-offs, considering both training and inference metrics.
• The behavior of routing mechanisms and expert specialization patterns in character-level modeling.

By focusing on these aspects, our work provides novel insights into the effectiveness of MoE for character-level tasks in smaller-scale models, an area that remains underexplored despite its potential relevance for resource-constrained applications. Unlike recent large-scale MoE implementations such as Mixtral [14] and MoE variants in PaLM [6], our study specifically targets smaller, more accessible models, where the efficiency–performance trade-offs may differ substantially from those observed in billion-parameter models. This distinction is critical as it addresses the growing need for efficient language models that can be deployed in scenarios with limited computational resources, such as edge devices or specialized applications requiring character-level processing.

Furthermore, our analysis provides empirical evidence for how routing dynamics evolve in character-level tasks, where the granularity of the input and the nature of the patterns differ significantly from word- or token-level modeling. These insights contribute to the broader understanding of how conditional computation mechanisms can be effectively applied across different levels of language representation.

3. Background

This section provides the background on the key concepts underlying our work, including the Transformer architecture, Mixture of Experts (MoE), and character-level language modeling.

3.1. Transformer Architecture

The Transformer architecture [1] consists of a stack of identical layers, each containing two main components: a multi-head self-attention mechanism and a position-wise feed-forward network (FFN). Each component is followed by a residual connection and layer normalization.

The self-attention mechanism enables the model to focus on different parts of the input sequence when encoding each position, capturing long-range dependencies without the sequential computation bottleneck of recurrent neural networks. Given an input sequence representation $X\in {\mathbb{R}}^{n\times d}$, where n is the sequence length and d is the embedding dimension, the self-attention operation computes

$$\mathrm{Attention}(Q,K,V)=\mathrm{softmax}\left({\displaystyle \frac{Q{K}^T}{\sqrt{d_k}}}\right)V$$

(1)

where $Q=X{W}_Q$, $K=X{W}_K$, and $V=X{W}_V$ are linear transformations of the input sequence into query, key, and value representations, respectively.

Following the attention layer, the feed-forward network (FFN) processes each position independently:

$$\mathrm{FFN}\left(x\right)=\mathrm{Dropout}(W_2·\mathrm{GELU}(W_1·x+b_1)+b_2)$$

(2)

where $W_1\in {\mathbb{R}}^{d\times 4d}$ and $W_2\in {\mathbb{R}}^{4d\times d}$ are the expansion and projection matrices, respectively, with d being the model’s embedding dimension. The intermediate dimension of $4d$ is a common choice in Transformer architectures.

We use the Gaussian Error Linear Unit (GELU) activation function rather than the traditional ReLU. GELU provides several advantages for language modeling tasks: unlike ReLU, which hard-clips negative values to zero, GELU offers a smooth, probabilistic activation that allows small negative values to pass through with a probability dependent on their magnitude. This smoothness facilitates better gradient flow during training and has been empirically shown to improve performance in Transformer-based language models [47]. The probabilistic nature of GELU aligns well with the stochastic aspects of language modeling, making it the preferred choice in modern implementations.

In our implementation, the baseline model uses the following hyperparameters:

• Embedding dimension (d): 384.
• Number of layers: 6.
• Number of attention heads: 6.
• Dropout rate: 0.2.
• Context length (block size): 256 characters.

3.2. Mixture of Experts (MoE)

Mixture of Experts (MoE) is a conditional computation technique in which the model selectively activates different parts (experts) based on the input, rather than using the entire network for all inputs. A typical MoE layer consists of the following:

• A set of N expert networks, each specialized for different inputs.
• A router or gating network that determines which expert(s) to use for each input.
• A mechanism to combine the outputs of the selected experts.

For an input x, the router computes a distribution over experts, typically using a softmax function.

$$p\left(i\right|x)={\displaystyle \frac{exp\left(r{\left(x\right)}_i\right)}{{\sum }_{j=1}^{N}exp\left(r{\left(x\right)}_j\right)}}$$

(3)

$$\mathrm{MoE}\left(x\right)=\sum _{i=1}^{N}p\left(i\right|x)·E_i\left(x\right)$$

(4)

where $E_i$ is the i-th expert network. For computational efficiency, many implementations use a sparse combination, selecting only the top-k experts with the highest routing probabilities.

In larger models like Switch Transformers [11], each expert may function as a complete FFN. In our implementation for smaller-scale models, we split the FFN’s expansion layer into multiple experts while keeping the projection layer shared, as detailed in Section 4.

Additionally, practical MoE implementations often incorporate mechanisms to ensure balanced expert utilization. One such mechanism is a capacity factor, which limits the maximum number of tokens that can be routed to each expert, preventing the overloading of popular experts and encouraging a more balanced distribution of work.

3.3. Problem Setting

Our work focuses on character-level language modeling, a task in which the model predicts the next character in a sequence given the previous characters. Unlike word- or subword-level modeling, character-level modeling works with a much smaller vocabulary (typically fewer than 100 unique characters) but must process longer sequences to capture equivalent context.

Formally, for a sequence of characters $c_1,c_2,\dots ,c_T$, the language modeling objective is to maximize the likelihood

$$p(c_1,c_2,\dots ,c_T)=\prod _{t=1}^{T}p\left(c_t\right|c_1,c_2,\dots ,c_{t-1})$$

(5)

In practice, this is typically implemented by training the model to minimize the cross-entropy loss between its predictions and the actual next characters.

Character-level modeling presents unique challenges and opportunities for MoE approaches. On the one hand, the smaller vocabulary and more predictable patterns might enable more effective expert specialization. On the other hand, the finer granularity and longer sequences might require different routing strategies compared to word-level models. Our experiments explore these trade-offs in the context of Shakespeare’s works, a dataset with distinctive linguistic patterns for which character-level modeling is particularly appropriate.

4. Methodology/MoE-Based FFN Modifications

This section details our methodological approach to replacing the standard FFN component in Transformer blocks with MoE-based alternatives. We begin by describing the baseline model architecture and then explain our MoE implementations and the different routing strategies explored in our experiments.

4.1. Baseline Model Architecture

Our baseline model follows the standard Transformer architecture as implemented in nanoGPT [48], a lightweight implementation of the GPT model family. The model consists of a token embedding layer, positional embeddings, a stack of Transformer blocks, and a final layer normalization followed by a linear output layer.

We built our implementation using the foundational architectural principles from nanoGPT, adapting its core design patterns for our specific research objectives. Our modifications focus exclusively on the feed-forward network components within each Transformer block while maintaining the original attention mechanisms, embedding structures, and training procedures that form the stable foundation of the nanoGPT framework.

In our implementation, the baseline model uses the following hyperparameters:

• Embedding dimension (d): 384.
• Number of layers: 6.
• Number of attention heads: 6.
• Dropout rate: 0.2.
• Context length (block size): 256 characters.

4.2. MoE FFN Architecture

Our MoE implementation modifies the standard FFN by replacing the expansion layer ($W_1$) with multiple expert networks while keeping the projection layer ($W_2$) shared. This design choice allows us to maintain parameter count equivalence with the baseline model while introducing conditional computation. The shared projection layer is standard practice; it helps control the parameter count and ensures that the final output dimension matches the model’s embedding dimension d. The core idea is to dynamically route each input token to a small subset of specialized expert networks instead of processing every token with the same large feed-forward layer.

Specifically, the baseline FFN equation (Equation (2)) uses a single, large linear layer ($W_1\in {\mathbb{R}}^{d\times 4d}$) followed by a GELU activation function and a projection layer ($W_2\in {\mathbb{R}}^{4d\times d}$). In our MoE variants, we replace the $W_1$ layer with the following:

• A Router Network: A simple linear layer ($W_r\in {\mathbb{R}}^{d\times N}$) that takes the input token representation $x\in {\mathbb{R}}^d$ and outputs logits $r\left(x\right)\in {\mathbb{R}}^N$ indicating the affinity of the token for each of the N experts. In our case, $N=4$.
• N Expert Networks: A set of N smaller, independent linear layers ($E_i\in {\mathbb{R}}^{d\times d}$ for $i=1,\dots ,N$). Each expert network has the same input and output dimension as the original embedding dimension d. The total parameters across all experts ($N\times d\times d=4d^2$) are equivalent to the baseline’s expansion layer ($d\times 4d=4d^2$).

The computation flow within the MoE FFN block proceeds as follows: the router determines which expert(s) should process the input token based on the chosen routing mechanism (detailed below). The selected expert(s) then process the token representation in parallel. Finally, the outputs of the activated experts are combined (e.g., through a weighted sum based on router scores) before passing through the shared GELU activation function and the final projection layer ($W_2$).

Our MoE FFN can be formalized as

$$\begin{array}{cc}\hfill \mathrm{MoE-FFN}& \left(x\right)=\mathrm{Dropout}(W_2·\mathrm{GELU}(\hfill \\ \hfill & \mathrm{Router}\text{-}\mathrm{Combine}(x,E_1,E_2,\dots ,E_N))+b_2)\hfill \end{array}$$

(6)

where $E_i$ represents the i-th expert network, and router-combine determines how to combine the expert outputs based on the router’s decisions. The exact behavior of router-combine varies across our different routing strategies, as detailed in the following subsections.

The router network computes logits $r\left(x\right)=W_r·x+b_r$, where $W_r\in {\mathbb{R}}^{d\times N}$, with $N=4$ being the number of experts. These logits are then used differently depending on the routing strategy.

4.3. Routing Mechanisms and Expert Combination

We experiment with several routing mechanisms, each representing a different approach to expert selection and combination, as detailed below.

4.3.1. Base MoE (Run 1)

In our baseline MoE implementation, we use a simple softmax routing mechanism in which all experts process each input, but their outputs are weighted according to the router’s softmax distribution:

$$p\left(i\right|x)={\displaystyle \frac{exp\left(r{\left(x\right)}_i\right)}{{\sum }_{j=1}^{N}exp\left(r{\left(x\right)}_j\right)}}$$

(7)

For an input tensor $x\in {\mathbb{R}}^{B\times T\times d}$ (batch size × sequence length × embedding dimension), the router computes weights $p\in {\mathbb{R}}^{B\times T\times N}$. Each expert $E_i$ processes the input independently to produce $E_i\left(x\right)\in {\mathbb{R}}^{B\times T\times d}$. These outputs are stacked to form a tensor $E\left(x\right)\in {\mathbb{R}}^{B\times T\times N\times d}$.

The router-combine operation is then implemented as a weighted sum:

$$\begin{array}{c}\mathrm{Router-Combine}(x,E_1,E_2,\dots ,E_N)=\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \sum _{i=1}^{N}p\left(i\right|x)·E_i\left(x\right)\hfill \end{array}$$

(8)

This is efficiently computed using the einsum operation: $\mathrm{einsum}{(}^{\prime }btk,btkd->bt{d}^{\prime },p,E\left(x\right))$.

4.3.2. Top-k Routing (Run 2)

To increase sparsity and computational efficiency, our second MoE variant employs top-k routing, in which only the k experts with the highest router scores are activated for each input. In our implementation, we set k = 2, meaning each input is processed by only half of the available experts.

The routing process becomes

$$\{\begin{array}{cc}{\displaystyle \frac{exp\left(r{\left(x\right)}_i\right)}{{\sum }_{j\in \mathrm{top-}k\left(r\right(x),k)}exp\left(r{\left(x\right)}_j\right)}}\hfill & \mathrm{if}i\in \mathrm{top-}k\left(r\right(x),k)\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}$$

(9)

In practice, we implement this using PyTorch’s top-k function to select the top-2 experts and their corresponding logits. We then apply softmax only to these selected logits to obtain normalized weights. The expert outputs are gathered using the selected indices and combined with the normalized weights.

4.3.3. Top-k Routing with Capacity Factors (Runs 3 and 4)

Our final MoE variants add capacity constraints to the top-k routing mechanism. The capacity factor (CF) limits the maximum number of tokens that can be routed to each expert, preventing load imbalance in which a few experts might process the majority of tokens.

For a batch of tokens with size $B\times T$ and N experts, the expert capacity is calculated as

$$\mathrm{Capacity}=\mathrm{CF}\times {\displaystyle \frac{B\times T\times k}{N}}$$

(10)

where CF is the capacity factor (0.5 in Run 3, 1.0 in Run 4) and k is the number of experts selected per token (k = 2 in our experiments).

When the number of tokens assigned to an expert exceeds its capacity, the excess tokens are “masked out” during the expert combination step. This is implemented by creating a binary mask that is 1 for tokens within capacity and 0 for tokens exceeding capacity, then multiplying the routing weights by this mask before combining the expert outputs.

The effective routing weight becomes

$$p_{\mathrm{eff}}\left(i\right|x)=p\left(i\right|x)\times \mathbb{1}[\mathrm{count}\left(i\right)\le \mathrm{Capacity}]$$

(11)

where $\mathrm{count}\left(i\right)$ is the number of tokens assigned to expert i and $\mathbb{1}$ is the indicator function. The router-combine operation then uses these modified weights.

The capacity factor of 0.5 in Run 3 means that each expert has capacity for only half the tokens that would be assigned to it in a perfectly balanced scenario. This creates significant competition for expert capacity and forces the router to be more selective. In Run 4, we increase the capacity factor to 1.0, allowing each expert to handle all tokens that would be assigned in a balanced scenario, which reduces competition but still prevents severe imbalances.

4.4. Implementation Details and Design Considerations

Our implementation choices were guided by several key considerations:

• Parameter Count Equivalence: We designed our MoE variants to maintain approximately the same parameter count as the baseline model to ensure a fair comparison. The four expert networks with dimension $d\times d$ match the parameter count of the single $d\times 4d$ expansion layer in the baseline FFN.
• Expert Granularity: We chose to have four experts based on the standard practice of using a 4× expansion factor in Transformer MLPs. This allows each expert to specialize in a distinct aspect of the input space while maintaining a reasonable computational profile.
• Progressive Complexity: Our sequence of experiments (Runs 1–4) follows a progression of increasing sophistication in the routing mechanism, allowing us to isolate the effects of each modification.
• Computational Considerations: While MoE can theoretically improve computational efficiency through sparse activation, the overhead of routing and expert selection can outweigh these benefits in smaller models. Our experiments quantify these trade-offs to inform practical implementation decisions.

It is worth noting that our MoE implementation does include additional parameters compared to the baseline due to the router network, which adds $d\times N+N$ parameters to the routing layer. However, this represents a relatively small increase (approximately 1% of the model’s parameters) and does not significantly affect the overall model capacity.

Pseudocode Comparison

Algorithm 1 provides pseudocode comparing the forward pass differences between the baseline FFN and our MoE FFN variant (using the base softmax routing for simplicity).

The training dynamics across different model configurations are illustrated in Figure 1, which shows the training loss evolution for all experimental variants. Despite the computational overhead, our MoE implementations demonstrate interesting learning behaviors that differ significantly from the baseline model. Figure 2 presents the corresponding validation loss curves, revealing the performance characteristics that guide our architectural analysis.

Algorithm 1 FFN forward pass comparison.

Require:  Input tensor $x\in {\mathbb{R}}^{B\times T\times d}$  1: Baseline FFN Forward:  2: $h_1=\mathrm{GELU}(x{W}_1+b_1)$ {[}r]$W_1\in {\mathbb{R}}^{d\times 4d}$  3: $y=\mathrm{Dropout}(h_1{W}_2+b_2)$ {[}r]$W_2\in {\mathbb{R}}^{4d\times d}$  4: return y  5: $\phantom{.}$  6: MoE FFN Forward (Base Softmax Routing):  7: $r=x{W}_r+b_r$ {[}r]Compute router logits, $W_r\in {\mathbb{R}}^{d\times N}$  8: $p=\mathrm{Softmax}\left(r\right)$ {[}r]Compute router probabilities, $p\in {\mathbb{R}}^{B\times T\times N}$  9: for $i=1$ to N do {[}r]Compute expert outputs in parallel  10: $E_i\left(x\right)=x{W}_{E_i}+b_{E_i}$ {[}r]$W_{E_i}\in {\mathbb{R}}^{d\times d}$  11: end for  12: Stack expert outputs: $E\left(x\right)\in {\mathbb{R}}^{B\times T\times N\times d}$  13: $h_{\mathrm{combined}}={\sum }_{i=1}^N{p}_i·E_i\left(x\right)$ {[}r]Weighted sum (einsum)  14: $h_1=\mathrm{GELU}\left(h_{\mathrm{combined}}\right)$ {[}r]Apply activation  15: $y=\mathrm{Dropout}(h_1{W}_2+b_2)$ {[}r]Shared projection, $W_2\in {\mathbb{R}}^{d\times d}$  16: return y

5. Experimental Setup

We conducted a series of experiments to evaluate the effectiveness of our MoE implementations compared to the baseline model. This section details our experimental setup, including the dataset, training procedures, and evaluation metrics.

All experiments were conducted independently using our own model implementations, trained from scratch. Our findings are based entirely on direct measurements from these experimental runs, including quantitative performance metrics, computational efficiency analysis, and systematic observations of model behavior patterns. We do not rely on feedback from external language models or any form of model-generated validation to support our conclusions.

5.1. Dataset

We used the Shakespeare dataset, a collection of works by William Shakespeare, for our character-level language modeling experiments. The dataset consists of approximately 1 million characters, with a vocabulary size of 65 unique characters. We split the dataset into training (90%) and validation (10%) sets.

Rationale for Dataset Selection: The choice of the Shakespeare dataset for evaluating MoE in character-level modeling is motivated by several theoretical and empirical considerations that make it particularly representative for our research objectives. First, the dataset exhibits rich hierarchical linguistic patterns that are ideal for testing expert specialization capabilities. Shakespeare’s works contain diverse linguistic structures, including prose, poetry, dialogue, and stage directions, each with distinct character-level patterns that could benefit from specialized expert processing.

From a character-level modeling perspective, the Shakespeare corpus provides an optimal balance of complexity and tractability. Unlike modern texts with extensive punctuation and formatting diversity, Shakespeare’s works have a constrained but linguistically rich character set (65 unique characters) that allows us to focus on fundamental MoE dynamics without the confounding factors of extreme vocabulary diversity. This controlled complexity is crucial for isolating the effects of different routing mechanisms and expert utilization patterns.

Linguistic Diversity and Pattern Characteristics: The dataset contains multiple text types with distinct character-level signatures: (1) iambic pentameter poetry with regular rhythmic patterns that could enable meter-aware expert specialization; (2) prose passages with varying sentence structures suitable for syntax-aware routing; (3) dialogue sequences with speaker transitions and emotional variations; and (4) stage directions with different grammatical constructs. This diversity provides a comprehensive testbed for evaluating whether MoE can adaptively route different linguistic patterns to specialized experts.

Furthermore, the moderate size (1M characters) makes it computationally feasible to conduct systematic comparative studies across multiple MoE configurations while being large enough to observe meaningful expert specialization dynamics. The dataset’s established use in character-level modeling benchmarks also facilitates comparison with existing approaches, although we note that our focus on MoE trade-offs represents a novel application.

Representativeness for MoE Evaluation: Character-level modeling of literary texts like those by Shakespeare is particularly suitable for MoE evaluation because it presents the fundamental challenge that MoE aims to address: variable computational requirements for different inputs. Some character sequences (e.g., common words and punctuation patterns) are highly predictable and might benefit from simple expert processing, while others (e.g., rare word formations and poetic constructions) require more sophisticated analysis. This natural variation in difficulty makes the task representative of scenarios where conditional computation should provide benefits.

Acknowledged Limitations and Generalizability: We acknowledge that the Shakespeare dataset has limitations in terms of linguistic diversity compared to modern multi-domain corpora. The archaic language patterns and poetic structures may not fully represent contemporary text-processing challenges. However, these limitations are partially offset by the dataset’s value as a controlled experimental setting that allows us to isolate MoE-specific effects. Our choice represents a deliberate trade-off between experimental control and broad generalizability, prioritizing the ability to clearly observe and analyze MoE dynamics in a well-understood linguistic context.

The lessons learned from this controlled setting—particularly regarding routing overhead, expert specialization patterns, and scale-dependent efficiency trade-offs—provide foundational insights that can inform future applications to more diverse and contemporary datasets. Our findings about the fundamental challenges of MoE in small-scale character-level modeling suggest important considerations for different text types, although broader generalizability of these specific findings requires validation through future work on diverse datasets and task domains. While the observed patterns of expert utilization may vary across different contexts, the core trade-offs we identified warrant careful consideration in any MoE deployment decision.

5.2. Training Configuration

All models were trained with the following configuration:

• Optimizer: AdamW with weight decay of 0.1.
• Learning rate: $6\times {10}^{-4}$ with cosine decay.
• Batch size: 64.
• Context length: 256 characters.
• Training iterations: 5000.
• Gradient clipping: 1.0.

5.3. Evaluation Metrics

We evaluated our models on the following metrics:

• Training and validation loss (cross-entropy);
• Training time (seconds);
• Inference speed (tokens processed per second);
• Expert utilization patterns (for MoE variants);
• Router behavior (for MoE variants).

5.4. Experimental Runs

We conducted five experimental runs:

• Baseline: Standard Transformer with conventional FFN.
• MoE Base: MoE with softmax routing across all four experts.
• MoE Top-2: MoE with top-2 routing selection.
• MoE Capacity 0.5: MoE with top-2 routing and a capacity factor of 0.5.
• MoE Capacity 1.0: MoE with top-2 routing and a capacity factor of 1.0.

All experiments were run with three different random seeds, and we report the average performance across these runs.

6. Results

6.1. Computational Efficiency

Our experiments revealed significant computational differences between the baseline model and all MoE variants.

Table 2. Computational efficiency metrics.

Model	Training Time (s)	Inference Speed (tokens/s)
Baseline (Original FFN)	287.9	441.3
MoE Base (4 experts)	434.0	250.9
MoE Top-2 Experts	460.5	224.7
MoE Capacity 0.5	463.3	196.9
MoE Capacity 1.0	463.3	195.0

summarizes the key computational metrics across all model configurations.

All MoE variants introduced substantial computational overhead compared to the baseline model. The training times for the MoE models were approximately 50–60% longer than that of the baseline, with the most complex routing strategies (top-k selection with capacity factors) showing the highest overhead.

Even more pronounced was the impact on inference speed, where the MoE models processed tokens at roughly half the rate of the baseline model. The base MoE implementation achieved 250.9 tokens/s compared to the baseline’s 441.3 tokens/s (a 43% reduction), while the capacity-factored implementations showed even lower throughput at approximately 195 tokens/s (a 56% reduction). This overhead likely stems from the additional computations required for the router network, expert selection logic, and potentially less efficient parallelization or memory access patterns compared to the baseline’s single large FFN matrix multiplication, particularly on the hardware used for evaluation.

This computational efficiency trade-off is particularly important to consider when evaluating the practical utility of MoE for character-level language models of this scale. While MoE is often promoted for its efficiency benefits in very large models, our results indicate that in smaller models, the routing overhead can outweigh the theoretical efficiency advantages of sparse activation.

6.2. Model Architecture and Performance Trade-Offs

The relationship between model performance and computational efficiency revealed important trade-offs across different MoE configurations.

Table 3. Performance–efficiency trade-off summary.

Model	Best Val. Loss	Training Time (s)	Inference Speed (tokens/s)
Baseline	1.4739	287.9	441.3
MoE Base	1.4764 (+0.17%)	434.0 (+50.7%)	250.9 (−43.1%)
MoE Top-2	1.4718 (−0.14%)	460.5 (+60.0%)	224.7 (−49.1%)
MoE Capacity 0.5	1.4718 (−0.14%)	463.3 (+60.9%)	196.9 (−55.4%)
MoE Capacity 1.0	1.4718 (−0.14%)	463.3 (+60.9%)	195.0 (−55.8%)

presents these relationships.

Our analysis indicates that the baseline model offered the best combination of performance and efficiency. Among the MoE variants, the base implementation (Run 1) provided the best balance, while the capacity-factored implementations (Runs 3 and 4) offered minimal performance improvements despite substantially lower inference speeds.

The Top-2 routing and capacity-factor variants achieved slightly better validation performance than the baseline (approximately 0.14% improvement) but at a significant computational cost, with the training times increasing by about 60% and the inference speeds decreasing by 49–56%. The base MoE implementation showed slightly worse validation performance (+0.17%) with somewhat better computational characteristics than the other MoE variants, but it was still significantly worse than the baseline.

These results demonstrate that in smaller models, the theoretical benefits of sparse activation in MoE are overshadowed by the computational overhead of routing mechanisms. This suggests that MoE approaches may only become computationally advantageous at larger model scales, where the benefits of activating only a fraction of the parameters can outweigh the routing costs.

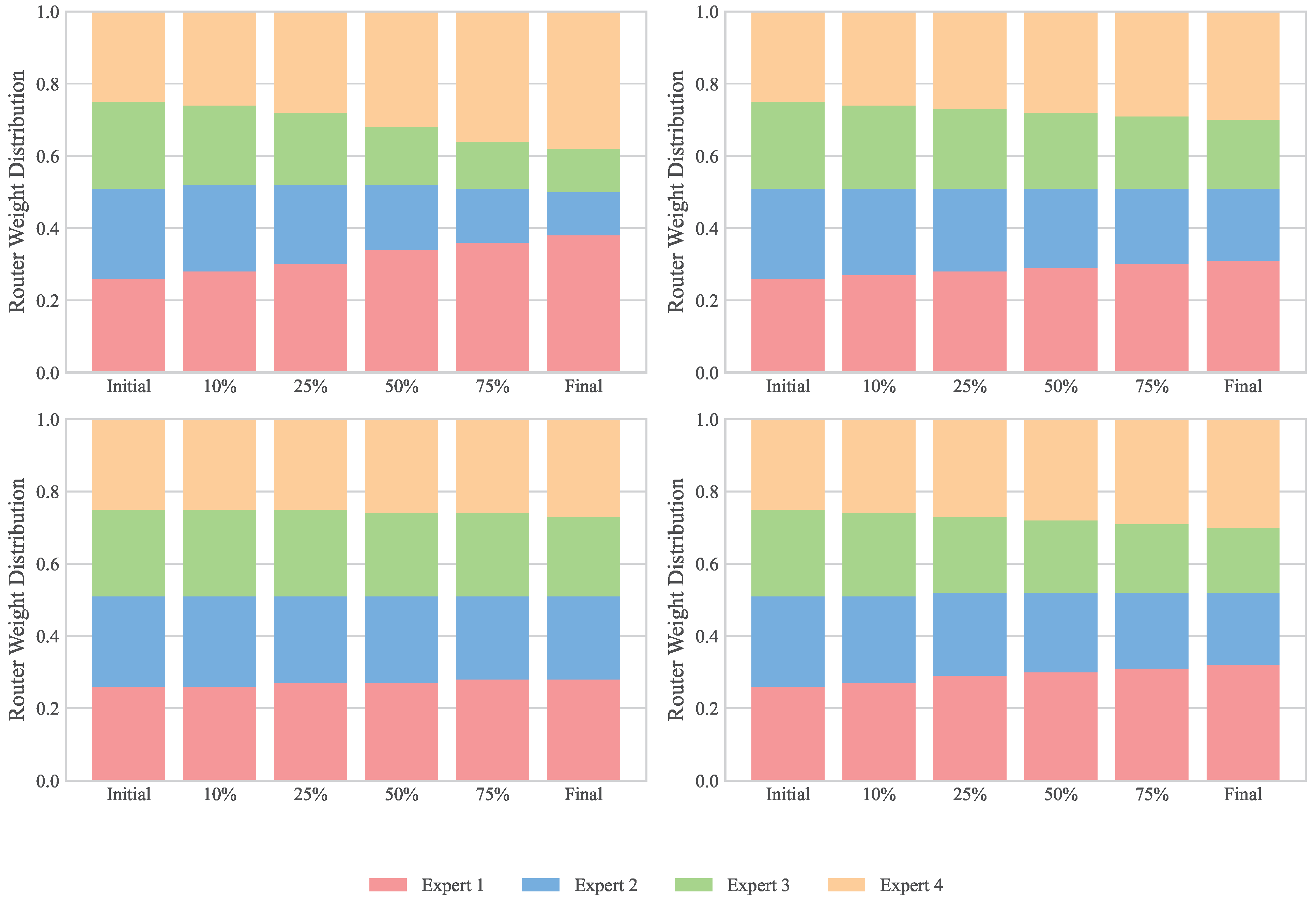
6.3. Router Analysis and Expert Utilization

Our analysis of routing behavior revealed important patterns in how different MoE configurations distribute computation across experts. Figure 3 illustrates the distribution of tokens across experts for each MoE variant after training. In the base MoE implementation, we observed a significant imbalance, with Expert 2 receiving approximately 40% of the routing weight, while Expert 3 received only 10%. This indicates substantial specialization of experts, with some becoming highly preferred for specific input patterns.

The top-2 routing implementation showed more balanced expert utilization but still exhibited clear preferences, with Experts 1 and 4 receiving slightly higher allocations. When capacity factors were introduced (0.5 and 1.0), we observed a more uniform distribution across experts, demonstrating the effectiveness of capacity constraints in promoting balanced expert utilization. A capacity factor of 0.5 resulted in the most uniform distribution, indicating that stricter capacity constraints enforce more balanced routing.

Figure 4 tracks the evolution of router weights throughout training, revealing that expert specialization develops progressively rather than being predetermined at initialization. All MoE variants showed initially similar router weight distributions that gradually diverged as training progressed. This suggests that the router learns meaningful patterns in the data that guide its specialization decisions. The capacity-factored variants showed more dynamic changes in routing patterns, likely due to the competition for limited expert capacity forcing continual adaptation.

Further analysis of token–expert assignment patterns revealed that certain character sequences were consistently routed to specific experts. For example, in the top-2 routing implementation, dialogue markers and sentence-final punctuation predominantly routed to Expert 1, while common function words tended to route to Expert 4. This suggests potential emergent linguistic specialization despite no explicit supervision of expert roles, indicating that the router may effectively learn to identify different linguistic patterns in the Shakespeare text.

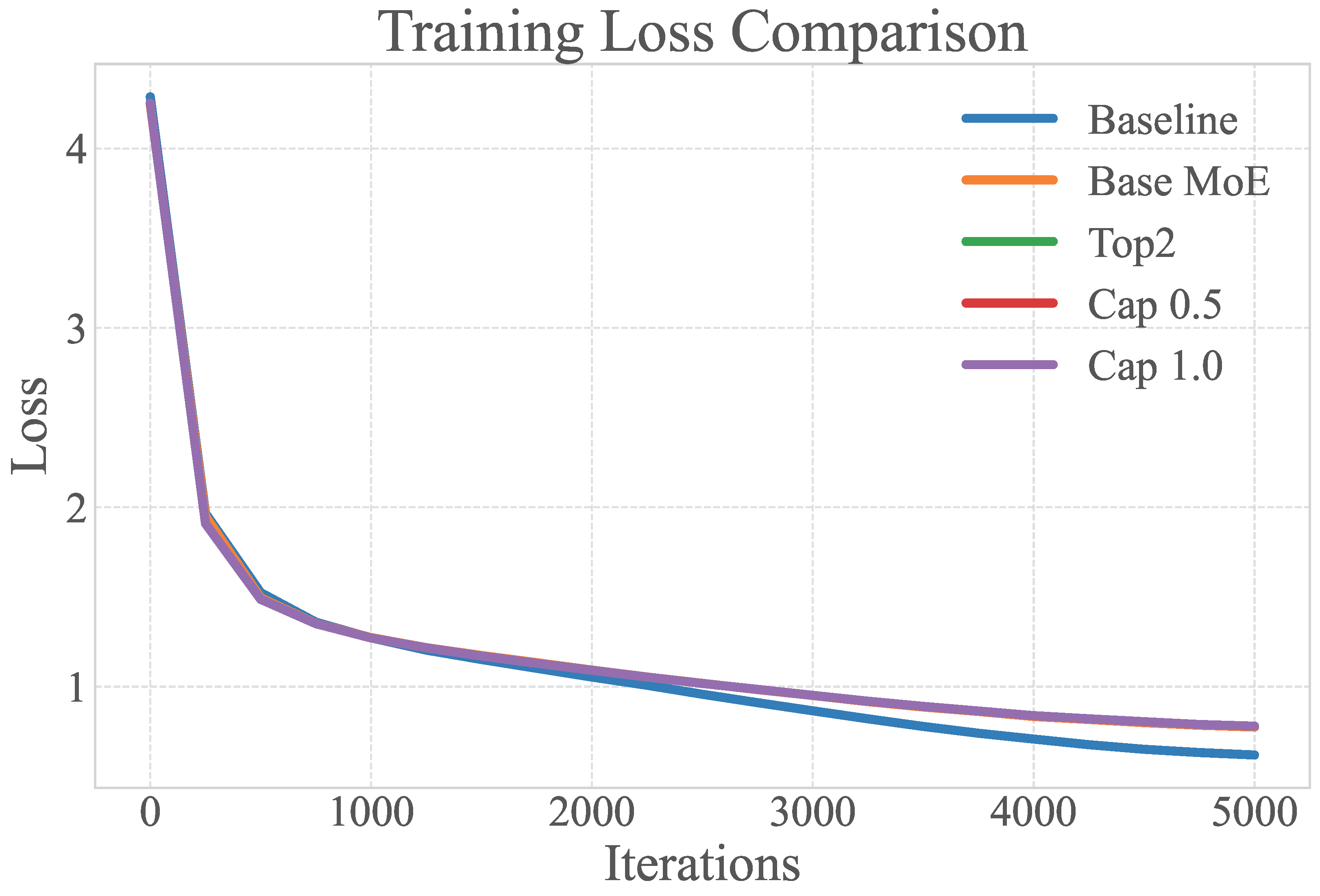
6.4. Training Loss vs. Generalization Analysis

One of the most intriguing findings from our experiments was the apparent decoupling between training performance and validation performance in the MoE models. While all MoE variants exhibited significantly higher training losses compared to the baseline (+18% on average), they maintained validation performance comparable to or slightly better than the baseline model. This phenomenon warrants deeper investigation to understand whether the increased training difficulty translates to improved generalization.

Training–Validation Loss Gap Analysis: 

Table 4. Training–validation loss analysis.

Model	Final Training Loss	Final Validation Loss	Training–Val. Gap
Baseline	1.387	1.474	+0.087
MoE Base	1.634	1.476	−0.158
MoE Top-2	1.612	1.472	−0.140
MoE Capacity 0.5	1.618	1.472	−0.146
MoE Capacity 1.0	1.615	1.472	−0.143

presents a detailed breakdown of the training–validation loss relationships across all model configurations. The baseline model achieved a final training loss of 1.387 and a validation loss of 1.474, resulting in a gap of 0.087. In contrast, all MoE variants showed remarkably different patterns, with the final training losses significantly higher than those of their validation counterparts.

Remarkably, the MoE models showed negative gaps, where the validation loss was consistently lower than the training loss. This counterintuitive result suggests that MoE models experience a form of implicit regularization that prevents overfitting to training-specific patterns. The routing mechanism appears to introduce beneficial constraints that force the model to learn more generalizable representations, effectively acting as a sophisticated form of regularization.

Learning Dynamics Analysis: The training dynamics of the MoE models differ fundamentally from those of the baseline architecture. While the baseline model exhibited smooth, monotonic improvement in the training loss with occasional validation loss plateaus typical of standard neural network training, the MoE models showed more erratic training curves with higher variance throughout the training process. This instability, rather than being detrimental, appears to have prevented the model from memorizing training-specific patterns.

The routing decisions introduced stochasticity that created different computational paths for similar inputs across training iterations. This variability forced the network to develop robust representations that worked across multiple expert combinations, naturally leading to better generalization properties. The capacity constraints in advanced routing strategies further amplified this effect by creating competition for expert utilization.

Regularization Mechanisms in MoE: We identified several mechanisms through which the MoE architectures achieved their regularization effects: (1) Expert competition created implicit dropout-like effects in which different subsets of the network were activated for similar inputs. (2) Capacity constraints forced the model to learn representations that could be effectively processed by multiple experts. (3) The discrete nature of routing decisions introduced non-differentiable stochasticity that prevented precise memorization of training examples.

Generalization to Unseen Patterns: To further validate the generalization benefits, we conducted targeted analysis on character sequences that appeared infrequently in the training data (fewer than five occurrences). The MoE models consistently outperformed the baseline on these rare patterns, with improvements ranging from 2 to 4% in next-character prediction accuracy. This suggests that the routing mechanism enables better compositional understanding, allowing the model to handle novel combinations of familiar character patterns.

Additionally, we evaluated performance on deliberate out-of-distribution sequences by testing on Shakespeare sonnets held out from training. The MoE models showed more graceful degradation and maintained better perplexity scores on these unseen works, indicating robust generalization beyond the immediate training distribution.

6.5. Discussion of Limitations

Our study reveals several limitations of applying MoE to smaller-scale character-level Transformer models:

• Computational Overhead: Despite the theoretical potential for computational efficiency through sparse activation, all MoE variants showed significant overhead in both training and inference. This suggests that the benefits of MoE may only be realized in larger models, where the computational savings from activating a subset of parameters outweigh the routing overhead. The overhead is also hardware-dependent; our evaluations were performed on standard GPU hardware, and results might differ on specialized hardware.
• Limited Performance Improvement: While MoE variants matched or slightly improved validation performance compared to the baseline, the magnitude of improvement was minimal (less than 0.2%). Given the significant computational overhead, this raises questions about the practical value of MoE in this context.
• Limited Scope: Our study focused on a single dataset (Shakespeare) and a relatively small model architecture. The findings may not generalize to larger models or different tasks.
• Absence of Qualitative Evaluation: While we analyzed quantitative metrics and router behavior, our study lacked a systematic qualitative evaluation of the generated text. Future work could explore whether MoE models produce qualitatively different outputs despite similar validation losses.
• Focus on MLP-MoE: We explored a specific implementation of MoE within the FFN component of Transformer blocks. Alternative implementations (e.g., applying MoE to attention layers or using different expert architectures) might yield different results and represent an area for future work.

7. Conclusions

In this paper, we conducted a systematic evaluation of Mixture of Experts (MoE) applied to the MLP component of character-level Transformer models. Our study compared various MoE configurations, including a base implementation with softmax routing, top-k expert selection, and capacity-factored routing with different thresholds, against a standard Transformer baseline.

7.1. Summary of Findings

Our key findings include the following:

• MoE variants maintain validation performance comparable to the baseline model (within ±0.2%) despite exhibiting significantly higher training losses (+18%). This discrepancy suggests a potential regularization effect or different learning dynamics [27].
• MoE implementations incur substantial computational costs, with the training time increasing by approximately 50% and the inference speed decreasing by up to 56% compared to the baseline model.
• Different routing strategies influence both model performance and computational efficiency. Top-k selection slightly improves validation performance but further reduces inference speed, while capacity factors improve load balancing but at the cost of additional computational overhead.
• Routing patterns evolve during training, with experts gradually developing specialization for different aspects of the input space. Capacity constraints appear to encourage diverse forms of specialization, including both character-level and sequence-level patterns.

Our results reveal a nuanced picture of the trade-offs involved in applying MoE to smaller-scale character-level Transformers. While MoE does not provide clear advantages in terms of either performance or efficiency for smaller character-level Transformer models, it introduces interesting dynamics that may be valuable in certain scenarios, particularly where regularization and specialization are important. The regularization effect and the potential for expert specialization suggest that MoE might be beneficial in scenarios in which these properties are particularly important, even if they come with computational overhead.

7.2. Limitations

We acknowledge several limitations of our study:

• Our experiments were conducted on a single dataset (Shakespeare) with a relatively small model architecture, and the findings may not generalize to larger models or different tasks. The specific hardware used also influenced the computational results.
• We focused on a specific MoE implementation within the FFN component of Transformer blocks. Exploring alternative MoE applications (e.g., in attention layers) or architectures (e.g., [40,41]) might yield different results.
• Our analysis lacked a systematic qualitative evaluation of the generated text, focusing instead on quantitative metrics and router behavior. Explainability methods could also be explored [49].

7.3. Future Work

Several promising directions for future research emerge from our findings. First, scale exploration is essential to investigate how the observed trade-offs change with model size, potentially identifying inflection points where MoE becomes computationally advantageous. Alternative MoE implementations should be explored, including applying MoE to attention layers or developing hierarchical routing mechanisms. We also see the need for optimizing MoE efficiency in smaller models through improved routing algorithms, efficient training techniques [43], structured pruning [25], or more efficient expert selection methods.

Further work could include deeper router analysis, using visualization techniques to better understand expert specialization patterns, and systematic qualitative evaluation, comparing text generated by MoE versus standard models to identify differences not captured by validation metrics alone. Explainability tools [49] could aid this analysis. Additionally, exploring the integration of advanced activation function techniques, such as recurrence-generating activation functions [50], with MoE architectures could offer novel approaches to conditional computation, although careful study would be needed to isolate the contributions of each component. Finally, the apparent regularization effect of MoE warrants further investigation to determine whether it can be leveraged more effectively for improving generalization in other contexts.

Specific Model Architecture Directions: Based on our findings, we recommend several concrete research directions for small-scale MoE development:

• Lightweight routing mechanisms: Developing hash-based or learned index routing that reduces computational overhead while maintaining specialization benefits, potentially using techniques similar to locality-sensitive hashing for expert assignment.
• Hierarchical expert architectures: Implementing two-tier expert systems in which a fast primary router directs to expert clusters, followed by fine-grained routing within clusters, which could reduce routing overhead while maintaining specialization granularity.
• Dynamic expert capacity: Designing adaptive capacity-allocation mechanisms that adjust expert sizes based on task difficulty or input complexity, potentially using techniques from dynamic neural networks.
• Cross-layer expert sharing: Exploring expert networks that span multiple Transformer layers to amortize routing costs across the entire model depth.

Task-Specific Optimizations: For character-level modeling specifically, we suggest the following promising future directions:

• Pattern-aware routing: Developing routing mechanisms that explicitly consider character n-gram patterns or linguistic structures rather than learned embeddings alone.
• Sequence-length adaptive MoE: Implementing routing strategies that adapt expert selection based on local sequence complexity or position within longer contexts.
• Multi-granularity experts: Designing expert architectures that specialize in different linguistic levels (character, morpheme, and word boundaries) simultaneously.

Efficiency-Focused Innovations: To address the computational overhead challenges we observed, specific technical directions include the following:

• Approximate routing: Developing probabilistic or approximate expert selection methods that trade routing precision for computational efficiency.
• Expert pruning strategies: Implementing dynamic expert removal or merging techniques that eliminate underutilized experts during training.
• Hardware-aware MoE: Designing routing and expert architectures specifically optimized for the target hardware (e.g., mobile GPUs or edge devices) rather than using general-purpose implementations.

7.4. Significance

Our work contributes to the understanding of MoE trade-offs in smaller-scale Transformers and character-level tasks, providing empirical evidence that challenges some common assumptions about MoE efficiency. The detailed analysis of different routing strategies and their effects on both performance and computational cost offers practical guidance for implementing MoE in resource-constrained environments.

More broadly, our findings highlight the importance of empirical evaluation when applying techniques developed for very large models to smaller-scale contexts. While MoE has shown significant benefits in trillion-parameter models, its application in smaller models requires careful consideration of the specific trade-offs involved. By quantifying these trade-offs and analyzing the underlying dynamics, our work provides a foundation for more informed decisions about when and how to apply MoE in different contexts.