Benchmarking Variants of Recursive Feature Elimination: Insights from Predictive Tasks in Education and Healthcare
Abstract
1. Introduction
2. A Narrative Review of RFE Algorithms and Their Applications in EDM
2.1. The Original RFE Algorithm
2.2. Four Major Types of RFE Variants
2.2.1. RFE Wrapped with Different ML Models
2.2.2. Combinations of ML Models or Feature Importance Metrics
2.2.3. Modifications to the RFE Process
2.2.4. RFE Hybridized with Other Feature Selection or Dimension Reduction Methods
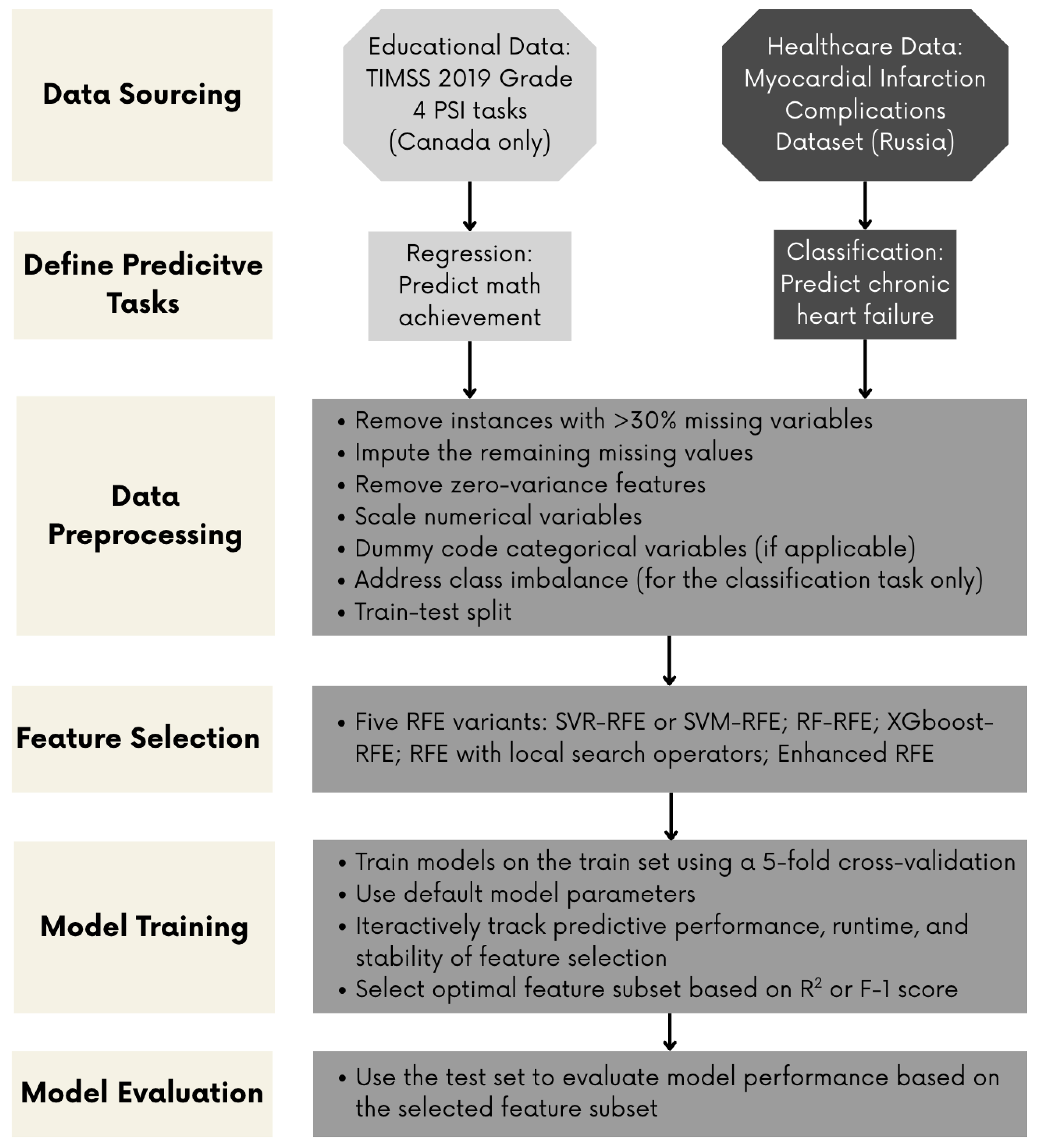
3. Methods
3.1. Datasets and Data Preprocessing
3.2. Model Training, Validation, and Evaluation
4. Results
4.1. Results for the Educational Dataset
4.1.1. Baseline: SVR-RFE
4.1.2. RF-RFE
4.1.3. XGBoost-RFE
4.1.4. RFE with Local Search Operators
4.1.5. Enhanced RFE
4.1.6. Summary of Regression Findings
4.2. Results for the Healthcare Dataset
4.2.1. Baseline: SVM-RFE
4.2.2. RF-RFE
4.2.3. XGBoost-RFE
4.2.4. Enhanced RFE
4.2.5. RFE with Local Search Operators
4.2.6. Summary of Classification Findings
5. Discussion
Limitations and Directions for Future Research
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AUC | Area Under the Curve |
| CV | Cross-Validation |
| DT | Decision Trees |
| EDM | Educational Data Mining |
| GI | Gini Index |
| LASSO | Least Absolute Shrinkage and Selection Operator |
| LR | Logistic Regression |
| LLM | Large Language Models |
| MAE | Mean Absolute Error |
| ML | Machine Learning |
| MOOC | Massive Open Online Courses |
| PCA | Principal Component Analysis |
| PSI | Problem Solving and Inquiry |
| RF | Random Forests |
| RFE | Recursive Feature Elimination |
| RMSE | Root Mean Square Error |
| SMOTE | Synthetic Minority Oversampling Technique |
| SVM | Support Vector Machine |
| SVR | Support Vector Regression |
| TIMSS | Trends in International Mathematics and Science Study |
| XGBoost | Extreme Gradient Boosting |
References
- Romero, C.; Ventura, S. Data mining in education. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2013, 3, 12–27. [Google Scholar] [CrossRef]
- Algarni, A. Data mining in education. Int. J. Adv. Comput. Sci. Appl. 2016, 7, 12–27. [Google Scholar] [CrossRef]
- Bulut, O.; Yavuz, H.C. Educational Data Mining: A Tutorial for the Rattle Package in R. Int. J. Assess. Tools Educ. 2019, 6, 20–36. [Google Scholar] [CrossRef]
- Romero, C.; Ventura, S. Educational data mining: A review of the state of the art. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2010, 40, 601–618. [Google Scholar] [CrossRef]
- Wongvorachan, T.; He, S.; Bulut, O. A comparison of undersampling, oversampling, and SMOTE methods for dealing with imbalanced classification in educational data mining. Information 2023, 14, 54. [Google Scholar] [CrossRef]
- Bulut, O.; Wongvorachan, T.; He, S.; Lee, S. Enhancing high-school dropout identification: A collaborative approach integrating human and machine insights. Discov. Educ. 2024, 3, 109. [Google Scholar] [CrossRef]
- Cui, Z.; Gong, G. The effect of machine learning regression algorithms and sample size on individualized behavioral prediction with functional connectivity features. Neuroimage 2018, 178, 622–637. [Google Scholar] [CrossRef]
- James, T.P.G.; Karthikeyan, B.Y.; Ashok, P.; Dhaasarathy; Suganya, R.; Maharaja, K. Strategic Integration of CNN, SVM, and XGBoost for Early-stage Tumor Detection using Hybrid Deep Learning Method. In Proceedings of the 2023 International Conference on Innovative Computing, Intelligent Communication and Smart Electrical Systems (ICSES), Chennai, India, 14–15 December 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Palo, H.K.; Sahoo, S.; Subudhi, A.K. Dimensionality reduction techniques: Principles, benefits, and limitations. In Data Analytics in Bioinformatics: A Machine Learning Perspective; Wiley: New York, NY, USA, 2021; pp. 77–107. [Google Scholar]
- Alalawi, K.; Athauda, R.; Chiong, R. Contextualizing the current state of research on the use of machine learning for student performance prediction: A systematic literature review. Eng. Rep. 2023, 5, e12699. [Google Scholar] [CrossRef]
- Venkatesh, B.; Anuradha, J. A review of feature selection and its methods. Cybern. Inf. Technol. 2019, 19, 3–26. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene selection for cancer classification using support vector machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Liu, W.; Wang, J. Recursive elimination–election algorithms for wrapper feature selection. Appl. Soft Comput. 2021, 113, 107956. [Google Scholar] [CrossRef]
- Albreiki, B.; Zaki, N.; Alashwal, H. A systematic literature review of student’performance prediction using machine learning techniques. Educ. Sci. 2021, 11, 552. [Google Scholar] [CrossRef]
- Chen, R.; Manongga, W.; Dewi, C. Recursive Feature Elimination for Improving Learning Points on Hand-Sign Recognition. Future Internet 2022, 14, 352. [Google Scholar] [CrossRef]
- Samb, M.L.; Camara, F.; Ndiaye, S.; Slimani, Y.; Esseghir, M.A. A novel RFE-SVM-based feature selection approach for classification. Int. J. Adv. Sci. Technol. 2012, 43, 27–36. [Google Scholar]
- Reunanen, J. Overfitting in making comparisons between variable selection methods. J. Mach. Learn. Res. 2003, 3, 1371–1382. [Google Scholar]
- Yeung, C.K.; Yeung, D.Y. Incorporating features learned by an enhanced deep knowledge tracing model for stem/non-stem job prediction. Int. J. Artif. Intell. Educ. 2019, 29, 317–341. [Google Scholar] [CrossRef]
- Pereira, F.D.; Oliveira, E.; Cristea, A.; Fernandes, D.; Silva, L.; Aguiar, G.; Alamri, A.; Alshehri, M. Early dropout prediction for programming courses supported by online judges. In Proceedings of the Artificial Intelligence in Education: 20th International Conference, AIED 2019, Chicago, IL, USA, 25–29 June 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 67–72. [Google Scholar]
- Lian, W.; Nie, G.; Jia, B.; Shi, D.; Fan, Q.; Liang, Y. An intrusion detection method based on decision tree-recursive feature elimination in ensemble learning. Math. Probl. Eng. 2020, 2020, 1–15. [Google Scholar] [CrossRef]
- Granitto, P.M.; Furlanello, C.; Biasioli, F.; Gasperi, F. Recursive feature elimination with random forest for PTR-MS analysis of agroindustrial products. Chemom. Intell. Lab. Syst. 2006, 83, 83–90. [Google Scholar] [CrossRef]
- Jeon, H.; Oh, S. Hybrid-recursive feature elimination for efficient feature selection. Appl. Sci. 2020, 10, 3211. [Google Scholar] [CrossRef]
- Chai, Y.; Lei, C.; Yin, C. Study on the influencing factors of online learning effect based on decision tree and recursive feature elimination. In Proceedings of the 10th International Conference on E-Education, E-Business, E-Management and E-Learning, Tokyo, Japan, 10–13 January 2019; pp. 52–57. [Google Scholar] [CrossRef]
- Alarape, M.A.; Ameen, A.O.; Adewole, K.S. Hybrid students’ academic performance and dropout prediction models using recursive feature elimination technique. In Advances on Smart and Soft Computing: Proceedings of ICACIn 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 93–106. [Google Scholar]
- Nguyen, H.N.; Ohn, S.Y. Drfe: Dynamic recursive feature elimination for gene identification based on random forest. In Proceedings of the International Conference on Neural Information Processing, Hong Kong, China, 3–6 October 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–10. [Google Scholar] [CrossRef]
- Artur, M. Review the performance of the Bernoulli Naïve Bayes Classifier in Intrusion Detection Systems using Recursive Feature Elimination with Cross-validated selection of the best number of features. Procedia Comput. Sci. 2021, 190, 564–570. [Google Scholar] [CrossRef]
- Wottschel, V.; Chard, D.T.; Enzinger, C.; Filippi, M.; Frederiksen, J.L.; Gasperini, C.; Giorgio, A.; Rocca, M.A.; Rovira, A.; De Stefano, N.; et al. SVM recursive feature elimination analyses of structural brain MRI predicts near-term relapses in patients with clinically isolated syndromes suggestive of multiple sclerosis. Neuroimage Clin. 2019, 24, 102011. [Google Scholar] [CrossRef] [PubMed]
- van der Ploeg, T.; Steyerberg, E.W. Feature selection and validated predictive performance in the domain of Legionella pneumophila: A comparative study. BMC Res. Notes 2016, 9, 147. [Google Scholar] [CrossRef]
- Chen, X.W.; Jeong, J.C. Enhanced recursive feature elimination. In Proceedings of the Sixth International Conference on Machine Learning and Applications (ICMLA 2007), Cincinnati, OH, USA, 13–15 December 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 429–435. [Google Scholar] [CrossRef]
- Ding, X.; Li, Y.; Chen, S. Maximum margin and global criterion based-recursive feature selection. Neural Netw. 2024, 169, 597–606. [Google Scholar] [CrossRef]
- Han, Y.; Huang, L.; Zhou, F. A dynamic recursive feature elimination framework (dRFE) to further refine a set of OMIC biomarkers. Bioinformatics 2021, 37, 2183–2189. [Google Scholar] [CrossRef]
- Nafis, N.S.M.; Awang, S. An enhanced hybrid feature selection technique using term frequency-inverse document frequency and support vector machine-recursive feature elimination for sentiment classification. IEEE Access 2021, 9, 52177–52192. [Google Scholar] [CrossRef]
- Paddalwar, S.; Mane, V.; Ragha, L. Predicting students’ academic grade using machine learning algorithms with hybrid feature selection approach. ITM Web Conf. 2022, 44, 03036. [Google Scholar] [CrossRef]
- Lei, H.; Govindaraju, V. Speeding Up Multi-Class SVM Evaluation by PCA and Feature Selection; Technical Report; Center for Unified Biometrics and Sensors, State University of New York at Buffalo: Amherst, NY, USA, 2005. [Google Scholar]
- Huang, X.; Zhang, L.; Wang, B.; Li, F.; Zhang, Z. Feature clustering based support vector machine recursive feature elimination for gene selection. Appl. Intell. 2018, 48, 594–607. [Google Scholar] [CrossRef]
- Almutiri, T.; Saeed, F. A hybrid feature selection method combining Gini index and support vector machine with recursive feature elimination for gene expression classification. Int. J. Data Min. Model. Manag. 2022, 14, 41–62. [Google Scholar] [CrossRef]
- Lin, X.; Wang, Q.; Yin, P.; Tang, L.; Tan, Y.; Li, H.; Yan, K.; Xu, G. A method for handling metabonomics data from liquid chromatography/mass spectrometry: Combinational use of support vector machine recursive feature elimination, genetic algorithm and random forest for feature selection. Metabolomics 2011, 7, 549–558. [Google Scholar] [CrossRef]
- Louw, N.; Steel, S. Variable selection in kernel Fisher discriminant analysis by means of recursive feature elimination. Comput. Stat. Data Anal. 2006, 51, 2043–2055. [Google Scholar] [CrossRef]
- Duan, K.B.; Rajapakse, J.C.; Wang, H.; Azuaje, F. Multiple SVM-RFE for gene selection in cancer classification with expression data. IEEE Trans. Nanobiosci. 2005, 4, 228–234. [Google Scholar] [CrossRef]
- Mao, Y.; Zhou, X.; Yin, Z.; Pi, D.; Sun, Y.; Wong, S.T. Gene selection using Gaussian kernel support vector machine based recursive feature elimination with adaptive kernel width strategy. In Proceedings of the Rough Sets and Knowledge Technology: First International Conference, RSKT 2006, Chongqing, China, 24–26 July 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 799–806. [Google Scholar]
- Zhou, X.; Tuck, D.P. MSVM-RFE: Extensions of SVM-RFE for multiclass gene selection on DNA microarray data. Bioinformatics 2007, 23, 1106–1114. [Google Scholar] [CrossRef]
- Zhang, L.; Zheng, X.; Pang, Q.; Zhou, W. Fast Gaussian kernel support vector machine recursive feature elimination algorithm. Appl. Intell. 2021, 51, 9001–9014. [Google Scholar] [CrossRef]
- Cao, J.; Zhang, L.; Wang, B.; Li, F.; Yang, J. A fast gene selection method for multi-cancer classification using multiple support vector data description. J. Biomed. Inform. 2015, 53, 381–389. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Sakyi, A.; Cui, Y. Identifying key contextual factors of digital reading literacy through a machine learning approach. J. Educ. Comput. Res. 2022, 60, 1763–1795. [Google Scholar] [CrossRef]
- Hu, J.; Peng, Y.; Ma, H. Examining the contextual factors of science effectiveness: A machine learning-based approach. Sch. Eff. Sch. Improv. 2022, 33, 21–50. [Google Scholar] [CrossRef]
- Zheng, S.; Liu, W. Lasso based gene selection for linear classifiers. In Proceedings of the 2009 IEEE International Conference on Bioinformatics and Biomedicine Workshop, Washington, DC, USA, 1–4 November 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 203–208. [Google Scholar] [CrossRef]
- Gitinabard, N.; Okoilu, R.; Xu, Y.; Heckman, S.; Barnes, T.; Lynch, C. Student Teamwork on Programming Projects: What can GitHub logs show us? arXiv 2020, arXiv:2008.11262. [Google Scholar] [CrossRef]
- Chen, F.; Cui, Y.; Chu, M.W. Utilizing game analytics to inform and validate digital game-based assessment with evidence-centered game design: A case study. Int. J. Artif. Intell. Educ. 2020, 30, 481–503. [Google Scholar] [CrossRef]
- Sánchez-Pozo, N.; Chamorro-Hernández, L.; Mina, J.; Márquez, J. Comparative analysis of feature selection techniques in predictive modeling of mathematics performance: An Ecuadorian case study. Educ. Sci. Manag. 2023, 1, 111–121. [Google Scholar] [CrossRef]
- Sivaneasharajah, L.; Falkner, K.; Atapattu, T. Investigating Students’ Learning in Online Learning Environment. In Proceedings of the 13th International Conference on Educational Data Mining (EDM 2020), Virtual Conference, 10–13 July 2020. [Google Scholar]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Mullis, I.V.; Martin, M.O.; Fishbein, B.; Foy, P.; Moncaleano, S. Findings from the TIMSS 2019 Problem Solving and Inquiry Tasks. 2021. Available online: https://timssandpirls.bc.edu/timss2019/psi (accessed on 5 June 2025).
- Martin, M.O.; von Davier, M.; Mullis, I.V.S. Methods and Procedures: TIMSS 2019 Technical Report. 2020. Available online: https://timssandpirls.bc.edu/timss2019/methods (accessed on 5 June 2025).
- Fishbein, B.; Foy, P.; Yin, L. TIMSS 2019 User Guide for the International Database. Hentet Fra. 2021. Available online: https://timssandpirls.bc.edu/timss2019/international-database (accessed on 5 June 2025).
- Ulitzsch, E.; Yildirim-Erbasli, S.N.; Gorgun, G.; Bulut, O. An explanatory mixture IRT model for careless and insufficient effort responding in self-report measures. Br. J. Math. Stat. Psychol. 2022, 75, 668–698. [Google Scholar] [CrossRef] [PubMed]
- Wongvorachan, T.; Bulut, O.; Liu, J.X.; Mazzullo, E. A Comparison of Bias Mitigation Techniques for Educational Classification Tasks Using Supervised Machine Learning. Information 2024, 15, 326. [Google Scholar] [CrossRef]
- Zhang, Z. Multiple imputation with multivariate imputation by chained equation (MICE) package. Ann. Transl. Med. 2016, 4, 30. [Google Scholar]
- Ahsan, M.M.; Mahmud, M.P.; Saha, P.K.; Gupta, K.D.; Siddique, Z. Effect of data scaling methods on machine learning algorithms and model performance. Technologies 2021, 9, 52. [Google Scholar] [CrossRef]
- Golovenkin, S.; Gorban, A.; Mirkes, E.; Shulman, V.; Rossiev, D.; Shesternya, P.; Nikulina, S.Y.; Orlova, Y.V.; Dorrer, M. Complications of Myocardial Infarction: A Database for Testing Recognition and Prediction Systems. 2020. Available online: https://archive.ics.uci.edu/dataset/579/myocardial+infarction+complications (accessed on 5 June 2025).
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Mao, A.; Huang, E.; Wang, X.; Liu, K. Deep learning-based animal activity recognition with wearable sensors: Overview, challenges, and future directions. Comput. Electron. Agric. 2023, 211, 108043. [Google Scholar] [CrossRef]
- Blagus, R.; Lusa, L. SMOTE for high-dimensional class-imbalanced data. BMC Bioinform. 2013, 14, 106. [Google Scholar] [CrossRef]
- Van Hulse, J.; Khoshgoftaar, T.M.; Napolitano, A.; Wald, R. Feature selection with high-dimensional imbalanced data. In Proceedings of the 2009 IEEE International Conference on Data Mining Workshops, Miami, FL, USA, 6 December 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 507–514. [Google Scholar]
- Gunn, S.R. Support Vector Machines for Classification and Regression; Technical Report; School of Electronics and Computer Science, University of Southampton: Southampton, UK, 1998. [Google Scholar]
- Li, Y.F.; Xu, Z.H.; Hao, Z.B.; Yao, X.; Zhang, Q.; Huang, X.Y.; Li, B.; He, A.Q.; Li, Z.L.; Guo, X.Y. A comparative study of the performances of joint RFE with machine learning algorithms for extracting Moso bamboo (Phyllostachys pubescens) forest based on UAV hyperspectral images. Geocarto Int. 2023, 38, 2207550. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Y.; Wei, Y.; Hu, J. Discrimination of the contextual features of top performers in scientific literacy using a machine learning approach. Res. Sci. Educ. 2021, 51, 129–158. [Google Scholar] [CrossRef]
- Han, Z.; He, Q.; Von Davier, M. Predictive feature generation and selection using process data from PISA interactive problem-solving items: An application of random forests. Front. Psychol. 2019, 10, 2461. [Google Scholar] [CrossRef] [PubMed]
- Syed Mustapha, S. Predictive analysis of students’ learning performance using data mining techniques: A comparative study of feature selection methods. Appl. Syst. Innov. 2023, 6, 86. [Google Scholar] [CrossRef]
- Kilinc, M.; Teke, O.; Ozan, O.; Ozarslan, Y. Factors Influencing the Learner’s Cognitive Engagement in a Language MOOC: Feature Selection Approach. In Proceedings of the 2023 Innovations in Intelligent Systems and Applications Conference (ASYU), Sivas, Turkiye, 11–13 October 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]

| RFE Variant Type | Description | Examples |
|---|---|---|
| RFE wrapped with different ML models | Using the original RFE process to eliminate features based on feature importance metrics computed by an algorithm other than SVR/SVM. | DT-RFE [21] RF-RFE [22] |
| Combination of ML models or feature importance metrics | Using the original RFE process to eliminate features based on multiple feature importance metrics (i.e., feature importance values from distinct ML models or different feature importance metrics from the same model). | SVM, RF, and generalized boosted regression algorithms [23]; SVM, LR, and DT ensemble [24]; SVM-NB hybrid classifier [25] |
| Modification to the RFE process | Changing or adding one or more steps in the original RFE process. | RFE + CV [26,27]; RFE + 4 resampling [28,29]; Enhanced-RFE [30]; Local search RFE [17]; Marginal improvement-based RFE [31]; Dynamic RFE [32] |
| RFE hybridized with other feature selection or dimension reduction methods | Using other feature selection methods or dimensionality reduction techniques together with RFE to select features. | TF-IDF + RFE [33]; Chi-square + RFE [34]; PCA + RFE [35]; K-means + RFE [36]; GI + RFE [37]; Other hybrids [38,39] |
| Algorithm | Features | RMSE | MAE | R2 | Time (s) | Stability |
|---|---|---|---|---|---|---|
| SVR-RFE | 82 | 57.357 | 45.957 | 0.359 | 430 | 0.633 |
| RF-RFE | 108 | 56.474 | 44.377 | 0.379 | 223,279 | 0.966 |
| XGBoost-RFE | 114 | 58.514 | 45.662 | 0.333 | 7321 | 0.949 |
| Enhanced RFE | 62 | 58.234 | 46.577 | 0.340 | 821 | 0.872 |
| RFE with local search operator | 85 | 57.442 | 46.091 | 0.357 | 473 | 0.581 |
| Algorithm | Features | F1 | Precision | Recall | AUC-ROC | Time (s) | Stability |
|---|---|---|---|---|---|---|---|
| SVM-RFE | 118 | 0.438 | 0.284 | 0.962 | 0.744 | 1011 | 0.632 |
| RF-RFE | 110 | 0.566 | 0.706 | 0.567 | 0.770 | 3358 | 0.938 |
| XGBoost-RFE | 56 | 0.665 | 0.725 | 0.645 | 0.799 | 5796 | 0.639 |
| Enhanced RFE | 120 | 0.604 | 0.600 | 0.624 | 0.692 | 12,940 | 0.778 |
| RFE with local search operator | 106 | 0.618 | 0.613 | 0.638 | 0.701 | 3334 | 0.563 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bulut, O.; Tan, B.; Mazzullo, E.; Syed, A. Benchmarking Variants of Recursive Feature Elimination: Insights from Predictive Tasks in Education and Healthcare. Information 2025, 16, 476. https://doi.org/10.3390/info16060476
Bulut O, Tan B, Mazzullo E, Syed A. Benchmarking Variants of Recursive Feature Elimination: Insights from Predictive Tasks in Education and Healthcare. Information. 2025; 16(6):476. https://doi.org/10.3390/info16060476
Chicago/Turabian StyleBulut, Okan, Bin Tan, Elisabetta Mazzullo, and Ali Syed. 2025. "Benchmarking Variants of Recursive Feature Elimination: Insights from Predictive Tasks in Education and Healthcare" Information 16, no. 6: 476. https://doi.org/10.3390/info16060476
APA StyleBulut, O., Tan, B., Mazzullo, E., & Syed, A. (2025). Benchmarking Variants of Recursive Feature Elimination: Insights from Predictive Tasks in Education and Healthcare. Information, 16(6), 476. https://doi.org/10.3390/info16060476







