A Novel Method for Community Detection in Bipartite Networks

Abstract

The community structure is a major feature of bipartite networks, which serve as a typical model for empirical networks consisting of two kinds of nodes. Over the past years, community detection has drawn a lot of attention. Numerous methods for community detection have been put forth. Nevertheless, some of them need a lot of time, which restricts their use in large networks. While several low-time complexity algorithms exist, their practical value in real-world applications is limited since they are typically non-deterministic. Typically, in bipartite networks, a unipartite projection of one part of the network is created, and then communities are detected inside that projection using methods for unipartite networks. Unipartite projections may yield incorrect or erroneous findings as they inevitably include a loss of information. In this paper, BiVoting, a two-mode and deterministic community detection method in bipartite networks, is proposed. This method is a consequence of bipartite modularity, which quantifies the strength of partitions and is based on how people vote in social elections. The proposed method’s performance was evaluated, and comparison with four common community detection methods in bipartite networks shows that for calculating the modularity score in large networks, BiVoting performs better than the best method.

1. Introduction

Networks display various complicated systems in different disciplines. The nodes and edges of a network inferred from complicated systems represent entities and relationships. An edge connects a pair of nodes if they have a particular relationship. Numerous studies have focused on unipartite or one-mode networks that only feature one kind of node. In contrast, real networks usually have a variety of node kinds. A bipartite or two-mode network has two different kinds of nodes, and connections are limited to distinct node kinds. A bipartite network is a natural model for various real-world complex systems. A better method to comprehend modular structures in bipartite networks is through the concept of community. Community detection in complex networks can aid in the understanding of these network structural characteristics. A straightforward approach to community detection was to apply the standard methods for community detection in unipartite networks after converting the bipartite networks into their unipartite counterparts. The issue of information loss in this procedure is a challenge. After, the concept of bipartite modularity, in which two independent parts of nodes are placed independently in modular structures, was presented; the idea of community detection was proposed without the need to change bipartite networks into unipartite networks. The task of precisely maximizing modularity is typically unsolvable. Some useful approaches for determining the nodes’ high modularity divisions have been presented. Centrality measures are commonly employed in social network analysis to ascertain the respective significance of nodes. Unfortunately, because of the requirement of full knowledge of network topology and the lack of proper measures for the detection of more behaviorally representative users in bipartite networks, the use of conventional centrality measures in the large-scale networks is a challenging issue.

HellRank is a precise metric for locating core nodes in bipartite networks that is very suitable for voting rules purposes in selecting candidates in our proposed method. The fact that there is no need to transform the bipartite network to its unipartite counterpart and there is no requirement of full knowledge of network topology for its output makes this measure ideal. In fact, without having to be converted into a unipartite counterpart, the proposed method, which makes use of the ideas of bipartite modularity and the HellRank centrality measure, has been able to be implemented directly in large-scale bipartite networks. Certain methods that have been suggested for community detection include issues such as excessive time and memory consumption, lack of assurance, inability to be applied in large-scale networks, and resolution issue limitations, but the proposed method has been able to be implemented directly in large-scale bipartite networks and significantly improve the calculation of modularity scores in networks, especially in large-scale networks. The proposed method is designed in two stages. The output of the first stage is some initial communities. Then, in the second stage, initial communities must be compared based on the similarity between them, and if this similarity exceeds a certain threshold, the process of examining their merging and calculating the increase in modularity resulting from this merging begins. This ensures that the execution time of the algorithm is not wasted to examine communities that have very low similarity. This is demonstrated by implementing the proposed method and four popular techniques for community detection on some artificial and real bipartite networks, and it can be seen that it was able to perform the community detection process with a high modularity score and acceptable execution time in large-scale bipartite networks. After the first section, in Section 2, various methods for community detection in bipartite networks will be reviewed, and following Section 2, some of the preliminary definitions and variables that were used in this paper will be demonstrated. In Section 3, the proposed method, the relevant voting rules, and its algorithm are explained in detail. In Section 4, the results obtained from implementing the proposed method on several artificial and real networks are presented and compared with four well-known methods for detecting communities in bipartite networks.

2. Related Work

A variety of methods, including non-negative matrix decomposition [1], label propagation [2], expansion from seed sets [3], evolutionary methods [4], game theoretical approaches [5], line graphs [6], and modularity optimization [7], have been suggested for unipartite community detection under various assumptions. One straightforward concept comes from the Zhou projection approach [8], which naturally adapts current community detection methods by converting bipartite networks into unipartite networks. However, scholars contend that projection approaches may result in incomplete information, as following projection, only a certain kind of node is kept while the other kind is lost [9]. Many methods have been devised to sustain two kinds of nodes following the division of communities. After expanding from unipartite modularity, Barber introduced bipartite modularity [10], and to impel two separate parts of nodes inside modular structures, BRIM was then created. It is noteworthy that bipartite network modularity has resolution limitations [11], as high modularity scores cannot reliably detect tiny communities. Lehmann introduced a method for biclique community detection, which is an extension of the k clique community detection algorithm [12]. Eigen vectors of matrices [13], modularity optimization [14], the clustering coefficient [15], the intimate degree [16], the stochastic block model [17], density-based modularity [18], and asymmetric intimacy [9] are just a few of the numerous methods with various assumptions in bipartite networks. Liu [19] presented a unified community detection method based on the probability of node similarity to handle unipartite and bipartite networks concurrently. With the exception of unipartite networks, there should be a greater focus on community detection in big bipartite networks with a lot of nodes and edges using existing methods. Currently available methods often need a temporal complexity that is at least quadratic, meaning that handling huge bipartite networks always takes several hours.

The BiAttractor algorithm is an approach based on distance dynamics that is proposed for community detection in big bipartite networks [20]. It draws inspiration from the ways in which human civilization is structured, with more interactions taking place inside communities and less between them. The community detection problem is traditionally solved using graph partitioning and hierarchical clustering methods. The Newman concept of modularity has quickly acquired traction as a standard for evaluating partition quality [21]. The ratio of edges inside communities to edges between them is known as modularity. Maximizing modularity using optimization approaches has been a prominent issue, as a high modularity value suggests a good partition [10]. There are several approximation methods to determine the precise best solution to the issue. Blondel [7] invented the Louvain algorithm, which is a greedy method. In [22], a two-stage method called the BiLouvain algorithm is presented for detecting community structure in bipartite networks.

In the following, more than forty new studies on community detection in the last two years will be reviewed. In these studies, some community detection methods for bipartite networks with various assumptions were proposed. Spectral-clustering-based, matrix-factorization-based, modularity-optimization-based, link-prediction-based, propagation-based, game-theory-based, machine-learning-based, different-seed-node-based, neural-network-based, non-negative matrix-factorization-based, stochastic agglomerative, link entropy, node-influence-based, distance-regularization-based, and parallel fuzzy cognitive maps are the most common community detection methods in the above studies. The main goal of all of them is to increase the accuracy of the community detection process. Other methods have also been introduced in this field, including community contrastive learning, multi-relational graph convolution, scalable community fitness function, and node-similarity-integrated stochastic competitive learning methods. In [23], a spectral-clustering-based community detection method is proposed for community detection in multilayer networks. In [24], tensor low-rank representation, spectral clustering, and distance regularization are combined in a method to enhance the accuracy of community detection in multiplex networks. In [25], a parallel algorithm is proposed to solve the community detection overlapping problem in graph streams. In [26], a new algorithm for community detection based on different seed nodes (RWBS) is proposed, whose goal is to comprehend community structure as a novel idea for allocating network resources. RWBS employs modularity as an optimization function to join communities. In [27], a neural-network-based method was used to overcome the drawback that user data lack temporal variation. Additionally, innovative techniques have been put forth to analyze community networks using a network embedding method based on the matrix factorization framework. In [28], a spectral clustering community detection algorithm, PMIK-SC, based on the point-wise mutual information graph kernel is proposed. Also, a quick approach called BI-CNE is suggested for determining the number of communities during spectral clustering. Link prediction, structure observation, network estimation, and community partitioning are the four parts of the LPGSE method which was developed and put into practice in [29] to overcome the difficulty of extracting useful community information from the limited network structure. In [30], the goal is to recognize the community that contains a particularly important node called the anchor and to monitor how it changes over time. To effectively mine evolutionary community-aware information and to construct dynamic similarity metrics for dynamic link prediction, link prediction methods must take into account actor-level temporal changes and associated evolutionary information. Developing and integrating such dynamic features with machine learning algorithms is the goal of [31]. A community detection method in complex networks was proposed in [32] by combining max–min modularity and a connectivity-based metric at the same time. This allowed for the development of a novel complementary graph by utilizing the connectivity-based metric and a heuristic algorithm. In [33], an improved method for community detection based on a scalable community fitness function is proposed. This method introduces a stringent strategy to filter the outputs and a new parameter to improve its scalability.

In [34], an unsupervised community detection algorithm called LNSSCL (local node-similarity-integrated stochastic competitive learning) is presented to overcome the community detection problem and enhance the stability and accuracy of stochastic competitive learning. A new online framework for concurrently learning node representations and detecting communities in a network, termed community contrastive learning (community-CL), is proposed in [35]. In [36], a new algorithm that uses non-negative matrix factorization (NMF) to detect sparse network communities is presented. In [37], a new method based on parallel fuzzy cognitive maps (FCMs) is suggested to locate critical nodes. In order to detect communities that contain one or more illegal Bitcoin addresses, the authors of [38] first look into the structure of Bitcoin transaction networks. After that, they gather a list of illegal addresses and use them to identify the communities that have been detected. In [39], a novel method for identifying societal issues from web-based data using network analysis is proposed, wherein social issue candidates within the designated time frame are extracted using a community detection method. In [40], a new method (CSIM) is put forth by providing details about the community structure from the standpoint of edge information encoding. In [41], a new approach is presented that synergizes community detection algorithms with different graph neural network (GNN) models to reinforce link prediction in scientific literature networks. In [42], an improved version of the link entropy method is proposed to solve the challenge of measuring the significance of edges in a complex network. In [43], entropy-based measures were introduced as a new way to describe student’s learning behaviors. By combining these measures with a proven community recognition technique, learning behaviors in student communities are analyzed.

In [44], a stochastic agglomerative algorithm to detect the local community of given seed nodes is proposed that has several superiorities, including hierarchical community structure detection, etc. In [45], the problem of estimating community memberships of nodes in directed networks is regarded. Here, a directed degree-corrected mixed membership (DiDCMM) model is proposed. In [46], a method to calculate the number of communities for weighted networks produced from an arbitrary distribution under the degree-corrected distribution-free model is proposed. In [47], unlike most studies, which consider the network topology to be a factor in community formation, the content of the network is considered. Here, a comprehensive online community detection method that simultaneously examines the network’s structure and content is offered. In [48], a user similarity measure based on the network structure is proposed to improve recommendations to users with special preferences and new users so that they deal with the gray sleep and cold start problems. In [49], a new method is suggested to construct and comprehend the structure of Reddit, which is based on crossposts that were crossposted to another subreddit after first appearing on one. In [50], using NLP techniques such as text embeddings, subreddit content is directly modeled, and a subreddit graph network is built. In [51], an asymmetric ladder-shaped architecture called RGCLN based on multi-relational graph convolution that can create node representations with significant representational strength by fusing deep node properties is proposed. In [52], a method called local greedy extended dynamic overlapping community detection (GLOD) is proposed to deal with the difficulties of detecting overlapping communities in complex networks. In [53], for community detection, a new QUBO-based approach that only requires number-of-nodes qubits and is shown using a QUBO matrix is introduced. In [54], a collaborative approach is proposed based on matrix factorization and spectral embedding to recuperate the groups for the layers and nodes together. In [55], the local expansion technique based on ordinary graphs is extended to hypergraphs, and an efficient hypernetwork community detection method based on local expansion (LE) and global fusion (GF), called HLEGF, is proposed. In [56], a new community-enhanced contrastive learning method is introduced to help the recommendation primary task called CECL, which uses a community detection algorithm in the bipartite graph.

In the traditional LPA, every node is considered to have an equivalent relationship, and unreliable nodes reduce the label propagation accuracy. Therefore, in [57], the influence-based community overlap propagation algorithm (INF-COPRA) to rank the labels and nodes influence is proposed. The community detection method has been emphasized as a practical technique for handling the LSGDM complexity. However, dealing with the reliability, hesitancy of information, and interpretability of the method is still challenging. Therefore, in [58], a new approach of a Z-hesitant fuzzy network with the implementation of the community detection method is introduced. Orthogonal non-negative matrix tri-factorization (ONMTF) displays noteworthy potential as a strategy for this. In [59], the application of ONMTF in multiplex networks is investigated with the goal of concurrently detecting exclusive and shared communities. In [60], a modularity function F2 as a new objective function is proposed. The modularity function F2 overcomes certain drawbacks of the previous modularity functions, such as the resolution limit. In [61], a community detection method based on node influence analysis is proposed, wherein Pareto dominance is employed to rank the node’s influence. In [62], a multi-objective community detection technique based on a pigeon-inspired optimization algorithm, MOPIO-Net, is proposed. In [63], a new centrality measure called density-based entropy for identifying the most significant nodes locally is proposed, which offers an efficient way to locally identify the most significant nodes and community detection. Community detection models based on non-negative matrix factorization are superficial and unable to completely recognize the internal organization of complex networks. So in [64], a new limited symmetric non-negative matrix factorization with deep autoencoders (CSDNMF) as a solution is introduced. In [65], a model based on convex game theory and a measure of community strength is proposed to tackle the problem of identifying meaningful communities. The main contribution of [66] is DISCO, a distributed protocol for community detection and management in a peer-to-peer dynamic environment. This protocol is mainly targeted to decentralized online social networks, but it can be applied in other distributed scenarios. An interesting family of community detection algorithms is working by overlapping node-centric techniques. In [67], an algorithm that aims to lower the computational complexity of earlier solutions while ensuring the identification of high-quality overlapping partitions was proposed.

2.1. Preliminary Definitions and Variables

2.1.1. Community Structure

A sub-graph whose nodes are more likely to link to one another than to nodes outside the sub-graph is called a network community. One of the key features of bipartite networks is their community structures, which divide networks into collections of nodes and edges. With tight connections between nodes in the same group and weak connections between groups of distinct nodes, the underlying networks are organized in a modular fashion. Coarse-grained sub-networks may be detected from underlying networks. Global average attributes are inadequate to describe the community structure features since various communities have varied structural characteristics [14]. Moreover, the community offers an improved comprehension of modularity in bipartite networks. There are two categories into which bipartite communities can be divided. Members of a bipartite network are categorized as belonging to the same type or to separate types. In bipartite networks, the community structure combines comparable nodes within the same part and shows the extent to which nodes in one part are connected to the other part’s nodes.

2.1.2. Centrality Measure

Centrality measures are frequently used in social network analysis to express the respective significance of nodes. It is possible to identify prominent users using social network analysis by applying this idea of centrality [68]. Numerous centrality measures, such as Betweenness, degree, and Closeness, have been put forth to identify network nodes. Utilizing these structural network measures necessitates a thorough comprehension of the network topology [69].

In order to transform bipartite networks into unipartite networks, some approaches have been applied to bipartite networks using various projection techniques. A few of the unipartite network measures have been applied to bipartite networks, despite the fact that unipartite networks are less informative than their bipartite counterparts [70]. Conventional centrality measures are problematic in large-scale social networks because they need a thorough grasp of network topology and because there are no suitable measures for detecting more behaviorally representative individuals inside bipartite social networks. A novel centrality measure known as HellRank was created by taking into account users’ significance indications while detecting core nodes [71]. Without initially generating a unipartite projection of the bipartite network, HellRank is a measure that may be applied to community detection in bipartite networks. One of the reasons for using this measure in the proposed method is this. The Hellinger distance, a kind of f-divergence metric, is the basis of HellRank and shows how similar a node is structurally to the other nodes. Empirical data indicate that nodes in bipartite networks exhibiting a high HellRank also have a high degree, Betweenness, and PageRank. A function that quantifies the difference between probability distributions P and Q is called a f-divergence, and its value is $D_H\left(P\right|\left|Q\right)$. For a convex function f and $f\left(1\right)=0$, the f-divergence of Q from P is defined as follows:

$$D_f\left(P\right|\left|Q\right)={\int }_{\Omega }f\left({\displaystyle \frac{dP}{dQ}}\right)dQ$$

(1)

where the set of all potential results is denoted by $\Omega$. The Hellinger distance for discrete probability distributions, $P=(p_1,p_2,...,p_m)$ and $Q=(q_1,q_2,...,q_m)$, where m is the vector’s length, is as follows:

$$D_H\left(P\right|\left|Q\right)={\displaystyle \frac{1}{\sqrt{2}}}\sqrt{\sum _{i=1}^m{(\sqrt{p_i}-\sqrt{q_i})}^2}$$

(2)

This is clearly connected to the Euclidean norm of the vector difference square root, as

$$D_H\left(P\right|\left|Q\right)={\displaystyle \frac{1}{\sqrt{2}}}\left|\right|\sqrt{P}-\sqrt{Q}{\left|\right|}_2$$

(3)

2.1.3. Modularity

The modularity measure, first proposed by Newman [21], quantifies the degree to which edges emerge inside communities rather than across communities. We can evaluate the quality of any node-to-community assignment by utilizing modularity. The task of precisely maximizing modularity is typically unsolvable. A number of useful approaches for determining the nodes’ high modularity divisions have been presented. It is also possible to define modularity by employing a matrix whose eigen spectrum is directly associated with the modularity of the network. Given that modularity is explicitly dependent on a null model, the choice of null model has a significant influence on modularity. In statistical physics, communities in bipartite networks are found by first building a unipartite projection of one part of the network, and then using community detection techniques related to working with unipartite networks. Unipartite projections are inherently less informative, notwithstanding their potential for usefulness. Barber offered a concept of modularity for bipartite networks based on creating a bipartite modularity matrix, which was an extension of the Newman work. These matrix eigen spectrum features have been identified, and the Newman method has been tailored for bipartite networks using these features. For bipartite, recursively induced modules, this technique is referred to as BRIM [72].

3. Proposed Method

Obtaining precise and high-quality community structures out of networks is still a difficult undertaking. The proposed method is significant because it can definitely detect distinct and high-quality community structures from networks. First, the voting patterns seen in election activities are used to model the network’s voting process. Every node votes for the candidates that have been nominated using the suggested voting criteria, and densely linked groups of nodes can rapidly come to an agreement on their choices. This process creates a cluster of candidates and their supporters. In order to create the final community structure, the clusters will serve as the first communities, and some of them will be effectively combined into larger ones. It was discovered through a thorough examination of community structures taken from several networks that the node and the majority of its neighbors are members of the same community. Furthermore, every node in a community forms a tiny cluster with its neighbors. Every community consists of several tiny clusters. There are always some nodes with a comparatively greater degree than others in every cluster. A cluster is a collection of nodes connected to a single, higher-degree node. In social systems, voting behavior is comparable to this phenomenon. There are always powerful local figures in networks that are detached from social systems, such as department heads and experts in certain domains. Assuming those people take part in an election where nominations are open to everybody, each voter will break ties by selecting the person nearest to them and casting their vote for the person who has more influence around them. A node group will be formed as a result of this process. The proposed method for community structure detection in networks is based on simulating the voting process. The approach that is being given uses a few predefined principles as voting guidelines, uses degree to indicate each node’s impact, and uses similarity between nodes to indicate how close they are. Stated differently, every node casts a vote for a neighbor whose degree exceeds its own. The voter node chooses the larger-degree node with the greatest similarity if there are many of them with the same impact among its neighbors. As a result, every node votes rapidly, and at the conclusion of the voting process, we will have a large number of little node clusters. Every community consists of many clusters. The clusters serve as the starting communities, which combine to form the final community structure.

Voting Rules

This study deals with a graph without direction or weight $G=(U,I,E)$, where two sets of distinct node kinds are represented by U and I, and various node kinds are connected by the edge e of E. There are no edges connecting any of the nodes in the same set. The proposed method simulates election voting patterns to detect groups inside networks. An important part of the detection procedure is the voting rules. Each node $u\in U$ votes throughout the detection procedure in accordance with the following guidelines:

• If node u has the highest degree among its second-order neighbors or has been nominated as a candidate, it casts a vote for itself.
• From among u’s second-order neighbors, a node with a greater degree than u is selected and designated as v. If there are many nodes that are similar to u, the most similar node is chosen and designated as v. The notation $sim(u,v)$ indicates the similarity between u and v. u proposes itself as a candidate and casts its own vote if $sim(u,v)=0$.
• If v has not cast a vote for any other nodes, u proposes node v as a candidate and casts a vote for it.
• If node v casts a vote for node w, i.e., if v has forfeited its right to be nominated as a candidate, then node u will also cast a vote for node w.

The voting arrangement of nodes can affect the arrangement in which nodes are nominated as candidates, as per the voting rules mentioned above. As a result, various voting orders may produce different outcomes.

The clustering coefficient of each node in the set U is computed according to Equation (4), and the nodes are then voted in ascending order based on their clustering coefficients. For any node $x\in U$, the clustering coefficient can be computed as a portion of the number of 4-paths centered on the focal node x to the subset of these in which the path’s first and last nodes share a common node that is not part of the 4-path (part of at least one 6-cycle) and can be calculated as follows [70]:

$$cc\left(x\right)={\displaystyle \frac{\mathit{closed} \mathit{4}\text{-}\mathit{paths} \mathit{centered} \mathit{on} \mathit{node} \mathit{x}}{\mathit{4}\text{-}\mathit{paths} \mathit{centered} \mathit{on} \mathit{node} \mathit{x}}}$$

(4)

The higher the number of edges that a certain node v has with its neighbors, the higher the clustering coefficient x. $cc\left(x\right)$ achieves its maximum, 1, whenever the sub-graph made up of node x’s second-order neighbors is a complete graph. However, in a sparse network, it is improbable that any node’s neighborhood sub-graph will be a full graph, particularly for nodes with higher degrees. Unless stated otherwise, a node with a higher degree always has a small clustering coefficient. The nodes with greater degrees can nominate a candidate early and surround themselves with their neighbors to create clusters by voting based on the ascendant order of the node’s clustering coefficients. Voting rule 2 states that the similarity between a node and u is utilized to decide which node u should vote for if there are many nodes in the neighborhood with degrees higher than u. As a result, voting heavily relies on node similarity. In the proposed method, the similarity between nodes u and v is determined using the following formula:

$$sim(u,v)={\displaystyle \frac{1}{\mathit{hellinger} \mathit{distance}(\mathit{u},\mathit{v})}}$$

(5)

Following the voting process, we will have several little clusters. These clusters deviate from the intended communities nonetheless. Several of these clusters may be present in a final community, based on the data mentioned above. Consequently, we regard these clusters as the starting communities and contemplate combining some of them to create the final communities. Only some communities are taken into consideration as pairings of communities that have a similarity higher than a certain level in order to guarantee high-quality results. The similarity between two communities $C_i$ and $C_j$ are computed as follows:

$$sim(C_i,C_j)=\sum _{x\in U_{C_i}}\sum _{y\in U_{C_j}}{\displaystyle \frac{1}{\mathit{hellinger} \mathit{distance}(\mathit{x},\mathit{y})}}$$

(6)

There are two stages to the proposed method, which is known as BiVoting. The voting process, which produces a number of little clusters, is the first stage. In order to build the final community structure, the smaller clusters will merge into bigger ones during the merging phase as a second stage. Two stages of the proposed method are displayed in Figure 1, and Algorithm 1 provides a description of the method framework.

Algorithm 1: BiVoting Community Detection Method

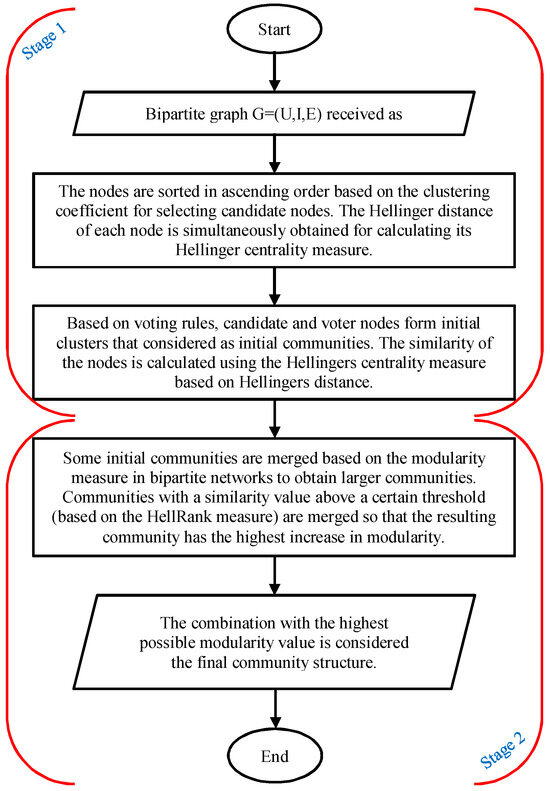
Figure 1. Two stages of the proposed method.

The BiVoting() function is equivalent to the voting process, wherein, according to the voting rules, every node in the network casts a vote for the node that has a bigger impact in its neighborhood. The reasoning of Algorithm 2 is given in pseudo-code, and several little clusters are the result. It should be mentioned that many of these little clusters can be combined to form a single community; they are not the final communities. The tiny clusters are used as the starting communities in the resultant community structure, and some communities are merged via the function BiMerge(). In the proposed method, using an approach similar to that of [72], this function is implemented by merging two communities whose merger would provide the biggest modularity increase in each iteration. The merging procedure pseudo-code is explained in Algorithm 3. This merging procedure results in a substantially lower joining time since each tiny cluster is regarded as an initial community instead of each node being a community. Also, the merging of two communities is only considered if their similarity exceeds a certain level, because doing so may have an adverse effect on the quality of the new community structure. Equation (6) is used for determining the similarity between two communities. Instead of continuing until every node is in the same community, the joining process can potentially end sooner if there is not similarity between any two communities that is higher than a predetermined threshold. As a result, the merging process is quite effective.

Algorithm 2: The Logic of Function BiVoting(G)

Algorithm 3: The Logic of Function BiMerge(G,$C{S}_{init}$)

4. Experimental Results

In this section, BiVoting will be compared with four popular methods for detecting communities in artificial and real bipartite networks. A quick explanation of these methods is provided below. BiVoting code was created in the Colab environment, and the results were achieved by implementing this code on an Intel E5-2683 v4 Broadwell @2.1GHz server.

• BiAttractor: Based on distance dynamics, Hong Sun created a unique technique for bipartite community detection in big bipartite networks [20]. The interactions that take place in human societies—where there are more interactions inside a society than between them—are the source of inspiration for it. It produces accurate community partitions and has $O\left(\right|E\left|\right)$ time complexity in networks that are sparse (the $\left|E\right|$ is the edge number).
• Adaptive BRIM: Barber introduced the concept of iteratively maximizing modularity $Q_b$ in bipartite networks, which led to the creation of BRIM (bipartite, recursively driven modules) [72]. It is ensured that $Q_b$ does not drop for each iteration. On the other hand, the observed splitting of bipartite networks results in a local maximum $Q_b$ instead of a global maximum. Furthermore, the maximization of modularity $Q_b$ also determines the number of modules. It has $O\left(cn\right)$ time complexity.
• LP BRIM: By putting out the combination BRIM and label propagation technique known as LP BRIM, Liu expanded on the work of BRIM [73]. It may be implemented in real networks because of its time complexity, which is $O\left(n^2\right)$ (where the number of nodes is n).
• AsymIntimacy: Considering the intimate degree between nodes of the same kind and nodes of different kinds, Wang established asymmetric parameters [9]. Because of the close degree of asymmetry, nodes of the same kind are first combined as subsets. To form core communities, the subsets from the previous stage are then combined with another sort of node. Core community pairings are combined as soon as the intersection ratio rises over a certain level. Until no other core communities can be combined, this procedure is repeated. $O(2n^2+mn)$ is its time complexity, where n and m are the number of nodes and edges.

In general, two measures may be employed to examine and contrast various approaches. Normalized Mutual Information (NMI) is used to compute a score in the range [0,1] when community splits across the underlying network are known beforehand. If not, modularity is used [10]. Modularity was first restricted to unipartite networks. Barber [72] has therefore expanded the concept of the community to include $Q_b$. There are more edges within the same community than predicted by the null model when the value from [0,1] is greater. Yet, because of the resolution limit [11], $Q_b$ has some restrictions.

4.1. Complexity Analysis

An algorithm’s low temporal complexity is beneficial when it comes to applying it to large-scale networks. There are two stages to the proposed method. To acquire the first communities, the voting process is simulated in the first stage. $O(md+nlogn)$ may be used to achieve it, where d is the average degree of nodes and n and m are the number of nodes in one of two distinct sets of nodes and edges, respectively. The final communities are acquired in the second stage, which has a complexity of $O\left(mk\right)$, where k is the cost of merging iterations and $k\ll n$, $d<k$ in general. Some of the initial communities are combined to generate the final communities. For sparse networks, this means that the proposed method’s overall time consumption is $O(md+nlogn+mk)\sim O\left(mk\right)$, or $O\left(nk\right)$. As a consequence, the experimental findings show that the proposed method is effective when used with large-scale networks. A comparison of the time complexity of the proposed method and the four compared methods in Table 1 shows that the proposed method is either better or at an equal level.

Table 1. Comparison of BiVoting and other methods on time complexity.

Method	AsymIntimacy	LP BRIM	Adaptive BRIM	BiAttractor	BiVoting
Time complexity	$O(2n^2+mn)$	$O\left(n^2\right)$	$O\left(cn\right)$	$O\left(\right|E\left|\right)$	$O\left(nk\right)$

4.2. Results in Artificial Networks

Numerous techniques for detecting communities rely on optimizing modularity. Nevertheless, the resolution limit issue may arise with these techniques [11]. Considering the network’s total size and internal connections, they are limited in their ability to detect communities on less than a certain scale. Rings of bicliques with various biclique numbers have been created to show off the usefulness of BiVoting. Three squares are used to fully link two circles, and each biclique contains two mode nodes. Table 2 provides an overview of these rings of bicliques fundamental topological structural characteristics, within which n and m are the number of members of two distinct node sets in a bipartite network, N is the total number of these nodes, M is the number of connections between the nodes of these sets, and K is the ratio of the number of connections to the average number of total nodes. Additional tests are conducted on rings with varying quantities of bicliques. In-depth findings are displayed in Figure 2 and Figure 3, where NMI denotes the degree of accuracy of various bipartite community detection methods and $N_C$ represents the total number of communities detected, respectively. The results show that the proposed method, like BiAttractor, can accurately detect the number of communities despite calculating a lower NMI, which is due to the ability of BiVoting to accurately replicate the voting process. It should be noted that as the biclique size increases, the calculated NMI gradually approaches the best value. These observations confirm that BiVoting outperforms other methods.

Table 2. Fundamental topological characteristics of rings of bicliques [20].

Bicliques	n	m	N	M	<K>	C
4bicliq.	12	8	20	28	2.8	0.482
8bicliq.	24	16	40	56	2.8	0.482
16bicliq.	48	32	80	112	2.8	0.482
64bicliq.	192	128	320	448	2.8	0.482
128bicliq.	384	256	640	896	2.8	0.482

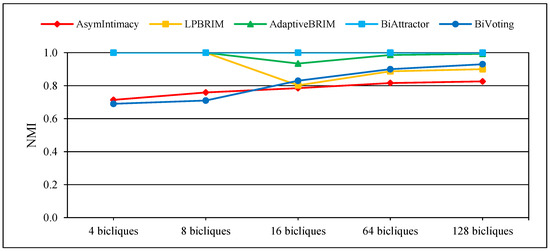
Figure 2. Performance of BiVoting and other methods on rings of bicliques for measurement NMI.

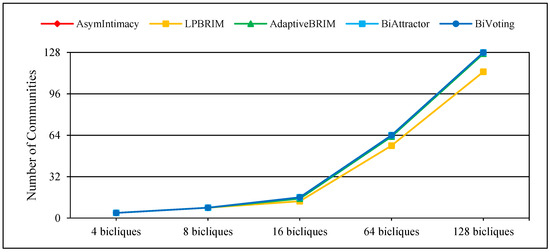
Figure 3. Performance of BiVoting and other methods on rings of bicliques for measurement $N_C$.

4.3. Results in Real Networks

Real bipartite networks with unknown modular structures were used for experimental research, and the modularity score ($Q_b$) was used to confirm correctness. The following real bipartite networks are included in our study: S.W., A.R., S.C.I., C.N., M.G., P.C.D., D.W., and D.P. Following is a brief explanation of these real networks. Also, Table 3 provides a summary of their fundamental topological structural properties, within which n and m are the number of members of two distinct node sets in a bipartite network, N is the total number of these nodes, M is the number of connections between the nodes of these sets, and K is the ratio of the number of connections to the average number of total nodes.

Table 3. Fundamental topological characteristics of real bipartite networks [20].

Network	n	m	N	M	<K>	C
S.W.	18	14	32	89	5.563	0.328
A.R.	136	5	141	160	2.270	0.781
S.C.I.	108	136	244	358	3.140	0.303
C.N.	829	551	1380	1476	2.139	0.427
M.G.	297	806	1103	2965	5.376	0.227
P.C.D.	680	739	1419	3690	1.746	0.407
D.W.	89,356	46,215	135,571	144,342	2.129	0.447
D.P.	48,833	138,839	187,672	207,268	2.209	0.514

• Southern Women (SW): In the context of bipartite network community detection, it is a widely recognized benchmark data set. Davis collected the information in and around Natchez, Mississippi in the 1930s in order to research race and class. It details how 18 women were divided up across 14 social gatherings. A bipartite network with 32 nodes and 89 edges is formed in this data set by women and the social activities they attend.
• American Revolution (AR): A total of 136 people’s membership details from five organizations that date back to the American Revolution are included in the data collection [74]. It is possible to think of the connection between well-known people and their organizations as a bipartite network. An edge indicating membership in an organization can be found between an individual and that organization.
• Scotland Corporate Interlock (SCI): Board members of Scottish corporations who served as directors on several occasions during 1904 and 1905 are included in this data collection. A bipartite network including 108 companies and 136 persons is upheld via directorships.
• Crime Network (CN): People who have been a victim, witness, or suspect in at least one criminal case are included in this data set [74]. A bipartite network with 1476 edges linking 829 individuals and 551 criminal cases is formed by the interactions between crime-related individuals and crime cases.
• Malaria and var Genes (MG): Using protein camouflages expressed in var genes, the malaria parasite eludes the human immune system. Regular recombination of Var genes results in a restricted genetic sub-string that generates novel camouflages [17]. As a result, var genes and their genetic sub-strings are linked in a way that creates a bipartite network with an inherent community structure. The 297 genes and 806 sub-strings that are connected by 2965 edges make up the MG network.
• The Protein Complex and Drug (PCD): Meaningful links between acute illnesses and protein complexes have been found in recent investigations. In order to determine the inter-connectivity in systems relevant to human and molecular diseases, Nacher and Schwartz examined a bipartite network including 680 medications and 739 protein complexes [75]. PCD consists of 3690 edges and 1419 nodes.
• DBpedia Writer (DW): DW has a lot of nodes and edges, making it difficult for current techniques to detect community patterns. The 46,215 authors and 89,356 works from DBpedia make up the DBpedia Writer network. The partnerships among writers to develop works are represented by the 144,342 edges [74].
• DBpedia Producer (DP): DBPedia is the source of the DBpedia Producer network. A total of 48,833 producers and their 138,839 works make up this bipartite network [74].

Figure 4, Figure 5 and Figure 6 display the comprehensive outcomes of the experiments conducted on the above small and medium real bipartite networks. Figure 7, Figure 8 and Figure 9 also show the results of the experiments on the large real bipartite networks. In these figures, $Q_b$ represents the modularity score of the various bipartite community detection methods, the number of communities detected is denoted by $N_C$, and the execution time of bipartite community detection methods is represented by $Time\left(s\right)$. In fact, the modularity score indicates the accuracy of a method for community detection, which can be used to evaluate the quality of each node-to-community assignment. Figure 4 and Figure 7 contrast BiVoting’s accuracy with other methods. Given that BiVoting and the other methods under comparison maximize modularity, we can deduce that BiVoting performs better than the other four methods when we see that its calculated modularity score is higher than that of BiAttractor and the other three methods under comparison. In BiVoting, although fewer communities are found, this reduction improves as the network gets bigger. Additionally, it must be noted that fewer communities are detected due to BiVoting’s ability to accurately replicate the voting process. The comparison charts of community detection methods on large real networks are separated from smaller real networks because in extremely big networks like DW and DP, AsymIntimacy, LPBRIM, and AdaptiveBRIM methods cannot be used, and after many hours of execution, they either fail or receive no specific result. BiVoting executes faster on small real networks like SW, AR, SCI, and CN than other methods, but in medium real networks like MG and PCD, it does not perform faster than all methods. Although in large real networks like DW and DP, compared to the BiAttractor method, the proposed method is implemented and executed in an acceptable time difference, which is a significant advantage given the large scale of the networks. These findings support the notion that BiVoting is a suitable technique for community detection in bipartite networks.

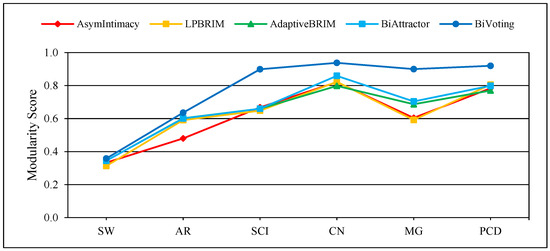
Figure 4. Performance of BiVoting and other methods on small and medium real networks for measurement $Q_b$.

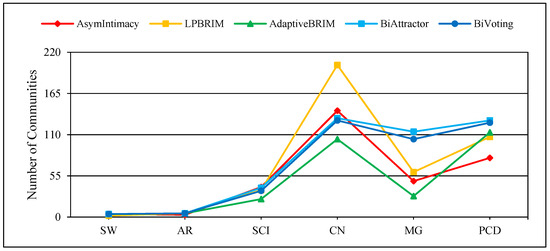
Figure 5. Performance of BiVoting and other methods on small and medium real networks for measurement $N_C$.

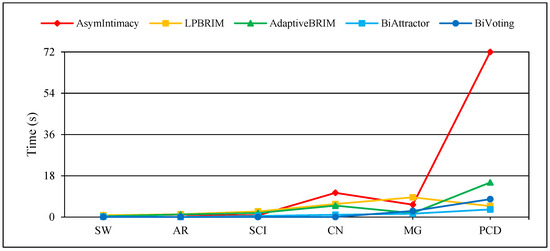
Figure 6. Time consumption comparison of BiVoting and other methods on small and medium real networks.

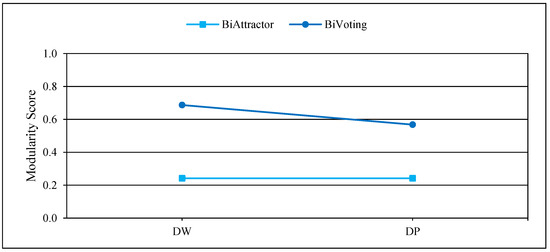
Figure 7. Performance of BiVoting and BiAttractor on large real networks for measurement $Q_b$.

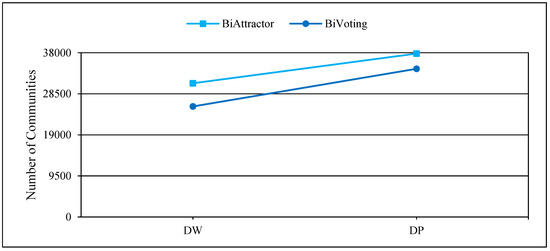
Figure 8. Performance of BiVoting and BiAttractor on large real networks for measurement $N_C$.

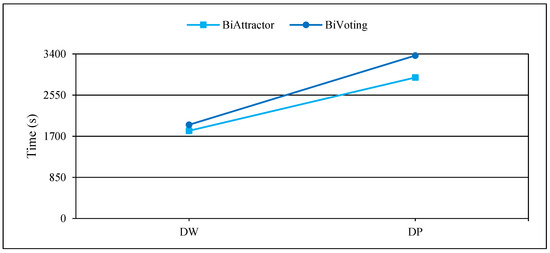
Figure 9. Time consumption comparison of BiVoting and BiAttractor on large real networks.

5. Conclusions and Future Work

A bipartite network is a natural model for various real-world complex systems. A better method to comprehend modular structures in bipartite networks is through the concept of community. Community detection in complex networks can aid in the understanding of these networks’ structural characteristics. Numerous methods for community detection have been put forth. Nevertheless, some of them need a lot of time, which restricts their use in large networks. While several low-time complexity algorithms exist, their practical value in real-world applications is limited since they are typically non-deterministic. A straightforward approach to community detection was to apply the standard methods for community detection in unipartite networks after converting the bipartite networks into their unipartite counterparts. The issue of information loss in this procedure is a challenge. After presenting the concept of bipartite modularity, in which two independent parts of nodes are placed independently in modular structures, the idea of community detection was proposed without the need to change bipartite networks into unipartite networks. Also, since the task of precisely maximizing modularity is typically unsolvable, some useful approaches are presented to determine the exact node’s modularity divisions. Centrality measures are commonly employed in social network analysis to ascertain the respective significance of nodes. HellRank is a precise metric for locating core nodes in bipartite networks. The fact that there is no need to transform the bipartite network to its unipartite counterpart makes this measure ideal.

In this paper, BiVoting, a two-mode and deterministic community detection method in bipartite networks, was proposed, which was defined with the help of two concepts of bipartite modularity and HellRank centrality measures and based on the simulation of the election voting patterns in human societies. The proposed method’s performance was evaluated, and the results of comparison with four common community detection methods on variable-size artificial and real bipartite networks show that BiVoting performs better than other methods. The results of tests on rings with varying quantities of biclique show that the proposed method, like BiAttractor, can accurately detect the number of communities despite calculating a lower NMI value, which is due to the ability of BiVoting to accurately replicate the voting process. It should be noted that as the biclique size increases, the calculated NMI value gradually approaches the best value. The outcomes of the experiments conducted on the real bipartite networks show that BiVoting can calculate a higher modularity score than other methods, which indicates the accuracy of a method for community detection and is used to evaluate the quality of each node-to-community assignment. The most important strength of BiVoting is calculating a higher modularity score in large-scale real bipartite networks. Of course, it should be noted that fewer communities are found, and this reduction improves as the network size increases. Fewer communities are detected due to BiVoting’s ability to accurately replicate the voting process. Some of the compared community detection methods like AsymIntimacy, LPBRIM, and AdaptiveBRIM cannot be used in large real bipartite networks like DW and DP because, after many hours of execution, they either fail or receive no specific result. But BiVoting in these networks is implemented and executed in an acceptable time difference compared to the BiAttractor method. This is another strength of BiVoting. Also, BiVoting executes faster in small real bipartite networks and somewhat faster in medium real networks. However, due to BiVoting’s ability to accurately replicate the voting process, fewer communities are detected in these networks. All of these findings support the notion that BiVoting is a suitable technique for community detection in bipartite networks.

It is proposed in the future to provide a method for community detection in bipartite networks using centrality measures that do not require full knowledge of the network topology and can meet the requirements of today’s complex social network environment and uses innovative ideas to discover the community structures in the shortest possible time.