A Modified Selected Mapping Scheme for Peak-to-Average Power Ratio Reduction in Polar-Coded Orthogonal Frequency-Division Multiplexing Systems
Abstract
1. Introduction
- Since the PAPR bits are a small subset of the frozen bits and the modulated signal vector corresponding to the PAPR bits can be precomputed offline, polar encoders and BPSK modulators are eliminated at the transmitter. We achieve a lower-complexity SLM transmitter compared to existing PC-SLM schemes without any code rate loss.
- At the receiver, the BP algorithm is applied to the SLM scheme, for the first time according to the authors’ knowledge. Our proposed SLM receiver utilizes a modified BP algorithm enhanced with detection capabilities to adapt to the SLM transmitter, eliminating the need for SI transmission.
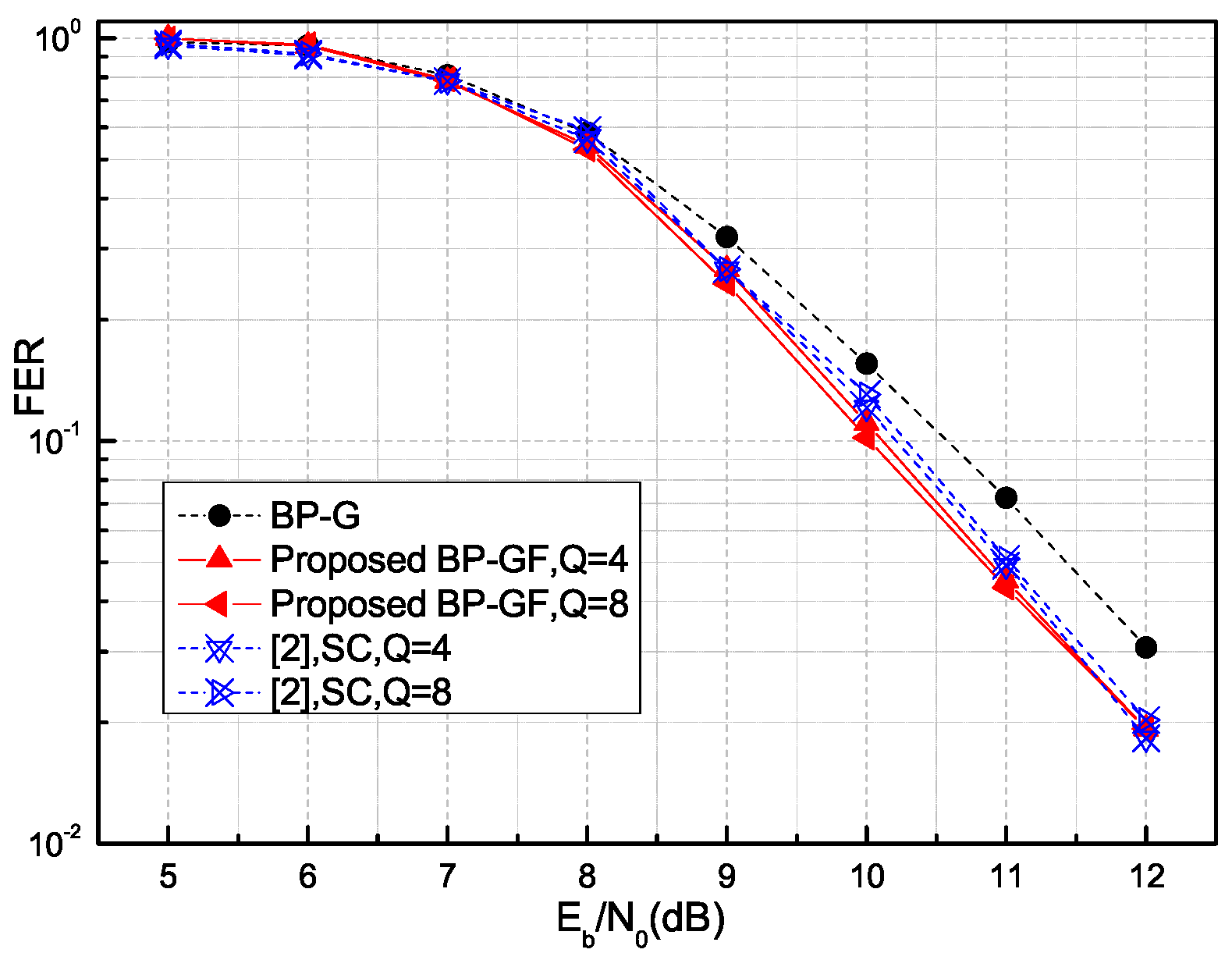
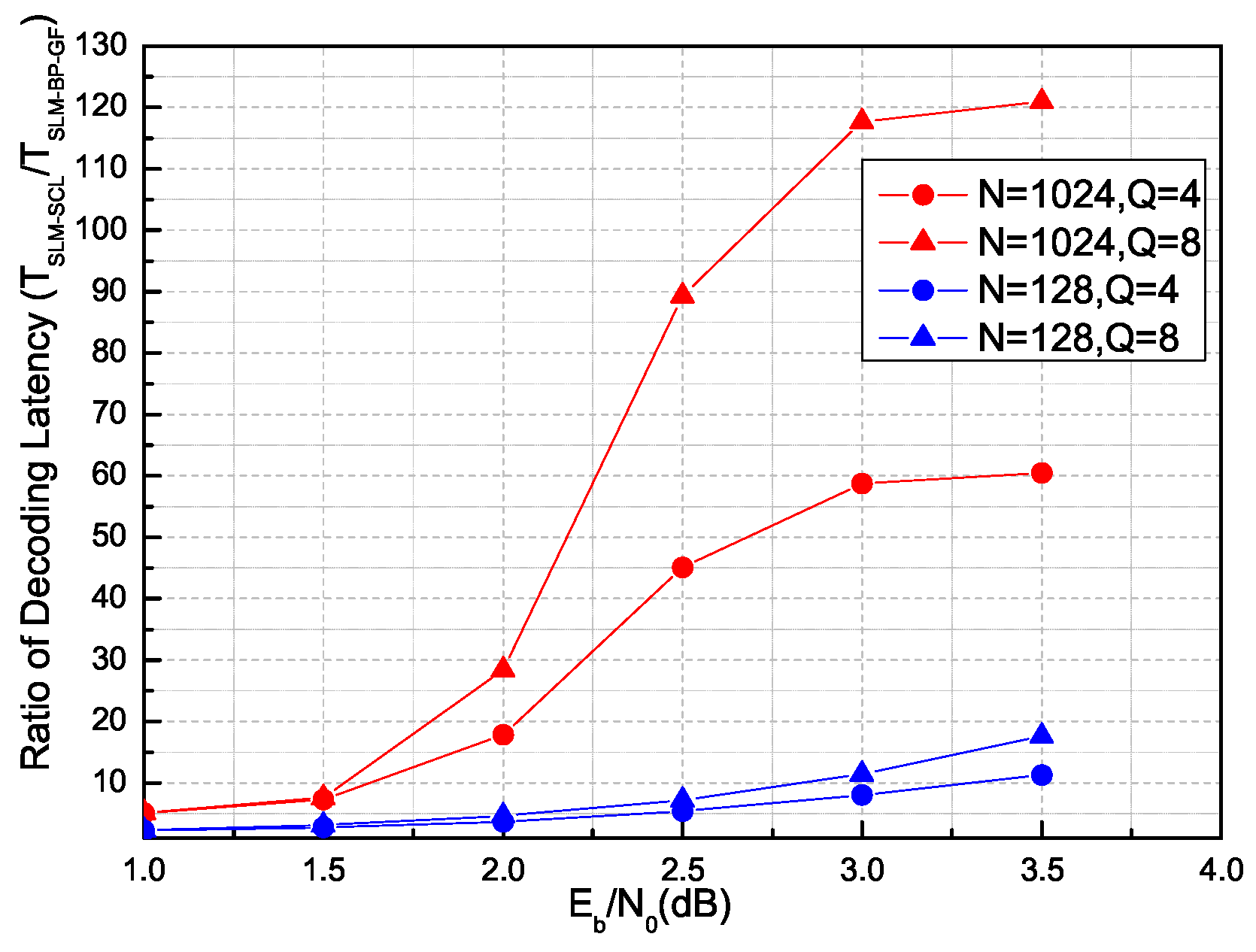
- For the PC-SLM approach based on the partially frozen bit method, the proposed BP-GF-based receiver achieves a PAPR reduction and error correction performance consistent with that of the successive cancellation (SC)-based receiver. Furthermore, its decoding latency is significantly lower than that of the SCL-based receiver.
2. Preliminaries
3. The Modified SLM Scheme for PAPR Reduction Based on Polar Coding
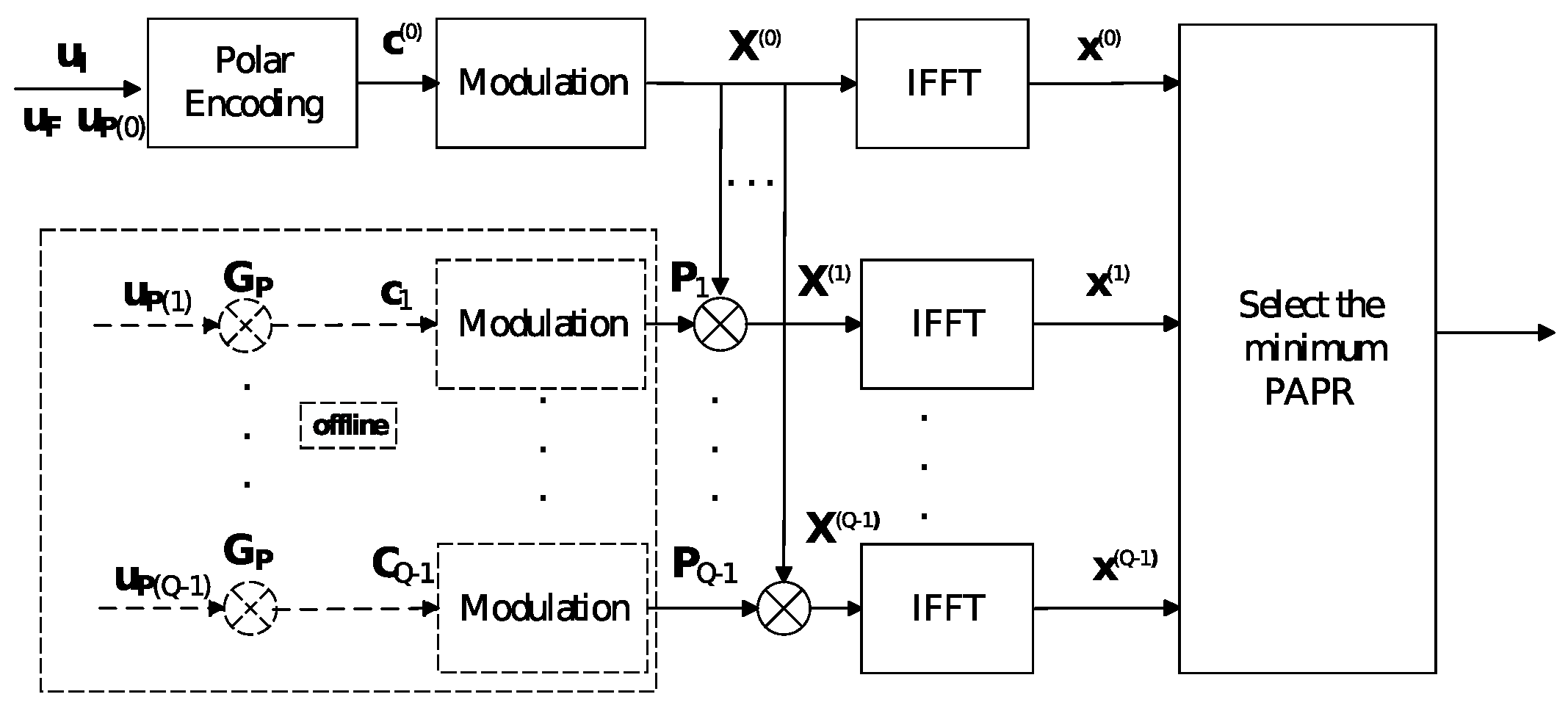
3.1. The Low-Complexity Transmitter
- 1.
- We construct the extended information set with cardinality using methods such as Bhattacharyya parameters [1], the generator matrix named .
- 2.
- Given the importance of PAPR bits, we select rows from with a Hamming weight in the range of to , which corresponds to higher reliability. The resulting matrix is denoted as
- 3.
- To perform a Monte Carlo simulation on the polar-coded OFDM system, we calculate the original PAPR () and the new PAPR() after flipping each bit in sequentially. We employ the metric presented in [2] to assess the PAPR impact of each bit in .
- 4.
- The PAPR metric is sorted in descending order, and the first l indices of are selected as PAPR set , while the remaining indices are used for information bit transmission.
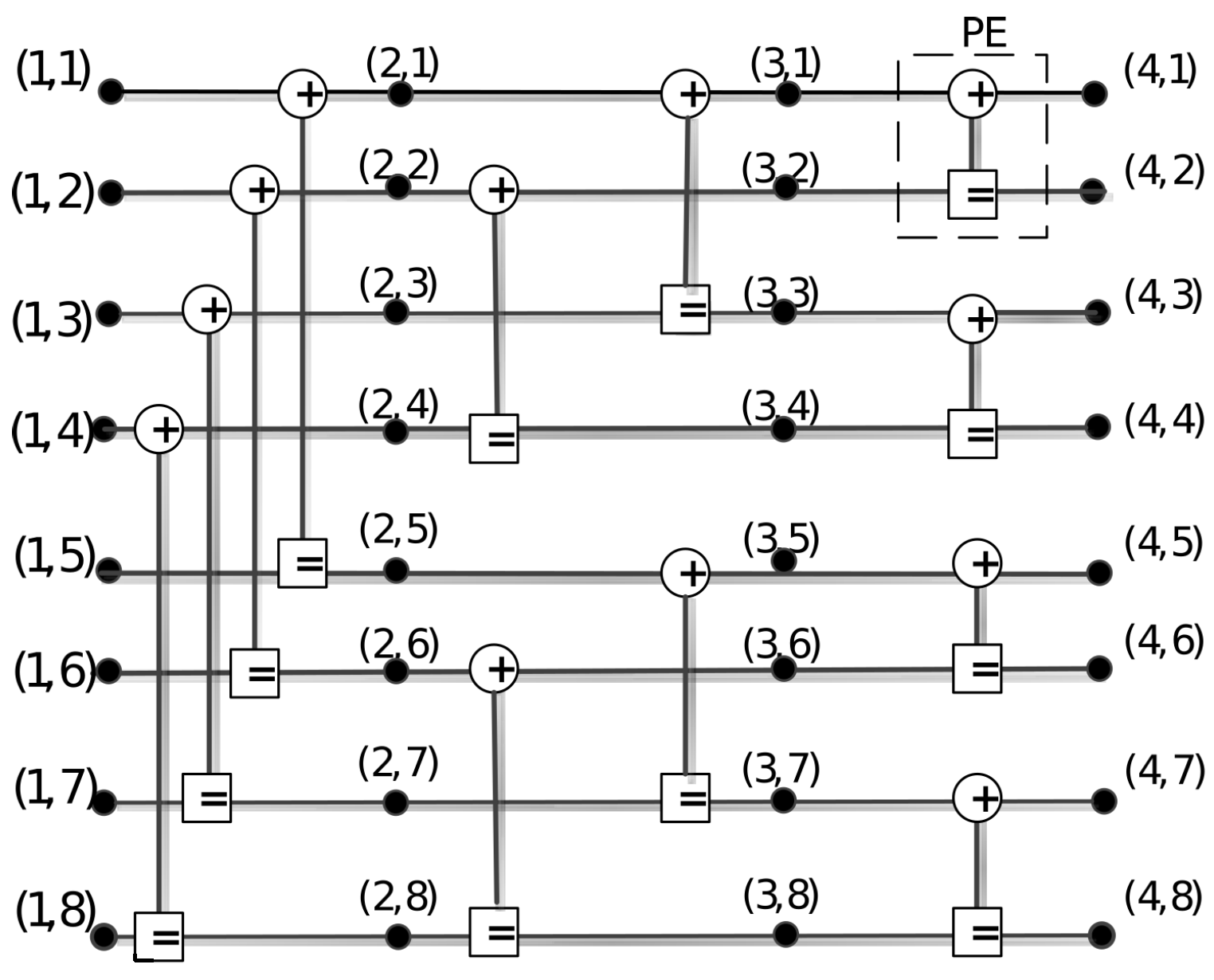
3.2. The Receiver Based on Modified BP Algorithm
| Algorithm 1 BP-GF |
| Input: LLR channel output and Output: estimated information bits
|
| Algorithm 2 GFcheck |
| Input: , L-matrix of BP factor graph , R-matrix of BP factor graph Output: isSatisfied
|
4. Simulation Results
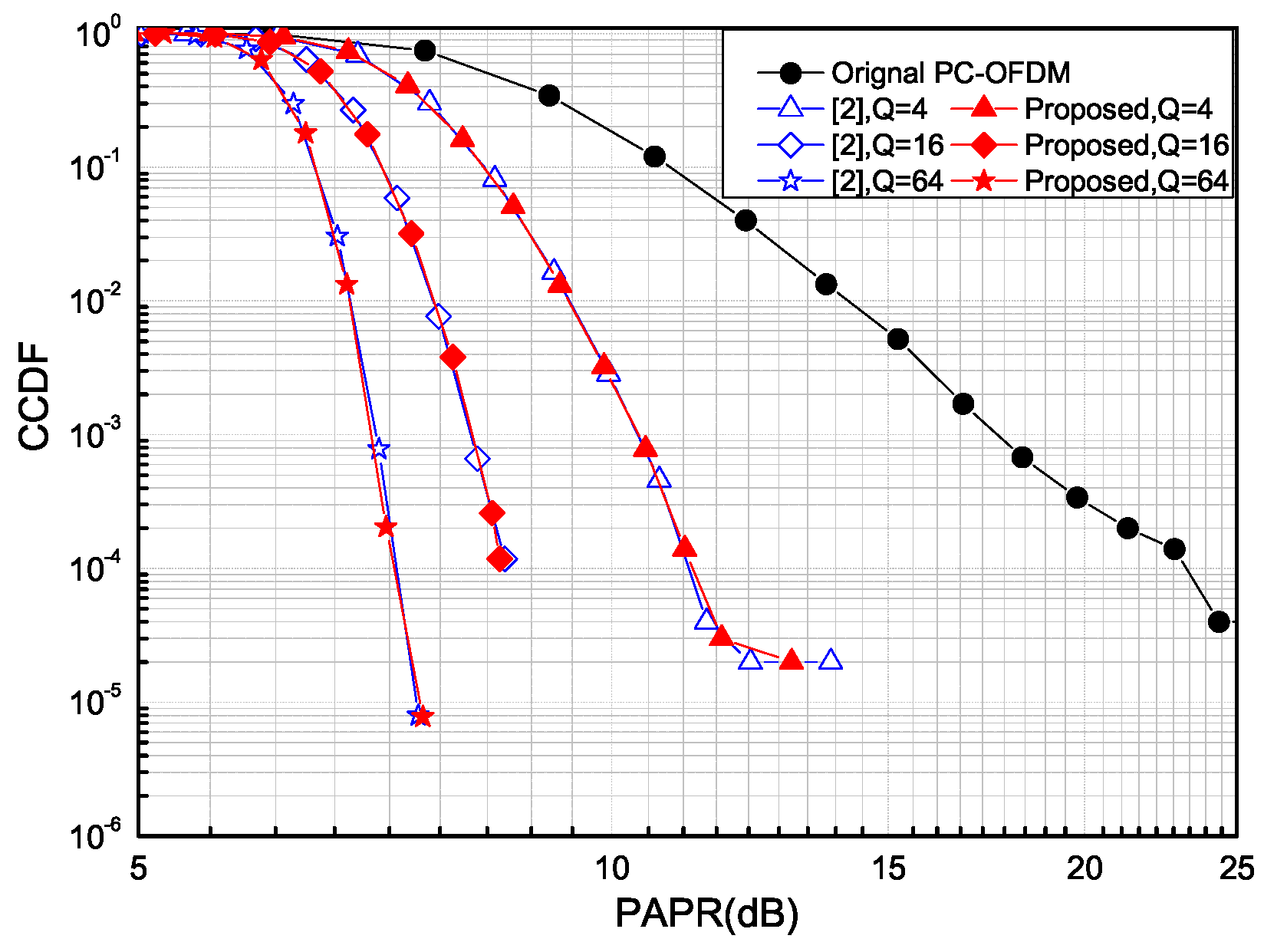
4.1. PAPR Performance
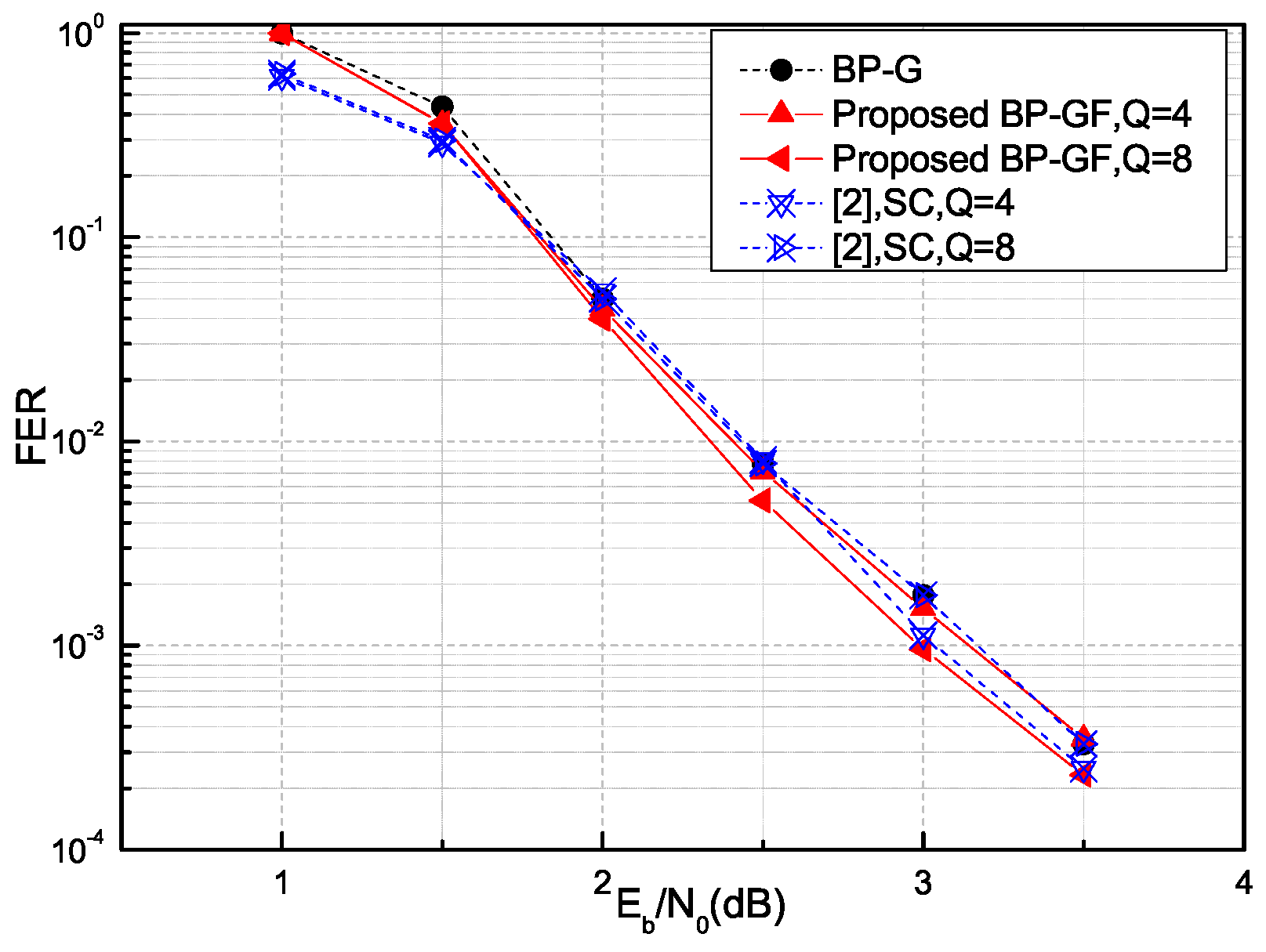
4.2. Frame Error Rate (FER) Performance
4.3. Latency Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Arikan, E. Channel Polarization: A Method for Constructing Capacity-Achieving Codes for Symmetric Binary-Input Memoryless Channels. IEEE Trans. Inf. Theory 2009, 55, 3051–3073. [Google Scholar] [CrossRef]
- Matsumine, T.; Ochiai, H. A Novel PAPR Reduction Scheme for Polar-Coded OFDM Systems. IEEE Commun. Lett. 2019, 23, 2372–2375. [Google Scholar] [CrossRef]
- Zhang, S.-Y.; Shahrrava, B. A SLM Scheme for PAPR Reduction in Polar Coded OFDM-IM Systems Without Using Side Information. IEEE Trans. Broadcast. 2021, 67, 463–472. [Google Scholar] [CrossRef]
- Lim, S.-C.; Kim, N.; Park, H. Polar Coding-Based Selective Mapping for PAPR Reduction Without Redundant Information Transmission. IEEE Trans. Broadcast. 2020, 24, 1621–1625. [Google Scholar] [CrossRef]
- Zhang, S.-Y.; Yue, X.; Shahrrava, B.; Zhang, Y.; Wang, G. A Polar-Coded PAPR Reduction Scheme Based On Hybrid Index Modulation. IEEE Open J. Commun. Soc. 2024; early access. [Google Scholar] [CrossRef]
- Tal, I.; Vardy, A. How to construct polar codes. IEEE Trans. Inf. Theory. 2013, 59, 6562–6582. [Google Scholar] [CrossRef]
- Arikan, E. Polar codes: A pipelined implementation. In Proceedings of the 2010 IEEE International Symposium on Broadband Communication, Melaka, Malaysia, 11–14 July 2010. [Google Scholar]
- Yuan, B.; Parhi, K.K. Early Stopping Criteria for Energy-Efficient Low-Latency Belief-Propagation Polar Code Decoders. IEEE Trans. Signal Process. 2014, 62, 1285–1288. [Google Scholar] [CrossRef]
- Çağrı Arlı, A.; Gazi, O. Noise-Aided Belief Propagation List Decoding of Polar Codes. IEEE Commun. Lett. 2019, 23, 1285–1288. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, J.; You, X.; Xu, S. Pipelined implementations of polar encoder and feed-back part for SC polar decoder. In Proceedings of the 2015 IEEE International Symposium on Circuits and Systems, Lisbon, Portugal, 24–27 May 2015; pp. 3032–3035. [Google Scholar]
- Yang, J.; Zhang, C.; Zhou, H.; You, X. Pipelined belief propagation polar decoders. In Proceedings of the 2016 IEEE International Symposium on Circuits and Systems, Montreal, QC, Canada, 22–25 May 2016; pp. 413–416. [Google Scholar]
- Yuan, B.; Parhi, K.K. Architecture optimizations for BP polar decoders. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 2654–2658. [Google Scholar]
- Leroux, C.; Tal, I.; Vardy, A.; Gross, W.J. Hardware architectures for successive cancellation decoding of polar codes. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing, Prague, Czech Republic, 22–27 May 2011; pp. 1665–1668. [Google Scholar]
- Balatsoukas-Stimming, A.; Raymond, A.J.; Gross, W.J.; Burg, A. Hardware Architecture for List Successive Cancellation Decoding of Polar Codes. IEEE Trans. Circuits Syst. II Exp. Briefs. 2014, 61, 609–613. [Google Scholar] [CrossRef]

| Scheme | Construction (Offline) | Frozen Bits Used | Transmitter | Receiver | SI Free | ||
|---|---|---|---|---|---|---|---|
| PC-SLM [2] | 1. set construction () 2. PAPR sort () | l | Q encoders | Q modulation | Q IFFT | SC | ✓ |
| PC-SLM [3] | set construction (K) | one encoder Q − 1 Scramble | Q modulation | Q IFFT | CA-SCL | ✓ | |
| PC-SLM [4] | set construction (K) | Q matrix product | Q modulation | Q IFFT | SCL | ✓ | |
| Proposed PC-SLM | 1. set construction () 2. Hamming weight of 3. PAPR sort () | l | one encoder Q − 1 AND operator | one modulation | Q IFFT | BP-GF | ✓ |
| Tap (samples) | 1 | 3 | 10 | 15 | 27 | 43 |
| Power level (dB) | −3.92 | −4.82 | −8.82 | −11.92 | −11.72 | −27.82 |
| SNR (dB) | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | |
|---|---|---|---|---|---|---|---|
| N = 128 | Q = 4 | 100.14 | 78.97 | 59.48 | 40.54 | 26.88 | 19.05 |
| Q = 8 | 189.98 | 139.92 | 94.53 | 60.34 | 38.05 | 24.51 | |
| N = 1024 | Q = 4 | 240 | 168.62 | 68.72 | 27.03 | 20.7 | 20.1 |
| Q = 8 | 480 | 323.32 | 86.3 | 27.3 | 20.67 | 20.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, C.; Hu, N.C.; Armada, A.G. A Modified Selected Mapping Scheme for Peak-to-Average Power Ratio Reduction in Polar-Coded Orthogonal Frequency-Division Multiplexing Systems. Information 2025, 16, 384. https://doi.org/10.3390/info16050384
Xing C, Hu NC, Armada AG. A Modified Selected Mapping Scheme for Peak-to-Average Power Ratio Reduction in Polar-Coded Orthogonal Frequency-Division Multiplexing Systems. Information. 2025; 16(5):384. https://doi.org/10.3390/info16050384
Chicago/Turabian StyleXing, Chao, Nixi Chen Hu, and Ana García Armada. 2025. "A Modified Selected Mapping Scheme for Peak-to-Average Power Ratio Reduction in Polar-Coded Orthogonal Frequency-Division Multiplexing Systems" Information 16, no. 5: 384. https://doi.org/10.3390/info16050384
APA StyleXing, C., Hu, N. C., & Armada, A. G. (2025). A Modified Selected Mapping Scheme for Peak-to-Average Power Ratio Reduction in Polar-Coded Orthogonal Frequency-Division Multiplexing Systems. Information, 16(5), 384. https://doi.org/10.3390/info16050384






