GC-MT: A Novel Vessel Trajectory Sequence Prediction Method for Marine Regions

Abstract

In complex marine environments, intelligent vessels require a high level of dynamic perception to process multiple types of information for mitigating collision risks. To ensure the safety of maritime traffic and enhance the efficiency of navigation information, vessel trajectory prediction is crucial for Automatic Identification Systems (AIS). This study introduces a Graph Convolutional Mamba Network (GC-MT) utilizing AIS data for predicting vessel trajectories. To capture motion interaction characteristics, we employed a Graph Convolutional Network (GCN) to construct a spatiotemporal graph that reflects the interaction relationships among various vessels within the maritime information flow. Furthermore, high-level spatiotemporal features were extracted using a Mamba Neural Network (MNN) to incorporate time-related dynamics. Validation against real-world historical AIS data demonstrates that the proposed model achieved improvements of approximately 35% and 28% in the Average Displacement Error (ADE) and Final Displacement Error (FDE), respectively, compared to the leading baseline model. The predictive capability of the proposed method demonstrates its effectiveness in improving maritime navigation safety in a shipping environment with multiple information sources.

1. Introduction

With the accelerated pace of economic globalization, the expanding scope of international trade, and the rapid advancement of the maritime transport sector, international maritime transport is assuming an increasingly pivotal role in the swiftly evolving global trade economy [1]. In densely trafficked oceans characterized by complex conditions, managing maritime traffic safety presents significant challenges [2,3]. Vessel collisions represent one of the most prevalent types of maritime accidents, and their rising frequency poses a serious threat to human interests and inter-country trade exchanges. Currently, maritime navigation typically requires human decision making by crew members during transit, supported by electronic charts, radar systems, sonar technology, and vessel traffic services. This navigational decision making heavily relies on human judgment. However, in intricate environments, such as harbors, where multiple adjacent entities interact, safety issues can easily arise due to crew inexperience or judgment errors. Consequently, the precise prediction of vessel trajectories in congested marine areas is crucial for effective management of maritime traffic and ensuring safe vessel operations. Prediction plays a vital role in maritime traffic safety by providing early warnings for collision avoidance, optimizing port operations through efficient berth allocation and reduced waiting times, and protecting the marine environment by minimizing unnecessary fuel consumption and emissions.

Vessel trajectory prediction is initially expressed through traditional physical model modeling, using physical laws and kinematic models to predict the future position of the vessel, and comprehensively considering various possible influencing factors, such as vessel mass and force. At the same time, some classical algorithms, such as the Kalman filter and Gaussian process model, are combined to realize the basic trajectory prediction [4,5,6,7,8]. However, the above trajectory prediction methods often rely heavily on a large number of mathematical equations and assumptions, and the performance of the model is constrained by these prior assumptions.

In recent years, with the development of machine learning technology, the field has begun to focus on Automatic Recognition System (AIS) data, turning to the use of statistical rules to improve prediction accuracy [9,10,11,12,13]. Vessel trajectory prediction based on statistical methods mainly uses statistical laws of historical data and mathematical model estimation to infer the future trajectory of vessels. This approach includes but is not limited to improved Markov models, Gray models, and Random Forest algorithms.

With the further mining of neural networks, deep learning algorithms are increasingly applied in the field of vessel trajectory prediction. As a subset of machine learning, the method primarily learns vessel movement patterns from historical AIS data to predict the future trajectory of the vessel. Due to its unique architectural design, Capobianco et al. proposed an innovative encoder–decoder Recurrent Neural Network (RNN) model for vessel trajectory prediction that effectively captures spatiotemporal correlations within sequential data [14]. Zhang et al. [15] preprocessed AIS data to ensure accuracy and integrity prior to developing a Long Short-Term Memory (LSTM) network model for predicting vessel trajectories. Forti et al. [16] devised a Seq2seq neural architecture featuring an LSTM encoder–decoder framework aimed at enhancing overall predictive performance. Additionally, Suo et al. [17] extracted and optimized principal trajectories utilizing a model based on Gated Recurrent Unit (GRU) alongside the Density-Based Spatial Clustering of Applications with Noise (DBSCAN) technique. Zhang et al.’s [18] integration of Convolutional Neural Networks (CNNs) with RNNs successfully captured both temporal and spatial attributes associated with vessel paths.

Due to its unique mechanism, the attention-based Transformer network helps to focus on the key parts of the input data and better grasp the key information when processing serial data. Xue et al. [19] introduced Transformer architecture and feature clustering to optimize a gated unit network, which effectively improved the fidelity of trajectory prediction in the long run. Donandt et al. [20] mixed the Gaussian model and the attention mechanism, and the generality of the method was demonstrated by using data from three different river segments, which improved the vessel’s ability to make perceptual predictions in inland waterway navigation.

With the comprehensive analysis of extensive AIS data sourced from various maritime authorities, the graphical structural analysis of inherent information has become increasingly clear [21]. The application of Graph Convolutional Networks (GCNs) to analyze and represent fixed structures within existing datasets has emerged as a significant research direction for trajectory tasks across diverse fields, including social networks and traffic flow assessment [22]. Wu et al. [23] borrowed the advantages of GCNs to capture the influence of the social diffusion process on user preferences within social networks, leading to a proposal of an effective social recommendation model based on a Graph Convolutional Neural Network. Zhao et al. [24] proposed a neural network that combines a GCN and a GRU, and the prediction results were better than the most advanced baselines on real-world traffic datasets.

Although some progress has been made in the field of vessel trajectory prediction, the task still faces challenges, such as insufficient anti-interference capabilities and limitations on the navigation of multiple vessels due to the quality issues of AIS data and the intricate spatiotemporal correlations among vessel trajectories. To address these limitations, this paper proposes a novel method for efficiently observing and capturing the spatial–temporal characteristics of vessels. In this prediction approach, multi-source AIS trajectory data are preprocessed to obtain historical samples, which are used as inputs to the Graph Convolution Mamba Network (GC-MT) model, enabling efficient vessel trajectory prediction.

The main contributions of this study can be summarized as follows:

(1)

This paper presents the GC-MT model, an innovative approach for intelligent spatiotemporal vessel trajectory prediction that operates without the need for an attention mechanism. By integrating GCN with the Mamba model, it effectively captures the motion characteristics, temporal features, and interaction relationships among moving vessels, thereby facilitating efficient sequence modeling and accurate forecasting of future trajectories.

(2)

Extensive experiments conducted on AIS data demonstrate that the proposed prediction method significantly outperforms other baseline approaches in terms of accuracy, underscoring its potential applicability in long-term and complex maritime environments.

(3)

Given the intricacies of real-world AIS data, this study incorporates feasibility analysis into existing preprocessing techniques to enhance the overall efficiency of the vessel trajectory prediction methodology.

The remainder of this paper is organized as follows: Section 2 details the definition of the problem, data processing, and model architecture of this paper (see Materials and Methods). Section 3 presents information about the experimental data, experimental design considerations, and results analysis (see Results). Section 4 compares this work with similar studies (see Discussion). Finally, Section 5 concludes the paper and provides future prospects (see Conclusions).

2. Materials and Methods

This section introduces the proposed method in three parts. First, the definitions related to vessel trajectory prediction are introduced. Then, the specific steps of data preprocessing are described in detail. Finally, the model architecture used is introduced.

2.1. Problem Explanation

This study primarily focuses on predicting vessel trajectories utilizing extensive AIS data. This subsection formally defines the basic concepts and the trajectory prediction problem under consideration.

The vessel trajectory can be defined as a series of spatiotemporal points, as shown in Equation (1):

$$T=\left\{P_1,P_2,\dots ,P_n\right\}$$

(1)

where each coordinate comprises the geographic position $P_i\left(1\le i\le n\right)$ of the vessel, including the latitude and longitude and the corresponding timestamp $t$. These coordinates are collected and recorded by AIS in this study.

A vessel network graph is an abstract data structure employed to represent spatial relationships and interactions among vessels. In this document, each vessel is typically represented as a node. Vessel attributes, such as the unique identification number (MMSI) and other characteristics, can be associated with nodes, while their relationships are modeled as edges. Edges serve to illustrate interactions among vessels. They capture various aspects, such as spatial proximity, communication links, or potential collision risks. Figure 1 illustrates the process of constructing a vessel network and presents a vessel network graph organized along the time dimension.

The locations and spatial relationships of the vessels at the present time step are described by the vessel network graph in each layer. ${\mathrm{G}}^{ST}=\left({\mathrm{V}}^{ST},{\mathrm{E}}^{ST}\right)$ is the definition of the vessel network graph at time step $t$, where $\mathrm{V}$ is a collection of nodes that represent the vessels and E is a set of edges that reflect the interactions among these vessels. In particular, ${\mathrm{V}}^t=\left\{{\mathrm{v}}_{\mathrm{n}}^t|\mathrm{n}=\mathrm{1,2},\dots ,\mathrm{N}\right\}$ and ${\mathrm{E}}^t=\left\{{\mathrm{e}}_{i,j}^t|\mathrm{i},\mathrm{j}=\mathrm{1,2},\dots ,\mathrm{N}\right\}$, where $\mathrm{N}$ denotes the number of vessels, ${\mathrm{v}}_{\mathrm{n}}^t$ denotes motion characteristics at the n-th vessel at time $t$, and ${\mathrm{e}}_{i,j}^t$ denotes the interaction between the i-th and j-th vessels at that location.

The adjacency matrix is used to describe the connection relationship between each node in the vessel network graph. It is a two-dimensional array of size N × N, where N represents the number of nodes (vessels) in the graph. The elements in the matrix represent the existence and weight of the edge between the nodes. In this paper, if the distance between node $i$ and node $j$ at time step $t$ is less than 6 nautical miles, it is considered that an interaction exists between the two vessels. In this case, this means that there is a connection between nodes $i$ and $j$, and the matrix element ${\mathrm{A}}_{\left[i\right]\left[j\right]}$ represents the weight of the edge between the two. If there is no connection between node $i$ and node $j$, ${\mathrm{A}}_{\left[i\right]\left[j\right]}$ = 0. The schematic diagram of the adjacency matrix is shown in Figure 2.

The interaction relationships among vessels in the water area are different. The weights of these interactions are proportional to the distance between the defined vessel nodes. Generally, vessels that are closer have more interactions than vessels that are farther away. The number of connections of a certain node to each node is also different, which has a specific generalization effect. Therefore, different weights should be assigned to the marginal ESTs in the vessel network graph to accurately reflect the interaction intensity between vessels. In order to quantify the weight representing the interaction between two vessels, the inverse of the distance between them is used, where vessels that are closer have larger weight values. Therefore, the adjacency matrix $\mathrm{A}$ mentioned above is converted into a weighted adjacency matrix, as shown in Equation (2):

$$A_{i,j}^t=\left\{\begin{array}{c} \begin{array}{c}{\displaystyle \frac{1}{d_{i,j}^t}}, if d_{i,j}^t\le 6nmiles\\ 0, otherwise\end{array}\end{array}\right.$$

(2)

where $d_{i,j}^t$ represents the distance between vessel points $i$ and $j$ at time step $t$, which is calculated by $d_{i,j}^t=\sqrt{{\left(x_i^t-x_j^t\right)}^2+{\left(y_i^t-y_j^t\right)}^2}$. Additionally, $x_i^t$ and $y_i^t$ refer to the longitude and latitude of vessel $i$ at time step $t$, respectively.

In addition, the node information of the vessel itself should also be considered. The unit matrix $I$ is introduced to represent the self-connection, thereby defining a new adjacency matrix, as shown in Equation (3):

$$\widehat{A^t}=A^t+I$$

(3)

To facilitate model learning and not change the above-mentioned adjacency and self-weight distribution, the adjacency matrix was normalized. This paper adopted the symmetric normalization method, that is, the adjacency matrix was scaled by the inverse square root of the node degree matrix. The normalized adjacency matrix was recorded as $\stackrel{\_\_\_}{A^t}$, as shown in Equation (4):

$$\stackrel{\_\_\_}{A^t}={\left(D^t\right)}^{-{\displaystyle \frac{1}{2}}}\widehat{A^t}{\left(D^t\right)}^{-{\displaystyle \frac{1}{2}}}$$

(4)

where $D^t$ is a diagonal matrix whose diagonal elements correspond to the number of additional nodes connected to each node in the adjacency matrix $\widehat{A^t}$, and all other diagonal elements are set to 0.

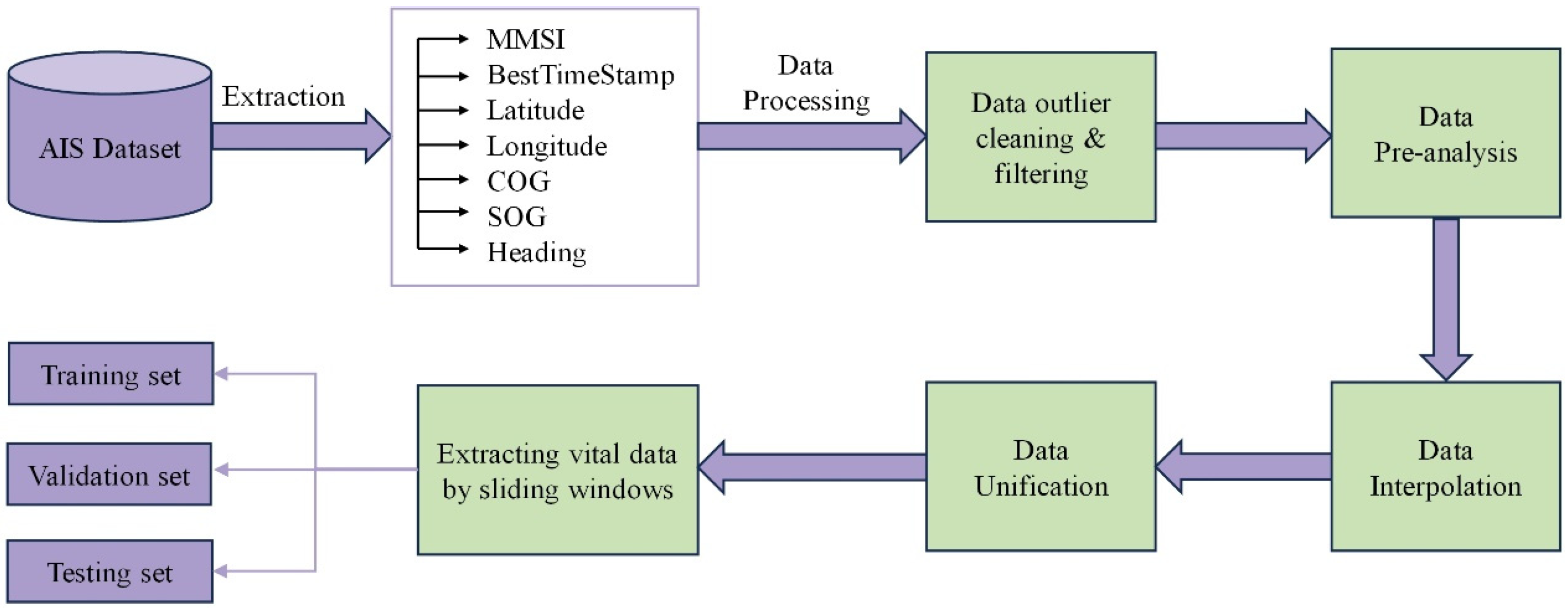
2.2. Data Preprocessing

Dynamic information is updated in real time within AIS data through sensors integrated into AIS devices. The process of obtaining vessel AIS data involves several steps, including creation, packaging, reception, and decoding. However, communication issues or environmental factors may lead to signal loss or sensor failure, resulting in challenges, such as data duplication, inaccuracies, and omissions. Therefore, it is imperative to conduct the necessary preprocessing before utilizing AIS system data for analysis to mitigate the adverse effects of anomalous data on model training. A typical data preparation pipeline encompasses essential steps: data cleaning and filtering, interpolation, standardization, and sampling via sliding windows. This paper introduces an additional step: data pre-analysis, which includes multi-feature correlation and trajectory stationarity analysis to ensure the standardization and rationality of the filtering process. The comprehensive procedure for preparing AIS data is illustrated in Figure 3. Each step is described in detail below using the Danish waters dataset as a case study.

2.2.1. Data Cleaning and Filtering

This step primarily involves removing entries that do not conform to established standards and regulations, including the following records:

(1) MMSI values that are not nine digits long: MMSI is a unique code used to identify AIS equipment. This code consists of nine digits. Therefore, the invalid part that does not meet the regulations is eliminated. (2) Data indicating a length of less than 3 m or a width of less than 2 m: Considering that the tracks of small ships are more susceptible to environmental factors, such as ocean currents, wind, and waves, these data may increase the risk of overfitting the model, so it is necessary to delete the information of these smaller ships. This study mainly considers ships with a length of 5 to 350 m and a width of 3 to 60 m. (3) Inconsistent vessel size entries, records exceeding valid ranges, and vessels lacking required information. (4) Remove outliers: Remove data that exceed the normal range, including longitude, latitude, ground speed, and ground heading. The latitude range for vessel trajectory positions is [53.56° N, 59.55° N], while the longitude range spans [0.65° W, 18.34° E]. Additionally, the speed over ground (SOG) range is defined as [0 kt, 51.2 kt], and the course over ground (COG) is constrained within [0°, 360°]. (5) Eliminate data records where the ground speed is zero at five consecutive time points: If the ground speed is zero at five consecutive time points, the ship is considered to be at anchor, and these data may interfere with subsequent track analysis if they are not removed.

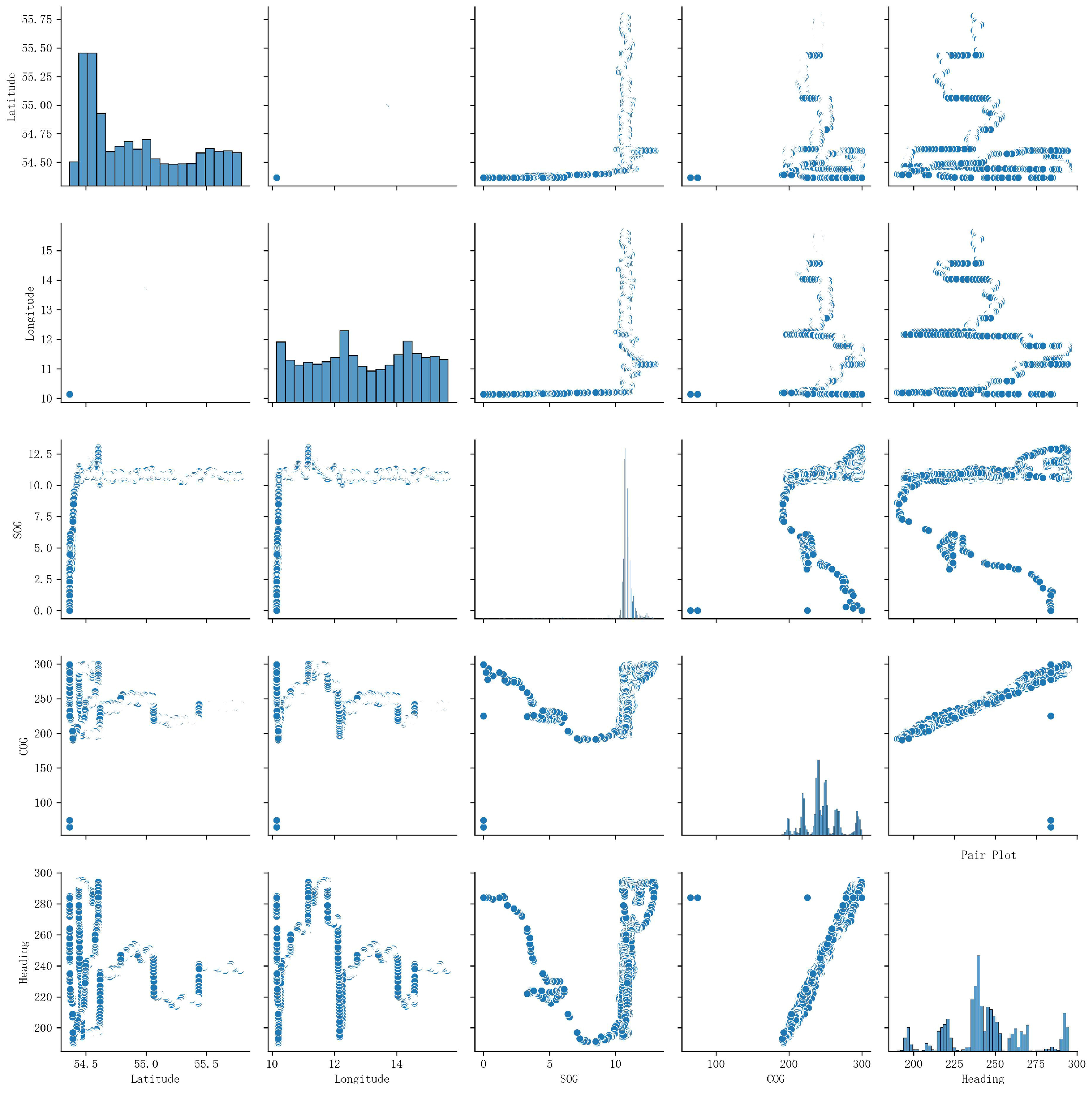
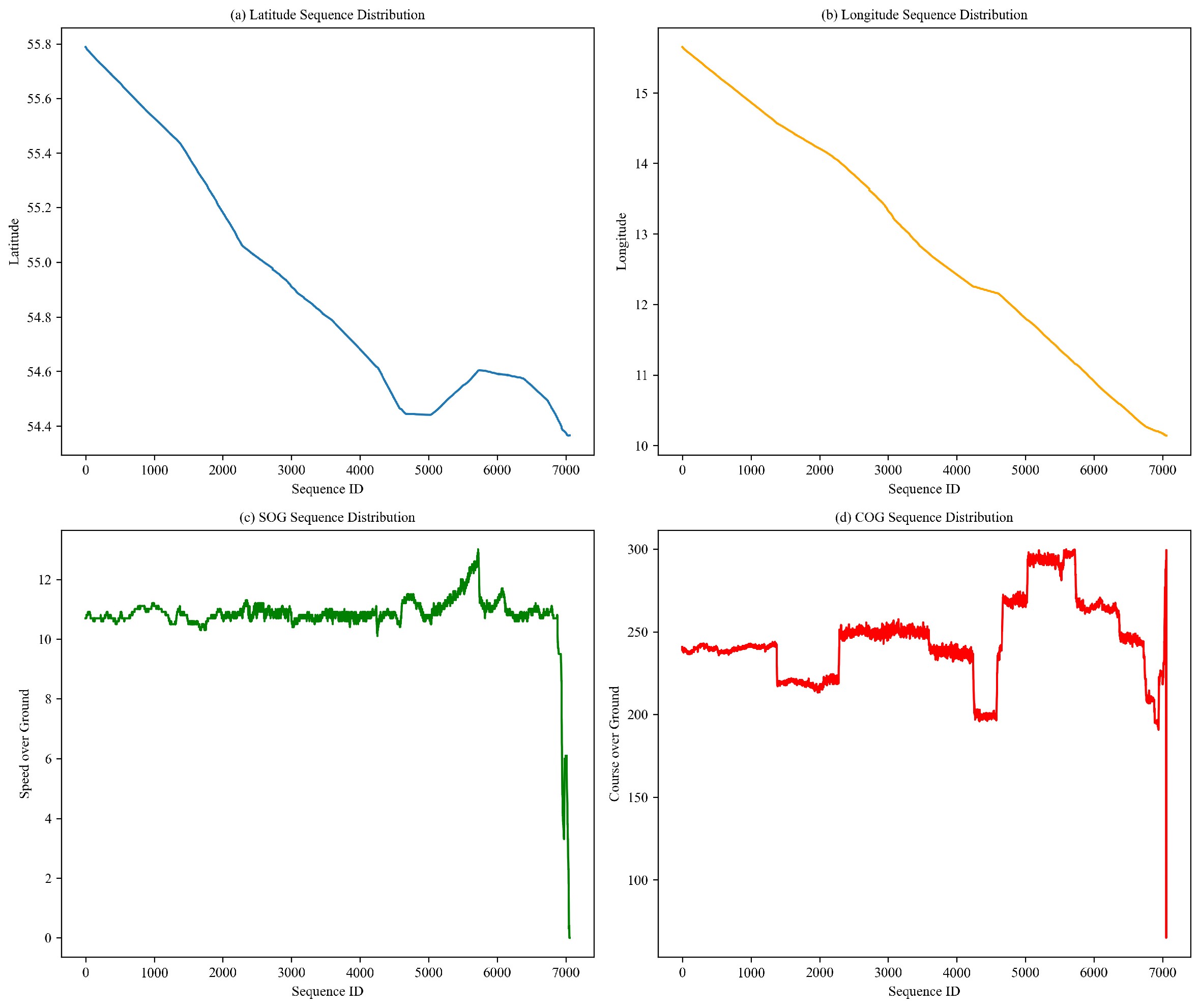
2.2.2. Data Pre-Analysis

All AIS data are segmented into multiple groups based on MMSI numbers, with track points arranged in ascending order according to BaseDateTime to derive a navigation track dataset corresponding to each vessel, represented by its specific MMSI, during a designated time period. When the time difference between two adjacent track points exceeds thirty minutes for trajectory series of the same vessel, they are classified as endpoints marking different tracks, thus segmenting an individual path into multiple sub-tracks. Each sub-trajectory is analyzed to generate a relationship matrix diagram that illustrates the connections among features, along with heat maps depicting the correlation coefficients across various eigenvalues for feature matrix correlation analysis purposes. Given that vessel trajectories represent typical multivariate time-series datasets, it becomes imperative to assess their stationarity prior to employing appropriate trajectory prediction methodologies during quantification processes using time-series analysis tools. Figure 4 and Figure 5 illustrate feature correlations, alongside the results of stationarity tests conducted on vessel trajectory predictions.

The vessel trajectory sequence is a typical multivariate time series. When using time-series analysis tools in the quantitative process, it is often necessary to first examine the stationarity of the trajectory sequence in order to select an appropriate trajectory prediction method. This code intuitively shows the sequence distribution of the characteristics of the vessel trajectory. Figure 6 shows the results of trajectory sequence stationarity.

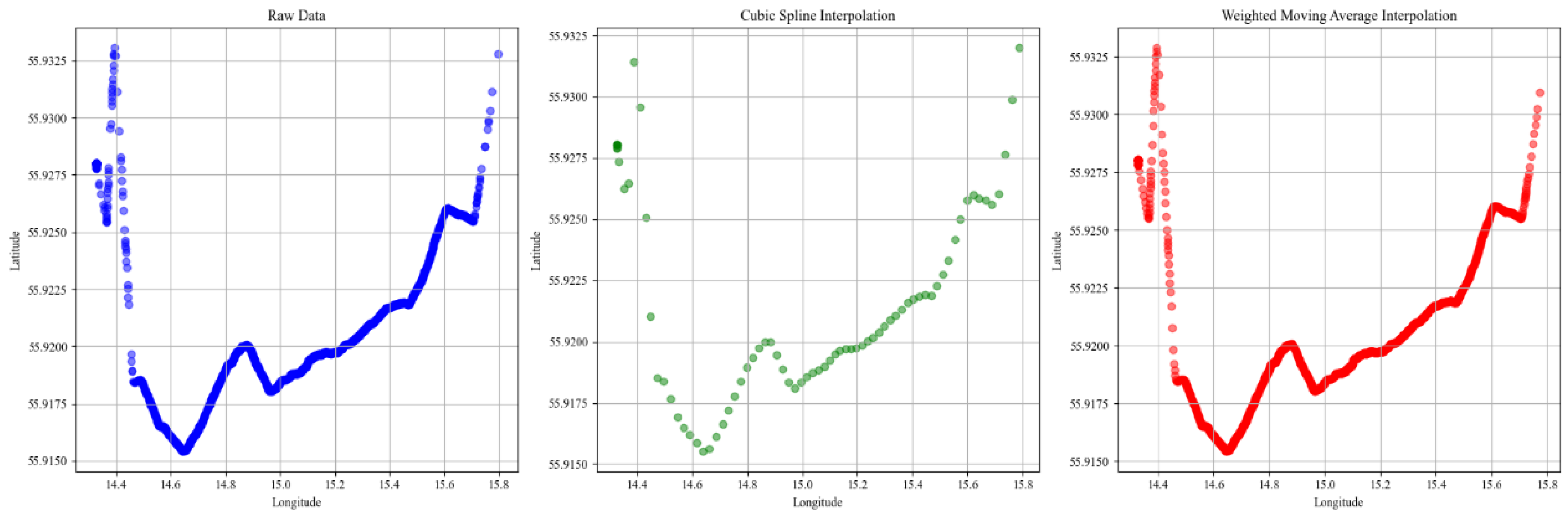
2.2.3. Data Interpolation

In the trajectory sequence, the time interval between any two adjacent positions may not be fixed. In order to effectively synchronize AIS data, when the interval between adjacent trajectory points of the same ship exceeds 1 min, interpolation is required to ensure that the interpolation timestamps are 1 min apart. In order to make the interpolated trajectory smoother and in line with ship navigation habits, for the missing LAT and LON values, the cubic spline interpolation function is used as a method, as shown in Equation (5):

$$S_i\left(t\right)=a_i+b_i\left(t-t_i\right)+c_i{\left(t-t_i\right)}^2+d_i{\left(t-t_i\right)}^3$$

(5)

where, in the interval [$t_i$, $t_{i+1}$], $t$, $t_i,$ and $t_{i+1}$ represent the timestamps of the moments $t$, the $i$-th moment, and the $i+1$-th moment to be interpolated in the trajectory sequence, respectively. The coefficients $a_i$, $b_i$, $c_i,$ and $d_i$ are determined according to the boundary conditions and smoothness requirements.

2.2.4. Data Standardization

After completing the outlier filtering and missing value completion of AIS data, data standardization steps need to be implemented to ensure the consistent data formats. The purpose of data standardization is to eliminate the influence of different dimensions on AIS data so as to reduce errors in model predictions. Each attribute in the vessel trajectory dataset is standardized using Equation (6) to aid in the convergence of model training:

$$\stackrel{\sim }{x}={\displaystyle \frac{x-\stackrel{\_\_}{x}\left(x_{data}\right)}{s\left(x_{data}\right)}}$$

(6)

where $x$ denotes the attribute value of a vessel, $\stackrel{\_\_}{x}(\cdot )$ denotes the dataset’s mean, $s(\cdot )$ denotes the dataset’s standard deviation, and $\stackrel{\sim }{x}$ is the standardized value of the corresponding vessel attribute. Figure 7 shows the comparison results of the original trajectory data and the interpolation results using two different interpolation methods.

2.2.5. Sampling Data by Sliding Windows

The capacity of the model to comprehend and forecast the dynamic changes in vessel trajectories is strongly correlated with the continuity and temporality of the data. In order to maintain the temporal consistency and continuity of the data, this work used sliding window sampling technology to efficiently retrieve data samples from the corrected trajectory sequence. To be more precise, each sliding window’s data length was (m + n), which was first determined by taking the input sequence length (m) and the anticipated output sequence length (n). At the beginning of the sequence, the sliding window advanced one time unit at a time along the time axis until the complete sequence was covered.

To make sure the model could pick up the properties of the trajectory at various times, the data in each window were utilized as separate samples for training. Finally, following preprocessing, a trajectory dataset of 852 vessels in Danish seas was created, containing 3,200,000 AIS data points over 30 days. Three subsets of these data were randomly selected, with 20% serving as validation sets, 60% serving as test sets, and the remaining 20% as model training sets.

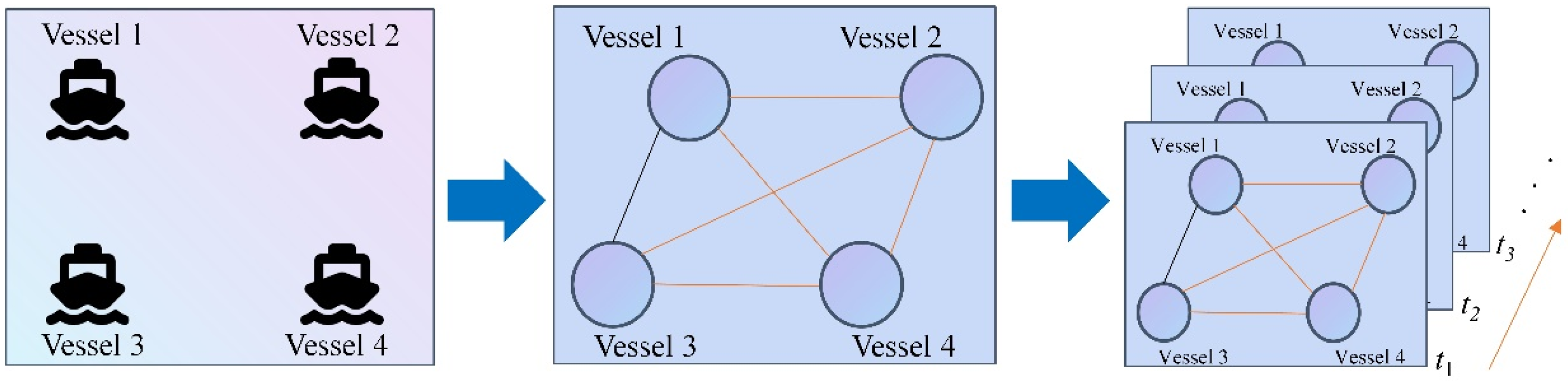
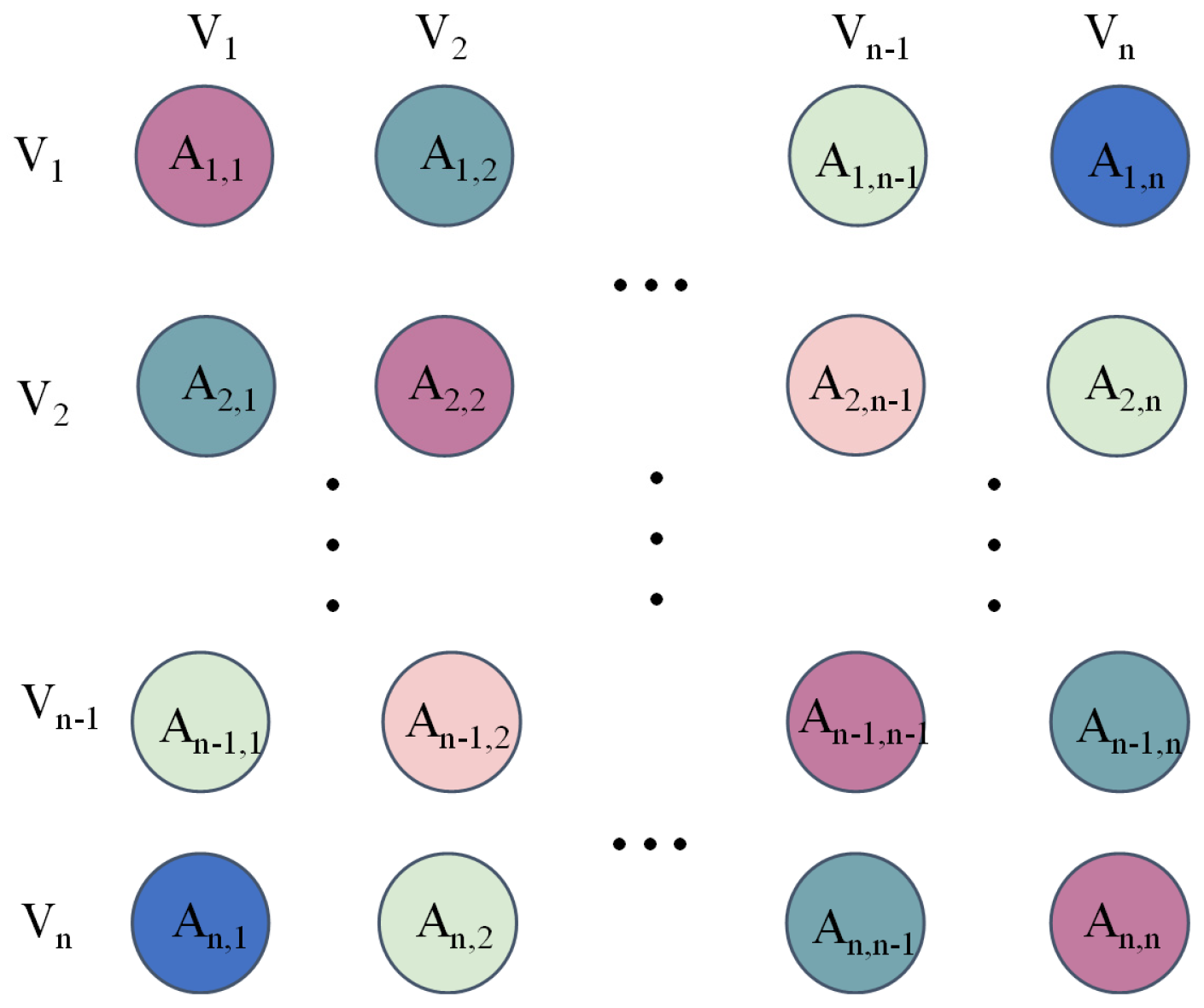
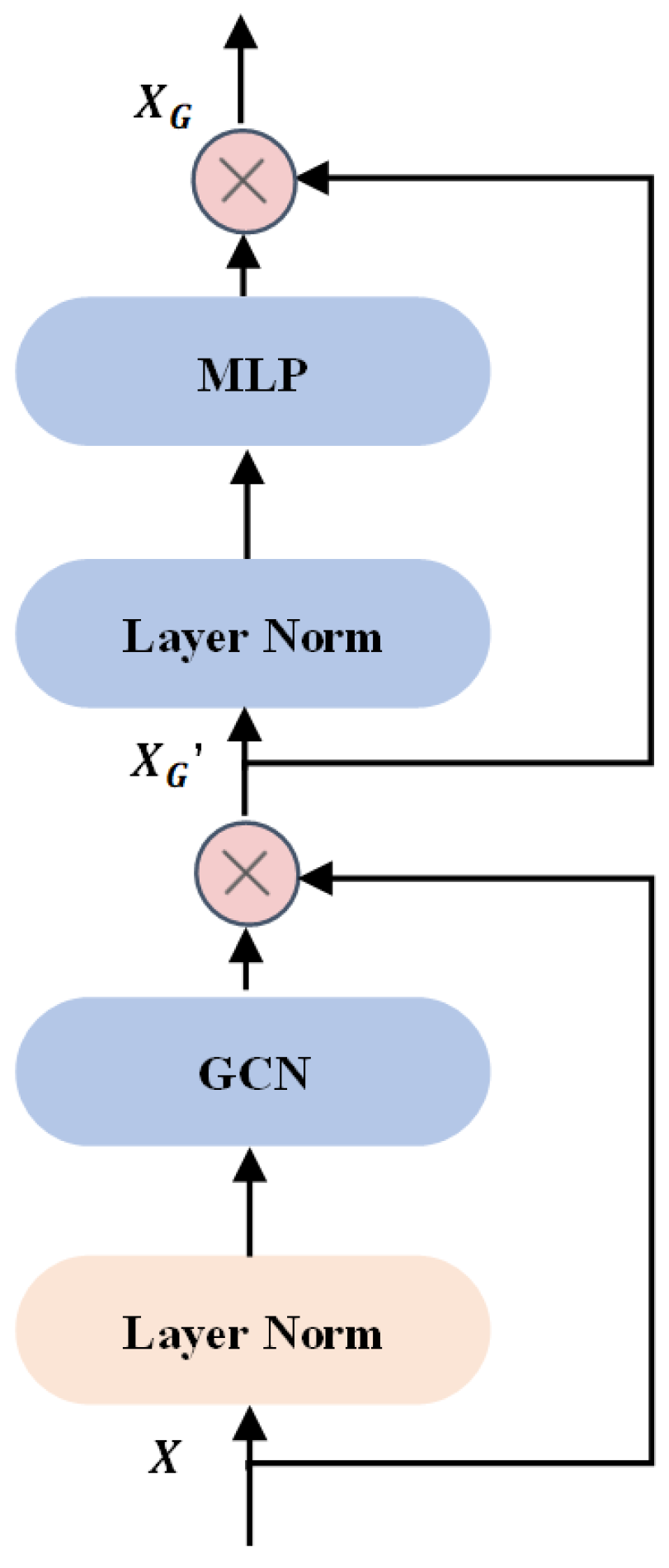
2.3. GCN Module

This paper proposes a new vessel trajectory prediction model that combines a GCN with a Selective State Space Model (SSSM) to address the problem of spatial interactions of vessels in AIS trajectory data over time [25]. In this work, Mamba was used to capture global dependencies with its high-quality and efficient long-range modeling capabilities [26]. At the same time, the GCN stream enhanced the functionality of Mamba by effectively capturing local dependencies between joints. This architecture ensured comprehensive and accurate vessel trajectory prediction. On this basis, we explored the GCN approach by designing an adjacency matrix. In this study, the GCN module used is defined as Equation (7):

$$\mathrm{G}\mathrm{C}\mathrm{N}\left(x\right)=\sigma \left(x+\mathrm{N}\mathrm{o}\mathrm{r}\mathrm{m}\left({\tilde{D}}^{-{\displaystyle \frac{1}{2}}}\tilde{A}{\tilde{D}}^{-{\displaystyle \frac{1}{2}}}x{W}_1+x{W}_2\right)\right)$$

(7)

where $\tilde{A}=A+I$ represents the addition of the self-connected adjacency matrix. $W_1$ and $W_2$ are trainable and learnable weight matrices. $\mathrm{N}\mathrm{o}\mathrm{r}\mathrm{m}(\cdot )$ and $\sigma (\cdot )$ represent batch normalization and activation function ReLU, respectively [27]. The key to GCNs is to construct the adjacency matrix $\tilde{A}$, which is represented by Equation (3) in this paper.

The GCN stream focuses on local spatial relationships to incorporate the interaction and motion effects of specific vessel nodes. The spatial GCN module structure used in this study is shown in Figure 8. Given $X\in {\mathrm{R}}^{B\times L}$, the output $X_G$ is obtained by the following Equation (8):

$$\begin{array}{c}{X}_G^{\prime }=X+\mathrm{GCN}\left(\mathrm{Norm}\right(X\left)\right)\\ X_G=X_G^{\prime }+\mathrm{MLP}\left(\mathrm{Norm}\right(X_G^{\prime }\left)\right)\end{array}$$

(8)

where $\mathrm{G}\mathrm{C}\mathrm{N}(\cdot )$ is taken as input by Equation (1).

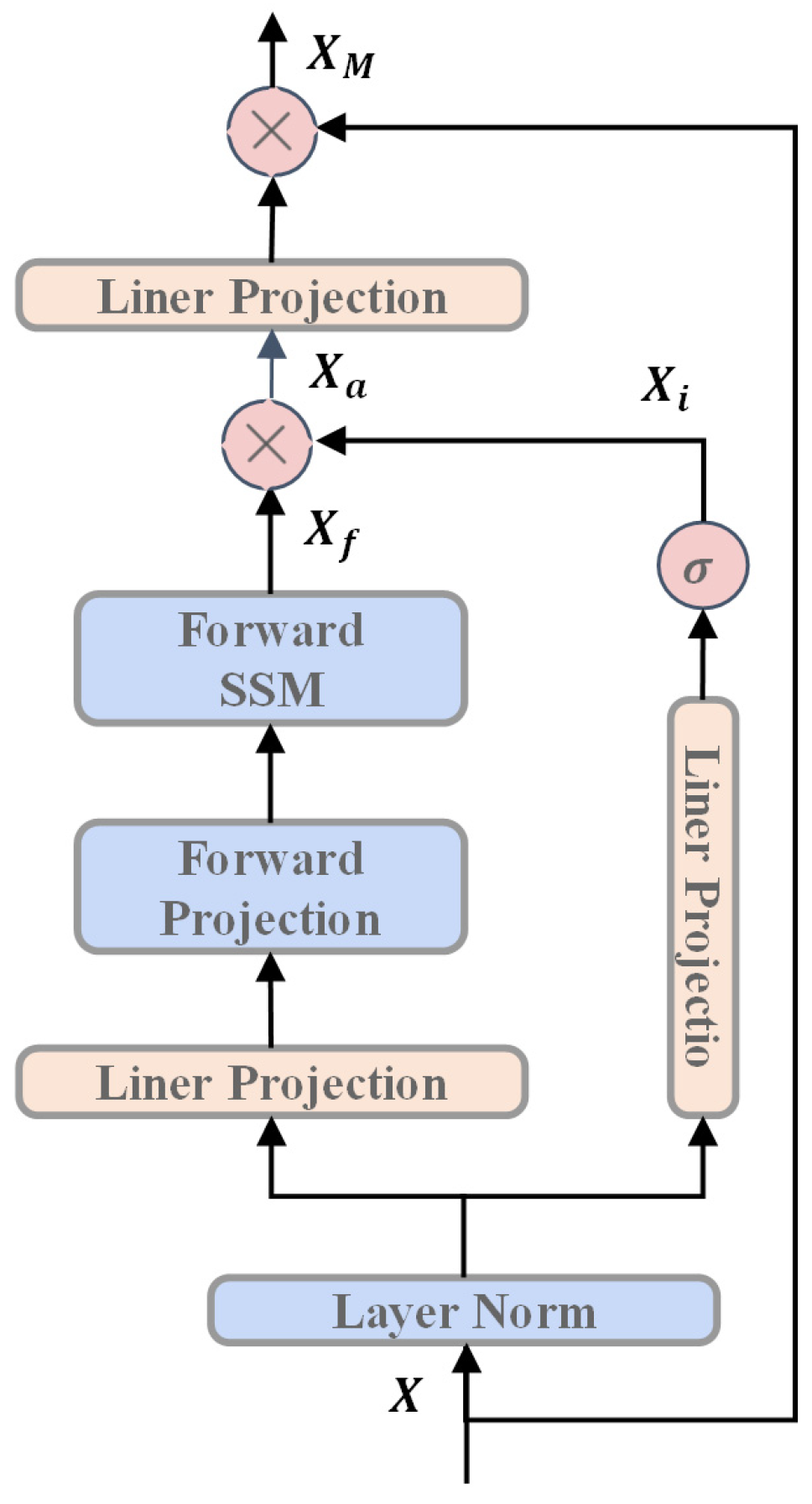
2.4. Mamba Module

Deep learning-based SSMs are a recently developed class of sequence models that are closely related to RNN architectures and classical state space models. These models are characterized by specific equations for continuous systems, which maps multidimensional input sequences to corresponding output sequences through implicit latent state representations.

SSMs define a continuous system that maps a 1D sequence $x\left(t\right)\in \mathrm{R}$ to $y\left(t\right)\in \mathrm{R}$ through implicit latent states $h\left(t\right)\in {\mathrm{R}}^N$. This process is described by ordinary differential equations in Equation (9), as follows:

$$\begin{array}{c}{h}^{\prime }\left(t\right)=\mathit{A}h\left(t\right)+\mathit{B}x\left(t\right),\\ y\left(t\right)=\mathit{C}h\left(t\right),\end{array}$$

(9)

where $\mathit{A}$, $\mathit{B},$ and $\mathit{C}$ are learned matrices. Instead of directly initializing $\mathit{A}$ randomly, a popular strategy is to impose a diagonal structure on $\mathit{A}$.

To enhance computational efficiency, it is necessary to discretize continuous variables $\mathit{A}$ and $\mathit{B}$. The choice of discretization criteria is varied, with zero-order hold [28] being a common approach, as shown in Equation (10):

$$\overline{A}=\exp \left(\Delta A\right) \overline{B}={\left(\Delta A\right)}^{-1}\left(\exp \left(\Delta A\right)-I\right)\cdot \Delta B$$

(10)

where $\Delta$ represents the step size, and $I$ is the identity matrix.

Therefore, the discrete version of Equation (9) can be written as Equation (11):

$$\begin{array}{c}{h}_t=\overline{A}{h}_{t-1}+\overline{B}{x}_t\hfill \\ y_t=C{h}_t\hfill \end{array}$$

(11)

This Linear Time-Invariant (LTI) discrete system allows for efficient computation in recursive or convolution forms, scaling linearly or near-linearly with sequence lengths.

The above framework facilitates efficient sequential modeling by enabling both linear and nonlinear computations. As a variant of traditional SSMs, SSSMs emphasize the construction of a selection mechanism atop standard SSM frameworks. This approach bears significant resemblance to the core principles underlying attention mechanisms, positioning it as a viable competitor to Transformer architectures. The selective state space model Mamba highlights that LTI constraints limit its capacity for effective data modeling due to the static nature of matrices in conventional SSMs—these matrices remain unchanged irrespective of input variations, thereby lacking content-based reasoning capabilities. Therefore, Mamba removes the LTI constraint and introduces time-varying parameters, as shown in Equations (12) and (13), respectively:

$$B={\mathrm{L}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{a}\mathrm{r}}_N\left(x\right),C={\mathrm{L}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{a}\mathrm{r}}_N\left(x\right)$$

(12)

$$\Delta =\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{p}\mathrm{l}\mathrm{u}\mathrm{s}\left(\mathrm{P}\mathrm{a}\mathrm{r}\mathrm{a}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{r}+{\mathrm{B}\mathrm{r}\mathrm{o}\mathrm{a}\mathrm{d}\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{t}}_D\left({\mathrm{L}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{a}\mathrm{r}}_1\left(x\right)\right)\right)$$

(13)

where ${\mathrm{L}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{a}\mathrm{r}}_N$ is a parameterized projection layer projected to d dimensions, and $\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{p}\mathrm{l}\mathrm{u}\mathrm{s}$ is an activation function. However, the lack of LTI will lead to a loss of equivalence with convolution, affecting training efficiency. To solve this problem, Mamba introduces hardware-aware algorithms that support parallelization. As a result, Mamba is able to achieve high-quality and efficient dynamic modeling.

To bidirectionally capture spatiotemporal information, this study adopts the structure of SSSM, as shown in Figure 9. The flow has two parallel processing paths: forward and independent. Formally, the input is $X\in {\mathrm{R}}^{B\times L\times d}$, where $B$ is the batch size, $L$ is the sequence length, and d is the dimension.

First, the information is processed forward along the sequence dimension, defined as Equation (14):

$$X_f={\mathrm{S}\mathrm{S}\mathrm{M}}_f\left(\sigma \left({\mathrm{N}\mathrm{o}\mathrm{r}\mathrm{m}}_l\left(X\right)W_{p1}{W}_f\right)\right)$$

(14)

The final path processes information independently, defined as Equation (15):

$$X_i=\sigma \left({\mathrm{N}\mathrm{o}\mathrm{r}\mathrm{m}}_l\left(X\right)W_{p2}\right)$$

(15)

where ${\mathrm{N}\mathrm{o}\mathrm{r}\mathrm{m}}_l(·)$ represents layer normalization, $\sigma (·)$ is the GELU activation function, and $\mathrm{f}\mathrm{l}\mathrm{i}\mathrm{p}(\cdot )$ indicates flipping along the sequence dimension. $W_{p1},{\widehat{ W}}_{p2},{ W}_f\in \widehat{{\mathrm{R}}^{d\times d}}$ are learnable matrices.

Next, information from the forward, backward, and independent paths is aggregated via multiplicative gating, defined as Equation (16):

$$X_a=X_f\odot X_i+X_b\odot X_i$$

(16)

where ⊙ denotes a Hadamard product.

Finally, a skip connection is added to compute the output, defined as Equation (17):

$$X_M=X+X_a{W}_{p3}$$

(17)

where $W_{p3}\in {\mathrm{R}}^{d\times d}$ is a learnable matrix.

Feature Fusion:

This study used the following method to aggregate the features extracted from the Mamba and GCN modules, as shown in Equations (18) and (19), respectively:

$$X\left(i\right)={\alpha }_M\left(i\right)\odot X_M\left(i-1\right)+{\alpha }_G\left(i\right)\odot X_G\left(i-1\right){\alpha }_M\left(i\right)$$

(18)

$${\alpha }_G\left(i\right)=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left(W\left[X_M\left(i-1\right),X_G\left(i-1\right)\right]\right)$$

(19)

where $X\left(i\right)$ represents the feature embedding extracted at node $i$,${ X}_M\left(i-1\right)$, and $X_G\left(i-1\right)$ represents the features extracted from the Mamba and GCN streams at node $i$ and node $i-1,$ respectively. $W$ is the learnable matrix.

2.5. End-to-End Learning

In the network architecture, after a certain amount of processing of the original data, multi-dimensional feature data are input and can be used directly. From the input end (input data) to the output end, a prediction result will be obtained, and an error will be obtained when compared with the actual result. This error will be transmitted (back propagation) in each layer of the model, and the representation of each layer will be adjusted according to this error until the model converges or achieves the expected effect. In this process, from the input of the original data to the output of the task result, the entire training and prediction process is completed in the model.

2.6. Overall Architecture

This paper proposes a novel method for predicting vessel trajectories, which is outlined as follows: First, essential preprocessing steps, such as the removal of anomalous data, trajectory segmentation, and interpolation, are applied to the original AIS data to ensure robust quality control. A network diagram representing spatial relationships among vessels is constructed based on their positional data over time; this time-series information serves as input features for the initial layer. Next, a GCN is employed to aggregate neighborhood information at each node to update its feature representation. In this context, nodes within the space–time graph represent positional information at distinct temporal points, while edges denote their spatial relationships. Simultaneously, a SSSM facilitates efficient sequence modeling by extracting motion feature sequences from historical trajectories of individual vessels and capturing temporal correlations within these datasets. This process yields both spatial interaction features and time-series attributes related to vessel movements, which are subsequently integrated into a comprehensive feature representation. Finally, this consolidated feature set is fed into an output layer designed to predict future positions of vessels over specified intervals. Figure 10 shows the specific process of vessel trajectory prediction.

3. Results

3.1. Dataset

To evaluate the effectiveness of the GC-MT model in predicting vessel trajectories within the target maritime area, this study constructed two datasets, referred to as Dataset-1 and Dataset-2, for training and analysis purposes. Dataset-1 comprises AIS records from Danish waters collected by the Danish Maritime Administration in November 2022; it encompasses selected latitude and longitude ranges of (53° to 59°) and (0° to 19°), containing available AIS records for 4438 vessels along the Danish coasts. Dataset-2 consists of AIS data obtained from the National Oceanic and Atmospheric Administration (NOAA) in March 2022, covering latitude and longitude ranges of (21° to 31°) and (−95° to −83°), which pertain to the Gulf of Mexico region. It includes available AIS records for 5556 vessels. Each AIS sample includes information related to several fields: MMSI (the unique vessel ID), BaseDateTime (timestamp), LAT (latitude), LON (longitude), SOG (speed over ground), COG (course over ground), heading angle, vessel name, IMO number, call sign, vessel type, navigational status, length, width, draft, and cargo. Although authoritative vessel identification services have rectified some inaccuracies within these datasets, many fields remain incomplete or outdated. For this experiment, we extracted values pertaining to the MMSI, BaseDateTime, LAT, LON, SOG, and heading. These data were utilized to derive historical trajectory information for vessels operating within the specified maritime regions, as illustrated in Figure 11.

Table 1. Specific parameters of the two datasets.

Water	Time Period	Vessel Quantity	SOG (NM/h)	Boundary
				Longitude (°)	Latitude (°)
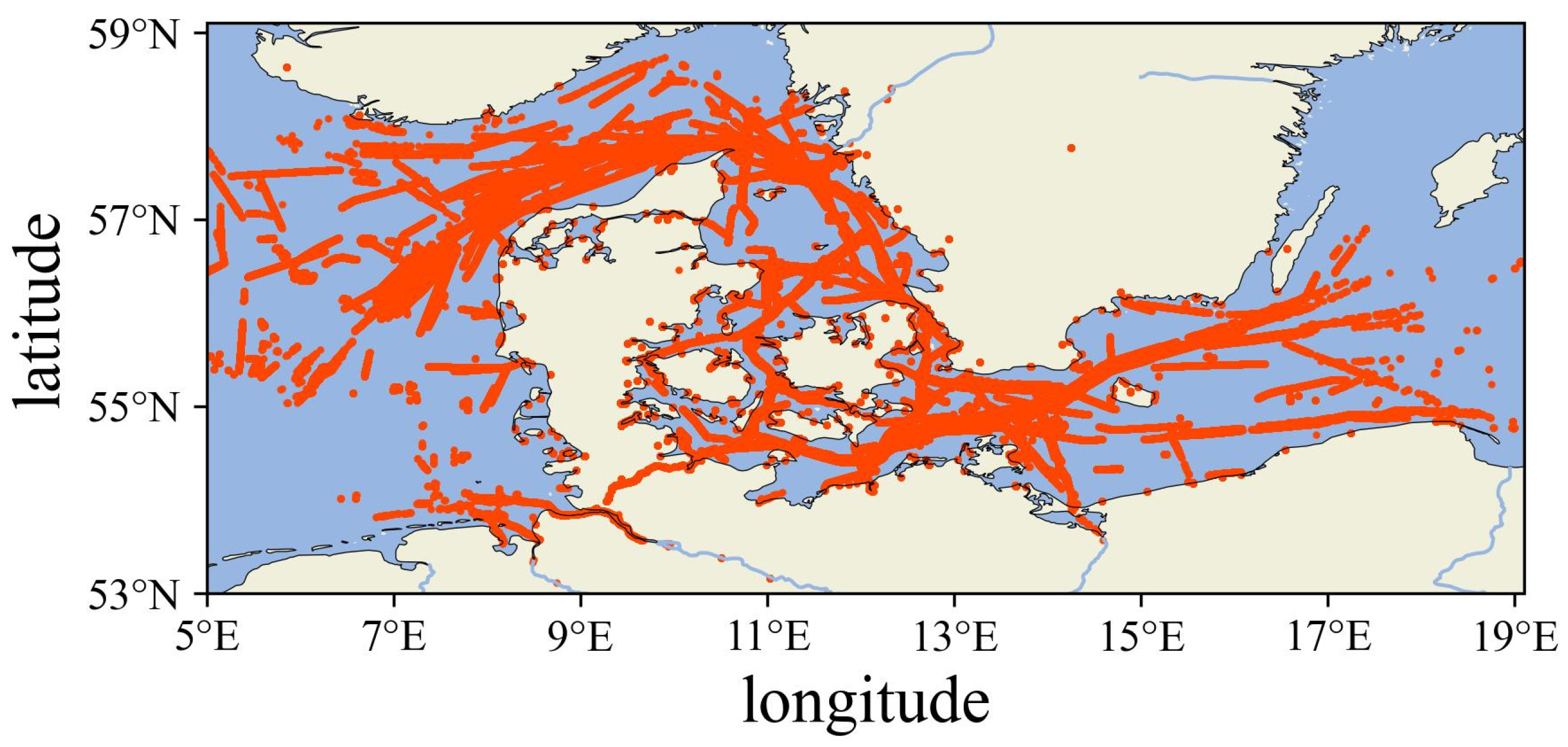
Danish	November 2022	4438	[1.0 kt, 51.2 kt]	[0.5°W, 21° E]	[53.56° N, 59.55° N]
Mexico	March 2022	5556	[1.0 kt, 22.0 kt]	[21°W, 31° W]	[−95° S, 83° S]

shows the specific details of the dataset used in this study.

3.2. Evaluation Metrics

In this study, the Average Displacement Error (ADE) and Final Displacement Error (FDE) were utilized as evaluation metrics to quantitatively assess the prediction results [29,30]. The ADE is defined as the average Euclidean distance between the predicted trajectory and the actual trajectory at each time step, while the FDE represents the average Euclidean distance between the predicted trajectory and the true trajectory at the final time point of the prediction period. These two indicators are calculated as shown in Equation (19) and Equation (20), respectively:

$$ADE={\displaystyle \frac{\sum _{n=1}^N \sum _{t=T_o+1}^{T_P} {∥{\widehat{p}}_t^n-p_t^n∥}_2}{N\times \left(T_p-\left(T_o+1\right)\right)}}$$

(20)

$$FDE={\displaystyle \frac{\sum _{n=1}^N {∥{\widehat{p}}_{T_p}^n-p_{T_p}^n∥}_2}{N}}$$

(21)

where N represents the number of vessels, and Δt denotes the total time interval for the corresponding period. To compare the distribution with the target value, we randomly selected 20 samples from the expected distribution. Subsequently, we utilized the sample that was closest to the true value to compute both the ADE and FDE.

3.3. Comparison Baselines

To evaluate the effectiveness of the proposed model, this study employed various commonly used deep learning models, such as LSTM and Seq2Seq architectures, as baseline comparison algorithms. We analyzed their performance differences in vessel trajectory prediction through various indicator results across different maritime environments. The competing trajectory prediction methods are described as follows: (1) LSTM: A type of recurrent neural network architecture designed to effectively capture long-term dependencies in sequential data by utilizing memory cells and specialized gating mechanisms, enabling it to retain and retrieve information over extended sequences [31]. (2) Seq2Seq: An encoder–decoder framework commonly used for tasks such as machine translation and text generation; here, an input sequence was encoded into a fixed-length vector representation by an encoder before being decoded by a separate decoder to generate an output sequence, enabling the handling of variable-length input and output sequences [16]. (3) GRU: As a variant of the LSTM model, the GRU simplifies the architecture by replacing both the forget gate and input gate found in LSTMs with a single reset gate. The update operation for this unit’s state is governed by an update gate, resulting in a more streamlined overall structure. These mechanisms enable GRUs to selectively update and reset their hidden states, effectively capturing long-term dependencies while mitigating the vanishing gradient problem [32]. (4) Social-STGCNN: A deep learning model specifically designed for modeling and predicting trajectories by integrating spatial and temporal information using graph convolutional neural networks [33].

3.4. Environment and Hyperparameters

In this section, we detail the parameters of the GC-MT model proposed in this study. Through the training regimen, a total of 96,280 trainable parameters were established. The results indicate that the loss value per epoch progressively decreased with each iteration, ultimately leading to convergence. All experiments were conducted under uniform hardware conditions utilizing a laptop equipped with an Intel Core i7-14700KF CPU @ 1.60 GHz and an NVIDIA GeForce RTX 4080 GPU. The software environment was consistent as well, featuring the WSL2 Ubuntu 22.04 operating system alongside the deep learning framework PyTorch 1.11.6.

For this experiment, both datasets were partitioned into training, validation, and testing subsets at a ratio of 6:2:2 using the holdout cross-validation method. The model employed features from 20 consecutive frames of vessel trajectory sequences as inputs to predict the subsequent trajectory sequence for the next ten frames; longitude, latitude, speed over ground, and course over ground were included among these dimensional input characteristics.

The AdamW optimizer was utilized for training across fifty epochs with a weight decay set at 0.01 [34]. The initial learning rate was established at 0.0001 while maintaining a batch size of 64. Additionally, the learning rate was adaptively decreased after each training epoch as part of an overall strategy to minimize loss function during eighty epochs of model training. The AdamW optimizer was implemented using PyTorch version 1.11.6.

3.5. Results and Analysis

Table 2. Performance metrics for different models on Danish and Mexico datasets.

Baseline	Danish		Mexico
	ADE	FDE	ADE	FDE
LSTM	0.6412	0.9800	0.7365	0.9384
GRU	0.6236	0.9681	0.6470	0.9622
Seq2seq	0.5226	0.7661	0.5286	0.8374
STGCNN	0.3512	0.4877	0.3552	0.5331
GC-MT	0.2281	0.3316	0.2557	0.3998
Impro (%)	35%	32%	28%	25%

presents the performance comparison results between the model and comparative models regarding the ADE and FDE metrics across different datasets (measured in nautical miles). Herein, bold black font indicates optimal results, while “Impro” signifies the percentage performance improvement of the model compared with that of optimal comparative models.

As demonstrated in Table 2, there was no statistically significant difference in predictive performance between LSTM and GRU; however, GRU exhibited a marginally superior predictive capability compared to LSTM. In contrast, the Seq2seq model successfully predicted vessel trajectories within 5 min for the Danish data, achieving ADE and FDE values of 0.5226 and 0.7661 nautical miles, respectively—significantly surpassing both the LSTM and GRU models. By integrating a decoder component to interpret the vessel sequence information captured by the encoder, Seq2seq established deeper internal relationships among the vessel trajectories and forecasted future trajectory distributions based on intermediate state vectors. Nevertheless, this approach does not account for spatial social interactions among vessels in complex scenarios. The social interactions of neighboring vessels significantly influence the future navigation intentions of the target vessel.

In this context, when compared to other baseline models, the proposed model demonstrated superior predictive performance based on the ADE and FDE metrics across various datasets while effectively capturing inter-vessel information interactions. Specifically, the results for the Danish dataset indicate an ADE value of 0.2281 nautical miles and an FDE value of 0.3316 nautical miles. Similarly, for the Mexico dataset, these values are reported as 0.2557 (ADE) and 0.3998 (FDE) nautical miles, respectively. These values indicate notably greater improvements in the Danish predictions, where the ADE improved by approximately 35% and the FDE by around 32% compared to the optimal baseline model outcomes. Therefore, it can be concluded that the proposed model consistently exhibits excellent predictive performance across diverse datasets, thereby underscoring its potential applicability and robustness.

In order to better demonstrate the predictive effectiveness of the proposed models, visual bar charts are used to represent the specific values of each model under different metrics on both datasets.

As shown in Figure 12, the tops of the models proposed in this paper (blue bars) are all located below the other baseline models, indicating that the present model exhibits superior performance in short-acting ship trajectory prediction, which provides a feasible solution for the safety of ship navigation at sea, the prevention of collision accidents, and the control of maritime transport.

To assess the long-term predictive performance of the GC-MT model in vessel trajectory forecasting, this study further compares its ADE and FDE values across various prediction time intervals. Specifically, prediction durations of 10, 30, and 60 min were analyzed to examine performance variations in the proposed model during extended forecasting periods.

Table 3. Performance metrics for different prediction lengths on two datasets.

Prediction Length	Danish		Mexico
	ADE	FDE	ADE	FDE
10	0.2836	0.4055	0.3112	0.4998
30	0.3106	0.4263	0.3274	0.5398
60	0.3785	0.5286	0.3536	0.5614

presents the experimental results for different datasets, with the ADE and FDE measured in nautical miles. As the prediction duration lengthened, there was a gradual increase in the average error, accompanied by a decrease in the predictive accuracy. Notably, the performance of the proposed model remained stable and robust across the different datasets.

The GC-MT model, excelling in accuracy and robustness, offers practical value by effectively supporting maritime decision-making processes in complex scenarios, such as enhancing traffic management in busy sea areas and improving route planning for vessels.

4. Discussion

In order to better understand the contributions of this study to the field of vessel trajectory prediction, a comparison is made between the GC-MT model and other similar studies. These studies have mainly focused on different model architectures, datasets, and evaluation indicators.

In terms of model architecture, the GC-MT model proposed in this study combines a GCN and SSSM, which can effectively capture the spatiotemporal characteristics of vessel motion. In contrast, other studies only used a single neural network model, such as LSTM or GRU, which has certain limitations in dealing with complex spatiotemporal interactions.

In terms of datasets, this study used AIS data from Denmark and the Gulf of Mexico, which have high diversity and complexity. In contrast, some similar studies used datasets of a smaller scale or single area, limiting the generalization ability of the model.

In terms of evaluation indicators, this study used ADE and FDE as evaluation indicators, which can comprehensively evaluate the prediction performance of the model. The experimental results show that the GC-MT model outperformed other baseline models in both indicators, especially in long-term prediction.

The Mamba network selected in this study combines the linear structure of the SSSM with the nonlinear MLP in deep learning to adapt to the characteristics of the vessel trajectory time-series prediction task. The weight in the Mamba network is essentially ${\mathrm{L}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{a}\mathrm{r}}_N\left(x\right)$, that is, the linear transformation result related to the input is set as a learnable parameter as the weight. This seemingly simple change directly transforms the SSSM from a time-invariant system to a time-varying system because the current weight change is no longer a parameter that does not change with time, but a learning parameter related to the input vessel motion characteristics that change with time. As a result, the SSM not only has a super long-range dependency ability but also has a time-varying screening ability. This allows it to target the characteristics of the trajectory prediction time-series task, screening and eliminating features that are not conducive to sequence order reasoning.

In the field of ship trajectory prediction, this study used graph theory approach to represent ship sequence information. Based on the research in recent years, the concept is relatively advanced, and for real-world AIS data, the prediction accuracy is higher and has more effective practical significance.

5. Conclusions

In conclusion, the significant task of predicting vessel trajectories in maritime environments is covered in this work. It emphasizes how crucial precise trajectory prediction is for proactive decision making, preventing collisions, and effectively planning routes for ASVs and USVs.

This paper introduces the GC-MT model, which combines the GCN and Mamba neural networks to capture the spatial and temporal correlations in vessel motion. This modeling is used to achieve accurate vessel trajectory prediction. The introduced GC-MT model integrates GCN and SSSM to effectively capture the spatial and temporal correlations of vessel movements, adeptly simulating the spatiotemporal dynamics of vessel trajectories by leveraging interactions and agent characteristics among sailing vessels to elucidate their temporal and spatial dependencies. The proposed GC-MT model leverages the power of deep learning techniques to effectively simulate the spatiotemporal dynamics of vessel trajectories. It combines temporal and spatial layers to capture the spatiotemporal dependencies among vessels. The Mamba architecture used in this model mitigates the modeling limitations of traditional neural networks, possibly due to the use of SSSM for global perception and dynamic weighting, thereby providing advanced modeling capabilities similar to Transformer. At the same time, by comparing the above baseline models with the quantitative analysis of the proposed model, it was found that the predictions of the GC-MT model had the smallest metric value in multiple datasets, thereby effectively reducing the distance error.

Looking ahead, future efforts will concentrate on studying trajectory predictions for ocean-going vessels utilizing satellite-based AIS data processing alongside transparency or multi-radar data integration. Additionally, reinforcement learning will be combined with transfer learning methodologies to develop collision avoidance warning algorithms aimed at ensuring traffic safety in maritime operations.