Quantum Edge Detection and Convolution Using Paired Transform-Based Image Representation
Abstract
1. Introduction
- A new paired transform-based quantum representation and computation of one-dimensional and 2D signal convolutions and gradients.
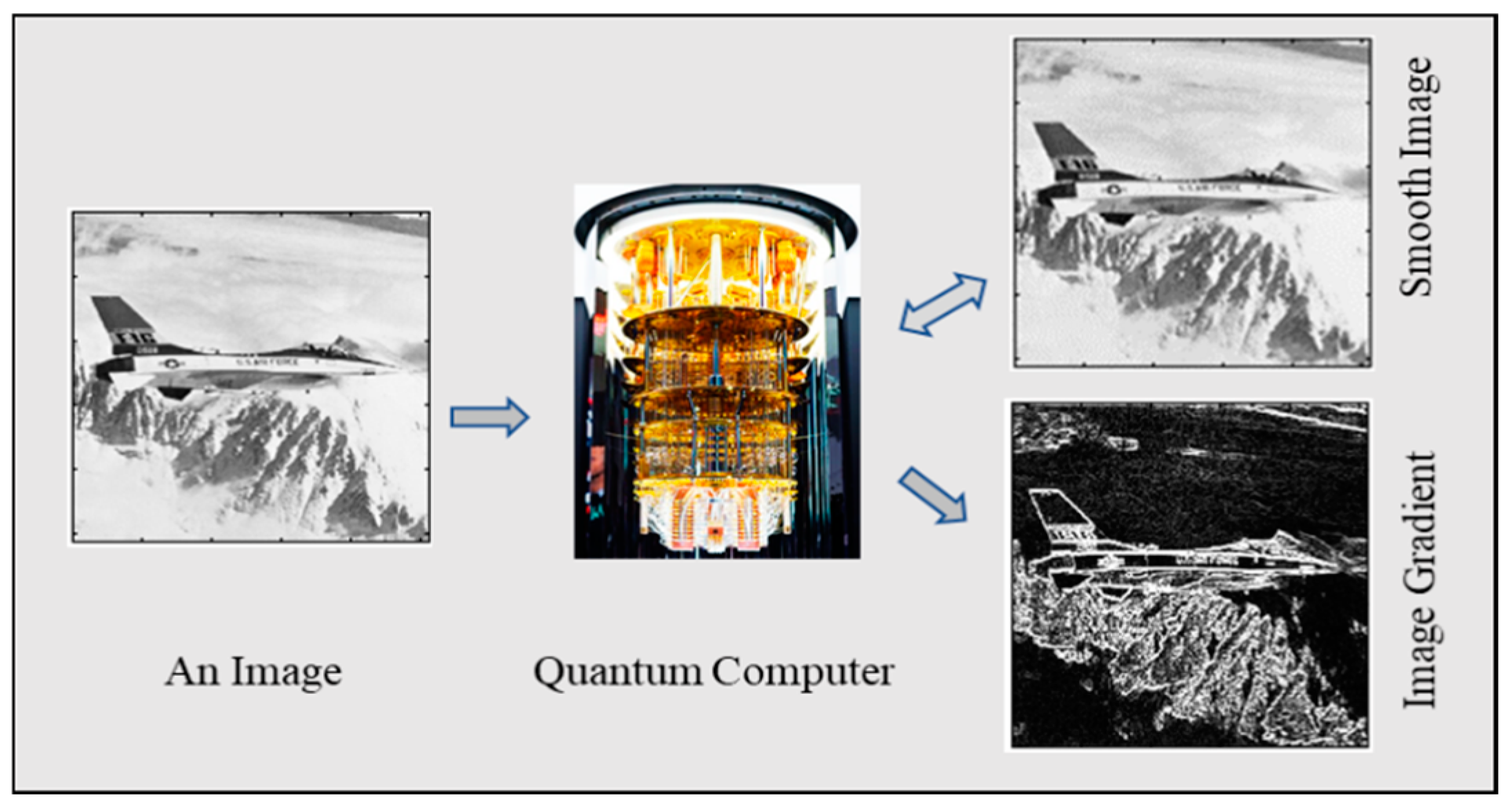
- Simultaneous computation of a few convolutions and gradients (Figure 1).
- Several illustrative examples of quantum algorithms involving two-qubit and three-qubit systems, including edge detection, gradients, and convolution algorithms.
2. Basic Concepts of Qubits
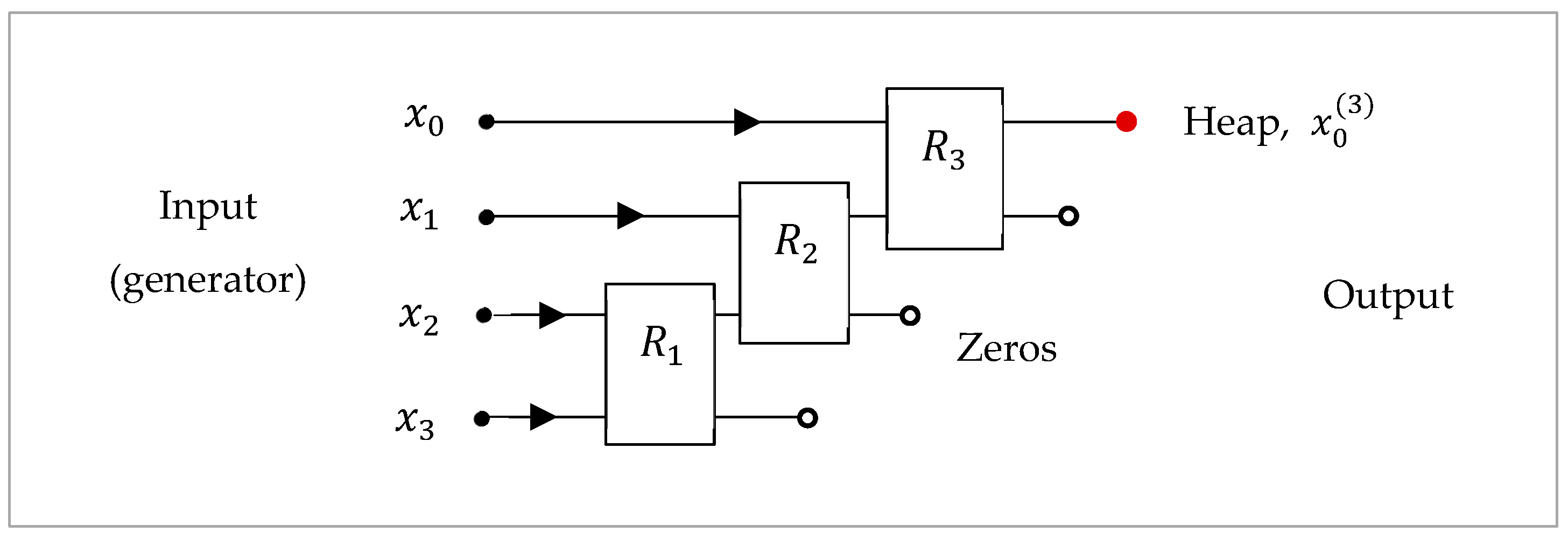
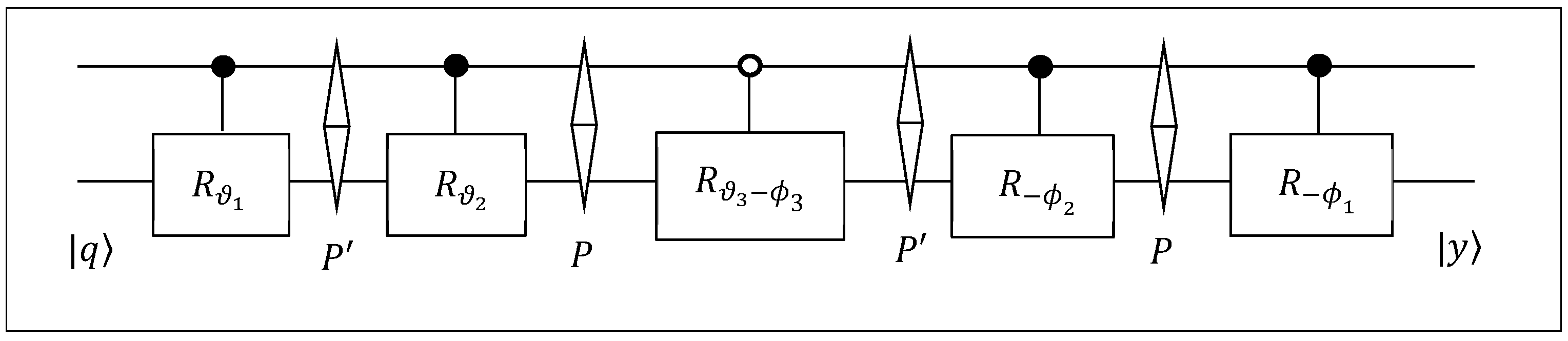
3. Method of 1-D Quantum Convolution
- (a)
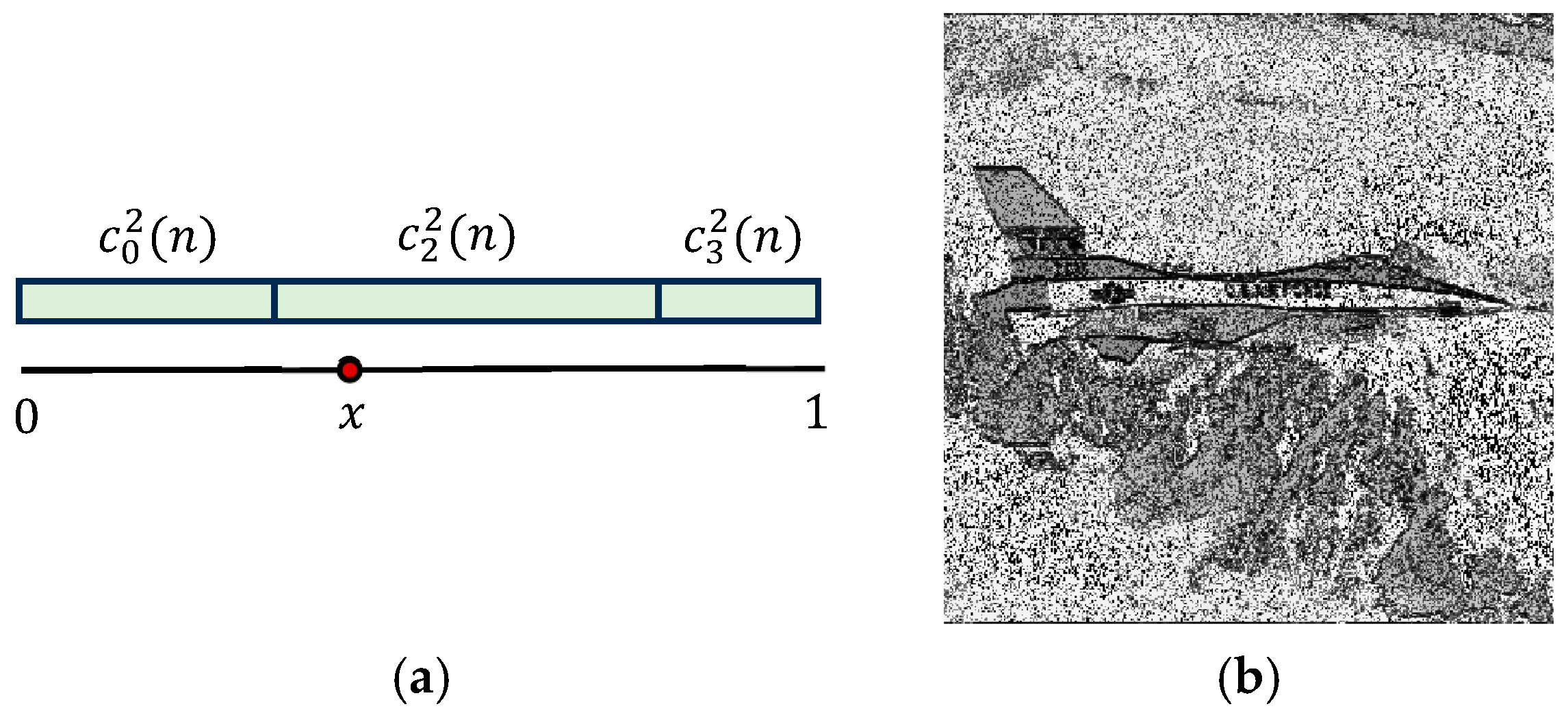
- First, a quantum representation of the convolution at each point, , is defined. Such a representation may be written in different ways and may lead to different results in calculations. The distinguished property of the proposed method is the fact that, in addition to the given convolution, quantum computing allows for parallel computing of other convolutions as well. Many of these additional convolutions or gradients can also be useful when processing signals. Therefore, both signal and convolution quantum representations, and we are confident of this, need to be analyzed separately for each specific case.
- (b)
- In the second step of the proposed method, the quantum paired transform is applied to parallelize a few convolutions and gradients.
Convolution Quantum Representation
- Circuit Definition and Manipulation: Users can define quantum circuits programmatically, add gates, and easily compose modular, reusable components.
- Simulation Tools: Qiskit’s Aer package allows for efficient simulation of large quantum circuits on classical hardware. This allows for rapid prototyping and debugging before running on an actual quantum device.
- Transpilation and Optimization: Qiskit can automatically optimize and transpile quantum circuits for different backends, ensuring that the circuits are physically realizable on specific quantum chips.
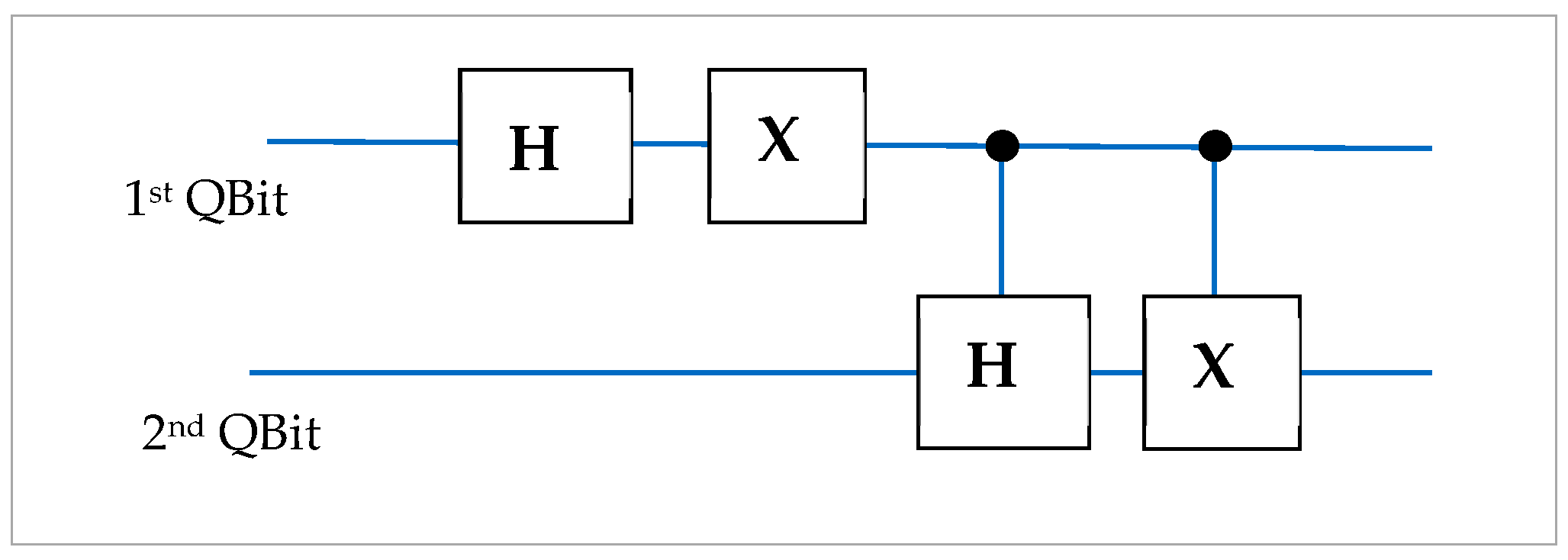
4. Gradient Operators and Numerical Simulations
5. Numerical Simulations: Sobel Gradient Operators
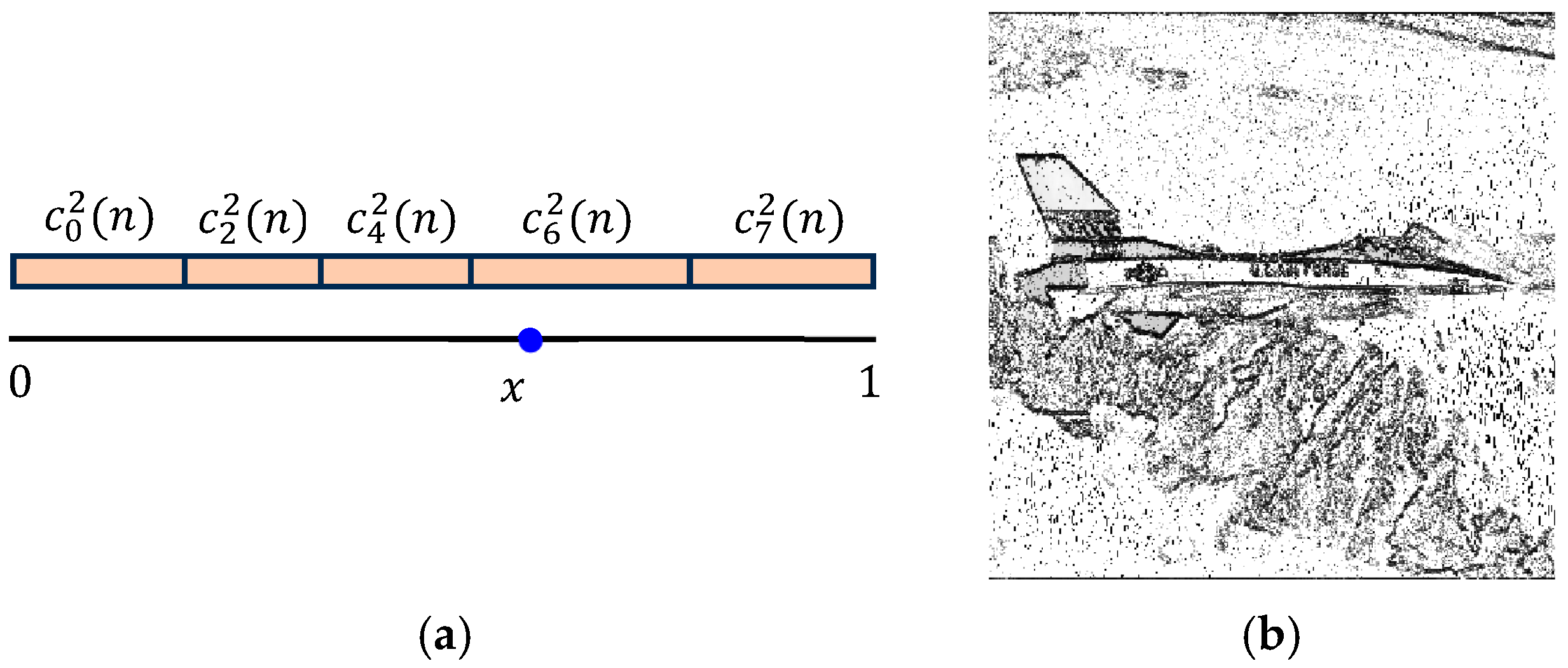
5.1. Three-Qubit Gradient Representation
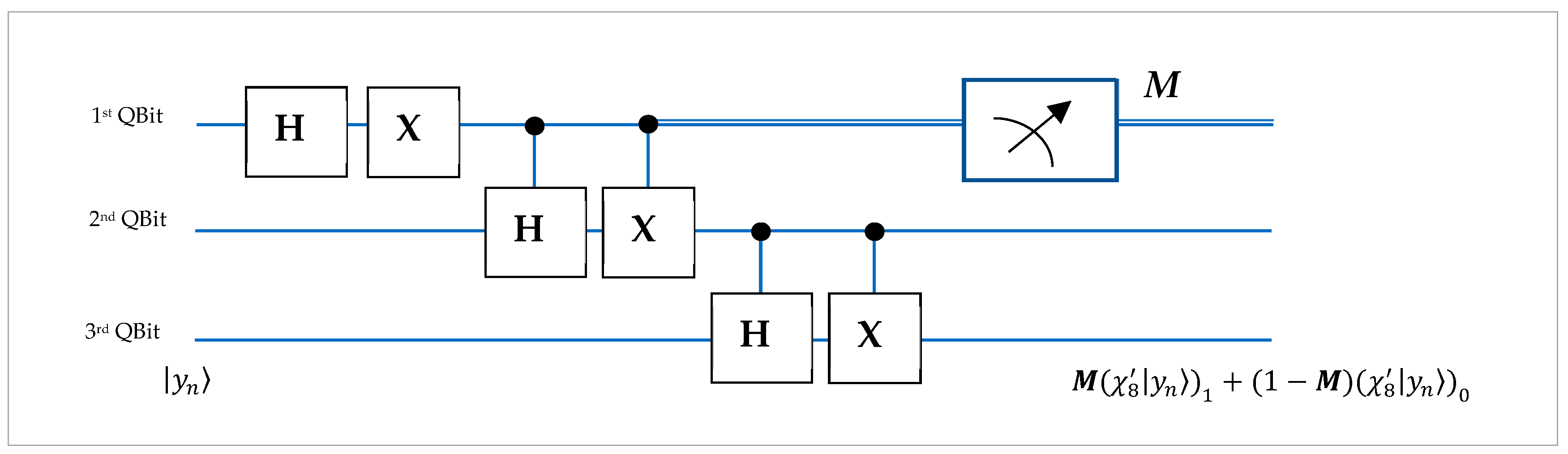
5.2. Three-Qubit Gradient Quantum Representation
5.3. Other Gradient Operators
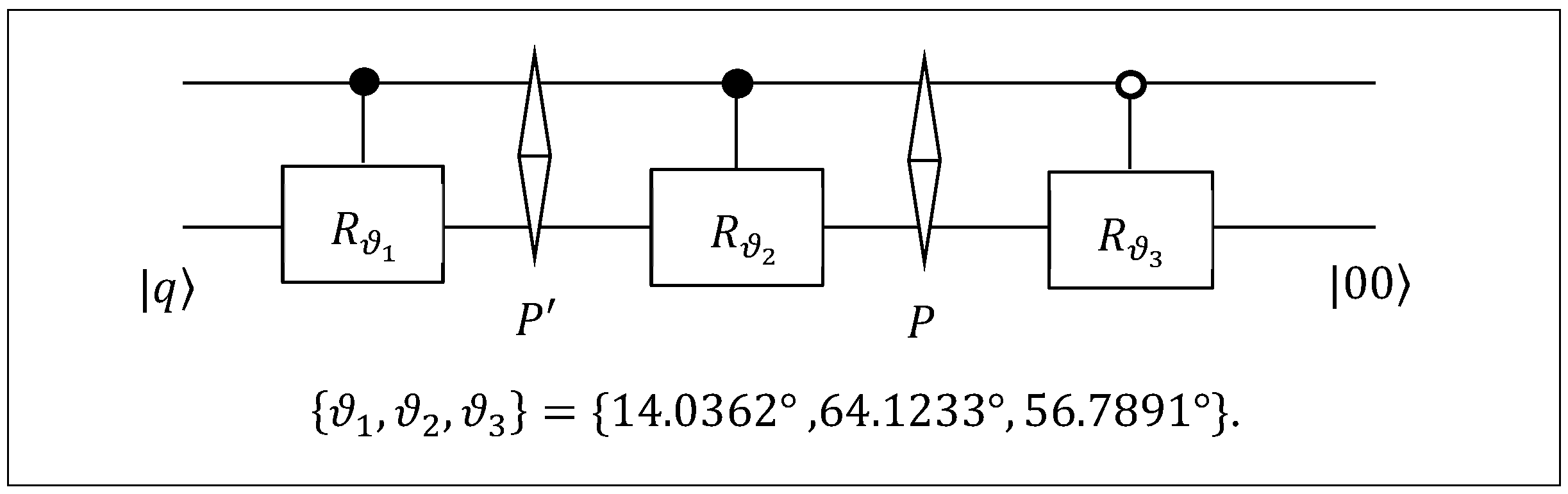
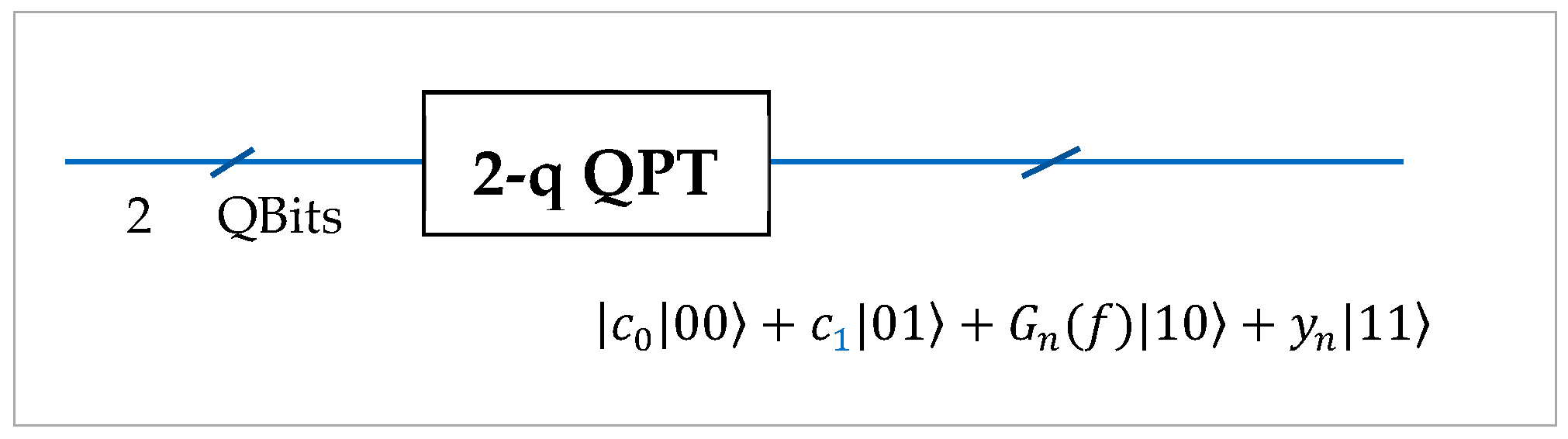
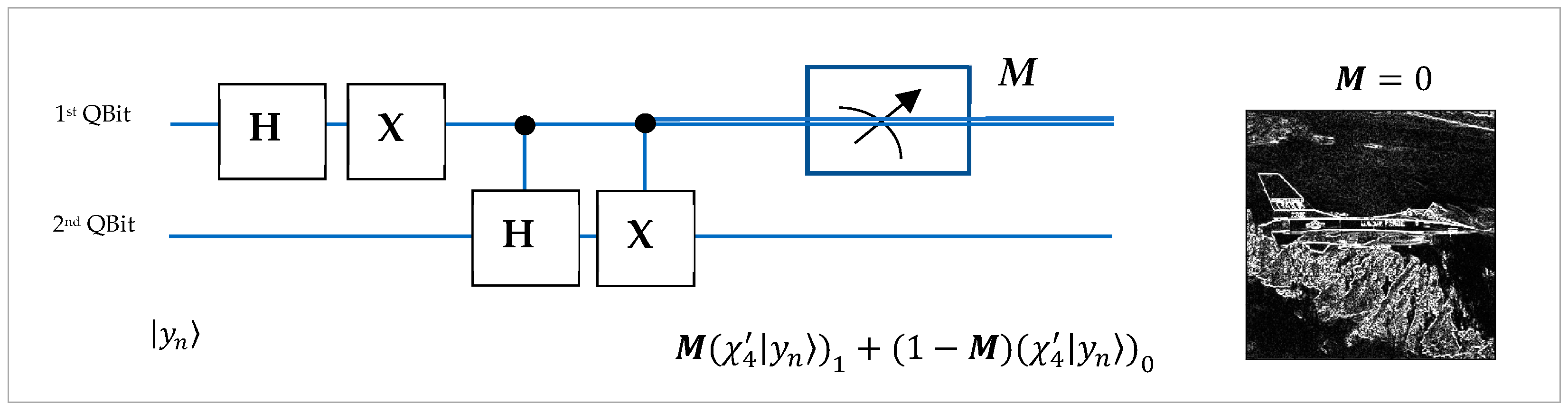
6. Results of Simulation of Quantum Circuits in Qiskit
- State Preparation: The classical pixel window is normalized and embedded into a quantum state through state preparation.
- Quantum Paired Transform: The three-qubit circuit QPT is applied to the encoded state.
- Measurement and Simulation: The circuit is simulated 100,000 times using Qiskit Framework’s Aer simulator, and output probabilities are used to reconstruct amplitude-based masks.
- Mask Extraction and Visualization: Specific amplitude components (selected from indices corresponding to computational basis states) are mapped back to the [0, 255] grayscale range and stored as individual masks for the corresponding pixel of the window.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Robinson, G.S. Edge detection by compass gradient masks. Comput. Graph. Image Process. 1977, 6, 492–501. [Google Scholar]
- Yuan, S.; Venegas-Andraca, S.E.; Wang, Y.; Luo, Y.; Mao, X. Quantum image edge detection algorithm. Int. J. Theor. Phys. 2019, 58, 2823–2833. [Google Scholar]
- Fan, P.; Zhou, R.G.; Hu, W.; Jing, N. Quantum circuit realization of morphological gradient for quantum grayscale image. Int. J. Theor. Phys. 2019, 58, 415–435. [Google Scholar]
- Robinson, G.S. Color edge detection. In Proceedings of the SPIE Symposium on Advances in Image Transmission Techniques, San Diego, CA, USA, 24–25 August 1976; Volume 87, pp. 126–133. [Google Scholar]
- Pratt, W.K. Digital Image Processing, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2001. [Google Scholar]
- Gonzalez, R.; Woods, R. Digital Image Processing, 2nd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Ulyanov, S.; Petrov, S. Quantum face recognition and quantum visual cryptography: Models and algorithms. Electron. J. Syst. Anal. Sci. Educ. 2012, 1, 17. [Google Scholar]
- Khan, M.Z.; Harous, S.; Hassan, S.U.; Khan, M.U.; Iqbal, R.; Mumtaz, S. Deep unified model for face recognition based on convolution neural network and edge computing. IEEE Access 2019, 7, 72622–72633. [Google Scholar]
- Tan, R.C.; Liu, X.; Tan, R.G.; Li, J.; Xiao, H.; Xu, J.J.; Yang, J.H.; Zhou, Y.; Fu, D.L.; Yin, F.; et al. Cryptosystem for grid data based on quantum convolutional neural networks and quantum chaotic map. Int. J. Theor. Phys. 2021, 60, 1090–1102. [Google Scholar]
- Cheng, C.; Parhi, K.K. Fast 2D convolution algorithms for convolutional neural networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 1678–1691. [Google Scholar]
- Schuld, M.; Sinayskiy, I.; Petruccione, F. An introduction to quantum machine learning. arXiv 2014, arXiv:1408.7005. [Google Scholar]
- Kerenidis, I.; Landman, J.; Prakash, A. Quantum algorithms for deep convolutional neural network. arXiv 2019, arXiv:1911.01117. [Google Scholar]
- Nielsen, M.; Chuang, I. Quantum Computation and Quantum Information, 2nd ed.; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Emms, D.; Wilson, R.C.; Hancock, E.R. Graph matching using the interference of discrete-time quantum walks. Image Vis. Comput. 2009, 27, 934–949. [Google Scholar]
- Dieks, D. Communication by EPR devices. Phys. Lett. A 1982, 92, 271–272. [Google Scholar]
- Schuld, M.; Sinayskiy, I.; Petruccione, F. The quest for a quantum neural network. Quantum Inf. Process. 2014, 13, 2567–2586. [Google Scholar]
- Cooley, J.W.; Tukey, J.W. An algorithm the machine computation of complex Fourier series. Math. Comput. 1965, 9, 297–301. [Google Scholar]
- Amerbaev, V.M.; Solovyev, R.A.; Stempkovskiy, A.L.; Telpukhov, D.V. Efficient calculation of cyclic convolution by means of fast Fourier transform in a finite field. In Proceedings of the IEEE East-West Design & Test Symposium (EWDTS 2014), Kiev, Ukraine, 26–29 September 2014; pp. 1–4. [Google Scholar]
- Paul, B.S.; Glittas, A.X.; Sellathurai, M.; Lakshminarayanan, G. Reconfigurable 2, 3 and 5-point DFT processing element for SDF FFT architecture using fast cyclic convolution algorithm. Electron. Lett. 2020, 56, 592–594. [Google Scholar]
- Blahut, R.E. Fast Algorithms for Digital Signal Processing; Addison-Wesley: Reading, UK, 1985. [Google Scholar]
- Cleve, R.; Watrous, J. Fast parallel circuits for the quantum Fourier transform. In Proceedings of the 41st Annual Symposium on Foundations of Computer Science, Redondo Beach, CA, USA, 12–14 November 2000; pp. 526–536. [Google Scholar]
- Yoran, N.; Short, A. Efficient classical simulation of the approximate quantum Fourier transform. Phys. Rev. A 2007, 76, 042321. [Google Scholar]
- Perez, L.R.; Garcia-Escartin, J.C. Quantum arithmetic with the quantum Fourier transform. Quantum Inf. Process 2017, 16, 14. [Google Scholar]
- Grigoryan, A.M.; Agaian, S.S. Paired quantum Fourier transform with log2N Hadamard gates. Quantum Inf. Process. 2019, 18, 26. [Google Scholar]
- Caraiman, S.; Manta, V.I. Quantum image filtering in the frequency domain. Adv. Electr. Comput. Eng. 2013, 13, 77–84. [Google Scholar]
- Grigoryan, A.M. Resolution map in quantum computing: Signal representation by periodic patterns. Quantum Inf. Process. 2020, 19, 21. [Google Scholar]
- Argyriou, V.; Vlachos, T.; Piroddi, R. Gradient-adaptive normalized convolution. IEEE Signal Process. Lett. 2008, 15, 489–492. [Google Scholar]
- Lomont, C. Quantum convolution and quantum correlation are physically impossible. arXiv 2003, arXiv:quant-ph/0309070. [Google Scholar]
- Yan, F.; Iliyasu, A.M.; Venegas-Andraca, S.E. A survey of quantum image representations. Quantum Inf. Process. 2016, 15, 1–35. [Google Scholar]
- Yan, F.; Iliyasu, A.M.; Jiang, Z. Quantum computation-based image representation, processing operations and their applications. Entropy 2014, 16, 5290–5338. [Google Scholar] [CrossRef]
- Grigoryan, A.M.; Agaian, S.S. Quantum Image Processing in Practice: A Mathematical Toolbox, 1st ed.; Wiley: Hoboken, NJ, USA, 2025; 320p. [Google Scholar]
- Wootters, W.K.; Zurek, W.H. A single quantum cannot be cloned. Nature 1982, 299, 802–803. [Google Scholar]
- Grigoryan, A.M.; Grigoryan, M.M. Brief Notes in Advanced DSP: Fourier Analysis with MATLAB; CRC Press Taylor and Francis Group: Boca Raton, FL, USA, 2009. [Google Scholar]
- Qiskit Development Team. Qiskit: An Open-Source Framework for Quantum Computing, Version 1.3.2. Computer software. IBM Quantum: Poughkeepsie, NY, USA, 2019.
- Yao, X.W.; Wang, H.; Liao, Z.; Chen, M.C.; Pan, J.; Li, J.; Zhang, K.; Lin, X.; Wang, Z.; Luo, Z.; et al. Quantum image processing and its application to edge detection: Theory and experiment. Phys. Rev. X 2017, 7, 031041. [Google Scholar]
- Grigoryan, A.M.; Agaian, S.S. 3-Qubit circular quantum convolution computation using the Fourier transform with illustrative examples. J. Quantum Comput. 2024, 6, 1–14. [Google Scholar]


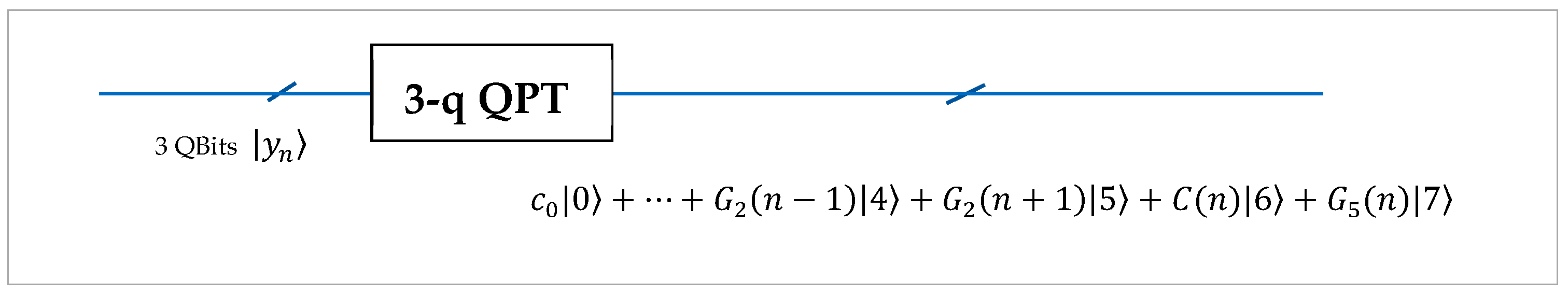








| Basis States | Magnitudes of | ||||
|---|---|---|---|---|---|
| Theoretical | 500 Shots | 1000 Shots | 10,000 Shots | 100,000 Shots | |
| 00 | 0.3162 | 0.3193 | 0.3209 | 0.3130 | 0.3167 |
| 01 | 0.4216 | 0.4449 | 0.4560 | 0.4172 | 0.4201 |
| 10 | 0.8432 | 0.8330 | 0.8264 | 0.8469 | 0.8434 |
| 11 | 0.1054 | 0.0774 | 0.0774 | 0.1024 | 0.1079 |
| MSRE | 0 | 6.76 × 10−3 | 1.04 × 10−2 | 1.89 × 10−3 | 3.57 × 10−4 |
| Gradient Image | MSRE of Different Image Magnitudes | ||||
|---|---|---|---|---|---|
| Jetplane | Leonardo | Peppers | Cameraman | House | |
| 2.78 × 10−3 | 5.50 × 10−4 | 7.87 × 10−4 | 2.75 × 10−3 | 3.26 × 10−3 | |
| 3.73 × 10−3 | 7.28 × 10−4 | 1.22 × 10−3 | 4.43 × 10−3 | 4.98 × 10−3 | |
| 1.05 × 10−3 | 4.20 × 10−4 | 5.76 × 10−4 | 2.19 × 10−3 | 7.17 × 10−3 | |
| 4.90 × 10−3 | 1.07 × 10−3 | 1.69 × 10−4 | 6.14 × 10−3 | 5.52 × 10−3 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grigoryan, A.; Gomez, A.; Agaian, S.; Panetta, K. Quantum Edge Detection and Convolution Using Paired Transform-Based Image Representation. Information 2025, 16, 255. https://doi.org/10.3390/info16040255
Grigoryan A, Gomez A, Agaian S, Panetta K. Quantum Edge Detection and Convolution Using Paired Transform-Based Image Representation. Information. 2025; 16(4):255. https://doi.org/10.3390/info16040255
Chicago/Turabian StyleGrigoryan, Artyom, Alexis Gomez, Sos Agaian, and Karen Panetta. 2025. "Quantum Edge Detection and Convolution Using Paired Transform-Based Image Representation" Information 16, no. 4: 255. https://doi.org/10.3390/info16040255
APA StyleGrigoryan, A., Gomez, A., Agaian, S., & Panetta, K. (2025). Quantum Edge Detection and Convolution Using Paired Transform-Based Image Representation. Information, 16(4), 255. https://doi.org/10.3390/info16040255










