A Method for Improving the Monitoring Quality and Network Lifetime of Hybrid Self-Powered Wireless Sensor Networks
Abstract
1. Introduction
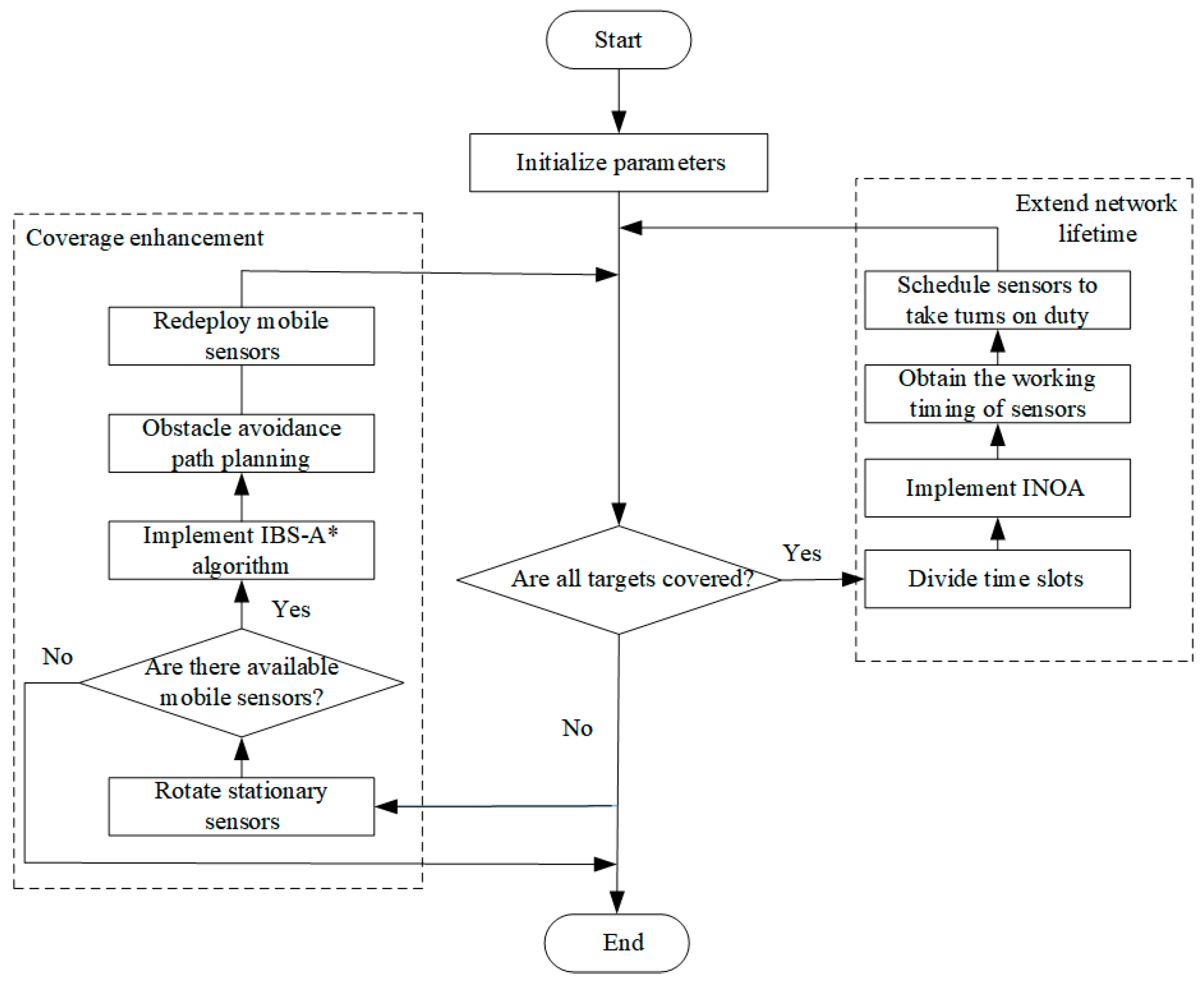
- This paper proposes a node deployment optimization method based on node sensing direction, location, and working state optimization to solve the problems of coverage quality and network lifetime in obstacle environments. This method improves coverage quality by repairing coverage holes and extends network lifetime through node sleep scheduling.
- We have designed a coverage quality enhancement method based on repairing coverage holes. This method first optimizes the sensing direction of stationary nodes and repairs coverage holes that are closer in distance. Then, an improved bidirectional A* algorithm is used to determine the shortest obstacle avoidance moving path, repair the remaining coverage holes, and improve the coverage quality of the network.
- We established a network lifetime optimization model with the residual energy and required number of sensors as targets and used an improved nutcracker optimizer algorithm to solve it. By scheduling the working status of nodes based on the optimal subset obtained, energy consumption can be reduced, thereby extending the network lifetime.
- We designed several simulation experiments to demonstrate the performance of the proposed method in coverage quality, mobile energy consumption, and network lifetime. The comparison with other advanced algorithms proves the effectiveness and superiority of the proposed algorithm.
2. Related Work
2.1. Coverage Enhancement Method Based on Repairing Coverage Holes
2.2. Network Lifetime Extension Method Based on Scheduling Nodes
3. Problem Statement
3.1. Network Model
3.2. Energy Consumption Model
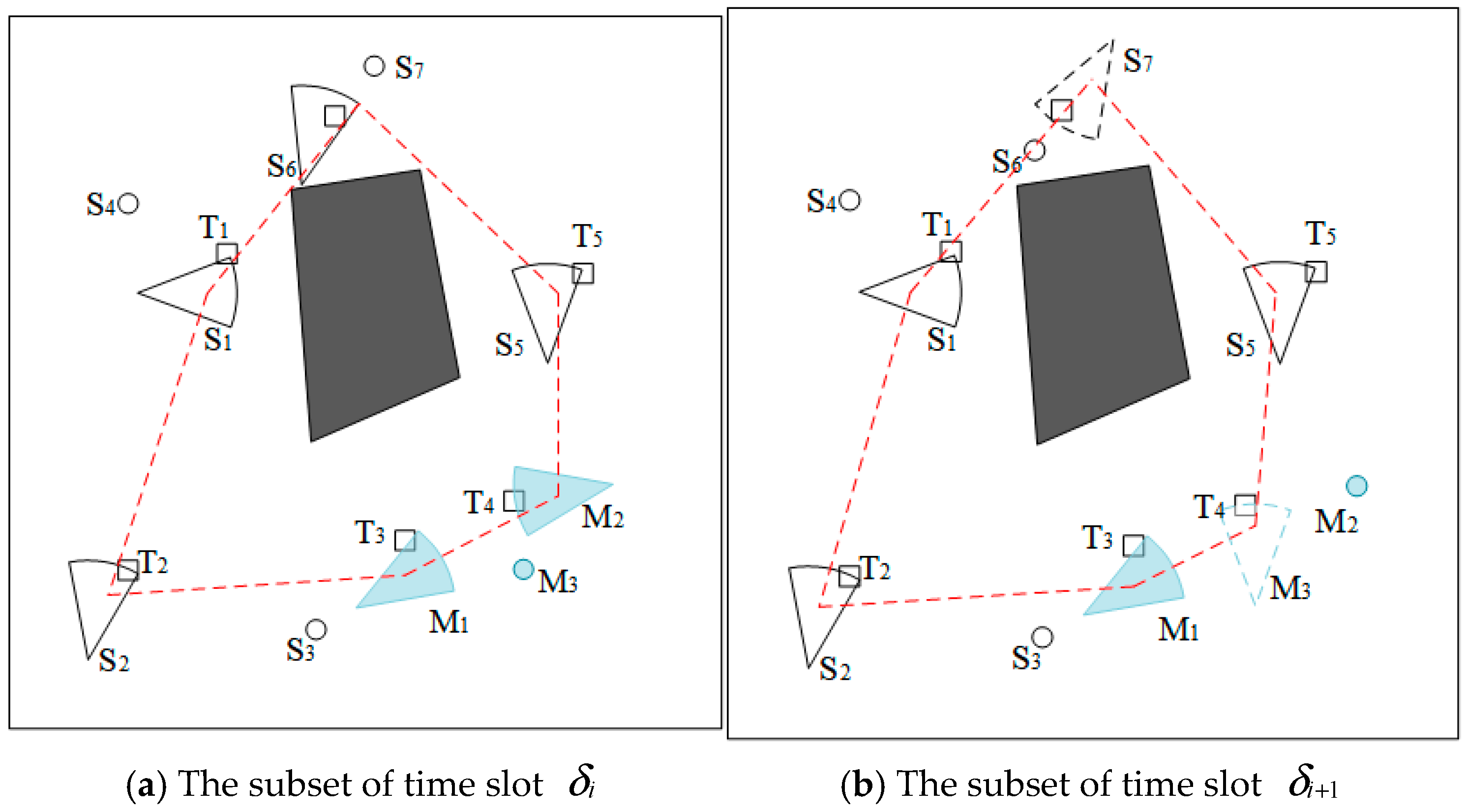
3.3. The Process of Repairing Coverage Holes and Extending Network Lifetime
3.4. Problem Formulation
3.4.1. Coverage Enhancement Problem
3.4.2. Extended Network Lifetime
4. Proposed Method
4.1. Node Scheduling Method for Enhancing Coverage in Obstacle Environments
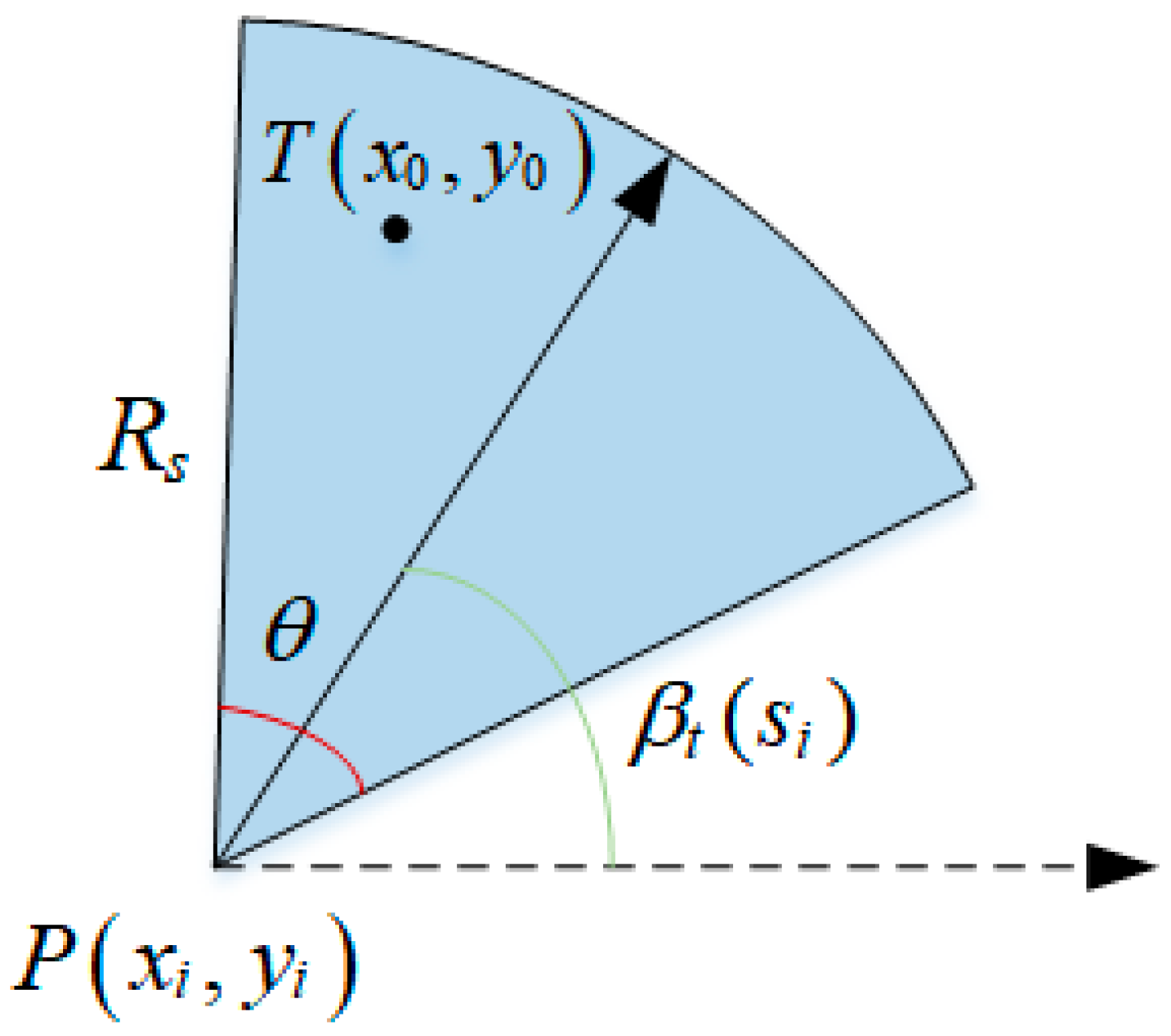
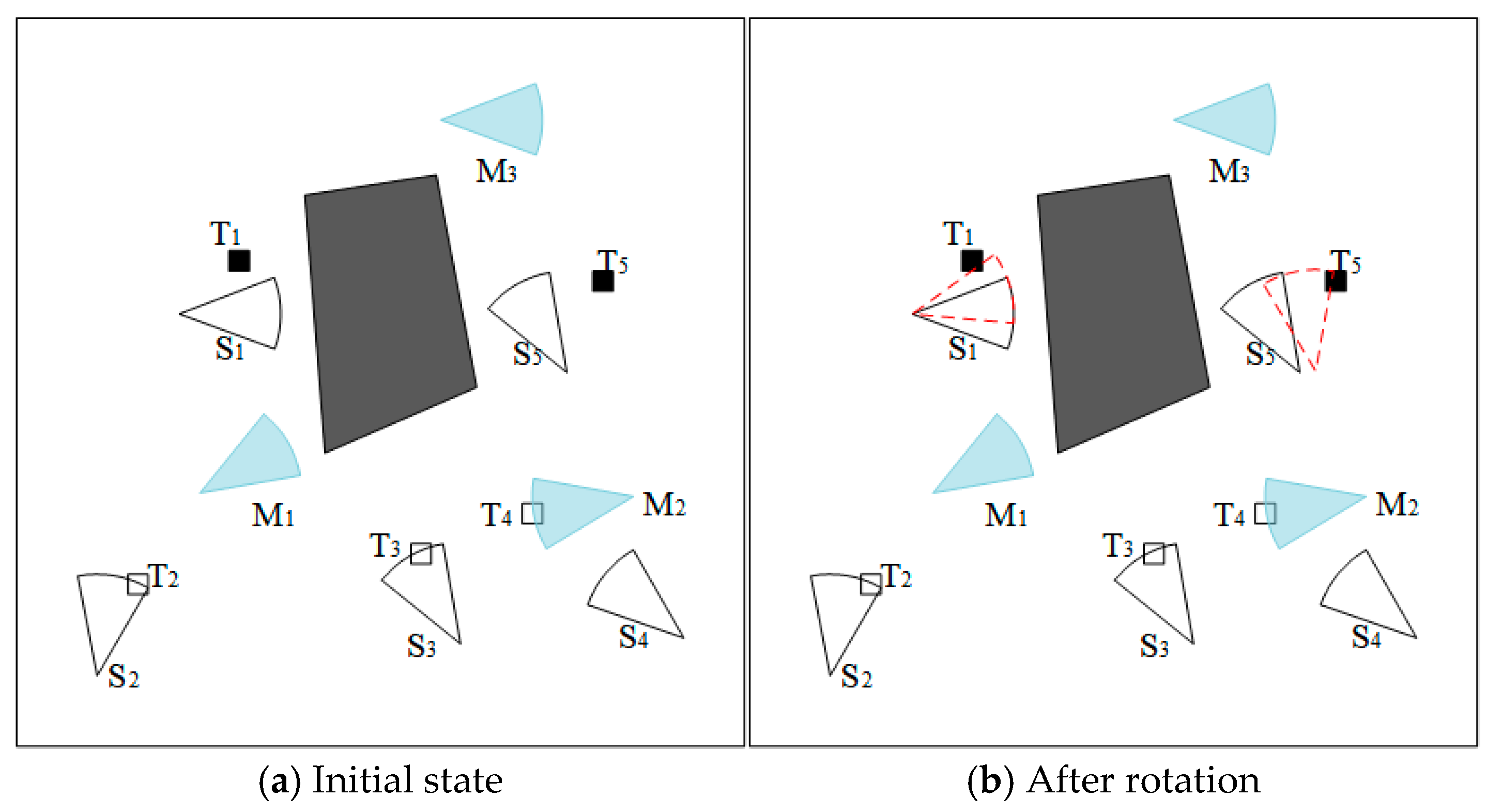
4.1.1. Repairing Coverage Hole Based on Adjusting Sensing Direction
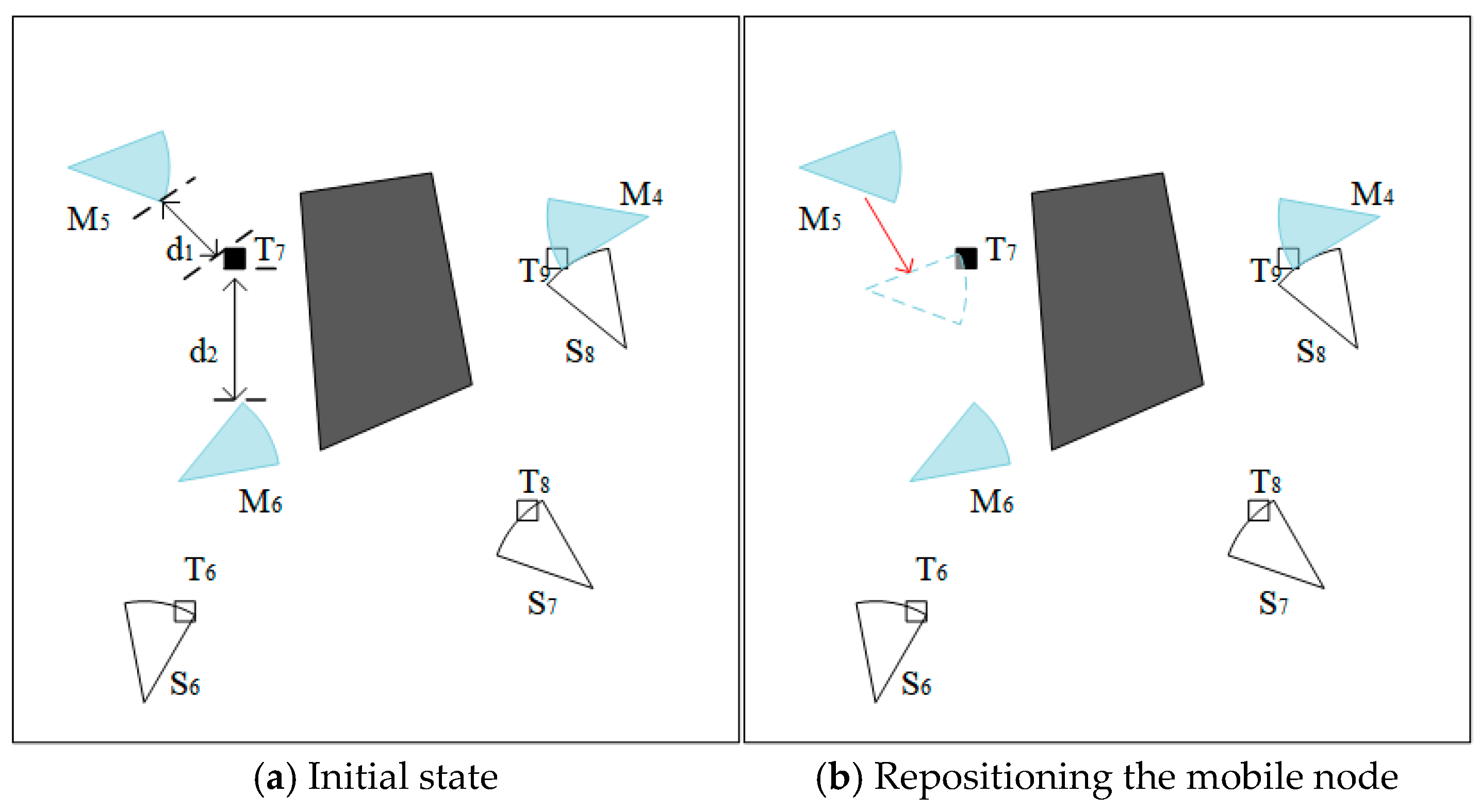
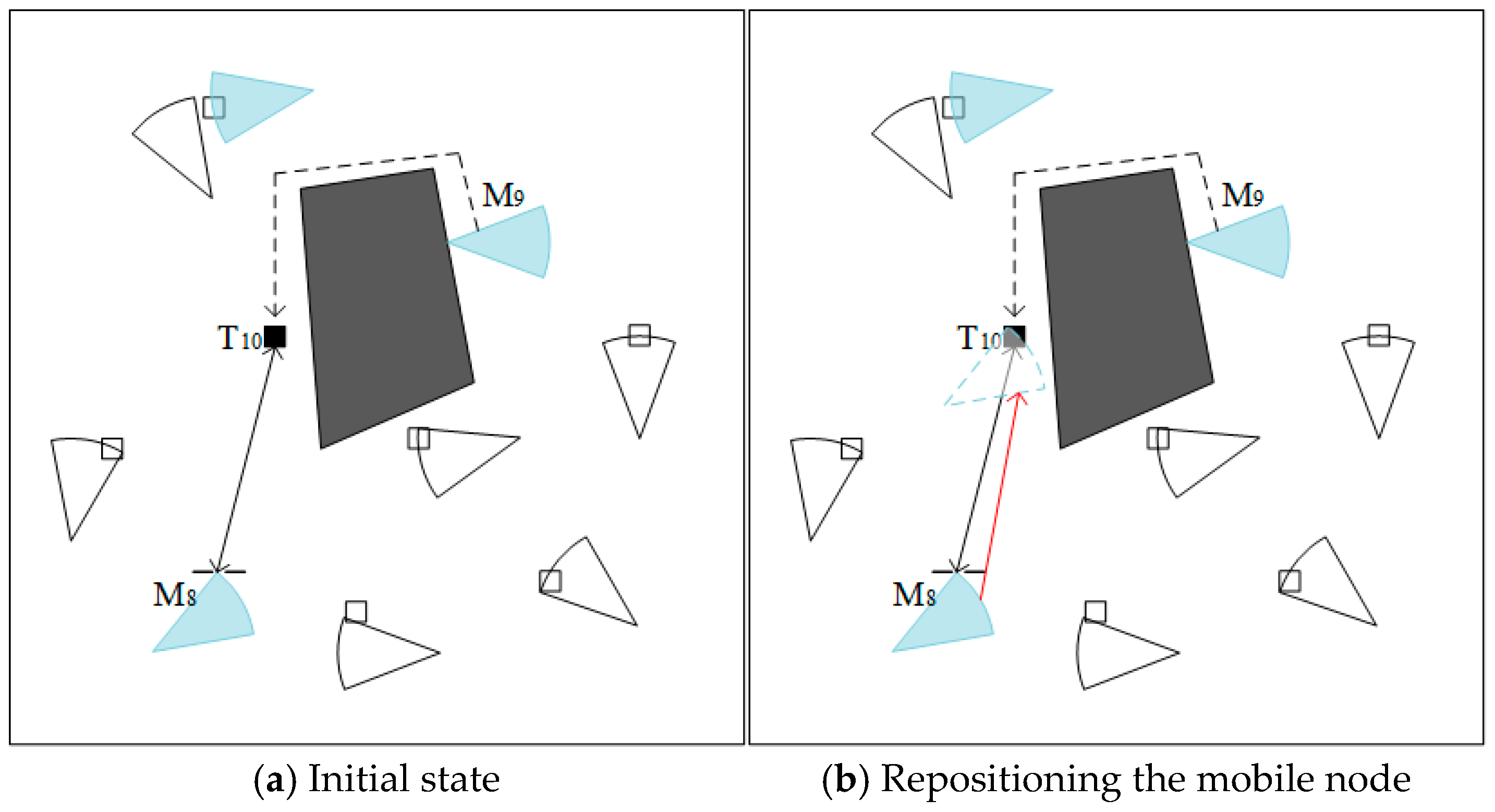
4.1.2. Obstacle Avoidance Path Planning Based on IBS-A* Algorithm
- (1)
- Adaptive heuristic function
- (2)
- Bidirectional search
- (3)
- Path smoothing strategy
4.2. Extending Network Lifetime Based on Improved Nutcracker Optimizer Algorithm
4.2.1. Nutcracker Optimizer Algorithm
- A.
- Foraging and storage strategy
- (1)
- Foraging stage: exploration phase 1
- (2)
- Storage stage: exploitation phase 1
- B.
- Cache-search and recovery strategy
- (1)
- Cache-search stage: exploration phase 2
- (2)
- Recovery stage: exploitation phase 2
4.2.2. Improvement of Nutcracker Optimizer Algorithm
- (1)
- Bidirectional local search
- (2)
- Cauchy mutation operation
- (3)
- Fusion improvement strategy
| Algorithm 1 Improved Nutcracker Optimization Algorithm (INOA) |
| Input: Output: 1: Initialize the population 2: Find the current solution with the highest fitness value 3: t = 1 4: while 5: from [0, 1] 6: //Foraging and storage strategy// 7: are random number within [0, 1] 8: for i = 1:N 9: for j = 1:d 10: 11: using Equations (20) and (30) 12: else 13: using Equations (22) and (30) 14: end if 15: t = t + 1 16: end for 17: else //Cache-search and recovery strategy// 18: Generate RP, and random numbers within [0, 1] 19: for i = 1:N 20: if 21: using Equations (25) and (30) 22: else 23: using Equations (28) and (30) 24: end if 25: t = t + 1 26: end for 27: else //Improvement strategy// 28: for i = 1:N 29: Calculate the fitness values of solutions under different improvement strategies 30: Compare fitness values 31: 32: end if 33: t = t + 1 34: end for 35: end while |
5. Simulation Result
5.1. Parameter Settings
5.2. Experiment A: Comparing of Coverage Enhancement Performance
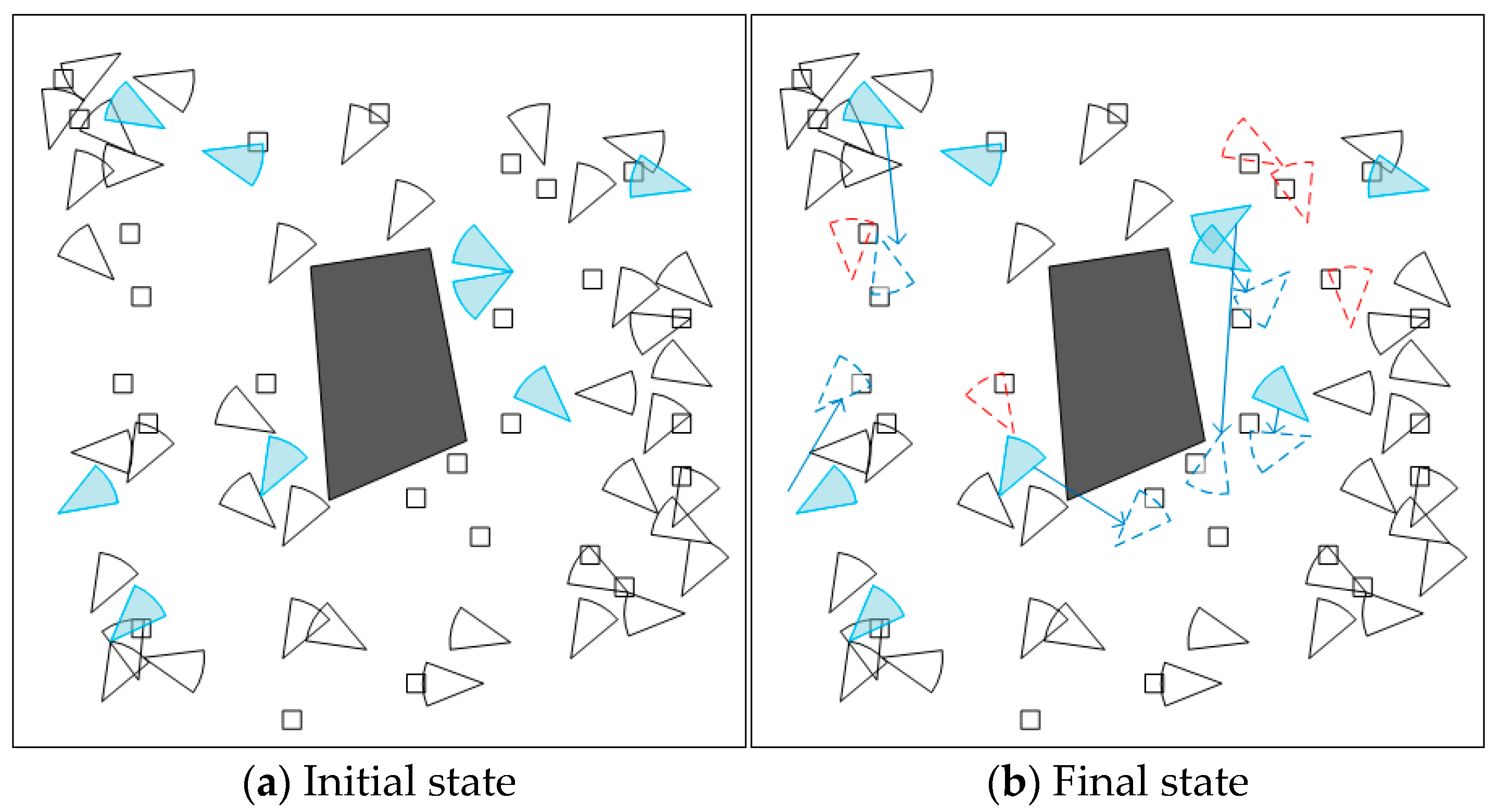
5.2.1. Visualization Example
5.2.2. Comparison of Obstacle Avoidance Path Lengths for Individual Sensors
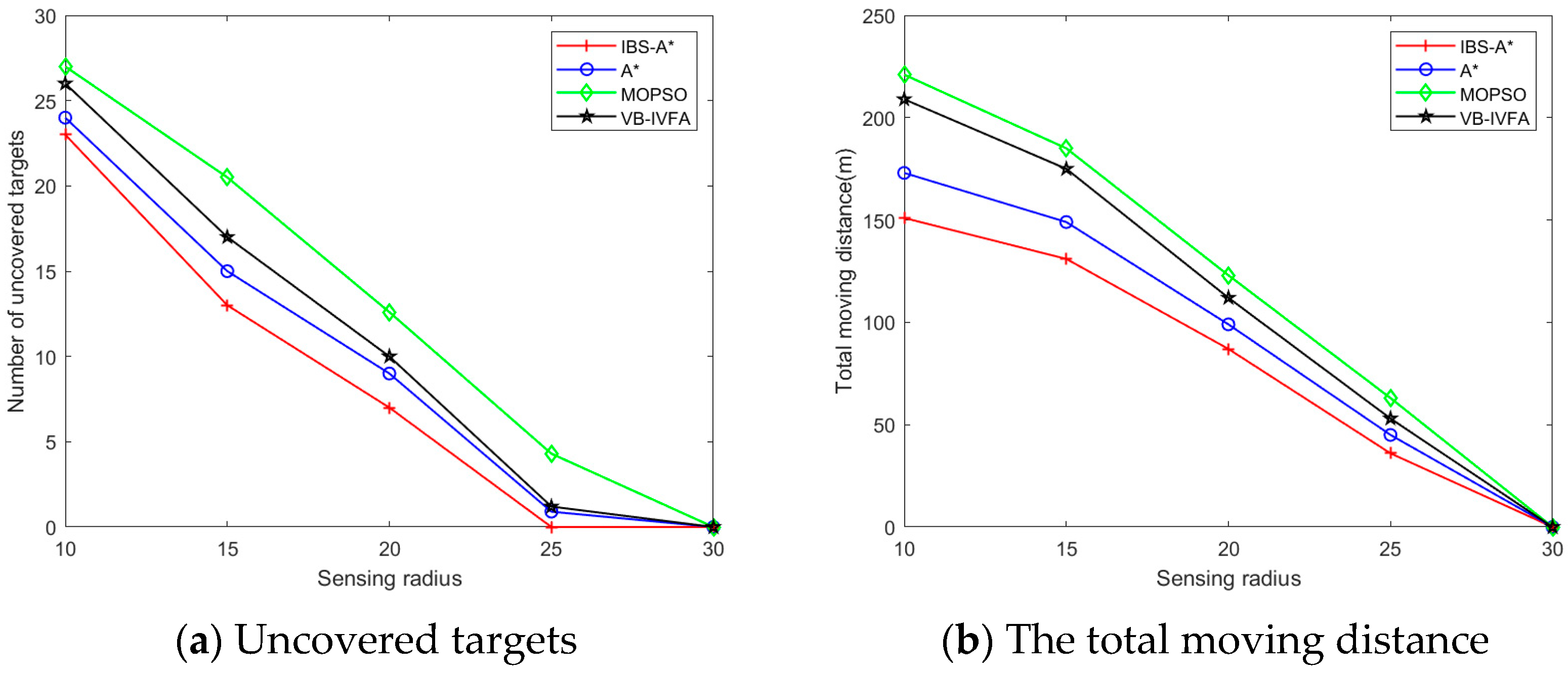
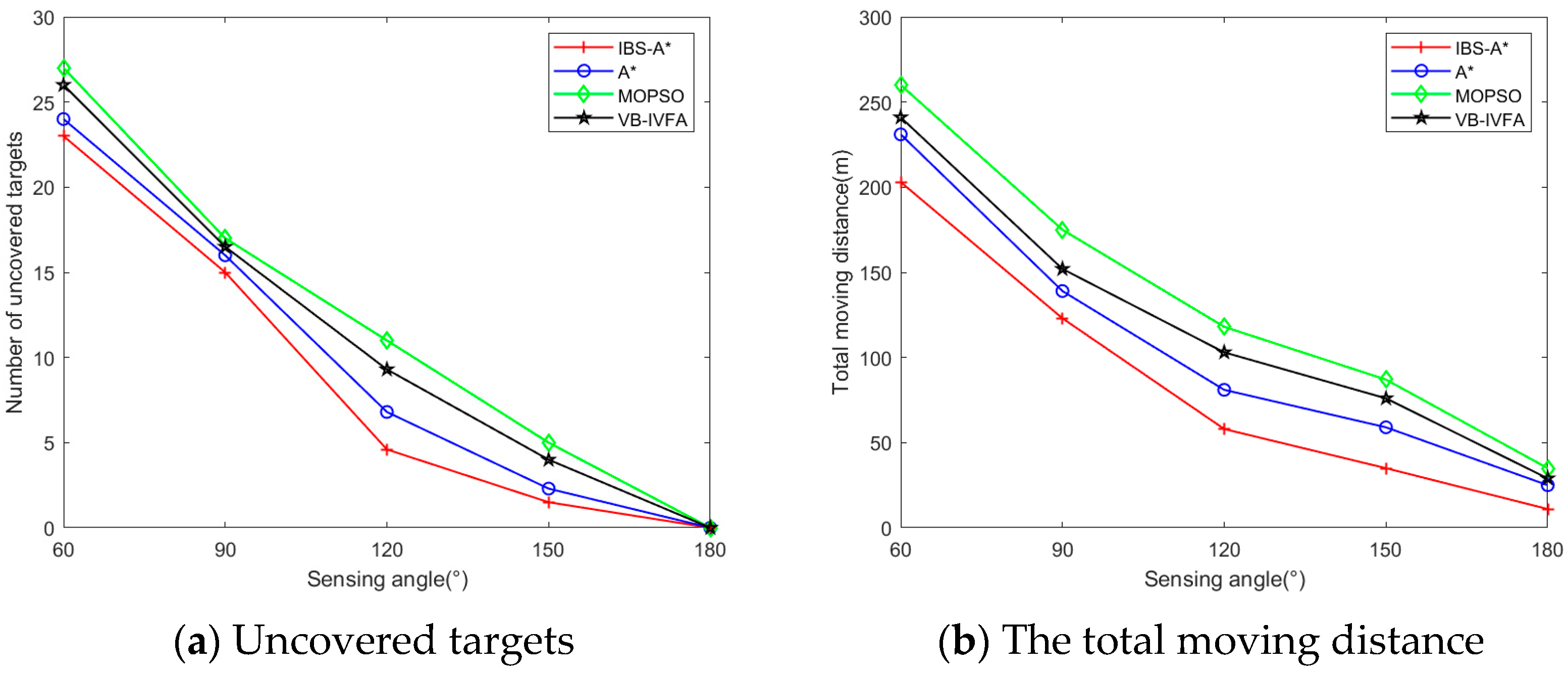
5.2.3. Comparison of Uncovered Targets and Total Moving Distance in Different Scenarios
5.3. Experiment B: Comparison of Network Lifetime
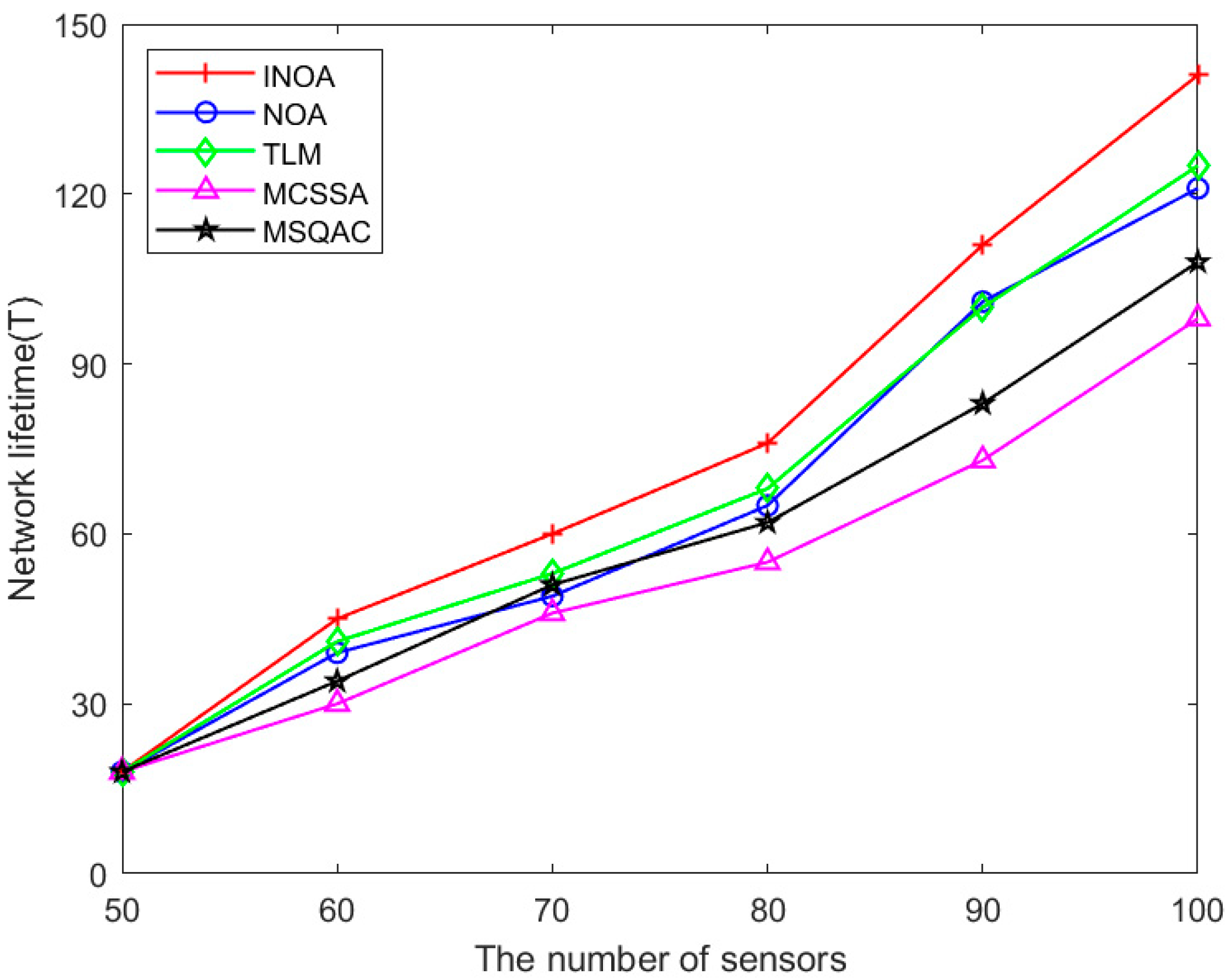
5.3.1. Comparing the Impact of Sensor Numbers on Network Lifetime
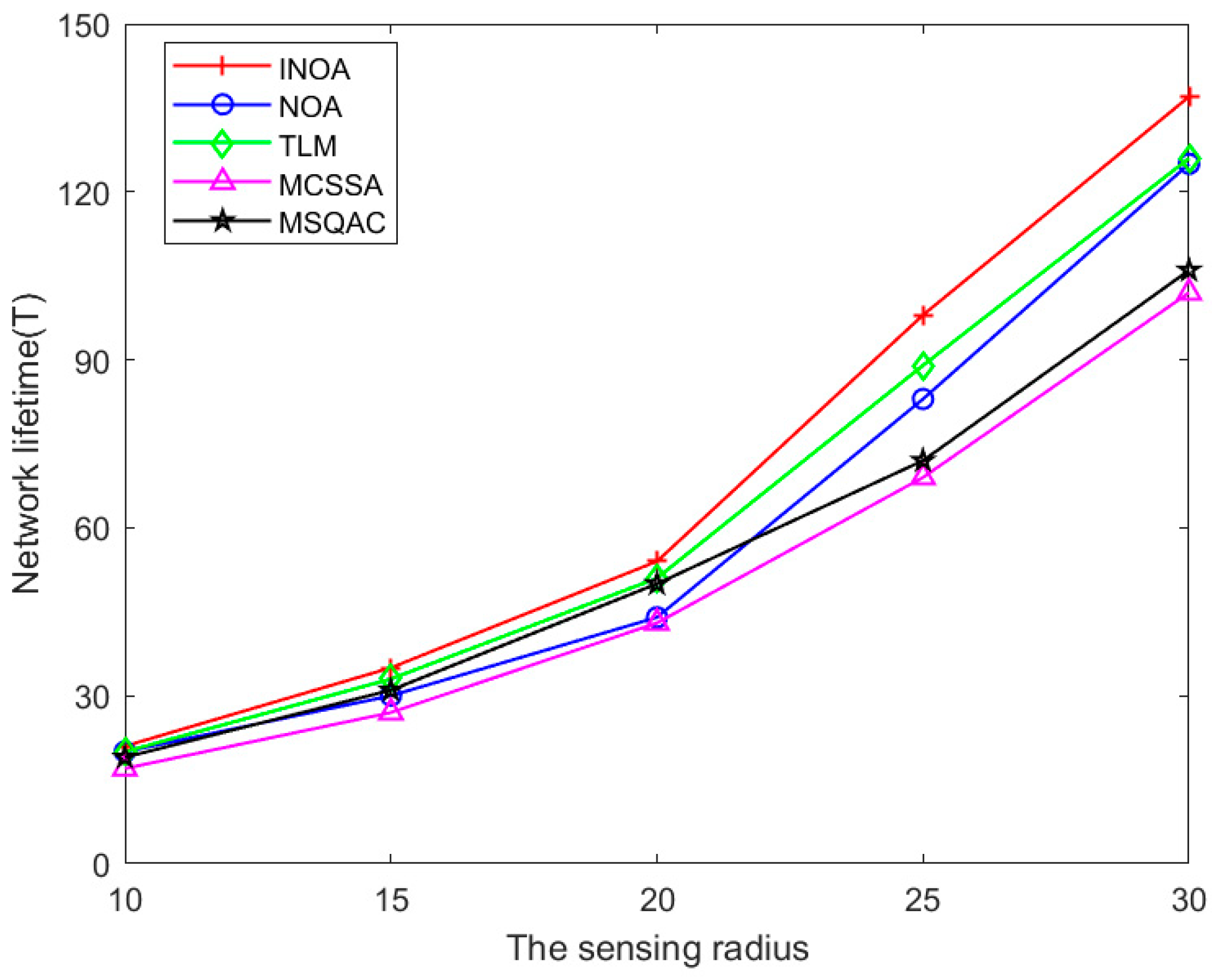
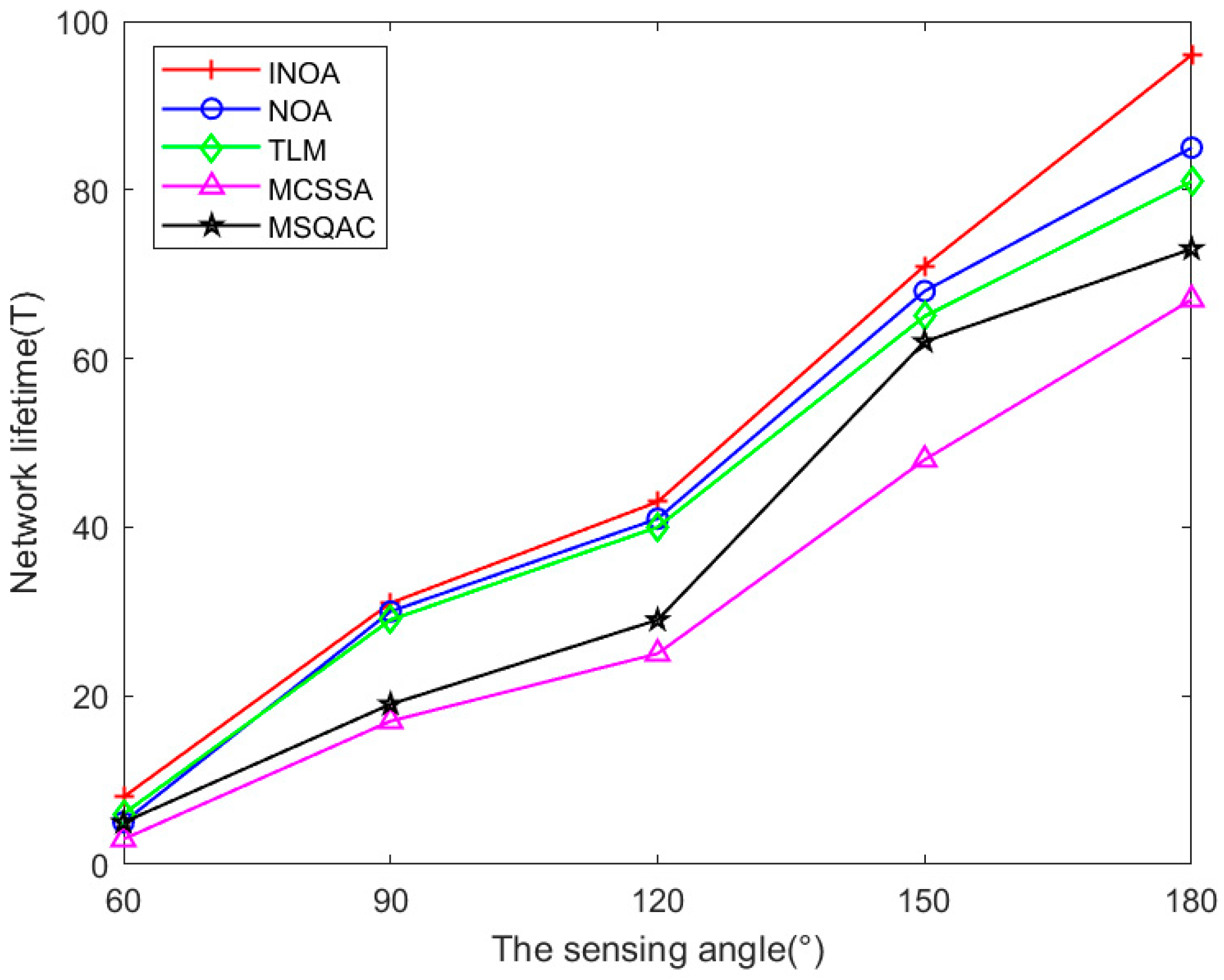
5.3.2. Comparing the Impact of Sensing Radii and Angles on Network Lifetime
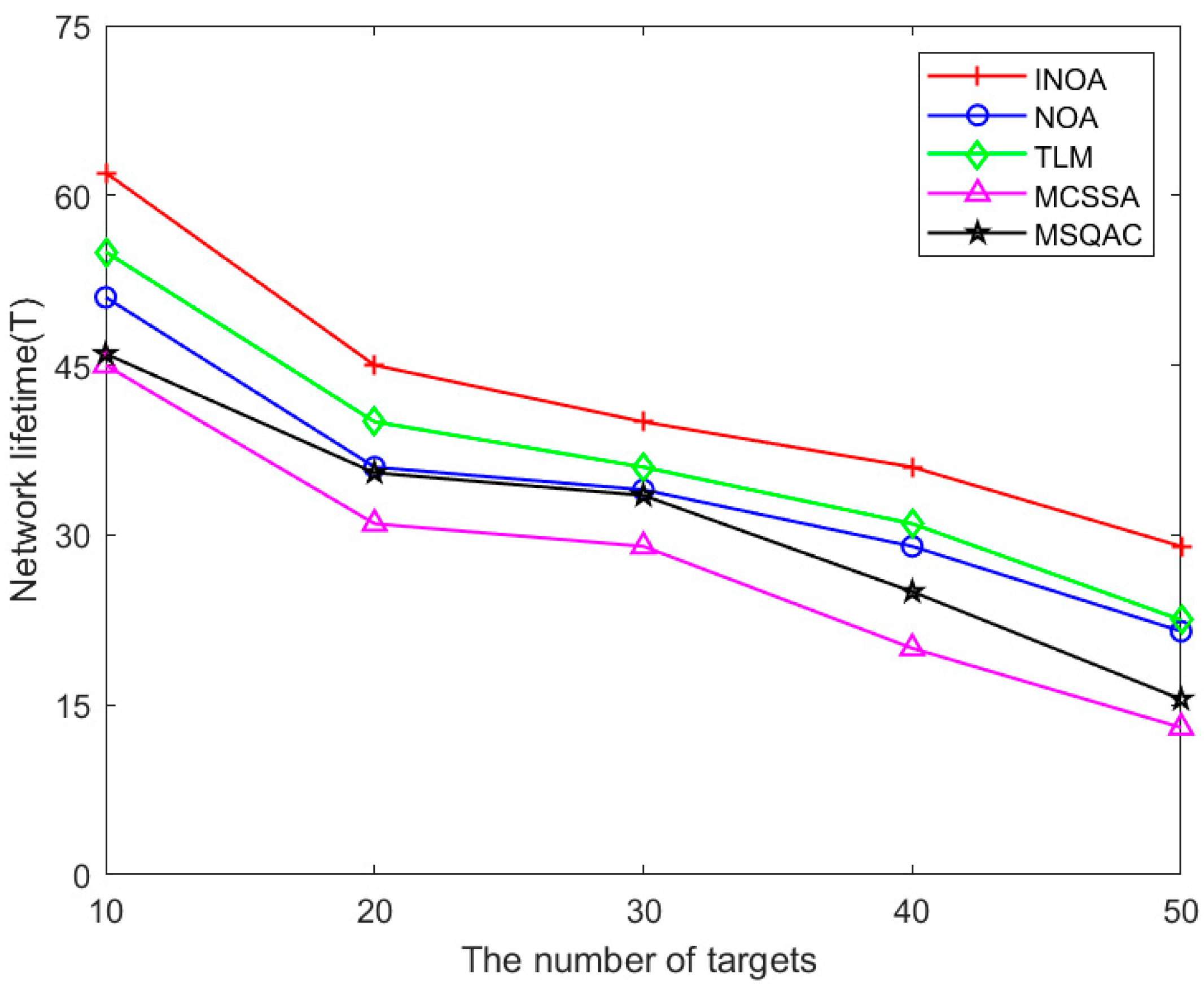
5.3.3. Comparing the Impact of Target Numbers on Network Lifetime
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liang, J.B.; Tu, J.K.; Leung, V.C.M. Mobile sensor deployment optimization algorithm for maximizing monitoring capacity of large-scale acyclic directed pipeline networks in smart cities. IEEE Internet Thing J. 2021, 8, 16083–16095. [Google Scholar] [CrossRef]
- Deng, C.; Fu, X.W. Low-AoI data collection in UAV-aided wireless-powered IoT based on aerial collaborative relay. IEEE Sens. J. 2024, 20, 33506–33521. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Pan, J.S.; Dao, T.K. A novel improved Bat algorithm based on hybrid parallel and compact for balancing an energy consumption problem. Information 2019, 10, 194. [Google Scholar] [CrossRef]
- Nkemeni, V.; Mieyeille, F.; Tsafack, P. Energy consumption reduction in wireless sensor network-based water pipeline monitoring systems via energy conservation techniques. Future Internet 2023, 15, 402. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Y.X.; Xu, P. Dynamic probabilistic sensing for enhanced target coverage in WRSNs. IEEE Sens. J. 2024, 24, 26699–26715. [Google Scholar] [CrossRef]
- Yao, Y.D.; Yang, Y.; Tian, Y.Y. Improved genetic algorithm-based MEP search strategy for DSNs intrusion detection. IEEE Sens. J. 2024, 24, 33544–33559. [Google Scholar] [CrossRef]
- Xu, C.J.; Su, S.C.; Wang, Y.W. An improved stochastic fractal search based on entropy multitrust fusion model for IoT-enabled WSNs clustering. IEEE Sens. J. 2023, 23, 29694–29704. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, Y.B.; Ge, Y.M. Game-theoretic power allocation scheme of cooperative localization in hybrid active–passive wireless sensor networks. IEEE Internet Thing J. 2024, 11, 33027–33039. [Google Scholar] [CrossRef]
- Mishra, A.M.; Agrawal, K.; Prakriya, S. Performance of a cluster-based multihop IoT network with battery-assisted energy harvesting. IEEE Internet Thing J. 2025, 12, 5901–5917. [Google Scholar] [CrossRef]
- Gonzalez, P.; Mujica, G.; Portilla, J. The application of evolutionary, swarm, and iterative-based task-offloading optimization for battery life extension in wireless sensor networks. IEEE Sens. J. 2024, 24, 26682–26698. [Google Scholar] [CrossRef]
- Cho, H.H.; Chien, W.C.; Tseng, F.H.; Chao, H.C. Artificial-intelligence-based charger deployment in wireless rechargeable sensor networks. Future Internet 2023, 15, 117. [Google Scholar] [CrossRef]
- Chen, Y.; Deng, T.D.; Tang, S.Q. A charging scheme for large-scale suburban WRSNs based on the collaboration of UAVs and mobile PADs. IEEE Sens. J. 2025, 25, 5615–5629. [Google Scholar] [CrossRef]
- Wang, P.; Xiong, Y.H. A method to optimize deployment of directional sensors for coverage enhancement in the sensing layer of IoT. Future Internet 2024, 16, 302. [Google Scholar] [CrossRef]
- Wang, P.; Xiong, Y.H.; She, J.H. A new closed-barrier covering optimization method for heterogeneous nodes in hybrid wireless sensor networks. In Proceedings of the 47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021. [Google Scholar]
- Yao, Y.D.; Wen, Q.; Cui, Y.P.; Zhao, B.Z. Discrete army ant search optimizer-based target coverage enhancement in directional sensor networks. IEEE Sens. Lett. 2022, 6, 1–4. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, R.L.; Shi, Y.H. Design of coverage algorithm for mobile sensor networks based on virtual molecular force. Comput. Commu. 2020, 15, 269–277. [Google Scholar] [CrossRef]
- Chen, G.; Xiong, Y.H.; She, J.H. A k-barrier coverage enhancing scheme based on gaps repairing in visual sensor network. IEEE Sens. J. 2023, 23, 2865–2877. [Google Scholar] [CrossRef]
- Yao, Y.D.; Li, Y.; Xie, D.Y. Coverage enhancement strategy for WSNs based on virtual force-directed ant lion optimization algorithm. IEEE Sens. J. 2021, 21, 19611–19622. [Google Scholar] [CrossRef]
- Wen, Q.; Zhao, X.Q.; Cui, Y.P.; Zeng, Y.P. Coverage enhancement algorithm for WSNs based on vampire bat and improved virtual force. IEEE Sens. J. 2022, 22, 8245–8256. [Google Scholar] [CrossRef]
- Peng, S.; Xiong, Y.H. A lifetime-enhancing method for directional sensor networks with a new hybrid energy-consumption pattern in Q-coverage scenarios. Energies 2020, 13, 824. [Google Scholar] [CrossRef]
- Tarip, U.U.; Ali, H.; Hussain, M. Shuffled ARSH-FATI: A novel meta-heuristic for lifetime maximization of range-adjustable wireless sensor networks. IEEE Trans. Green. Commun. Netw. 2023, 7, 1217–1233. [Google Scholar]
- Chen, Z.G.; Lin, Y.; Gong, Y.J. Maximizing lifetime of range-adjustable wireless sensor networks: A neighborhood-based estimation of distribution algorithm. IEEE Intern. Trans. Cyber. 2021, 51, 5433–5444. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.X.; Jian, P.; Xu, W.Z. Maximizing sensor lifetime via multi-node partial-charging on sensors. IEEE Trans. Mobile. Comput. J. 2023, 22, 6571–6584. [Google Scholar] [CrossRef]
- Xiong, Y.H.; Chen, G.; Lu, M.J. A two-phase lifetime-enhancing method for hybrid energy-harvesting wireless sensor network. IEEE Sens. J. 2020, 20, 1934–1946. [Google Scholar] [CrossRef]
- Xu, P.; Wang, X.F.; Chang, C.Y. JMLA: Joint monitoring quality and network lifetime for range-adjustable sensors in WRSNs. IEEE Sens. J. 2024, 24, 33522–33543. [Google Scholar] [CrossRef]
- Xiong, D.; Liu, Y.F.; Zhu, C.; Jin, L.; Wang, L.M. Delay-dependent stability analysis of haptic systems via an auxiliary function-based integral inequality. Actuators 2021, 10, 171. [Google Scholar] [CrossRef]
- Basset, M.A.; Mohamed, R.; Jameel, M. Nutcracker optimizer: A novel nature-inspired metaheuristic algorithm for global optimization and engineering design problems. Knowl. System. 2023, 262, 110248. [Google Scholar] [CrossRef]
- Evangeline, S.I.; Darwin, S.; Anandkumar, P.P. Investigating the performance of a surrogate-assisted nutcracker optimization algorithm on multi-objective optimization problems. Expert. System. Appli. 2024, 245, 123044. [Google Scholar] [CrossRef]
- Mahamed, A.B.; Reda, M.; Ibrahim, M.H. An improved nutcracker optimization algorithm for discrete and continuous optimization problems: Design, comprehensive analysis, and engineering applications. Heliyon 2024, 10, e36678. [Google Scholar]
- Dande, B.; Chang, C.Y.; Liao, W.H. MSQAC: Maximizing the surveillance quality of area coverage in wireless sensor networks. IEEE Sens. J. 2022, 22, 6150–6163. [Google Scholar] [CrossRef]
- Luo, C.W.; Hong, Y.; Li, D.Y. Maximizing network lifetime using coverage sets scheduling in wireless sensor networks. Ad. Hoc. Netw. 2020, 98, 102037. [Google Scholar] [CrossRef]

| Region of Interest (ROI) | 200 m × 200 m |
|---|---|
| Number of targets (k) | |
| Number of sensors (n) | |
| Number of stationary sensors () | |
| Number of mobile sensors () | |
| Sensing angles () | |
| Sensing radius () | 10 m |
| Communication radius () | 20 m |
| Initial energy () | 10 U |
| Energy threshold () | 0.6 |
| Sensing energy consumption () | 0.5 U/T |
| Mobile energy consumption () | 0.1 U/m |
| Charging rate () | 0–0.5 U/T |
| The Length of Obstacle Avoidance Path (m) | Search Time (s) | |
|---|---|---|
| A* | 39.75 | 7.81 |
| MOPSO | 46.62 | 9.53 |
| VB-IVFA | 45.33 | 11.56 |
| IBS-A* | 37.25 | 3.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Xiong, Y. A Method for Improving the Monitoring Quality and Network Lifetime of Hybrid Self-Powered Wireless Sensor Networks. Information 2025, 16, 228. https://doi.org/10.3390/info16030228
Wang P, Xiong Y. A Method for Improving the Monitoring Quality and Network Lifetime of Hybrid Self-Powered Wireless Sensor Networks. Information. 2025; 16(3):228. https://doi.org/10.3390/info16030228
Chicago/Turabian StyleWang, Peng, and Yonghua Xiong. 2025. "A Method for Improving the Monitoring Quality and Network Lifetime of Hybrid Self-Powered Wireless Sensor Networks" Information 16, no. 3: 228. https://doi.org/10.3390/info16030228
APA StyleWang, P., & Xiong, Y. (2025). A Method for Improving the Monitoring Quality and Network Lifetime of Hybrid Self-Powered Wireless Sensor Networks. Information, 16(3), 228. https://doi.org/10.3390/info16030228







