EquiFlowShard: A Blockchain Sharding Protocol with Optimized Account Distribution
Abstract
1. Introduction
- 1.
- A dynamic Optimized Account State Distribution Algorithm (OASDA) is proposed to allocate ordinary accounts to the optimal shard while selecting the most active accounts as LinkAgents and segmenting their states across an optimal set of shards. This reduces cross-shard transaction proportions, balances cross-shard workloads, and significantly enhances throughput.
- 2.
- The State Flow (SFlow) mechanism is designed, comprising two parts: one for the system’s optimization phase, where state redistribution is achieved via a communication mechanism based on OASDA results, and another for the consensus phase, where state transfers between segmented sub-accounts are executed through transactions.
- 3.
- To ensure smooth state updates, a Smooth Transition scheme is developed. During state reconfiguration, fine-grained account locking is used to minimize the impact on system performance. Additionally, a transitional phase is introduced for LinkAgent deactivation, establishing a three-phase life cycle.
- 4.
- The EquiFlowShard protocol is implemented and simulated using Ethereum historical transaction data. Experimental results show that this protocol outperforms other benchmark protocols in terms of throughput, transaction confirmation latency, and the proportion of cross-shard transactions.
2. Related Work
2.1. Blockchain Sharding
2.2. Processing a Cross-Shard Transaction
3. Overview of EquiFlowShard
3.1. System Model
- Optimization Shard (O-shard): O-shard is responsible for optimizing the distribution of account states. In each epoch, it adaptively allocates account states and updates the LinkAgent.
- Processing Shard (P-shard): P-shard is responsible for generating blocks during the consensus phase by processing transactions and achieving intra-shard consensus.
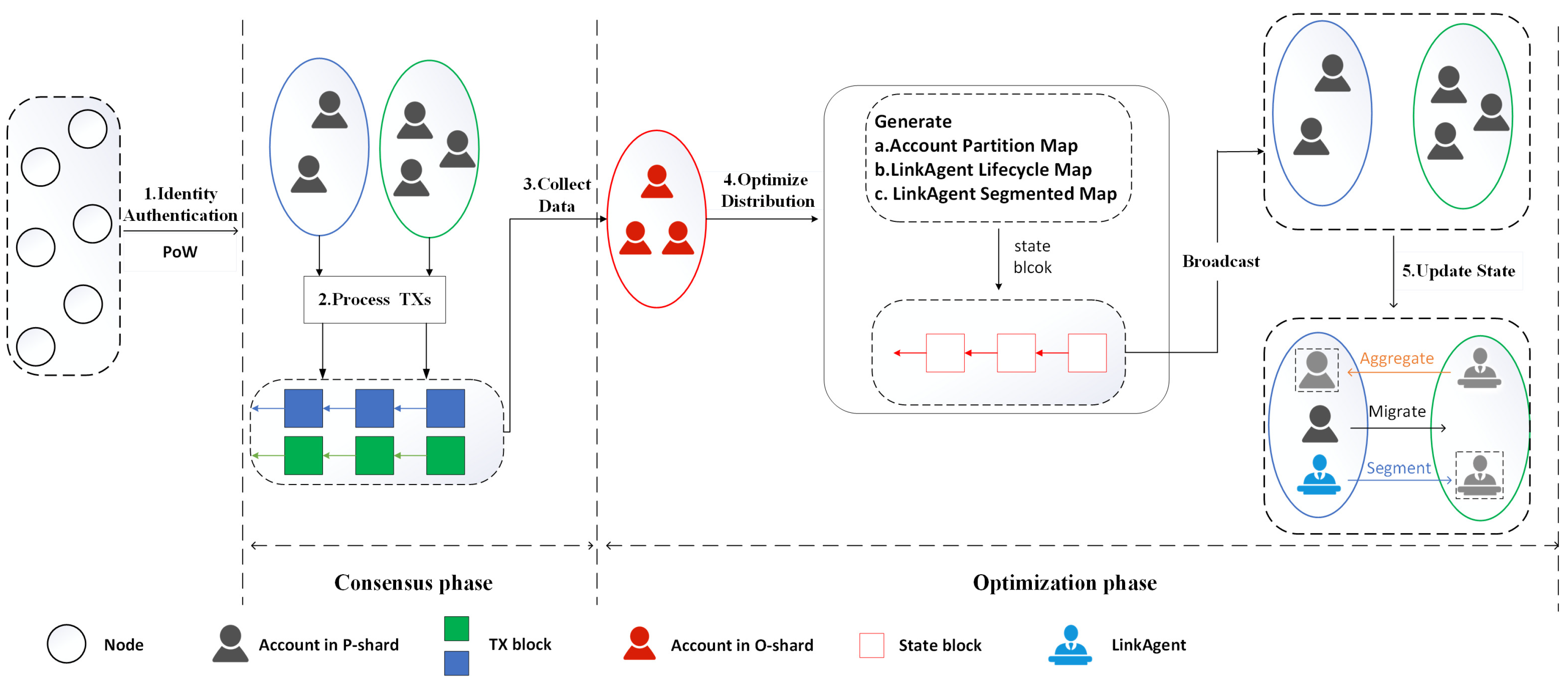
3.2. Workflow of EquiFlowShard
- Step 1, identity authentication: To prevent Sybil attacks, at the beginning of each epoch, all consensus nodes generate unbiased and unpredictable randomness based on a Verifiable Random Function (VRF). Similar to [9], nodes must solve a PoW puzzle using their IP address, public key, randomness from the previous epoch, and a flag indicating their willingness to become a LinkAgent in order to obtain a valid identity for this epoch. Accounts intending to become LinkAgents must stake tokens in advance.
- Step 2, process transactions: The P-shard continuously receives user transactions and adds them to the transaction pool. During each epoch, the P-shard packages the transactions from the pool, generates blocks, broadcasts them to the shard network, and reaches consensus using the PBFT consensus algorithm.
- Step 3, collect data: The O-shard continuously receives block information broadcasted by the P-shard and uses the transactions within the blocks to construct and update a transaction distribution graph.
- Step 4, optimize distribution: Based on the transaction distribution graph, the O-shard periodically executes the OSADA to generate the optimal account partition map and updates the composition of LinkAgents and the segmentation map. The O-shard reaches consensus on the algorithm results, generates a state block, and then sends a state reconfiguration message to all P-shards.
- Step 5, update state: The P-shard updates its ledger state and transaction pool based on the state block. Active LinkAgents will segment the shard’s state according to the segmentation map and distribute it to the respective shards. LinkAgents in the reintegration phase must aggregate all segmented states back into the main shard.
4. EquiFlowShard Protocol Design
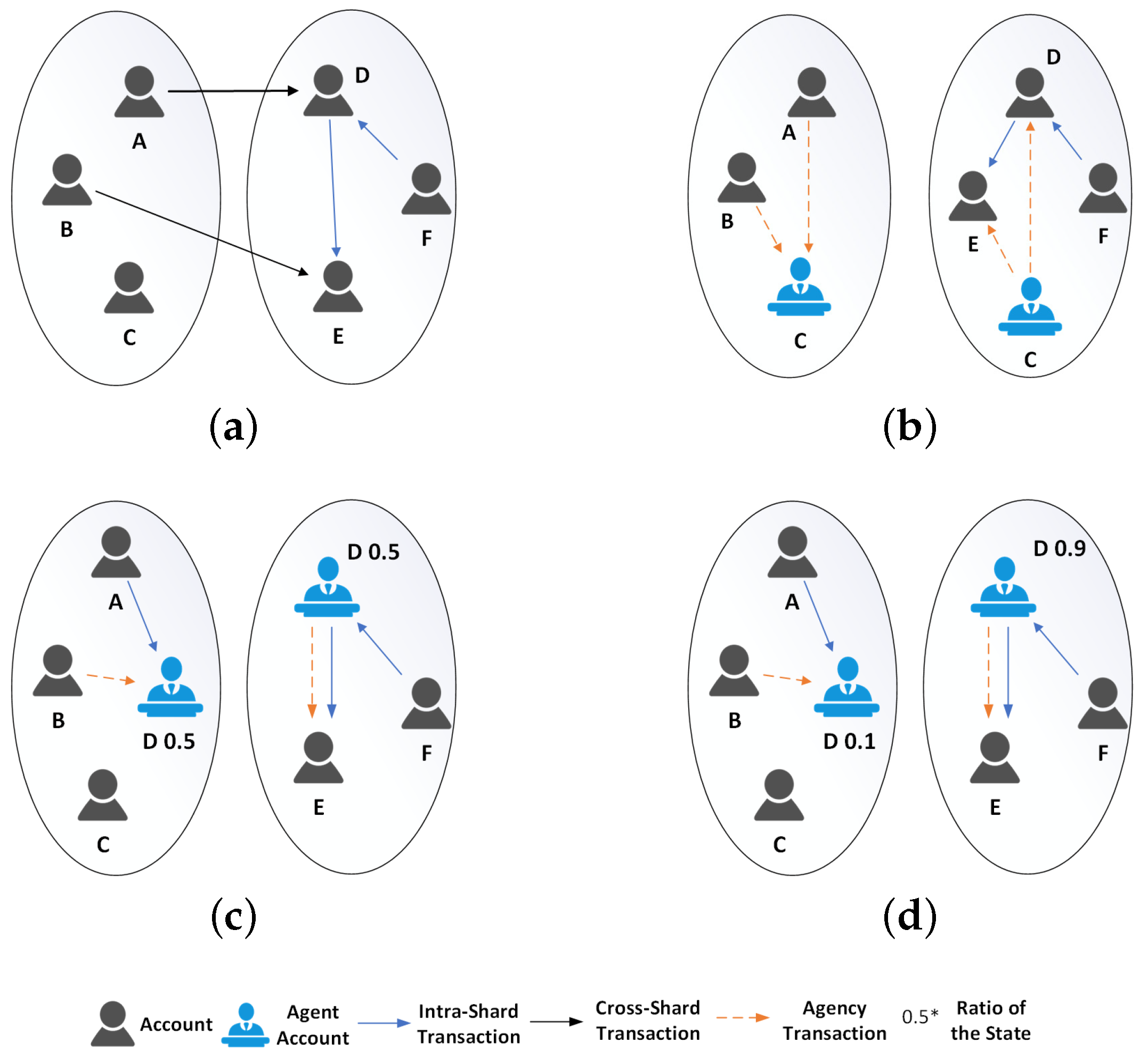
4.1. Formulation of Distribution Problem
4.2. Optimized Account State Distribution Algorithm
4.3. State Flow Mechanism
- Verify : Confirm that and that account a has an existing state in shard .
- Construct and transmit the message: Shard sends a message to shard : . The corresponds to the current epoch of , preventing account migration desynchronization due to transmission delays. To protect against malicious nodes replaying to increase account a’s balance, a nonce field is included in the message. The is a digest of the message content to ensure its integrity and immutability. is the signature of shard , guaranteeing the authenticity of the message and preventing repudiation.
- Update local ledger: When receives the message , it verifies the signature and hash values, verifies the nonce and EpochId, and then updates the local ledger state accordingly.
- Account i initiates a withdraw transaction on source shard , specifying destination shard and transfer amount . To minimize the frequency of CSAT triggers, account i may adjust the transfer amount based on its circumstances, provided the amount is not less than the CSAT-triggering transaction amount . After broadcasting transaction in , once is confirmed, i’s state in is reduced by , and i receives proof of the successful deduction, denoted as .
- LinkAgent i, based on and , constructs a deposit transaction on destination shard . Upon broadcasting transaction in , and after is confirmed, i’s state in is increased by .
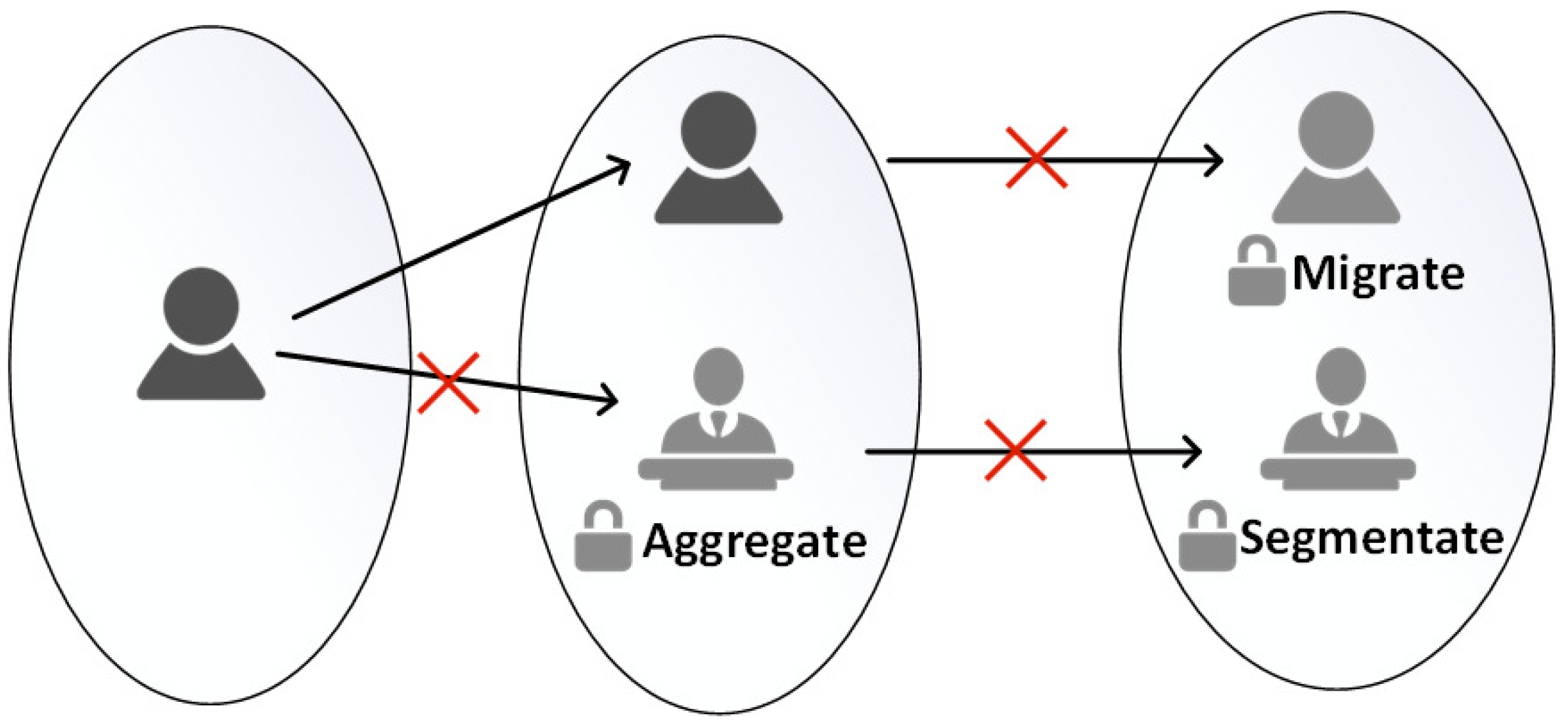
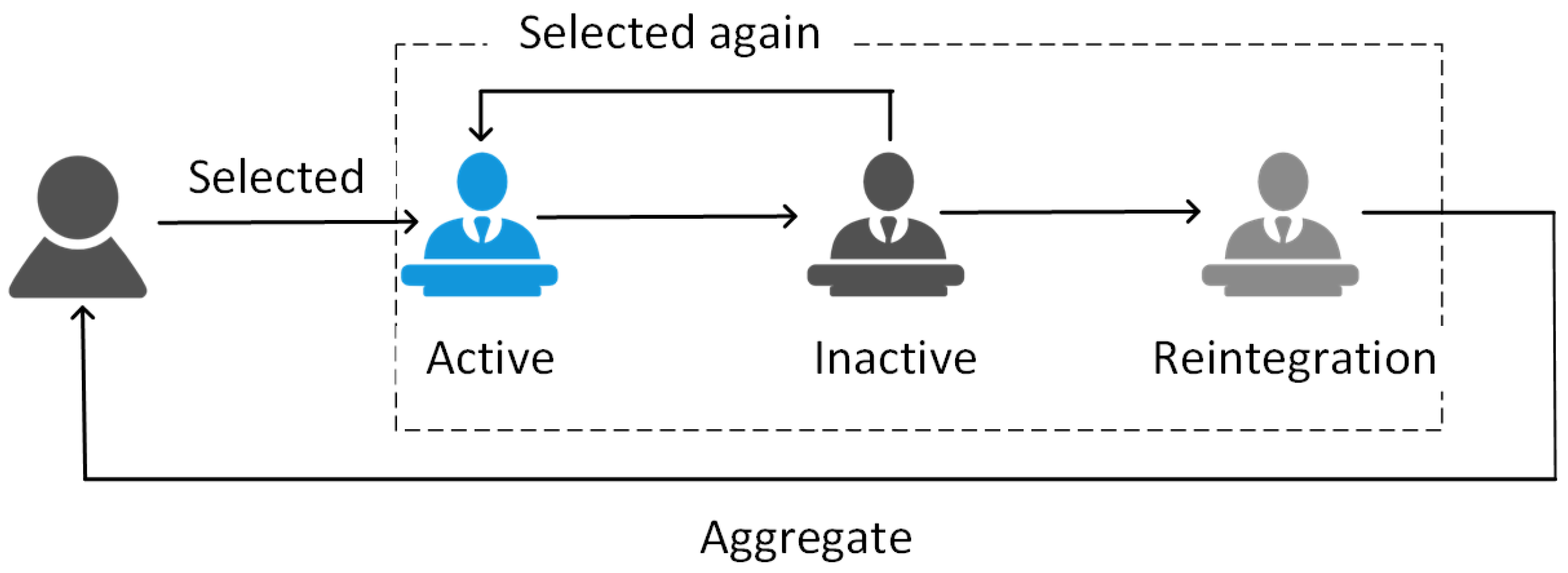
4.4. Smooth Transition
4.5. Real-Time Monitoring and Feedback
5. Experimental Results
- (1).
- Monoxide [5]: Monoxide allocates accounts by taking the first few bits of the hash address and applying modulo with the number of shards to determine the shard assignment. For cross-shard transactions, Monoxide employs a relay transaction mechanism. When a cross-shard transaction occurs, the source shard generates a relay transaction and updates its internal state. This relay transaction is then broadcast to the destination shard, which directly references the updated state from the source shard without requiring direct synchronization.
- (2).
- BrokerChain [9]: Similar to Monoxide, BrokerChain allocates accounts using the first few bits of the hash address and applying modulo with the number of shards. However, for cross-shard transactions, BrokerChain introduces intermediary accounts called brokers. Cross-shard transactions are split into two sub-transactions: the first half involves the sender transferring assets to the broker in the source shard. Once confirmed, the broker initiates the second half of the transaction, transferring the assets to the recipient in the destination shard. The transaction is considered successful once the second sub-transaction is confirmed.
- (3).
- CLPA-Broker [11]: CLPA-Broker uses the CLPA community detection algorithm for account allocation. Its approach to handling cross-shard transactions is similar to BrokerChain, utilizing brokers to split transactions into two phases for secure processing.
5.1. Comparing with Baselines
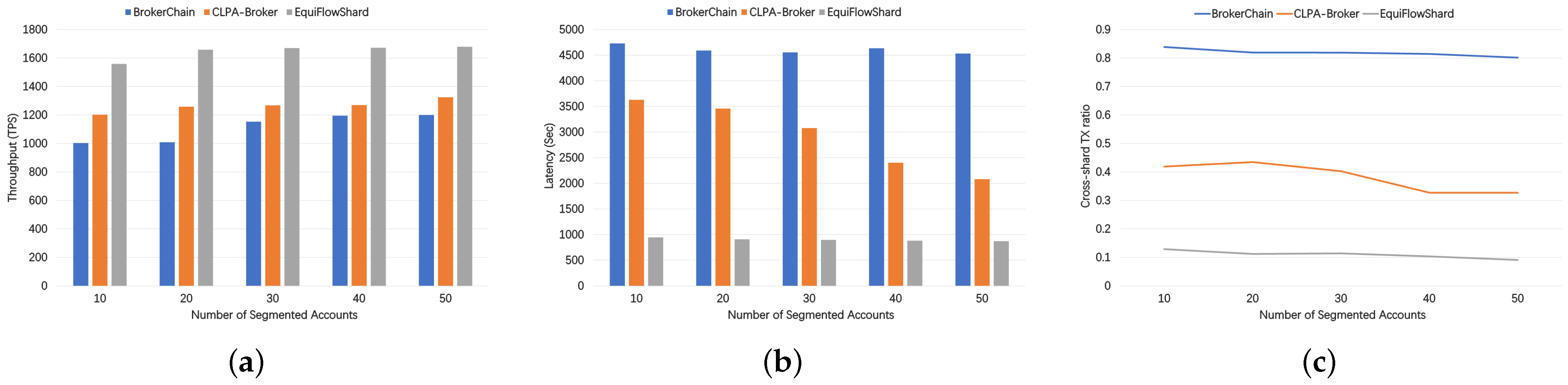
5.2. The Effect of the Number of Segmented Accounts
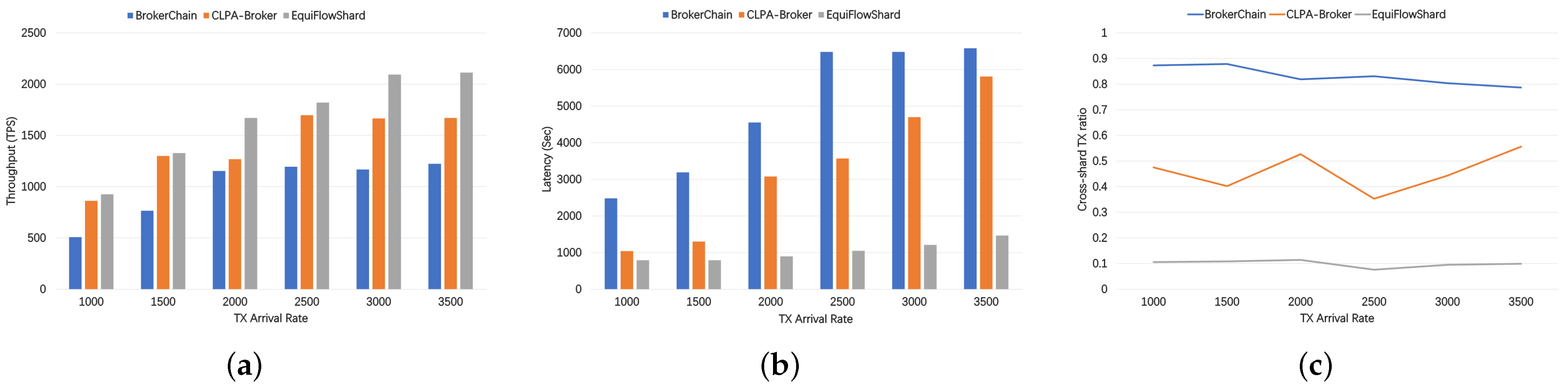
5.3. The Effect of TX Arrival Rate
6. Discussion
6.1. System Security
6.2. LinkAgent Security
- (a).
- Sending meaningless requests: Malicious LinkAgents may generate a large number of invalid cross-shard transaction requests, increasing inter-shard communication overhead. This can cause transaction queues in the pools to grow rapidly, leading to system performance degradation or even congestion. To address this, the system can employ real-time monitoring to identify accounts generating frequent invalid requests and impose penalties, such as revoking LinkAgent status, confiscating collateral, or expelling the account. Additionally, request frequency limits can be established to flag and penalize accounts exceeding thresholds. Nodes can further prioritize economically valuable transactions when generating blocks, effectively filtering out invalid requests to optimize system throughput.
- (b).
- Delay attacks: Malicious LinkAgents may intentionally delay processing cross-shard transaction requests during periods of high congestion, creating cascading delays that increase transaction confirmation times and degrade user experience. To mitigate this, the system can dynamically adjust the distribution of LinkAgents, introducing additional agents to alleviate congestion. Real-time monitoring of transaction processing times can identify and penalize LinkAgents causing abnormal delays. However, defining and adapting delay thresholds dynamically based on network conditions remains challenging, and future work will explore effective solutions in this area.
- (c).
- Malicious exit or offline behavior: Malicious LinkAgents may intentionally exit or go offline at critical moments, disrupting the completion of cross-shard transactions. As previously explained, even if a LinkAgent exits or goes offline, token lock mechanisms and timeout rollback mechanisms ensure the atomicity of cross-shard transactions. However, such behavior increases the system’s resource burden for handling rollbacks and amplifies the load on other LinkAgents, further degrading performance under high congestion. To counteract this, the system can pre-configure backup global LinkAgents to automatically take over transaction processing when primary LinkAgents fail. Furthermore, designing improved cross-shard transaction mechanisms to penalize malicious LinkAgents by confiscating their collateral while completing transactions without triggering rollbacks will be prioritized in future research. These measures aim to enhance the robustness and reliability of the sharding system under adverse scenarios.
6.3. Future Prospects
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Luu, L.; Narayanan, V.; Zheng, C.; Baweja, K.; Gilbert, S.; Saxena, P. A secure sharding protocol for open blockchains. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 17–30. [Google Scholar]
- Zamani, M.; Movahedi, M.; Raykova, M. Rapidchain: Scaling blockchain via full sharding. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, Toronto, ON, Canada, 15–19 October 2018; pp. 931–948. [Google Scholar]
- Kokoris-Kogias, E.; Jovanovic, P.; Gasser, L.; Gailly, N.; Syta, E.; Ford, B. Omniledger: A secure, scale-out, decentralized ledger via sharding. In Proceedings of the 2018 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 21–23 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 583–598. [Google Scholar]
- Nguyen, L.N.; Nguyen, T.D.; Dinh, T.N.; Thai, M.T. Optchain: Optimal transactions placement for scalable blockchain sharding. In Proceedings of the 2019 IEEE 39th International Conference on Distributed Computing Systems (ICDCS), Dallas, TX, USA, 7–9 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 525–535. [Google Scholar]
- Wang, J.; Wang, H. Monoxide: Scale out blockchains with asynchronous consensus zones. In Proceedings of the 16th USENIX Symposium on Networked Systems Design and Implementation (NSDI 19), Boston, MA, USA, 26–28 February 2019; pp. 95–112. [Google Scholar]
- Hong, Z.; Guo, S.; Li, P.; Chen, W. Pyramid: A layered sharding blockchain system. In Proceedings of the IEEE INFOCOM 2021-IEEE Conference on Computer Communications, Virtual, 10–13 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–10. [Google Scholar]
- Li, M.; Lin, Y.; Zhang, J.; Wang, W. Jenga: Orchestrating smart contracts in sharding-based blockchain for efficient processing. In Proceedings of the 2022 IEEE 42nd International Conference on Distributed Computing Systems (ICDCS), Bologna, Italy, 10–13 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 133–143. [Google Scholar]
- Okanami, N.; Nakamura, R.; Nishide, T. Load balancing for sharded blockchains. In Proceedings of the Financial Cryptography and Data Security: FC 2020 International Workshops, AsiaUSEC, CoDeFi, VOTING, and WTSC, Kota Kinabalu, Malaysia, 14 February 2020; Revised Selected Papers 24. Springer: Berlin/Heidelberg, Germany, 2020; pp. 512–524. [Google Scholar]
- Huang, H.; Peng, X.; Zhan, J.; Zhang, S.; Lin, Y.; Zheng, Z.; Guo, S. Brokerchain: A cross-shard blockchain protocol for account/balance-based state sharding. In Proceedings of the IEEE INFOCOM 2022-IEEE Conference on Computer Communications, Virtual, 2–5 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1968–1977. [Google Scholar]
- Li, M.; Wang, W.; Zhang, J. LB-Chain: Load-balanced and low-latency blockchain sharding via account migration. IEEE Trans. Parallel Distrib. Syst. 2023, 34, 2797–2810. [Google Scholar] [CrossRef]
- Li, C.; Huang, H.; Zhao, Y.; Peng, X.; Yang, R.; Zheng, Z.; Guo, S. Achieving scalability and load balance across blockchain shards for state sharding. In Proceedings of the 2022 41st International Symposium on Reliable Distributed Systems (SRDS), Vienna, Austria, 19–22 September 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 284–294. [Google Scholar]
- Al-Bassam, M.; Sonnino, A.; Bano, S.; Hrycyszyn, D.; Danezis, G. Chainspace: A sharded smart contracts platform. arXiv 2017, arXiv:1708.03778. [Google Scholar]
- Bagaria, V.; Kannan, S.; Tse, D.; Fanti, G.; Viswanath, P. Prism: Deconstructing the blockchain to approach physical limits. In Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, London, UK, 11–15 November 2019; pp. 585–602. [Google Scholar]
- Tao, Y.; Li, B.; Jiang, J.; Ng, H.C.; Wang, C.; Li, B. On sharding open blockchains with smart contracts. In Proceedings of the 2020 IEEE 36th International Conference on Data Engineering (ICDE), Dallas, TX, USA, 20–24 April 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1357–1368. [Google Scholar]
- Jia, L.; Liu, Y.; Wang, K.; Sun, Y. Estuary: A Low Cross-Shard Blockchain Sharding Protocol Based on State Splitting. IEEE Trans. Parallel Distrib. Syst. 2024, 35, 405–420. [Google Scholar] [CrossRef]
- Jiang, S.; Cao, J.; Tung, C.L.; Wang, Y.; Wang, S. Sharon: Secure and Efficient Cross-shard Transaction Processing via Shard Rotation. In Proceedings of the IEEE INFOCOM 2024—IEEE Computer Communications, Vancouver, BC, Canada, 20–23 May 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 2418–2427. [Google Scholar]
- Li, P.; Song, M.; Xing, M.; Xiao, Z.; Ding, Q.; Guan, S.; Long, J. SPRING: Improving the Throughput of Sharding Blockchain via Deep Reinforcement Learning Based State Placement. In Proceedings of the ACM on Web Conference 2024, Virtual, 13–17 May 2024; pp. 2836–2846. [Google Scholar]
- Castro, M.; Liskov, B. Practical byzantine fault tolerance. In Proceedings of the OsDI, New Orleans, LA, USA, 22–25 February 1999; Volume 99, pp. 173–186. [Google Scholar]
- Zhang, S.; Lee, J.H. Double-spending with a sybil attack in the bitcoin decentralized network. IEEE Trans. Ind. Inform. 2019, 15, 5715–5722. [Google Scholar] [CrossRef]
- Puttaswamy, K.P.; Zheng, H.; Zhao, B.Y. Securing structured overlays against identity attacks. IEEE Trans. Parallel Distrib. Syst. 2008, 20, 1487–1498. [Google Scholar] [CrossRef]
- Awerbuch, B.; Scheideler, C. Towards a scalable and robust DHT. In Proceedings of the Eighteenth Annual ACM Symposium on Parallelism in Algorithms and Architectures, Cambridge, MA, USA, 30 July–2 August 2006; pp. 318–327. [Google Scholar]
- Xie, J.; Szymanski, B.K.; Liu, X. Slpa: Uncovering overlapping communities in social networks via a speaker-listener interaction dynamic process. In Proceedings of the 2011 IEEE 11th International Conference on Data Mining Workshops, Vancouver, BC, Canada, 11 December 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 344–349. [Google Scholar]
- Huang, H.; Ye, G.; Chen, Q.; Yin, Z.; Luo, X.; Lin, J.; Yang, Q.; Zheng, Z. Blockemulator: An emulator enabling to test blockchain sharding protocols. arXiv 2023, arXiv:2311.03612. [Google Scholar]
- Wood, G. Ethereum: A secure decentralised generalised transaction ledger. Ethereum Proj. Yellow Pap. 2014, 151, 1–32. [Google Scholar]
- Chen, Q.; Huang, H.; Yin, Z.; Ye, G.; Yang, Q. Broker2Earn: Towards Maximizing Broker Revenue and System Liquidity for Sharded Blockchains. In Proceedings of the IEEE INFOCOM 2024-IEEE Conference on Computer Communications, Vancouver, BC, Canada, 20–23 May 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 251–260. [Google Scholar]

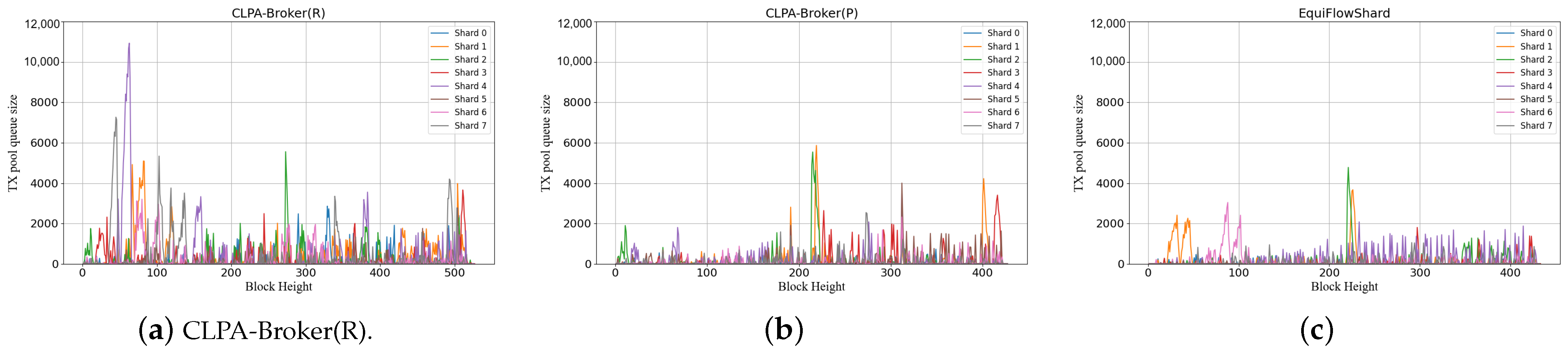
| Method | TPS | TCL (s) | CTR |
|---|---|---|---|
| Monoxide | 1052 | 1,427,721 | 0.8817 |
| BrokerChain(R) | 918 | 6499 | 0.8535 |
| CLPA-Broker(R) | 1296 | 1691 | 0.4527 |
| BrokerChain(P) | 1595 | 1271 | 0.3572 |
| CLPA-Broker(P) | 1607 | 967 | 0.1583 |
| EquiFlowShard | 1685 | 862 | 0.0632 |
| Method | Number |
|---|---|
| BrokerChain(H) | 18,261 |
| CLPA-Broker(H) | 26,565 |
| EquiFlowShard () | 24,973 |
| EquiFlowShard () | 17,499 |
| EquiFlowShard () | 3298 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Wu, Y.; Li, T. EquiFlowShard: A Blockchain Sharding Protocol with Optimized Account Distribution. Information 2025, 16, 92. https://doi.org/10.3390/info16020092
Chen Y, Wu Y, Li T. EquiFlowShard: A Blockchain Sharding Protocol with Optimized Account Distribution. Information. 2025; 16(2):92. https://doi.org/10.3390/info16020092
Chicago/Turabian StyleChen, Yemin, Yongdong Wu, and Tong Li. 2025. "EquiFlowShard: A Blockchain Sharding Protocol with Optimized Account Distribution" Information 16, no. 2: 92. https://doi.org/10.3390/info16020092
APA StyleChen, Y., Wu, Y., & Li, T. (2025). EquiFlowShard: A Blockchain Sharding Protocol with Optimized Account Distribution. Information, 16(2), 92. https://doi.org/10.3390/info16020092





