Exchangeability and Bayesian Inference: A Theoretical and Computational Framework for Reliable Experimental Data Analysis

Abstract

Exchangeability is a foundational concept in Bayesian statistics, crucial for ensuring the validity and generalizability of inferences from experimental data. This paper presents a theoretical and computational framework for understanding the role of exchangeability in the reliability of scientific conclusions, with specific reference to psychology, neuroimaging, and clinical trials. We build on de Finetti’s representation theorem to show how exchangeability enables using hierarchical Bayesian models, and we analyze how its violation can lead to interpretative errors and paradoxes, such as Simpson’s Paradox. In addition to theoretical discussion, we present practical strategies to evaluate and enforce exchangeability, including randomization, matching, stratification, and hierarchical modeling. We also introduce computational tools—such as the Shuffle Test and Stratified Bootstrap—to empirically test for exchangeability and detect latent structures in the data. The novelty of this work lies in unifying theoretical reasoning and empirical testing within a single framework that bridges de Finetti’s representation theorem and resampling-based diagnostics. By providing concrete tools to evaluate exchangeability prior to model fitting, the proposed approach introduces a pre-analysis verification step that strengthens the reliability and transparency of Bayesian inference. Our results emphasize that exchangeability is not merely a technical assumption, but a structural property that governs the coherence and informational integrity of the data. This framework provides both conceptual clarity and operational tools for researchers aiming to perform robust Bayesian inference in complex and heterogeneous datasets.

1. Introduction

Recent years have witnessed a huge increase in the volume and complexity of data accessible to scientists across many different disciplines such as machine learning, pattern recognitions, and genetics, just to name a few. This “deluge of data” [1] has led some to suggest that a new epistemological paradigm has arisen in which models and theories have become redundant. Although the grandiose claims about the “end of theory” [1] and the obsolescence of the scientific method have not been substantiated, the notion persists that data alone can provide enough information to address scientific questions. This perspective overlooks that employing big data presents certain problems, as noted in [2]. In particular, the heterogeneous nature of big data can pose significant concerns regarding the stability and replicability of experimental outcomes.

Several studies have shown that a significant fraction of the scientific literature has reproducibility problems. For example, in psychology, a famous 2015 study attempted to reproduce 100 experiments published in high-impact journals and found that less than 40 percent produced significant results similar to the originals [3]; in neuroimaging, using different analysis pipelines can lead to discordant results, calling into question the reliability of conclusions [4]; and in clinical trials, differences in patient selection or randomization can lead to outcomes that do not replicate in different settings [5].

There are many factors that can compromise the replicability or reproducibility of trials: selection bias, variations in experimental protocols, use of inappropriate statistical models, selective publication, and p-hacking [6]. To date, several solutions have been proposed to improve reproducibility, including pre-analytic recording of studies, publication of data and source code, and independent replication of results [7].

A commonly overlooked factor in replicating scientific experiments is assuming that collected data are exchangeable. According to de Finetti’s concept of exchangeability [8,9,10] data are exchangeable if their joint distribution of data does not depend on the order of observations. This principle is essential to ensure that statistical inferences are valid and generalizable.

Despite its foundational role in Bayesian inference, exchangeability has received limited attention in empirical applications. While de Finetti’s theorem is widely cited in theoretical discussions (e.g., [9]), few studies have investigated how to verify exchangeability in real-world data. Gelman and Hill [11] and Kruschke [12] advocate for hierarchical models under the assumption of exchangeability, but do not provide diagnostic tools for testing it.

Some recent works have proposed algorithmic or graphical approaches to assess exchangeability, particularly in time series ([13,14]) and causal inference contexts [15], but these remain domain-specific and underutilized. Nonparametric tests such as permutation methods and bootstrap techniques have been suggested as general tools for checking structural assumptions, but their application to exchangeability has not been systematically explored.

Our contribution is twofold: (1) we clarify the conceptual and inferential role of exchangeability in Bayesian analysis, and (2) we propose a practical, general-purpose procedure—based on Shuffle and Stratified Bootstrap tests—to empirically assess whether the data structure supports the use of exchangeability-based models.

De Finetti’s Theorem provides a formal basis for the Bayesian approach: it shows that if a sequence of random variables is exchangeable, then it can be interpreted as a mixture of independent and identically distributed (iid) distributions, conditional on a latent parameter. In other words, exchangeability justifies using probabilistic models based on a latent hierarchical structure, rather than requiring absolute independence among observations.

Several authors have addressed the role of exchangeability in Bayesian inference and probabilistic modeling. Foundational work by Diaconis and Freedman [9] and Aldous [10] expanded de Finetti’s representation to finite and partially exchangeable sequences. More recent treatments, such as those by Gelman et al. [16], Kruschke [12], and Dawid [17], emphasize the practical implications of exchangeability in hierarchical modeling and causal inference.

However, while the theoretical basis is well-established, relatively few studies have focused on empirical methods to assess exchangeability in applied contexts. Strategies such as randomization and stratified design are commonly suggested [18,19], but more recent contributions have proposed resampling-based techniques—including permutation tests, bootstrap procedures, and simulation-based diagnostics—to test for violations of exchangeability under realistic data conditions [11]. Despite these efforts, a general, operational framework for empirically verifying exchangeability in experimental data remains lacking.

This property has critical implications for data analysis in psychology, neuroimaging, and clinical trials, where the presence of hidden subgroups or uncontrolled factors can make observations non-exchangeable, leading to erroneous conclusions. A famous example is Simpson’s Paradox [20,21,22], in which an effect observed in separate groups can reverse when data are aggregated without adequately considering their latent structure.

This paper seeks to provide a clear picture of the concept of exchangeability, illustrating its role in Bayesian statistics through de Finetti’s Theorem, using concrete examples of how violations of exchangeability can distort results and lead to interpretive paradoxes, such as Simpson’s Paradox. We then propose a computational approach based on resampling methods (Shuffle Test and Stratified Bootstrap) to empirically assess exchangeability, and we discuss strategies—including hierarchical Bayesian models and stratified analysis—to control for its violation in experimental data.

• Statement of the Problem

While the theoretical foundations of exchangeability are well established, current research lacks a general, operational framework that allows scientists to empirically verify whether this assumption holds in real-world data before applying hierarchical Bayesian models. This gap has important consequences: if the data are not exchangeable, probabilistic models built upon this assumption may yield biased or non-replicable conclusions. This issue is particularly critical in disciplines such as psychology, neuroimaging, and clinical research, where heterogeneous samples and hidden subgroups are common.

The purpose of this paper is therefore to address this gap by integrating theoretical reasoning and empirical diagnostics into a single framework. Specifically, we reinterpret two nonparametric techniques—the Shuffle Test and the Stratified Bootstrap—as empirical tests of permutation-invariance and within-stratum stability, thus providing a concrete way to assess exchangeability before inference.

• Contributions

This work contributes both conceptually and operationally to the study of exchangeability in Bayesian inference.

First, it unifies theoretical, methodological, and computational perspectives by linking de Finetti’s representation theorem with empirical diagnostics.

Second, it reinterprets classical resampling methods—the Shuffle Test and the Stratified Bootstrap—as direct tests of the exchangeability assumption, quantifying permutation-invariance and within-stratum stability in observed data.

Third, it provides a practical protocol that researchers can apply before hierarchical or regression modeling, serving as a “pre-analysis gate” to verify whether the foundational assumption of exchangeability is plausible in their dataset.

Finally, the paper illustrates applications in psychology, neuroimaging, and clinical trials, emphasizing how violations of exchangeability can explain replication failures and paradoxical effects such as Simpson’s Paradox.

2. The Concept of Exchangeability

As stated in the introduction, exchangeability is a fundamental concept in Bayesian statistics and plays a key role in the proper interpretation of experimental data. Introduced by Bruno de Finetti [23], the principle of exchangeability states that the order in which we observe data should not influence the statistical inferences we draw from them. This concept is closely related to the idea that, if we have no special reason to distinguish observations, we should treat them as if they were generated from the same underlying distribution.

In intuitive terms, a sequence of data is exchangeable if the probability of observing a certain set of outcomes does not change if we reorder the observations. A simple example is as follows: suppose we have a set of responses to a psychological test collected from a sample of participants. If we can exchange the results between subjects without altering the distribution of observed scores, then we can say that the data are exchangeable. However, if the sample consists of two distinct groups (e.g., adolescents and adults), treating all the data as a single exchangeable population may lead to erroneous inferences.

From a mathematical point of view, a sequence of random variables $\{X_1,X_2,...,X_n\}$ is exchangeable if the following property holds for each permutation π of the indices:

$$P\left(X_1,X_2,\dots ,X_n\right)=P\left(X_{\pi \left(1\right)},X_{\pi \left(2\right)},\dots ,X_{\pi \left(n\right)}\right)$$

(1)

In other words, the joint distribution of variables is invariant to any rearrangement of observations.

Note that exchangeability is a structural property. We define a structural property as an invariance constraint on a dataset’s joint probability distribution that remains unchanged under a transformation group 𝔾 acting on the observation indices. A property is structural when it limits the admissible transformations of the data without altering the information relevant to inference.

To make this property clear consider the permutation group 𝔾 on n indices. For any permutation π of {1, …, n} then $p(x_1,x_2,\dots ,x_n)=p(x_{\pi \left(1\right)},x_{\pi \left(2\right)},\dots ,x_{\pi \left(n\right)})$.

This formulation clarifies that structural is not to be intended in a “conceptual” or “philosophical” sense: it refers to a precise invariance condition—permutation-invariance—that preserves the informational integrity of the data and underlies de Finetti’s representation theorem.

A trivial case of exchangeability occurs when the random variables are independent. Two, or more, random variables are independent if and only if $P\left(X_1,X_2,...,X_n\right)$ can be factorized in the product of the probability of each random variable, and thus, exchangeability is ensured by the commutativity of the product. In other words, exchangeability is a weaker condition than independence: exchangeability does not exclude the presence of structured dependence between observations. For instance, consider a bivariate normal distribution of variables x and y with the same means $\mu =0$, ${\sigma }_x={\sigma }_y=1$ and correlation coefficient $\rho \ne 0$: the probability density is

$$p\left(x,y\right)=p\left(y,x\right)\propto \exp [-{\displaystyle \frac{1}{2\left(1-{\rho }^2\right)}}\left(x^2+y^2-2\rho xy\right)]$$

(2)

Clearly the variables are exchangeable but not independent.

It is straightforward to prove that linear combinations of independent variables are exchangeable, a sufficient condition is that the transformation be invertible. Although there are cases in which linear combinations of independent variables are in turn independent, the Damois–Skitovic theorem states that normal distribution is necessary—but not sufficient—for independence, meaning some variables can be exchangeable without being independent.

In experimental design, exchangeability guarantees homogeneity—even with correlations—since subdividing data yields the same results as using the aggregated data. On the other hand, verification of exchangeability in experimental data is essential to ensure the validity of statistical inferences. If observations are not exchangeable, using models that assume independence or homogeneity can lead to incorrect conclusions. Let us look at some real-world examples where exchangeability is respected and others where it is violated, with possible consequences for data analysis.

For example, consider an experiment in which reaction time to a visual stimulus is measured in a random sample of college students of the same age and background. Since the subjects have similar characteristics and are randomly selected, we can reasonably assume that their responses are exchangeable: the order in which we analyze the data does not change their distribution.

Suppose now that the same experiment is performed in two separate groups: college students (20–25 years old) and seniors (65–75 years old). If data from both groups are aggregated without regard to age, exchangeability is violated, since responses are affected by systematic differences in cognitive and motor skills. An analysis that ignores this distinction could lead to misleading conclusions, as in the case of Simpson’s Paradox, where an effect observed in subgroups may reverse when the data are aggregated. Similarly in a neuroimaging (fMRI) experiment in several subjects, each of whom is examined in a single independent experimental session. If participants are randomly sampled and their data have no dependencies, we can assume that observations are exchangeable between subjects. If, on the other hand, we analyze data from the same subject over the course of a neuroimaging session that lasts an hour, exchangeability is lost as brain activation levels change over time due to fatigue or adaptation to the stimulus, and later instants are correlated with earlier ones (time dependence).

Finally, in a clinical trial, a drug is tested on different patients, each of whom receives a single dose and is monitored for effects. If patients are randomly assigned to treatment and control groups, we can assume that observations are exchangeable between subjects. If, on the other hand, we consider repeated measures on the same patient receiving the drug for multiple weeks, the data are no longer exchangeable because the patient may develop tolerance or sensitization to the drug over time, and early and late responses are not interchangeable as the experimental context changes with treatment progression. If we treat these observations as independent and exchangeable, we may underestimate or overestimate drug efficacy.

Thus, violation of exchangeability can compromise statistical inferences in different experimental contexts. A well-known case is provided by the Simpson’s Paradox, a counterintuitive statistical phenomenon that occurs when an observed trend in subgroups of data is reversed when the data are aggregated. This paradox occurs when data aggregation ignores a latent factor affecting the results, leading to misinterpretations. The violation of exchangeability is often the main cause of this phenomenon: if data come from different populations or are influenced by hidden variables, treating them as a single set can distort conclusions.

Formally, Simpson’s Paradox occurs when for two variables. $X$ e $Y$, the relationship observed at the aggregate level is opposite to the relationship observed within subgroups defined by a third variable $Z$:

$$P\left(Y\mid X\right)>P\left(Y\mid X^{\prime }\right)$$

(3)

for aggregate data, but

$$P\left(Y\mid X,Z\right)<P\left(Y\mid X^{\prime },Z\right)$$

(4)

Within each subgroup $Z$. This implies that if we do not properly consider the structure of the data, we may draw incorrect conclusions about causal relationships.

Suppose we analyze the success rate of two medical treatments, A and B, to treat a disease. The aggregate data (

Table 1. Aggregated treatment success rates before stratification.

Treatment	Successes	Failures	Percentage Successes
A	200	800	20%
B	400	600	40%

) show that treatment B has a higher success rate than treatment A: this table presents the overall success rates of two medical treatments, A and B, before stratification based on disease severity. The aggregate data suggests that treatment B has a higher success rate (40%) compared to treatment A (20%). However, this conclusion does not account for possible confounding factors such as the severity of the disease, which may influence treatment outcomes. This unstratified analysis demonstrates the risk of misinterpretation due to the assumption of exchangeability.

Based solely on these data, treatment B shows more favorable results. Now consider patients to be divided into two subgroups based on disease severity (mild or severe) (

Table 2. Treatment success rates stratified by disease severity.

Gravity	Treatment	Successes	Failures	Percentage Successes
Mild	A	190	10	95%
Mild	B	350	50	87.5%
Severe	A	10	790	1.25%
Severe	B	50	550	8.3%

). The table below shows the success rates of treatments A and B after stratification based on disease severity (mild vs. severe cases). When analyzed within each severity group, treatment A consistently demonstrates a higher success rate than treatment B. However, in the aggregated data (Table 1), the overall trend was reversed due to a higher proportion of severe cases receiving treatment A. This illustrates Simpson’s Paradox, emphasizing the importance of stratification when exchangeability is violated.

In both subgroups, treatment A has a higher success rate than treatment B. But when the data are aggregated, the opposite appears to be true. This happens because more severe patients received treatment A, while more patients with mild disease received treatment B, introducing a selection bias. Thus, aggregation without considering hidden variables can completely overturn the interpretation of the data.

Considering the domains we have considered this means, for example, that in a psychology experiment if the number of males and females in the sample is unbalanced, the aggregated result could give a misleading indication. In neuroimaging this situation can occur if the results are aggregated without considering the differences in the methods of obtaining a spurious effect that could lead to erroneous conclusions because the differences could be due to pre-processing and not to actual biological differences. Finally, in clinical trials if a new drug is tested on a heterogeneous population of patients without stratification by age, for example, The drug appears ineffective.

In conclusion, Simpson’s Paradox shows that data aggregation can lead to misinterpretation if exchangeability is not considered. In the fields of psychology, neuroimaging, and clinical trials, it is essential to follow criteria such as stratifying into relevant subgroups, checking for exchangeability before making statistical inferences and using Bayesian models to handle heterogeneity in the data.

Theoretical Justification for the Proposed Method

The computational approach we propose—based on the Shuffle Test and the Stratified Bootstrap—is grounded in the conceptual framework of exchangeability, as formalized by de Finetti’s theorem. According to this theorem, an exchangeable sequence of random variables can be represented as a mixture of i.i.d. distributions conditional on a latent parameter. This insight provides the epistemic foundation for Bayesian hierarchical models: if the observations are exchangeable, then we can model them as arising from a shared underlying distribution with latent parameters.

However, in real-world experimental settings, the assumption of exchangeability cannot be taken for granted. Violations may arise due to the presence of latent subgroups, uncontrolled variables, or hidden biases in sampling. The methods we propose aim to empirically assess whether the assumption of exchangeability is justified in the observed data, before applying any hierarchical Bayesian model.

The Shuffle Test evaluates whether reordering labels affects the distribution of a test statistic, under the null hypothesis that data are exchangeable. The Stratified Bootstrap resamples within predefined groups and constructs a null distribution for the statistic of interest, allowing us to assess whether the observed difference is compatible with exchangeability. These techniques thus serve as empirical diagnostics for verifying the assumptions underpinning hierarchical Bayesian modeling.

3. De Finetti’s Theorem and Its Implication

Exchangeability implies a similarity among random variables that is made precise by De Finetti’s Theorem, one of the fundamental results of Bayesian statistics: the theorem states that if a sequence of random variables $X_1,X_2,X_3,\dots$ is exchangeable, then there exists a latent variable $\theta$ such that, conditional on $\theta$, the variables $X_i$ are independent and identically distributed (iid):

$$\left(X_1,X_2,\dots ,X_n\right)=\int P\left(X_1,X_2,\dots ,X_n\mid \theta \right)P\left(\theta \right)d\theta$$

(5)

Thus, exchangeable variables can be viewed as drawn from a mixture of iid distributions, with their variability explained by a latent parameter. In other words, if a sequence of data is assumed to be exchangeable any finite subset of them is the random sample of some model.

This result has profound implications in statistical modeling, particularly when the data comes from heterogeneous populations, as in clinical trials or neuroimaging studies. A direct consequence is that if we observe a sequence of data that appears exchangeable, we can model it as a distribution conditional on an unknown parameter governing its behavior. This is the principle on which hierarchical Bayesian models are based.

The theorem implies that if the data are exchangeable, there is no single underlying iid distribution, but rather a mixture of iid distributions, weighted by an a priori distribution on $\theta$. This result in Bayesian terms leads to the interpretation of $\theta$ as a measure of the latent heterogeneity in the data, the distribution $P\left(\theta \right)$ as the a priori distribution on population variability and finally that conditional on $\theta$, the data follow an iid distribution.

If we do not consider the role of $\theta$, we risk treating as homogeneous data that come from heterogenous subgroups, and as if they were i.i.d. without considering $\theta$. This factor frequently undermines the reliability of experimental replication.

In conclusion, de Finetti’s Theorem provides mathematical justification for the use of Bayesian inference, while in experimental practice it allows if the data are exchangeable to model their structure with a priori distribution over a latent parameter. It also tells us that if we do not verify exchangeability, we can make errors in the interpretation of results, and non-verification is a major cause of statistical bias, as in the case of Simpson’s Paradox.

In conclusion, de Finetti’s Theorem provides mathematical justification for using Bayesian inference, while in experimental practice it allows if the data are exchangeable to model their structure with a priori distribution over a latent parameter. It also tells us that if we do not verify exchangeability, we can make errors in the interpretation of results, and non-verification is a major cause of statistical bias, as in the case of Simpson’s Paradox. Finally, note that De Finetti’s theorem is an existence theorem and, as such, does not specify the parameter, which needs to be inferred from the properties of the process under study. This point is explained in the examples that follow. Another example can be found in [24].

• Example 1: episodic memory task

Suppose we study short-term memory using a free recall task. Each subject is shown a list of $m$ words and asked to recall as many as possible. For each subject $i$, we observe the number $x_i$ of correctly recalled words. Assuming all participants receive the same list, the maximum number of items recalled is fixed across subjects.

If the participants are similar (e.g., students from the same course, similar age, no known neurological conditions), it is reasonable to assume that the sequence $x_1,x_2,\dots ,x_n$ is exchangeable. De Finetti’s representation theorem then tells us that the observations are conditionally i.i.d. binomial given a latent parameter $\theta$, representing the average probability of recalling a word:

$$x_i\mid \theta \sim \mathrm{Binomial}(m,\theta )$$

(6)

The joint distribution of the data can then be written as:

$$P(x_1,\dots ,x_n)=\int {\prod }_{i=1}^n\mathrm{Binomial} (x_i\mid m,\theta )\hspace{0.17em}p(\theta )\hspace{0.17em}d\theta$$

(7)

A common choice for the prior $p\left(\theta \right)$, in the absence of prior information, is a non-informative Beta distribution:

$$\theta \sim \mathrm{Beta}(1,1)$$

(8)

After observing the data, the posterior distribution becomes:

$$\theta \mid x_1,\dots ,x_n\sim \mathrm{Beta}\left(1+\sum x_i,1+n\cdot m-\sum x_i\right)$$

(9)

This can be used to make predictions for a new subject via the Beta-Binomial predictive distribution.

• Example 2: reaction times in an attention task

To illustrate exchangeability using a Gaussian model, consider a selective attention experiment in which we measure participants’ reaction times (RTs) to a target stimulus. Participants are shown a series of visual stimuli on a screen. Occasionally, a target appears (e.g., a red arrow among blue arrows), and the subject must press a key as quickly as possible. We record the mean reaction time for each subject, resulting in a real-valued sequence $x_1,x_2,\dots ,x_n$.

If the subjects belong to a relatively homogeneous population—e.g., university students of similar age, education, and experimental conditions—we may assume that the order of the observations carries no information. This means we assume exchangeability of the sequence $x_1,x_2,\dots ,x_n$, which implies:

$$P(x_1,\dots ,x_n)=\int {\prod }_{i=1}^n\mathcal{N}(x_i\mid \mu ,{\sigma }^2)\hspace{0.17em}p(\mu ,{\sigma }^2)\hspace{0.17em}d\mu d{\sigma }^2$$

(10)

Under de Finetti’s theorem, this representation implies that there exists a latent distribution over parameters $\mu$ and ${\sigma }^2$ such that the $x_i$ are i.i.d. normal conditionally on those parameters:

$$x_i\mid \mu ,{\sigma }^2\sim \mathcal{N}(\mu ,{\sigma }^2)$$

(11)

In the absence of prior information, one can adopt a noninformative prior such as Bernardo’s reference prior. After observing the data, the posterior for $\mu$ follows a Student’s t distribution:

$$\mu \mid \mathbf{x}\sim t_{n-1}\left(\bar{x},{\displaystyle \frac{s^2}{n}}\right)$$

(12)

where $\bar{x}$ is the sample mean and $s^2$ the sample variance. The predictive distribution for the next observation also follows Student’s t:

$$x_{\mathrm{new}}\mid \mathbf{x}\sim t_{n-1}\left(\bar{x},s^2\left(1+{\displaystyle \frac{1}{n}}\right)\right)$$

(13)

• Example 3: Detecting Hidden Subgroup Structure

To illustrate how our methods can detect violations of exchangeability in realistic scenarios, we simulated a dataset composed of two latent subgroups. Specifically, we generated two samples of size $n=100$ each, drawn from normal distributions with different means:

• Group A: $\mathcal{N}\left(\mathrm{0,1}\right)$
• Group B: $\mathcal{N}\left(\mathrm{2,1}\right)$

The combined dataset mimics a situation in which data are collected from two distinct populations, but analyzed without accounting for subgroup structure.

When applying the Shuffle Test, the null distribution of the mean difference (obtained by permuting group labels) centered around 0, while the observed difference was far from the null and consistently fell in the tails—leading to rejection of exchangeability.

Similarly, the Stratified Bootstrap—performed by resampling within each group separately—produced a confidence interval that did not include the null value, correctly indicating a statistically significant difference. These results demonstrate the ability of our method to detect hidden structure in the data that would invalidate standard Bayesian models assuming full exchangeability.

This example highlights the importance of empirically testing the exchangeability assumption before applying statistical inference, particularly in fields where latent heterogeneity is common, such as psychology, neuroimaging, and clinical research.

4. Methods

In the previous section, we have seen that, for exchangeable variables, de Finetti’s representation theorem supports using Bayesian models [24], where the observed data are modeled as conditionally iid given a group-level or population-level distribution.

In practical applications, however, exchangeability can be compromised by the presence of hidden subgroups, stratification variables, or time dependencies; in these cases, using hierarchical models based on the assumption of exchangeable variables can lead to biased estimates and misleading inferences. Thus, effective strategies are needed to verify exchangeability: some methods will be reviewed next [17,18,19].

Our Approach vs. standard resampling.

Traditional permutation and bootstrap methods are typically used to test hypotheses about mean differences, variances, or distributional equality. In this paper, however, we reinterpret these tools as diagnostics of exchangeability itself.

Under this view, the Shuffle Test becomes a direct assessment of permutation-invariance of a target statistic under the null hypothesis of exchangeability, while the Stratified Bootstrap quantifies within-stratum stability and between-stratum divergence as indicators of structural non-exchangeability.

This reframing turns generic resampling tools into empirical tests of a model assumption, linking de Finetti’s representation theorem to operational data diagnostics. In doing so, our approach bridges the gap between theoretical Bayesian principles and practical model validation.

Randomization is the most effective method for ensuring exchangeability in experimental data. By randomly assigning subjects to experimental and control groups, we reduce the risk of confounding factors influencing the results. However, randomization is not always possible (e.g., observational studies) and does not guarantee that subgroups are perfectly balanced, especially in small samples.

If randomization is not feasible, matching can be used, which involves selecting pairs of similar observations (e.g., by age, gender, educational level) and comparing them directly. There exist different techniques for matching, among others propensity score matching (PSM), which pairs subjects based on an estimated probability of receiving a certain treatment, and exact matching, which couples only subjects with identical values for all key variables.

Another method is provided by hierarchical Bayesian models (or multilevel models) [11,20], which are powerful tools for dealing with non-exchangeability in experimental data because they allow for modeling variability between subgroups and individuals. With this method, data are treated as coming from multiple latent populations, each with its own parameter, and it avoids the assumption that all data are iid (independent and identically distributed), which is often unrealistic. Finally, if the data are not exchangeable, an effective technique is to perform stratified analysis, that is, to analyze subgroups separately to see if the results change. This technique consists of separating the data into relevant subgroups before performing statistical analyses, checking whether the effects observed in the subgroups are consistent with those aggregated, and using statistical interaction tests to check whether the subgroups respond differently to the treatment.

However, these methods involve identifying the various components to correctly generate the relevant groups. It is possible, however, to find out whether the data are exchangeable or not, without making any assumption on how to partition the sample. One such way is to generate data under the assumption of exchangeability and compare the results with the observed data, as is performed in the Shuffle Test, which is based on the idea that if the data are indeed exchangeable, then shuffling the observations between the groups should not change the distribution of the tested statistic (e.g., difference in averages); on the other hand, if after shuffling the statistic changes significantly, it means that the data are not exchangeable.

Our proposed method seeks to fill this gap by empirically testing the plausibility of exchangeability in the observed data, before such models are applied. In particular:

• The Shuffle Test exploits the principle that, under exchangeability, the test statistic (e.g., group difference) should not systematically change when the group labels are permuted. The choice of the mean difference as test statistic is motivated by its simplicity and interpretability. It captures the expected group-level effect under the hypothesis of no structural difference and is widely used in both classical and Bayesian frameworks. However, the method is flexible and can be extended to other statistics depending on the nature of the data. For instance, median difference or Kolmogorov–Smirnov statistics can be used when distributional assumptions are violated or when robustness is preferred.
  The key idea is that, under exchangeability, the distribution of the test statistic should remain invariant under permutations. A substantial deviation of the observed statistic from this distribution indicates a breakdown of the exchangeability assumption.
• The Stratified Bootstrap builds on the same logic, generating empirical confidence intervals within subgroups to detect whether between-group variability exceeds what would be expected under exchangeability. The Stratified Bootstrap maintains the original group sizes while resampling within each group independently. This procedure preserves the empirical group-level structure and prevents artificial mixing that would violate stratification.
  One important caveat, however, is that large imbalances in group sizes may affect the estimation of variance and lead to biased confidence intervals. In such cases, more robust resampling strategies or balanced bootstrap techniques may be considered.
  Overall, the Stratified Bootstrap allows for nonparametric inference while explicitly controlling for group membership, making it well-suited for assessing exchangeability in structured datasets.

Both techniques provide operational tools for assessing whether the assumption of exchangeability holds well enough to justify a hierarchical Bayesian modeling approach—or whether alternative strategies (e.g., stratification, matching, or separate modeling) should be considered.

In summary, our method operationalizes de Finetti’s and Bayesian principles by offering empirical diagnostics that test whether the foundational assumption of exchangeability is met in the data to which probabilistic models will be applied.

Practical protocol (pre-analysis gate)

To make the proposed framework operational, we outline a step-by-step protocol that can be integrated into any analysis pipeline before model estimation:

Step 1—Identify the target statistic.

Select a summary statistic relevant to the hypothesis or model to be tested (e.g., mean difference, regression coefficient, correlation).

Step 2—Run the Shuffle Test.

Under the null hypothesis of exchangeability, permute observation labels and recompute the statistic to generate an empirical null distribution. If the observed value falls within this distribution, the assumption of exchangeability is plausible.

Step 3—Run the Stratified Bootstrap (if subgroups are present).

When covariates or known strata exist, perform bootstrapping within each stratum. Compare confidence intervals or predictive intervals across groups. Large between-stratum divergence signals a violation of exchangeability.

Step 4—Gate hierarchical modeling.

Proceed with hierarchical Bayesian or regression models only if diagnostics support exchangeability (globally or within strata). Otherwise, stratify the analysis, reweight samples, or adopt explicitly non-exchangeable models.

This protocol provides a concrete “pre-analysis gate” that links empirical diagnostics with the theoretical assumption of exchangeability, improving transparency and robustness in Bayesian data analysis.

The following table (

Table 3. Comparative strategies to assess and control exchangeability.

Strategy	Assumptions	Advantages	Limitations
Randomization	Feasible design	High internal validity	Not always possible
Matching	Measured covariates	Balances groups	Limited to observed variables
Stratification	Known subgroups	Improves interpretability	May reduce power
Hierarchical Models	Exchangeability within strata	Models latent structure	Requires model specification
Shuffle Test	Exchangeable under null	No distributional assumption	Computationally intensive
Stratified Bootstrap	Strata defined a priori	Respects group structure	Dependent on stratification quality

) summarizes the main strategies discussed above, comparing their assumptions, strengths, and limitations in addressing exchangeability in experimental data.

Controlling for exchangeability is essential to ensure the validity of experiments. Before drawing conclusions from experimental data, always check exchangeability to avoid interpretive errors.

5. Results

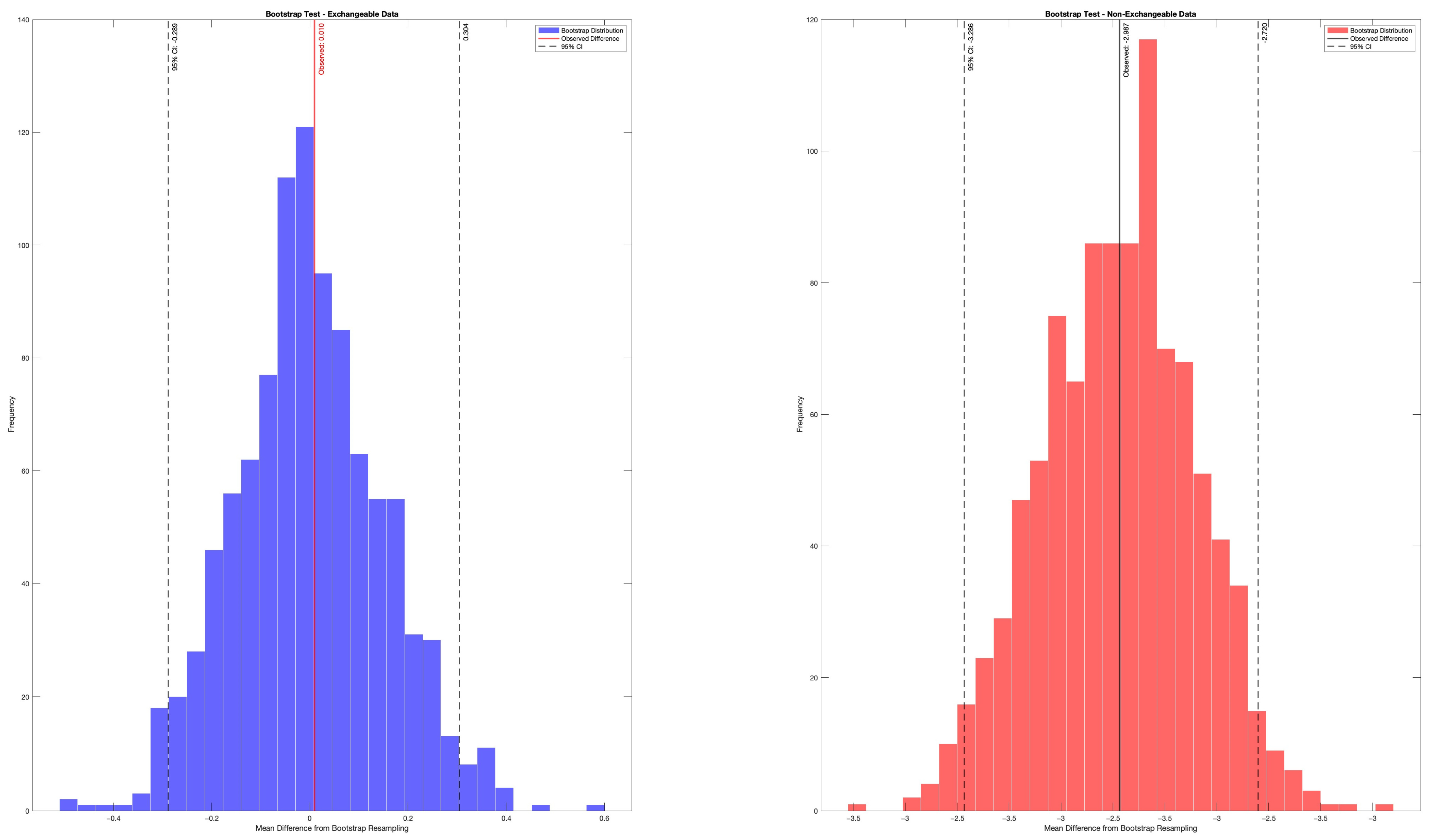
Before describing the algorithms in detail, we present two benchmark scenarios that illustrate how the proposed diagnostics behave under exchangeable and non-exchangeable conditions.

In the exchangeable scenario, data are generated from a single homogeneous population, and the observed statistic lies well within the empirical null distribution produced by the Shuffle Test; the corresponding bootstrap confidence intervals largely overlap across strata.

In the non-exchangeable scenario, hidden subgroup structure or systematic bias causes the observed statistic to fall in the tails of the permuted distribution and the bootstrap confidence intervals to diverge between strata.

These contrasting patterns provide an intuitive and empirical way to assess whether exchangeability holds before applying hierarchical or regression-based Bayesian models.

The algorithm considers two groups of data $X_1$ e $X_2$ and calculates a statistic of interest, for instance the difference of averages:

$$D_{\mathrm{orig}}=\mathrm{mean}\left(X_1\right)-\mathrm{mean}\left(X_2\right),$$

(14)

the two groups are then combined into a single dataset and the observations are randomly shuffled and assigned to two groups. Next, the statistics are recalculated for the new groups:

$$D_{\mathrm{perm}}^{\left(i\right)}=\mathrm{mean}\left(X_1^{\left(i\right)}\right)-\mathrm{mean}\left(X_2^{\left(i\right)}\right)$$

(15)

This procedure is repeated $N$ times (typically N = 1000), thus obtaining an empirical distribution of differences under the assumption of exchangeability. Finally, the p-value is calculated, which measures how many of the permuted differences $D_{\mathrm{perm}}$ are equal to or more extreme than the original difference $D_{\mathrm{orig}}$:

$$={\displaystyle \frac{\sum \mid D_{\mathrm{perm}}\mid \ge \mid D_{\mathrm{orig}}\mid }{N}}$$

(16)

If $p$ is small (e.g., <0.05), the exchangeability hypothesis is rejected.

The distribution of permuted differences and the position of the observed statistic under the null hypothesis of exchangeability are illustrated in Figure 1, which compares an exchangeable scenario with a non-exchangeable one.

The Shuffle Test is particularly useful for testing whether two groups come from the same distribution, identifying the presence of a hidden factor (confounder) and validating exchangeability hypotheses in Bayesian models.

An alternative to the Shuffle Test is provided by Layered Bootstrap, which is an extension of the classical bootstrap method, designed to handle situations in which data come from different subgroups (layers) (Figure 2). It is used when it is suspected that the data are not exchangeable, that is, each subgroup has different characteristics. The key idea is to sample with replacement within each stratum separately, instead of treating all data as a single set. This avoids introducing bias due to structural differences between groups.

The algorithm divides the data into strata by, for example, identifying membership groups defined by a variable C (e.g., gender, ethnicity, department, etc.). Each observation $X_i$ is associated with a layer $C_i$ And sampling with replacement is carried out within each layer. For each layer $S_k$, a new sample is randomly drawn with replacement, keeping the original stratum size. For example, if a group has 50 observations, the new sample will still contain 50 data but randomly chosen with replacement. For each bootstrap sample generated, a statistic (e.g., mean, variance, difference between groups) is computed and the process is repeated for N iterations (typically 1000+ times). From these results, a distribution of the statistics obtained from the bootstrap samples is created and confidence intervals, variances, and other metrics are calculated to assess the stability of the estimates. If the bootstrap distributions of the statistics differ significantly between groups, it means that the data are not exchangeable. Whereas if the confidence intervals overlap and the distributions are similar, the data are exchangeable.

Applications of this method are useful to correct bias due to inhomogeneous subgroups, analyze nonexchangeable data by separating subgroups with different characteristics, handle Simpson’s Paradox by analyzing whether the observed effect changes within subgroups, and improve statistical inference on heterogeneous data.

Limitations and Scope.

The proposed framework provides a practical diagnostic for assessing the plausibility of exchangeability, but it has some inherent limitations.

First, it evaluates exchangeability relative to a chosen statistic (e.g., mean difference or regression coefficient), not to the entire data-generating process.

Second, the reliability of both the Shuffle Test and the Stratified Bootstrap depends on sample size, group balance, and the quality of stratification; highly unbalanced or small samples may yield unstable results.

Third, these diagnostics do not replace model comparison or formal Bayesian updating—they serve as pre-analysis checks to ensure that subsequent modeling rests on coherent assumptions.

Finally, in datasets with temporal or spatial dependence, violations of exchangeability may require explicit non-exchangeable models (e.g., Gaussian processes, state-space models).

Future work should focus on extending these diagnostics to multivariate and hierarchical contexts and on developing automated procedures for detecting latent structure in complex datasets.

6. Conclusions

Exchangeability is a key concept in Bayesian statistics and probabilistic modeling, with deep implications for statistical inference and the validity of conclusions drawn from experiments. Its importance is often underestimated, but as it has been shown in this article, a violation of exchangeability can seriously compromise the interpretation of data, leading to misleading and sometimes paradoxical results, as in the case of Simpson’s Paradox.

De Finetti’s Theorem provides a sound theoretical basis for understanding exchangeability by showing how a sequence of exchangeable data can be viewed as a mixture of independent, identically distributed (iid) distributions, conditional on a latent parameter. This perspective provides a justification for using hierarchical Bayesian models, which allow for more accurate modeling of the structure of the data and allow for any heterogeneity present in the samples.

One of the most critical aspects of exchangeability concerns its impact on the reproducibility and replicability of scientific experiments. The reproducibility crisis that has affected many disciplines, from psychology to neuroimaging to clinical trials, is partly related to misuse of statistical models that incorrectly assume exchangeability of data. If data are not exchangeable, aggregating them without considering their latent structure can lead to incorrect inferences, compromising the ability to replicate results in subsequent studies.

We examined several methods to check and verify exchangeability in experimental data. Of these, randomization is the most effective tool to ensure that the collected data are indeed exchangeable, reducing the risk of bias due to uncontrolled latent factors. However, randomization is not always feasible, especially in observational studies, and in these cases, alternative strategies such as matching (e.g., Propensity Score Matching) or stratified analysis can be adopted, which allow comparison of more homogeneous groups and reduce bias due to differences in sample composition.

Another particularly effective approach is using hierarchical Bayesian models, which allow variability between subgroups to be modeled explicitly and incorporate a priori information about the structure of the data. These models are a particularly useful solution in contexts where exchangeability cannot be guaranteed a priori, such as in neuroimaging studies or clinical trials with heterogeneous populations.

In addition to theoretical methods and statistical models, we also discussed computational techniques that allow us to empirically verify exchangeability. The Shuffle Test and the Stratified Bootstrap are two particularly useful tools for testing whether data can be considered exchangeable or whether instead there are subgroups with different characteristics. These methods allow the observed distribution to be compared with simulated distributions under the assumption of exchangeability, providing empirical evidence on the validity of this assumption.

In this paper, we addressed a fundamental but often neglected issue in statistical modeling: whether the collected data can be legitimately treated as exchangeable. Building on the theoretical foundations laid by de Finetti, we developed a computational framework based on the Shuffle Test and Stratified Bootstrap to empirically assess this assumption in experimental datasets.

Through simulations and illustrative examples, we showed how violations of exchangeability—such as the presence of hidden subgroups—can lead to misleading statistical conclusions, even when standard assumptions like independence or identical distribution appear to hold.

Our approach offers a simple, interpretable, and general-purpose method to test the adequacy of exchangeability assumptions before applying Bayesian or frequentist models. This is particularly relevant in fields such as psychology, neuroscience, and medicine, where latent heterogeneity is common and sample sizes are often limited.

Nevertheless, the method has some limitations: it relies on resampling strategies that may be sensitive to unbalanced designs or small sample sizes, and it does not provide a formal statistical decision rule, but rather a diagnostic interpretation. Future work will extend this approach to multivariate and longitudinal data and investigate its integration into model selection and Bayesian updating pipelines.

7. Future Perspectives

As datasets continue to grow in size and complexity, the need for rigorous validation of statistical assumptions becomes more critical. Exchangeability plays a pivotal role in maintaining the informational coherence required for valid inference. Future directions include the development of automated diagnostic tools for exchangeability in large-scale data, integration of these diagnostics into machine learning workflows, and the creation of open-source frameworks to guide users in detecting and modeling violations of exchangeability.

In addition, with the increasing adoption of artificial intelligence and machine learning approaches, it will be critical to integrate methods for verifying exchangeability into predictive models to avoid making inferences about data with inadequately modeled latent structures.

8. General Conclusions

In an age when scientific reproducibility is under scrutiny, understanding and assessing exchangeability should be a standard step in every experimental analysis. This concept is not merely theoretical—it impacts the structural validity of our inferences. By combining formal theory, practical guidelines, and computational tools, researchers can ensure their analyses rest on solid statistical ground.

Deepening and spreading awareness of the importance of exchangeability is not only a methodological issue, but a necessity to ensure that scientific progress is based on sound and replicable statistical foundations.