A Simulation Modeling of Temporal Multimodality in Online Streams

Abstract

Temporal variability in online streams arises in information systems where heterogeneous modalities exhibit varying latencies and delay distributions. Efficient synchronization strategies help to establish a reliable flow and ensure a correct delivery. This work establishes a formal modeling foundation for addressing temporal dynamics in streams with multimodality using a discrete-event system specification framework. This specification captures different latencies and interarrival dynamics inherent in multimodal flows. The framework also incorporates a Markov variant to account for variations in delay processes, thereby capturing timing uncertainty in a single modality. The proposed models are modular, with built-in mechanisms for diverse temporal integration, thereby facilitating heterogeneity in information flows and communication. Various structural and behavioral forms can be flexibly represented and readily simulated. The devised experiments demonstrate, across several model permutations, the time-series behavior of individual stream components and the overall composed system, highlighting performance metrics in both, quantifying composability and modular effects, and incorporating learnability into the simulation of multimodal streams. The primary motivation of this work is to enhance the degree of fitting within formal simulation frameworks and to enable adaptive, learnable distribution modeling in multimodal settings that combine synthetic and real input data. We demonstrate the resulting errors and degradation when replacing real sensor data with synthetic inputs at different dropping probabilities.

1. Introduction

Temporal multimodality provides avenues for heterogeneous information processing. Efficient handling of such phenomena significantly enhances the ability to account for a wide range of diverse data types in unified platforms and environments. Recent artificial intelligence (AI) models [1,2,3] process multimodality in unprecedented ways, often quite natively using deep neural architectures [4,5]. From real-time language translation to reasoning over images and video processing and captioning, the breakthroughs in recent models are expected to drive a new era of products and innovations that leverage these advances (e.g., [6,7,8]).

Handling such diversity requires a foundation that lays the groundwork for various accounts in terms of forms and latencies. Especially in time-sensitive domains, the synchronization of different, time-varying forms must be continually assessed to ensure a seamless flow with minimal discrepancies. The computational complexity of new AI-driven solutions must be examined and thoroughly tested to select candidates that offer potential improvements and novelty over traditional methods.

Data in many applications often rely on timely transmission to remain valid [9,10,11]. When data are inherently asynchronous, they can pose the challenge of handling delays and drops without undermining the fidelity of the flow and communication. Multimodality introduces new challenges, primarily when operating under hard, real-time constraints, as in online streams. The time base on which such a flow depends may significantly contribute to the interpretability of the transmitted data. While strict constraints are necessary in many domains, handling errors and missing values is also important. Diffusion algorithms and models [2] have recently achieved a significant milestone in generative performance. In some domains, conditional diffusion models [12] have shown 40–65% improvements when applied to imputing over missing values in time series. The goal of this work is to equip traditional simulators with learnability to reduce staleness caused by drops or delays in multimodal streams while adhering to the formal temporal properties of the underlying modeling framework.

Thus, this paper establishes a computational foundation for simulating information flow that inherently accommodates temporal multimodality (e.g., neural encoding and diffusion) and offers significant solutions to regular timing and delays. Combining methods across layers—from symbolic reasoning to signal processing—can be challenging due to interdisciplinary barriers. However, having a framework that enables such multilayered assessment by leveraging recent AI models stands to offer significant resolutions for widely known challenging issues.

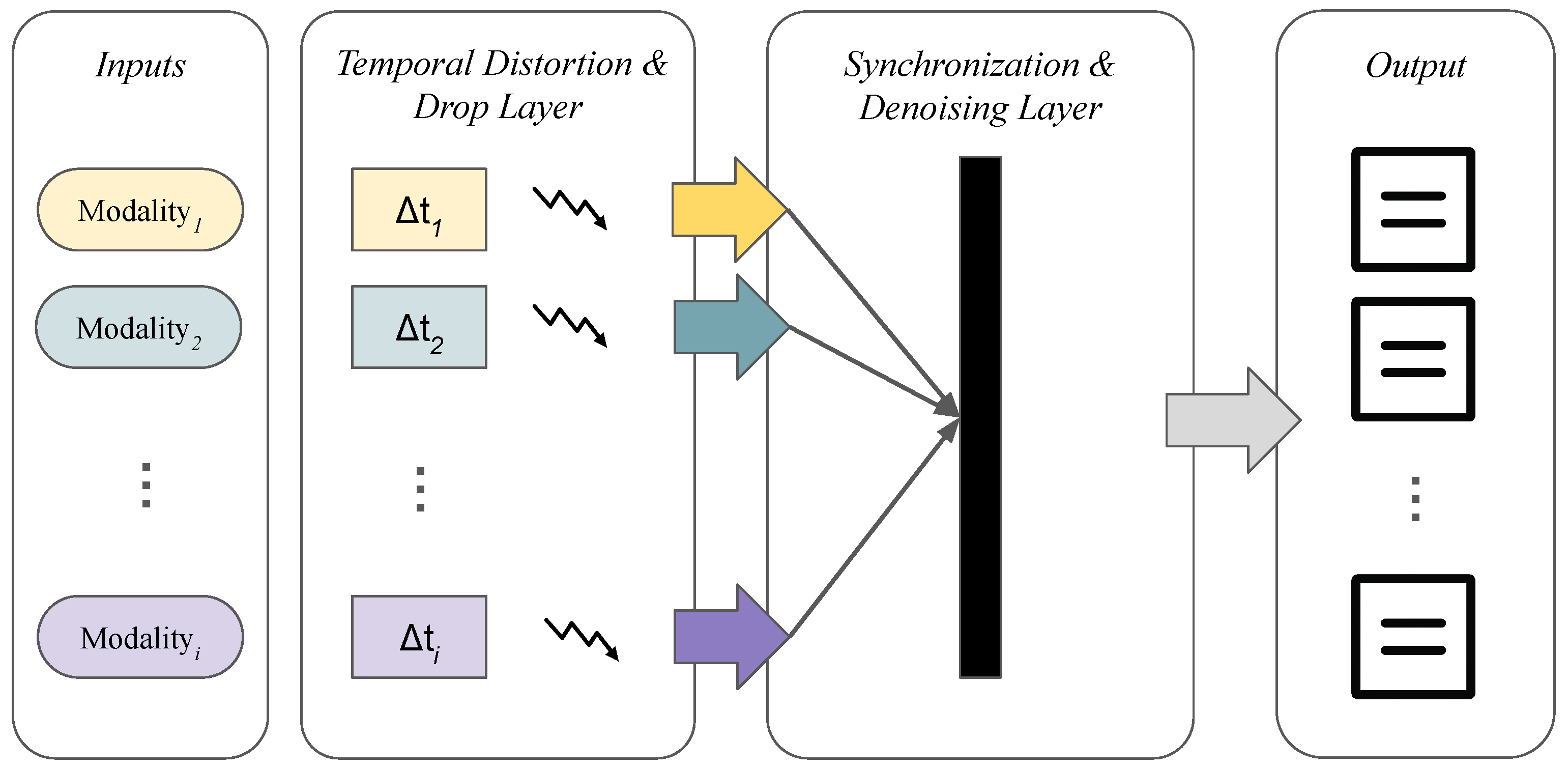
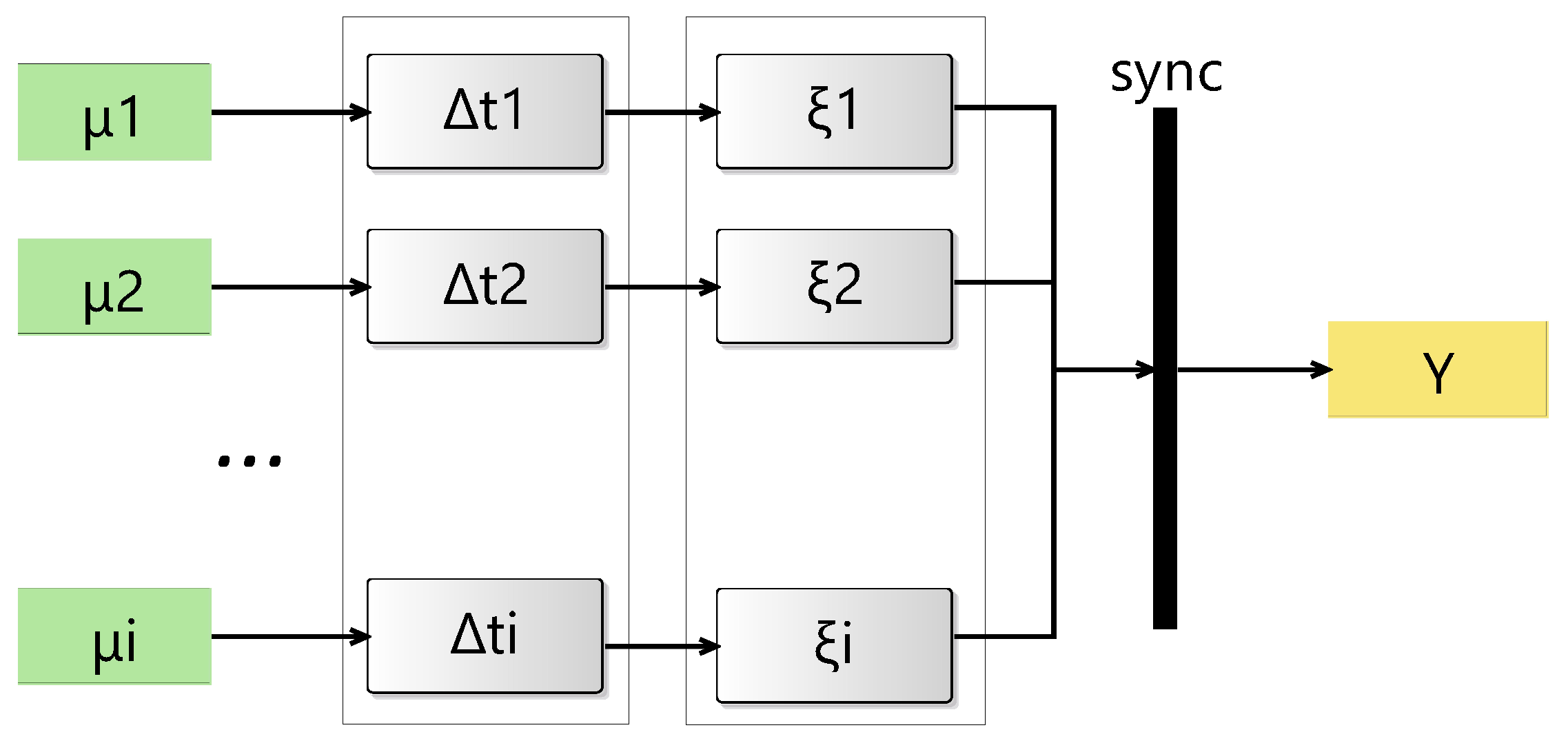
Figure 1 illustrates how modern communications may take place given temporal multimodality. Various forms of inputs enter the pipeline through different ports and channels. A different latency sanctions each form. Additionally, jitter during transmission further increases flow variability due to differences in the modalities’ latencies. The synchronization layer must therefore accommodate such variations. To effectively reconstruct the flow, the layer uses a suitable AI model tailored to each modality for denoising. The outcome is a correctly constructed stream according to a defined quality threshold.

Thus, a simulation modeling framework is proposed in this work to precisely account for the variability and jitter in multimodal flows. The framework models each modality as an incoming input to the system, characterized by distinct latency and jitter. Each input encounters variable delays derived from a predetermined distribution. It simulates the varying latencies each modality encounters, as well as the jitter each latency may undergo. Specific dropping semantics can also be introduced at this stage. At the synchronization layer, the implemented model expects incoming inputs with various latencies and combines them to form the corresponding flow. At this layer, the model can be tuned to minimize waiting and optimize overall performance within a well-defined experimental framework.

Background information on the underlying formulations is provided in the next section. Then, Section 3 explains in detail the methodology of creating the modeling & simulation (M&S) framework in light of the given background. The approach is demonstrated with example simulations and experiments in Section 4, and discusses the results in Section 5.

2. Background

In this section, the necessary background information is provided. The Discrete Event System Specification (DEVS) is used to formulate the layers and building blocks of the framework. The framework also draws on a background in models of computation to address heterogeneous systems. Activity diagrams are used as an interface language to describe the DEVS model’s overall behavior before mapping them to formal specifications and execution, along with other related background.

2.1. The DEVS Formalism

The DEVS formalism [13] is used to describe the overall architecture of the proposed system, featuring multiple layers that leverage its modularity and hierarchical expressiveness. The formalism has been employed to guide the development of simulations in various domains, such as the Internet of Things [14] and cyberphysical system design [15]. It is also used to describe the simulation’s basic building blocks (atomic models) that drive its computational execution. Due to the unique combination of these two features, it is well-suited to modularize components with various temporal modalities. The coupled DEVS model allows hierarchical construction of components. It does not describe the behavior of transition functions as in the atomic model. The coupled model may consist of sub-components (i.e., atomic and other coupled). It also consists of couplings: external input coupling connects entry points to sub-components, external output coupling connects sub-components to exit points and ports, and internal coupling connects sub-components to each other according to a well-defined set of basic rules. The X and Y sets are used to handle the arrival of input and departure of output events, respectively.

The atomic model mainly defines the following. X and Y are the sets of inputs and outputs (I/O). S is the set of states with $s_0$ as an initial state. The external transition function ${\delta }_{ext}$ handles the arrival of inputs and their effects on the model behavior by defining the state transition. The internal transition function ${\delta }_{int}$ works in a similar manner; however, it is triggered internally after elapsing $\sigma$, which is defined by the time advance function ($ta$). The output function $\lambda$ defines how the model generates and emits outputs. It is triggered prior to calling ${\delta }_{int}$. In parallel DEVS, ${\delta }_{conf}$ acts as a select function to handle the confluence of ${\delta }_{ext}$ and ${\delta }_{int}$ when it arises. ${\delta }_{ext}$, ${\delta }_{int}$, and $ta$ can include deterministic, probabilistic transitions, or both.

The system behavior in the DEVS Markov formulation [16] is expressed as a composition of independent atomic components whose state transitions follow discrete-event dynamics governed by stochastic processes. Internal transition functions and time advance are determined solely by the current state of the atomic model and stochastic parameters. Coupling determines how local state changes influence global behavior and, therefore, how synchronization emerges across modalities. The simulation protocol provides the operational semantics for event scheduling and execution, following Markovian transition probabilities in state updates.

The DEVS Markov model is particularly effective for simulating irregularities in temporal multimodal streams. The modularity support in DEVS can be leveraged to construct multiple flows, components, layers, and levels within streams. The devised DEVS-based architecture captures multimodalities and supports time-based simulation of their streams with various distributions. The root-coupled model represents the system in a modular manner, allowing the observation of a wide range of performance and behavioral metrics while ensuring simulation correctness. This is the underlying reason for using the DEVS Markov formalism even under various conditions for delay and jitter. In modular construction, the goal is to quantify the effects on the model by introducing delay and jitter in separate modules and measuring their impact on synchronization via staleness. Real-world multimodal streams operate under strict time windows and deadlines. Timely transmission is essential to data validity, yet is compounded by multimodality. Discussion on the model formulation and experimental details is given in Section 3 and Section 4, respectively.

2.2. Activities and Other Related Background

Activity diagrams intuitively describe the flow dynamics [17]. Previous research has employed DEVS as a foundation for modeling and simulating these diagrams [18]. In this work, the activity abstraction describes various flow logic in multimodal streams and leverages the predefined code-generation facility to streamline the development of their corresponding simulation models. The experimental frame [19] initiates the execution and derives the performance metrics of interest. The dual-layer approach further ensures the correctness of the devised models and supports behavioral modeling and the interpretation of simulation results.

The modal model is an actor model in Ptolemy [20] that primarily governs the transitions between different modes in systems. This work relates to that notion in that the system may operate differently across different modalities. In the example of passing inputs cleanly rather than introducing Gaussian noise, the system exhibits heterogeneous behavior, as shown in the combined plot that concatenates two trajectories from different modes. In this approach, the composition of different time trajectories is achieved by deriving the results through coupling and via the experimental frame. Further refinement in the modal model is enabled through a hierarchical finite-state machine that dictates the system’s behavior.

Additionally, incorporating diffusion models [21] is prompting a substantial shift in how traditional systems approach multimodality more broadly. Assessing the incorporation of various models via the synchronization layer provides a foundation for their proper adoption in time-sensitive domains. This work explores how to enhance learnability in a simulation model by leveraging diffusion.

3. Methods

First, the model is specified at a high level using an activity flow diagram. Each modality is presented as an input parameter. Upon arrival, different modalities follow parallel paths with varying latencies and jitter specifications. Each path consists of atomic steps/actions with a distinct timing and state characterizations. Each action may optionally have a queue to manage multiple arrivals and input pressure. It can also be used to define dropping semantics. However, it is an optional feature of the model, and the flow may choose to drop inputs that arrive while actions are in a processing state. After completing these steps, each input modality ultimately reaches the synchronization node. Now, the underlying model allows different combining mechanisms to occur across various accounts of timing, order, and type. For example, inputs received through different channels can be combined arbitrarily or according to a predefined mechanism. It can also be extended to accommodate a live stream and time windows.

The underlying formulation specifies the overall structure of the system with models, layers, hierarchical levels, and couplings. It also specifies the state transition and time-advance functions for each atomic model. A generic overall structure of the model is depicted as an activity flow diagram in Figure 2. Horizontal layers highlight the stages through which the stream undergoes state changes, where hierarchical levels determine depth. Note that the diagram can be readily simulated by following the stages as described below.

The diagram is transformed into a fully specified coupled model. The coupled model consists of multiple atomic models. It is initially a one-level model but it will later be expanded to cover more detailed cases with a multi-level hierarchy and to examine its effect on the observed analytics. Each modality is represented in the coupled model as an external input to the root model. Each modality stream undergoes a distinct latency at the beginning, specified by an atomic model with a deterministic or probabilistic timing assignment and state changes. At the second stage of this layer, a new set of atomic models introduces timing variability into the stream by using various distributions within a modular DEVS Markov model. It can be a single atomic model but it can also consist of multiple models in various structural and hierarchical arrangements.

3.1. Synchronization and Denoising Layer

In this layer, the aim is to describe how to handle multiple incoming flows that have been processed by the model over the previous stages. These flows are characterized by both deterministic and stochastic variations introduced along the stream. Now, the goal is to synchronize all these incoming flows into a unified flow. By doing so, the output can be reconstructed into a consistent stream. The underlying mechanisms within the model support reconstruction and calibration, ensuring that the combined stream can proceed and later be assessed by the transducer at the experimental frame.

In the model, multiple queues are implemented at the synchronization layer to handle a variety of inputs from different streams. Different mechanisms are also implemented to handle both the arrival and departure of elements within these queues.

Initially, these inputs may be treated arbitrarily, but predefined ordering and matching mechanisms are introduced to organize the multimodal inputs across different queues. These mechanisms rely on timestamps or identity annotations added at earlier stages of the model and the generation process. The synchronization process ensures that inputs are aligned and merged coherently. All of this can be specified within this model in a configurable manner, starting with some initial default assignments. In the experimental section of this paper, an initial basic scenario is presented to demonstrate how changing configurations affect the simulation results and analytics.

3.2. DEVS Modeling

This subsection describes the formulation of the entire DEVS specification in three steps. First, the coupled model serves as the root model, providing the overall architecture of the approach. Then, templates for coupled models represent each stream in a more modular, hierarchical manner. Finally, a foundation is laid out to create templates for all the different types of atomic models, serving as the fundamental building blocks that run the executable simulation.

3.2.1. The Root Coupled Model

The root model’s structure and hierarchy capture multiple layers horizontally. First, each modality is treated by a distinct external input port. Then, each layer is represented by a coupled model across the flow. Finally, an external output port represents the final stage at which the flow is directed to its ultimate destination. In the simulation experiment, this port is linked to the transducer model, from which the performance metrics are then derived. The root coupled model is formulated as follows:

Let there be i modalities ${\mu }_1,\dots ,{\mu }_i$. The root-level coupled model is as follows:

$${\mathcal{M}}_{\mathrm{root}}=\langle X_{\mathrm{root}},Y_{\mathrm{root}},D,\{M_d\mid d\in D\},EIC,EOC,IC\rangle ,$$

where

$$X_{\mathrm{root}}=\{{\mathtt{in}}_k\mid k=1,\dots ,i\},Y_{\mathrm{root}}=\left\{\mathtt{out}\right\}.$$

${\mathcal{M}}_{\mathrm{root}}$ contains three coupled models representing each layer, that is, a delay layer ${\mathcal{C}}_{\mathrm{\Delta }}$, a jitter layer ${\mathcal{C}}_{\xi }$, and a synchronizer $\mathsf{Sync}$ where the following is true:

$$D=\{\mathrm{\Delta },\xi ,\mathsf{Sync}\},\left\{M_d\right\}=\{{\mathcal{C}}_{\mathrm{\Delta }},{\mathcal{C}}_{\xi },\mathsf{Sync}\}.$$

Delay layer:

$${\mathcal{C}}_{\mathrm{\Delta }}=\langle X_{\mathrm{\Delta }},Y_{\mathrm{\Delta }},D_{\mathrm{\Delta }},\{{\mathsf{Delay}}_k\mid k=1,\dots ,i\},EI{C}_{\mathrm{\Delta }},EO{C}_{\mathrm{\Delta }},I{C}_{\mathrm{\Delta }}\rangle ,$$

where the following is true:

$$X_{\mathrm{\Delta }}={\left\{{\mathtt{in}}_k^{\mathrm{\Delta }}\right\}}_{k=1}^i,Y_{\mathrm{\Delta }}={\left\{{\mathtt{out}}_k^{\mathrm{\Delta }}\right\}}_{k=1}^i.$$

Each ${\mathsf{Delay}}_k$ is represented by an atomic model with time advance ${\sigma }_k>0$ (realizing $\mathrm{\Delta }{t}_k$) and ports $\mathrm{In}\left({\mathsf{Delay}}_k\right)=\left\{\mathtt{in}\right\}$, $\mathrm{Out}\left({\mathsf{Delay}}_k\right)=\left\{\mathtt{out}\right\}$. External couplings of ${\mathcal{C}}_{\mathrm{\Delta }}$ are specified as follows:

$$EI{C}_{\mathrm{\Delta }}={\left\{({\mathtt{in}}_k^{\mathrm{\Delta }},{\mathsf{Delay}}_k.\mathtt{in})\right\}}_{k=1}^i,EO{C}_{\mathrm{\Delta }}={\left\{({\mathsf{Delay}}_k.\mathtt{out},{\mathtt{out}}_k^{\mathrm{\Delta }})\right\}}_{k=1}^i,I{C}_{\mathrm{\Delta }}=⌀.$$

Jitter layer:

$${\mathcal{C}}_{\xi }=\langle X_{\xi },Y_{\xi },D_{\xi },\{{\mathsf{Jitter}}_k\mid k=1,\dots ,i\},EI{C}_{\xi },EO{C}_{\xi },I{C}_{\xi }\rangle ,where$$

$$X_{\xi }={\left\{{\mathtt{in}}_k^{\xi }\right\}}_{k=1}^i,Y_{\xi }={\left\{{\mathtt{out}}_k^{\xi }\right\}}_{k=1}^i.$$

Each $Jitte{r}_k$ is an atomic model with a time advance function that is drawn from a stochastic parametrization (e.g., ${\xi }_k$ specifying a delay distribution in DEVS Markov), ports $\mathrm{In}\left(Jitte{r}_k\right)=\left\{\mathtt{in}\right\}$, $\mathrm{Out}\left(Jitte{r}_k\right)=\left\{\mathtt{out}\right\}$. External coupling of ${\mathcal{C}}_{\xi }$ are specified as follows:

$$EI{C}_{\xi }={\left\{({\mathtt{in}}_k^{\xi },Jitte{r}_k.\mathtt{in})\right\}}_{k=1}^i,EO{C}_{\xi }={\left\{(Jitte{r}_k.\mathtt{out},{\mathtt{out}}_k^{\xi })\right\}}_{k=1}^i,I{C}_{\xi }=⌀.$$

Synchronizer: With $Sync$ as an atomic model [18] that receives i number of inputs and dispatches a unified stream:

$$\mathrm{In}\left(Sync\right)={\left\{{\mathtt{in}}_k^{Sync}\right\}}_{k=1}^i,\mathrm{Out}\left(Sync\right)=\left\{{\mathtt{out}}^{Sync}\right\}.$$

The remaining specification of the root coupled model follows:

$$\begin{array}{cc}\hfill EIC& =\{({\mathtt{in}}_k,{\mathcal{C}}_{\mathrm{\Delta }}.{\mathtt{in}}_k^{\mathrm{\Delta }})\mid k=1,\dots ,i\}\hfill \\ \hfill EOC& =\left\{(\mathsf{Sync}.{\mathtt{out}}^{\mathsf{S}},\mathtt{out})\right\}\hfill \\ \hfill IC& =\{({\mathcal{C}}_{\mathrm{\Delta }}.{\mathtt{out}}_k^{\mathrm{\Delta }},{\mathcal{C}}_{\xi }.{\mathtt{in}}_k^{\xi }),({\mathcal{C}}_{\xi }.{\mathtt{out}}_k^{\xi },\mathsf{Sync}.{\mathtt{in}}_k^{\mathsf{S}})\mid k=1,\dots ,i\}.\hfill \end{array}$$

External input couplings $EIC$ route each modality to its designated flow. External output coupling $EOC$ links the synchronizer output to the final destination while internal couplings $IC$ establish the full flow for each modality.

3.2.2. Jitter Couplings

${\mathcal{C}}_{\xi }$ primarily consists of i models for representing jitter and dropping semantics for each modality flow. By leveraging hierarchy in DEVS Markov, each one of these models can be either an atomic or a coupled model. A generic coupled model is formulated to better capture stochastic behavior across a broader range. The coupling of this newly formulated model with the root coupled model remains unchanged, preserving the original interface. That is, for $Jitte{r}_k$, the following is true:

$$\mathrm{In}\left({\mathcal{C}}_k^{\xi }\right)=\left\{{\mathtt{in}}^{{\xi }_k}\right\},\mathrm{Out}\left({\mathcal{C}}_k^{\xi }\right)=\left\{{\mathtt{out}}^{{\xi }_k}\right\}.$$

Now, the jitter model is further decomposed for each modality by formulating a coupled model as follows:

$${\mathcal{C}}_{\xi }^k=〈X_{{\xi }_k},Y_{{\xi }_k},D_k,\{J^{k,m}\mid m\in D_k\},EI{C}_{{\xi }_k},EO{C}_{{\xi }_k},I{C}_{{\xi }_k}〉$$

where

$$X_{{\xi }_k}=\left\{{\mathtt{in}}_{{\xi }_k}\right\},Y_{{\xi }_k}=\left\{{\mathtt{out}}_{{\xi }_k}\right\}.$$

Each $J^{k,m}$ is an atomic model with a time-advance function and transitions that specify various aspects of the model, such as random jitter and dropping conditions. Once each atomic model is specified, the couplings can be specified, forming a coupled, modular DEVS Markov system that can be readily simulated by a DEVS-compliant simulator.

The following describes the DEVS tuple of this atomic model generally:

$$J^{k,m}=\langle X^{k,m},Y^{k,m},S^{k,m},{\delta }_{\mathrm{ext}}^{k,m},{\delta }_{\mathrm{int}}^{k,m},{\lambda }^{k,m},{\mathrm{ta}}^{k,m}\rangle ,$$

with $X^{k,m}=\left\{\mathtt{in}\right\}$ and $Y^{k,m}=\left\{\mathtt{out}\right\}$.

More details about the inner functions are provided in the following subsection. The constructed coupling essentially forms a graph [22] that mimics a directed acyclic graph, with nodes representing atomic models and edges representing couplings. In such a way, ${\mathcal{C}}_{\xi }^k$ acts as a stochastic kernel inducing DEVS Markov modulation. As such, a function exists that maps an input arrival time at the port $i{n}^{{\xi }_k}$ to a random output time at the port $ou{t}^{{\xi }_k}$. For example, if ${\mathcal{C}}_{\xi }^k$ consists of two atomic models in sequence where $J_{k,1}$ feeds $J_{k,2}$, then the total delay distribution is obtained by the convolution of each individual distribution. Let $R_{k,1}$ and $R_{k,2}$ denote the nonnegative random variables associated with $J_{k,1}$ and $J_{k,2}$, respectively. Then, the total delay is as follows:

$$R_k^{★}=R_{k,1}+R_{k,2},$$

with the following probability density:

$$f_{R_k^{★}}\left(r\right)={\int }_0^r{f}_{R_{k,2}}(r-r^{\prime })f_{R_{k,1}}\left(r^{\prime }\right)d{r}^{\prime },r\ge 0.$$

Therefore, the composed mapping of this particular kernel form is as follows:

$$L_k^{★}(t\mid s)={\int }_s^t{L}_{J_{k,2}}(t\mid u)L_{J_{k,1}}(u\mid s)du,t\ge s.$$

where s is the input arrival time, u is the output departure time from $J_{k,1}$ and instantaneously entering $J_{k,2}$, and t is the output departure time from $J_{k,2}$ and thereby ${\mathcal{C}}_{\xi }^k$. The components $R_{k,1}$ and $R_{k,2}$ are assumed statistically independent. When a dependency is present (e.g., coupling), empirical tests show that moderate correlation has a negligible impact on overall staleness when synthesis is activated.

In Section 4, the use of various DEVS Markov structures is demonstrated, as well as variations in processing and dropping semantics.

3.2.3. Atomic Models

The formulation specifies three types of atomic models. The first type is a delayed action with an optional queue. The second one represents a decision point with a preassigned probability for dropping. The third one is for synchronizing the arrival of multiple streams. The specifications of each model are presented, with a particular focus on the external transition functions.

First, upon input arrival, an atomic model (action) specifies the time advance function that governs the transition to the next state and thereby generates the output. Each modality can be governed by a different distribution type. For example, an exponential distribution might be used with network packets and sensor data. More specific determinations using other distribution types might be more suitable with other forms of data and communication (e.g., video, acoustic). It can also be specified deterministically.

Thus, each deterministic/stochastic delay action is specified as an atomic DEVS as follows:

$$\begin{array}{cc}\hfill {\mathcal{A}}^k& =\langle X^k,Y^k,S^k,{\delta }_{\mathrm{ext}}^k,{\delta }_{\mathrm{int}}^k,{\lambda }^k,{\mathrm{ta}}^k\rangle ,where\hfill \\ \hfill X^k& =\left\{\mathtt{in}\right\},Y^k=\left\{\mathtt{out}\right\},\hfill \\ \hfill S^k& =\{(phase,\sigma ,v)\mid \sigma \in {\mathbb{R}}_{\ge 0},v\in {\mathcal{V}}^k\},\hfill \\ \hfill {\delta }_{ext}((phase,\sigma ),e,(in,v))& =(\mathsf{active},\tau (in,v),(in,v\left)\right);\hfill \\ \hfill {\delta }_{int}(phase,\sigma )& =(\mathsf{passive},\infty );\hfill \\ \hfill \lambda (\mathsf{active},\sigma )& =(out,v)\mathrm{where}input=(in,v).\hfill \end{array}$$

While the time advance function ($t{a}^k$) is given by a random variable $R_k$ drawn from a distribution chosen according to the modality:

$${\mathrm{ta}}_k\left(s\right)=R_k,R_k\sim F_k,$$

where $F_k$ is the delay distribution with typical parameterizations such that the following is true:

$$F_k=\left\{\begin{array}{c}\mathrm{Uniform}(a_k,b_k),\hfill \\ \mathcal{N}({\mu }_k,{\sigma }_k^2),\hfill \\ \mathrm{Exponential}\left({\lambda }_k\right),\hfill \\ \mathrm{Lognormal}({\mu }_k,{\sigma }_k^2),\hfill \end{array}\right.$$

where each flow can be assigned to components specified according to the modular DEVS Markov variant with the appropriate parametrization for each form (e.g., audio, video, sensor feeds, heterogeneous).

The other two types of atomic models follow accordingly, differing mainly in their definition of the state transition function (i.e., ${\delta }_{ext}$ and ${\delta }_{int}$). The atomic model for dropping involves drawing a random variable from a predefined probability distribution for input dropping. The other atomic model in the synchronization layer defines the external transition function as follows:

$$\begin{array}{cc}\hfill {\delta }_{ext}((phase,\sigma ,T,C),e,(in,v))& =\left\{\begin{array}{cc}(\mathsf{waiting},\infty ,T\cup \{(in,v)\},C[in\mapsto \top \left]\right),\hfill & \exists in:C\left(in\right)=\perp ,\hfill \\ (\mathsf{enabled},0,T\cup \{(in,v)\},C[in\mapsto \top \left]\right),\hfill & \forall in:C\left(in\right)=\top ,\hfill \end{array}\right.\hfill \end{array}$$

where $C\left(in\right)$ is a boolean condition associated with each incoming stream to the synchronizer. The output is enabled when all incoming inputs have arrived and their associated conditions have been marked as true. The internal of $sync$ policy may be windowed, timestamped, or constrained. Listing 1 shows the implementation of the external transition function of the sync atomic model. It is written in Java for the model implementation in the MS4 Me environment [23].

Listing 1. External transition for the synchronizer.

3.3. Diffusion

A diffusion-based time-series model is used to synthesize the dropped data during the simulation. The model learns the underlying temporal dependencies across multivariate sequences, enabling a robust synthesis and reconstruction process of dropped and missing data. Given a time series as follows:

$$X={\{x_t\in {\mathbb{R}}^F\}}_{t=1}^T,$$

with F features and T timesteps, a binary mask is defined as follows:

$$M={\{m_t\in {\{0,1\}}^F\}}_{t=1}^T,$$

where $m_t=1$ indicates observed input and $m_t=0$ indicates missing input.

The observed sequence is thus $X_{\mathrm{obs}}=M\odot X$, while the target for synthesis is $X_{\mathrm{rec}}=(1-M)\odot X$. During training, the model applies Gaussian noise for the forward diffusion process. While a denoising network learns to reverse the process while being conditioned on the partially observed input. During inference, the model masks a subset of the data according to the defined dropping probability. The synthesis takes place in two settings. First, the model uses the entire dataset to synthesize the dropped input. Second, future observations are masked, leaving only past observations available, mimicking a forward-time simulation.

To quantify synthesis fidelity, the mean absolute error (MAE) and mean squared error (MSE) are used for evaluation, along with MAE per feature. The metric is computed after running simulations for each setting (causal and non-causal) for each dataset subset. Both metrics are calculated as follows:

$$\mathrm{MAE}={\displaystyle \frac{1}{N}}\sum |X-\widehat{X}|$$

$$\mathrm{MSE}={\displaystyle \frac{1}{N}}\sum {(X-\widehat{X})}^2$$

4. Experiments

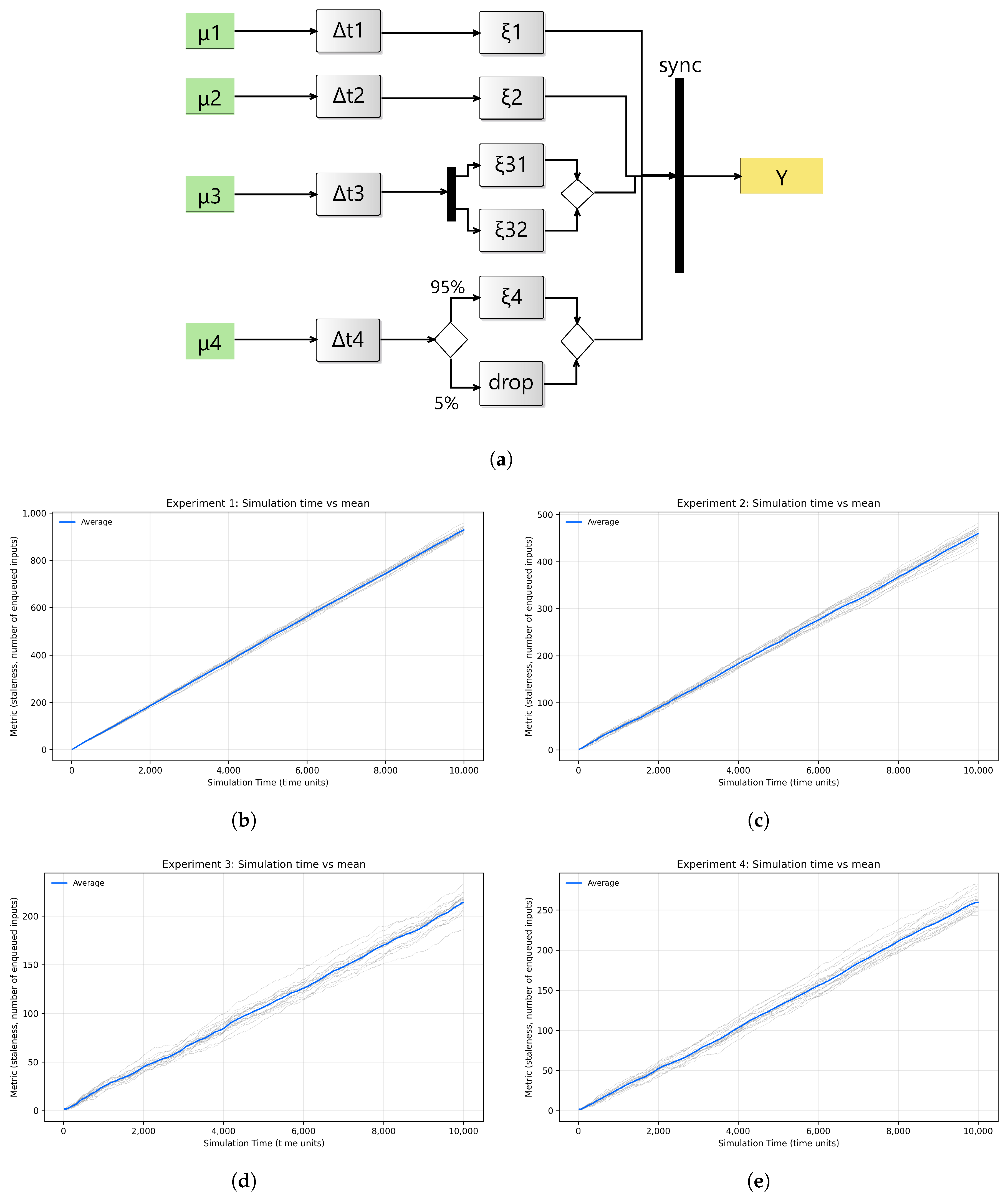
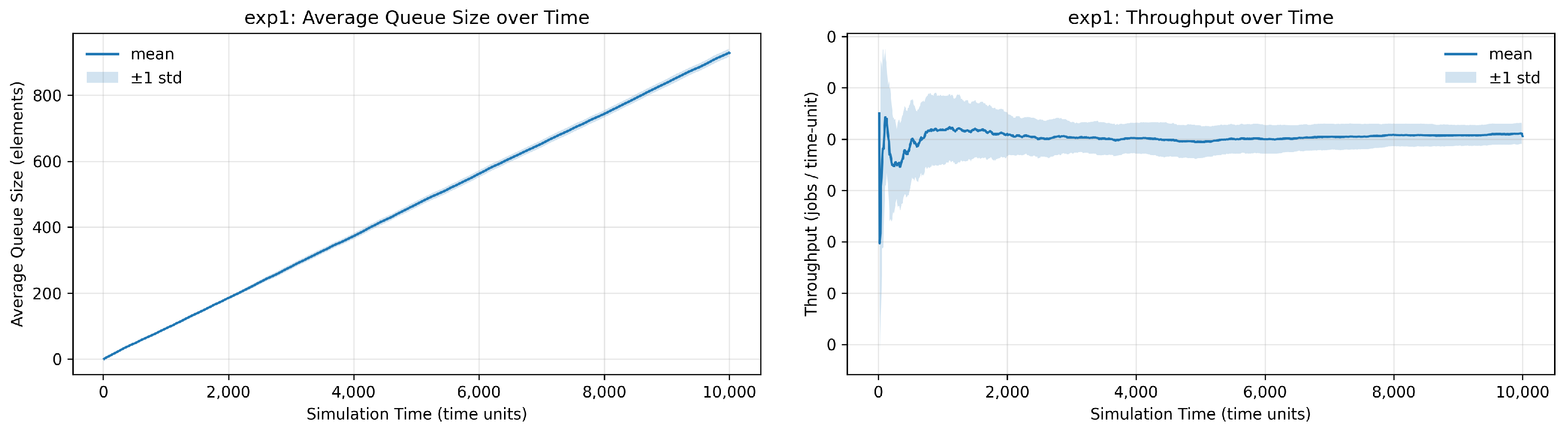
An exemplary model illustrates the key aspects of the framework. Figure 3 shows the devised activity along with some sample simulation results. In this experiment, staleness is observed at the synchronizer via average queue size. The larger the average size, the greater the staleness. Since each stream feeds into the synchronization layer via a channel queue, the average queue size across the four incoming flows indicates the waiting time for inputs arriving through each flow. The focus on staleness and average queue size stems from their relevance to synchronization and input freshness in this context. While throughput can be measured, the model actively synthesizes and reconstructs missing or delayed inputs rather than processing a complete flow. The relationship between staleness and throughput is generally asymmetric. In conventional queuing systems, larger queues increase waiting times and reduce throughput. In the proposed model, as queues grow, the diffusion process synthesizes the missing inputs, thereby maintaining effective throughput despite delays. The resulting trade-off is that lower staleness is achieved at the potential cost of reduced stream quality. A simple baseline of the experiment corresponds to conservative interarrival rates, where all modalities exhibit varying timing behavior and no synthesis, under which the model self-manages staleness with a simple synchronization control.

Table 1. Per-message latency for baseline timestamp matching experiments (in time units).

Experiment	Interarrival	Mean	SD	Median	p90	p99	Max
Timestamp 1	4	2299.48	2065.63	1924.50	5407.95	6377.77	6654.70
Timestamp 2	10	2358.93	2015.90	2166.40	5230.96	6000.31	6140.47
Timestamp 3	20	1678.66	1491.94	1660.84	3919.25	4361.91	4452.24

shows the simulation results for timestamp matching with different interarrival rates without dropping.

The activity in Figure 3a illustrates four modalities ${\mu }_1,{\mu }_2,{\mu }_3,{\mu }_4$ each undergoing a latency stage ($\mathrm{\Delta }t$) followed by stochastic jitter $\xi$ before entering the synchronizer. Modality ${\mu }_1$ encounters a delay $\mathrm{\Delta }{t}_1$ specified by a uniform distribution $R_{\mathrm{\Delta }{t}_1}$∼$\mathrm{Uniform}(0,1)$, representing a lightweight latency. Modality ${\mu }_2$ encounters a delay $\mathrm{\Delta }{t}_2$ specified as $R_{\mathrm{\Delta }{t}_2}$∼$\mathrm{Uniform}(1,2)$. Modality ${\mu }_3$ encounters a delay $\mathrm{\Delta }{t}_3$ specified by an exponential distribution $R_{\mathrm{\Delta }{t}_3}$∼$\mathrm{Exponential}(\lambda =1)$, followed by two parallel jitter models ${\xi }_{31},{\xi }_{32}$. Their outputs are merged afterward. Modality ${\mu }_4$ goes through a delay $\mathrm{\Delta }{t}_4$ specified by a Gaussian distribution $R_{\mathrm{\Delta }{t}_4}$∼$\mathcal{N}(\mu =10,{\sigma }^2=1)$, representing higher latency. After this step, the flow undergoes a probabilistic branching. The input is forwarded to jitter ${\xi }_4$ with probability $0.95$, and with probability $0.05$, the input is dropped.

All jitter outputs are routed into the synchronizer block, which produces the combined output stream Y. All jitter models ${\xi }_k$ time advance function is specified with an exponential distribution $R_{{\xi }_2}$∼$\mathrm{Exponential}(\lambda =1)$.

The delay distributions are arbitrarily selected to mimic diversity in latency behaviors observed in multimodal streams. The uniform distributions represent a lightweight delay with near-constant time. The exponential delay reflects a memoryless arrival typical of asynchronous event-driven streams, while the Gaussian delay $R_{\mathrm{\Delta }{t}_4}$∼$\mathcal{N}(\mu =10,{\sigma }^2=1)$ introduces a high-latency, tightly clustered modality analogous to slow, periodic sensors. The probabilistic drop and the additional exponential jitter ${\xi }_k$ further add sporadic interruptions and noise. Additionally, a sensitivity analysis was conducted in which the distributions’ parameters were perturbed to different values. Lower staleness behavior is observed with consistent modalities, and similar staleness was observed when the diffusion model is introduced across all modalities, confirming that the synchronization behavior is qualitatively invariant to moderate variations in the underlying latency distributions. This indicates that the synchronizer primarily adapts to the temporal order and frequency of missing data rather than to the exact form of the delay distribution.

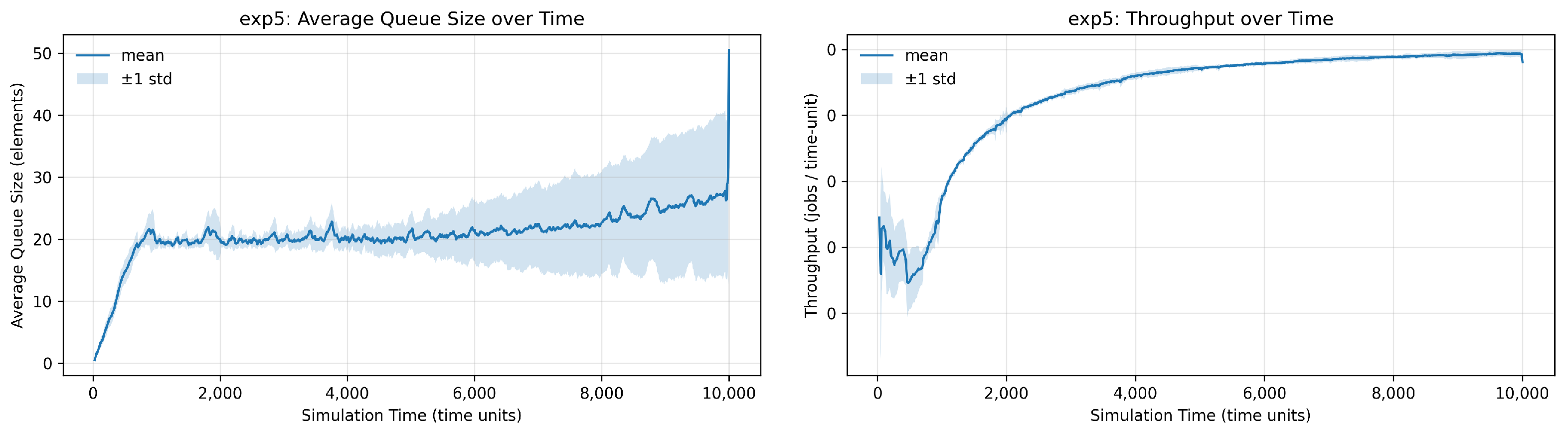
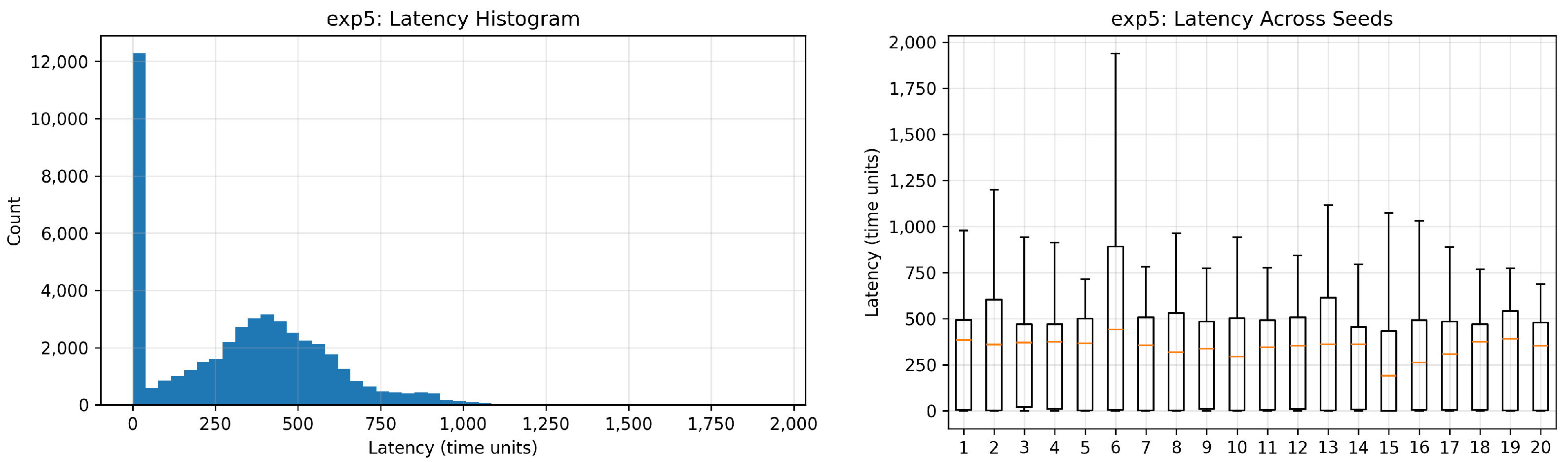
Four experimental setups are devised to evaluate the effect of interarrival rate and dropping probability on the average waiting time within the synchronizer queues, thereby quantifying staleness by averaging through queue sizes. Each experiment is run over 10,000 time units. In the first setup, a new input is generated at every time unit and fed consecutively into one of the streams. In other words, an input is generated for each stream every four time units (i). This produces the largest buildup of inputs in the synchronizer queues, since arrivals are frequent and often wait for higher-latency streams. The result is shown in Figure 3b, where staleness increases steadily. In the second setup, a new input is generated every 3 time units. 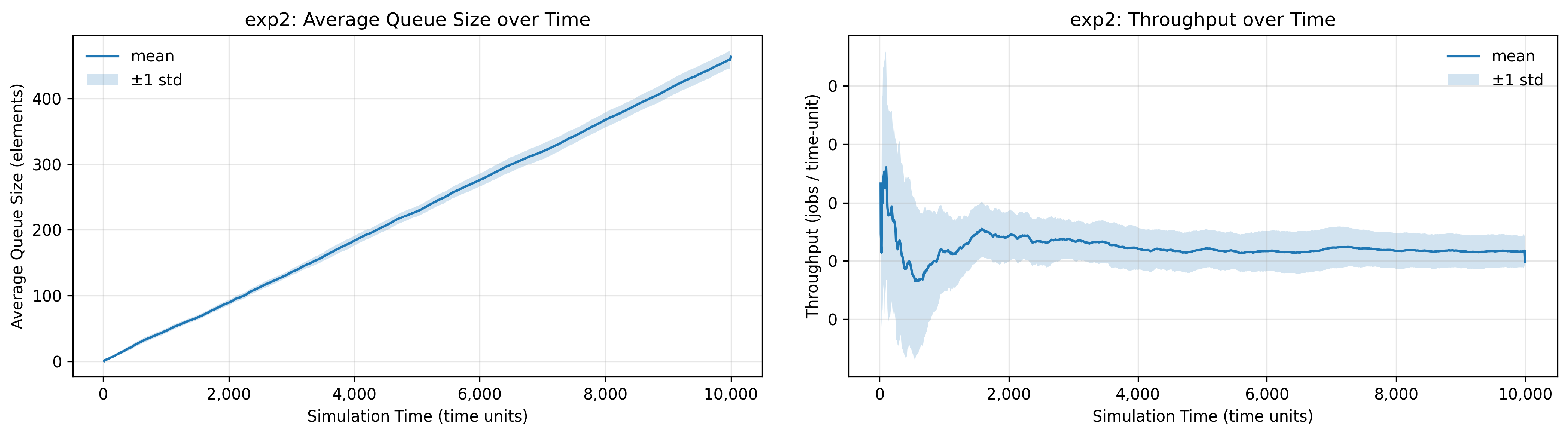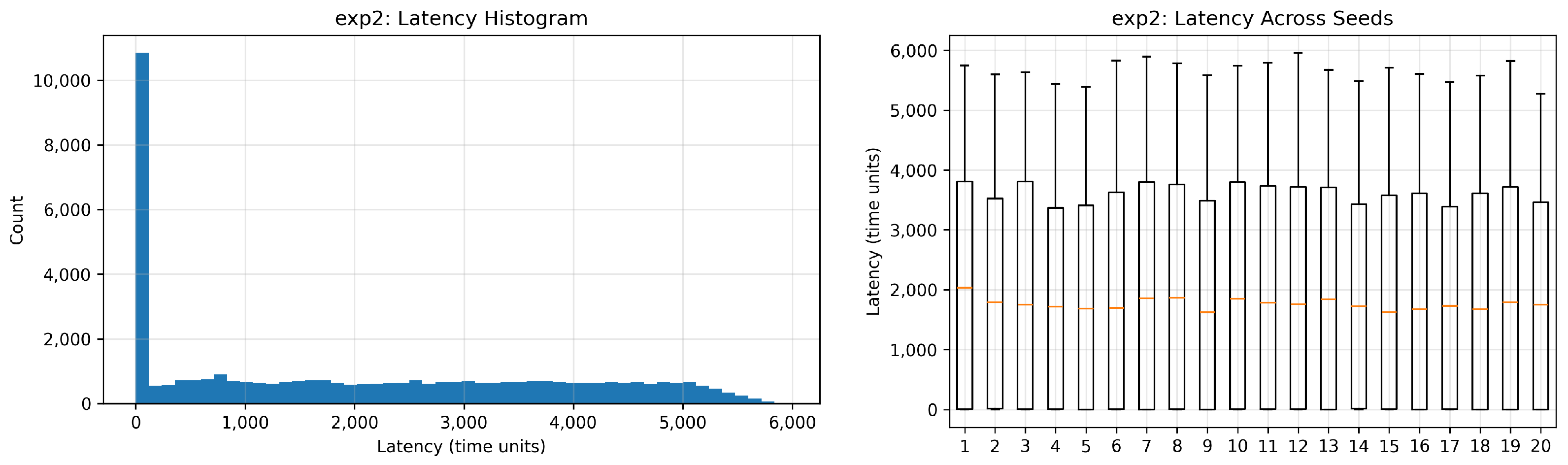As expected, the staleness is significantly smaller in Figure 3c. In the third setup, with inputs generated only every five time units, queue pressure is further reduced while showing some staleness fluctuations, highlighting a typical dissipation behavior in queuing systems (Figure 3d).

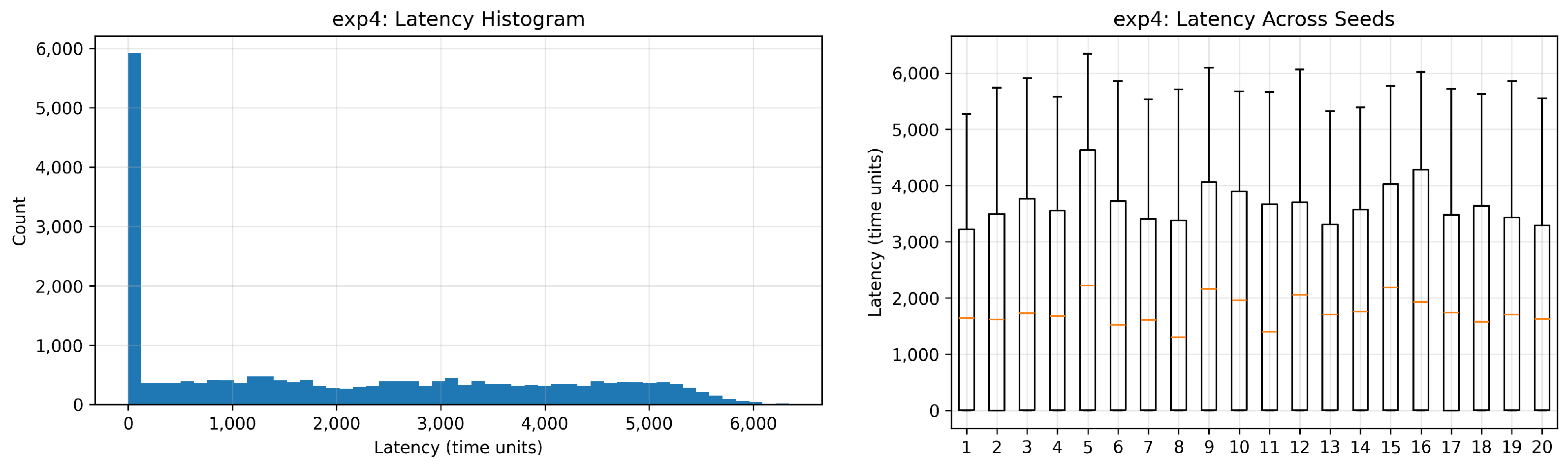
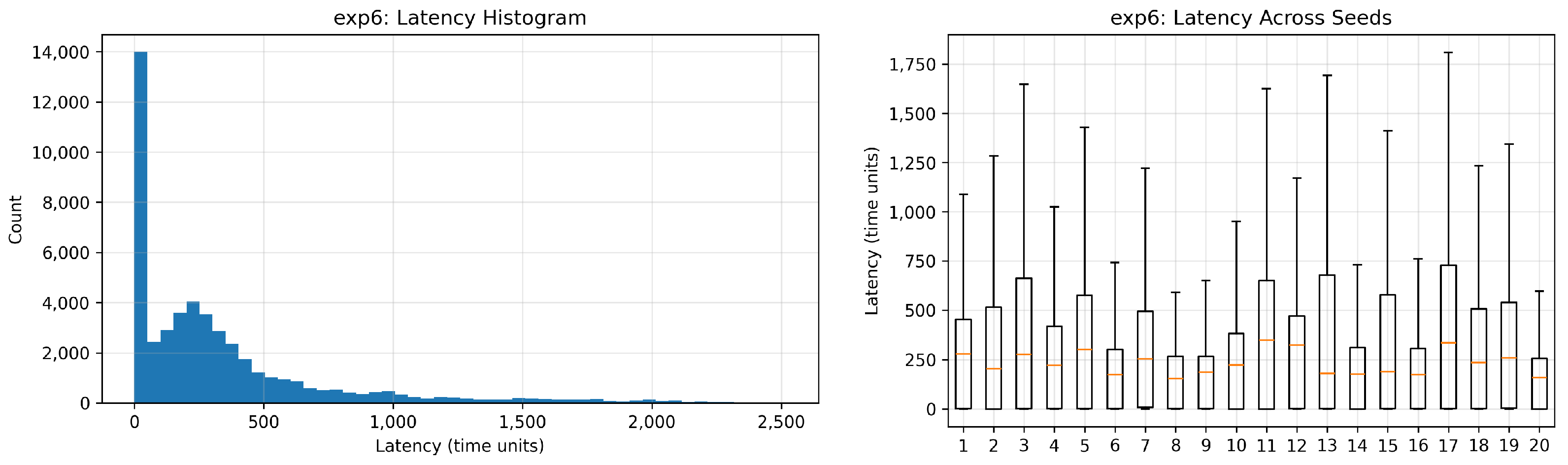
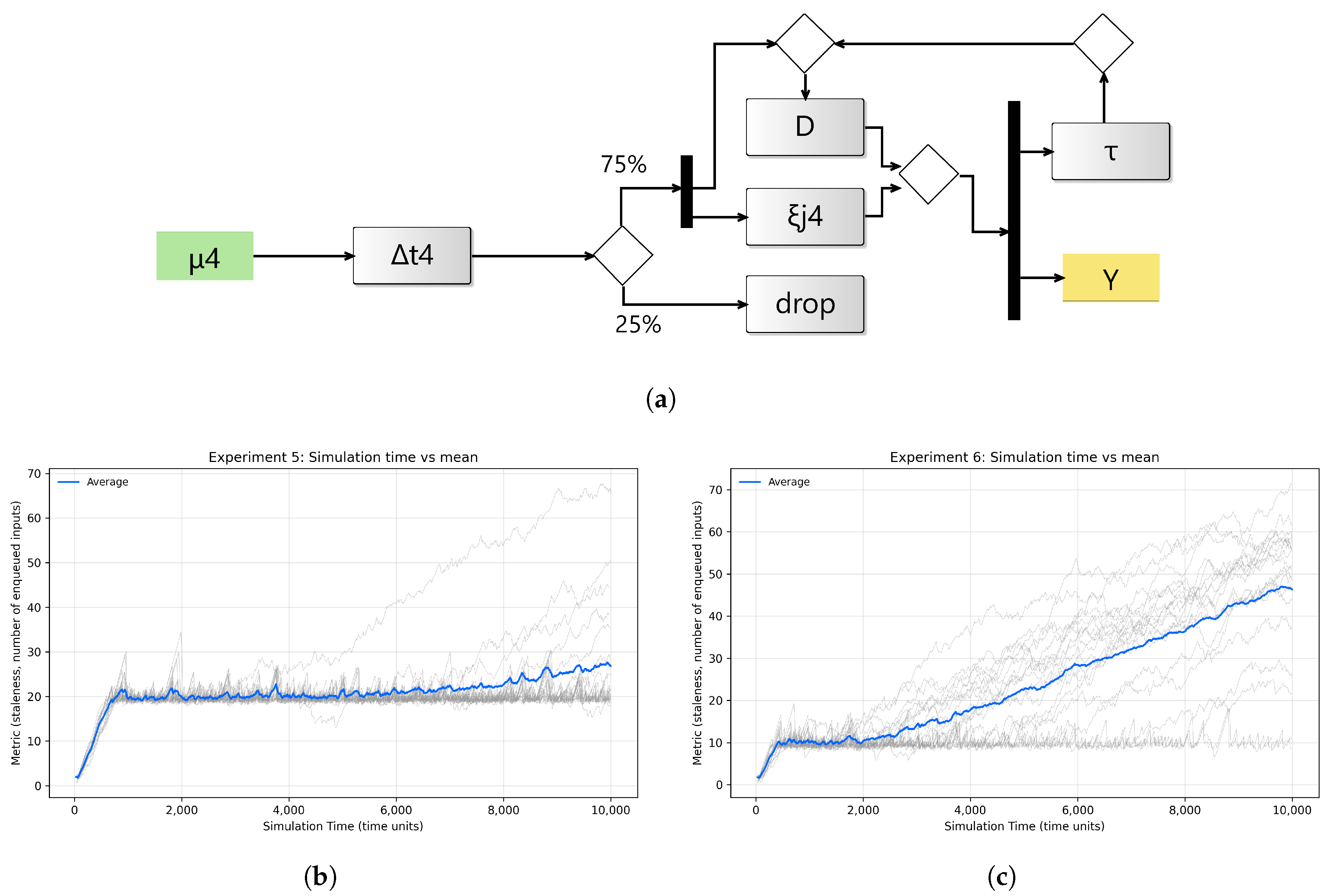
In the fourth setup, the input rate is kept at every five time units, but the drop probability at the probabilistic branch of modality ${\mu }_4$ is increased to 25%. The goal is to introduce additional pressure by increasing the drop rate and then observing staleness at the synchronizer. As expected, the results in Figure 3e show an increase in staleness due to the increased wait time of other, more frequent arrivals in faster streams.

Overall, the results of these four experiments validate the simulation in two respects. First, it confirms that higher input rates directly increase synchronizer queue occupancy. Second, increasing the dropping probability results in more waiting time for the incoming flow from other streams. These results highlight the trade-off between aspects of throughput and input pressure in synchronizing temporal multimodal streams.

4.1. Event-Driven Restoration with Staleness Threshold

Now, the restoration of staleness levels in Figure 3d is demonstrated by introducing a diffusion model at the synchronizer. When the staleness level reaches a certain arbitrary threshold (e.g., 20), the synchronizer dispatches an output to the diffusion model to synthesize a replacement for the stream experiencing higher delays or a higher drop rate. The experiment is run again with the same dropping rate (i.e., 25%) in ${\mu }_4$. The goal is to restore the same level of staleness as when the dropping rate was 5%. Thus, the diffusion model learns from previous inputs and is triggered when needed, when the dropping rate increases. It can also be used as a tool to manipulate staleness and conduct further assessment and observation within the experimental frame. Figure 4a shows the part of the overall activity after adjusting for the diffusion model. Figure 4b shows the attempt to restore staleness in Figure 3d. In Figure 4c, lowering the staleness threshold further (set to 10) demonstrates the matching of multi-rate multimodal streams with temporal variability. The staleness stayed around 10 at the beginning of the simulation run. However, as queues built up and began to accumulate from other flows, the upward trend accelerated, and the effect of the threshold for ${\mu }_4$ diminished.

MS4 Me simulation environment [23] is used to develop the framework and models, and to run the experiments. Matplotlib [24] is used for visualizing the simulation results. More results are reported in the Appendix A.

4.2. Empirical Evaluation on Multivariate Sensor Data

The empirical evaluation of synthesis is conducted using publicly available sensor data from Beach Weather Stations operated by the Chicago Park District [25]. The proposed diffusion synthesis is evaluated on multivariate, timestamped weather streams. Training is conducted at each location (single-station) and on the combined dataset. The combined dataset is constructed by concatenating all available station records and shuffling temporally. While evaluation is performed at each station, it is also performed at both stations to test the model’s robustness.

Nine channels are considered a feature set in a fixed order. For readability, feature indices are denoted as $F_0$–$F_8$ corresponding respectively to: Air Temperature, Wet Bulb Temperature, Humidity, Rain Intensity, Interval Rain, Wind Speed, Maximum Wind Speed, Barometric Pressure, Battery Life. All features are z-score normalized using training statistics. Reconstruction and metrics are reported in original units.

Training. The model is trained on a single station (Oak Street), comprising $69,473$ timestamped rows. It is also trained at another station (Foster), comprising $74,918$ rows, as well as the combined dataset.

Evaluation (eight runs). Results are reported under the different training conditions and two inference regimes (non-causal/causal), and on two stations:

• Oak Street Weather Station (station 1): non-causal and causal reconstruction.
• Foster Weather Station (station 2): non-causal and causal reconstruction.

Note that “Wet Bulb Temperature” and “Rain Intensity” are not available at station 2. In this procedure, these are treated as missing throughout the evaluation. Consequently, metrics for those features are undefined and appear as $NA$ in the tables (no valid ground-truth positions contribute to the average).

During evaluation, dropping is simulated with a binary drop mask $M\in {\{0,1\}}^{T\times F}$ applied to available values. Metrics are computed exclusively over positions that (i) have ground-truth and (ii) were dropped by the simulation:

$$\mathrm{MAE}={\displaystyle \frac{\sum |X-\widehat{X}|·\{M=0\}}{\sum \{M=0\}}},\mathrm{MSE}\mathrm{analogously}.$$

Overall, MAE/MSE and MAE-by-feature are all reported. Non-causal inference uses the full context, while causal inference reconstructs sequentially using only past inputs.

Table 2. Overall synthesis error on dropped entries with separate training for each station.

Station	Causal	MAE	MSE
Station 1	No	4.462316293620372	88.62497246441211
Station 1	Yes	5.012455509464308	130.1108624856918
Station 2	No	8.193623126906719	245.95552317981088
Station 2	Yes	8.206198785008374	235.35899747817228

summarizes overall MAE/MSE across the four runs where the training is performed per station.

Table 3. Overall synthesis error on dropped entries with training on the combined dataset.

Station	Causal	MAE	MSE
Station 1	No	4.477697375141572	93.25408713008477
Station 1	Yes	4.602957818414336	103.12671188698077
Station 2	No	5.472566442807675	96.4500224050607
Station 2	Yes	5.767469694843806	107.60615252597336

reports the same results when the training is performed for the combined dataset. Partial input dropping is emulated by randomly masking approximately 25% of the values using a Bernoulli process (bernoulli_p = 0.25).

Table 4. Per-feature MAE for each station with separate training.

Station	Causal	${\mathit{F}}_0$	${\mathit{F}}_1$	${\mathit{F}}_2$	${\mathit{F}}_3$	${\mathit{F}}_4$	${\mathit{F}}_5$	${\mathit{F}}_6$	${\mathit{F}}_7$	${\mathit{F}}_8$
Station 1	No	5.01	6.12	16.64	0.81	0.74	1.24	1.69	7.28	0.12
	Yes	5.04	5.72	21.21	0.45	0.65	1.29	2.41	7.40	0.13
Station 2 *	No	12.13	-	25.54	-	2.05	2.47	3.75	10.98	0.21
	Yes	14.54	-	23.83	-	1.51	2.25	4.27	10.80	0.23

* Channel data in $F_1$ and $F_3$ are absent at Station 2.

reports the MAE per feature with the training conducted per station.

Table 5. Per-feature MAE for each station with training on the combined set.

Station	Causal	${\mathit{F}}_0$	${\mathit{F}}_1$	${\mathit{F}}_2$	${\mathit{F}}_3$	${\mathit{F}}_4$	${\mathit{F}}_5$	${\mathit{F}}_6$	${\mathit{F}}_7$	${\mathit{F}}_8$
Station 1	No	4.28	4.60	18.51	0.50	0.7	1.14	1.65	7.46	0.72
	Yes	5.15	4.38	18.25	0.47	0.53	1.18	1.96	8.03	0.84
Station 2	No	11.08	-	16.59	-	0.46	1.52	2.19	5.64	1.07
	Yes	12.34	-	16.34	-	0.53	1.51	2.82	6.02	1.12

reports the same results for evaluation while conducting the training on the combined datasets.

Table 6. Per-feature MAE for each station with training on the combined set while fully synthesizing inputs (bernoulli_p = 1.0).

Station	Causal	${\mathit{F}}_0$	${\mathit{F}}_1$	${\mathit{F}}_2$	${\mathit{F}}_3$	${\mathit{F}}_4$	${\mathit{F}}_5$	${\mathit{F}}_6$	${\mathit{F}}_7$	${\mathit{F}}_8$
Station 1	No	10.01	7.89	18.99	0.7	0.61	2.06	3.2	7.35	2.46
	Yes	10.8	8.15	19.91	0.64	0.57	2.01	3.25	7.36	2.47
Station 2	No	9.2	-	17.94	-	0.53	1.6	2.47	6.64	0.84
	Yes	10.13	-	17.38	-	0.47	1.79	2.51	6.45	0.76

shows the results with fully synthetic inputs drawn from the training on the combined dataset. The results highlight the degradation of MAE for some features.

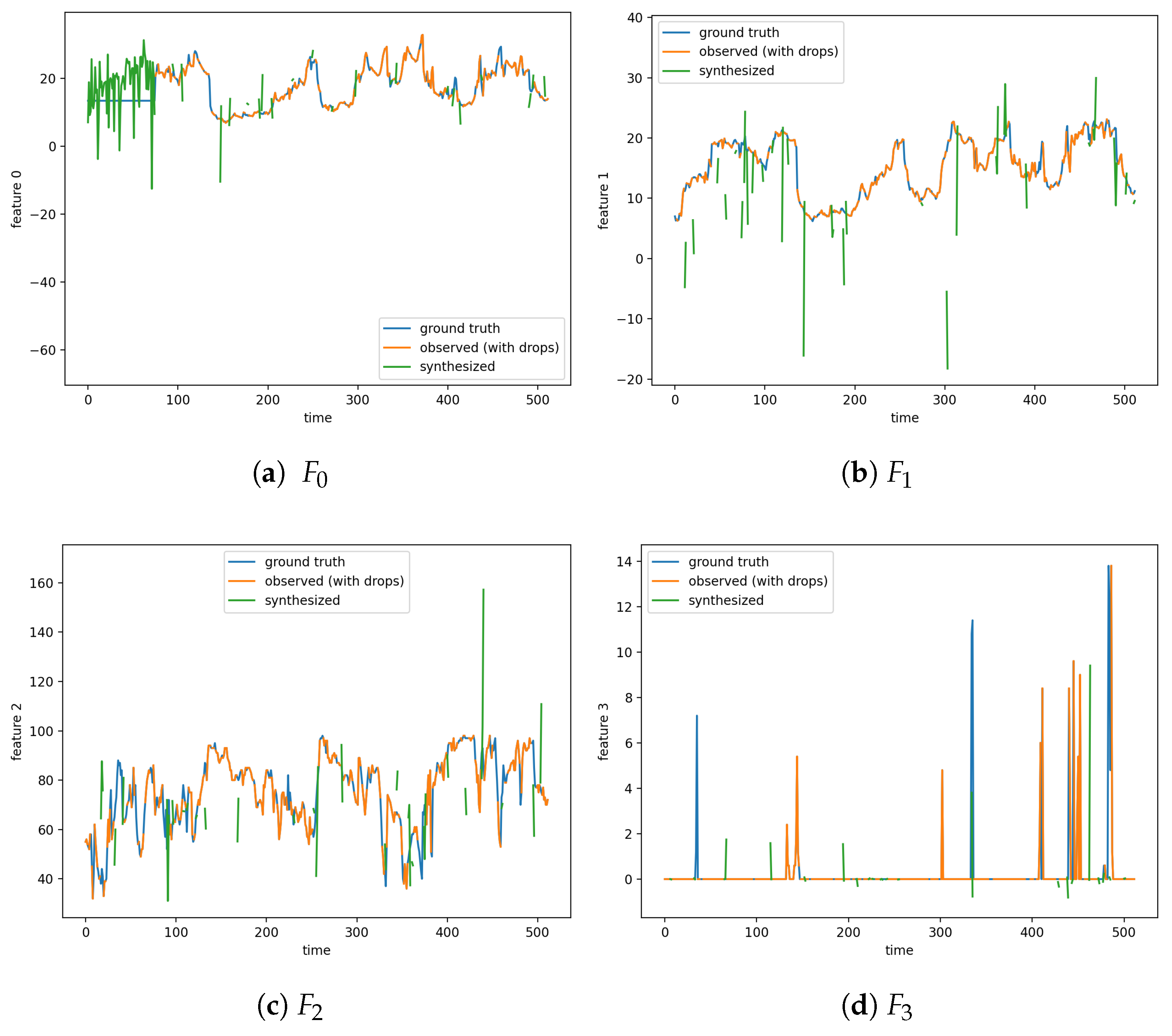
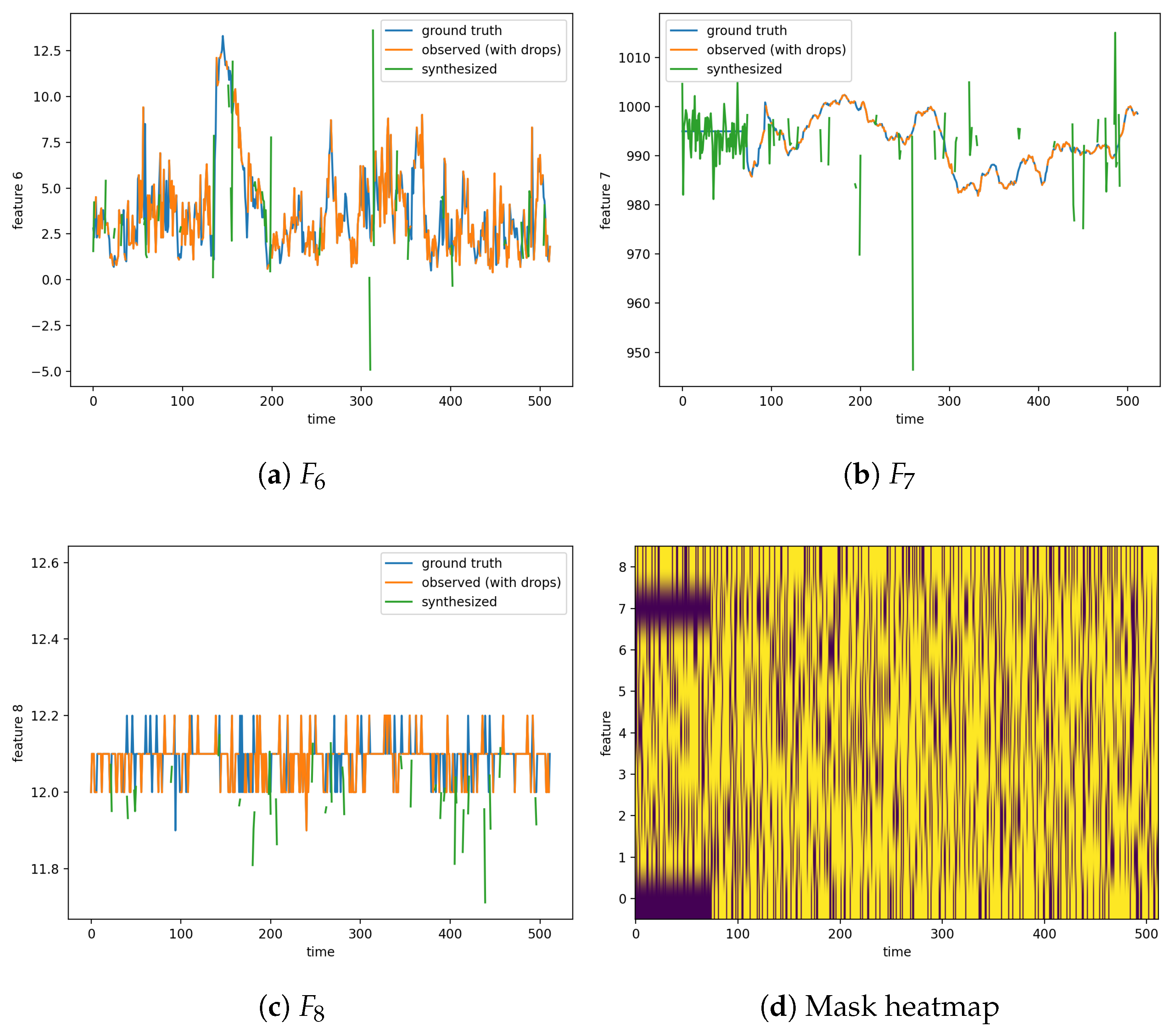
For each run and feature, ground-truth visualizations are provided, along with observed values and synthesized inputs during the simulation, where values are dropped. Figure 5 and Figure 6 show the results of the simulation with station 1 while dropping 25% of the inputs. The results for the other 13 experiments are available in the code repository.

Computational Overheads

The simulations were run on a standard workstation equipped with an NVIDIA GeForce RTX 3070 GPU (Nvidia Corporation, Santa Clara, CA, USA) and an Intel Core i9-12900H CPU with 32 GB of RAM (Intel Corporation, Santa Clara, CA, USA). Each diffusion training run required around 5 s per epoch, and full convergence was typically reached within 10 epochs. In the DEVS-based simulation with four modalities, the overall runtime for 10,000 time units was about 4337–11,039 ms per seed, with both the viewer and logging disabled. In modest cases, these overheads remain manageable but provide a basis for assessing the practical feasibility of integrating learnable imputation into a formal simulation framework, while acknowledging the computational trade-off. 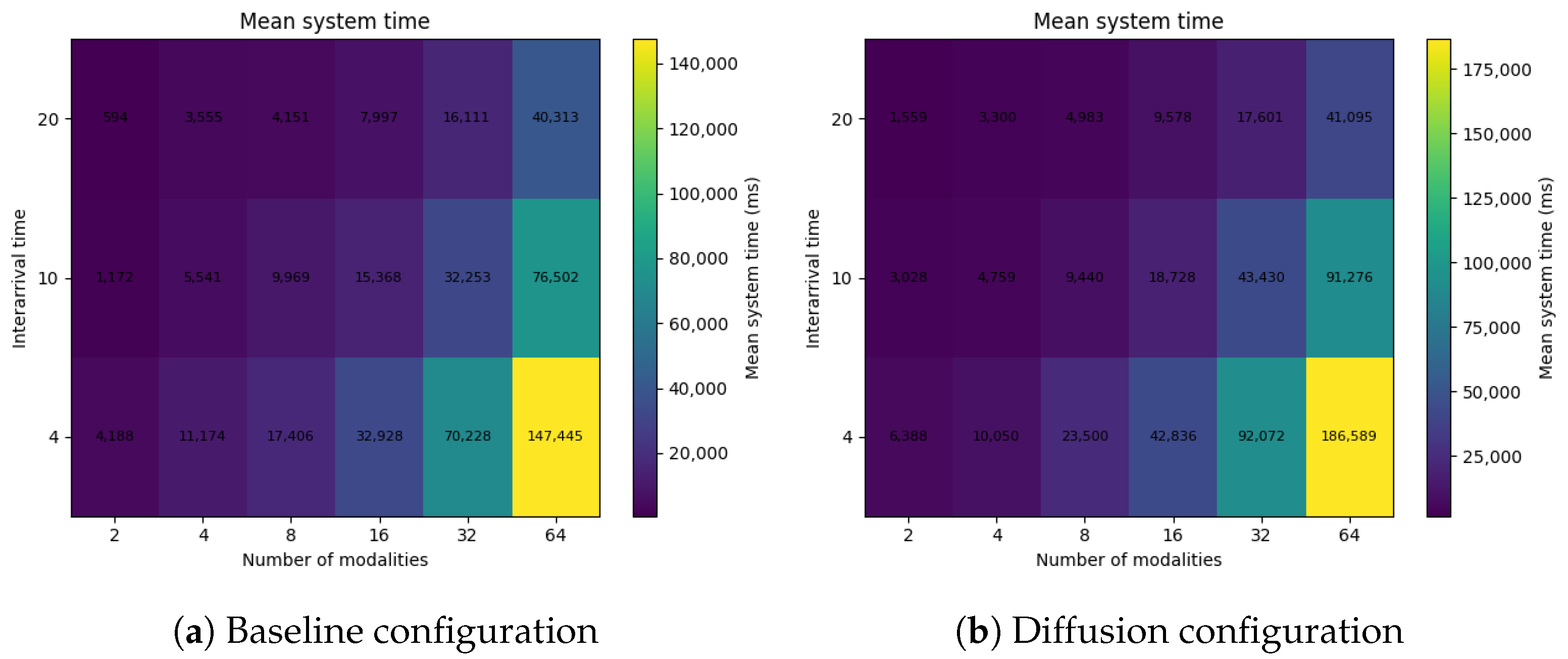Figure 7 compares the mean system time across configurations defined by interarrival interval and number of modalities, with the drop rate fixed at 25%. Each cell shows the average of 20 runs. The basic configuration (Figure 7a) demonstrates a gradual increase in processing time as the system load grows, whereas the diffusion configuration (Figure 7b) exhibits a steeper rise at higher modality counts.

The performance of the proposed framework is influenced by several external factors, including data characteristics and computational constraints. Variations in inter-arrival times and the simulated drop probability directly affect the quality of the stream and staleness behavior. Overfitting can occur when the model is trained with limited data. This can be mitigated within the modular framework and through accurate system decomposition. In the sensor data example, this can be achieved via cross-station evaluation with dedicated modules.

5. Discussion

This work aims to establish an M&S foundation to assess temporal multimodality. All experiments highlight the complexity and sensitivity in modeling such streams. They also demonstrate the prospects and challenges that may arise from the emergence of new modalities. By combining the inherent capabilities of AI models with a foundational simulation framework, the aim is to deepen the understanding of and, consequently, enhance their use to improve information streaming and communication at a broader scale.

The results in Section 4 demonstrate how variability in interarrival rates and dropping probabilities affects the overall model. By doing so, the goal is to validate the simulation’s correctness. Modelers can then modify the structure, add modalities, and calibrate the model to accurately represent various flow designs, thereby running and producing simulation results readily. Observed input staleness helps assess the efficiency of synchronizing multiple incoming flows and demonstrates the sensitivity of this metric to external factors in other model components. The model is tested with various synchronization policies for matching and ordering inputs. Note that a matching policy is used to combine incoming flows on a FIFO basis. However, the framework allows for the simulation of various policies, including timestamping, watermarking, event-driven, and multi-rate and latency synchronization.

There are still current limitations for integrating AI models, especially for time-sensitive streams. The goal is to continuously explore more practical, computationally efficient ways to integrate different models (e.g., diffusion) into the overall pipeline. Previous works address some underlying aspects of these limitations. Researchers have thoroughly discussed the problems of alignment among information streams [26], including jitter [27], dropping [28,29], and expiration [30], among others. However, the emergent enhancement requires revisiting these issues and fostering innovative approaches to leverage these capabilities.

6. Conclusions

Continuous assessment and calibration of temporal multimodality across information streams can be challenging. However, recent AI models have made significant advances, enabling more ways and removing some essential barriers to transformation in heterogeneous communication and information flows. In this paper, these models can be tailored to address time-sensitive streams in a modular modeling and simulation environment. The flexibility of the modular DEVS Markov model enables the simulation of a wide range of scenarios in multimodal streaming, with high configurability and the ability to calibrate structural compositions and stochastic parameterization. Such support allows for a time-aware simulation of heterogeneous compositions of current and emerging modalities in information systems.

Limitations and Future Work

The integration between a continuous-time base and discrete time steps needs to be addressed more thoroughly. Heterogeneity can pose challenges when various concatenation and composition schemes are used, while maintaining temporal consistency without jeopardizing formal guarantees. The fragmentation between discrete-event modeling and other development environments must be remedied to achieve concrete results in real-time simulation. Currently, there are two segregated suites of developed models, with substantial gaps that are addressed ad hoc. Also, the training is conducted with relatively small-scale data. Further work with substantial computational resource assessment is needed for domains that require high-dimensional data. Ethical concerns might arise in using this approach to breach privacy and synthesize sensitive information.

The proposed framework contributes to enhancing the fidelity of simulation models in representing challenging real phenomena by enabling them to capture complex temporal and data dynamics. Ongoing and future work includes conducting experiments to elaborate on synchronization policies and explore how they can accommodate diffusion and sampling enhancements to ensure the flow’s integrity. It also includes examining different, more aggressive interarrival and drop rates with different numbers of modalities and reassessing the staleness and quality of the flow, as well as the computational overhead and scalability. Adaptive simulations with an optimized mix of real and synthetic inputs are also of particular interest for examination within well-established quality-versus-efficiency trade-offs. Future experimental designs could offer substantial automation for assessing the validity and calibrating domain-specific performance and design metrics for applications, including autonomous decision-making via sensor fusion and high-speed streaming of high-dimensional data. A rigorous extension to incorporate discrete-event dynamics with diffusion atomic models is also considered.