Efficiency Analysis and Classification of an Airline’s Email Campaigns Using DEA and Decision Trees
Abstract
1. Introduction
2. Literature Review
2.1. DEA Studies on Campaign Efficiency
2.2. DEA–Machine Learning Studies
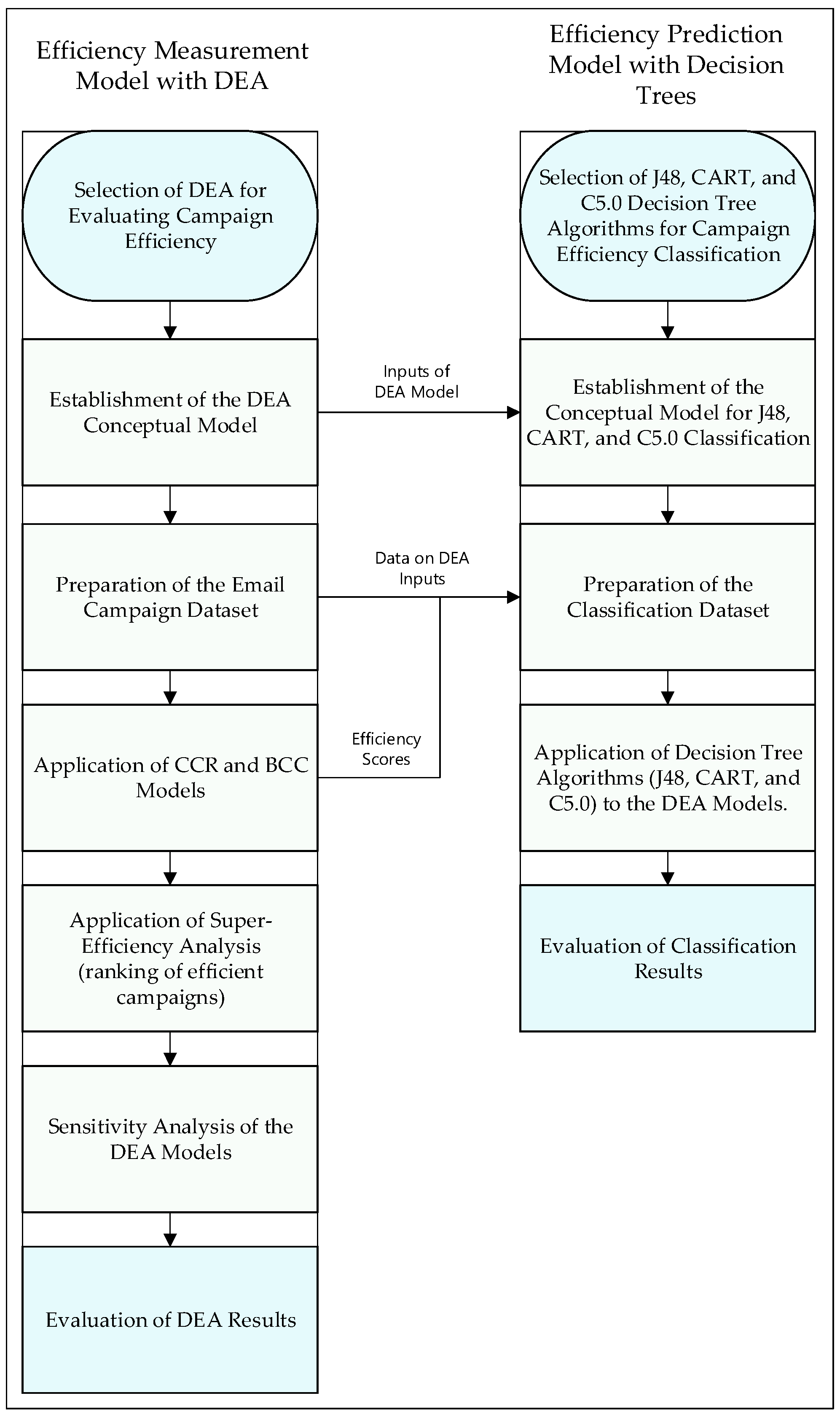
3. Methodology
3.1. Efficiency Measurement with DEA
3.1.1. DMUs Definitions
3.1.2. Inputs and Outputs
- •
- Literature survey on campaign evaluation indicators
- •
- Selection of inputs and outputs for this study
3.1.3. Choice of DEA Methodology
3.1.4. Orientation Choice
3.1.5. Scale Type: CCR and BCC
- •
- CCR Model
- •
- BCC Model
3.1.6. Super Efficiency DEA Model
3.1.7. DEA Models Applied in the Study
3.2. Efficiency Prediction with Decision Trees
4. Results
4.1. Results of the DEA Models
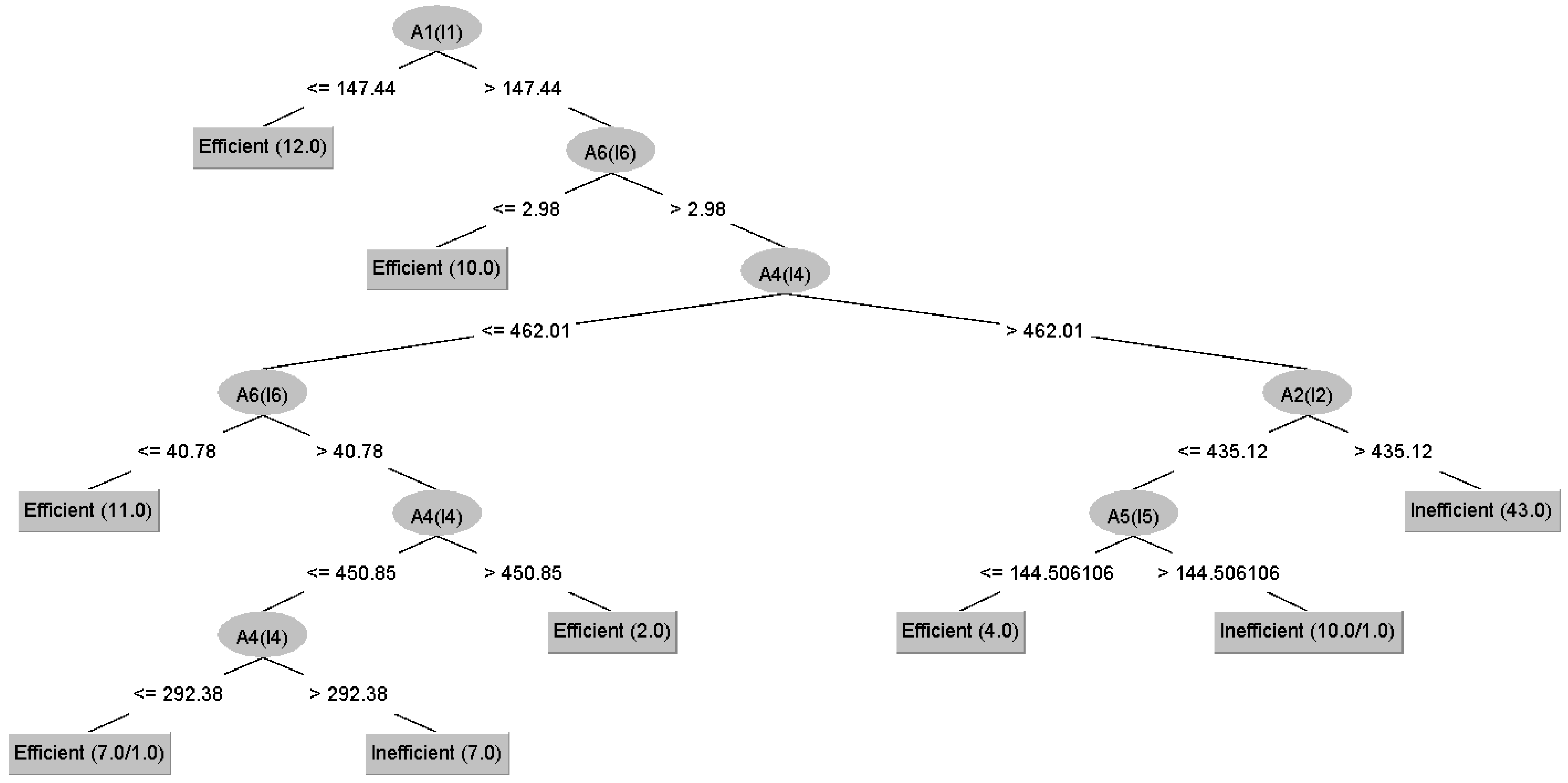
4.2. Results of the Decision Tree Classification Algorithms
5. Conclusions
Limitations and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DEA | Data Envelopment Analysis |
| CCR | Charnes, Cooper and Rhodes |
| BCC | Banker, Charnes and Cooper |
| CART | Classification and Regression Trees |
| CRM | Customer Relationship Management |
| SFA | Stochastic Frontier Analysis |
| ES | Efficiency Score |
| CTOR | Click-to-Open Rate |
| ML | Machine Learning |
| DMU | Decision-Making Unit |
| CTR | Click-Through Rate |
| CRS | Constant Returns to Scale |
| VRS | Variable Returns to Scale |
| WEKA | Waikato Environment for Knowledge Analysis |
| NN | Neural Network |
| CIT | Classification and Interaction Trees |
| SVM | Support Vector Machine |
| K-NN | K-Nearest Neighbors |
| RF | Random Forest |
| ANN | Artificial Neural Network |
| AUC | Area Under the Curve |
| AM | Additive Model |
| F-M | F-Measure |
| MAE | Mean Absolute Error |
| RMSE | Root Mean Squared Error |
| MCC | Matthews Correlation Coefficient |
Appendix A
| Study | DEA Models | Purpose | Type of Decision Tree (DT) Classification Algorithm | Attributes of the Classification Algorithms | Target Variables, and Number of Classes | Accuracy and Other Evaluation Metrics of the Main Algorithm(s) | Algorithms * Compared and Their Evaluation Metrics |
|---|---|---|---|---|---|---|---|
| [20] | 131 IT development projects, BCC, output oriented, 6 inputs 3 outputs | to predict efficiency of new IT development projects | C4.5 | 9 environmental factors for technology commercialization | efficiency class, 2 classes, based on efficiency scores of DEA model, Efficient: ES = 1 Inefficient: ES < 1 | not specified | No comparison |
| [25] | 444 Bank branches in Ghana, CCR (2- stage DEA), 4 inputs, 2 outputs | to predict efficiencies of bank branches | C5.0 | inputs and outputs of DEA model | efficiency class, 2 classes, based on efficiency scores of DEA model, Efficient: ES * ≥ 0.8 Inefficient: ES < 0.8 | 100, Kappa = 1 | RF (98.5) Kappa = 0.95, NN (86) Kappa = −0.014 |
| [19] | 21 health centers in Jordan, 3 input 2 output | to predict efficiencies of a new health centers | J48 (with WEKA) | only inputs of DEA model | efficiency class, 2 classes, based on efficiency scores of DEA model, Efficient: ES = 1 Inefficient: ES < 1 | imbalanced 76.19 F-M: 0.747, balanced 88.09 F-M: 0.875 | imbalanced NB (52.38) SVM (52.38), balanced NB (86.9) F-M = 0.87 SVM (87.47) F-M = 0.835 |
| both ofinputs and outputs of DEA model | imbalanced: 71.42 F-M = 0.714, balanced: 89.29 F-M = 0.888 | imbalanced NB (52.38) SVM (61.9), balanced: NB (69.04) F-M = 0.692 SVM (91.66) F-M = 0.893 | |||||
| [26] | 23 suppliers of a firm CCR, BCC data were taken from a paper originally 6 inputs and 5 outputs this study added 2 new factors. | to predict efficiencies of potential suppliers and make selection | C4.5 (with WEKA) | inputs and outputs of DEA model | efficiency class, 2 classes, based on efficiency scores of DEA model | CCR: 90.91 BCC: 81.82 | for NN; CCR: 72.3 BCC: 100 |
| [29] | 15 manufacturers firms of automotive parts in Iran MPI Based DEA, output oriented, 3 inputs 2 outputs, data belongs to years of 2013–2016 | to Assess the green supply chain performance of auto parts manufacturers with higher accuracy and determining the rules behind high performance | J48 (with WEKA) | inputs and outputs of DEA model | efficiency class, 2 classes, based on efficiency scores of MPI based DEA model, Inefficient MPI < 1 Efficient MPI > 1 | not specified | no comparison |
| [73] | 53 industrial companies listed on the stock Exchange in Amman, input and output orientation for both VRS and CRS model, 11 inputs 11 outputs, data belongs to years of 2012–2015 | predicting the performance of companies | J48 (with WEKA) | inputs and outputs of DEA model, to determine ultimate attributes for J48, variable Importance Ranker in WEKA was applied to data | efficiency class, 2 classes, based on aggregated efficiency scores of DEA models Efficient: ES = 1 Inefficient: ES < 1 | 79.9 F-M = 0.804, 81.6 (after application of DECORATE) F-M: 0.818 | no comparison |
| [24] | 22 cement producers in Iran, 2-Stage MPI based CCR, BCC and AM, 2 inputs, 4 outputs for single stage, data belongs to years of 2015–2019 | to develop a method to predict and analyze the Eco-efficiency values of cement companies and the factors affecting them. | not specified (with WEKA, Rapid Miner and Tanagra) | inputs and outputs of the single stage DEA models | efficiency class, 2 classes, based on efficiency scores of single stage MPI based DEA model, Inefficient MPI < 1 Efficient MPI > 1 | different accuracy rates in WEKA, Rapid Miner and Tanagra highest degree of 91.23 is with WEKA. | with WEKA K-N (89.51) NB (79.25) with other software K-N and NB are better |
| [28] | 200 bank branches in Iran, CCR input oriented, 3 inputs 5 outputs | to predict efficiency of a new branch without running DEA model. | C4.5 | inputs and outputs of DEA model | efficiency class, 10 classes with equal intervals, based on efficiency scores of DEA model | 86.5 | no comparision |
| [27] | energy assessment project offered to 7548 medium and small-scale manufacturing companies in USA, Projects belong to years of 1981–2020, CCR, BCC CCR-Tier, BCC-Tier models, 6 inputs, 1 output | to predict efficiencies of energy assessment projects | not specified | inputs and outputs of DEA model | efficiency class, 2, 3, 5, 10 classes, based on efficiency scores of DEA model | as the number of classes increases, the accuracy rate decreases, conventional DEA modeling provides more accurate predictions than DEA-Tier modeling, for conventional: CCR (2): 98.24 CCR (5): 86.29 CCR (10): 69.94 BCC (2) 98.85 BCC (5): 91.55 BCC (10): 82.62 | SVM K-NN Linear Discrimination Analysis RF overall, the best algorithms are RF and SVM. for 2 of classes, DT is the second after RF |
| [21] | 18 Insurance branches of an insurance company in Iran, MPI based DEA (MPI based Latent Variable VRS model), 3 inputs 3 outputs, data belongs to 2008–2010 | to explore rules behind the productivity based on CART algorithm using 8 internal and external factors | CART | 8 internal and external factors | efficiency class, 3 classes, based on efficiency scores MPI based DEA model, Inefficient MPI < 1 Constant MPI = 1 Efficient MPI > 1 | for period I 98.02 for period II 100 (with Bootstrap) | no comparison |
| [22] | 151 Banks in MENA countries, VRS input and output oriented, 5 inputs, 4 outputs, data on 2008–2010 | to asses impact of environmental factors on banking performance and predict banking performance based on environmental factors | CART CIT | 15 environmental factors | efficiency class, 2 classes, based on efficiency scores of DEA model, Efficient: ES = 1 Inefficient: ES < 1 | CART: 75.50 AUC: 0.7466 CIT: 67.55 AUC: 0.7077 | RF-CART: 82.78 AUC: 0.9293 RF-CIT: 75.50 AUC: 0.8516 ANN: 68.21 AUC: 0.6951 Bagging: 84.11 AUC: 0.9221 Bootstrap except ANN |
| [23] | 36 banks in Gulf Cooperation Council countries, VRS, output oriented, 3 inputs 2 outputs, use of bootstrap | to predict efficiency of bank based on internal and external factors and discover reasons behind inefficiencies | CART | 12 internal and external factors | efficiency class, 2 classes, based on efficiency scores of DEA model, Efficient: ES = 1 Inefficient: ES < 1 | 97.93 | no comparison |
| [74] | 200 service units of a hypothetical firm, Pure outputs DEA model, 11 outputs | to find inefficient service units and inefficient process es in inefficient service units. | CART | efficiency scores of processes in service units | efficiency class, 2 classes, based on efficiency scores of DEA model, Efficient: ES = 1 Inefficient: ES < 1 | not specified | no comparison |
References and Note
- Shafiee Roodposhti, M.; Behrang, K.; Kamali, H.; Rezadoost, B. An Evaluation of the Advertising Media Function Using DEA and DEMATEL. J. Promot. Manag. 2022, 28, 923–943. [Google Scholar] [CrossRef]
- Luo, X.; Donthu, N. Benchmarking Advertising Efficiency. J. Advert. Res. 2001, 41, 7–18. [Google Scholar] [CrossRef]
- Luo, X.; Donthu, N. Assessing advertising media spending inefficiencies in generating sales. J. Bus. Res. 2005, 58, 28–36. [Google Scholar] [CrossRef]
- Guido, G.; Prete, M.I.; Miraglia, S.; De Mare, I. Targeting direct marketing campaigns by neural networks. J. Mark. Manag. 2011, 27, 992–1006. [Google Scholar] [CrossRef]
- Hudák, M.; Kianičková, E.; Madleňák, R. The importance of e-mail marketing in e-commerce. Procedia Eng. 2017, 192, 342–347. [Google Scholar] [CrossRef]
- Litmus Software. The 2023 State of E-Mail Report; Litmus: Boston, MA, USA, 2023. [Google Scholar]
- Păvăloaia, V.-D.; Anastasiei, I.-D.; Fotache, D. Social Media and E-mail Marketing Campaigns: Symmetry versus Convergence. Symmetry 2020, 12, 1940. [Google Scholar] [CrossRef]
- Qabbaah, H.; Sammour, G.; Vanhoof, K. Decision Tree Analysis to Improve e-mail Marketing Campaigns. Int. J. Inf. Theor. Appl. 2019, 26, 3–36. [Google Scholar]
- Ayanso, A.; Mokaya, B. Efficiency Evaluation in Search Advertising. Decis. Sci. 2013, 44, 877–913. [Google Scholar] [CrossRef]
- Farvaque, E.; Foucault, M.; Vigeant, S. The politician and the vote factory: Candidates’ resource management skills and electoral returns. J. Policy Model. 2020, 42, 38–55. [Google Scholar] [CrossRef]
- Sexton, T.R.; Lewis, H.F. Measuring efficiency in the presence of head-to-head competition. J. Product. Anal. 2012, 38, 183–197. [Google Scholar] [CrossRef]
- Götz, G.; Herold, D.; Klotz, P.-A.; Schäfer, J.T. Efficiency in COVID-19 Vaccination Campaigns—A Comparison across Germany’s Federal States. Vaccines 2021, 9, 788. [Google Scholar] [CrossRef]
- Lohtia, R.; Donthu, N.; Yaveroglu, I. Evaluating the efficiency of Internet banner advertisements. J. Bus. Res. 2007, 60, 365–370. [Google Scholar] [CrossRef]
- Lo, Y.C.; Fang, C.-Y. Facebook marketing campaign benchmarking for a franchised hotel. Int. J. Contemp. Hosp. Manag. 2018, 30, 1705–1723. [Google Scholar] [CrossRef]
- Cordero-Gutiérrez, R.; Lahuerta-Otero, E. Social media advertising efficiency on higher education programs. Span. J. Mark.—ESIC 2020, 24, 247–262. [Google Scholar] [CrossRef]
- Kongar, E.; Adebayo, O. Impact of Social Media Marketing on Business Performance: A Hybrid Performance Measurement Approach Using Data Analytics and Machine Learning. IEEE Eng. Manag. Rev. 2021, 49, 133–147. [Google Scholar] [CrossRef]
- Hamelin, N.; Al-Shihabi, S.; Quach, S.; Thaichon, P. Forecasting Advertisement Effectiveness: Neuroscience and Data Envelopment Analysis. Australas. Mark. J. 2022, 30, 313–330. [Google Scholar] [CrossRef]
- Ejlal, A.; Roodposhti, M.S. Providing a framework for evaluating the advertising efficiency using data envelopment analysis technique. Middle East J. Manag. 2019, 6, 451. [Google Scholar] [CrossRef]
- Najadat, H.; Najadat, H.; Althebyan, Q.; Khamaiseh, A.; Al-Saad, M.; Rawashdeh, A.A. The Society of Digital Information and Wireless Communication Efficiency Analysis of Health Care Centers Using Data Envelopment Analysis. Int. J. E-Learn. Educ. Technol. Digit. Media 2018, 4, 34–38. [Google Scholar] [CrossRef]
- Sohn, S.Y.; Moon, T.H. Decision Tree based on data envelopment analysis for effective technology commercialization. Expert Syst. Appl. 2004, 26, 279–284. [Google Scholar] [CrossRef]
- Alinezhad, A. An Integrated DEA and Data Mining Approach for Performance Assessment. Iran. J. Optim. 2016, 8, 968–987. [Google Scholar]
- Anouze, A.L.M.; Bou-Hamad, I. Data envelopment analysis and data mining to efficiency estimation and evaluation. Int. J. Islam. Middle East. Financ. Manag. 2019, 12, 169–190. [Google Scholar] [CrossRef]
- Emrouznejad, A.; Anouze, A.L. Data envelopment analysis with classification and regression tree—A case of banking efficiency. Expert Syst. 2010, 27, 231–246. [Google Scholar] [CrossRef]
- Mirmozaffari, M.; Shadkam, E.; Khalili, S.M.; Kabirifar, K.; Yazdani, R.; Asgari Gashteroodkhani, T. A novel artificial intelligent approach: Comparison of machine learning tools and algorithms based on optimization DEA Malmquist productivity index for eco-efficiency evaluation. Int. J. Energy Sect. Manag. 2021, 15, 523–550. [Google Scholar] [CrossRef]
- Appiahene, P.; Missah, Y.M.; Najim, U. Predicting Bank Operational Efficiency Using Machine Learning Algorithm: Comparative Study of Decision Tree, Random Forest, and Neural Networks. Adv. Fuzzy Syst. 2020, 2020, 8581202. [Google Scholar] [CrossRef]
- Wu, D. Supplier selection: A hybrid model using DEA, decision tree and neural network. Expert Syst. Appl. 2009, 36, 9105–9112. [Google Scholar] [CrossRef]
- Perroni, M.G.; Veiga, C.P.D.; Forteski, E.; Marconatto, D.A.B.; Da Silva, W.V.; Senff, C.O.; Su, Z. Integrating Relative Efficiency Models with Machine Learning Algorithms for Performance Prediction. Sage Open 2024, 14, 21582440241257800. [Google Scholar] [CrossRef]
- Dalvand, B.; Jahanshahloo, G.; Lotfi, F.H.; Rostami, M. Using C4.5 Algorithm for Predicting Efficiency Score of DMUs in DEA. Adv. Environ. Biol. 2014, 8, 473–477. [Google Scholar]
- Khalili, J.; Alinezhad, A. Performance Evaluation in Green Supply Chain Using BSC, DEA and Data Mining. Int. J. Supply Oper. Manag. 2018, 5, 182–191. [Google Scholar] [CrossRef]
- Patel, B.R.; Rana, K.K. A Survey on Decision Tree Algorithm For Classification. Int. J. Eng. Dev. Res. 2014, 2, 1–5. [Google Scholar]
- Song, Y.; Lu, Y. Decision tree methods: Applications for classification and prediction. Shanghai Arch. Psychiatry 2015, 27, 130–135. [Google Scholar] [CrossRef]
- Isbilen-Yucel, L. Veri Zarflama Analizi, 1st ed.; Der Yayinlari: Istanbul, Türkiye, 2017; ISBN 978-975-353-484-0. [Google Scholar]
- Heiets, I.; Ng, S.; Singh, N.; Farrell, J.; Kumar, A. Social media activities of airlines: What makes them successful? J. Air Transp. Res. Soc. 2024, 2, 100017. [Google Scholar] [CrossRef]
- Murphy, D. Increasing clicks through advanced targeting: Applying the third-party seal model to airline advertising. J. Tour. Herit. Serv. Mark. 2019, 5, 24–30. [Google Scholar] [CrossRef]
- Sakas, D.P.; Reklitis, D.P. The Impact of Organic Traffic of Crowdsourcing Platforms on Airlines’ Website Traffic and User Engagement. Sustainability 2021, 13, 8850. [Google Scholar] [CrossRef]
- Vlassi, E.; Papatheodorou, A. Towards a Method to Assess the Role of Online Marketing Campaigns in the Airline–Airport–Destination Authority Triangular Business Relationship: The Case of Athens Tourism Partnership. In Air Transport and Regional Development Policies; Routledge: London, UK, 2020; pp. 227–239. [Google Scholar]
- Vlassi, E.; Papatheodorou, A.; Karachalis, N. Evaluating the Effectiveness of Online Destination Marketing Campaigns from a Sustainability and Resilience Viewpoint: The Case of “This Is Athens & Partners” in Greece. Sustainability 2024, 16, 7649. [Google Scholar] [CrossRef]
- Lorente-Páramo, Á.-J.; Hernández-García, Á.; Chaparro-Peláez, J. Modelling e-mail marketing effectiveness—An approach based on the theory of hierarchy-of-effects. Manag. Lett. 2021, 21, 19–27. [Google Scholar] [CrossRef]
- Bonfrer, A.; Dréze, X. Real-Time Evaluation of E-mail Campaign Performance. Mark. Sci. 2009, 28, 251–263. [Google Scholar] [CrossRef]
- Smart, K.L.; Cappel, J. Assessing the Response to and Success of Email Marketing Promotions. Issues Inf. Syst. 2003, 4, 309–315. [Google Scholar]
- Sahni, N.S.; Wheeler, S.C.; Chintagunta, P. Personalization in Email Marketing: The Role of Non-Informative Advertising Content. Mark. Sci. 2018, 37, 177–331. [Google Scholar] [CrossRef]
- Skačkauskienė, I.; Nekrošienė, J.; Szarucki, M. A Review on Marketing Activities Effectiveness Evaluation Metrics. In Proceedings of the 13th International Scientific Conference “Business and Management 2023”, Vilnius, Lithuania, 11–13 May 2023. [Google Scholar]
- Hartemo, M. Conversions on the rise—Modernizing e-mail marketing practices by utilizing volunteered data. J. Res. Interact. Mark. 2022, 16, 585–600. [Google Scholar] [CrossRef]
- Wiesel, T.; Pauwels, K.; Arts, J. Marketing’s Profit Impact: Quantifying Online and Off-line Funnel Progression. Mark. Sci. 2011, 30, 604–611. [Google Scholar] [CrossRef]
- Sarkis, J. Preparing Your Data for DEA. In Modeling Data Irregularities and Structural Complexities in Data Envelopment Analysis; Zhu, J., Cook, W.D., Eds.; Springer US: Boston, MA, USA, 2007; pp. 305–320. ISBN 978-0-387-71606-0. [Google Scholar]
- Boussofiane, A.; Dyson, R.G.; Thanassoulis, E. Applied data envelopment analysis. Eur. J. Oper. Res. 1991, 52, 1–15. [Google Scholar] [CrossRef]
- Golany, B.; Roll, Y. An application procedure for DEA. Omega 1989, 17, 237–250. [Google Scholar] [CrossRef]
- Friedman, L.; Sinuany-Stern, Z. Combining ranking scales and selecting variables in the DEA context: The case of industrial branches. Comput. Oper. Res. 1998, 25, 781–791. [Google Scholar] [CrossRef]
- Cooper, W.W.; Seiford, L.M.; Tone, K. (Eds.) Data Envelopment Analysis: A Comprehensive Text with Models, Applications, References and DEA-Solver Software, 2nd ed.; Springer Science & Business Media, LLC: Boston, MA, USA, 2007; ISBN 978-0-387-45281-4. [Google Scholar]
- Dyson, R.G.; Allen, R.; Camanho, A.S.; Podinovski, V.V.; Sarrico, C.S.; Shale, E.A. Pitfalls and protocols in DEA. Eur. J. Oper. Res. 2001, 132, 245–259. [Google Scholar] [CrossRef]
- Tone, K.; Tsutsui, M. Dynamic DEA: A slacks-based measure approach. Omega 2010, 38, 145–156. [Google Scholar] [CrossRef]
- Ray, S.C. Data Envelopment Analysis: An Overview; University of Connecticut: Mansfield, CT, USA, 2014. [Google Scholar]
- Cook, W.D.; Tone, K.; Zhu, J. Data envelopment analysis: Prior to choosing a model. Omega 2014, 44, 1–4. [Google Scholar] [CrossRef]
- Barros, C.P.; Athanassiou, M. Efficiency in European Seaports with DEA: Evidence from Greece and Portugal. Marit. Econ. Logist. 2004, 6, 122–140. [Google Scholar] [CrossRef]
- Cooper, W.W.; Seiford, L.M.; Tone, K. Introduction to Data Envelopment Analysis and Its Uses: With DEA-Solver Software and References; Springer US: Boston, MA, USA, 2006; ISBN 978-0-387-28580-1. [Google Scholar]
- Cooper, W.W.; Seiford, L.M.; Tone, K. Data Envelopment Analysis, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2007; ISBN 0-387-45283-4. [Google Scholar]
- Kutlar, A.; Bakirci, F. Veri Zarflama Analizi Teori ve Uygulama; Orion: Ankara, Türkiye, 2018; ISBN 978-605-9524-22-3. [Google Scholar]
- Yang, L.; Ouyang, H.; Fang, K.; Ye, L.; Zhang, J. Evaluation of regional environmental efficiencies in China based on super-efficiency-DEA. Ecol. Indic. 2015, 51, 13–19. [Google Scholar] [CrossRef]
- Andersen, P.; Petersen, N.C. A Procedure for Ranking Efficient Units in Data Envelopment Analysis. Manag. Sci. 1993, 39, 1261–1264. [Google Scholar] [CrossRef]
- Frontier Analyst, version 4.0; Commercial computer software; Banxia Software Ltd.: Kendal, UK, 2025.
- Tanza, A.; Utari, D.T. Comparison of the Naïve Bayes Classifier and Decision Tree J48 for Credit Classification of Bank Customers. EKSAKTA J. Sci. Data Anal. 2022, 3, 70–77. [Google Scholar] [CrossRef]
- Quinlan, J.R. Improved Use of Continuous Attributes in C4.5. J. Artif. Intell. Res. 1996, 4, 77–90. [Google Scholar] [CrossRef]
- Mahboob, T.; Irfan, S.; Karamat, A. A machine learning approach for student assessment in E-learning using Quinlan’s C4.5, Naive Bayes and Random Forest algorithms. In Proceedings of the 2016 19th International Multi-Topic Conference (INMIC), Islamabad, Pakistan, 5–6 December 2016; pp. 1–8. [Google Scholar]
- Bujlow, T.; Riaz, T.; Pedersen, J.M. A method for classification of network traffic based on C5.0 Machine Learning Algorithm. In Proceedings of the 2012 International Conference on Computing, Networking and Communications (ICNC), Maui, HI, USA, 30 January–2 February 2012; pp. 237–241. [Google Scholar]
- Montazeri, M.; Montazeri, M.; Beygzadeh, A.; Javad Zahedi, M. Identifying efficient features in diagnose of liver disease by decision tree models. HealthMED 2014, 8, 1115–1124. [Google Scholar]
- Kalmegh, S. Analysis of WEKA Data Mining Algorithm Reptree, Simple Cart and RandomTree for Classification of Indian News. Int. J. Innov. Sci. Eng. Technol. 2015, 2, 438–446. [Google Scholar]
- Weka Homepage. Available online: https://ml.cms.waikato.ac.nz/weka/ (accessed on 1 May 2025).
- Banker, R.D.; Morey, R.C. The Use of Categorical Variables in Data Envelopment Analysis. Manag. Sci. 1986, 32, 1613–1627. [Google Scholar] [CrossRef]
- Banker, R.D.; Morey, R.C. Efficiency Analysis for Exogenously Fixed Inputs and Outputs. Oper. Res. 1986, 34, 513–521. [Google Scholar] [CrossRef]
- Chen, K.; Zhu, J. Scale efficiency in two-stage network DEA. J. Oper. Res. Soc. 2019, 70, 101–110. [Google Scholar] [CrossRef]
- Elliott, A.C.; Hynan, L.S. A SAS® macro implementation of a multiple comparison post hoc test for a Kruskal–Wallis analysis. Comput. Methods Programs Biomed. 2011, 102, 75–80. [Google Scholar] [CrossRef] [PubMed]
- Dogan, N.; Dogan, I. Determination of the number of bins/classes used in histograms and frequency tables: A short bibliography. J. Stat. Res. 2010, 7, 77–86. [Google Scholar]
- Najadat, H.; Al-Daher, I.; Alkhatib, K. Performance Evaluation of Industrial Firms Using DEA and DECORATE Ensemble Method. Int. Arab J. Inf. Technol. 2020, 17, 750–757. [Google Scholar] [CrossRef]
- Seol, H.; Choi, J.; Park, G.; Park, Y. A framework for benchmarking service process using data envelopment analysis and decision tree. Expert Syst. Appl. 2007, 32, 432–440. [Google Scholar] [CrossRef]

| Study | DMU(s)/Unit of Analysis | Orientation and DEA Model | Input(s) | Output(s) |
|---|---|---|---|---|
| [13] | 37 internet banner ads, multiple firms | orientation not specified (implicitly output-oriented), DEA model not specified | color level presence of emotion presence of incentive presence of interactivity presence of animation message length | CTR |
| CTR attitude toward the ad recall | ||||
| [9] | 200 online retailers in search advertising, multiple firms | output-oriented, BCC | number of paid keywords, number of organic keywords keyword length cost per click (CPC) cost per day number of ad copies | online sales impressions CTR conversion rate ad-rank percentile for sponsored links organic ranking |
| [14] | 60 Facebook marketing campaigns, single firm | input-oriented, CCR, BCC | text length number of pictures number of colors | people reached reactions, comments and shares post clicks |
| [15] | 45 Facebook ads, single institution | not specified | ad duration (in days) amount spent | reach impressions clicks reactions post engagement |
| [16] | 43 U.S. furniture retailers, multiple firms | CCR with benevolent cross-efficiency ranking, orientation not specified (implicitly output-oriented) | number of employees total assets | annual sales |
| number of employees total assets tweets | annual sales likes followers friends list count | |||
| [2] | 23 outdoor billboard campaigns, multiple firms | not specified | number of large words number of concepts color vs. black-and-white level of graphics | consumer recall expert-rated ad quality |
| [17] | 14 real-estate print ads, single firm | output-oriented, BCC | no inputs used | joy engagement positive attention |
| [18] | 15 Iranian food brands, multiple firms | input-oriented, BCC | advertising budget campaign duration | sales brand familiarity attractiveness of implementation |
| Study | Campaign Evaluation Indicators |
|---|---|
| [33] | followers, post frequency, total interactions (comments, likes), content type (advertising, informational, customer care, interactive, entertainment, promotional), platform efficiencies (Facebook, Instagram, X, LinkedIn, TikTok) |
| [34] | impressions, reach, clicks, CTR, cost per click (CPC) |
| [35] | organic traffic, paid keywords, paid traffic cost, average visit duration, unique visitors, user engagement, global rank |
| [36] | destination awareness, emotional proximity, intention to visit incremental spending, ROI |
| [37] | destination awareness, campaign awareness, campaign engagement, intention to visit, conversion, average cost per visitor, ROI, perception, emotional proximity, additional spending |
| Study | Evaluation Indicators |
|---|---|
| [38] | open rate (Attention), CTR (Interest), unsubscribe rate (Retention), conversion (Action), (Desire excluded) |
| [39] | open rate, CTOR, CTR, emails sent, opens per campaign, clicks per campaign, time-to-first-open, time-to-first-click, doubling time |
| [40] | CTR, conversion rate |
| [41] | open rate, sales leads, unsubscribe rate |
| [42] | delivery metrics: delivery rate, bounce rate, spam complaint rate open metrics: open rate, unique open rate click metrics: CTR, unique click rate conversion metrics: conversion rate, revenue per email, ROI engagement metrics: forward rate, sharing rate, reply rate list growth metrics: new subscribers, list growth rate, unsubscribe rate |
| Variable Code | Variable Name | Variable Definition |
|---|---|---|
| I1 | booking period | time period during which tickets can be purchased as part of the campaign |
| I2 | travel period | time period during which travel is possible as part of the campaign |
| I3 | number of emails sent | the number of campaign emails sent to customers |
| I4 | number of flights taken | average number of flights taken by customers to whom campaign emails were sent in the last 18 months prior to the campaign |
| I5 | market share | the market share of the company within the routes and travel periods targeted by each campaign |
| I6 | market size | total customers carried by all airlines on the campaign’s relevant routes and dates |
| Variable Code | Variable Name | Variable Definition |
|---|---|---|
| O1 | CTOR (click-to-open rate) | the ratio of recipients who clicked on a link after opening the campaign email |
| O2 | tickets sold | the total number of tickets sold during the campaign period |
| Model No. | Categorical Variable | Segment | Inputs | Outputs |
|---|---|---|---|---|
| CCR_C * | I1, I2, I3, I4, I5, I6 | O1, O2 | ||
| CCR_G | G (group size) | all | ||
| CCR_G_I | I (individual) | |||
| CCR_G_G | G (group) | |||
| CCR_S | S (seasonality) | all | ||
| CCR_S_L | L (low) | |||
| CCR_S_H | H (high) | |||
| CCR_R | R (route type) | all | ||
| CCR_R_O | O (one-way) | |||
| CCR_R_R | R (round-trip) | |||
| CCR_R_B | B (both) | |||
| BCC_C * | I1, I2, I3, I4, I5, I6 | O1, O2 | ||
| BCC_G | G (group size) | I (individual) | ||
| BCC_G_I | G (group) | |||
| BCC_G_G | all | |||
| BCC_S | S (seasonality) | L (low) | ||
| BCC_S_L | H (high) | |||
| BCC_S_H | all | |||
| BCC_R | R (route type) | O (one-way) | ||
| BCC_R_O | R (round-trip) | |||
| BCC_R_R | B (both) | |||
| BCC_R_B | I (individual) |
| Model No. | Number of Efficient Campaigns (Score = 100) | Number of Inefficient Campaigns (Score < 100) | Mean | Median | Std | Min |
|---|---|---|---|---|---|---|
| CCR_C | 26 | 50 | 69.5 | 74.6 | 28.6 | 12.7 |
| CCR-G-I CCR-G-G | 22 9 | 45 0 | 70.2 100 | 75.6 100 | 27.6 0 | 12.7 100 |
| CCR-S-L CCR-S-H | 20 16 | 35 5 | 76.5 94 | 82.9 100 | 23.9 16.6 | 19.7 34.2 |
| CCR-R-O CCR-R-R CCR-R-B | 10 15 11 | 1 33 6 | 98.8 71.3 84.5 | 100 77.1 100 | 4 27.2 27.8 | 86.9 12.8 28.2 |
| BCC-C | 46 | 30 | 80.8 | 100 | 27.7 | 13.3 |
| BCC-G-I BCC-G-G | 41 9 | 26 0 | 81.4 100 | 100 100 | 26.9 0 | 13.3 100 |
| BCC-S-L BCC-S-H | 41 20 | 14 1 | 90.4 98.6 | 100 100 | 20.2 6.6 | 20.7 69.6 |
| BCC-R-O BCC-R-R BCC-R-B | 11 31 14 | 0 17 3 | 100 84 87.8 | 100 100 100 | 0 25.9 27.2 | 100 13.3 30.4 |
| DEA Model | Models | Categorical Variables | Mean | Median | Std | Min |
|---|---|---|---|---|---|---|
| CCR_C—BCC_C | 0.87 | 0.97 | 0.19 | 0.32 | ||
| CCR_G—BCC_G | G I | 1 0.87 | 1 0.96 | 0 0.17 | 1 0.38 | |
| SE | CCR_S—BCC_S | L H | 0.85 0.95 | 0.94 1 | 0.18 0.15 | 0.36 0.34 |
| CCR_R—BCC_R | R O B | 0.86 0.99 0.96 | 0.96 1 1 | 0.19 0.04 0.1 | 0.31 0.87 0.61 |
| Models | Chi-Square (χ2) | Degrees of Freedom (df) | p-Value |
|---|---|---|---|
| CCR | 41.12 | 7 | 1 × 10−6 |
| BCC | 22.68 | 7 | 1.934 × 10−3 |
| Model Comparison | Z-Statistic | Adjusted p-Value (Bonferroni) |
|---|---|---|
| CCR_G_G—CCR_C | 3.56 | 0.010 |
| CCR_S_H—CCR_C | 3.78 | 0.004 |
| CCR_R_O—CCR_C | 3.61 | 0.008 |
| CCR_G_G—CCR_G_I | 3.50 | 0.013 |
| CCR_S_H—CCR_G_I | 3.69 | 0.006 |
| CCR_R_O—CCR_G_I | 3.55 | 0.011 |
| CCR_G_G—CCR_R_R | 3.38 | 0.020 |
| CCR_S_H—CCR_R_R | 3.47 | 0.015 |
| CCR_R_O—CCR_R_R | 3.41 | 0.018 |
| Group 1 | Group 2 | Rank-Biserial r |
|---|---|---|
| CCR_C | CCR_G_G | 0.65 |
| CCR_C | CCR_S_H | 0.49 |
| CCR_C | CCR_R_O | 0.62 |
| CCR_G_G | CCR_G_I | −0.67 |
| CCR_G_I | CCR_S_H | 0.51 |
| CCR_G_G | CCR_R_R | −0.69 |
| CCR_G_I | CCR_R_O | 0.64 |
| CCR_R_R | CCR_S_H | 0.52 |
| CCR_R_R | CCR_R_O | 0.64 |
| Range | CCR Models | |||||||
|---|---|---|---|---|---|---|---|---|
| CCR_C | CCR_G_I | CCR_G_G | CCR_S_L | CCR_S_H | CCR_R_O | CCR_R_R | CCR_R_B | |
| [100–250) | 18 | 14 | 5 | 13 | 12 | 7 | 8 | 5 |
| [200–400) | 4 | 4 | 1 | 3 | 2 | 0 | 5 | 3 |
| [400–550) | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| [550–700) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| [700–850) | 1 | 2 | 0 | 1 | 1 | 0 | 1 | 0 |
| [850–1000] | 3 | 2 | 2 | 3 | 1 | 3 | 1 | 3 |
| Range | BCC Models | |||||||
|---|---|---|---|---|---|---|---|---|
| BCC_C | BCC_G_I | BCC_G_G | BCC_S_L | BCC_S_H | BCC_R_O | BCC_R_R | BCC_R_B | |
| [100–250) | 7 | 7 | 0 | 4 | 3 | 2 | 0 | 1 |
| [200–400) | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| [400–550) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| [550–700) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| [700–850) | 2 | 2 | 0 | 1 | 0 | 0 | 1 | 0 |
| [850–1000] | 36 | 32 | 9 | 36 | 16 | 9 | 30 | 13 |
| Model | Output Variable | Variation (%) | Range of Mean Model Differences | Spearman’s ρ | Number of Efficient Campaigns |
|---|---|---|---|---|---|
| CCR_C | O1 | ±5, ±10 | 0 to 2.63 × 10−4 0 | 1 | 26 |
| O2 | |||||
| CCR_S_L | O1 | ±5, ±10 | −1.82 × 10−4 to 0 | 1 | 20 |
| O2 | 0 | ||||
| CCR_S_H | O1 | ±5, ±10 | 0 | 1 | 16 |
| O2 |
| Input Removed | Δ Mean Model | Spearman’s ρ | Number of Efficient Campaigns |
|---|---|---|---|
| I1 | −7.83 | 0.88 | 21 |
| I2 | −5.29 | 0.95 | 22 |
| I3 | −0.56 | 0.99 | 25 |
| I4 | −4.93 | 0.93 | 22 |
| I5 | −7.42 | 0.94 | 18 |
| I6 | −13.55 | 0.65 | 16 |
| Input Removed | Δ Mean Model | Spearman’s ρ | Efficient Campaigns |
|---|---|---|---|
| I1 | −10.89 | 0.80 | 17 |
| I2 | −7.17 | 0.89 | 16 |
| I3 | −0.50 | 0.98 | 19 |
| I4 | −1.79 | 0.97 | 19 |
| I5 | −10.02 | 0.91 | 14 |
| I6 | −9.60 | 0.64 | 13 |
| Input Removed | Δ Mean Model | Spearman’s ρ | Efficient Campaigns |
|---|---|---|---|
| I1 | −1.27 | 0.90 | 15 |
| I2 | −1.74 | 1.00 | 16 |
| I3 | −0.29 | 1.00 | 16 |
| I4 | 0.00 | 1.00 | 16 |
| I5 | −6.24 | 0.64 | 13 |
| I6 | −28.05 | 0.62 | 8 |
| Model | Scenario | Δ Mean Model | Spearman’s ρ | Efficient Campaigns |
|---|---|---|---|---|
| CCR_C | 3 campaigns removed | 6.12 | 0.88 | 26 |
| CCR_S_L | 3 campaigns removed | 4.40 | 0.92 | 19 |
| CCR_S_H | 1 campaign removed | 0 | 1 | 15 |
| Variable | Potential Improvement (%) |
|---|---|
| O1 | 44 |
| O2 | 44 |
| I1 | 0 |
| I2 | −34 |
| I3 | −26 |
| I4 | 0 |
| I5 | 0 |
| I6 | 0 |
| Campaign | Variable | Contribution (%) |
|---|---|---|
| 42 | O1 | 36 |
| O2 | 91 | |
| I1 | 39 | |
| I2 | 55 | |
| I3 | 83 | |
| I4 | 23 | |
| I5 | 17 | |
| I6 | 99 |
| Variable | Contribution (%) | Input/Output |
|---|---|---|
| I1 | 21 | Input |
| I2 | 0 | Input |
| I3 | 0 | Input |
| I4 | 1.52 | Input |
| I5 | 0.69 | Input |
| I6 | 77 | Input |
| O1 | 12 | Output |
| O2 | 88 | Output |
| Model | Correctly Classified Campaigns (n) | J48 | CART | C5.0 |
|---|---|---|---|---|
| CCR_C | accuracy rate (%) | 76.3 | 67.1 | 73.7 |
| correctly classified instances | 58 | 51 | 56 | |
| BCC_C | accuracy rate (%) | 71.1 | 68.4 | 78.9 |
| correctly classified instances | 54 | 52 | 60 |
| Algorithm | Model | Efficiency | Classified as Efficient | Classified as Inefficient |
|---|---|---|---|---|
| J48 | CCR_C | efficient | 12 | 14 |
| inefficient | 4 | 46 | ||
| BCC_C | efficient | 31 | 15 | |
| inefficient | 7 | 23 | ||
| CART | CCR_C | efficient | 7 | 19 |
| inefficient | 6 | 44 | ||
| BCC_C | efficient | 36 | 10 | |
| inefficient | 14 | 16 | ||
| C5.0 | CCR_C | efficient | 8 | 18 |
| inefficient | 2 | 48 | ||
| BCC_C | efficient | 39 | 7 | |
| inefficient | 9 | 21 |
| Correctly Classified Campaigns (n) | J48 | CART | C5.0 |
|---|---|---|---|
| accuracy rate (%) | 76.3 | 72.3 | 75.0 |
| correctly classified instances | 58 | 55 | 57 |
| Algorithm | Efficiency | Classified as Efficient | Classified as Inefficient |
|---|---|---|---|
| J48 | efficient | 36 | 10 |
| inefficient | 8 | 22 | |
| CART | efficient | 34 | 12 |
| inefficient | 9 | 21 | |
| C5.0 | efficient | 40 | 6 |
| inefficient | 13 | 17 |
| Model | Efficiency | TP Rate | FP Rate | Precision | Recall | F-Measure | Kappa | ROC Area |
|---|---|---|---|---|---|---|---|---|
| J48 | efficient | 0.783 | 0.267 | 0.818 | 0.783 | 0.800 | 0.510 | 0.763 |
| inefficient | 0.733 | 0.217 | 0.688 | 0.733 | 0.710 | |||
| weighted average | 0.763 | 0.247 | 0.767 | 0.763 | 0.764 | |||
| CART | efficient | 0.739 | 0.300 | 0.791 | 0.739 | 0.764 | 0.432 | 0.758 |
| inefficient | 0.700 | 0.261 | 0.636 | 0.700 | 0.667 | |||
| weighted average | 0.724 | 0.285 | 0.73 | 0.724 | 0.726 | |||
| C5.0 | efficient | 0.870 | 0.433 | 0.755 | 0.870 | 0.808 | 0.455 | 0.684 |
| inefficient | 0.567 | 0.130 | 0.739 | 0.567 | 0.642 | |||
| weighted average | 0.750 | 0.314 | 0.749 | 0.750 | 0.749 |
| Study | Number of DMUs | Accuracy Rates (%) |
|---|---|---|
| [26] | 23 | using C4.5; CCR (90.9), BCC (81.8) |
| [29] | 15 | not specified |
| [73] | 53 | using J48 for aggregated scores of VRS and CRS DEA models; imbalanced (79.9), balanced (81.6) (after DECORATE) |
| [24] | 22 | MPI-based AM model (91.2) |
| [28] | 200 | using C4.5; CCR (86.5) |
| [27] | 7548 | CCR (98.2)-2 *, BCC (98.9)-2 * |
| [20] | 131 | not specified |
| [25] | 444 | using C5.0; CCR (100) |
| [19] | 21 | using J48; for use of only inputs: imbalanced (76.2), balanced (88.1) for use of both inputs and outputs: imbalanced (71.4) balanced (89.3) |
| [21] | 18 | using CART based on Latent Variable VRS DEA model; for Period I: 98.02, period II: 100 (with Bootstrap) |
| [22] | 151 | using CART; VRS DEA (75.5), for CIT; VRS DEA (67.5) |
| [23] | 36 | using CART; VRS DEA (97.9) (with Bootstrap) |
| [74] | 200 | not specified |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Inci, G.; Polat, S. Efficiency Analysis and Classification of an Airline’s Email Campaigns Using DEA and Decision Trees. Information 2025, 16, 969. https://doi.org/10.3390/info16110969
Inci G, Polat S. Efficiency Analysis and Classification of an Airline’s Email Campaigns Using DEA and Decision Trees. Information. 2025; 16(11):969. https://doi.org/10.3390/info16110969
Chicago/Turabian StyleInci, Gizem, and Seckin Polat. 2025. "Efficiency Analysis and Classification of an Airline’s Email Campaigns Using DEA and Decision Trees" Information 16, no. 11: 969. https://doi.org/10.3390/info16110969
APA StyleInci, G., & Polat, S. (2025). Efficiency Analysis and Classification of an Airline’s Email Campaigns Using DEA and Decision Trees. Information, 16(11), 969. https://doi.org/10.3390/info16110969






