Modular Reinforcement Learning for Multi-Market Portfolio Optimization
Abstract
1. Introduction
- We present a modular reinforcement learning framework for multi-market portfolio optimization.
- We integrate four RL algorithms into MPLS and analyze their scenario-wise performance (Sharpe ratio, CVaR, drawdown, turnover) across stable, crisis, recovery, and sideways regimes.
- We report robustness analyses, including stability across multiple runs and ablation studies, to quantify the non-redundant contribution of each module.
- We show that MPLS consistently achieved higher risk-adjusted returns than traditional baselines, while maintaining moderate turnover.
2. Related Work
2.1. Portfolio Optimization in Dynamic Markets
2.2. Reinforcement Learning in Finance
2.3. Modular Architectures and Multi-Signal Integration
2.4. Comparative Evaluation of RL Algorithms
3. Preliminaries
3.1. Reinforcement Learning in Portfolio Management
3.2. Reinforcement Learning Algorithms Compared
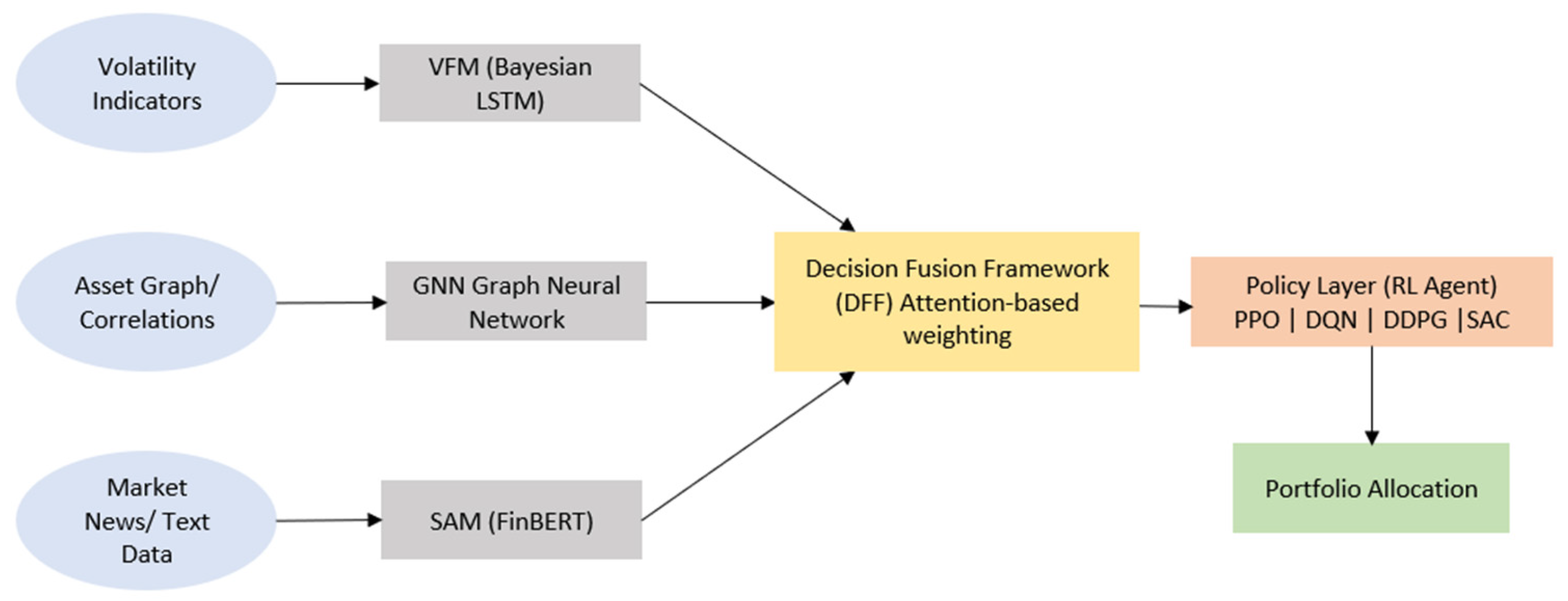
3.3. Modular Portfolio Learning System (MPLS)
- Sentiment Analysis Module (SAM)—Employs the transformer-based NLP model FinBERT to extract market sentiment from financial news, capturing behavioral shifts not evident in price data [27].
- Volatility Forecasting Module (VFM)—Employs Bayesian LSTM networks to anticipate regime changes and quantify predictive uncertainty, guiding risk-sensitive allocations [28].
- Structural Dependency Module (GNN)—Uses Graph Neural Networks to model evolving inter-asset relationships via dynamic correlation graphs [29].
4. Methodology
4.1. System Overview
4.2. Modular Design
4.2.1. Sentiment Analysis Module (SAM)
4.2.2. Volatility Forecasting Module (VFM)
4.2.3. Structural Dependency Module (SDM)
4.3. Decision Fusion Framework (DFF)
4.4. Reinforcement Learning Backbone
- State (): asset prices, technical indicators, and the DFF-fused latent vector , which encapsulates sentiment, volatility, and structural information extracted from the SAM, VFM, and GNN modules.
- Action (): portfolio weights across N assets, with
- Reward (): risk-adjusted return incorporating transaction costs:
4.5. Training Procedure
- Module Pretraining: Each module (SAM, VFM, SDM) is pretrained on domain-specific tasks (e.g., sentiment classification, volatility forecasting, correlation prediction).
- Fusion Learning: The DFF learns to align module outputs with RL objectives through attention updates.
- Policy Optimization: The RL backbone updates policy parameters θ by maximizing the expected cumulative reward:
- Sample market trajectories
- Update expert modules
- Fuse signals via DFF
- Update RL policy parameters
- Repeat until convergence
5. Experimental Setup
5.1. Data Sources and Markets
5.2. Preprocessing and Feature Engineering
5.3. Market Scenarios
- Stable Pre-crisis (January–December 2019)—low volatility and sustained growth.
- Crisis (COVID-19 Crash, February–April 2020)—sharp drawdowns and extreme uncertainty [51].
- Recovery (June–August 2020)—rebound following crisis-driven lows.
- Sideways Market (October–December 2020)—stagnant returns with increased noise.
- Full-Year Generalization (2020)—long-term consistency across heterogeneous regimes.
5.4. Benchmarks
5.5. Algorithmic Configurations
5.6. Evaluation Metrics
6. Results and Analysis
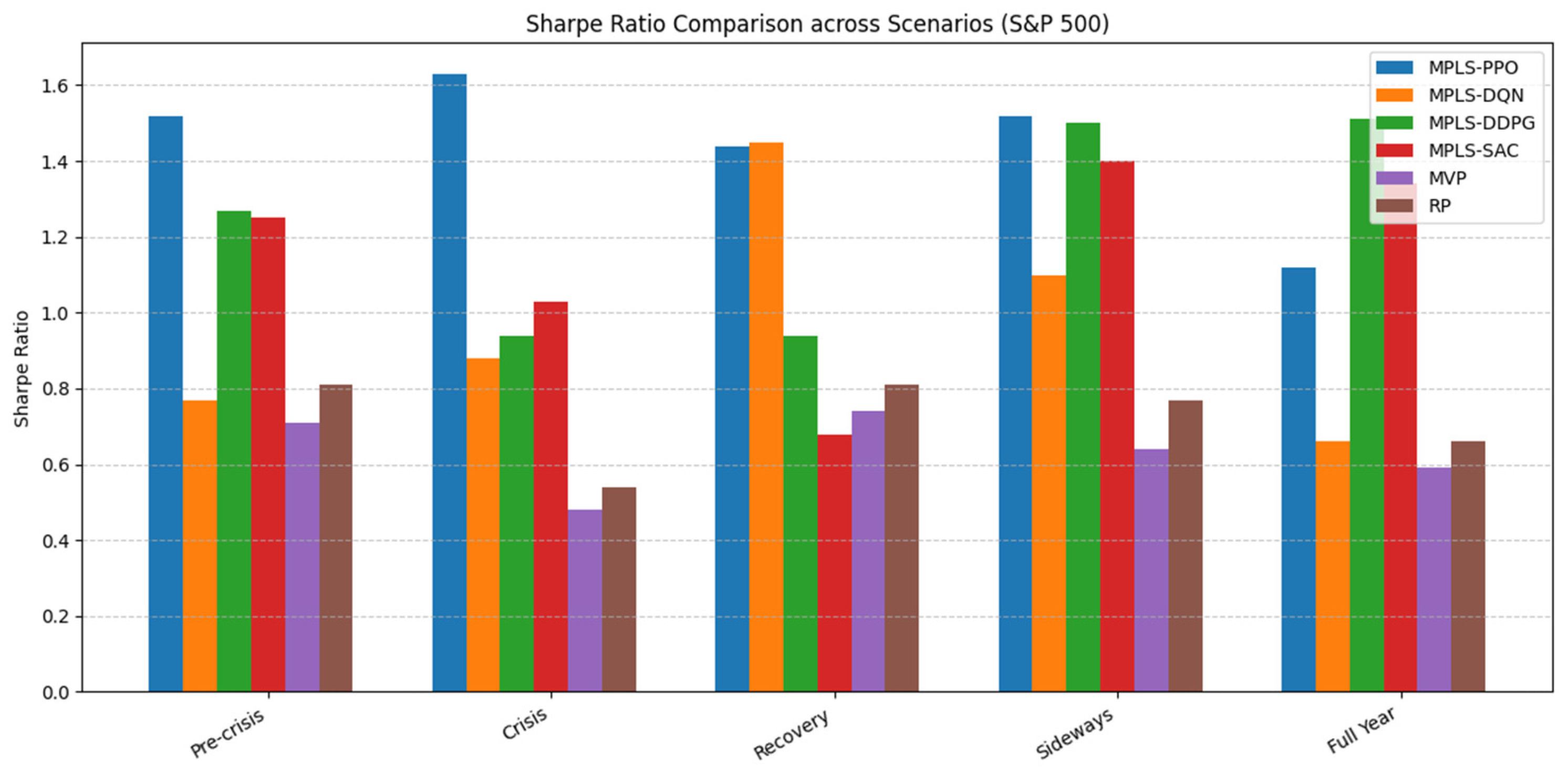
6.1. S&P 500 Market Evaluation
6.1.1. Scenario-Based Performance
6.1.2. Insights and Discussion
- Crisis regimes: MPLS-PPO outperformed, indicating resilience under stress while maintaining attractive risk-adjusted performance.
- Recovery and sideways markets: MPLS-DQN showed notable strength in balancing risk and return, particularly through effective CVaR control.
- Long-term evaluation: MPLS-DDPG showed the most stable profile, combining strong Sharpe ratios with low volatility.
- Aggressive strategies: MPLS-SAC, while capable of delivering higher returns, tended to be associated with higher volatility and tail risk.
6.1.3. Performance Variance Across Runs
6.1.4. Ablation Study
6.2. DAX 30 Market Evaluation
6.2.1. Quantitative Summary
6.2.2. Insights and Discussion
- Crisis resilience: MPLS-PPO consistently provided higher risk-adjusted returns during periods of extreme turbulence.
- Recovery dynamics: The system effectively captured rebounds while containing downside risks, outperforming both MVP and RP in Sharpe ratio and CVaR.
- Adaptive flexibility: MPLS variants retained high performance in sideways regimes, demonstrating stability under low-trend environments where static strategies faltered.
6.2.3. Performance Variance Across Multiple Runs
6.2.4. DAX Ablation Analysis
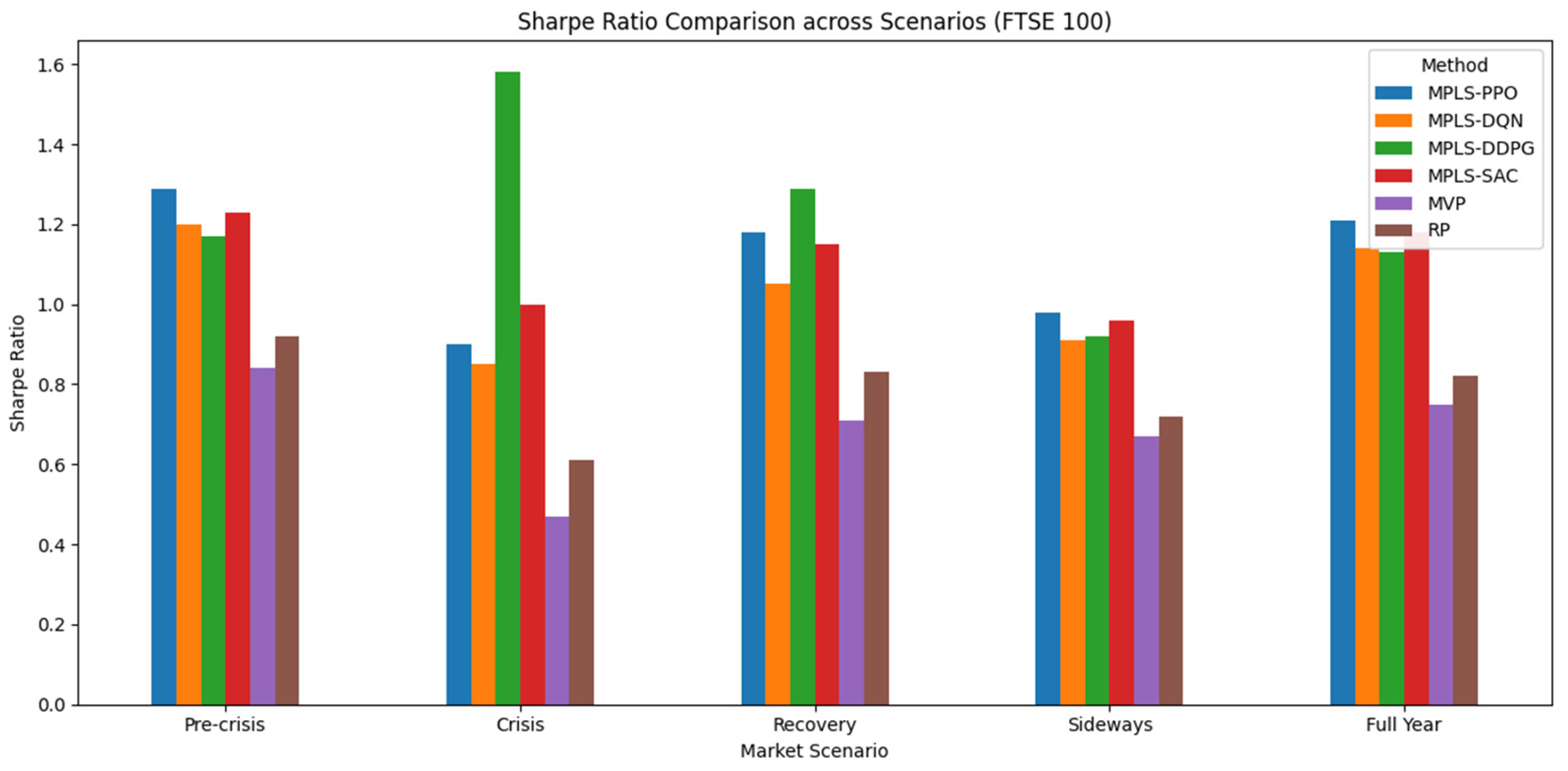
6.3. FTSE 100 Market Evaluation
6.3.1. Scenario-Based Performance
6.3.2. Insights and Discussion
- Crisis adaptability: MPLS-DDPG clearly outperformed during the COVID crash, showing that continuous action policies handle extreme volatility more effectively than static baselines.
- Recovery resilience: Both PPO and DDPG sustained high Sharpe ratios while controlling CVaR, confirming the framework’s ability to capture rebounds without excessive tail risk.
- Structural flexibility: In sideways markets, MPLS variants maintained positive risk-adjusted returns where MVP and RP failed, indicating the benefit of modular integration in noise-driven regimes.
- Cross-market perspective: Compared to the S&P and DAX, the FTSE results emphasize the importance of volatility and structural modules, as commodity-driven shocks create sharper but shorter-lived risks.
6.3.3. Performance Variance Across Multiple Runs
6.3.4. FTSE 100 Ablation Analysis
6.4. Robustness and Limitations
6.4.1. Robustness Across Markets and Scenarios
6.4.2. Limitations and Nuances
7. Discussion
7.1. Theoretical Implications
7.2. Practical Implications
7.3. Methodological Limitations
7.4. Future Research Directions
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vuković, D.B.; Dekpo-Adza, S.; Matović, S. AI integration in financial services: A systematic review of trends and regulatory challenges. Humanit. Soc. Sci. Commun. 2025, 12, 562. [Google Scholar] [CrossRef]
- Sutiene, K.; Schwendner, P.; Sipos, C.; Lorenzo, L.; Mirchev, M.; Lameski, P.; Cerneviciene, J. Enhancing Portfolio Management Using Artificial Intelligence: Literature Review. Front. Artif. Intell. 2024, 7, 1371502. [Google Scholar] [CrossRef] [PubMed]
- Armour, J.; Mayer, C.; Polo, A. Regulatory Sanctions and Reputational Damage in Financial Markets. J. Financ. Quant. Anal. 2017, 52, 1429–1448. [Google Scholar] [CrossRef]
- Lintner, J. The Valuation of Risk Assets and the Selection of Risky Investments in Stock Portfolios and Capital Budgets. Rev. Econ. Stat. 1965, 47, 13–37. [Google Scholar] [CrossRef]
- Fama, E.F.; French, K.R. Common risk factors in the returns on stocks and bonds. J. Financ. Econ. 1993, 33, 3–56. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Jiang, Z.; Xu, D.; Liang, J. A Deep Reinforcement Learning Framework for the Financial Portfolio Management Problem. arXiv 2017, arXiv:1706.10059. [Google Scholar] [CrossRef]
- Moody, J.; Saffell, M. Learning to trade via direct reinforcement. IEEE Trans. Neural Netw. 2001, 12, 875–889. [Google Scholar] [CrossRef]
- Doshi-Velez, F.; Kim, B. Towards a Rigorous Science of Interpretable Machine Learning. arXiv 2017, arXiv:1702.08608. [Google Scholar] [CrossRef]
- Khemlichi, F.; Idrissi Khamlichi, Y.; El Haj Ben Ali, S. MPLS: A Modular Portfolio Learning System for Adaptive Portfolio Optimization. Math. Model. Eng. Probl. 2025, 12, 1959–1970. [Google Scholar] [CrossRef]
- Yan, Y.; Zhang, C.; An, Y.; Zhang, B. A Deep-Reinforcement-Learning-Based Multi-Source Information Fusion Portfolio Management Approach via Sector Rotation. Electronics 2025, 14, 1036. [Google Scholar] [CrossRef]
- Espiga-Fernández, F.; García-Sánchez, Á.; Ordieres-Meré, J. A Systematic Approach to Portfolio Optimization: A Comparative Study of Reinforcement Learning Agents, Market Signals, and Investment Horizons. Algorithms 2024, 17, 570. [Google Scholar] [CrossRef]
- Shabe, R.; Engelbrecht, A.; Anderson, K. Incremental Reinforcement Learning for Portfolio Optimisation. Computers 2025, 14, 242. [Google Scholar] [CrossRef]
- Clarke, R.G.; de Silva, H.; Thorley, S. Minimum-Variance Portfolios in the U.S. Equity Market. J. Portf. Manag. 2006, 33, 10–24. [Google Scholar] [CrossRef]
- Maillard, S.; Roncalli, T.; Teiletche, J. On the Properties of Equally-Weighted Risk Contributions Portfolios. J. Portf. Manag. 2010, 36, 60–79. [Google Scholar] [CrossRef]
- Ahmadi-Javid, A. Entropic Value-at-Risk: A New Coherent Risk Measure. J. Optim. Theory Appl. 2012, 155, 1105–1123. [Google Scholar] [CrossRef]
- Acerbi, C. Spectral measures of risk: A coherent representation of subjective risk aversion. J. Bank. Financ. 2002, 26, 1505–1518. [Google Scholar] [CrossRef]
- Chekhlov, A.; Uryasev, S.; Zabarankin, M. Drawdown measure in portfolio optimization. Int. J. Theor. Appl. Financ. 2005, 8, 13–58. [Google Scholar] [CrossRef]
- Yan, R.; Jin, J.; Han, K. Reinforcement Learning for Deep Portfolio Optimization. Electron. Res. Arch. 2024, 32, 5176–5200. [Google Scholar] [CrossRef]
- Wang, X.; Liu, L. Risk-Sensitive Deep Reinforcement Learning for Portfolio Optimization. J. Risk Financ. Manag. 2025, 18, 347. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, S.; Pan, J. Two-Stage Distributionally Robust Optimization for an Asymmetric Loss-Aversion Portfolio via Deep Learning. Symmetry 2025, 17, 1236. [Google Scholar] [CrossRef]
- Li, H.; Hai, M. Deep Reinforcement Learning Model for Stock Portfolio Management Based on Data Fusion. Neural Process. Lett. 2024, 56, 108. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Sun, R.; Xi, Y.; Stefanidis, A.; Jiang, Z.; Su, J. A novel multi-agent dynamic portfolio optimization learning system based on hierarchical deep reinforcement learning. Complex Intell. Syst. 2025, 11, 311. [Google Scholar] [CrossRef]
- Khemlichi, F.; Idrissi Khamlichi, Y.; El Haj Ben Ali, S. Hierarchical Multi-Agent System with Bayesian Neural Networks for Portfolio Optimization. Math. Model. Eng. Probl. 2025, 12, 1257–1267. [Google Scholar] [CrossRef]
- Bai, Y.; Gao, Y.; Wan, R.; Zhang, S.; Song, R. A Review of Reinforcement Learning in Financial Applications. arXiv 2024, arXiv:2411.12746. [Google Scholar] [CrossRef]
- Araci, D. FinBERT: Financial Sentiment Analysis with Pre-Trained Language Models. arXiv 2019, arXiv:1908.10063. [Google Scholar] [CrossRef]
- Wang, Z.; Qi, Z. Future Stock Price Prediction Based on Bayesian LSTM in CRSP. In Proceedings of the 3rd International Conference on Internet Finance and Digital Economy (ICIFDE 2023), Chengdu, China, 4–6 August 2023; Atlantis Press: Paris, France, 2023; pp. 219–230. [Google Scholar] [CrossRef]
- Korangi, K.; Mues, C.; Bravo, C. Large-Scale Time-Varying Portfolio Optimisation Using Graph Attention Networks. arXiv 2025, arXiv:2407.15532. [Google Scholar] [CrossRef]
- Du, S.; Shen, H. Reinforcement Learning-Based Multimodal Model for the Stock Investment Portfolio Management Task. Electronics 2024, 13, 3895. [Google Scholar] [CrossRef]
- Choudhary, H.; Orra, A.; Sahoo, K.; Thakur, M. Risk-Adjusted Deep Reinforcement Learning for Portfolio Optimization: A Multi-reward Approach. Int. J. Comput. Intell. Syst. 2025, 18, 126. [Google Scholar] [CrossRef]
- Pippas, N.; Ludvig, E.A.; Turkay, C. The Evolution of Reinforcement Learning in Quantitative Finance: A Survey. ACM Comput. Surv. 2025, 57, 1–51. [Google Scholar] [CrossRef]
- Khemlichi, F.; Elfilali, H.E.; Chougrad, H.; Ali, S.E.B.; Khamlichi, Y.I. Actor-Critic Methods in Stock Trading: A Comparative Study. In Proceedings of the 2023 3rd International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME), Tenerife, Spain, 19–21 July 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Sharpe, W.F. The Sharpe Ratio. J. Portf. Manag. 1994, 21, 49–58. [Google Scholar] [CrossRef]
- Deng, Y.; Bao, F.; Kong, Y.; Ren, Z.; Dai, Q. Deep Direct Reinforcement Learning for Financial Signal Representation and Trading. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 653–664. [Google Scholar] [CrossRef]
- Zhang, Z.; Zohren, S.; Roberts, S. Deep Reinforcement Learning for Trading. arXiv 2019, arXiv:1911.10107. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2019, arXiv:1509.02971. [Google Scholar] [CrossRef] [PubMed]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor. arXiv 2018, arXiv:1801.01290. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. arXiv 2017, arXiv:1706.03762. [Google Scholar] [CrossRef]
- Tetlock, P.C. Giving Content to Investor Sentiment: The Role of Media in the Stock Market. J. Finance 2007, 62, 1139–1168. [Google Scholar] [CrossRef]
- Neal, R.M. Bayesian Learning for Neural Networks. Lecture Notes in Statistics; Springer: New York, NY, USA, 2012; Volume 118. [Google Scholar] [CrossRef]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph Attention Networks. arXiv 2018, arXiv:1710.10903. [Google Scholar] [CrossRef]
- Battiston, S.; Puliga, M.; Kaushik, R.; Tasca, P.; Caldarelli, G. DebtRank: Too Central to Fail? Financial Networks, the FED and Systemic Risk. Sci. Rep. 2012, 2, 541. [Google Scholar] [CrossRef]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural Machine Translation by Jointly Learning to Align and Translate. arXiv 2016, arXiv:1409.0473. [Google Scholar] [CrossRef]
- Rockafellar, R.T.; Uryasev, S. Optimization of conditional value-at-risk. J. Risk 2000, 2, 21–41. [Google Scholar] [CrossRef]
- Yahoo Finance. Yahoo Finance—Stock Market Live, Quotes, Business & Finance News. Available online: https://finance.yahoo.com/ (accessed on 14 August 2025).
- Investing.com. Stock Market Quotes & Financial News. Available online: https://www.investing.com/ (accessed on 14 August 2025).
- Lopez de Prado, M. Advances in Financial Machine Learning; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Little, R.J.A.; Rubin, D.B. Statistical Analysis with Missing Data; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Baker, S.R.; Bloom, N.; Davis, S.J.; Kost, K.; Sammon, M.; Viratyosin, T. The Unprecedented Stock Market Reaction to COVID-19. Rev. Asset Pricing Stud. 2020, 10, 742–758. [Google Scholar] [CrossRef]
- Markowitz, H. Portfolio Selection. J. Finance 1952, 7, 77–91. [Google Scholar] [CrossRef]
- Magdon-Ismail, M.; Atiya, A.F.; Pratap, A.; Abu-Mostafa, Y.S. On the Maximum Drawdown of a Brownian Motion. J. Appl. Probab. 2004, 41, 147–161. [Google Scholar] [CrossRef]
- Tsay, R.S. Analysis of Financial Time Series, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]


| Scenario | Method | Sharpe | Volatility (%) | Max Drawdown (%) | CVaR (%) | Turnover |
|---|---|---|---|---|---|---|
| Pre-crisis | MPLS-PPO | 1.52 | 8.3 | −8.0 | −8.4 | 0.80 |
| MPLS-DQN | 0.77 | 7.7 | −6.6 | −9.1 | 1.55 | |
| MPLS-DDPG | 1.27 | 7.5 | −9.2 | −8.8 | 1.00 | |
| MPLS-SAC | 1.25 | 6.5 | −12.7 | −9.0 | 0.79 | |
| MVP | 0.71 | 8.5 | −9.8 | −14.3 | 0.72 | |
| RP | 0.81 | 9.2 | −8.8 | −13.1 | 0.65 | |
| Crisis | MPLS-PPO | 1.63 | 15.8 | −12.6 | −12.7 | 1.61 |
| MPLS-DQN | 0.88 | 13.3 | −9.4 | −14.2 | 1.17 | |
| MPLS-DDPG | 0.94 | 7.1 | −13.5 | −11.5 | 1.08 | |
| MPLS-SAC | 1.03 | 9.0 | −15.1 | −13.6 | 0.99 | |
| MVP | 0.48 | 8.4 | −14.1 | −15.0 | 0.76 | |
| RP | 0.54 | 9.2 | −13.3 | −14.1 | 0.69 | |
| Recovery | MPLS-PPO | 1.44 | 12.2 | −14.5 | −10.9 | 1.14 |
| MPLS-DQN | 1.45 | 6.8 | −9.9 | −9.6 | 0.73 | |
| MPLS-DDPG | 0.94 | 9.6 | −14.0 | −11.2 | 1.30 | |
| MPLS-SAC | 0.68 | 16.9 | −14.5 | −12.3 | 0.82 | |
| MVP | 0.74 | 8.9 | −11.2 | −13.5 | 0.79 | |
| RP | 0.81 | 8.4 | −9.5 | −11.7 | 0.68 | |
| Sideways | MPLS-PPO | 1.52 | 6.8 | −7.2 | −9.0 | 0.70 |
| MPLS-DQN | 1.10 | 8.5 | −4.2 | −8.7 | 0.55 | |
| MPLS-DDPG | 1.50 | 11.0 | −10.0 | −9.8 | 1.15 | |
| MPLS-SAC | 1.40 | 12.0 | −7.5 | −8.5 | 0.58 | |
| MVP | 0.64 | 8.2 | −9.3 | −11.2 | 0.61 | |
| RP | 0.77 | 8.8 | −8.9 | −10.6 | 0.68 | |
| Full Year | MPLS-PPO | 1.12 | 8.8 | −11.5 | −11.9 | 0.93 |
| MPLS-DQN | 0.66 | 9.1 | −16.0 | −12.7 | 0.86 | |
| MPLS-DDPG | 1.51 | 6.8 | −6.2 | −9.4 | 0.65 | |
| MPLS-SAC | 1.34 | 14.4 | −8.6 | −10.2 | 1.40 | |
| MVP | 0.59 | 9.1 | −12.2 | −13.4 | 0.69 | |
| RP | 0.66 | 9.5 | −10.8 | −12.1 | 0.71 |
| Scenario | MPLS-PPO | MPLS-DQN | MPLS-DDPG | MPLS-SAC |
|---|---|---|---|---|
| Scenario 1 | 0.039 | 0.061 | 0.052 | 0.049 |
| Scenario 2 | 0.043 | 0.066 | 0.057 | 0.053 |
| Scenario 3 | 0.041 | 0.062 | 0.053 | 0.050 |
| Scenario 4 | 0.036 | 0.057 | 0.050 | 0.047 |
| Scenario 5 | 0.042 | 0.065 | 0.056 | 0.051 |
| Sharpe | Max Drawdown (%) | Turnover | |
|---|---|---|---|
| MPLS | 1.12 | −11.5 | 0.93 |
| MPLS w/o SAM | 0.98 | −27.0 | 1.31 |
| MPLS w/o VFM | 0.94 | −29.5 | 1.46 |
| MPLS w/o GNN | 0.96 | −25.5 | 1.28 |
| Scenario | Method | Sharpe | Volatility (%) | Max Drawdown (%) | CVaR (%) | Turnover |
|---|---|---|---|---|---|---|
| Pre-crisis | MPLS-PPO | 1.34 | 8.6 | −4.1 | −6.2 | 0.11 |
| MPLS-DQN | 1.17 | 9.2 | −5.0 | −7.3 | 0.14 | |
| MPLS-DDPG | 1.15 | 9.4 | −5.1 | −7.5 | 0.15 | |
| MPLS-SAC | 1.29 | 8.9 | −4.3 | −6.5 | 0.12 | |
| MVP | 0.84 | 8.5 | −6.2 | −8.2 | 0.10 | |
| RP | 0.92 | 8.7 | −5.4 | −7.7 | 0.09 | |
| Crisis | MPLS-PPO | 0.91 | 12.9 | −8.1 | −10.3 | 0.17 |
| MPLS-DQN | 0.70 | 13.8 | −9.5 | −12.2 | 0.20 | |
| MPLS-DDPG | 0.69 | 14.0 | −9.3 | −12.0 | 0.21 | |
| MPLS-SAC | 0.87 | 13.2 | −8.3 | −10.7 | 0.18 | |
| MVP | 0.49 | 13.6 | −12.9 | −14.8 | 0.14 | |
| RP | 0.62 | 12.7 | −10.7 | −12.9 | 0.13 | |
| Recovery | MPLS-PPO | 1.35 | 10.2 | −3.9 | −6.1 | 0.16 |
| MPLS-DQN | 1.18 | 10.8 | −4.8 | −7.1 | 0.20 | |
| MPLS-DDPG | 1.12 | 11.0 | −4.5 | −7.0 | 0.21 | |
| MPLS-SAC | 1.31 | 10.4 | −4.1 | −6.4 | 0.18 | |
| MVP | 0.78 | 10.9 | −6.0 | −8.5 | 0.12 | |
| RP | 0.84 | 11.1 | −5.5 | −7.9 | 0.10 | |
| Sideways | MPLS-PPO | 1.06 | 8.4 | −2.4 | −5.2 | 0.15 |
| MPLS-DQN | 0.95 | 9.1 | −2.9 | −5.9 | 0.18 | |
| MPLS-DDPG | 0.93 | 9.3 | −3.0 | −6.0 | 0.19 | |
| MPLS-SAC | 1.01 | 8.6 | −2.5 | −5.4 | 0.16 | |
| MVP | 0.65 | 9.1 | −3.1 | −6.7 | 0.11 | |
| RP | 0.72 | 9.4 | −2.8 | −6.2 | 0.10 | |
| Full Year | MPLS-PPO | 1.36 | 9.1 | −3.9 | −6.6 | 0.21 |
| MPLS-DQN | 1.23 | 9.7 | −4.7 | −7.6 | 0.25 | |
| MPLS-DDPG | 1.19 | 9.9 | −4.9 | −7.9 | 0.26 | |
| MPLS-SAC | 1.31 | 9.3 | −4.1 | −6.9 | 0.23 | |
| MVP | 0.78 | 9.2 | −4.9 | −8.1 | 0.11 | |
| RP | 0.84 | 9.4 | −4.6 | −7.8 | 0.12 |
| Scenario | MPLS-PPO | MPLS-DQN | MPLS-DDPG | MPLS-SAC |
|---|---|---|---|---|
| Scenario 1 | 0.034 | 0.056 | 0.049 | 0.045 |
| Scenario 2 | 0.045 | 0.069 | 0.058 | 0.052 |
| Scenario 3 | 0.038 | 0.059 | 0.051 | 0.048 |
| Scenario 4 | 0.031 | 0.053 | 0.047 | 0.043 |
| Scenario 5 | 0.043 | 0.066 | 0.055 | 0.050 |
| Sharpe | Max Drawdown (%) | Turnover | |
| MPLS | 1.36 | −3.9 | 0.21 |
| MPLS w/o SAM | 1.19 | −5.2 | 0.29 |
| MPLS w/o VFM | 1.22 | −5.4 | 0.31 |
| MPLS w/o GNN | 1.25 | −5.1 | 0.29 |
| Scenario | Method | Sharpe | Volatility (%) | Max Drawdown | CVaR (%) | Turnover |
|---|---|---|---|---|---|---|
| Pre-crisis | MPLS-PPO | 1.29 | 12.6 | −4.3 | −6.1 | 0.12 |
| MPLS-DQN | 1.20 | 14.9 | −4.9 | −6.8 | 0.14 | |
| MPLS-DDPG | 1.17 | 15.2 | −5.1 | −7.1 | 0.15 | |
| MPLS-SAC | 1.23 | 13.8 | −4.5 | −6.4 | 0.14 | |
| MVP | 0.84 | 12.2 | −6.3 | −9.0 | 0.12 | |
| RP | 0.92 | 14.8 | −5.9 | −8.2 | 0.15 | |
| Crisis | MPLS-PPO | 0.90 | 7.0 | −1.3 | −2.2 | 0.11 |
| MPLS-DQN | 0.85 | 13.0 | −0.9 | −1.8 | 0.11 | |
| MPLS-DDPG | 1.58 | 15.5 | −1.2 | −2.5 | 0.15 | |
| MPLS-SAC | 1.00 | 8.8 | −1.45 | −2.6 | 0.10 | |
| MVP | 0.47 | 12.0 | −1.9 | −3.1 | 0.16 | |
| RP | 0.61 | 11.0 | −1.5 | −2.7 | 0.14 | |
| Recovery | MPLS-PPO | 1.18 | 8.2 | −1.03 | −1.9 | 0.09 |
| MPLS-DQN | 1.05 | 9.1 | −1.12 | −2.0 | 0.10 | |
| MPLS-DDPG | 1.29 | 8.9 | −1.01 | −1.8 | 0.09 | |
| MPLS-SAC | 1.15 | 8.7 | −1.08 | −1.9 | 0.09 | |
| MVP | 0.71 | 9.0 | −1.50 | −2.5 | 0.08 | |
| RP | 0.83 | 8.2 | −1.10 | −2.0 | 0.07 | |
| Sideways | MPLS-PPO | 0.98 | 8.1 | −2.6 | −4.1 | 0.17 |
| MPLS-DQN | 0.91 | 9.0 | −3.0 | −4.8 | 0.19 | |
| MPLS-DDPG | 0.92 | 8.8 | −2.9 | −4.7 | 0.20 | |
| MPLS-SAC | 0.96 | 8.5 | −2.8 | −4.6 | 0.17 | |
| MVP | 0.67 | 8.7 | −3.5 | −5.2 | 0.12 | |
| RP | 0.72 | 8.6 | −3.6 | −5.3 | 0.13 | |
| Full Year | MPLS-PPO | 1.21 | 9.2 | −4.3 | −6.8 | 0.18 |
| MPLS-DQN | 1.14 | 9.7 | −5.0 | −7.2 | 0.20 | |
| MPLS-DDPG | 1.13 | 9.5 | −4.6 | −7.0 | 0.20 | |
| MPLS-SAC | 1.18 | 8.9 | −4.1 | −6.5 | 0.18 | |
| MVP | 0.75 | 10.0 | −5.7 | −8.8 | 0.22 | |
| RP | 0.82 | 9.8 | −5.1 | −8.2 | 0.21 |
| Scenario | MPLS-PPO | MPLS-DQN | MPLS-DDPG | MPLS-SAC |
|---|---|---|---|---|
| Scenario 1 | 0.041 | 0.059 | 0.049 | 0.046 |
| Scenario 2 | 0.044 | 0.061 | 0.055 | 0.051 |
| Scenario 3 | 0.042 | 0.060 | 0.053 | 0.048 |
| Scenario 4 | 0.039 | 0.056 | 0.050 | 0.045 |
| Scenario 5 | 0.043 | 0.063 | 0.054 | 0.050 |
| Sharpe | Max Drawdown (%) | Turnover | |
|---|---|---|---|
| MPLS | 1.21 | −4.3 | 0.18 |
| MPLS w/o SAM | 1.04 | −5.7 | 0.26 |
| MPLS w/o VFM | 1.06 | −5.9 | 0.28 |
| MPLS w/o GNN | 1.09 | −5.5 | 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khemlichi, F.; Idrissi Khamlichi, Y.; Elhaj Ben Ali, S. Modular Reinforcement Learning for Multi-Market Portfolio Optimization. Information 2025, 16, 961. https://doi.org/10.3390/info16110961
Khemlichi F, Idrissi Khamlichi Y, Elhaj Ben Ali S. Modular Reinforcement Learning for Multi-Market Portfolio Optimization. Information. 2025; 16(11):961. https://doi.org/10.3390/info16110961
Chicago/Turabian StyleKhemlichi, Firdaous, Youness Idrissi Khamlichi, and Safae Elhaj Ben Ali. 2025. "Modular Reinforcement Learning for Multi-Market Portfolio Optimization" Information 16, no. 11: 961. https://doi.org/10.3390/info16110961
APA StyleKhemlichi, F., Idrissi Khamlichi, Y., & Elhaj Ben Ali, S. (2025). Modular Reinforcement Learning for Multi-Market Portfolio Optimization. Information, 16(11), 961. https://doi.org/10.3390/info16110961






